降低直升机振动水平及噪声大小是直升机优化设计中关注的主要问题。近年来,旋翼主动襟翼控制(Active flap control, AFC)[1-2]技术凭借良好的减振[1]作用及降噪[3-4]特性逐渐成为直升机界的研究热点。
AFC技术最早由Lemnios和Smith在使用伺服襟翼降低旋翼振动载荷[5]的研究中被提出。马里兰大学的Milgram在文献[2]中将其发展应用于降低旋翼气动载荷。而后,Schmitz等人将其用于旋翼厚度噪声的降噪研究[3],Aoyama又将其发展应用于降低桨-涡干扰噪声[4]。在国内,夏品奇等也对AFC旋翼的载荷控制[6]与气动特性[7]进行了相关的研究。
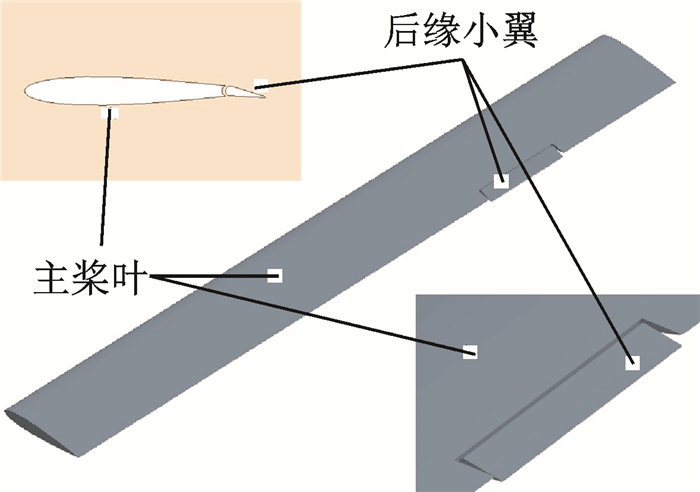
图 1给出了AFC旋翼桨叶的示意图,与常规直升机旋翼桨叶相比,AFC旋翼桨叶不仅具有复杂的外形和结构,且其后缘小翼在伴随桨叶运动的同时还具有相对独立的偏转运动,使得流场非定常变化,难以精确模拟。另外,在网格生成方面, 要求能准确处理主桨叶和后缘小翼间缝隙处的网格。此外,考虑到旋翼本身的挥舞、摆振及变距,这将使得后缘小翼的运动相当复杂,运动嵌套的实现也变得更为棘手。其复杂性使得目前针对AFC旋翼气动特性的研究并不多见,而详细探究AFC旋翼翼型参数对其尾涡产生的影响,并能用于指导AFC旋翼设计的工作则更为少见。
|
图 1 AFC旋翼桨叶示意图 Figure 1 Schematic of AFC rotor blade |
针对上述问题,本文采用基于Euler方程与Jameson中心格式的数值模拟求解方法,编写了可用于非结构多重嵌套条件下的嵌套网格处理程序,并结合基于坐标系变换的运动描述方式,提出可用于AFC旋翼数值模拟的运动嵌套网格方法。然后建立了适于AFC旋翼翼型复杂运动条件下的流场数值模拟方法。应用所建立的方法,深入地开展了AFC旋翼翼型参数对翼型涡量影响的计算研究,并得出了一些新的结论。
1 计算方法和模型 1.1 流场控制方程针对AFC旋翼流场的复杂性,并考虑计算效率,本文以欧拉方程为主控方程,其微分方程形式为
| $ \frac{{\partial \boldsymbol{W}}}{{\partial t}} + \frac{{\partial \boldsymbol{F}}}{{\partial x}} + \frac{{\partial \boldsymbol{G}}}{{\partial y}} + \frac{{\partial \boldsymbol{H}}}{{\partial z}} = 0 $ | (1) |
式中:W为守恒变量;F,G和H为对流通量,其具体表达式如下
| $ \begin{array}{l} \boldsymbol{W} = {[\rho, \rho u, \rho v, \rho w]^{\rm{T}}}\\ \boldsymbol{F} = {[\rho u, \rho {u^2} + p, \rho uv, \rho uw]^{\rm{T}}}\\ \boldsymbol{G} = {[\rho v, \rho uv, \rho {v^2} + p, \rho w]^{\rm{T}}}\\ \boldsymbol{H} = {[\rho w, \rho uw, \rho vw, \rho {w^2} + p]^{\rm{T}}} \end{array} $ | (2) |
式中:ρ,p分别为流体密度和压强;u,v,w为速度在3个方向上的分量。
空间离散采用Jameson中心格式,其表达式为
| $ F{\left( \boldsymbol{W} \right)_{ij}} = F\left( {\frac{1}{2}({W_i} + {W_j})} \right) $ | (3) |
本文构建的嵌套网格方法与常规的inverse-map或hole-map方法不同,这里先进行网格贡献单元搜索以确定是否有贡献单元及贡献单元所在位置,再根据网格分类准则参数来决定网格所属分类,所得分类单元的边界即为嵌套网格边界。该嵌套网格方法能处理相互嵌套的网格块,因此非常适合AFC旋翼主桨叶与后缘小翼间的网格嵌套。
关于网格分类准则,考虑到在流场计算中网格尺度对流场求解的精度和收敛效果有很大影响,网格尺度越小,求解精度越高、收敛性越好,故本文使用Löhner[8]的物面距和网格尺度组合参数s作为判据进行分类,s定义为
| $ s = {d^p}{h^q} $ | (4) |
式中:d为物面距,h为网格尺度,通过对指数p和q的调节可以改变物面距和网格尺度的权重。本文选取p=1,q=1,这样既考虑了物面距影响,又考虑了网格尺度影响。
对于贡献单元搜索,本文采用相邻单元搜索算法与交流数字树(Alter-nating digital tree, ADT)搜索算法[9]相结合的方法。对网格单元i,其在网格块b中贡献单元搜索算法如下:
(1) 取目标坐标点为单元i的形心。
(2) 在网格块b中,初始化搜索的出发单元作为当前单元ic。
(3) 连线当前单元ic的形心与目标坐标点,判断该线段与单元边的相交情况,如果无相交边,则当前单元为网格单元i的贡献单元,并结束搜索;否则,继续执行步骤(4)。
(4) 判断相交边的类型,如果为中间面,即相邻单元存在,则以该单元为新的出发单元,跳转执行步骤(3);如果为外边界(通常为压力远场),则该单元保留为活动单元,搜索结束;如果该边为内边界(通常为物面边界),则继续执行步骤(5)。
(5) 采用ADT算法,判断步骤(3)中得到的线段与内边界相交情况,如果相交边(或面)个数为奇数,则目标坐标点位于物面内,即单元i在内边界内,并标记为非活动单元;如果为偶数,则取距目标坐标点最近的内边界,并以其相邻单元作为新的出发单元,跳转到步骤(3)并继续。
数值实践表明,上述嵌套网格方法适应范围广、效率高,并具有良好的鲁棒性。
1.3 运动描述方式旋翼桨叶运动除绕旋转轴旋转外,还具有挥舞、摆振和变距运动。特别地,对包含后缘小翼的AFC旋翼,该小翼还将绕其安装轴运动。上述运动的合成使得描述小翼对地面运动变得十分复杂。
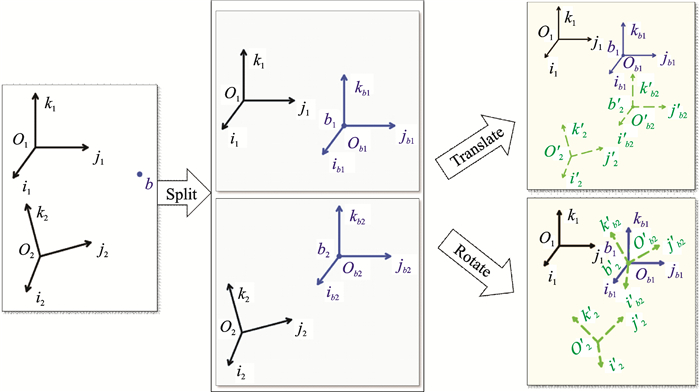
本文提出一种基于坐标系变换的运动描述方式,其基本思路是:通过描述一个坐标系相对另一个坐标系的运动,使得复杂运动能经过多次简单描述后转换为对地面运动的表示。该方法分为建立装配关系以及对运动进行描述两大部分,见图 2。
|
图 2 坐标系变换示意图 Figure 2 Schematic of coordinate transformation |
(1) 处理装配关系。对两个已知坐标系O1,O2,处理装配关系时先固定参考点,可在空间中任取点b, 记其在坐标系O1,O2中的坐标为b1,b2。然后,固定参考方向,即过参考点b建立新坐标系Ob1,Ob2,得坐标系基向量在O1,O2中的向量组nb1和nb2。注意到点b1,b2虽在两坐标系中具有不同坐标值,但实际上为同一位置点。于是,对空间中任意点P, 类似的有坐标P1,P2, 若已知b1,nb1,b2,nb2及P2,便可求得P1为
| $ {P_{1}} = {\rm{ }}{\boldsymbol{n}_{b1}}^{-1}{\boldsymbol{n}_{b2}} \times ({P_{2}}-{b_{2}}) + {b_1} $ | (5) |
(2) 在装配的基础上,增加运动描述项。设时刻t时坐标系Ob1,Ob2变为运动后的O′b1,O′b2,点P1,P2成为P′1,P′2。定义运动平动分量为函数向量T(t),转动分量为函数矩阵R(t)。由于P2相对坐标系Ob2静止,即P′2 = P2,于是在已知b1,nb1,b2,nb2,P′2,T(t)及R(t)的条件下,可解得P1 ′为
| $ P{'_1} = {(\boldsymbol{R}\left( t \right) \times {\boldsymbol{n}_{b1}})^{-1}}{\boldsymbol{n}_{b2}} \times ({P_2}-{b_2}) + {b_1} + \boldsymbol{T}\left( t \right) $ | (6) |
实践表明,描述两个原本重合的坐标系间的相对运动容易实现。对于AFC后缘小翼,只需依次建立后缘小翼坐标系-主桨叶坐标系-扭转坐标系-摆振坐标系-挥舞坐标系-桨毂坐标系-地面坐标系,便可完整地描述具有挥摆扭运动的AFC旋翼后缘小翼对地面运动方式。
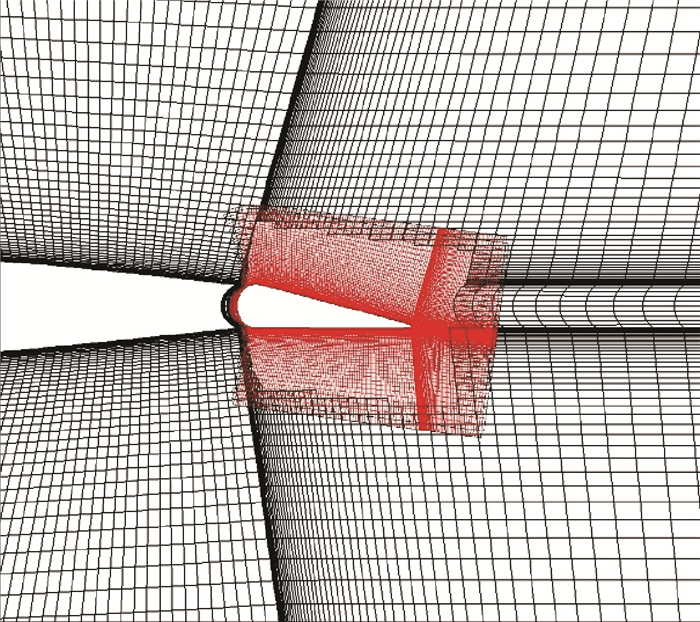
2 算例验证 2.1 运动嵌套网格验证图 3给出了某时刻下AFC后缘小翼附近的嵌套网格,图中后缘部分网格与主旋翼部分相互嵌套,网格嵌套情况符合预期要求。
|
图 3 AFC后缘小翼附近的嵌套网格 Figure 3 Overset grid near AFC rotor trailing edge |
2.2 “30P30N”多段翼型算例验证
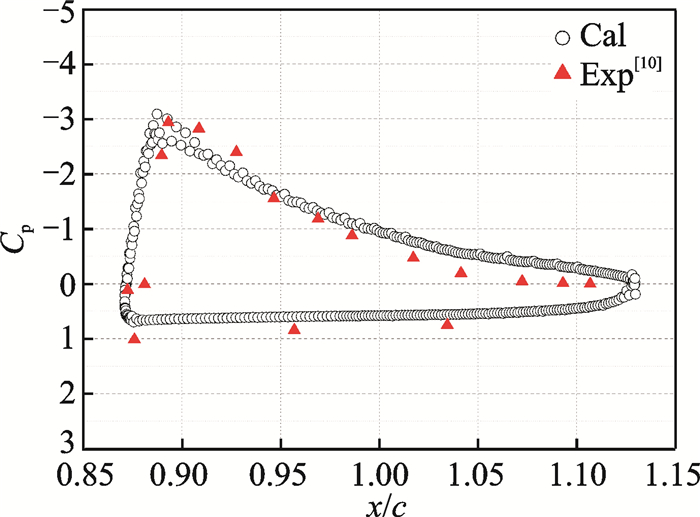
为验证CFD方法对AFC翼型的计算准确性,选取类似的“30P30N”多段翼型[10],图 4给出了Ma=0.2、迎角8.5°下“30P30N”翼型后缘襟翼部分对应的压力系数计算结果与文献[10]实验值的对比。由图可见,其吻合程度是合理的,可用于后文的分析。
|
图 4 “30P30N”翼型后缘压力系数计算结果 Figure 4 Calculation results of pressure coefficient at trailing edge of ″30P30N″ airfoil compared with experimental results[10] |
2.3 C-T旋翼算例验证
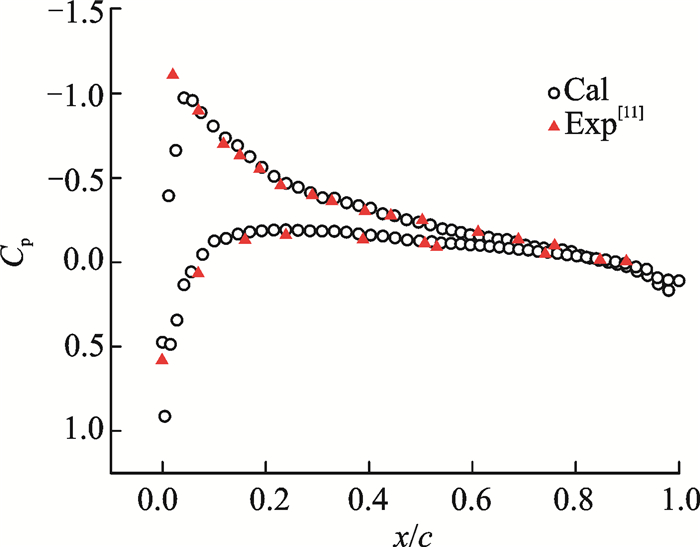
图 5给出了桨尖马赫数0.439下C-T旋翼在0.96R处的翼型表面压力系数分布与实验值[11]的对比,结果吻合良好,说明对于典型旋翼工作条件下本文运动嵌套数值模拟方法能有效地模拟桨叶表面压强分布。
|
图 5 C-T旋翼表面压力系数计算结果 Figure 5 Calculation results of C-T rotor surface pressure coefficient compared with experimental results[11] |
3 AFC旋翼翼型数值模拟 3.1 AFC旋翼翼型数值模拟条件
与典型固定翼多段翼型相比,旋翼AFC后缘小翼工作环境存在较大差别。固定翼后缘襟翼多用于起飞降落阶段, 来流速度通常在Ma=0.1~0.2之间,且襟翼转动缓慢,可视为定常或准定常流场;但后者位于靠近桨尖部分,其周围流场呈现明显的非定常特性,两者有着显著差别,故需为AFC后缘小翼开展单独的分析工作。本文中AFC旋翼数值模拟的基准条件如表 1, 2所示。
| 表 1 AFC旋翼主桨叶参数 Table 1 Parameters of AFC rotor main blade |
| 表 2 AFC后缘小翼参数 Table 2 Parameters of AFC trailing edge |
3.2 AFC翼型涡的特性
AFC旋翼对气动特性影响主要通过尾部所产生的涡来实现。图 6给出了后缘小翼某一摆动周期内其附近的涡量图。从图中可以观察到,后缘小翼是AFC旋翼涡的主要产生部件,后缘上下表面均可从后缘小翼与主桨叶间缝隙处产生涡。其中,上表面涡沿顺时针方向旋转,而下表面为逆时针。由于总距角的存在,使得下表面涡的强度总体上较上表面强。此外,从图 6中还可以观察到,在后缘小翼向下摆动过程中,由于小翼对下表面涡的阻塞,使得两个涡发生了合并,表现出非定常特性。
综上所述,可以得出结论:AFC旋翼翼型涡主要从后缘小翼与主桨叶间缝隙产生,上下表面涡旋转方向相反,并呈现显著的非定常特性。
|
图 6 不同时刻下后缘小翼附近涡分布图 Figure 6 Vortex near trailing edge at different time |
4 AFC翼型参数化特性分析
为探究影响涡产生的因素,并为日后开展AFC旋翼设计、运动控制方式设计等提供参考依据,有必要进行AFC翼型参数对涡的影响研究。
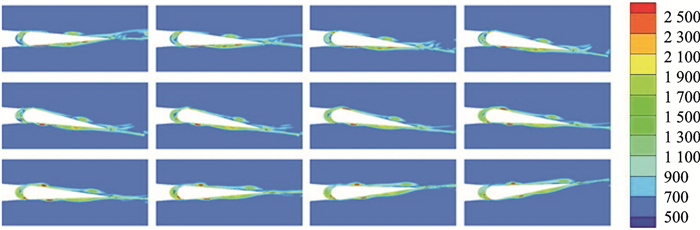
4.1 桨尖速度对涡的影响在第3节的基准桨叶参数基础上,改变旋翼桨尖速度进行算例计算。图 7给出了旋翼桨尖马赫数从Ma=0.4开始,以Ma=0.05步进、后缘小翼同一摆动角度下的涡量分布图。可以观测到,随着旋翼桨尖速度的增大,涡产生速度加快,且单个涡强度增大。
|
图 7 不同桨尖马赫数下后缘小翼处涡量分布 Figure 7 Vorticity distribution of trailing edge with different tip Mach numbers |
4.2 总距角对涡的影响
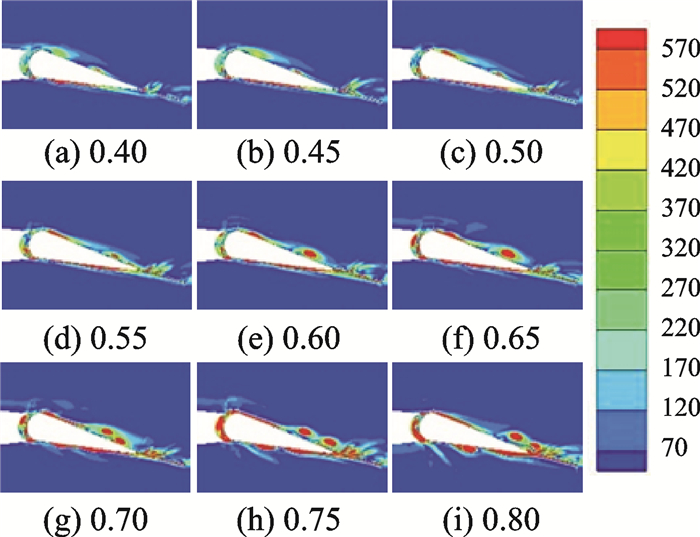
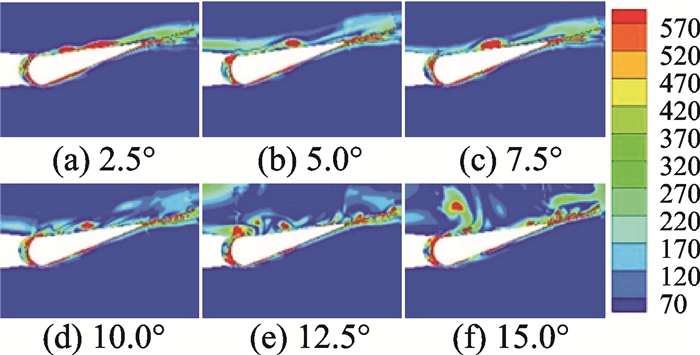
图 8给出了旋翼总距从2.5°开始,以2.5°步进、后缘小翼同一摆动角度下的涡量分布图。可观察到,随着旋翼总距角的增加,单个涡强度逐渐增大,且在迎角过大时主桨叶也将产生一定量的涡。
|
图 8 不同总距角下后缘小翼处涡量分布 Figure 8 Vorticity distribution of trailing edge with different collective pitch angles |
4.3 后缘小翼摆动频率对涡的影响
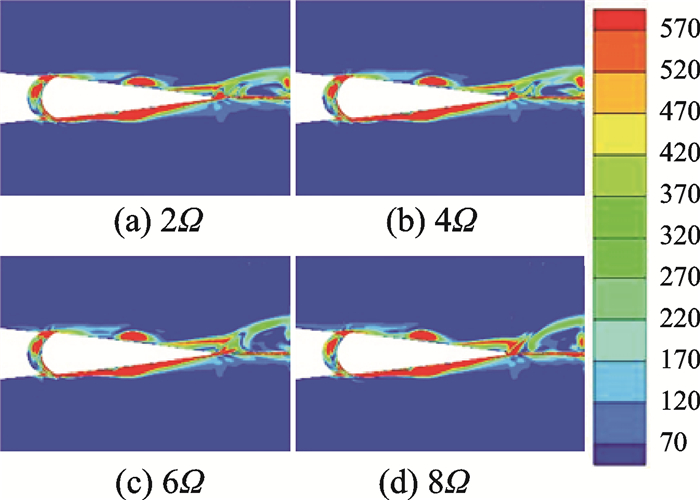
AFC旋翼摆动周期通常为桨叶片数k与旋翼转速Ω乘积的整倍数。图 9给出了后缘小翼摆动角速度2Ω,4Ω,6Ω,8Ω时后缘小翼同一摆动角度下的涡量分布图。图中不同摆动频率下观察到的涡数目几乎相同,即随着后缘小翼摆动频率的增加,单位时间内产生涡的数目也增多。另外,还可看出单个涡的强度略有减小。
|
图 9 不同后缘小翼摆动频率下涡量分布 Figure 9 Vorticity distribution of trailing edge with different oscillating frequencies |
4.4 后缘小翼摆动幅度对涡的影响
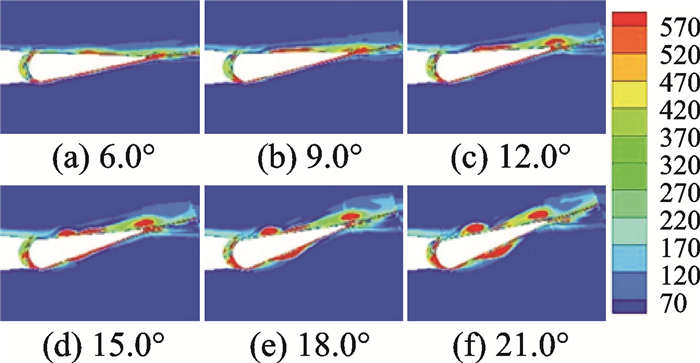
图 10给出了后缘小翼摆动幅度从6°开始,以3°步进、后缘小翼同一摆动角度下的涡量分布图。对比可看出,随着摆动幅度的增加,涡的强度将明显增大。
|
图 10 不同后缘小翼摆动幅度下涡量分布 Figure 10 Vorticity distribution of trailing edge with different swing amplitudes |
4.5 后缘小翼缝隙宽度对涡的影响
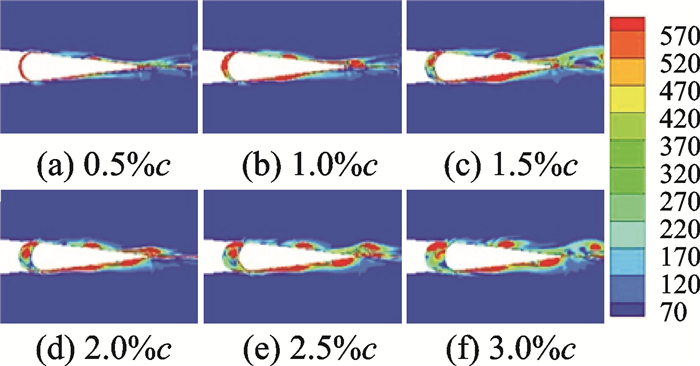
根据第3节涡的历程可知,后缘小翼与主桨叶间缝隙是绝大部分涡的形成区域,为此,本节分析缝隙宽度改变对涡的影响。图 11给出了缝隙宽度在0.5%c~3%c,以0.5%c步进、后缘小翼同一摆动角度下的涡量分布图。可以观测到,从0.5%c开始,随着缝隙的增大,单个涡强度逐渐增大,但缝隙宽度3%c下单个涡的强度却较2.5%c时下降,即在一定范围内,增大缝隙宽度,单个涡的强度将增大。
|
图 11 不同后缘小翼与主桨叶间间距下涡量分布 Figure 11 Vorticity distribution of trailing edge with different gap widths |
4.6 后缘小翼长度对涡的影响
图 12给出了后缘小翼弦长在0.1c~2c,以0.025c步进、后缘小翼同一摆动角度下的涡量分布图。可见,随着后缘小翼弦长的增大,涡逐渐由连续的贴体涡转变为分离涡,单个涡强度逐渐增加,但涡产生频率逐渐减少。

|
图 12 不同后缘小翼长度下涡量分布 Figure 12 Vorticity distribution of trailing edge with different chord lengths |
5 结论
本文建立的运动嵌套数值模拟方法满足AFC旋翼翼型的数值模拟要求。应用该方法对AFC旋翼翼型后缘小翼涡的数值模拟可得到如下结论:
(1) AFC旋翼涡主要从后缘小翼与主桨叶间缝隙产生,对本文算例,涡在上表面顺时针旋转,而下表面旋向相反为逆时针,呈现显著非定常现象。
(2) 提高桨尖马赫数、增加后缘小翼摆动频率能加快翼型涡产生速度;而提高桨尖马赫数、增大后缘小翼摆动幅度及增加后缘小翼长度能增大单个涡强度。
(3) 在一定范围内,增加总距角能提高AFC旋翼翼型单个涡强度;增大后缘小翼与主桨叶缝隙间距也能提高单个涡强度,但间距过大时涡强度反而减少。
| [1] |
FRIEDMANN P P, MILLOTT T A.
Vibration reduction in rotorcraft using active control:A comparison of various approaches[J]. AIAA Journal of Guidance, Control, and Dynamics, 1995, 18(4): 664–673.
DOI:10.2514/3.21445
|
| [2] |
MILGRAM J H. A comprehensive aeroelastic analysis of helicopter main rotors with trailing edge flaps for vibration reduction[C]//47th AIAA Aerospace Sciences Meeting and Including.[S.l.]:AIAA, 1997:9736601. |
| [3] |
SCHMITZ F H, GOPALAN G. High-speed impulsive helicopter noise reduction possibilities through on-blade acoustic control[C]//Proceedings of the International Forum on Rotorcraft Multidisciplinary Technology.Seoul, Korea:[s.n.], 2007. |
| [4] |
AOYAMA T. Comparison of noise reduction effect between AFC and conventional IBC by moving overlapped grid method[C]//27th AIAA Aeroacoustics Conference.[S.l.]:AIAA, 2006:8-10. |
| [5] |
MILLOTT T, FRIEDMANN P. Vibration reduction in helicopter rotors using an active control surface located on the blade[C]//33rd Structures, Structural Dynamics and Materials Conference. Dallas, TX, USA:[s.n.], 1992. |
| [6] |
王荣, 夏品奇.
多片后缘小翼对直升机旋翼桨叶动态失速及桨毂振动载荷的控制[J]. 航空学报, 2013, 34(5): 1083–1091.
WANG Rong, XIA Pinqi. Control of helicopter rotor blade dynamic stall and hub vibration by multiple trailing edge flaps[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(5): 1083–1091. |
| [7] |
马奕扬, 招启军, 赵国庆.
基于后缘小翼的旋翼翼型动态失速控制分析[J]. 航空学报, 2017, 38(3): 127–137.
MA Yiyang, ZHAO Qijun, ZHAO Guoqing. Dynamic stall control of rotor airfoil via trailing-edge flap[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(3): 127–137. |
| [8] |
LÖHNER R, SHAROV D, LUO H. Overlapping unstructured grids[C]//39th AIAA Aerospace Sciences Meeting and Exhibit.[S.l.]:AIAA, 2001:8-11. |
| [9] |
田书玲. 基于非结构网格方法的重叠网格算法研究[D]. 南京: 南京航空航天大学, 2008.
TIAN Shuling. Investigation of overset unstructured grids algorithm[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2008. |
| [10] |
PASCIONI K, CATTAFESTA L N, CHOUDHARI M M.An experimental investigation of the 30P30N multi-element high-lift airfoil[C]//35th AIAA Aeroacoustics Conference.[S.l.]:AIAA, 2014, 204(1):1-13. |
| [11] |
CARADONNA F X, TUNG C. Experimental and analytical studies of a model helicopter rotor in hover[R]. NASA TM-81232, 1981. |
 2018, Vol. 50
2018, Vol. 50


