复合材料蜂窝夹层结构由厚而轻质的蜂窝芯材胶接上下复合材料薄面板构成,高比强度、高比刚度的复合材料面板主要承受面内和弯曲载荷,而蜂窝芯材使得上下面板分离,从而极大地增加了结构弯曲刚度,且同时承受横向剪切载荷。夹层结构形式极大地发挥了材料的性能,具有最优的比弯曲刚度、比弯曲强度,良好的吸声、隔振性能,因此在航空航天领域具有广泛的应用。目前,国内外学者和工程科技人员对复合材料蜂窝夹层结构开展了广泛的研究工作,取得了一系列成果[1-6]。
进气道结构作为歼击机飞机结构的重要组成部件,其主要功能是为发动机进气气流进行整流和控制,随着飞机性能的不断提高,进气道载荷越来越大,环境越来越复杂,对进气道结构提出了轻量化、高承载、高可靠性的要求[7-8]。对比复合材料蜂窝夹层结构的优点,选用其设计进气道结构具有较大的优势。本文以复合材料蜂窝夹层结构进气道为研究对象,进行其优化设计方法研究。
1 优化设计方法 1.1 工程化选取设计参数在面板材料和蜂窝芯材选定的情况下,复合材料蜂窝夹层结构设计变量包括:上下面板铺层角度、铺层厚度、铺层顺序以及蜂窝芯厚度。
实际飞机结构设计中为了简化铺层工艺,只采用由0°,90°,45°和-45°组成的标准铺层,从而消除了复合材料面板的铺层角度变化。根据设计指南[9-10]:为了避免受载时拉弯和拉剪耦合效应及成型后固化变形翘曲,需采用对称均衡铺层;同时还须遵守其他设计规则,如90°层不成组以及同方向最小原则,同时要求高的抗冲击性能。一般而言,薄面板铺层层数较少,外加上述设计原则约束,使得面板铺层顺序设计具有较大的限制性,因此舍弃面板铺层中的铺层顺序优化。
复合材料夹层结构实际工程设计和生产中,单层材料以预浸料的形式提供,因此铺层厚度变量为预浸料厚度的整数倍,同时在蜂窝厚度设计中也多选用整数或者小数点后一位。因此,在复合材料蜂窝夹层进气道优化设计中,优化变量应选用离散型变量。
1.2 复合材料进气道设计要求复合材料结构设计中,首当其冲的便是铺层比例约束,即:0°,±45°,90°的4种铺层中每一种至少要占10%,其中0°铺层10%~70%之间,45°铺层10%~40%之间,90°铺层10%~70%之间[9-10]。
对于进气道结构,由于发动机工作时,进气量大,气流速度高,进气道承受的气动力大。在一般的进气道结构设计中主要考虑以下两种受力情况[7]:
(1) 地面试车工况,进气道结构承受吸力,称为Ⅰ状态;
(2) 某飞行工况,进气道处于充压状态,称为Ⅱ状态。
在复合材料蜂窝夹层结构进气道优化设计中,必须考虑静强度、刚度和声疲劳寿命等要求,须进行全面约束。
复合材料蜂窝夹层结构在拉伸、压缩、弯曲、剪切以及各种复合载荷作用下静强度问题包括面板和芯子材料失效,主要设计约束为:
(1) 面板应变约束:设计载荷下,面板工作应变小于考虑损伤容限的设计许用应变[9], 即
| $ \varepsilon \le \left[ \varepsilon \right] $ | (1) |
式中:ε为设计载荷下各单层工作应变;[ε]为设计许用应变。
(2) 蜂窝芯材强度校核[9]:芯材应具有足够的厚度和强度,以保证在设计载荷作用下,不发生剪切破坏。
| $ \begin{array}{l} {\tau _{xz}} \le \left[ {{\tau _{xz}}} \right] \times 0.7\\ {\tau _{yz}} \le \left[ {{\tau _{yz}}} \right] \times 0.7 \end{array} $ | (2) |
式中:τ为蜂窝剪切应力;[τ]为蜂窝剪切强度;xz表示蜂窝纵向;yz表示蜂窝横向。
对于复合材料蜂窝夹层结构刚度的要求,主要分为两部分:
(1) 面板和芯材应具有足够的刚度,以防止设计载荷下发生面板起皱破坏、面板格间失稳及剪切皱折破坏。
面板起皱失稳[10]
| $ {N^{{\rm{wr}}}} = 0.82{E_{\rm{f}}}{t_{\rm{f}}}\sqrt {\frac{{{E_{\rm{c}}}{t_{\rm{f}}}}}{{{E_{\rm{f}}}{t_{\rm{c}}}}}} $ | (3) |
面板格间失稳[10]
| $ {N^{{\rm{dp}}}} = \frac{{2{E_{\rm{f}}}t_{\rm{f}}^3}}{{\left( {1 - {\nu ^2}} \right)}}\frac{1}{{{S^2}}} $ | (4) |
剪切皱折[10]
| $ {N^{{\rm{crim}}}} = {G_{\rm{c}}}{t_{\rm{c}}} $ | (5) |
式(3~5)中:Ef表示面板模量;Ec表示蜂窝厚度方向压缩模量;Gc表示蜂窝剪切模量;tf表示面板厚度;tc表示蜂窝芯厚度;S为蜂窝芯格尺寸。
组合载荷作用下,采用相互作用曲线法来分析[10]
| $ {R_{\rm{c}}} + R_{\rm{s}}^2 = 1 $ | (6) |
式中:Rc = Nx / Nxi, Rs=Nxy / Nxyi,而i代表wr, db和crim。
(2) 夹层结构刚度:进气道结构在Ⅰ状态设计载荷作用下(地面试车),必须保证结构总体不失稳。考虑到制造缺陷及使用中可能损伤,设计预留一定的安全裕度,即:限制屈曲分析的一阶屈曲因子大于1.2。
同时进气道壁板在机体使用寿命期内,应能经受声载荷和振动的作用。文献[11]认为进气道在强噪音和发动机振动环境下,噪音脉动和发动机振动机理的频率分布与进气道结构固有频率分布具有交集或者相接近时,使得进气道结构产生振动,导致破坏。因此,在进气道结构优化设计中,应使得结构固有频率位于使用环境下所有可能频率之上一定的区间。
1.3 分析模型对复合材料夹层结构而言,横向剪切变形影响显著,采用薄板理论计算结果误差较大,因此须采用厚壳单元以考虑横向剪切效应的影响。在单层厚壳单元模拟复合材料蜂窝夹层结构时,将蜂窝芯材作为复合材料属性的中间单层建模。
在优化实施中,为了消除面板铺层顺序对优化结果影响,对整个复合材料蜂窝夹层结构采用“SMCORE”算法[12]进行弯曲刚度计算。具体实施过程如下:
(1) 根据厚壳理论,可知
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{N}}\\ \mathit{\boldsymbol{M}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&\mathit{\boldsymbol{B}}\\ \mathit{\boldsymbol{B}}&\mathit{\boldsymbol{D}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\varepsilon }}\\ \mathit{\boldsymbol{\kappa }} \end{array}} \right];\left[ \mathit{\boldsymbol{Q}} \right] = \left[ \mathit{\boldsymbol{C}} \right]\left[ \mathit{\boldsymbol{\gamma }} \right] $ | (7) |
式中:N为薄膜内力矢量;M为面外弯矩矢量;Q为横向剪切力矢量;A为面内刚度矩阵;B为面内-弯曲耦合刚度矩阵;D为弯曲刚度矩阵;C为剪切刚度矩阵;ε为面内应变矢量;κ为弯曲曲率矢量;γ为剪切应变矢量。
(2) 由于整个复合材料夹层结构中,面板的面内刚度属性较蜂窝夹芯刚度属性大得多,因此在计算A矩阵时只计及面板的贡献。假设芯子对面内刚度无贡献, A矩阵各分量计算公式如下
| $ {A_{ij}} = \sum\limits_{k = 1}^n {{Q_{ij}}\left( {{z_k} - {z_{k - 1}}} \right)} $ | (8) |
且上下面板铺层关于整个夹层结构中面对称,则[B]=0。
(3) 计算面板的等效刚度属性,其中tf为面板厚度
| $ \begin{array}{*{20}{c}} {{\nu _{xy}} = \frac{{ - \left[ A \right]_{12}^{ - 1}}}{{\left[ A \right]_{11}^{ - 1}}};{\nu _{yx}} = \frac{{ - \left[ A \right]_{12}^{ - 1}}}{{\left[ A \right]_{22}^{ - 1}}};{G_{xy}} = \frac{{{A_{33}}}}{{{t_{\rm{f}}}}}}\\ {{E_x} = \frac{{{A_{11}}\left( {1.0 - {\nu _{xy}}{\nu _{yx}}} \right)}}{{{t_{\rm{f}}}}};{E_y} = \frac{{{A_{22}}\left( {1.0 - {\nu _{xy}}{\nu _{yx}}} \right)}}{{{t_{\rm{f}}}}}} \end{array} $ | (9) |
(4) 计算复合材料夹层结构的截面惯性矩
| $ {I_{xx}} = {I_{yy}} = \frac{{{t_{\rm{f}}}{{\left( {{t_{\rm{c}}} + \frac{{{t_{\rm{f}}}}}{2}} \right)}^2}}}{4} + \frac{{t_{\rm{f}}^3}}{{48}} $ | (10) |
(5) 计算整个复合材料蜂窝夹层结构的弯曲刚度,从而形成弯曲刚度矩阵D
| $ \begin{array}{*{20}{c}} {{D_{11}} = \frac{{{E_x}{I_{xx}}}}{{1.0 - {\nu _{xy}}{\nu _{yx}}}};{D_{22}} = \frac{{{E_y}{I_{yy}}}}{{1.0 - {\nu _{xy}}{\nu _{yx}}}}}\\ {{D_{12}} = {D_{21}} = \frac{{{D_{11}}{\nu _{xy}}{E_y}}}{{{E_x}}}}\\ {{D_{66}} = {G_{xy}}{I_{xx}};{D_{16}} = {D_{61}} = {D_{26}} = {D_{62}} = 0} \end{array} $ | (11) |
(6) 计算剪切刚度[9]
| $ {C_{xz}} = \frac{{{{\left( {{t_{\rm{f}}} + {t_{\rm{c}}}} \right)}^2}}}{{{t_{\rm{c}}}}}{G_{xz}};{C_{yz}} = \frac{{{{\left( {{t_{\rm{f}}} + {t_{\rm{c}}}} \right)}^2}}}{{{t_{\rm{c}}}}}{G_{yz}} $ | (12) |
式中:Gxz和Gyz为蜂窝夹芯下xz和yz方向的剪切刚度。
1.4 载荷处理通过有限元分析获得的复合材料蜂窝夹芯结构的内力或应力结果,不能全部满足设计约束的需求,须对结果进行合理的处理。
对于面板起皱失稳和面板格间失稳须求得面板承担的内力,其计算公式如下[10]
| $ \begin{array}{*{20}{c}} {N_x^{\rm{f}} = {N_x} \pm \frac{{{M_x}}}{{{t_{\rm{c}}} + \frac{{{t_{\rm{f}}}}}{2}}}}\\ {N_y^{\rm{f}} = {N_y} \pm \frac{{{M_y}}}{{{t_{\rm{c}}} + \frac{{{t_{\rm{f}}}}}{2}}}}\\ {N_{xy}^{\rm{f}} = {N_{xy}} \pm \frac{{{M_{xy}}}}{{{t_{\rm{c}}} + \frac{{{t_{\rm{f}}}}}{2}}}} \end{array} $ | (13) |
而对于蜂窝芯材的强度校核,则须求得蜂窝芯材所受的剪切应力,其计算公式如下[9]
| $ {\tau _{xz}} = \frac{{{Q_{xz}}}}{{{t_{\rm{f}}} + {t_{\rm{c}}}}};{\tau _{yz}} = \frac{{{Q_{yz}}}}{{{t_{\rm{f}}} + {t_{\rm{c}}}}} $ | (14) |
考虑制造工艺性要求和各种性能约束,以复合材料蜂窝夹层结构进气道重量为目标函数,优化数学模型可描述为
| $ \begin{array}{l} \min W = {W_{\rm{f}}} + {W_{\rm{c}}} = \sum\limits_{i = 0,90,45, - 45} {{\rho _i}{t_i}{S_i} + {\rho _{\rm{c}}}{t_{\rm{c}}}{S_{\rm{c}}}} \\ {\rm{s}}.\;{\rm{t}}.\;{g_j}\left( {{t_i},{t_{\rm{c}}}} \right) \le 0\;\;\;\;j = 1,2, \cdots ,h\\ \;\;\;\;\;\;{t_i} \in \left\{ {{T_1},{T_2}, \cdots ,{T_l}} \right\}\\ \;\;\;\;\;\;{t_{\rm{c}}} \in \left\{ {{T_{1{\rm{c}}}},{T_{2{\rm{c}}}}, \cdots ,{T_{k{\rm{c}}}}} \right\} \end{array} $ | (15) |
式中:W为结构重量;ρ为材料密度;t为材料厚度;S为材料面积;下标f表示面板;c表示蜂窝芯材;Tl为考虑制造约束的i方向角度可选厚度离散值,Tkc为蜂窝芯厚度的可选离散值,gj (ti, tc)为指定的优化约束条件。
为了实现所有设计参数的优化,目前工程研究人员采用对复合材料蜂窝夹层结构进行参数化建模,通过各种优化算法直接驱动进行优化设计。其中涉及优化算法包括[1-6]:满应力(应变)法、可行方向法、序列二次规划法、遗传算法、神经网络算法以及模拟退火算法等。
本文所建立的复合材料蜂窝夹层结构进气道优化设计有其特殊性,表现在复合材料面板和蜂窝芯材厚度在考虑工程制造约束及实际设计后,都是离散设计变量。对于离散优化问题,本文采用HyperStudy软件自带的全局响应面法(Global response surface method, GRSM),相比于其他优化方法,该算法具有适用于离散变量问题、避免陷入局部最优、计算效率和准确性高等优点,其优化流程如图 1所示。
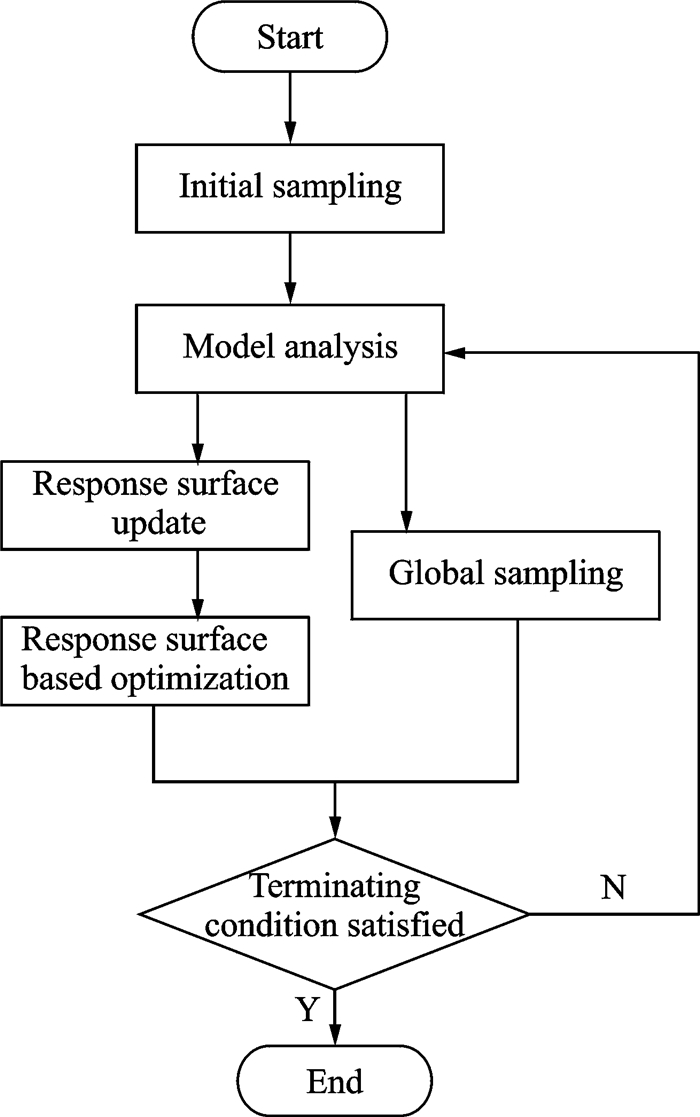
|
图 1 GRSM优化算法流程图 Figure 1 Flow chart for GRSM optimization algorithm |
2 优化算例分析
为了验证上述复合材料蜂窝夹层结构进气道优化设计方法的可行性,建立如下算例。
2.1 算例介绍以1/3圆柱面为待设计进气道理论外形,采用25 mm×25 mm的单元大小划分有限元网格,有限元模型如图 2所示。面板选用T300/环氧预浸料,预浸料单层厚度0.125 mm,密度为1 570 kg/m3,材料力学性能如表 1所示,上下面板铺层关于蜂窝夹芯中面对称,初始铺层为[452/-452/902/02]。蜂窝芯选用NRH-3-64,初始厚度10.0 mm,密度为64 kg/m3,材料力学性能如表 2所示。

|
图 2 算例有限元模型 Figure 2 Finite element model |
| 表 1 T300复合材料力学性能 Table 1 Mechanical properties of T300 |
| 表 2 NRH-3-64蜂窝材料力学性能 Table 2 Mechanical properties of NRH-3-64 |
复合材料蜂窝夹层结构进气道通过双排钉与周边结构相连,有限元模型中简化为四边固支。施加Ⅰ状态吸力工况和Ⅱ状态压力工况,以及吸力载荷下的屈曲工况,同时计算结构的固有频率。
2.2 优化结果分析根据本文所建立的优化设计方法,建立算例结构的优化模型。由于上下面板铺层关于蜂窝夹芯对称,因此只设置上面板各铺层角度的厚度变量,其中:t0为上面板0°层厚度,t90为上面板90°层厚度,t45为上面板45°层厚度,45°与-45°均衡。离散可选值如表 3所示,按照表 4所给上下限约束各个响应。
| 表 3 设计变量取值范围及最优结果 Table 3 Ranges and optimal results of design variables |
| 表 4 约束条件限制及最终值 Table 4 Restrictions and final values of constraints |
首先对初始结构进行分析,总质量4.00 kg。将各响应结果整理到表 4中,可以看出初始结构具有较大的减重空间。
对算例模型进行优化,图 3给出了优化过程中结构总质量的变化,第4个迭代过程之后结构总质量达到最小,为2.2 kg,最终优化设计的面板铺层为[45/-45/90/0],蜂窝芯厚8.0 mm,减重效果明显,验证了所选优化算法的高效特征。

|
图 3 质量迭代历史 Figure 3 History of mass iteration |
以最终优化设计为输入,建立强度校核模型,并进行分析计算,将强度校核所关注的各响应最终值整理于表 4中,可以看出所有指标满足强度要求,验证了本文所建立的复合材料蜂窝夹芯进气道结构优化设计方法的有效性和合理性。相比于初始结果,材料利用率有了极大的提升。
3 结论(1) 本文论述的优化设计方法以工程实用为目的,考虑了复合材料结构设计一般原则和生产制造中真实工艺状态,全面考察了复合材料蜂窝夹层结构的各种失效模式以及进气道工作需求。
(2) 算例表明:此优化设计方法合理,效果明显,结果可靠,解决了复合材料蜂窝夹层结构进气道设计问题,具有工程实际意义。
| [1] |
DING Y.
Optimum design of honeycomb sandwich constructions with buckling constraints[J]. Computers & Structures, 1989, 33(6): 1355–1364.
|
| [2] |
VINSON J R.
The behavior of sandwich structures of isotropic and composite materials[M]. Lancaster, PA, USA: TECHNOMIC Publishing Company, Inc, 1999.
|
| [3] |
MALOTT B, AVERILL R C, GOODMAN E D. Use of genetic algorithms for optimal design of laminated composite sandwich panels with bending twisting coupling: AIAA-96-1538-CP[R]. USA: AIAA, 1996: 1874-1879. |
| [4] |
KAM T Y, LAI F M.
Optimum design of laminated composite foam-filled sandwich plates subjected to strength constraint[J]. Solids and Structures, 1999, 36: 2865–2889.
DOI:10.1016/S0020-7683(98)00133-4
|
| [5] |
修英姝, 崔德刚.
复合材料蜂窝夹层结构的优化设计[J]. 北京航空航天大学学报, 2004, 30(9): 855–858.
XIU Yingshu, CUI Degang. Optimal design of composite sandwich structure[J]. Journal of Beijing University of Aeronautics & Astronautics, 2004, 30(9): 855–858. |
| [6] |
梁海州, 张元龙.
复合材料蜂窝夹层结构翼梁优化设计[J]. 机械制造研究, 2009, 38(3): 3–5.
LIANG Haizhou, ZHANG Yuanlong. Optimal design of composite wing beam with honeycomb sandwich[J]. Machine Building & Automation, 2009, 38(3): 3–5. |
| [7] |
许泽, 许希武, 曾宁, 等.
歼击机进气道结构强度设计方法研究[J]. 应用力学学报, 2006, 23(1): 159–162.
XU Ze, XU Xiwu, ZENG Ning, et al. Air inlet structural strength design method[J]. Chinese Journal of Applied Mechanics, 2006, 23(1): 159–162. |
| [8] |
杨永文. 复合材料层合板及飞机进气道铺层设计和分析[D]. 哈尔滨: 哈尔滨工业大学, 2009.
YANG Yongwen. Design and analysis of placement layers for composite laminates and aircraft inlet[D]. Harbin: Harbin Institute of Technology, 2009. |
| [9] |
中国航空研究院.
复合材料结构设计手册[M]. 北京: 航空工业出版社, 2001.
Chinese Aviation Academy. Design handbook of composites structure[M]. Beijing: Aviation Industry Press, 2001. |
| [10] |
(荷)克里斯托斯·卡萨波格罗. 飞机复合材料结构设计与分析[M]. 颜万亿, 译. 上海: 上海交通大学出版社, 2011.
|
| [11] |
隋立军.
某型飞机进气道有限元应力及振动疲劳分析[J]. 航空计算技术, 2014, 44(4): 26–28.
SUI Lijun. Vibration fatigue analysis of aircraft inlet using FEM[J]. Aeronautical Computing Technique, 2014, 44(4): 26–28. |
| [12] |
Altair Engineering, Inc. Hyperworks 13. 0 online help[M]. . [S. l. ]: Altair Engineering, Inc., 2014. |
 2018, Vol. 50
2018, Vol. 50

