复合材料在航空结构中常以层合板、层合壳的形式出现。这些结构一般较薄,常常通过设置加强筋来增强整体刚度或局部刚度,但结构的静强度失效中仍有很大一部分是由于失稳所引起的,所以结构的稳定性问题非常突出。
在早期稳定性的设计中,考虑到复合材料的脆性,屈曲会造成结构损伤,所以把设计载荷设定在初始屈曲载荷以下,以确保结构使用过程中的安全性。随着制造工艺的改善,纤维和基体性能的提高,人们发现这样的设计要求使很大一部分复合材料承载能力没有发挥,造成结构的浪费。已有的研究表明[1-3]:复合材料加筋板在处于较低的应力水平时可能产生局部失稳现象,但不一定产生破坏,仍具有很大的承载能力,最终的承载能力可能是初始屈曲载荷的2~3倍,甚至更高。要充分发挥结构的承载能力,提高材料、结构的使用效率,就必须利用复合材料加筋板(壳)的后屈曲段承载性能。
要发挥复合材料加筋结构的承载能力,就必须加强后屈曲阶段的研究。在结构的初步设计中,如果要利用后屈曲承载能力来设计层合板,就要对层合板在不同载荷和边界约束组合下的屈曲/后屈曲问题进行快速且有效的计算。现有的研究通常通过推导各种形式的载荷和边界条件下的屈曲/后屈曲行为的解析公式,以达到快速计算的目的。正交各向异性的复合材料层合板屈曲问题很早就有了比较成熟的解析解法[4],Pevzner等[5]将筋条对面板的约束简化成简支约束或固支约束,得到了纵向筋条加强的复合材料圆柱壳屈曲载荷的解析解。这种简化方法没有考虑筋条的扭转刚度,过低(简支约束)或过高(固支约束)地估计了筋条对面板的约束作用。Paik等[6]将筋条简化为扭转杆,对面板进行扭转约束,得到了各向同性板在弹性约束下屈曲载荷的解析解,并通过数值方法进行了验证。Bisagni等[7, 8]将这种方法推广到复合材料加筋板模型,模拟其在均布压缩载荷下的屈曲和后屈曲形态,模型中筋条被简化为扭力杆,整体加筋板模型转化为两扭力杆和其间面板的局部模型,再利用里兹法得到屈曲载荷的解析解和后屈曲行为的半解析解。Qiao等[9-13]建立了离散板分析方法,将复合材料型材简化成一系列板件,每个板件都转化为边界(与其他板件连接处)受到弹性约束或自由边的正交各向异性板,对整个型材的分析就转化为受各种边界约束和载荷方式的局部板件的分析。Mittelstedt等[14]用里兹法研究对称铺层层合板压缩载荷下的屈曲载荷与屈曲模态,求解中考虑弯扭耦合刚度,讨论了耦合刚度对屈曲分析结果的影响。
与特征值屈曲分析相比,复合材料层合板后屈曲解析解法的文献相对较少。Mittelstedt等[15]利用伽辽金法得到了简支和固支边界矩形板在剪切载荷下的屈曲与后屈曲的解析解,并在后屈曲中引入了初始缺陷,但忽略了弯扭耦合项。Beerhorst等[16]将该方法推广到弹性约束下的复合材料层合板在压剪复合载荷下的屈曲/后屈曲求解,考虑了弯扭耦合项,但未考虑横向边界的约束情况。Byklum等[17]基于最小势能原理,考虑几何非线性,分析双向轴压载荷下双向加筋板的后屈曲行为,解析结果与数值结果在前屈曲阶段吻合较好,后屈曲阶段有一定的误差。Brubak等[18]用半解析方法研究筋条方向任意的复合材料加筋板在压剪载荷作用下的屈曲和后屈曲行为,所得结果与数值模拟结果误差很小。以上屈曲和后屈曲的解析解法都是针对对称铺层的层合板(加筋板),任意铺层的层合板因刚度矩阵存在拉弯耦合和弯扭耦合项,很难得到解析解。Diaconu等[19]研究了简支约束下的任意铺层层合板在压缩载荷下的后屈曲问题,通过引入无量纲参数将大挠度后屈曲的平衡方程和协调方程无量纲化,根据简支边界条件和由铺层不对称而引起扭曲的屈曲模态构造挠度函数,考虑前屈曲挠度,利用伽辽金法对控制方程进行求解,得到压缩载荷和挠度的显式表达式。Nie等[20]将该方法推广到求解弹性约束下的任意铺层层合板在剪切载荷下的后屈曲问题,通过边界上承受扭转约束的边界条件,构造屈曲挠度函数,并利用伽辽金法得到剪切载荷和挠度的显式表达式。
本文针对任意铺层的复合材料加筋板,通过将加筋板简化为受弹簧约束的层合板,利用伽辽金法,得到了加筋板受压缩、剪切和压剪载荷下的屈曲/后屈曲解析解。求解中引入了无量纲参数,使得结果更具一般性;在后屈曲行为中考虑了初始曲线和耦合刚度引起的前屈曲挠度,使得结果更加准确。通过与有限元结果的比较,讨论了几何参数、弹簧刚度等对解的影响。最后将该方法应用于T形加筋对称铺层复合材料加筋板的屈曲分析中,考虑T形筋对复合材料层板粘结区的刚度增强作用,采用刚度平均化方法引入增强效果,并与两种T形筋刚度简化模型以及有限元结果进行了比较,验证了粘结区刚度平均对加筋板后屈曲行为分析的有效性。
1 复合材料层合板屈曲/后屈曲解析分析方法在复合材料加筋板的初步设计阶段,采用解析方法可以提高设计效率。
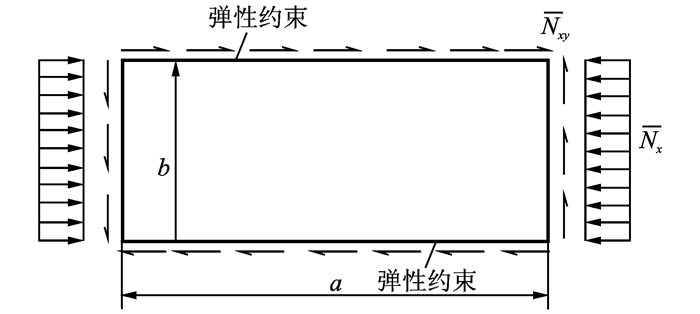
在复合材料加筋板的屈曲/后屈曲问题求解中,通常的做法是将筋条简化为扭转弹簧(见图 1)[7],原问题即转化为求解边界含弹性约束的板的屈曲/后屈曲问题。为了使分析更具一般性,本文考虑的复合材料加筋板的面板为任意铺层的复合材料层合板。
|
图 1 复合材料加筋板分析模型 Figure 1 Analysis model of stiffened composite panels |
1.1 基本方程
根据经典层合板理论和基于基尔霍夫假设的薄壁理论,中面上单位长度的薄膜应力{Nx, Ny, Nxy},力矩{Mx, My, Mxy}和应变{εx0, εy0, γxy0},曲率{κx, κy, κxy}满足关系式[21]
| $ \left( {\begin{array}{*{20}{c}} {{N_x}}\\ {{N_y}}\\ {{N_{xy}}}\\ {{M_x}}\\ {{M_y}}\\ {{M_{xy}}} \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}&{{A_{16}}}&{{B_{11}}}&{{B_{12}}}&{{B_{16}}}\\ {{A_{21}}}&{{A_{22}}}&{{A_{26}}}&{{B_{21}}}&{{B_{22}}}&{{B_{26}}}\\ {{A_{61}}}&{{A_{62}}}&{{A_{66}}}&{{B_{61}}}&{{B_{62}}}&{{B_{66}}}\\ {{B_{11}}}&{{B_{12}}}&{{B_{16}}}&{{D_{11}}}&{{D_{12}}}&{{D_{16}}}\\ {{B_{21}}}&{{B_{22}}}&{{B_{26}}}&{{D_{21}}}&{{D_{22}}}&{{D_{26}}}\\ {{B_{61}}}&{{B_{62}}}&{{B_{66}}}&{{D_{61}}}&{{D_{62}}}&{{D_{66}}} \end{array}} \right]\left( {\begin{array}{*{20}{c}} {\varepsilon _x^0}\\ {\varepsilon _y^0}\\ {\gamma _{xy}^0}\\ {{\kappa _x}}\\ {{\kappa _y}}\\ {{\kappa _{xy}}} \end{array}} \right) $ | (1) |
层合板大挠度后屈曲平衡方程可由薄膜应力表示为
| $ \left\{ \begin{array}{l} \frac{{\partial {N_x}}}{{\partial x}} + \frac{{\partial {N_{xy}}}}{{\partial y}} = 0\\ \frac{{\partial {N_{xy}}}}{{\partial x}} + \frac{{\partial {N_y}}}{{\partial y}} = 0\\ \begin{array}{*{20}{c}} {\frac{{{\partial ^2}{M_x}}}{{\partial {x^2}}} + 2\frac{{{\partial ^2}{M_{xy}}}}{{\partial x\partial y}} + \frac{{{\partial ^2}{M_y}}}{{\partial {y^2}}} + {N_x}\frac{{{\partial ^2}w}}{{\partial {x^2}}} + }\\ {2{N_{xy}}\frac{{{\partial ^2}w}}{{\partial x\partial y}} + {N_y}\frac{{{\partial ^2}w}}{{\partial {y^2}}} = 0} \end{array} \end{array} \right. $ | (2) |
薄膜应力可由应力函数ψ表示[22]
| $ {N_x} = \frac{{{\partial ^2}\psi }}{{\partial {y^2}}},\;\;\;\;{N_y} = \frac{{{\partial ^2}\psi }}{{\partial {x^2}}},\;\;\;\;\;{N_{xy}} = - \frac{{{\partial ^2}\psi }}{{\partial x\partial y}} $ | (3) |
当复合材料层合板受到压缩载荷Nx和剪切载荷Nxy单独或共同作用时,设其中占主导作用的载荷为Nd;若两者相等,则Nd可取两者中的任意值。
应变和曲率可分别定义为[22]
| $ \left\{ \begin{array}{l} \varepsilon _x^0 = \frac{{\partial {u_0}}}{{\partial x}} + \frac{1}{2}{\left( {\frac{{\partial w}}{{\partial x}}} \right)^2},\varepsilon _y^0 = \frac{{\partial {v_0}}}{{\partial y}} + \frac{1}{2}{\left( {\frac{{\partial w}}{{\partial y}}} \right)^2}\\ \gamma _{xy}^0 = \frac{{\partial {u_0}}}{{\partial y}} + \frac{{\partial {v_0}}}{{\partial x}} + \frac{{\partial w}}{{\partial x}}\frac{{\partial w}}{{\partial y}} \end{array} \right. $ | (4) |
| $ {\kappa _x} = - \frac{{{\partial ^2}w}}{{\partial {x^2}}},\;\;\;{\kappa _y} = - \frac{{{\partial ^2}w}}{{\partial {y^2}}},\;\;\;\;{\kappa _{xy}} = - 2\frac{{{\partial ^2}w}}{{\partial x\partial y}} $ | (5) |
联合式(1~5),并引入无量纲参数(见附录),层合板后屈曲问题的无量纲基本微分方程为
| $ \begin{array}{l} \frac{1}{{\alpha _D^2}}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^4}}} + 4\frac{{{\gamma _D}}}{{{\alpha _D}}}\frac{{{\partial ^2}\bar w}}{{\partial {\xi ^3}\partial \eta }} + 2{\beta _D}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^2}\partial {\eta ^2}}} + 4{\alpha _D}{\delta _D}\frac{{{\partial ^4}\bar w}}{{\partial \xi \partial {\eta ^3}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\alpha _D^2\frac{{{\partial ^4}\bar w}}{{\partial {\eta ^4}}} + {\alpha _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^4}}} + {\gamma _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^3}\partial \eta }} + {\beta _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^2}\partial {\eta ^2}}} + \\ \;\;\;\;\;\;\;\;\;\;\;{\delta _B}\frac{{{\partial ^4}\bar \psi }}{{\partial \xi \partial {\eta ^3}}} + {\eta _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\eta ^4}}} = \frac{{{\partial ^2}\bar \psi }}{{\partial {\eta ^2}}}\frac{{{\partial ^2}\bar w}}{{\partial {\xi ^2}}} - 2\frac{{{\partial ^2}\bar \psi }}{{\partial \xi \partial \eta }}\frac{{{\partial ^2}\bar w}}{{\partial \xi \partial \eta }} + \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{{\partial ^2}\bar \psi }}{{\partial {\xi ^2}}}\frac{{{\partial ^2}\bar w}}{{\partial {\eta ^2}}} \end{array} $ | (6) |
| $ \begin{array}{l} \frac{1}{{\alpha _A^2}}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^4}}} - 2\frac{{{\delta _A}}}{{{\alpha _A}}}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^3}\partial \eta }} + 2{\beta _A}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^2}\partial {\eta ^2}}} - 2{\gamma _A}{\alpha _A}\frac{{{\partial ^4}\bar \psi }}{{\partial \xi \partial {\eta ^3}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\alpha _A^2\frac{{{\partial ^4}\bar \psi }}{{\partial {\eta ^4}}} - \left( {{\alpha _B}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^4}}} + {\gamma _B}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^3}\partial \eta }} + {\beta _B}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^2}\partial {\eta ^2}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {{\delta _B}\frac{{{\partial ^4}\bar w}}{{\partial \xi \partial {\eta ^3}}} + {\eta _B}\frac{{{\partial ^4}\bar w}}{{\partial {\eta ^4}}}} \right) = {\left( {\frac{{{\partial ^2}\bar w}}{{\partial \xi \partial \eta }}} \right)^2} - \frac{{{\partial ^2}\bar w}}{{\partial {\xi ^2}}}\frac{{{\partial ^2}\bar w}}{{\partial {\eta ^2}}} \end{array} $ | (7) |
方程(6,7)是层合板后屈曲问题的无量纲基本微分方程。
假设层合板具有已知的初始缺陷w0,层合板的后屈曲实际挠度包含由载荷产生的挠度w和初始挠度w0两部分,把总挠度w+w0代入中面应变的表达式(4),并忽略其中的高阶项,得到具有初始挠度的层合板应变表达式
| $ \left\{ \begin{array}{l} \varepsilon _x^0 = \frac{{\partial {u_0}}}{{\partial x}} + \frac{1}{2}{\left( {\frac{{\partial w}}{{\partial x}}} \right)^2} + \frac{{\partial w}}{{\partial x}}\frac{{\partial {w_0}}}{{\partial x}}\\ \varepsilon _y^0 = \frac{{\partial {v_0}}}{{\partial y}} + \frac{1}{2}{\left( {\frac{{\partial w}}{{\partial y}}} \right)^2} + \frac{{\partial w}}{{\partial y}}\frac{{\partial {w_0}}}{{\partial y}}\\ \gamma _{xy}^0 = \frac{{\partial {u_0}}}{{\partial y}} + \frac{{\partial {v_0}}}{{\partial x}} + \frac{{\partial w}}{{\partial x}}\frac{{\partial w}}{{\partial y}} + \frac{{\partial w}}{{\partial x}}\frac{{\partial {w_0}}}{{\partial y}} + \frac{{\partial w}}{{\partial y}}\frac{{\partial {w_0}}}{{\partial x}} \end{array} \right. $ | (8) |
同时应变εx0,εy0,γxy0表达式也可由关系式(1)结合应力函数表达式(3)给出
| $ \left\{ \begin{array}{l} \varepsilon _x^0 = {{\bar A}_{11}}\frac{{{\partial ^2}\psi }}{{\partial {y^2}}} + {{\bar A}_{12}}\frac{{{\partial ^2}\psi }}{{\partial {x^2}}} - {{\bar A}_{16}}\frac{{{\partial ^2}\psi }}{{\partial x\partial y}} - {{\bar B}_{11}}\frac{{{\partial ^2}w}}{{\partial {x^2}}} - \\ \;\;\;\;\;\;\;{{\bar B}_{12}}\frac{{{\partial ^2}w}}{{\partial {y^2}}} - 2{{\bar B}_{16}}\frac{{{\partial ^2}w}}{{\partial x\partial y}}\\ \varepsilon _y^0 = {{\bar A}_{12}}\frac{{{\partial ^2}\psi }}{{\partial {y^2}}} + {{\bar A}_{22}}\frac{{{\partial ^2}\psi }}{{\partial {x^2}}} - {{\bar A}_{26}}\frac{{{\partial ^2}\psi }}{{\partial x\partial y}} - {{\bar B}_{21}}\frac{{{\partial ^2}w}}{{\partial {x^2}}} - \\ \;\;\;\;\;\;\;{{\bar B}_{22}}\frac{{{\partial ^2}w}}{{\partial {y^2}}} - 2{{\bar B}_{26}}\frac{{{\partial ^2}w}}{{\partial x\partial y}}\\ \gamma _{xy}^0 = {{\bar A}_{16}}\frac{{{\partial ^2}\psi }}{{\partial {y^2}}} + {{\bar A}_{26}}\frac{{{\partial ^2}\psi }}{{\partial {x^2}}} - {{\bar A}_{66}}\frac{{{\partial ^2}\psi }}{{\partial x\partial y}} - {{\bar B}_{61}}\frac{{{\partial ^2}w}}{{\partial {x^2}}} - \\ \;\;\;\;\;\;\;{{\bar B}_{62}}\frac{{{\partial ^2}w}}{{\partial {y^2}}} - 2{{\bar B}_{66}}\frac{{{\partial ^2}w}}{{\partial x\partial y}} \end{array} \right. $ | (9) |
消去式(8)中的位移u0,v0,并将应变表达式(9)代入,可得具有初始缺陷的层合板应变协调方程,引入无量纲参数后为
| $ \begin{array}{l} \frac{1}{{\alpha _A^2}}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^4}}} - 2\frac{{{\delta _A}}}{{{\alpha _A}}}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^3}\partial \eta }} + 2{\beta _A}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^2}\partial {\eta ^2}}} - 2{\gamma _A}{\alpha _A}\frac{{{\partial ^4}\bar \psi }}{{\partial \xi \partial {\eta ^3}}} + \\ \;\;\;\;\;\;\;\;\;\;\alpha _A^2\frac{{{\partial ^4}\bar \psi }}{{\partial {\eta ^4}}} - \left( {{\alpha _B}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^4}}} + {\gamma _B}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^3}\partial \eta }} + {\beta _B}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^2}\partial {\eta ^2}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{\delta _B}\frac{{{\partial ^4}\bar w}}{{\partial \xi \partial {\eta ^3}}} + {\eta _B}\frac{{{\partial ^4}\bar w}}{{\partial {\eta ^4}}}} \right) = {\left( {\frac{{{\partial ^2}\bar w}}{{\partial \xi \partial \eta }}} \right)^2} - \frac{{{\partial ^2}\bar w}}{{\partial {\xi ^2}}}\frac{{{\partial ^2}\bar w}}{{\partial {\eta ^2}}} + \\ \;\;\;\;\;\;\;\;\;\;2\frac{{{\partial ^2}\bar w}}{{\partial \xi \partial \eta }}\frac{{{\partial ^2}{{\bar w}_0}}}{{\partial \xi \partial \eta }} - \frac{{{\partial ^2}\bar w}}{{\partial {\xi ^2}}}\frac{{{\partial ^2}{{\bar w}_0}}}{{\partial {\eta ^2}}} - \frac{{{\partial ^2}{{\bar w}_0}}}{{\partial {\xi ^2}}}\frac{{{\partial ^2}\bar w}}{{\partial {\eta ^2}}} \end{array} $ | (10) |
对于平衡方程(6),等号左端项代表弯曲薄膜应力,它仅与由其产生的挠度w有关。等号右端项表示力在坐标系下的投影,应该按照包含初始缺陷w0在内的实际位置进行投影,将总挠度w+w0代替w并代入方程(6)的右端,得到考虑初始缺陷的平衡微分方程
| $ \begin{array}{l} \frac{1}{{\alpha _D^2}}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^4}}} + 4\frac{{{\gamma _D}}}{{{\alpha _D}}}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^3}\partial \eta }} + 2{\beta _D}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^2}\partial {\eta ^2}}} + 4{\alpha _D}{\delta _D}\frac{{{\partial ^4}\bar w}}{{\partial \xi \partial {\eta ^3}}} + \\ \;\;\;\;\;\;\;\;\;\;\alpha _D^2\frac{{{\partial ^4}\bar w}}{{\partial {\eta ^4}}} + {\alpha _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^4}}} + {\gamma _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^3}\partial \eta }} + {\beta _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^2}\partial {\eta ^2}}} + \\ \;\;\;\;\;\;\;\;\;\;{\delta _B}\frac{{{\partial ^4}\bar \psi }}{{\partial \xi \partial {\eta ^3}}} + {\eta _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\eta ^4}}} = \frac{{{\partial ^2}\bar \psi }}{{\partial {\eta ^2}}}\left( {\frac{{{\partial ^2}\bar w}}{{\partial {\xi ^2}}} + \frac{{{\partial ^2}{{\bar w}_0}}}{{\partial {\xi ^2}}}} \right) - \\ \;\;\;\;\;\;\;\;\;\;2\frac{{{\partial ^2}\bar \psi }}{{\partial \xi \partial \eta }}\left( {\frac{{{\partial ^2}\bar w}}{{\partial \xi \partial \eta }} + \frac{{{\partial ^2}{{\bar w}_0}}}{{\partial \xi \partial \eta }}} \right) + \frac{{{\partial ^2}\bar \psi }}{{\partial {\xi ^2}}}\left( {\frac{{{\partial ^2}\bar w}}{{\partial {\eta ^2}}} + \frac{{{\partial ^2}{{\bar w}_0}}}{{\partial {\eta ^2}}}} \right) \end{array} $ | (11) |
方程(10,11)即为考虑初始缺陷的关于挠度函数w和应力函数ψ的微分方程组。
1.2 屈曲/后屈曲问题的求解为了得到微分方程组(10,11)的解析解,首先需要假设挠度函数,亦称位移函数。由于本文研究的是任意铺层的复合材料层合板,存在拉弯、弯扭耦合刚度,当受到面内压缩、剪切或压剪复合载荷时,在屈曲发生之前会产生较大的离面位移,称为前屈曲挠度,并对后屈曲变形产生影响。因此,为了准确地计算层合板的后屈曲问题,除了初始缺陷w0,假设层合板的挠度w还包含两部分
| $ \bar w = {{\bar w}_1} + {{\bar w}_2} $ | (12) |
式中w1为前屈曲挠度。根据挠度函数在两纵向边界满足的自然边界条件,这个挠度函数可以假设为
| $ {{\bar w}_1} = g\eta \left( {\eta - 1} \right) $ | (13) |
式中g为待定系数。同时,这个挠度函数在两纵向边界还满足层合板的弯曲刚度和所受弹性约束的扭转刚度相协调的关系
| $ \begin{array}{l} {M_\eta } = - {\eta _B}\frac{{{\partial ^2}\bar \psi }}{{\partial \eta }} - {\rho _B}\frac{{{\partial ^2}\bar \psi }}{{\partial {\xi ^2}}} + {\tau _B}\frac{{{\partial ^2}\bar \psi }}{{\partial {\eta ^2}}} - {\eta _D}\frac{{{\partial ^2}{{\bar w}_1}}}{{\partial {\xi ^2}}} - \\ \;\;\;\;\;\;\;\alpha _D^2\frac{{{\partial ^2}{{\bar w}_1}}}{{\partial {\eta ^2}}} - 2{\alpha _D}{\delta _D}\frac{{{\partial ^2}{{\bar w}_1}}}{{\partial \xi \partial \eta }} = \bar K\alpha _D^2\overline {AD} \frac{{\partial {{\bar w}_1}}}{{\partial \eta }} \end{array} $ | (14) |
将式(13)代入式(14),可以得到g的表达式
| $ g = \frac{{\left( {{\eta _B}{{\bar N}_x} + {\tau _B}\alpha {{\bar N}_{xy}}} \right){{\rm{ \mathit{ π} }}^2}}}{{\left( {\bar K + 2} \right)\alpha _D^2}} $ | (15) |
式(12)中的第2项w2为面内载荷作用下层合板后屈曲阶段产生的位移。为了能够得到复合材料层合板在扭转约束下的后屈曲问题解析解,假设在层合板发生屈曲后的一定载荷范围内,屈曲模态的倾斜角和半波长没有发生变化,挠度函数可以通过屈曲模态和边界条件构造成
| $ \begin{array}{l} {{\bar w}_2}\left( {\xi ,\eta } \right) = W\sin \left( {{\rm{ \mathit{ π} }}\left( {\xi - \phi \eta } \right)} \right)\left[ {\left( {1 - t} \right)\sin \left( {{\rm{ \mathit{ π} }}\eta } \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{t}{2}\left( {1 - \cos \left( {2{\rm{ \mathit{ π} }}\eta } \right)} \right)} \right] \end{array} $ | (16) |
式中:W表示挠度函数的振幅;t(0 ≤ t ≤ 1)为待求参数, 表示扭转边界条件介于简支边界条件和固支边界条件之间;ϕ表示屈曲模态的倾斜角;半波长α通过无量纲的变量ξ表示。
假设的挠度函数w2除了满足基本的自然边界条件外,在层合板纵向边界的弯曲刚度和扭转刚度同样满足下面的协调关系
| $ {M_\eta } = \left\{ \begin{array}{l} \bar K\alpha _D^2\overline {AD} \frac{{\partial {{\bar w}_2}}}{{\partial \eta }}\;\;\;\;\;\eta = 1\\ - \bar K\alpha _D^2\overline {AD} \frac{{\partial {{\bar w}_2}}}{{\partial \eta }}\;\;\;\eta = 0 \end{array} \right. $ | (17) |
将式(16)代入式(17),可以得到未知参数t为
| $ t = \frac{{\bar K}}{{\bar K + 2{\rm{ \mathit{ π} }}}} $ | (18) |
同时,假设考虑初始缺陷的位移函数w0和理想情况下的位移函数w2具有相同的形式
| $ \begin{array}{l} {{\bar w}_0}\left( {\xi ,\eta } \right) = {W_0}\sin \left( {{\rm{ \mathit{ π} }}\left( {\xi - \phi \eta } \right)} \right)\left[ {\left( {1 - t} \right)\sin \left( {{\rm{ \mathit{ π} }}\eta } \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{t}{2}\left( {1 - \cos \left( {2{\rm{ \mathit{ π} }}\eta } \right)} \right)} \right] \end{array} $ | (19) |
对于薄板后屈曲无量纲应变协调微分方程(11),一个常用的齐次通解为[16]
| $ {{\bar \psi }_h} = \frac{{{{\rm{ \mathit{ π} }}^2}}}{2}\left( {{{\bar N}_x}{\eta ^2} - 2{{\bar N}_{xy}}\alpha \xi \eta } \right) $ | (20) |
方程(11)的一个特解ψh的表达式较长,列于附录中,这里不再写出。方程(11)中应力函数ψ的通解可表达为
| $ \bar \psi = {{\bar \psi }_h} + {{\bar \psi }_p} $ | (21) |
方程(10)可采用伽辽金法进行求解[23]
| $ \int_0^2 {\left( {\int_0^1 {L\left( {\bar w,\bar \psi } \right)\frac{{\partial \bar w}}{{\partial W}}{\rm{d}}\eta } } \right){\rm{d}}\xi } = 0 $ | (22) |
式中算子L(w, ψ)定义如下
| $ \begin{array}{l} L\left( {\bar w,\bar \psi } \right) = \frac{1}{{\alpha _D^2}}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^4}}} + 4\frac{{{\gamma _D}}}{{{\alpha _D}}}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^4}\partial \eta }} + 2{\beta _D}\frac{{{\partial ^4}\bar w}}{{\partial {\xi ^4}\partial {\eta ^2}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;4{\alpha _D}{\delta _D}\frac{{{\partial ^4}\bar w}}{{\partial \xi \partial {\eta ^3}}} + \alpha _D^2\frac{{{\partial ^4}\bar w}}{{\partial {\eta ^4}}} + {\alpha _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^4}}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;{\gamma _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^3}\partial \eta }} + {\beta _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\xi ^2}\partial {\eta ^2}}} + {\delta _B}\frac{{{\partial ^4}\bar \psi }}{{\partial \xi \partial {\eta ^3}}} + {\eta _B}\frac{{{\partial ^4}\bar \psi }}{{\partial {\eta ^4}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\partial ^2}\bar \psi }}{{\partial {\eta ^2}}}\left( {\frac{{{\partial ^2}\bar w}}{{\partial {\xi ^2}}} + \frac{{{\partial ^2}{{\bar w}_0}}}{{\partial {\xi ^2}}}} \right) + 2\frac{{{\partial ^2}\bar \psi }}{{\partial \xi \partial \eta }}\left( {\frac{{{\partial ^2}\bar w}}{{\partial \xi \partial \eta }} + \frac{{{\partial ^2}{{\bar w}_0}}}{{\partial \xi \partial \eta }}} \right) - \\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{{\partial ^2}\bar \psi }}{{\partial {\xi ^2}}}\left( {\frac{{{\partial ^2}\bar w}}{{\partial {\eta ^2}}} + \frac{{{\partial ^2}{{\bar w}_0}}}{{\partial {\eta ^2}}}} \right) \end{array} $ | (23) |
将式(16,19,21)代入方程(22),得到关于挠度W的3次方程
| $ \begin{array}{l} {\gamma _1}{W^3} + 3{\gamma _1}{W_0}{W^2} + 2{\gamma _1}W_0^2W - \left( {{\gamma _2} + {\gamma _3}} \right)W - \\ \;\;\;\;\;\;{\gamma _4}{{\bar N}_d}\left( {W - {W_0}} \right) = 0 \end{array} $ | (24) |
式中γ1~γ4为半波长α和倾斜角ϕ的函数,具体表达式见附录。
为了求解关于挠度W的3次方程(24),首先需要得到屈曲模态的半波长α和倾斜角ϕ。考虑理想情况下没有初始缺陷的层合板,即W0=0,这样方程(24)就变为关于W的二次方程
| $ {\gamma _1}{W^2} - \left( {{\gamma _2} + {\gamma _3} + {\gamma _4}{{\bar N}_d}} \right) = 0 $ | (25) |
方程(25)存在一个正根
| $ W = \sqrt {\frac{{{\gamma _2} + {\gamma _3} + {\gamma _4}{{\bar N}_d}}}{{{\gamma _1}}}} $ | (26) |
当外部载荷达到某个临界值时,复合材料层合板发生屈曲,这时还没有面外位移产生,即W=0,则式(26)化为
| $ {\gamma _2} + {\gamma _3} + {\gamma _4}{{\bar N}_d} = 0 $ | (27) |
同时在所有满足方程(27)的载荷Nd中,屈曲载荷是最小值,因此有
| $ \frac{{\partial {{\bar N}_d}}}{{\partial \alpha }} = 0,\;\;\;\frac{{\partial {{\bar N}_d}}}{{\partial \phi }} = 0 $ | (28) |
联立式(28)的两个方程,并通过简单的牛顿迭代就可以求出未知量α和ϕ的值。把这两个值代入方程(27),就得到屈曲载荷Nd的解析表达式
| $ {{\bar N}_d} = - \frac{{{\gamma _2} + {\gamma _3}}}{{{\gamma _4}}} $ | (29) |
同样地,把α和ϕ代入方程(24),可以得到挠度W和载荷Nd的关系式。
| $ \begin{array}{l} W = \frac{1}{{3\sqrt[3]{{{\gamma _1}}}}}\sqrt[3]{{ - 27{W_0}\left( {{\gamma _2} + {\gamma _3}} \right) + 3\sqrt {{\gamma _5}} }} + \\ \;\;\;\;\frac{{{\gamma _1}W_0^2 + {\gamma _2} + {\gamma _3} + {\gamma _4}{{\bar N}_d}}}{{\sqrt[3]{{\left( { - 27{W_0}\left( {{\gamma _2} + {\gamma _3}} \right) + 3\sqrt {{\gamma _5}} } \right)\gamma _1^2}}}} - {W_0} \end{array} $ | (30) |
式中
| $ \begin{array}{l} {\gamma _5} = - 3\left\{ {4\gamma _1^3W_0^6 + 12\gamma _1^2W_0^4\left( {{\gamma _4}{{\bar N}_d} + {\gamma _2} + {\gamma _3}} \right) + } \right.\\ \;\;\;\;\;\;\;3{\gamma _1}W_0^2\left[ {4\gamma _4^2\bar N_d^2 - 10{\gamma _2}{\gamma _3} + \left( {{\gamma _2} + {\gamma _3}} \right)\left( {8{\gamma _4}{{\bar N}_d} - } \right.} \right.\\ \;\;\;\;\;\;\;\left. {\left. {5{\gamma _2} + 5{\gamma _3}} \right)} \right] + 4\left( {{\gamma _2} + {\gamma _3}} \right)\left[ {3\gamma _4^2\bar N_d^2 + \left( {{\gamma _2} + } \right.} \right.\\ \;\;\;\;\;\;\;\left. {{{\left. {{\gamma _3}} \right)}^2}} \right] + 12\gamma _4^2\bar N_d^2\left( {3{\gamma _2} + {\gamma _4}{{\bar N}_d}} \right) + \\ \;\;\;\;\;\;\;\left. {36{\gamma _3}{\gamma _4}{{\bar N}_d}\left( {{\gamma _3} + 2{\gamma _2}} \right)} \right\}/{\gamma _1} \end{array} $ | (31) |
在对任意铺层复合材料加筋板屈曲/后屈曲问题的求解中,加筋板是被当作无限长板来处理的,忽略了横向边界约束的影响,再结合筋条刚度和面板耦合刚度(前屈曲挠度),对屈曲/后屈曲结果会产生不同程度的影响。因此,须根据不同的长宽比对解析解进行验证。对比解是基于有限元计算的结果。
本文采用ABAQUS软件。加筋板模型参见图 1,板宽设为150 mm,长度由长宽比决定,计算时采用4节点壳单元S4R,单元尺寸为5 mm×5 mm;进行单元尺寸的收敛性分析,结果证实在该尺寸下的结果是收敛的;上下边的筋条简化为弹性约束,采用Spring弹簧单元模拟,弹簧单元的刚度为筋条的扭转刚度,四边均约束离面位移。
复合材料单层材料参数[7]为:E11=113 GPa,E22=9 GPa,G12=3.82 GPa,ν12=0.302,厚度0.25 mm。加筋板长宽比λ=a/b,取为1≤λ≤7;筋条扭转刚度k取0,1,10和100。面板铺层方式很多,此处只选取一般的不对称铺层[0/45/-45/90]。
以下为压缩、剪切和压剪(压剪比1:1)3种载荷的有限元和本文解析解结果的对比。
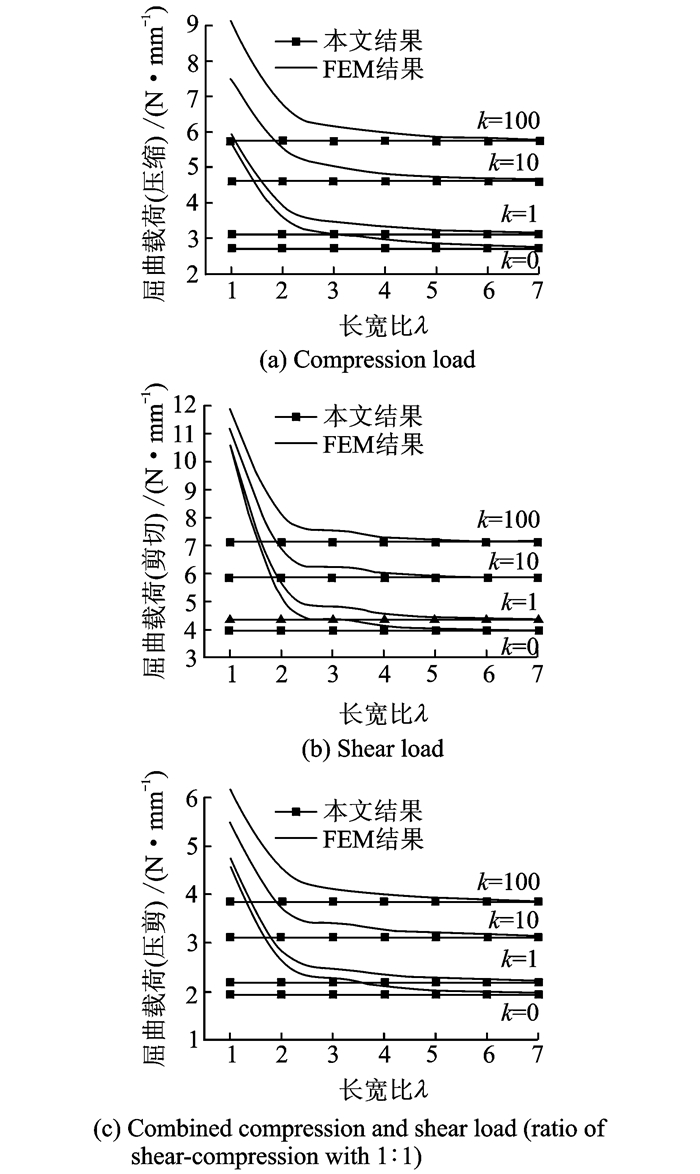
1.3.1 屈曲载荷加筋板的屈曲载荷解析结果可由式(29)解得,有限元结果由特征值分析获得。图 2为3种载荷形式下屈曲载荷的结果比较。
|
图 2 不同弹性约束和长宽比下的复合材料层合板在3种载荷下的屈曲载荷 Figure 2 Buckling loads of laminated composite panels with different elastic restraints and aspect ratios subjected to three kinds of loads |
由图 2的结果比较可知,当长宽比较小时,解析解的屈曲载荷与有限元结果偏差较大;但当λ≥3后,3种载荷下屈曲载荷的解析结果和有限元结果的偏差小于10%,并随着长宽比的增大而趋向有限元结果。该现象也适用于其他铺层,限于篇幅,不再给出。
1.3.2 后屈曲响应复合材料层合板为任意铺层时,可能存在不对称性引起的耦合刚度,在屈曲前就会产生较大的挠度,加上筋条扭转刚度约束性的差异,对后屈曲响应会有不同程度的影响。因此,本节除解析解与有限元结果的比较外,还比较了考虑前屈曲挠度(本文结果1)和不考虑前屈曲挠度(本文结果2)对结果的影响。
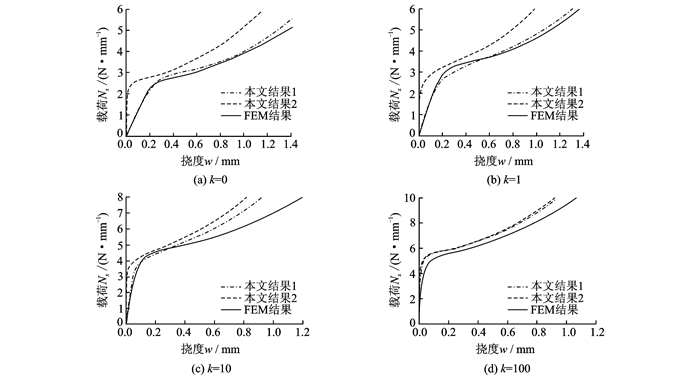
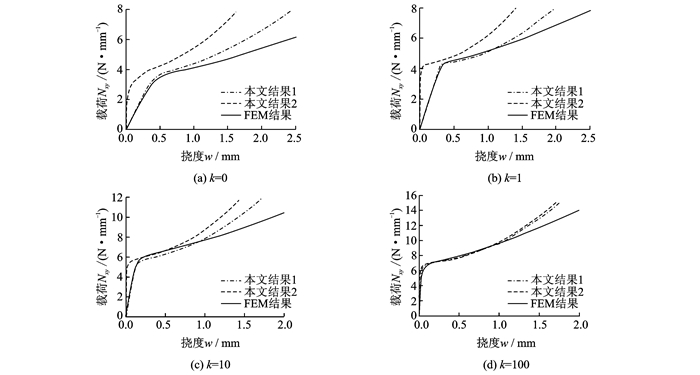
图 3,4为压缩载荷和剪切载荷下的载荷-挠度曲线。由图 3,4可见,一般铺层复合材料层合板在压缩和剪切载荷作用下产生了较大的前屈曲挠度,当筋条扭转刚度较小时,约束力较弱,对后屈曲影响较大,若不予以考虑,对后屈曲的挠度计算结果影响较大;只有在筋条扭转刚度很大、约束力非常强时,前屈曲的影响才可忽略。压剪载荷是压缩和剪切载荷的组合,结果与两者一致,在此不再给出。
|
图 3 不同扭转刚度约束下的复合材料层合板在压缩载荷下的载荷-挠度曲线 Figure 3 Load-deflection curves for laminated composite panels with different rotational stiffness restraints subjected to compression loads |
|
图 4 不同扭转刚度约束下的复合材料层合板在剪切载荷下的载荷-挠度曲线 Figure 4 Load-deflection curves for laminated composite panels with different rotational stiffness restraints subjected to shear loads |
图 5给出了加筋板受压缩和剪切载荷共同作用时,不同压剪比(Nx=0.5Nxy,Nx=Nxy和Nx=2Nxy)下的载荷-挠度曲线。由图可见,解析结果和有限元结果吻合很好。

|
图 5 在不同压剪比压剪载荷作用下的载荷-挠度曲线 Figure 5 Load-deflection curves for laminated composite panels with different rotational stiffness restraints subjected to combined compression and shear loads |
2 解析解法的应用
复合材料加筋板的面板一般采用对称铺层,以避免成型后的翘曲。筋条与面板通过粘结区粘结为一个整体,粘结区会提高面板刚度,但面板和粘结区的整体铺层往往会失去对称性。因此,该区域存在耦合刚度。而目前的分析方法均不考虑粘结区的刚度增强效果,屈曲载荷值相对偏低,影响加筋板承载力的发挥。
本节以工程中最常用的T形筋复合材料加筋板为例,通过刚度平均化方法,引入粘结区的刚度增强作用,采用上节任意铺层层合板屈曲/后屈曲解析解法进行求解。
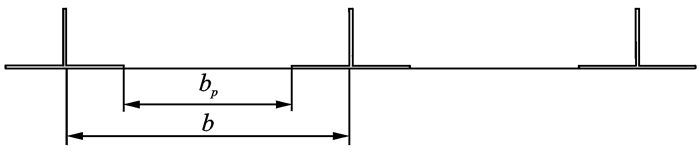
2.1 刚度平均方法图 6为工程中常用的T形筋复合材料加筋板截面结构示意图,其中b为筋间距,bp为无筋区面板宽度,则粘结区宽度为b-bp。
|
图 6 T形筋加筋板截面结构示意图 Figure 6 Structural representation of T-shaped stiffened panels |
以面板的中面为基准面,假设面板的厚度为tp,铺层数为n,粘结区的厚度为tf,铺层数为m。根据经典层合板理论,面板的拉伸刚度系数Aijp,耦合刚度系数Bijp和弯曲刚度系数Dijp分别为
| $ \begin{array}{l} A_{ij}^p = \sum\limits_{k = 1}^n {{{\left( {\bar Q_{ij}^p} \right)}_k}\left( {{z_k} - {z_{k - 1}}} \right)} ,B_{ij}^p = \frac{1}{2}\sum\limits_{k = 1}^n {{{\left( {\bar Q_{ij}^p} \right)}_k}\left( {z_k^2 - } \right.} \\ \;\;\;\;\;\;\;\left. {z_{k - 1}^2} \right),D_{ij}^p = \frac{1}{3}\sum\limits_{k = 1}^n {{{\left( {\bar Q_{ij}^p} \right)}_k}\left( {z_k^3 - z_{k - 1}^3} \right)} \end{array} $ | (32) |
由于加筋板的面板是对称铺层,所以刚度矩阵是对称的,且耦合刚度Bijp=0,拉弯耦合刚度系数A12p,A16p和弯扭耦合刚度系数D12p,D16p与其他量相比是小量,并随着铺层数的增加而减小。因此,为求解方便,在通常的分析中一般取零值,但在本文中无须忽略。
采用同样方法可以得到粘结区各刚度系数,由于粘结区的铺层可能是非对称的,即以下刚度系数均不为零
| $ \begin{array}{l} A_{ij}^F = \sum\limits_{k = 1}^m {{{\left( {\bar Q_{ij}^F} \right)}_k}\left( {{z_k} - {z_{k - 1}}} \right)} ,B_{ij}^F = \frac{1}{2}\sum\limits_{k = 1}^m {{{\left( {\bar Q_{ij}^F} \right)}_k}\left( {z_k^2 - } \right.} \\ \;\;\;\;\;\;\;\left. {z_{k - 1}^2} \right),D_{ij}^F = \frac{1}{3}\sum\limits_{k = 1}^m {{{\left( {\bar Q_{ij}^F} \right)}_k}\left( {z_k^3 - z_{k - 1}^3} \right)} \end{array} $ | (33) |
采用平均化方法,将粘结区刚度叠加到层合板上
| $ \begin{array}{l} {A_{ij}} = \frac{1}{b}\left[ {\left( {b - {b_p}} \right)A_{ij}^F + {b_p}A_{ij}^P} \right],{B_{ij}} = \frac{1}{b}\left[ {\left( {b - {b_p}} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\;\left. {B_{ij}^F + {b_p}B_{ij}^P} \right],{D_{ij}} = \frac{1}{b}\left[ {\left( {b - {b_p}} \right)D_{ij}^F + {b_p}D_{ij}^P} \right] \end{array} $ | (34) |
粘结区的铺层非对称性,使得刚度系数Aij,Bij和Dij均不为零。
2.2 算例及结果分析考虑筋条间距100 mm,粘结区宽度40 mm,筋条高度20 mm,长度300 mm的T形筋复合材料加筋板。面板铺层为[45°/(0°, 90°)/45°],筋条为[45°/0°/0°/0°/0°/45°],筋条粘结区为[45°/0°/0°],其中(0°, 90°)和45°层材料为碳纤维布,0°层材料为碳纤维单向带。材料性能见表 1。
| 表 1 铺层材料性能 Table 1 Layer material properties |
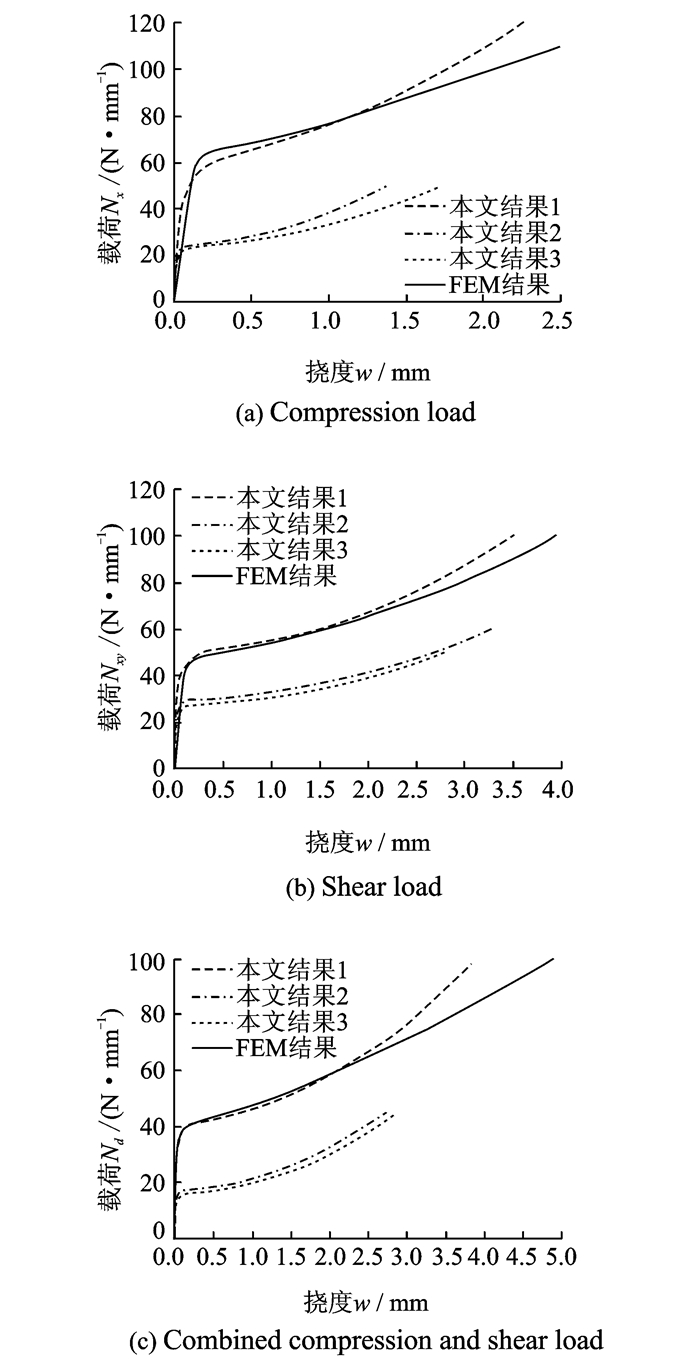
利用式(32~34),可得到平均化后的刚度阵,采用第1节中的方法可以得到加筋板屈曲/后屈曲响应,在此称解法1。工程中常用的求解方法是将T形筋条简化为扭转弹簧,弹簧刚度的计算分为只考虑筋条立面并忽略粘结区,和两者都考虑的两种方法,在此称解法2和3。面板为对称铺层,按式(32)计算。解法1~3及有限元方法计算结果见表 2和图 7。
| 表 2 特征值屈曲载荷 Table 2 Eigenvalue buckling load |
|
图 7 复合材料加筋板的载荷-挠度曲线比较 Figure 7 Comparison for load-deflection curves of stiffened composite panels |
由表 2和图 7可知,解法2和3没有体现粘结区的刚度增强效果,屈曲载荷偏低;而解法1考虑了粘结区的增强效果,屈曲载荷与FEM结果相比,偏差为2.8%。解法2和3的载荷-挠度曲线与FEM相比,尽管趋势相近,但由于面板刚度的差别,使曲线在数值上相差较远,而解法1的载荷-挠度曲线与FEM的吻合较好。
3 结论本文给出了一种弹性约束下的任意铺层复合材料层合板在压缩、剪切或压剪载荷下的屈曲/后屈曲问题解析解法,讨论了不同几何尺寸、前屈曲挠度、弹簧扭转刚度对屈曲/后屈曲响应的影响:
(1) 加筋板面板长宽比λ≥ 3时,屈曲载荷的解析结果和有限元结果的偏差小于10%;
(2) 前屈曲挠度对屈曲/后屈曲响应影响随筋条扭转刚度的提高而减弱。
考虑筋条粘结区对面板刚度的增强效果,将本文解析解应用于对称铺层的复合材料加筋板中,通过算例结果的对比表明本文方法能够更准确地预测复合材料加筋板的屈曲/后屈曲响应,为加筋板的设计提供了有效的分析方法。
附录无量纲参数
| $ \xi = \frac{x}{a},\eta = \frac{y}{b},\bar u = \frac{{ua}}{{{{\overline {AD} }^2}}},\bar v = \frac{{vb}}{{{{\overline {AD} }^2}}},\bar w = \frac{w}{{\overline {AD} }},{{\bar w}_0} = \frac{{{w_0}}}{{\overline {AD} }},\overline {AD} = \sqrt[4]{{{{\bar A}_{11}}{{\bar A}_{22}}{{\bar D}_{11}}{{\bar D}_{22}}}},\alpha = \frac{a}{b},\bar K = \frac{{Kb}}{{{{\bar D}_{22}}}},\\\bar \psi = \frac{\psi }{{\sqrt {{{\bar D}_{11}}{{\bar D}_{22}}} }},{\alpha _A} = \frac{a}{b}\sqrt[4]{{\frac{{{{\bar A}_{11}}}}{{{{\bar A}_{22}}}}}} $ |
| $ {\beta _A} = \frac{{2{{\bar A}_{12}} + {{\bar A}_{66}}}}{{2\sqrt {{{\bar A}_{11}}{{\bar A}_{22}}} }},{\gamma _A} = \frac{{{{\bar A}_{16}}}}{{\sqrt[4]{{\bar A_{11}^3{{\bar A}_{22}}}}}},{\delta _A} = \frac{{{{\bar A}_{26}}}}{{\sqrt[4]{{{{\bar A}_{11}}\bar A_{22}^3}}}},{\eta _A} = \frac{{{{\bar A}_{12}}}}{{\sqrt {{{\bar A}_{11}}{{\bar A}_{22}}} }},{\alpha _D} = \frac{a}{b}\sqrt[4]{{\frac{{{{\bar D}_{22}}}}{{{{\bar D}_{11}}}}}},{\beta _D} = \frac{{{{\bar D}_{12}} + 2{{\bar D}_{66}}}}{{\sqrt {{{\bar D}_{11}}{{\bar D}_{22}}} }},{\gamma _D} = \frac{{{{\bar D}_{16}}}}{{\sqrt[4]{{\bar D_{11}^3{{\bar D}_{22}}}}}} $ |
| $ {\delta _D} = \frac{{{{\bar D}_{26}}}}{{\sqrt[4]{{{{\bar D}_{11}}\bar D_{22}^3}}}},{\eta _D} = \frac{{{{\bar D}_{12}}}}{{\sqrt {{{\bar D}_{11}}{{\bar D}_{22}}} }},{\alpha _B}\frac{{{b^2}}}{{{a^2}}}\frac{{{{\bar B}_{21}}}}{{\overline {AD} }},{\beta _B} = \frac{{{{\bar B}_{11}} + {{\bar B}_{22}} - 2{{\bar B}_{66}}}}{{\overline {AD} }},{\gamma _B} = \frac{b}{a}\frac{{2{{\bar B}_{26}} - {{\bar B}_{61}}}}{{\overline {AD} }},{\delta _B} = \frac{a}{b}\frac{{2{{\bar B}_{16}} - {{\bar B}_{62}}}}{{\overline {AD} }},{\eta _B} = \frac{{{a^2}}}{{{b^2}}}\frac{{{{\bar B}_{12}}}}{{\overline {AD} }} $ |
| $ {\mu _B} = \frac{{{{\bar B}_{11}}}}{{\overline {AD} }},{\rho _B} = \frac{{{{\bar B}_{22}}}}{{\overline {AD} }},{\omega _B} = \frac{{{{\bar B}_{66}}}}{{\overline {AD} }},{\nu _B} = \frac{a}{b}\frac{{2{{\bar B}_{16}}}}{{\overline {AD} }},{\tau _B} = \frac{a}{b}\frac{{{{\bar B}_{62}}}}{{\overline {AD} }},{\theta _B} = \frac{b}{a}\frac{{{{\bar B}_{61}}}}{{\overline {AD} }},{\zeta _B} = \frac{b}{a}\frac{{2{{\bar B}_{26}}}}{{\overline {AD} }},{{\bar N}_x} = \frac{{{N_x}{b^2}}}{{{\pi ^2}\sqrt {{{\bar D}_{11}}{{\bar D}_{22}}} }},\\{{\bar N}_{xy}} = \frac{{{N_{xy}}{b^2}}}{{{\pi ^2}\sqrt {{{\bar D}_{11}}{{\bar D}_{22}}} }} $ |
特解ψh的表达式
| $ \begin{array}{*{20}{l}} {{{\bar \psi }_h} = W\left[ {{P_1}\sin {f_1} + {P_2}\cos {f_2} + {P_3}\cos {f_3} + {P_4}\sin {f_4} + {P_5}\sin {f_5} + \left( {W + 2{W_0}} \right)\left( {{P_6}\sin {f_6} + {P_7}\cos {f_7}} \right.} \right.} \\ {\;\;\;\;\;\;\;\left. {\left. { + {P_8}\sin {f_8} + {P_9}\cos {f_9} + \sum\limits_{i = 10}^{13} {{P_i}\sin {f_i}} + \sum\limits_{j = 14}^{16} {{P_i}\cos {f_i}} } \right)} \right]} \end{array} $ |
其中
| $ {f_1} = {\rm{ \mathit{ π} }}\left( {\xi - \phi \eta } \right),{f_{2,3}} = {\rm{ \mathit{ π} }}\left( {\xi - \left( {\phi \mp 1} \right)\eta } \right),{f_{4,5}} = {\rm{ \mathit{ π} }}\left( {\xi - \left( {\phi \mp 2} \right)\eta } \right),{f_6} = {\rm{ \mathit{ π} }}\eta ,{f_7} = 2{\rm{ \mathit{ π} }}\eta ,{f_8} = 3{\rm{ \mathit{ π} }}\eta ,{f_9} = 4{\rm{ \mathit{ π} }}\eta $ |
| $ {f_{10,11}} = {\rm{ \mathit{ π} }}\left( {2\xi - \left( {2\phi \mp 1} \right)\eta } \right),{f_{12,13}} = {\rm{ \mathit{ π} }}\left( {2\xi - \left( {2\phi \mp 3} \right)\eta } \right),{f_{14}} = 2{\rm{ \mathit{ π} }}\left( {\xi - \phi \eta } \right),{f_{15,16}} = 2{\rm{ \mathit{ π} }}\left( {\xi - \left( {\phi \mp 1} \right)\eta } \right) $ |
| $ {P_1} = \frac{{\alpha _A^2t\left( {{\eta _B}{\phi ^4} - {\delta _B}{\phi ^3} + {\beta _B}{\phi ^2} - {\gamma _B}\phi + {\alpha _B}} \right)}}{{2\left( {\alpha _A^2{\phi ^4} + 2\alpha _A^3{\gamma _A}{\phi ^3} + 2\alpha _A^2{\beta _A}{\phi ^2} + 2{\alpha _A}{\delta _A}\phi + 1} \right)}},{P_{2,3}} = \frac{{ \mp \alpha _A^2\left( {1 - t} \right)\left[ {{\eta _B}{{\left( {\phi \mp 1} \right)}^4} - {\delta _B}{{\left( {\phi \mp 1} \right)}^3} + {\beta _B}{{\left( {\phi \mp 1} \right)}^2} - {\gamma _B}\left( {\phi \mp 1} \right) + {\alpha _B}} \right]}}{{2\left[ {\alpha _A^4{{\left( {\phi \mp 1} \right)}^4} + 2\alpha _A^3{\gamma _A}{{\left( {\phi \mp 1} \right)}^3} + 2\alpha _A^2{\beta _A}{{\left( {\phi \mp 1} \right)}^2} + 2{\alpha _A}{\delta _A} + 1} \right]}} $ |
| $ {P_{4,5}} = \frac{{ - \alpha _A^2t\left[ {{\eta _B}{{\left( {\phi \mp 2} \right)}^4} - {\delta _B}{{\left( {\phi \mp 2} \right)}^3} + {\beta _B}{{\left( {\phi \mp 2} \right)}^2} - {\gamma _B}\left( {\phi \mp 2} \right) + {\alpha _B}} \right]}}{{4\left[ {\alpha _A^4{{\left( {\phi \mp 2} \right)}^4} + 2\alpha _A^3{\gamma _A}{{\left( {\phi \mp 2} \right)}^3} + 2\alpha _A^2{\beta _A}{{\left( {\phi \mp 2} \right)}^2} + 2{\alpha _A}{\delta _A}\left( {\phi \mp 2} \right) + 1} \right]}},{P_6} = - \frac{{3t\left( {1 - t} \right)}}{{8\alpha _A^2}},{P_7} = \frac{{\left( {1 - 2t + 2{t^2}} \right)}}{{32\alpha _A^2}},{P_8} = - \frac{1}{{27}}{P_6} $ |
| $ {P_9} = - \frac{{{t^2}}}{{512\alpha _A^2}},{P_{10,11}} = \frac{{ \pm 11\alpha _A^2t\left( {1 - t} \right)}}{{16\left[ {\alpha _A^2{{\left( {2\bar \phi + 1} \right)}^4} + 4\alpha _A^3{\gamma _A}{{\left( {2\bar \phi + 1} \right)}^3} + 8\alpha _A^2{\beta _A}{{\left( {2\bar \phi + 1} \right)}^2} + 16{\alpha _A}{\delta _A}\left( {2\bar \phi + 1} \right) + 16} \right]}} $ |
| $ {P_{12,13}} = \frac{{ \mp \alpha _A^2t\left( {1 - t} \right)}}{{16\left[ {\alpha _A^4{{\left( {2\phi \mp 3} \right)}^4} + 4\alpha _A^3{\gamma _A}{{\left( {2\phi \mp 3} \right)}^3} + 8\alpha _A^2{\beta _A}{{\left( {2\phi \mp 3} \right)}^2} + 16{\alpha _A}{\delta _A}\left( {2\phi \mp 3} \right) + 16} \right]}} $ |
| $ {P_{14}} = \frac{{\alpha _A^2\left( {1 - 2t + 2{t^2}} \right)}}{{32\left( {\alpha _A^4{\phi ^4} + 2\alpha _A^3{\gamma _A}{\phi ^3} + 2\alpha _A^2{\beta _A}{\phi ^2} + 2{\alpha _A}{\delta _A}\phi + 1} \right)}} $ |
| $ {P_{15,16}} = \frac{{ - \alpha _A^2{t^2}}}{{64\left[ {\alpha _A^4{{\left( {\phi \mp 1} \right)}^4} + 2\alpha _A^3{\gamma _A}{{\left( {\phi \mp 1} \right)}^3} + 2\alpha _A^2{\beta _A}{{\left( {\phi \mp 1} \right)}^2} + 2{\alpha _A}{\delta _A}\left( {\phi \mp 1} \right) + 1} \right]}} $ |
γ1~γ4的值
| $ {\gamma _1} = {S_9}{P_6} + {S_{10}}{P_7} + {S_{11}}{P_8} + {S_{12}}{P_9} + {S_{13}}\left( {{P_{10}} - {P_{11}}} \right) + {S_{14}}\left( {{P_{12}} - {P_{13}}} \right) + {S_{15}}{P_{14}} + {S_{16}}\left( {{P_{15}} + {P_{16}}} \right) $ |
| $ {\gamma _2} = {S_4}{P_1} - {S_5}{P_2} + {S_6}{P_3} - {S_7}{P_4} - {S_8}{P_5} $ |
| $ {\gamma _3} = \frac{{{S_1}}}{{\alpha _D^2}} - \frac{{4{\gamma _D}\phi {S_1}}}{{{\alpha _D}}} + 2{\beta _D}\left( {{S_1}{\phi ^2} + {S_2}} \right) - 4{\alpha _D}{\delta _D}\left( {{S_1}{\phi ^3} + 3{S_2}\phi } \right) + \alpha _D^2\left( {{S_1}{\phi ^4} + 6{S_2}{\phi ^2} + {S_3}} \right) $ |
| $ {\gamma _4} = - {S_1}\left( {\frac{{{{\bar N}_x}}}{{{{\bar N}_d}}} + \frac{{2{{\bar N}_{xy}}}}{{{{\bar N}_d}}}\phi \alpha } \right) $ |
其中
| $ {S_1} = \left( {\frac{{7{\rm{ \mathit{ π} }}}}{8} - \frac{8}{3}} \right){t^2} - \left( {{\rm{ \mathit{ π} }} - \frac{8}{3}} \right)t + \frac{{\rm{ \mathit{ π} }}}{2},{S_2} = \left( {{\rm{ \mathit{ π} }} - \frac{8}{3}} \right)\left( {t - 1} \right)t + \frac{{\rm{ \mathit{ π} }}}{2},{S_3} = \left( {\frac{{5{\rm{ \mathit{ π} }}}}{2} - \frac{{20}}{3}} \right){t^2} - \left( {{\rm{ \mathit{ π} }} - \frac{{20}}{3}} \right)t + \frac{{\rm{ \mathit{ π} }}}{2} $ |
| $ \begin{array}{*{20}{l}} {{S_4} = \left( {\frac{{{\rm{\pi }}t}}{2} - 2t + 2} \right)\left( {{\eta _B}{\phi ^4} - {\delta _B}{\phi ^3} + {\beta _B}{\phi ^2} - {\gamma _B}\phi + {\alpha _B}} \right),{S_{5,6}} = \left( { - \frac{{{\rm{\pi }}t}}{2} + \frac{{4t}}{3} + \frac{{\rm{\pi }}}{2}} \right)}\\ {\;\;\;\;\;\;\;\left[ {{\eta _B}{{\left( {\phi \mp 1} \right)}^4} - {\delta _B}{{\left( {\phi \mp 1} \right)}^3}} \right. + {\beta _B}{{\left( {\phi \mp 1} \right)}^2} - \left. {{\gamma _B}\left( {\phi \mp 1} \right) + {\alpha _B}} \right]} \end{array} $ |
| $ {S_{7,8}} = \left( {\frac{{{\rm{ \mathit{ π} }}t}}{4} - \frac{{2t}}{3} + \frac{2}{3}} \right)\left[ {{\eta _B}{{\left( {\phi \mp 2} \right)}^4} - {\delta _B}{{\left( {\phi \mp 2} \right)}^3} + {\beta _B}{{\left( {\phi \mp 2} \right)}^2} - {\gamma _B}\left( {\phi \mp 2} \right) + {\alpha _B}} \right],\\{S_9} = \left( { - \frac{{3{\rm{ \mathit{ π} }}}}{4} + \frac{{12}}{5}} \right){t^2} + \left( {\frac{{3{\rm{ \mathit{ π} }}}}{4} - \frac{8}{3}} \right)t + \frac{4}{3} $ |
| $ {S_{10}} = \left( { - 2{\rm{ \mathit{ π} }} + \frac{{32}}{5}} \right)\left( {t - 1} \right)t - {\rm{ \mathit{ π} }},{S_{11}} = \left( {\frac{{9{\rm{ \mathit{ π} }}}}{4} - \frac{{228}}{{35}}} \right){t^2} + \left( { - \frac{{9{\rm{ \mathit{ π} }}}}{4} + \frac{{24}}{5}} \right)t - \frac{{12}}{5},{S_{12}} = \left( {{\rm{ \mathit{ π} }} - \frac{{128}}{{35}}} \right){t^2} + \frac{{128}}{{35}}t $ |
| $ {S_{13}} = \left( {\frac{{11{\rm{ \mathit{ π} }}}}{8} - \frac{{14}}{3}} \right){t^2} + \left( { - \frac{{11{\rm{ \mathit{ π} }}}}{8} + 4} \right)t - 2,{S_{14}} = - \left( {\frac{{\rm{ \mathit{ π} }}}{8} + \frac{2}{{15}}} \right){t^2} + \left( {\frac{{\rm{ \mathit{ π} }}}{8} + \frac{4}{3}} \right)t - \frac{2}{3},\\{S_{15}} = \left( { - 2{\rm{ \mathit{ π} }} + \frac{{16}}{3}} \right)\left( {t - 1} \right)t - {\rm{ \mathit{ π} }} $ |
| $ {S_{16}} = \left( {\frac{{\rm{ \mathit{ π} }}}{2} - \frac{{32}}{{15}}} \right){t^2} + \frac{{32}}{{15}}t $ |
| [1] |
STEVENS K A, RICCI R, DAVIES G A O.
Buckling and postbuckling of composite structures[J]. Composite Structures, 1995, 26(3): 189–199.
|
| [2] |
HEATH B. Advanced structural efficiency (ADSTREFF): State of Art Report, BETC-1039[R]. [S. l. ]: CORDIS, 2000. |
| [3] |
LANZI L.
A numerical and experimental investigation on composite stiffened panels into post-buckling[J]. Thin-Walled Structures, 2004, 42(12): 1645–1664.
DOI:10.1016/j.tws.2004.06.001
|
| [4] |
LEKHNITSKⅡ S G.
Anisotropic plate[M]. New York: Gordon and Breach, 1968.
|
| [5] |
PEVZNER P, ABRAMOVICH H, WELLER T.
Calculation of the collapse load of an axially compressed laminated composite stringer-stiffened curved panel—An engineering approach[J]. Composite Structures, 2008, 83(4): 341–353.
DOI:10.1016/j.compstruct.2007.05.001
|
| [6] |
PAIK J K, THAYAMBALLI A K.
Buckling strength of steel plating with elastically restrained edges[J]. Thin-Walled Structures, 2000, 37(1): 27–55.
DOI:10.1016/S0263-8231(00)00009-4
|
| [7] |
BISAGNI C, VESCOVINI R.
Analytical formulation for local buckling and post-buckling analysis of stiffened laminated panels[J]. Thin-Walled Structures, 2009, 47(3): 318–334.
DOI:10.1016/j.tws.2008.07.006
|
| [8] |
BISAGNI C, VESCOVINI R.
Fast tool for buckling analysis and optimization of stiffened panels[J]. Journal of Aircraft, 2009, 46(6): 2041–2053.
DOI:10.2514/1.43396
|
| [9] |
QIAO P, DAVALOS J F, WANG J.
Local buckling of composite FRP shapes by discrete plate analysis[J]. Journal of Structural Engineering, 2001, 127(3): 245–255.
DOI:10.1061/(ASCE)0733-9445(2001)127:3(245)
|
| [10] |
QIAO P, SHAN L.
Explicit local buckling analysis and design of fiber-reinforced plastic composite structural shapes[J]. Composite Structures, 2005, 70(4): 468–483.
DOI:10.1016/j.compstruct.2004.09.005
|
| [11] |
QIAO P, SHAN L.
Explicit local buckling analysis of rotationally restrained composite plates under biaxial loading[J]. International Journal of Structural Stability, 2007, 7(3): 487–517.
DOI:10.1142/S021945540700240X
|
| [12] |
QIAO P, HUO X.
Explicit local buckling analysis of rotationally restrained composite plates under uniaxial compression[J]. Engineering Structures, 2008, 30(1): 126–140.
DOI:10.1016/j.engstruct.2007.02.023
|
| [13] |
QIAO P, HUO X.
Explicit local buckling analysis of rotationally-restrained orthotropic plates under uniform shear[J]. Composite Structures, 2011, 93(11): 2785–2794.
DOI:10.1016/j.compstruct.2011.05.026
|
| [14] |
MITTELSTEDT C.
Stability behavior of arbitrarily laminated composite plates with free and elastically restrained unloaded edges[J]. International Journal of Mechanical Sciences, 2007, 49(7): 819–833.
DOI:10.1016/j.ijmecsci.2006.11.011
|
| [15] |
MITTELSTEDT C, ERDMANN H, SCHROEDER K.
Postbuckling of imperfect rectangular composite plates under inplane shear closed-form approximate solutions[J]. Archive of Applied Mechanics, 2011, 81(10): 1409–1426.
DOI:10.1007/s00419-010-0491-y
|
| [16] |
BEERHORST M, SEIBEL M, MITTELSTEDT C.
Fast analytical method describing the postbuckling behavior of long, symmetric, balanced laminated composite plates under biaxial compression and shear[J]. Composite Structures, 2012, 94(6): 2001–2009.
DOI:10.1016/j.compstruct.2012.01.026
|
| [17] |
BYKLUM E, AMDAHL J.
A simplified method for elastic large deflection analysis of plates and stiffened panels due to local buckling[J]. Thin-Walled Structures, 2002, 40(11): 925–953.
DOI:10.1016/S0263-8231(02)00042-3
|
| [18] |
BRUBAK L, HELLESLAND J.
Semi-analytical postbuckling analysis of stiffened imperfect plates with a free or stiffened edge[J]. Computers & Structures, 2011, 89(17): 1574–1585.
|
| [19] |
DIACONU C G, WEAVER P M.
Postbuckling of long unsymmetrically laminated composite plates under axial compression[J]. International Journal of Solids and Structures, 2006, 43(22/23): 6978–6997.
|
| [20] |
NIE Kun, LIU Yi, DAI Ying.
Closed-form solution for the postbuckling behavior of long unsymmetrical rotationally-restrained laminated composite plates under inplane shear[J]. Composite Structures, 2015, 122: 31–40.
DOI:10.1016/j.compstruct.2014.11.036
|
| [21] |
WHITNEY J M.
Structural analysis of laminated anisotropic plates[M]. USA: Technomic Pub, 1987.
|
| [22] |
TIMOSHENKO S P, GERE J M.
Theory of elastic stability[M]. New York: McGraw-Hill, 1961.
|
| [23] |
CHIA C Y.
Nonlinear analysis of plates[M]. New York: McGraw-Hill, 1980.
|
 2018, Vol. 50
2018, Vol. 50


