2. 上海宇航系统工程研究所,上海,201108
2. Shanghai Institute of Aerospace System Engineering, Shanghai, 201108, China
液体运载火箭推进系统主要由火箭发动机、低温贮箱和增压输送系统组成,推进系统为飞行器贮存和提供推进剂,推进剂贮箱作为液体运载火箭必备的燃料储存和供给设备,在箭体升空过程中向发动机连续提供过冷低温液体燃料[1]。低温推进剂储罐排出液体燃料过程中,储罐内部需要有一定的压力,用自生增压方式将低温推进剂由储槽向发动机供液,是目前普遍采用的一种加压方式。而在推进剂排出之前,常有一个预增压过程,以便保证推进剂能够顺利流入发动机。在这一过程中,储罐内液体推进剂受气枕内高温气体以及壁面漏热影响,会有部分液体气化,气液界面两侧都会产生一定程度的温度分层,研究预增压过程低温推进剂蒸发与沸腾现象,确定推进剂温度变化,掌握增压之前液体推进剂在储箱内部物理特性,这对于自身增压过程推进剂的稳定输送以及发动机的安全工作非常重要。
数值仿真是目前研究低温储箱内部流场分布的一种有效途径和重要手段,并且能为储箱系统的结构设计提供重要的理论基础和技术指导。对贮箱内低温推进剂的传热传质过程仿真主要采用集总参数法和CFD方法。由于均相集总参数模型[2-4]在计算箱体增压过程中做了过多的简化与假设,该模型由于因素考虑不全面,限定性假设较粗糙,在预测箱体压增及温度场时往往与实际情况偏离较大。已有的CFD模型[5-7]在一定范围内能够较好预测箱体增压过程。
现有文献中,储罐自生增压过程仿真研究大多局限于对二维定温或定热流边界的过程,且对低温推进剂的蒸发特性分析较少[8]。而实际操作中,储箱在加速上升时先经过高温气体预增压过程后,推进剂才从储箱内部逐渐流出,储箱加速上升过程随着高度的升高,外界大气温逐渐降低,由于其飞行速度在不断增加,当Ma大于一定值后外界空气通过气动加热与储箱近壁面进行剧烈地换热,因此实际过程与多数文献模拟工况存在一定的差异。本文在考虑气动加热的影响下,用变热流边界条件,采用三维模型数值模拟液氧储箱预增压上升阶段箱内物理场变化特性,对液氧相变特征以及温度分层发展规律进行了分析。
1 模型的建立 1.1 物理模型以某一低温液氧贮箱为例,对其在加速上升中预增压过程进行模拟。本文计算选取的储箱结构如图 1所示,直径为2.25 m的液氧贮箱由圆柱筒体及上下两个椭圆形封头组成,上下底封头高800 mm,贮箱顶部开有氧排气阀、散流器,散流器壁面开有孔,预增压过程高温氧气通过散流器喷射进入气枕空间,以避免对气液相界面造成的冲击作用,增压管路内径50 mm。

|
图 1 贮箱结构示意图 Figure 1 Schematic of tank |
在进行储箱预增压过程模拟计算前,储箱已在地面停放一段时间,由于壁面漏热作用,储箱内液氧已经形成一定程度的温度分层,从气液界面至储箱底部液氧温度从89.51 K变化至89 K,气枕区平均温度为95 K,预增压过程中增压气体流量0.18 kg/s、密度5.3 kg/m3,增压气体平均温度360 K。
贮箱壁面为铝合金材料,厚4.0 mm,金属壁密度取2 800 kg/m3,导热系数159 W/(m·K),比热容830 J/(kg·K),贮箱外包裹不同厚度的绝热材料,考虑到贮箱顶部非对称结构,以及储箱经历一个非稳态过程后逐步趋稳定,因此计算采用三维非稳态模型,根据贮箱结构特点,对其网格进行分区划分并且局部加密,近壁面处采用了边界层网格划分形式,网格数量为627 210个。
在FLUENT软件平台中采用三维单精度求解器对储箱内部流场进行数值模拟,采用VOF模型来捕捉气液界面的变化,界面的质量、动量以及能量平衡均通过加载到离散项中的源项来实现。从文献[9]中多次模拟与实验相验证知Realizable形式的k~ε湍流模型的预测性能大大高于Standard模型,本次模拟采用Realizable形式的k~ε湍流模型,选用PISO的压力与速度耦合形式,体积分数项采用Geo-Reconstruct的格式。
在计算过程中,由于储箱受到漏热及高温增压气体共同作用,液氧温度不断发生变化,设液氧密度随着温度升高而减小,氧气采用理想气体模型。
1.2 相变模型在预增压过程,高温增压气体不断进入气枕区与液氧进行传热作用,假设气液界面处于准稳态过程,界面温度为气枕压力对应下的饱和温度,计算过程中通过对比网格温度与相对大小作为气液界面是否发生相变的判据。针对多相流的气液界面的相变,Lee[10]提出的蒸发冷凝模型也常被采用,但该模型适用于Mixture和Eulerian多相流模型,不适合本文采取VOF描述的多相流。相界面处的相变蒸发和冷凝过程,为储箱内纯质之间的两相过程,针对储箱内的相变模型参考文献[11]提出的相界面模型描述气液界面处相变情况。
| $m = \left\{ \begin{array}{l}\frac{{2{f_e}}}{{2-{f_e}}}\sqrt {\frac{M}{{2\pi R{T_{{\rm{sat}}}}}}} \frac{{\Delta _l^g{H_m}{P_g}}}{{R{T_g}}}\frac{{T-{T_{{\rm{sat}}}}}}{{{T_{{\rm{sat}}}}}}\left| {\nabla F} \right|\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Evaporation}}\\\frac{{2{f_e}}}{{2-{f_e}}}\sqrt {\frac{M}{{2\pi R{T_{{\rm{sat}}}}}}} \frac{{\Delta _g^l{H_m}{P_g}}}{{R{T_g}}}\frac{{{T_{{\rm{sat}}}} - T}}{{{T_{{\rm{sat}}}}}}\left| {\nabla F} \right|\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Condensation}}\end{array} \right.$ | (1) |
储箱在加速上升过程中,由于其飞行速度不断增加,当Ma>1时考虑外界大气对储箱的气动加热,此时储箱漏热量大,近壁面处液氧过热度较大,故在模拟计算中同时考虑近壁面处液氧沸腾现象,参考文献[11]中相变模型描述近壁面处液氧沸腾现象。
| $m = \frac{{2{f_e}}}{{2-{f_e}}}\sqrt {\frac{M}{{2\pi R{T_{{\rm{sat}}}}}}} \frac{{\Delta _l^g{H_m}{P_g}}}{{R{T_g}}}\frac{{T-{T_{{\rm{sat}}}}}}{{{T_{{\rm{sat}}}}}}\frac{{Na \cdot {A_{ns}}}}{{\Delta l}}$ | (2) |
式中
| $\begin{array}{l}Na = 0.34 \times {10^4}\left( {1-\cos \theta } \right)\Delta T_w^2\\\Delta {T_{{\rm{ONB}}}} < \Delta {T_W} < 15{\rm{K}}\end{array}$ | (3) |
式中:fe为蒸发系数;M相对分子质量;ΔlgHm为汽化潜热;P压力;T温度;▽F网格梯度;Ans为汽化核心的表面积,Ans=πr2,Δl为网格的尺寸;θ接触角;下标g表示气体,l表示液体。
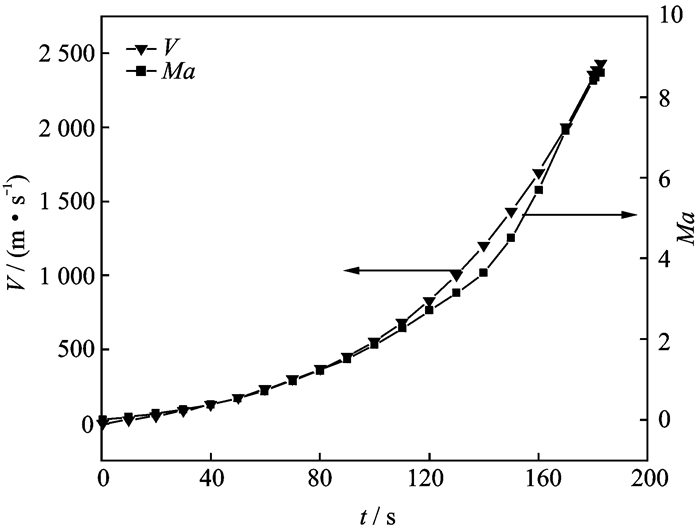
2 边界条件的计算假定储箱上封头为288 K定温边界,下封头考虑外界风速3 m/s,环境温度283 K。筒段大气层飞行中,马赫数(Ma)大于1情况下需要考虑气动加热,其余时间根据流速按照对流换热计。储箱飞行期间速度V及Ma数随时间变化规律如图 2所示。
|
图 2 储箱飞行期间速度V及Ma数随时间变化规律 Figure 2 Variation of the tank velocity and Ma with time |
前72 s马赫数小于1,此时根据强制对流考虑筒段换热,来流的大气参数与实际飞行高度有关,这一时段内升空高度在91 km以下,参考文献[12]知此时大气参数随高度的变化关系式为
| $\left\{ \begin{array}{l}H = \frac{Z}{{1 + \frac{{\rm Z}}{{{R_0}}}}}\\T = 288.15 \times \left( {1-\frac{H}{{44.330\;8}}} \right)\\\frac{\rho }{{{\rho _{{\rm{地面}}}}}} = {\left( {1-\frac{H}{{44.330\;8}}} \right)^{4.255\;9}}\\\frac{P}{{{P_{{\rm{地面}}}}}} = {\left( {1-\frac{H}{{44.330\;8}}} \right)^{5.255\;9}}\end{array} \right.\;\;\;\;0 \le Z \le 91$ | (4) |
当Ma>1时考虑气动加热的影响,气动加热[13]是指在大气层内高速飞行时,飞行器表面附近的边界层内的空气有非常大的速度梯度,由于受黏性或剪切力的作用,将动能转化成热能,从而引起附面层和箭体表面温度的迅速升高。
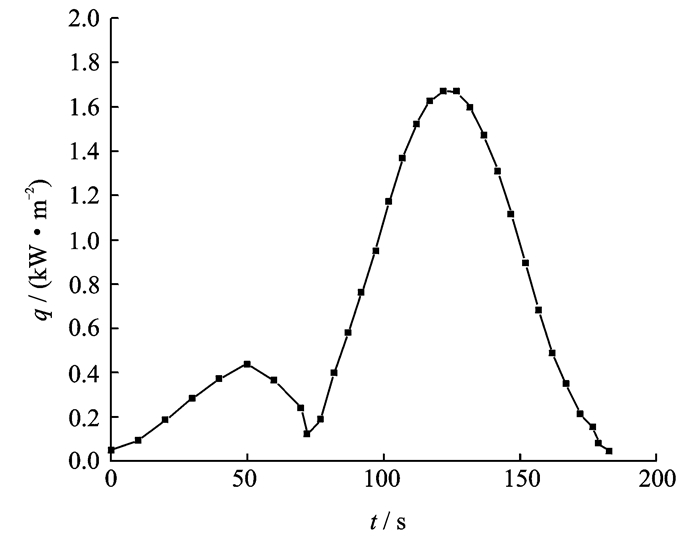
筒段整个飞行期间筒段外界热流密度随时间变化曲线如图 3所示。
|
图 3 储箱飞行期间筒段外界热流密度随时间变化规律 Figure 3 Heat flux of the outside cylinder wall with 17:13:13 |
通过计算将气动加热期间外界漏热量作为第二类边界条件,作为变热流密度条件加载在储箱筒段。
3 计算结果分析 3.1 液氧相变速率分析液氧储箱在进行预增压上升时,在大气层内,当考虑气动加热的影响时,近壁面处液氧与外界环境进行大量的换热,近壁面处液氧温度高于其压力对应的饱和温度,在储箱上升过程中近壁面处液氧会发生沸腾。由于高温增压气体持续进入气枕区,使得气枕区温度逐渐升高,气枕区与液氧界面进行传热作用,使得气液界面处液氧不断蒸发。故在模拟中同时考虑近壁面处液氧沸腾现象以及气液界面处液氧蒸发作用,现分别对这二种相变速率进行分析。
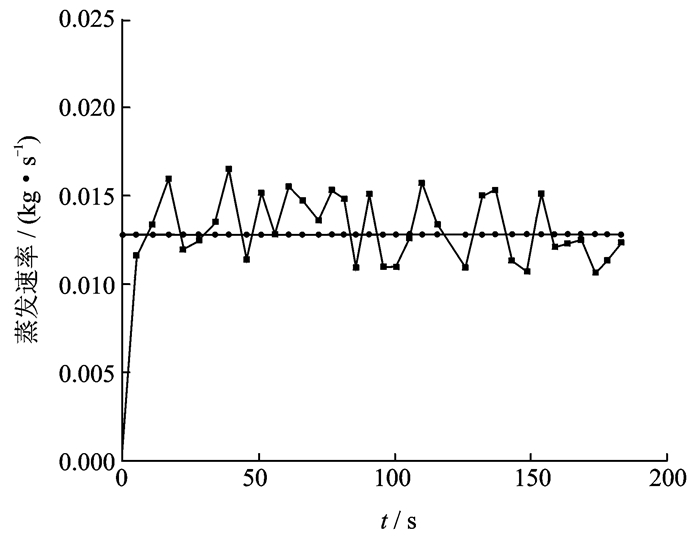
图 4为气液相界面处液氧蒸发速率随时间变化图,当360 K的高温增压气体进入储箱内部,气枕区温度压力不断升高,气枕区同时与气液界面进行导热和对流作用,使得气液界面发生相变作用。高温增压气体的进入,使得气枕区压力不断升高,气液界面处气枕区压力对应的饱和温度即为液氧发生蒸发的最低温度,气枕区压力升高使得液氧蒸发饱和温度升高,液氧蒸发速率随之下降,吸热量减少,气枕区不断传递给气液界面热量,使之蒸发速率又相应升高,故储箱上升期间气液界面处蒸发速率不是常数,而是呈现上下震荡趋势,在183 s预增压期间气液界面处蒸发速率平均值为0.012 6 kg/s。
|
图 4 气液界面处液氧蒸发速率随时间变化图 Figure 4 Evaporation rate of liquid oxygen at gas-liquid interface with time |
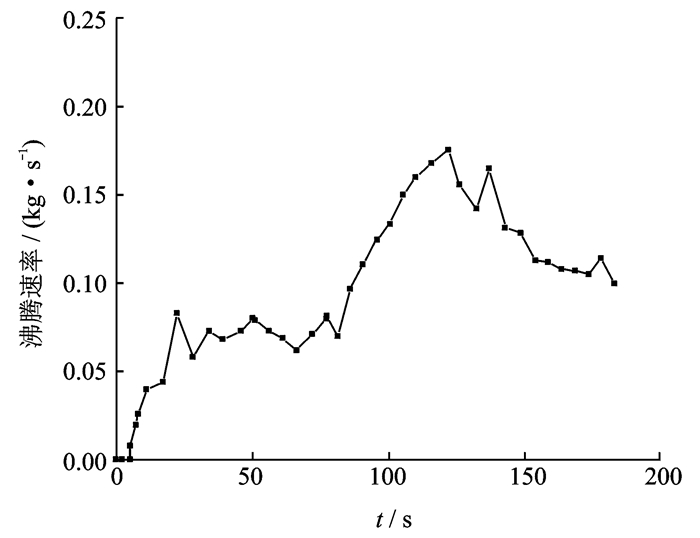
储箱在加速上升过程中,大气层飞行中,初期由于其速度较小,Ma较小,此时储箱与外界空气进行对流换热,当Ma>1时,考虑气动加热的影响,此时储箱与外界的换热更加剧烈,故储箱在大气层飞行期间考虑储箱近壁面处液氧沸腾。大气层飞行期间,近壁面处液氧沸腾相变速率随时间的变化曲线图如图 5所示。
|
图 5 近壁面处液氧沸腾相变速率随时间变化曲线图 Figure 5 Boiling rate of liquid oxygen near wall with 17:14:17 |
储箱在飞行前期,速度不高,外界大气与储箱对流换热系数较小,储箱漏热量较小而不足以使箱内近壁面处液氧沸腾,可看到前5 s近壁面处液氧沸腾速率近似为0,随着飞行的持续,筒段与外界进行的换热不断增强,近壁面处液氧温度逐渐升高,5 s之后出现沸腾迹象,前72 s储箱通过强制对流与外界环境进行对流换热,从图 3外界热流密度随着飞行时间先增加后降低,液氧沸腾相变速率也呈现同样变化趋势,0~72 s储箱与外界大气进行强制对流换热过程,近壁面处液氧沸腾速率平均值为0.045 kg/s。72 s之后,由于此时储箱与箱外气流相对速度已经很高,Ma>1,气动加热效果不可忽略,气动加热量随着飞行时间的增长呈现先增大后减小趋势,从图 5可看出液氧沸腾速率同时呈现出该趋势,气动加热期间沸腾速率最大值为0.175 kg/s,整个气动加热期间液氧沸腾速率平均值为0.12 kg/s。
从图 5可以看出,近壁面处液氧沸腾速率整体变化趋势基本与外界漏热量相一致。整个预增压过程沸腾速率平均值为0.086 kg/s,而气液界面处液氧蒸发速率平均值0.012 6 kg/s,因此储箱在预增压上升期间,储箱内液氧相变速率主要受外界漏热的影响。
3.2 温度分层的分析当储箱进行预增压上升时,随着高温气体的持续进入,气枕区压力不断升高,其对应饱和温度随着升高,气液界面处液氧始终存在蒸发现象,即相界面处液氧温度随着增压气体的进入不断升高,相界面处温度首先升高并随着时间逐渐影响下部液体。
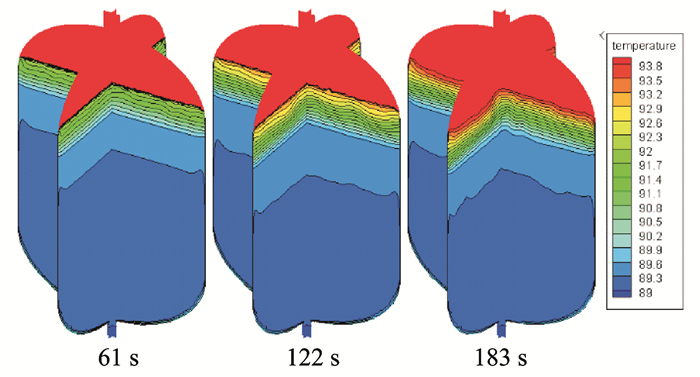
储箱上升期间,不同时刻下储箱内液氧温度云图如图 6所示,其中红色区域为气枕区,其温度高于93.8 K,在此只关注液氧区温度分区,故不对气枕区温度进行讨论分析。由于增压气体通过向四周喷射进入气枕区间,故对气液界面扰动较小,从图 6可看出,储箱内液氧主体出现了平稳的温度分层,相界面处温度较高,温度分层程度明显,离相界面越远,液氧温度梯度越小。随着预增压时间的增长,近相界面处温度分层层数不断增多。
|
图 6 预增压结束时液氧温度分层发展图 Figure 6 Development of the liquid oxygen temperature stratification after the pre-pressurization |
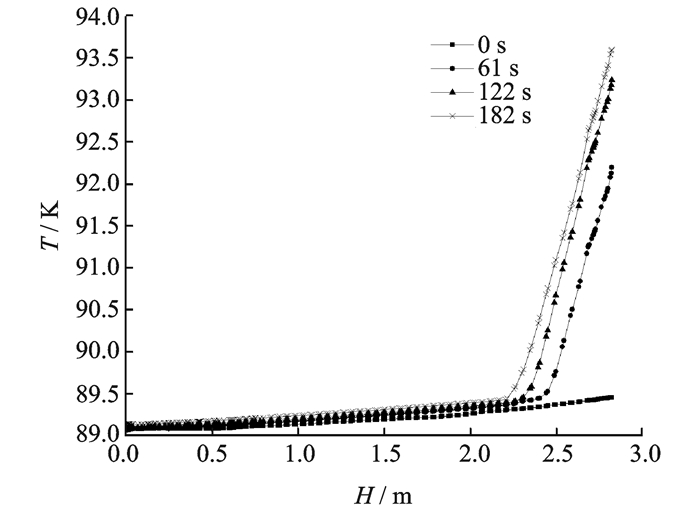
储箱预增压上升期间液氧主体在轴线处温度变化趋势如图 7所示,其中高度坐标原点建在储箱底部。
|
图 7 不同时刻液氧在轴线处温度值 Figure 7 Temperature of liquid oxygen at the z-axis for different periods |
储箱在在地面停放一段时间后,再进行增压,随后上升,停放期间由于壁面的漏热,液氧主体温度出现不均匀趋势,即0 s液氧主体已出现温度分层现象。
增压气体温度为360 K,进入储箱后,将不可避免与低温液氧进行换热,另外由于筒壁漏热也会导致液氧被加热,故液氧温度在不断上升,相界面处温度首先升高并随着时间的持续影响下部液体,故距相界面越近液氧温度越高。随着预增压时间延长,热流不断影响下层液氧,液氧主体温度不断升高,储箱内轴向温度分层愈加明显。
储箱在预增压过程中,由于气枕区压力不断升高,其对应饱和温度不断升高,相界面处液氧温度随之升高,相界面处液氧温度在预增压期间随时间的变化规律如图 8所示。

|
图 8 相界面温度随时间变化规律 Figure 8 Temperature at gas-liquid interface varies with time |
由图 8可看出,随着增压气体的流入,相界面处液氧温度随之不断升高,初始阶段,由于液氧主体温度较低,高温气体进入后,与气液界面进行剧烈的换热,使得相界面处温度迅速升高至一定数值后再缓慢增加,预增压后期,相界面处温度几乎呈线性增加,其温升速率近似为0.017 K/s,整个预增压183 s过程,相界面处温度从89.51 K上升至93.61 K,温升速率为0.022 K/s。
4 结论本文在考虑气动加热的影响下,同时考虑储箱气液界面处液氧蒸发以及近壁面处液氧沸腾现象,采用三维模型数值模拟直径为2.25 m,初始液位高度2.962 m的液氧储箱在前底、筒段、后底边界条件各不相同下,预增压上升过程箱内液氧相变速率和温度分布随时间变化规律,根据模拟结果可以看出:
(1) 储箱上升期间气液界面处蒸发速率并不是常数,而是呈现一定振荡形态,整个183 s预增压过程气液界面处平均蒸发速率平均值为0.012 6 kg/s。
(2) 近壁面处液氧沸腾速率随时间总的变化趋势与外界漏热量变化规律相一致,整个飞行期间液氧沸腾速率平均值为0.086 kg/s,与气液界面处液氧蒸发速率相比可知,储箱在预增压上升期间,相变速率主要受外界漏热的控制。
(3) 随着高温增压气体的进入,相界面处温度首先升高并随着时间的持续向下扩散,距相界面越近液氧温度越高。随着预增压时间的增长,热量不断向下传递,液氧主体温度不断升高,储箱内轴向温度分层愈加明显。
(4) 随着增压气体的不断流入,相界面处液氧温度随之不断升高,整个预增压过程,相界面处液氧温度从89.51 K上升至93.61 K,温升速率为0.022 K/s。
| [1] |
廖少英.
液体火箭推进增压输送系统[M]. 北京: 国防工业出版社, 2008.
LIAO Shaoying. The system of propulsion the pressurization with liquid rocket[M]. Beijing: National Defence of Industry Press, 2008. |
| [2] |
王赞社, 顾兆林, 冯诗愚, 等.
低温推进剂贮箱增压过程的传热传质数学模拟[J]. 低温工程, 2008(6): 28–31.
WANG Zanshe, GU Zhaolin, FENG Shiyu, et al. Simulation of heat transfer and mass transfer in cryogenic propellant tank pressurization process[J]. Cryogenics, 2008(6): 28–31. |
| [3] | PANZARELLA C H, KASSEMI M. On the validity of purely thermodynamic descriptions of two-phase cryogenic fluid storage[J]. Journal of Fluid Mechanics, 2003, 484: 41–68. DOI:10.1017/S0022112003004002 |
| [4] | ZILLIAC G, KARABEYOGLU M A. Modeling of propellant tank pressurization[J]. AIAA Paper, 2005, 3549: 10–13. |
| [5] |
尚存存, 耑锐, 王文.
液氧贮箱增压过程中气枕空间温度场的数值模拟[J]. 低温工程, 2011(6): 47–51.
SHANG Cuncun, ZHUAN Rui, WANG Wen. Numerical simulation of ullage temperature field in pressurization process of liquid oxygen tank[J]. Cryogenics, 2011(6): 47–51. |
| [6] | PANZARELLA C H, KASSEMI M. Self-pressurization of large spherical cryogenic tanks in space[J]. Journal of Spacecraft and Rockets, 2005, 42(2): 299–308. DOI:10.2514/1.4571 |
| [7] | MATTICK S J, LEE C P, HOSANGADI A, et al. Progress in modeling pressurization in propellant tanks[C]//Joint Propulsion Conference & Exhibit. Nashville:[s.n.], 2010.http://www.researchgate.net/publication/267566348_Progress_in_Modeling_Pressurization_in_Propellant_Tanks |
| [8] |
程向华, 厉彦忠, 陈二锋, 等.
新型运载火箭射前预冷液氧贮箱热分层的数值研究[J]. 西安交通大学学报, 2008, 42(9): 1132–1136.
DOI:10.7652/xjtuxb200809015 CHENG Xianghua, LI Yanzhong, CHEN Erfeng, et al. Numerical investigation of thermal stratification in liquid oxygen tank for new-style launch vehicle during ground precooling[J]. Journal of Xi′an Jiao Tong University, 2008, 42(9): 1132–1136. DOI:10.7652/xjtuxb200809015 |
| [9] |
刘展, 厉彦忠, 王磊, 等.
在轨运行低温液氢箱体蒸发量计算与增压过程研究[J]. 西安交通大学学报, 2015, 49(2): 135–140.
DOI:10.7652/xjtuxb201502023 LIU Zhan, LI Yanzhong, WANG Lei, et al. Numerical investigation of thermal stratification in liquid oxygen tank for new-style launch vehicle during ground precooling[J]. Journal of Xi′an Jiao Tong University, 2015, 49(2): 135–140. DOI:10.7652/xjtuxb201502023 |
| [10] | LEE W H. A pressure iteration scheme for two-phase flow modeling[J]. Multiphase Transport Fundamentals, Reactor Safety, Applications, 1980, 1: 407–431. |
| [11] | KUANG Y W, WANG W, ZHUAN R, et al. Simulation of boiling flow in evaporator of separate type heat pipe with low heat flux[J]. Annals of Nuclear Energy, 2015, 75: 158–167. DOI:10.1016/j.anucene.2014.08.008 |
| [12] |
杨炳尉.
标准大气参数的公式表示[J]. 宇航学报, 1983, 4(1): 86–89.
YANG Bingwei. The formula of standard atmosphere parameter[J]. Journal of Astronautics, 1983, 4(1): 86–89. |
| [13] |
吴丹, 许常悦, 孙建红.
来流马赫数对座舱气动加热影响的数值模拟[J]. 南京航空航天大学学报, 2011, 43(4): 464–469.
WU Dan, XU Changyue, SUN Jianhong. Numerical simulation about effect of mach number on aerodynamic heating around cabin[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 43(4): 464–469. |
 2017, Vol. 49
2017, Vol. 49


