常规单旋翼带尾桨构型的直升机由于存在前行桨叶激波和后行桨叶失速等限制因素难以实现高速飞行。而共轴式刚性双旋翼直升机通过上下两副旋翼共轴反向旋转,相互抵消反扭矩,省去尾桨从而提高了功率利用效率。该构型直升机通过对后行桨叶进行卸载,并充分发挥前行桨叶的升力潜能,突破了常规构型大速度前飞时旋翼的气动约束,从而具备高速飞行的能力。悬停是旋翼类飞行器一个非常重要的工作状态,研究悬停状态共轴刚性旋翼气动特性是认识该构型高速直升机旋翼气动布局的第一步。
国内外许多学者对共轴双旋翼悬停状态进行了相关的试验和计算研究。文献[1]中进行了共轴旋翼悬停状态不同转速下的性能试验,结果表明适当增加旋翼转速可以提高共轴旋翼的悬停性能。唐正飞等人[2-3]用三维激光多普勒测速仪对共轴双旋翼悬停状态下的流场进行了试验测量,得到了流场诱导速度试验数据。文献[4~7]均建立了适合于悬停状态的共轴双旋翼动量/叶素理论,并在此基础上研究了共轴旋翼悬停状态气动特性,结果表明上下旋翼的气动力特征存在明显差异。文献[8]中发展了适于共轴双旋翼悬停流场模拟的CFD方法,开展了对桨-涡干扰和涡-涡干扰的研究,初步揭示了双旋翼的流场干扰机理。童自力等[9-10]则在N-S方程中用动量源项取代桨叶作用,快速地预估共轴双旋翼的气动特性。许和勇等[11-12]基于非结构滑移网格技术、通过求解Euler方程对悬停状态共轴旋翼的气动特性进行了数值模拟。叶靓等[13]发展了基于自适应技术的非结构嵌套网格方法,对共轴双旋翼桨尖涡轨迹进行了捕捉。朱正等[14]建立了悬停状态共轴刚性旋翼流场模拟的高精度CFD方法,对流场干扰机理和气动特性进行了研究。
上述研究工作为揭示共轴旋翼气动特性的变化规律及流动机理提供了结果和基础,但是关于气动外形参数对共轴刚性旋翼气动特性的影响研究较少,以常规单旋翼桨叶外形参数影响为主[15-18]。目前仅有Jun[6]和Rand[7]等开展了悬停状态共轴旋翼的气动布局参数分析工作,但是这些工作均是基于动量/叶素理论而展开的,很难准确考虑共轴旋翼悬停状态复杂的非定常干扰现象对气动特性的影响。鉴于此,为了解桨叶外形对悬停状态共轴旋翼的影响规律,本文基于高精度的CFD方法进行了悬停状态下的共轴刚性双旋翼流场气动特性计算分析,着重开展了多种桨叶平面外形参数对旋翼气动性能的影响分析,获得了一些对于提高共轴刚性旋翼直升机悬停气动性能有意义的结论。
1 数值计算方法与算例验证 1.1 非定常流场模拟方法悬停状态时,常规单旋翼旋转过程中桨叶气动特性随时间变化较小,流场可视为准定常。而共轴刚性双旋翼由两副共轴、反向旋转的旋翼构成,旋转过程中上下旋翼桨叶的相对位置不停变化,这使得共轴旋翼流场即使是在悬停状态也呈现明显的非定常特征。为此,不能将悬停状态的共轴旋翼流场视为准定常流场,需要发展相应的非定常流场求解方法。
鉴于此,为了求解共轴刚性双旋翼的非定常流场,将计算坐标轴定义于惯性坐标系下,建立以绝对物理量为参数的守恒积分形式的可压非定常RANS方程,方程如下
| $ \frac{\partial }{{\partial t}}\iiint\limits_V \boldsymbol{W}{\rm{d}}V + \iint\limits_S {\left( {{\boldsymbol{F}_c} - {\boldsymbol{F}_v}} \right)}{\rm{d}}S = 0 $ | (1) |
式中:守恒变量W、对流通量Fc和黏性通量Fv分别为
| $ \boldsymbol{ W} = \left[ \begin{gathered} \rho \\ \rho u \\ \rho c \\ \rho w \\ \rho E \\ \end{gathered} \right],\boldsymbol{F}_c = \left[ \begin{gathered} \rho \left( {\boldsymbol{V} - {\boldsymbol{V}_\omega }} \right) \cdot \boldsymbol{n} \\ \rho u\left( {\boldsymbol{V} - {\boldsymbol{V}_\omega }} \right) \cdot \boldsymbol{n} + {n_x}p \\ \rho v\left( {\boldsymbol{V} - {\boldsymbol{V}_\omega }} \right) \cdot \boldsymbol{n} + {n_y}p \\ \rho w\left( {\boldsymbol{V} - {\boldsymbol{V}_\omega }} \right) \cdot \boldsymbol{n} + {n_z}p \\ \rho H\left( {\boldsymbol{V} - {\boldsymbol{V}_\omega }} \right) \cdot \boldsymbol{n} + {\boldsymbol{V}_\omega } \cdot \boldsymbol{n}p \\ \end{gathered} \right], \\ {\boldsymbol{F}_v} = \left[ \begin{gathered} 0 \\ {n_x}{\tau _{xx}} + {n_y}{\tau _{xy}} + {n_z}{\tau _{xz}} \\ {n_x}{\tau _{yx}} + {n_y}{\tau _{yy}} + {n_z}{\tau _{yz}} \\ {n_x}{\tau _{zx}} + {n_y}{\tau _{zy}} + {n_z}{\tau _{zz}} \\ {n_x}{\mathit{\Theta} _{x}} + {n_y}{\mathit{\Theta} _{y}} + {n_z}{\mathit{\Theta} _z} \\ \end{gathered} \right] \\ $ | (2) |
式中:V为控制体体积;S为控制体表面积;Vω=(ue, ve, we)为牵连速度,即网格运动速度;V=(u, v, w)为气流速度;n=(nx, ny, nz)为控制体表面单位法矢;ρ,p,E和H分别为密度、压力、总能和总焓;τ(·)为黏性应力张量项分量;Θ(·)为与黏性应力和热传导作用相关的项。
黏性应力τ的各分量定义为
| $ \begin{gathered} \left\{ \begin{gathered} {\tau _{xx}} = 2\mu {u_x} - \left( {2/3} \right)\mu \nabla \cdot \boldsymbol{V},{\tau _{xy}} = \mu \left( {{u_y} + {v_x}} \right) \\ {\tau _{yy}} = 2\mu {u_y} - \left( {2/3} \right)\mu \nabla \cdot \boldsymbol{V},{\tau _{yz}} = \mu \left( {{v_z} + {w_y}} \right) \\ {\tau _{zz}} = 2\mu {u_z} - \left( {2/3} \right)\mu \nabla \cdot \boldsymbol{V},{\tau _{xz}} = \mu \left( {{u_z} + {w_x}} \right) \\ \end{gathered} \right. \\ \left\{ \begin{gathered} {\mathit{\Theta} _x} = u{\tau _{xx}} + v{\tau _{xy}} + w{\tau _{xz}} + \kappa \frac{{\partial T}}{{\partial x}} \\ {\mathit{\Theta} _y} = u{\tau _{yx}} + v{\tau _{yy}} + w{\tau _{yz}} + \kappa \frac{{\partial T}}{{\partial y}} \\ {\mathit{\Theta} _z} = u{\tau _{zx}} + v{\tau _{zy}} + w{\tau _{zz}} + \kappa \frac{{\partial T}}{{\partial z}} \\ \end{gathered} \right. \\ \end{gathered} $ | (3) |
式中:μ, κ, T分别为黏性系数、热传导系数和绝对温度;ux,uy,uz,vx,vy,vz,wx,wy和wz的下标表示对该方向的偏导数。
对于共轴刚性旋翼悬停流场的数值模拟,RANS方程能够较好地体现湍流对流体的整体影响。空间离散格式采用精度高、耗散低的Roe-MUSCL[19-20],在伪时间的推进中采用计算效率高、收敛性好的隐式LU-SGS算法[21],湍流计算模型为Spalart-Allmaras模型。共轴旋翼系统中操纵量配平方法采用Newton-Rhapson迭代法。
1.2 运动嵌套网格方法共轴旋翼嵌套网格包含围绕各片桨叶的网格和包围桨叶网格的背景网格,二者之间存在着流场信息传递。本文中不同时刻上下旋翼桨叶之间的相对位置关系也不同,设置桨叶网格外边界时应当避免旋翼旋转过程中桨叶网格间出现交叉问题(桨叶网格不能穿过桨叶实体),从而规避对流场信息交换产生的不利影响。
图 1给出了悬停状态共轴双旋翼运动嵌套网格示意图,此时上下旋翼桨叶恰好平行,即是上下旋翼桨叶网格位置关系最为敏感的时刻。从图中可见,上下旋翼桨叶贴体网格部分区域发生了重叠,但是从细节图中可知上下旋翼桨叶实体并无网格穿过,能满足流场信息传递的要求。

|
图 1 悬停状态共轴双旋翼运动嵌套网格示意图 Figure 1 Schematic diagram of moving-embedded grid system |
1.3 共轴旋翼悬停流场算例验证
本文采用了有试验结果可供对比的Harrington 2旋翼进行了气动特性CFD计算的验证。该共轴刚性旋翼系统由两副共轴、反向旋转的旋翼构成,每副旋翼有两片桨叶。图 2给出了悬停状态Harrington 2共轴旋翼拉力系数随扭矩系数变化曲线的计算值和试验值[22]的对比,其中CQ为扭矩系数,CT为拉力系数。从图中可见,虽然扭矩系数计算值普遍比试验值略小,但是总体与试验值吻合较好,表明本文建立的共轴双旋翼流场模拟方法能够有效性地用于共轴刚性旋翼的气动性能计算。扭矩系数计算值偏小的原因可能是共轴旋翼流场中存在着严重的桨-涡干扰现象,桨叶附面层气动环境复杂,使得数值模拟结果未能全部计入黏性力的影响。

|
图 2 气动性能计算值与试验值的对比 Figure 2 Comparisons of aerodynamic characteristics between calcula ted results and experimental data[22] |
为了验证本文方法对共轴旋翼流场流动细节的模拟能力,对共轴旋翼桨盘下方的时均轴向诱导速度进行了计算。
图 3给出了计算值与试验值[3]的比较,计算位置位于下旋翼平面下方0.1R处,时均轴向诱导速度Vy用桨尖速度ΩR进行了无量纲化。从图中可以看出,在旋翼下方位置上的轴向诱导速度计算值与试验值吻合度较好,验证了本文方法模拟共轴旋翼干扰流场流动细节的能力。

|
图 3 轴向诱导速度计算值与试验值的对比 Figure 3 Comparisons of axial induced velocities between calculated results and experimental data[3] |
2 共轴刚性双旋翼气动特性分析
本文计算采用的共轴刚性双旋翼模型的每副旋翼由两片外形相同的桨叶组成。设上旋翼为右旋,两片桨叶初始方位角为90°和270°;下旋翼为左旋,两片桨叶初始方位角为0°和180°。模型桨叶的半径(R)为2 m,基准弦长0.2 m,根切为0.2R。上下旋翼的轴间距定为0.15R。扭转分布为线性-10°扭转(从旋转中心到桨尖),采用单一翼型NACA0012。桨叶平面形状为矩形,无下反。分别给4片桨叶命名:上旋翼两片桨叶分别命名为“U-1”(初始方位角为90°)、“U-2”(初始方位角为270°);下旋翼两片桨叶分别命名为“L-1”(初始方位角为0°)、“L-2” (初始方位角为180°)。图 4给出了初始时刻共轴刚性旋翼示意图。验证算例所采用的共轴刚性旋翼桨叶网格数量为197(周向)×36(法向)×79(展向),悬停状态计算使用的背景网格数量为241×141×241。

|
图 4 共轴刚性旋翼计算模型示意图 Figure 4 Schematic diagram of coaxial rigid rotor calculation model |
以共轴旋翼总拉力为0.013的状态为典型算例进行共轴刚性旋翼悬停状态气动分析研究。图 5给出了上下旋翼不同方位角处桨叶展向拉力系数分布曲线。可以看出,上旋翼桨叶尖部拉力随方位角变化剧烈,尤其是在上、下桨叶相遇位置。以45°方位角为例,此时上、下桨叶相遇,桨叶尖部0.6R至1.0R的区域拉力骤减。下旋翼桨叶始终处于上旋翼较强的下洗流之中,导致下旋翼桨叶有效迎角较小,同时上旋翼桨叶脱落的尾涡运动至下旋翼桨叶上,使得下旋翼桨叶内侧拉力减小、外侧拉力增大。下旋翼桨叶尖部拉力变化较小,而中段拉力变化较为剧烈,这主要是因为上旋翼桨叶脱落的桨尖涡运动至下旋翼桨叶中段,使得其气动载荷出现非定常特性。下旋翼尖部的拉力高于上旋翼尖部的拉力,一方面是由于“厚度效应”对上旋翼尖部的拉力产生不利影响,另一方面是由于下旋翼会对上旋翼桨叶诱导产生下洗流,而上旋翼对下旋翼的尖部的下洗流影响较小。

|
图 5 不同方位角处桨叶剖面展向拉力系数分布 Figure 5 Spanwise thrust coefficient distributions of blade sections in different azimuth angles |
图 6, 7分别给出了上下旋翼瞬态拉力系数和扭矩系数变化曲线。可看出,上下旋翼桨叶从相遇转为离开时,旋翼的拉力均会下降,而当桨叶逐渐接近时,上下旋翼的拉力又逐渐增加。和常规旋翼相比,悬停状态下共轴旋翼桨叶表面载荷呈现出明显的非定常周期性变化,每个旋转周期包含4个载荷周期。这与上下旋翼反向旋转一周过程中的相遇4次相对应。方位角分别为45°、135°、225°和315°时,上下旋翼的桨叶正好处于相互平行位置,拉力出现了较大的负脉冲。而在0°、90°、180°和270°时,上下旋翼正好处于相互垂直位置。从上下旋翼瞬态扭矩系数图中可知,上下旋翼扭矩基本满足了平衡条件。

|
图 6 上下旋翼瞬态拉力系数变化曲线 Figure 6 Transient thrust coefficient distributions of upper and lower rotors |

|
图 7 上下旋翼瞬态扭矩系数变化曲线 Figure 7 Transient torque coefficient distributions of upper and lower rotors |
当上下旋翼桨叶相互分开时,拉力均会逐渐上升,随后迅速下降,且上旋翼拉力系数下降速度比下旋翼快。桨叶在旋转一周过程中间存在多种干扰现象,上下旋翼气动力的变化是由共轴双旋翼流场多种干扰现象共同作用所造成的结果。在图中也可看出在主脉冲前后两侧伴有方向相反的小扰动,这是由于翼型几何形状呈前钝后尖的特点,使得上下桨叶相遇时流管出现扩张、收缩和扩张的过程,主脉冲出现在流管的收缩阶段,而小扰动则出现在扩张阶段。
3 外形参数对旋翼悬停性能的影响 3.1 后掠角度的影响为了研究后掠桨叶后掠角度对共轴刚性旋翼悬停状态气动特性的影响,本文设计了3种不同后掠角的后掠桨叶共轴刚性旋翼,后掠位置均为0.9R,后掠角度为10°、20 °和30°。图 8给出了矩形桨叶(图中以Rect表示)共轴刚性旋翼和后掠桨尖共轴刚性旋翼不同拉力状态下悬停效率的对比,4个拉力状态的总拉力系数分别为0.013 0, 0.010 2, 0.007 3和0.004 9。本文中σ表示旋翼实度。从图中可看出,后掠桨叶共轴旋翼的悬停性能明显优于矩形旋翼,且在相同拉力状态下悬停效率随着后掠角的增大而增大。这说明后掠桨叶有助于提高共轴刚性旋翼悬停性能。

|
图 8 不同后掠角桨叶共轴旋翼悬停性能的比较 Figure 8 Comparisons of FM of coaxial rotors with different swept angles |
图 9给出了总拉力系数为0.013时,上下旋翼夹角为30°时上下旋翼桨叶上表面压强分布云图。从图中可看出,相对于矩形桨叶,后掠桨叶桨尖的负压区域和强度都明显减小,并且随着桨尖后掠角度的增大,负压中心向桨尖前缘移动。这是因为,随着后掠角度的增加,桨尖处剖面法向来流速度减小,可以减弱空气的压缩性,提高阻力发散马赫数和减缓阻力突增。对于下旋翼桨叶而言,由于受上旋翼气动干扰影响较大,所以后掠桨尖对其产生的效果没有上旋翼桨叶显著。

|
图 9 不同后掠角桨叶上表面压强系数云图 Figure 9 Pressure contour distributions of upper surfaces of coaxial rotors with different swept angles |
图 10, 11分别给出了总拉力系数为0.013时,上下旋翼夹角为30°时上下旋翼桨叶0.90R和0.95R剖面处的压强系数分布比较。在0.90R剖面处(后掠起始位置),具有后掠桨尖的桨叶在该剖面的负压峰值明显减小,尤其是上表面减弱最为明显,这有利于减小桨尖处的逆压梯度。随着后掠角的增大,负压峰值和逆压梯度越小,更加有效地缓解了气流分离现象。与0.90R剖面的特征不同的是,矩形桨叶在0.95R剖面上表面负压值高于后掠桨叶,并且随着后掠角的增加,后掠桨叶上表面负压值也略微增加。这是因为后掠桨叶使得负压中心向桨尖移动,导致了桨尖局部升力的增加,因此靠近桨尖的剖面负压较大。虽然这可能引起局部阻力的增加,但由于此时的负压中心更加靠近前缘,因此阻力增加也不会很多。这些结论和上表面压强系数云图分析结果相一致。

|
图 10 不同后掠角桨叶剖面压强系数分布(r/R=0.90) Figure 10 Pressure coefficient distributions of coaxial rotor sections with different swept angles(r/R=0.90) |

|
图 11 不同后掠角桨叶剖面压强系数分布(r/R=0.95) Figure 11 Pressure coefficient distributions of coaxial rotor sections with different swept angles(r/R=0.95) |
3.2 后掠位置的影响
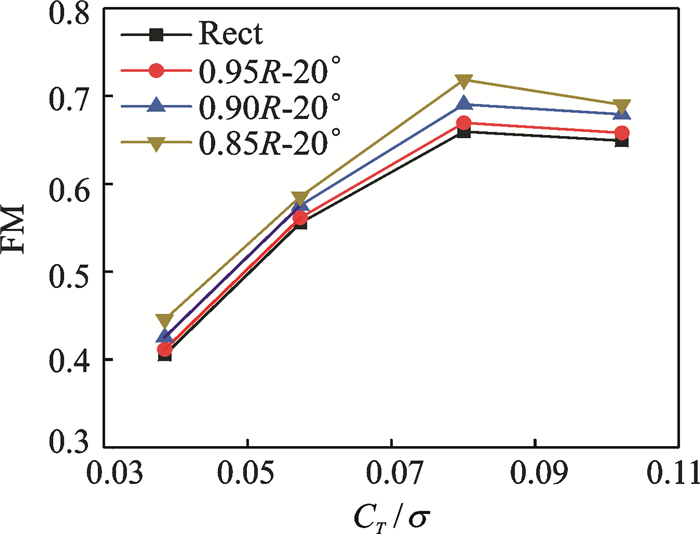
为了研究后掠桨叶后掠起始位置对共轴刚性旋翼悬停状态气动特性的影响,本文设计了3种不同后掠位置的后掠桨叶共轴刚性旋翼,后掠角度均为20°,后掠起始位置分别为0.95R, 0.90R和0.85R。图 12给出了共轴刚性旋翼矩形桨叶和后掠桨尖桨叶在不同拉力下悬停效率的比较,四个拉力状态的总拉力系数分别为0.013 0, 0.010 2, 0.007 3和0.004 9。从结果可知在当前的计算状态下,共轴刚性旋翼悬停性能随着桨叶后掠范围的扩大而增大。
|
图 12 不同后掠起始位置共轴旋翼悬停性能的比较 Figure 12 Comparisons of FM of coaxial rotors with different swept positions |
图 13给出了拉力系数为0.013时,上下旋翼夹角为30°时桨叶上表面压强分布云图,图 14则给出了展向拉力分布对比。从图 13中可看出,相对于矩形桨叶,后掠桨叶后掠区域的负压值明显减小,并且随着后掠范围的增大,负压中心向桨尖移动。比较展向拉力可知,后掠桨叶在尖部后掠段的拉力比矩形桨叶大,这和前文分析的负压中心向桨尖移动的结论相一致。随着后掠起始位置向桨叶内侧移动,后掠段范围扩大,桨尖产生的拉力也越大。由于负压中心偏离桨叶内侧以及共轴刚性旋翼总拉力相同,因此随着后掠范围的扩大,后掠桨叶中段拉力有所减小。从图 14可看出,与矩形桨叶相比,后掠桨叶在尖部外段能够获得更大的升力,并且后掠起始位置越向内侧靠近的桨叶在尖部获得升力越大,但是在后掠桨叶在桨叶中段获得的升力有所减小。

|
图 13 不同后掠起始位置桨叶上表面压强系数云图 Figure 13 Pressure contour distributions of upper surfaces of coaxial rotors with different swept positons |

|
图 14 不同后掠起始位置桨叶展向拉力分布 Figure 14 Spanwise thrust coefficient distributions of coaxial rotors with different swept positons |
3.3 尖削及变弦长的影响
为了研究非线性弦长分布对共轴旋翼悬停性能的影响,本文仿照X2TD桨叶[23]设计了3种非线性弦长分布的桨叶。这3种桨叶的弦长大小从桨根到桨尖先逐渐增大然后逐渐减小。3种桨叶最大弦长分别为1.20c, 1.35c和1.35c,最大弦长位置分别为0.7R, 0.7R和0.6R。设定桨尖弦长均为0.6倍的基准弦长,这种桨叶同时具备尖削以及中段弦长增大的特点。图 15给出了矩形桨叶和这3种弦长非线性分布桨叶的平面形状和弦长分布。矩形桨叶旋翼桨盘实度为0.098,“0.7R-1.20c”旋翼桨盘实度为0.102,“0.7R-1.35c”旋翼桨盘实度为0.109,“0.6R-1.35c”旋翼桨盘实度为0.108。

|
图 15 平面形状和弦长分布 Figure 15 Planform and chord distributions of coaxial rotors |
图 16给出了不同弦长分布方案的共轴旋翼悬停效率随拉力的变化,4个拉力状态的总拉力系数分别为0.013 0、0.010 2、0.007 3和0.004 9。可以发现,在大拉力时,弦长较大的“0.7R-1.35c”的悬停性能大于“0.7R-1.20c”。“0.7R-1.35c”和“0.6R-1.35c”的最大弦长相同,但是“0.7R-1.35c”的最大弦长位置更靠近桨尖,比较可知“0.7R-1.35c”的悬停效率高于“0.6R-1.35c”。这3种弦长分布的共轴刚性旋翼的悬停效率均高于矩形桨叶共轴刚性旋翼,这说明采用尖削变弦长分布桨叶的共轴刚性旋翼有利于提高悬停性能。

|
图 16 不同弦长分布方案的共轴旋翼悬停效率比较 Figure 16 Comparisons of FM of coaxial rotors with different chord distributions |
图 17给出了总拉力系数为0.013时,上下旋翼夹角为30°时桨叶上表面压强分布云图。可以很明显地看出,采用这种变弦长分布的桨叶在桨叶中段和桨尖有较大差别。尖削桨叶桨尖前缘处和后掠桨尖类似,剖面入流速度减小,减弱了空气的压缩性。另一方面,尖削桨叶由于尖部区域面积较小,增强了激波压缩性的影响,可能会增加一定阻力。从图中可知3种尖削桨叶桨尖的负压区域范围和强度均比矩形桨叶小,且“0.7R-1.35c”桨尖负压强度最小。这是由于“0.7R-1.35c”最大弦长位置更加靠近桨尖且弦长最大,而悬停时桨叶负压中心主要集中在桨尖区域,因此“0.7R-1.35c”悬停效率最高。比较“0.7R-1.35c”和“0.7R-1.20c”可知,最大弦长较小的“0.7R-1.20c”在改善桨叶载荷分布的效果不如“0.7R-1.35c”。

|
图 17 不同弦长分布桨叶上表面的压强系数云图 Figure 17 Pressure contour distributions of upper surfaces of coaxial rotors with different chord distributions |
图 18给出了展向拉力系数分布的对比。这种变弦长桨叶中段弦长较大,因此也承担了较多的拉力载荷。尖削的桨尖区域负压强度和范围都较小,因此产生的拉力比矩形桨叶小。比较“0.7R-1.35c”和“0.6R-1.35c”可知,“0.6R-1.35c”最大弦长位置远离桨尖,因此展向最大拉力位置也比“0.7R-1.35c”更加靠近桨叶内侧,且“0.6R-1.35c”桨叶中段拉力比“0.7R-1.35c”大、桨尖拉力比“0.7R-1.35c”小。比较“0.7R-1.35c”和“0.7R-1.20c”可知,虽然“0.7R-1.35c”在相同位置的弦长均比“0.7R-1.20c”大,但是由于当前共轴旋翼总拉力相同的情况下,两者的展向拉力分布曲线差别较小。综上可知,选取合适的非线性弦长分布可以改善展向气动载荷分布,能够有效对桨尖进行卸载,提高共轴刚性旋翼整体的悬停性能。

|
图 18 不同弦长分布桨叶剖面展向拉力系数分布 Figure 18 Spanwise thrust coefficient distributions of coaxial rotors with different chord distributions |
4 结论
通过使用基于运动嵌套网格技术和可压缩RANS方程等建立的共轴刚性双旋翼非定常流场模拟方法,开展了对悬停状态共轴刚性双旋翼的流场模拟和气动特性计算分析。着重针对共轴刚性双旋翼的气动性能进行了桨叶平面外形的参数分析,包括后掠角、后掠起始位置以及非线性弦长分布。主要结论如下:
(1) 与常规旋翼相比,由于上下旋翼在反向旋转过程中的相互干扰,悬停状态下共轴刚性双旋翼桨叶表面载荷呈现出明显的非定常周期性变化,每个旋转周期包含N个载荷周期(N为共轴旋翼桨叶总片数)。
(2) 在相同拉力状态下,后掠桨叶共轴旋翼的悬停性能优于矩形旋翼,且悬停效率随着后掠角和后掠范围的增大而增大。相对于矩形桨叶,后掠桨尖的负压区域明显减小,并且随着桨尖后掠角和后掠范围的增大,负压中心向桨尖前缘移动。
(3) 采用非线性弦长分布的共轴刚性旋翼的悬停性能优于常规矩形桨叶共轴旋翼。中段弦长大且桨尖尖削的非线性弦长分布的共轴旋翼桨叶在桨尖区域的拉力小于矩形桨叶,而在桨叶中段拉力大于矩形桨叶。选取合适的非线性弦长分布可以改善展向气动载荷分布,能够对桨尖进行有效卸载,提高共轴刚性旋翼的悬停性能。
这些方法和结论为进一步开展桨叶外形对共轴刚性旋翼的前飞性能的影响研究打下基础。
| [1] | HO J C, YEO H, BHAGWA T M. Validation of rotorcraft comprehensive a nalysis performance predictions for coaxial rotors in hover[C]//Journal of the American Helicopter Society, 2017, 1(2): 732-751.http://www.ingentaconnect.com/content/ahs/jahs/2017/00000062/00000002/art00005 |
| [2] |
唐正飞, 高正.
共轴双旋翼与单旋翼悬停流场实验测量值的对比[J]. 南京航空航天大学学报, 1997, 29(6): 627–632.
TANG Zhen gfei, GAO Zheng. Comparison of experimental data for the coaxial-rotor and single-rotor flowfield in hovering[J]. Journal of Nanjing University of Aeronauti cs and Astronautics, 1997, 29(6): 627–632. |
| [3] |
唐正飞, 李锋.
用三维激光多谱勒测速仪对共轴双旋翼悬停流场的测定[J]. 流体力学实验与测量, 1998, 12(1): 81–87.
TANG Zhengfei, LI Feng. Measurement of the coaxial-rotor flowfield in hovering using 3-d laser doppler velocimeter[J]. Experiments and Measurements in fluid Mechanics, 1998, 12(1): 81–87. |
| [4] | LEISHMAN J G, ANANTHAN S. Aerody namic optimization of a coaxial proprotor[C]//Proceedings of the 62th Annual Forum of the American Helicopter Society. Phoenix: American Helicopter Society, 2006: 64-85. |
| [5] | WACHSPRESS D A, QUACKENBUSH T R. Impact of rotor design on coaxial rotor performance, wake geometry and noise[C]//Proceedings of the 62th Annual Forum of the American Helicopter Society.Phoenix: American Helicopter Soci ety, 2006: 41-63.https://www.mendeley.com/research-papers/impact-rotor-design-coaxial-rotor-performance-wake-geometry-noise/ |
| [6] | JUN S, YEE K, LEE J. Robust design optimization of unmanned aerial vehicle coaxial rotor considering operational uncertainty[J]. Journal of Aircraft, 2011, 48(2): 353–367. DOI:10.2514/1.C001016 |
| [7] | RAND O, KHROMOV V. Aerodynamic optimiza tion of coaxial rotor in hover and axial flight[C]//27th Congress of the Inte rnational Council of the Aeronautical Sciences 2010. Nice, France: ICAS Secretariat, 2010: 893-905.https://www.mendeley.com/research-papers/aerodynamic-optimization-coaxial-rotor-hover-axial-flight/ |
| [8] | LAKSHMINARAYAN V K, BAEDER J D. High-resolution computational investigation of trimmed coaxial rotor aerodynamics in hover[J]. Journal of the American Helicopter Society, 2009, 54(4): 42008–42008. DOI:10.4050/JAHS.54.042008 |
| [9] |
童自力, 孙茂.
共轴式双旋翼流动的N-S方程模拟[J]. 航空学报, 1998, 19(1): 1–5.
TONG Zili, SUN Mao. Navier-Stokes calculations of coaxial rotor aerodynamics[J]. Acta Aeronautica et Astronautica Sinica, 1998, 19(1): 1–5. |
| [10] |
童自力, 孙茂.
共轴式双旋翼气动力特性的计算研究[J]. 航空学报, 1999, 20(4): 348–350.
TONG Zi li, SUN Mao. Navier-Stokes analysis of the aerodynamic properties of coaxial rotors[J]. Acta Aeronautica et Astronautica Sinica, 1999, 20(4): 348–350. |
| [11] | XU H Y, YE Z Y. Coaxial rotor helicopter in hover based on unstructured dynamic overset Grids[J]. Journal of Aircraft, 2010, 47(5): 1820. DOI:10.2514/1.C031079 |
| [12] |
许和勇, 叶正寅.
悬停共轴双旋翼干扰流动数值模拟[J]. 航空动力学报, 2011, 26(2): 453–457.
XU Heyong, YE Zhengyin. Numerical simulation of interaction unsteady flows[J]. Journal of Aerospace Power, 2011, 26(2): 453–457. |
| [13] |
叶靓, 徐国华.
共轴式双旋翼悬停流场和气动力的CFD计算[J]. 空气动力学学报, 2012, 30(4): 437–442.
YE Liang, XU Guohua. Calculation on flow field and aerodynamic force of coaxial rotors in hover with CFD method[J]. Acta Aerodynamica Sinica, 2012, 30(4): 437–442. |
| [14] |
朱正, 招启军, 李鹏.
悬停状态共轴刚性双旋翼非定常流动干扰机理[J]. 航空学报, 2016, 37(2): 568–578.
ZHU Zheng, ZHAO Qijun, LI Peng. Unsteady flow interaction mechanism of coaxial rigid rotors in hover[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 568–578. |
| [15] | BROCKLEHURST A, BARAKOS G N. A review of helicopter rotor blade tip shapes[J]. Progress in Aerospace Science, 2013, 56: 35–74. DOI:10.1016/j.paerosci.2012.06.003 |
| [16] | SPIVEY W A, MOREH OUSE G G. New insights into the design of swept-tip rotor blades[C]//26th National Annual Forum Proceedings of the American Helicopter Society. Washington, DC:[s.n.], 1970. |
| [17] | ZHAO Q J, XU G H, ZHAO J G. New hybrid method for predicting the flowfields of helicopter rotors[J]. Journal of Aircraft, 2006, 43(2): 372–380. DOI:10.2514/1.14863 |
| [18] |
招启军, 徐国华.
新型桨尖旋翼悬停气动性能试验及数值研究[J]. 航空学报, 2009, 30(3): 422–429.
ZHAO Qijun, XU Guohua. Aerodynamic performance of rotor with new type blade-tip in hover based upon test and numerical investigations[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(3): 422–429. |
| [19] | ROE P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357–372. DOI:10.1016/0021-9991(81)90128-5 |
| [20] | HARIHARAN N, SANKAR L N.Application of ENO schemes to rotary flow field[R]. AIAA paper 95-1892, 1995. |
| [21] | YOON S, JAMESON A. Lower-upper symmetric-Gauss-Seidel method for the Euler and Navier-Stokes equations[J]. AIAA Journal, 1988, 26(9): 1025–1026. DOI:10.2514/3.10007 |
| [22] | HARRINGTON R D. Full-scale-tunnel investigation of the static-thrust performance of a coaxial helicopter rotor[J]. NACA TN-2318, 1951. |
| [23] | BAGAI A. Aerodynamic design of the X2 technology demonstratorTM[C]// Americ an Helicopter Society 64th Annual Forum. Montreal, Canada:[s.n.], 2008. |
 2017, Vol. 49
2017, Vol. 49


