飞机装配是飞机制造的关键环节,需要采用大量的工艺装备(简称工装)来保证装配精度,满足协调性要求[1-2]。工装设计、制造的周期和成本占据了飞机制造的周期和成本中的较大比重,柔性工装以其柔性的特点,不仅降低了飞机制造成本,还缩短了更新周期,同时实现了数字量在制造过程中的全流通[3-4]。因此,柔性工装相关技术的突破将为航空制造业的发展带来巨大的机遇。
柔性工装存在设计、制造误差,且在飞机装配中会发生柔性形变,再加上飞机零、部件本身的设计、制造误差与柔性形变,最终反映为装配件上特征点的实际位置与理论位置之间存在定位误差,这势必将导致装配精度降低[5]。因此,需要采用误差控制策略来建立实际与理论之间的精确映射关系。工程中常用预防法控制定位误差,即通过修改结构设计、材料属性等减少误差源至误差之间的数量转换关系。考虑到可重构柔性工装的可重构性与柔性的特点,预防法的另一途径(通过优化对装配件的定位/支撑布局来减小误差)更具有经济性,且已逐渐成为研究热点。文献[6, 7]中分析了“N-2-1”定位原则,并使用遗传算法优化了薄壁件的支撑布局,以减小加工过程中薄壁件的形变;文献[8]展开了误差溯源分析,兼顾分析了装配过程的刚性和柔性误差,通过改进的遗传算法优化定位点布局,减小了误差的影响;文献[9]基于启发式优化算法提出定位策略的设计方法,并显著降低了蒙皮在装配中产生的形变;文献[10]还将该技术用到了飞机总装,结合有限元模型优化了定位器的数量、布局,提高了装配准确度。以上研究大多都是针对壁板类弱刚性零件,对于非壁板类零件,由于其本身较好的刚性,在以往研究中通常被忽略。但是,在机身立式装配中,框件的定位误差也将对装配精度产生较大的影响。因此,优化框件的定位/支撑布局,这一误差控制策略具有一定的研究必要性。
考虑到框件的复杂工艺特征,定位/支撑布局优化需要作为约束优化问题来处理。约束优化问题中的约束处理技术受到了国内外学者的关注。文献[11]提出基于违反程度的自适应惩罚函数法来处理约束优化问题;与其相似的还有DEB[12],他将自适应策略用于增广拉格朗日乘子法,提出改进的约束优化遗传算法,实例证明该法具有高效性和精确性;文献[13]中提出α约束法,该法采用约束满足水平表示个体满足约束条件的程度。以上研究均采用了常见的约束处理技术,这些已有技术的“保留并改善”处理策略通常会产生大量不可行解,导致在具有复杂约束时算法不稳定与低效,在工程中甚至造成被调用的其他软件(如有限元分析软件)无法正常运行。
本文针对机身立式装配中可重构柔性工装上框件定位误差问题,首先基于可重构柔性工装分析误差,然后通过优化框件的定位/支撑布局来减小误差,从而在实际装配任务开始之前的设计阶段抑制误差,提高装配精度。具体的方法如下:分析可重构柔性工装的结构和原理,根据其基于交点孔的定位/支撑方式追溯误差的来源,建立误差的数学模型;针对工装各部件由于柔性形变带来的柔性定位误差,通过优化定位/支撑布局进行抑制;分析优化汇总的工艺特征约束,建立约束的广义数学模型,提出修补算法,基于修补算法设计改进的遗传算法,建立优化的数学模型;基于APDL语言开发ANSYS参数化模型,通过MATLAB运行优化算法并调用模型完成有限元仿真计算,实现改进的遗传算法对布局的优化。
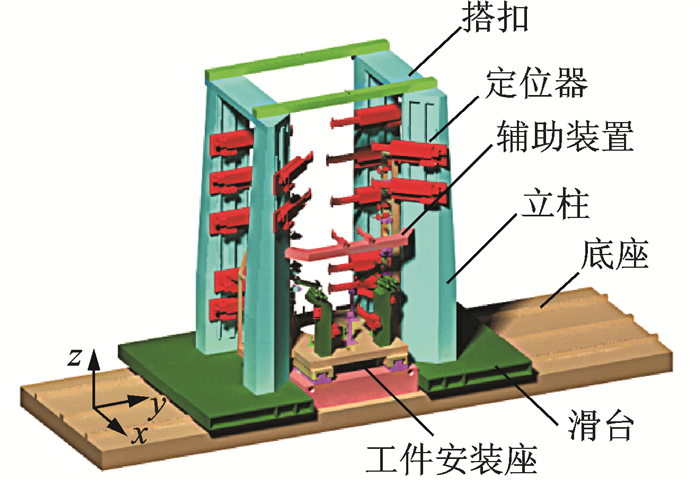
1 可重构柔性工装原理与误差分析 1.1 工装组成及功能需求分析本文笔者所在课题组针对某型飞机机身的立式装配工艺,设计了一种龙门式可重构柔性工装(见图 1),其功能是实现预装配,为其后的自动化钻铆工序做准备。工装包括底座、滑台、立柱、工件安装座、定位器和辅助装置。其中立柱底座上布置两个具有y向移动自由度的滑台,滑台上布置立柱,立柱上布置可以沿立柱z向运动的定位器,定位器可以实现3个自由度的运动,两套立柱底座中间布置工件安装座。装配过程中,4个定位器的末端接头采用交点孔式的定位和支撑确定框件的空间位置。根据需求,装配件关键特性定位精度为±0.1mm。
|
图 1 可重构柔性工装 Figure 1 Reconfigurable flexible fixture |
1.2 基于交点孔的定位/支撑方式
飞机装配中常用预先加工的工艺基准孔(即交点孔)对整体刚度较好的数控加工件进行定位。这种定位方式只需要产品与定位接头形成“销-孔”配合即可完成定位和支撑,省去了辅助支撑工装,提升了工装的开敞性和装配成本、效率。
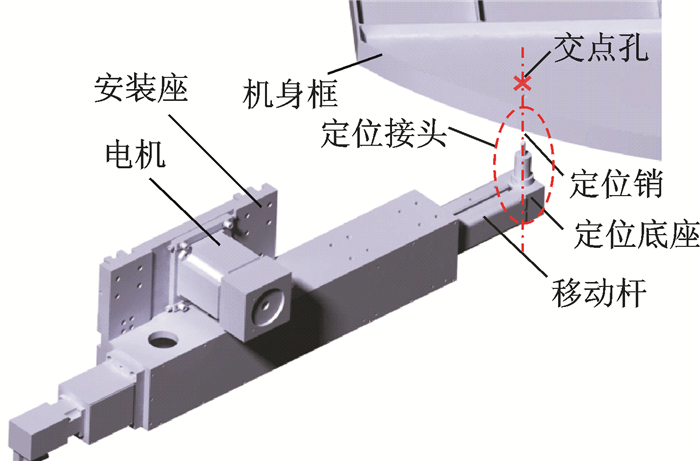
本文可重构柔性工装的交点孔定位/支撑方式如图 2所示。其中定位器由电机、驱动系统、移动杆、定位接头组成,通过定位器安装座安装在立柱导轨上,可实现3个自由度的运动。定位器末端的可拆卸定位接头由高精度铣削加工而成,能够较好地贴合机身框端面,加上定位销与交点孔的配合,实现定位和支撑框件。定位接头具有可拆卸、体积小的特点,极大增强了定位器的实用性。
|
图 2 基于交点孔的定位/支撑方式 Figure 2 Locating/supporting mode based on intersection hole |
根据本文工装的结构特点和基于交点孔的定位/支撑方式可见,该工装能够针对不同型号机身框的不同交点孔分布情况,通过调整定位器完成交点孔定位/支撑。针对不同交点孔尺寸,可以通过调整定位器接头实现定位/支撑。
1.3 误差分析装配误差包括定位误差、自动化钻铆的加工误差和热变形误差等,其中定位误差主要受制造、安装、控制系统、夹具运动、柔性形变和运行工况影响[14-15]。本文将分析机身立式装配的定位误差,以从误差的根源减小误差的影响。工装定位误差流如图 3所示,底座与滑台、滑台与立柱的误差主要来自形变、安装和制造,产品的变化对其产生的影响可以忽略,作为系统误差;定位器安装座到移动杆、移动杆到接头的误差同时受控制系统、制造、安装和变形的影响,作为刚性和柔性误差的混合过程;定位器接头到框件受变形的影响,作为柔性误差。

|
图 3 可重构柔性工装定位误差流 Figure 3 Locating err or flow of reconfigurable flexible fixture |
考虑到本文对定位/支撑布局的研究主要针对柔性误差,因此做出假设[16]:工装和工件制造、安装正确且工装各部件能正常运动到规定工位,即误差主要产生于框件、定位器等各部件的柔性形变影响。下文将分别对各误差进行分析,从而求解框件上任一待钻铆点(特征点)Pi的柔性定位误差δi
| $ {\mathit{\boldsymbol{\delta }}_i} = \mathit{\boldsymbol{P'}}_i^G - \mathit{\boldsymbol{P}}_i^G $ | (1) |
式中:P′iG,PiG分别为特征点在全局坐标系CS-G下的实际位置和理论位置。
(1) 框件柔性误差ΔDiFRA
在框件坐标系CS-FRA下,任一特征点Pi的理论坐标为PiFRA,在其上级坐标系CS-LA1下的理论坐标PiLA1可通过齐次坐标变换矩阵求得
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}}_i^{{\rm{LA1}}}}\\ 1 \end{array}} \right] = _{{\rm{LA1}}}^{{\rm{FRA}}}\mathit{\boldsymbol{T}} \cdot \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}}_i^{{\rm{FRA}}}}\\ 1 \end{array}} \right] $ | (2) |
式中:
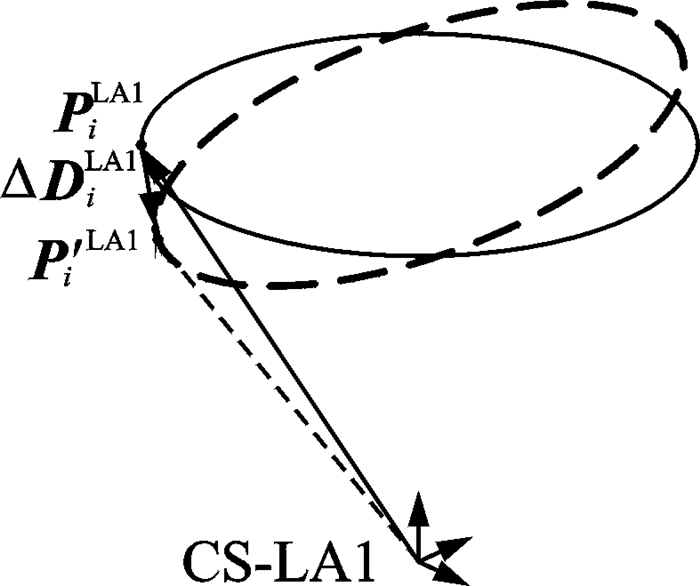
框件柔性误差如图 4所示。框件坐标系下,柔性误差ΔDiFRA可以通过有限元分析获得,特征点变形后的坐标P′iFRA 可由式(3)求得
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P'}}_i^{{\rm{FRA}}}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{D}}_i^{{\rm{FRA}}}}\\ 1 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}}_i^{{\rm{FRA}}}}\\ 1 \end{array}} \right] $ | (3) |
|
图 4 框件柔性定位误差 Figure 4 Flexible locating error of frame |
于是,特征点在上级坐标系下的实际坐标可表示为
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P'}}_i^{{\rm{LA1}}}}\\ 1 \end{array}} \right] = _{{\rm{LA1}}}^{{\rm{FRA}}}\mathit{\boldsymbol{T}} \cdot \left( {\left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{D}}_i^{{\rm{FRA}}}}\\ 1 \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}}_i^{{\rm{FRA}}}}\\ 1 \end{array}} \right]} \right) $ | (4) |
结合式(4)可得,根据误差流依次向上级LAx(x=1, 2)迭代,直到全局坐标系,便能求得柔性定位误差。
由于框件由4个定位器支撑并定位,换言之,决定框件坐标系的为4个交点孔定位点对应的空间位置关系,定位点分别由4个定位器提供,属于并联装配。4个交点孔定位点组成特征坐标系CS-FFRA,由于误差的存在,特征坐标系到框件坐标系和上级坐标系到特征坐标系存在变化
| $ \begin{array}{l} _{{\rm{LA1}}}^{{\rm{FRA}}}\mathit{\boldsymbol{T}} = _{{\rm{LA1}}}^{{\rm{FFRA}}}\mathit{\boldsymbol{T}} \cdot _{{\rm{FFRA}}}^{{\rm{FRA}}}\mathit{\boldsymbol{T}}\\ _{{\rm{LA1}}}^{{\rm{FRA}}}\mathit{\boldsymbol{T}} = _{{\rm{LA1}}}^{{\rm{FFRA'}}}\mathit{\boldsymbol{T}} \cdot _{{\rm{FFRA'}}}^{{\rm{FRA}}}\mathit{\boldsymbol{T}} \end{array} $ | (5) |
式中:
(2) 定位器柔性误差ΔJLOC
定位器作为框件的上级误差源,其柔性误差如图 5所示。

|
图 5 定位器柔性定位误差 Figure 5 Flexible locating error of locator |
因此可得定位器柔性误差
| $ \left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{J}}^{{\rm{LOC}}}}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{J'}}}^{{\rm{LOC}}}}}\\ 1 \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}^{{\rm{LOC}}}}}\\ 1 \end{array}} \right] $ | (6) |
式中:J′ LOC,JLOC分别为接头在定位器坐标系CS-LOC下的实际和理论坐标。
通过坐标变换可求得其上级坐标系CS-LA2中接头理论坐标JLA2、实际坐标J′LA2为
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}^{{\rm{LA2}}}}}\\ 1 \end{array}} \right] = _{{\rm{LA2}}}^{{\rm{LOC}}}\mathit{\boldsymbol{T}} \cdot \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{J}}^{{\rm{LOC}}}}}\\ 1 \end{array}} \right]}\\ {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{J'}}}^{{\rm{LA2}}}}}\\ 1 \end{array}} \right] = _{{\rm{LA2}}}^{{\rm{LOC}}}\mathit{\boldsymbol{T}} \cdot \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{J'}}}^{{\rm{LOC}}}}}\\ 1 \end{array}} \right]} \end{array} $ | (7) |
式中:LA2LOCT为CS-LA2到CS-LOC的变换矩阵。
(3) 系统误差ΔSG
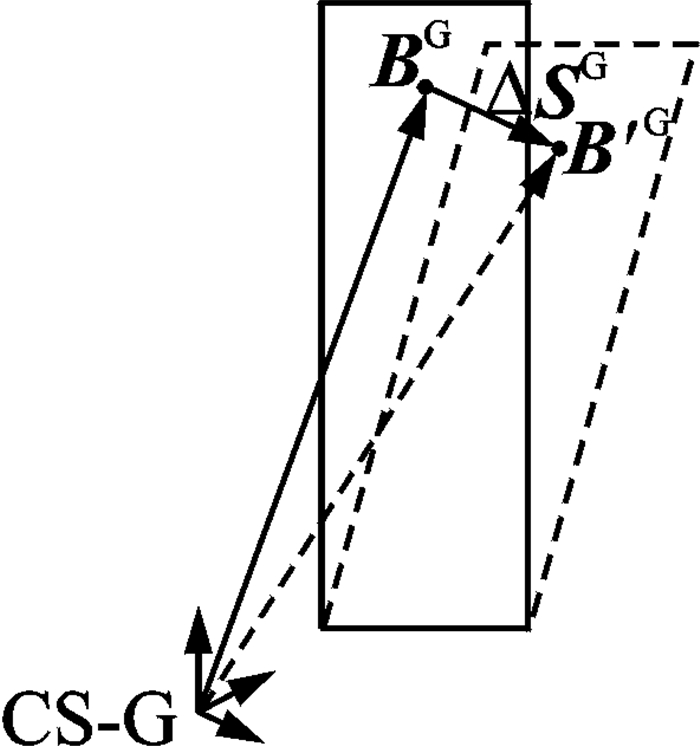
立柱、滑台等作为定位器的上级误差源,产生系统误差,且在全局坐标系CS-G中建立(如图 6所示)。
|
图 6 系统误差 Figure 6 System error |
可得系统误差
| $ \left[ {\begin{array}{*{20}{c}} {\Delta {\mathit{\boldsymbol{S}}^{\rm{G}}}}\\ 1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{B'}}}^{\rm{G}}}}\\ 1 \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}^{\rm{G}}}}\\ 1 \end{array}} \right] $ | (8) |
式中:B′G,BG为CS-G下,定位器安装座的实际定位坐标和理论定位坐标。
综合式(2~8)可得
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}}_i^{\rm{G}}}\\ 1 \end{array}} \right] = _{\rm{G}}^{{\rm{LOC}}}\mathit{\boldsymbol{T}} = _{{\rm{LOC}}}^{{\rm{FFRA}}}\mathit{\boldsymbol{T}} \cdot _{{\rm{FFRA}}}^{{\rm{FRA}}}\mathit{\boldsymbol{T}} \cdot \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}}_i^{{\rm{FRA}}}}\\ 1 \end{array}} \right]\\ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P'}}_i^{\rm{G}}}\\ 1 \end{array}} \right] = _{\rm{G}}^{{\rm{LOC}}}\mathit{\boldsymbol{T}} = _{{\rm{LOC}}}^{{\rm{FFRA'}}}\mathit{\boldsymbol{T}} \cdot _{{\rm{FFRA'}}}^{{\rm{FRA}}}\mathit{\boldsymbol{T}} \cdot \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{P'}}_i^{{\rm{FRA}}}}\\ 1 \end{array}} \right] \end{array} $ | (9) |
结合式(1, 9)便可得到任一待钻铆点的柔性定位误差δi。
2 基于交点孔定位的定位/支撑布局优化工程中,通常需要在钻铆工序开始前测量各关键特性的定位误差信息,从而通过自动化钻铆工序中精度补偿技术减小定位误差。误差过大不仅影响精度补偿的效率和实施难度,还会影响产品的质量。考虑到柔性定位误差可以通过优化定位/支撑布局的策略在前期设计阶段控制到最小,且机身框件的交点孔布局不会对框整体力学特性造成影响,因此本文优化交点孔布局,旨在提高前期装配精度,同时减小后期精度补偿的难度、提高装配效率。
优化过程中,布局受工艺特征约束限制,为约束优化问题。工艺特征约束是约束条件在实际中的体现,狭义上指框件上交错布置的加强筋、不规则边缘、凹槽等限制交点孔布置的特征;广义上指约束数学模型中的等式、不等式约束和设计变量定义区间约束(如设计变量定义区间不连续且设计域离散)。求解约束优化问题的方法有确定性算法和智能型算法[17]。由于确定性算法对目标函数定义域的限制,通常使用智能算法,并加以适当的约束处理技术[18]。约束处理技术是智能算法解决约束优化问题的关键,常见的包括惩罚函数法、转化法、修补法等[19]。惩罚函数法通过添加惩罚项,从而将约束问题变为无约束问题[12, 20]。转化法将违背约束的程度作为优化目标,从而将约束优化转化为无约束多目标优化问题。转化法或将个体区分为可行解和不可行解分别处理[21]。相比于以上两种方法对不可行解的“保留并改善”策略,修补法能够避免不可行解的产生,且复杂度低,更适合应用于工程中。本文建立工艺特征约束的数学模型,设计相应的修补算法,然后设计改进的优化算法。
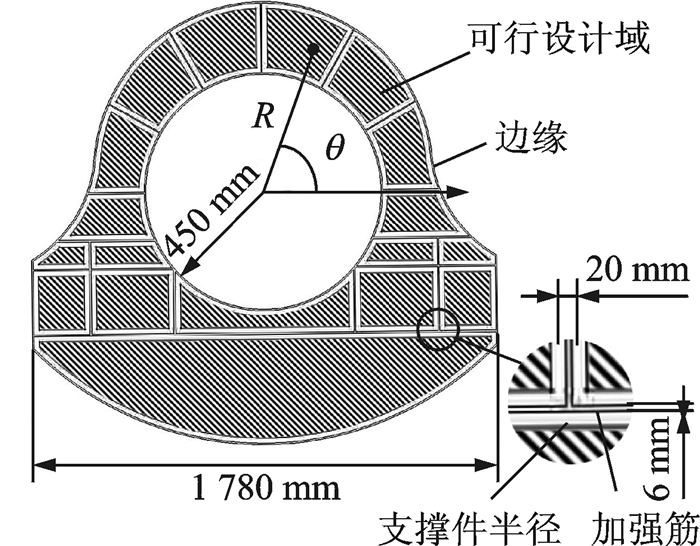
2.1 约束分析和处理定位/支撑点在框件上的可行设计域如图 7所示。产生的主要原因为:
|
图 7 框件的可行设计域 Figure 7 Feasible design region of frame |
(1) 设计区间约束:在图中极坐标下,半径与角度成函数关系,点的半径应处于各角度对应的半径区间内。广义数学模型上为不等式约束。
(2) 加强筋和边缘约束:定位器不能与加强筋和边缘干涉,需要使定位销与加强筋和边缘至少保持半径的距离;复杂布置的加强筋和不规则的边缘将设计域分隔为不规则的块。广义数学模型上为不连续的定义区间和离散设计域。
上述约束分析可得,工艺特征约束在广义数学模型上包括:不等式约束、设计变量定义区间不连续、设计域离散等约束。不失一般性,添加等式约束建立约束数学模型
| $ \begin{array}{l} \left\{ \begin{array}{l} {x_{1,\min }} \le {x_1} \le x_{1,1}^{\rm{U}},x_{1,2}^{\rm{U}} \le {x_1} \le x_{1,2}^{\rm{U}}, \cdots ,x_{1,m}^{\rm{D}} \le \\ \;\;\;\;\;\;{x_1} \le {x_{1,\max }}\\ {x_{2,\min }} \le {x_2} \le x_{2,1}^{\rm{U}},x_{2,2}^{\rm{U}} \le {x_2} \le x_{2,2}^{\rm{U}}, \cdots ,x_{2,m}^{\rm{D}} \le \\ \;\;\;\;\;\;{x_2} \le {x_{2,\max }}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {x_{n,\min }} \le {x_n} \le x_{n,1}^{\rm{U}},x_{n,2}^{\rm{U}} \le {x_n} \le x_{n,2}^{\rm{U}}, \cdots ,x_{n,m}^{\rm{D}} \le \\ \;\;\;\;\;\;{x_n} \le {x_{n,\max }} \end{array} \right.\\ {f_e}\left( {{x_{e,1}},{x_{e,2}}, \cdots ,{x_{e.k}}} \right) = 0\\ \left\{ \begin{array}{l} {f_{ne1}}\left( {{x_{ne1,1}},{x_{ne1,2}}, \cdots ,{x_{ne1.k}}} \right) \ne 0\\ {f_{ne2}}\left( {{x_{ne2,1}},{x_{ne2,2}}, \cdots ,{x_{ne2.k}}} \right) < 0\\ {f_{ne3}}\left( {{x_{ne3,1}},{x_{ne3,2}}, \cdots ,{x_{ne3.k}}} \right) > 0 \end{array} \right. \end{array} $ | (10) |
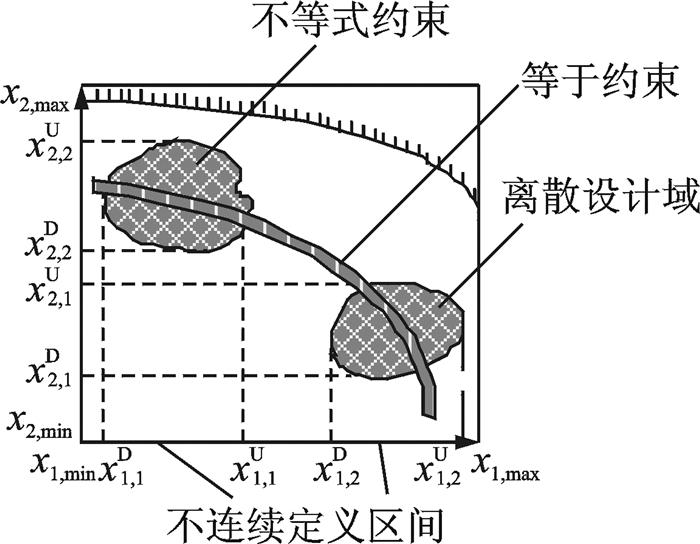
该式表示:优化问题有n个独立的设计变量xi(i=1, 2, …, n),变量在上下界中有m+1个不连续的定义区间;有k个独立变量满足等式约束,l个独立变量满足不等式约束;xn, min,xn, max为设计变量极值,xn, mD,xn, mU为区间边界。图 8为2个设计变量时的二维约束。
|
图 8 2个设计变量的二维约束 Figure 8 2-D constrains for two design variables |
针对任意设计变量xi进行讨论,设其在上下界区间[xi, min, xi, max]内具有不连续的定义区间(xi, 1D, xi, 1U] ∪[xi, 2D, xi, 2U]。采用修补法,算法流程为:
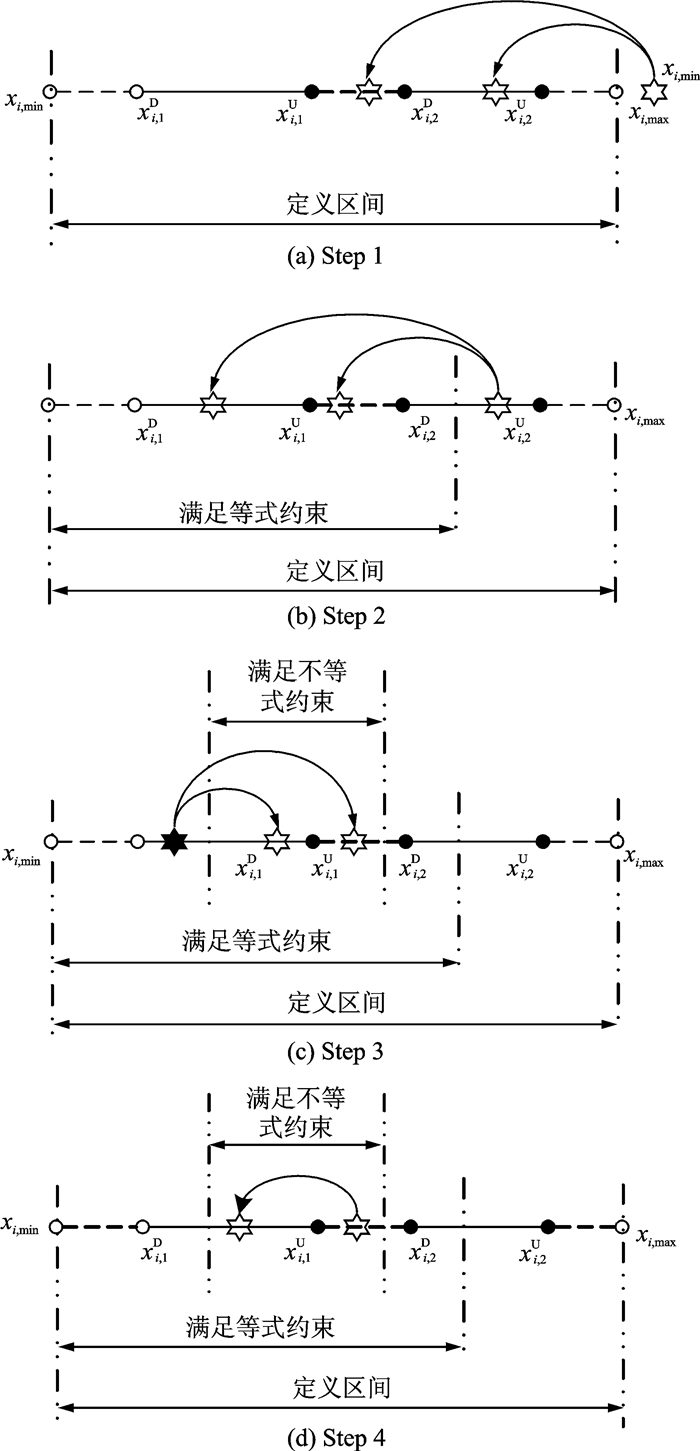
步骤1 检查xi是否处于[xi, min, xi, max]中。若否,则在区间内随机生成新值(见图 9(a))。
|
图 9 修补算法流程 Figure 9 Process of repairing method |
步骤2 检查xi是否满足等式约束。若否,根据等式fe=0获取xi与其他设计变量的关系,在[xi, min, xi, max]内调整xi,并相应调整其他设计变量,使等式约束条件成立(见图 9(b))。
步骤3 检查xi是否满足不等式约束。若否,根据不等式fne1≠0,fne2 < 0,fne3>0获取xi与其他设计变量的关系,在[xi, min, xi, max]中满足等式约束的区间内调整xi,并相应调整其他设计变量,使等式约束条件成立的同时不等式约束条件也成立(见图 9(c))。
步骤4 检查xi是否落入不连续的定义区间。若否,则在满足等式与不等式约束的区间内调整xi至定义区间,同时根据上述变量关系相应调整其它未落入区间的设计变量,直至所有设计变量落入定义区间(见图 9(d))。
步骤5 算法结束,修补完成。
n个设计变量时,该修补法复杂度为
| $ \begin{array}{l} T\left( n \right) = O\left( n \right) + O\left( {4n} \right) + O\left( n \right) + O\left( {{n^2} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. n \right) = O\left( {{n^2}} \right) \end{array} $ | (11) |
由此可知,该算法计算复杂度低,若结合灵敏度分析精简变量个数,能够高效地处理约束问题。
2.2 约束优化算法设计考虑到遗传算法参数结构简单且不失一般性,本文采用遗传算法,并基于修补法进行改进。设计变量为4个定位器接头中心(即交点孔定位点)的极坐标X=(θ1, R1, θ2, R2, θ3, R 3, θ4, R4);约束条件为定位点的可行设计域Afeasible;目标函数为装配过程中工装与工件产生柔性形变后,工件上各特征点相对于理论位置的定位误差δ(X)。优化模型如下
| $ \begin{array}{*{20}{c}} {\min \mathit{\boldsymbol{\delta }}\left( X \right)}\\ {{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\left\{ \begin{array}{l} \left( {{\theta _1},{R_1}} \right) \in {A_{{\rm{feasible}}}}\\ \left( {{\theta _2},{R_2}} \right) \in {A_{{\rm{feasible}}}}\\ \left( {{\theta _3},{R_3}} \right) \in {A_{{\rm{feasible}}}}\\ \left( {{\theta _4},{R_4}} \right) \in {A_{{\rm{feasible}}}} \end{array} \right.} \end{array} $ | (12) |
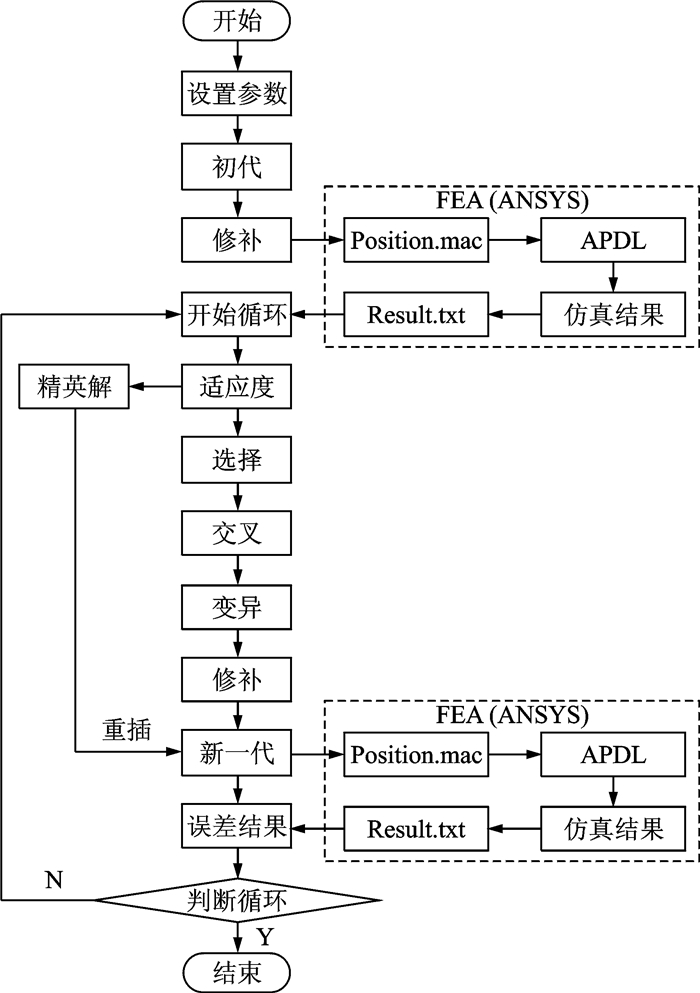
改进后的遗传算法流程图如图 10所示。
|
图 10 改进的遗传算法流程图 Figure 10 Flow chart of improved genetic algorithm |
该遗传算法个体染色体使用实数编码,并采用精英保留策略,确保算法收敛。运行过程中,调用有限元软件,然后将计算结果返回主程序,最后根据误差模型计算误差,得到最优方案。
3 实例分析与讨论本文采用图 11(a)所示机身框作为实例,验证误差分析和优化算法。该框采用铝合金材料,密度2.82 g/cm3,弹性模量72 GPa,泊松比0.33。在MA T LAB环境下编写误差矩阵和改进的遗传算法,设置种群大小分别为40,60,80,100,进化代数为100,交叉概率为0.8,变异概率为0.2。结合ANSYS环境下APDL语言建立参数化模型并完成有限元分析,得到优化结果。选取框件上需要钻铆的点P1,P2,P3,P4,P5作为特征点,如图 11(b)所示。

|
图 11 某型飞机机身框件模型 Figure 11 Frame model of fuselage |
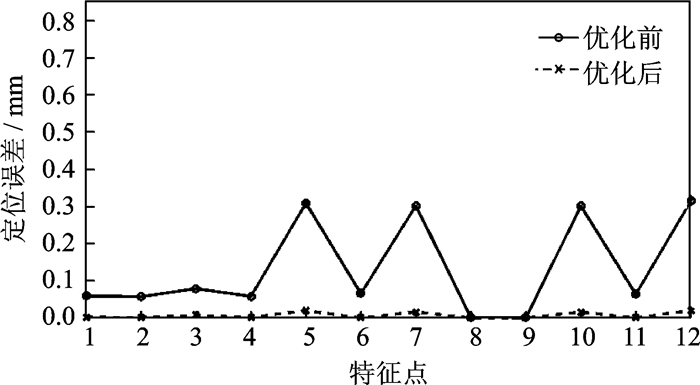
提取特征点优化前后的定位误差(见表 1),定位误差对比图如图 12所示。分析可知,特征点定位误差明显小于优化前,且都满足精度要求(0.1 mm);最大误差(0.019 8 mm)相比于优化前(0.314 5 mm)减小93.7%;各特征点变动标准差0.007 9,小于优化前的0.124 1,且从变化曲线可以看出,变动更加平缓,更利于自动钻铆加工。
| 表 1 优化前后特征点定位误差 Table 1 Locating errors of feature points before/after optimization |
|
图 12 优化前后特征点定位误差变化曲线 Figure 12 Curves of locating errors of feature points before/aft er optimization |
优化前后交点孔的变化如图 13所示。在该布局下,误差分布均匀,不仅保证了特征孔定位精度,还保证了框面整体形变不会过大。

|
图 13 优化前后交点孔布局 Figure 13 Layout of intersection holes before/after optimization |
分析可知,交点孔应该在定位器刚度满足的情况下,尽量布置在加强筋分布密集的框中部。该部位框面承受较大的重力,易产生较大的柔性形变。且框中部通常布置较多特征孔,更应该保证较高的定位精度。考虑到定位器的可达性,在工程实际中不能因为盲目追求工装的柔性而导致装配精度降低,必要时可以添加刚性定位器来保证定位精度。
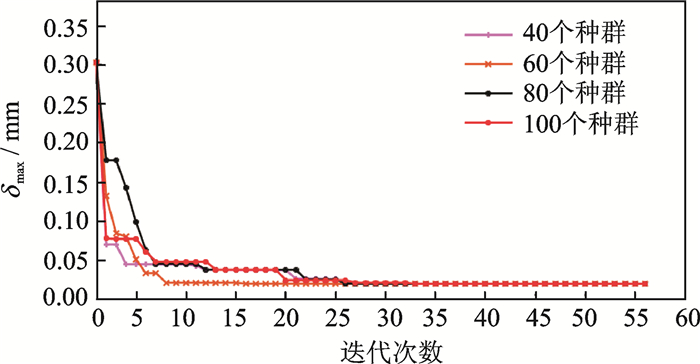
本文提出解决工艺特征约束的修补算法,基于此算法改进遗传算法完成定位/支撑布局优化,优化过程迭代图如图 14所示。由图 14可知,该算法在不同的种群试验时收敛速度快,具有较好的收敛性和优化效率。同时,由于约束模型的建立从广义数学模型出发,考虑了可能出现的各种约束模式,该修补算法具有普遍适用性。因此,该修补算法能有效解决工程中的约束优化问题。
|
图 14 优化迭代图 Figure 14 Iteration graph of optimization |
4 结论
(1) 飞机立式装配可重构柔性工装的定位误差主要来源于工装和工件的安装、制造等刚性误差和柔性形变产生的柔性误差。针对柔性定位误差,考虑到工装基于交点孔的定位方式和可重构性、柔性的特点,可以使用优化定位/支撑布局的方式来控制柔性误差。在飞机产品更新换代时,该误差控制策略可以不需要改变工装本体的设计,便能减小柔性误差的影响,很好的迎合了柔性工装的特点。
(2) 针对柔性定位误差的分析,可以通过分析工装的结构和原理,搭建误差传递流,然后基于齐次坐标变换原理建立误差的数学模型,从而进行误差的分析和计算。误差的传递可以根据实际结构特点分为并联和串联两种基本形式,以及它们的混合方式。
(3) 针对约束优化问题,可以采用修补的思想建立相应的约束处理方法。在工程应用中,考虑到约束的复杂性,以及其他处理技术在不可行解方面的处理缺陷,修补算法具有较强的优势。且简单的算法结构使修补算法处理约束优化问题时具有高效性和稳定性。本文针对机身装配中的工艺特征约束,从理论上建立约束的数学模型,针对约束数学模型提出的修补算法具有普遍意义,能够适用于各种约束优化问题。
(4) 通过应用实例可以看出,经优化后特征点的定位误差明显降低,装配精度提高,且框件平缓的误差波动更利于自动钻铆工艺。因此,本文提出的改进遗传算法和误差控制策略具有有效性和工程意义。
| [1] | QIU Y, ZHENG G L, RAO Y F, et al. Process-condition-driven automatic location of components[J]. Chinese Journal of Aeronautics, 2010, 23(4): 470–477. DOI:10.1016/S1000-9361(09)60243-0 |
| [2] |
王亮, 李东升.
飞机数字化装配柔性工装的低成本化[J]. 南京航空航天大学学报, 2012, 44(S): 27–31.
WANG Liang, LI Dongsheng. Low cost of flexible tooling technology for aircraft digital assembly[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(S): 27–31. |
| [3] |
沈建新, 田威.
基于工业机器人的飞机柔性装配技术[J]. 南京航空航天大学学报, 2014, 46(2): 181–189.
SHEN Jianxin, TIAN Wei. Aircraft flexible assembly technology based on industrial robots[J]. Journal of Nanjin g University of Aeronautics & Astronautics, 2014, 46(2): 181–189. |
| [4] |
田威, 廖文和, 唐金成.
面向复杂产品装配的柔性工装共性技术研究[J]. 中国机械工程, 2010, 21(22): 2699–2704.
TIAN Wei, LIAO Wenhe, Tang Jincheng. Common technology on flexible tooling for complex product assembly[J]. China Mechanical Engineering, 2010, 21(22): 2699–2704. |
| [5] |
韩锋, 田威, 廖文和, 等.
基于并联机构的轻型自主爬行钻铆系统法向调姿算法[J]. 航空学报, 2015, 36(6): 2083–2090.
HAN Feng, TIAN Wei, LIAO Wenhe, et al. Normal posture adjustment a lgori thm for lightweight auto-crawling drilling and riveting system based on parallel mechanism[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 2083–2090. |
| [6] | LU C, ZHAO H W. Fixture layout optimization for deformable sheet metal workpiece[J]. The International Journal of Advanced Manufacturing Technology, 2015, 78(1): 85–98. |
| [7] | XIONG L, MOLFINO R, ZOPPI M. Fixture la yout optimization for flexible aerospace parts based on self-reconfigurable swarm intelligent fixture system[J]. The International Journal of Advanced Manufac turing Technology, 2013, 66(9): 1305–1313. |
| [8] |
齐振超, 张开富, 李原, 等.
大型壁板自动钻铆定位误差分析与优化[J]. 航空学报, 2015, 36(10): 3439–3449.
QI Zh enchao, ZHANG Kaifu, LI Yuan, et al. Analysis and optimization for locating erro rs of large wing panel during automatic drilling and riveting[J]. Acta Aeronau tica et Astronautica Sinica, 2015, 36(10): 3439–3449. |
| [9] |
王仲奇, 黄杰, 康永刚, 等.
基于萤火虫算法的飞机弱刚性件装配定位策略优化[J]. 机械科学与技术, 2016, 35(4): 626–629.
WANG Zhongqi, HUANG Jie, KANG Yonggang, et al. Loca ting strategy optimization of aircraft weakly rigid parts assembly based on fire fly algorithm[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(4): 626–629. |
| [10] |
盖宇春, 朱伟东, 柯映林.
大型飞机总装配中支撑点设计分析技术[J]. 浙江大学学报(工学版), 2013, 47(12): 2176–2183.
GAI Yuchun, ZHU Weidong, KE Yinglin. Design and analysis of fuselage supporting posi tion for aircraft final assembly[J]. Journal of Zhejiang University(Engineerin g Science), 2013, 47(12): 2176–2183. |
| [11] | BARBOSA H J C, LEMONGE A C C. An adaptive penalty method for genetic algorithms in constrained optimi zation problems[M]. Vienna: I-Tech Education and Publishing, 2008: 9-34. |
| [12] | DEB K, SRIVASTAVA S. A genetic algorithm based augmented lagrangia n method f or constrained optimization[J]. Computational Optimization Applications, 2012, 53(3): 869–902. DOI:10.1007/s10589-012-9468-9 |
| [13] | TAKAHAMA T, SAKAI S. Constrained optimization by applyi ng the α constrained method to the nonlinear simplex method with mutations[J]. IEEE Transactions on Evolutionary Computation, 2005, 9(5): 437–451. DOI:10.1109/TEVC.2005.850256 |
| [14] |
朱嘉, 李醒飞, 谭文斌, 等.
基于激光干涉仪的测量机几何误差检定技术[J]. 机械工程学报, 2010, 46(10): 25–30.
ZHU Jia, LI Xingfei, TAN Wenbin, et al. Method of geometric error detection for measuring machine based on laser interferometer[J]. Journal of Mechanical Engineering, 2010, 46(10): 25–30. |
| [15] |
郭飞燕, 王仲奇, 康永刚, 等.
飞机立柱式柔性工装定位误差分析与精度保障[J]. 计算机集成制造系统, 2013, 19(8): 2036–2042.
GUO Feiyan, WANG Zhongqi, KANG Yonggang, et al. Error analysis and accuracy guarantee for column flexible tooling positioning of aircraft[J]. Computer Integrated Manufacturing Systems, 2013, 19(8): 2036–2042. |
| [16] |
李欣, 于乃辉, 曹玉君, 等.
基于状态空间模型的航天器装配角偏误差研究[J]. 国防科技大学学报, 2014, 36(1): 104–109, 115.
DOI:10.11887/j.cn.201401019 LI Xin, YU Naihui, CAO Yujun, et al. Angular variation analysis of spacecraft assembly based on state space model[J]. Journal of National University of Defense Tec hnology, 2014, 36(1): 104–109, 115. DOI:10.11887/j.cn.201401019 |
| [17] |
王勇, 蔡自兴, 周育人, 等.
约束优化进化算法[J]. 软件学报, 2009, 20(1): 11–29.
WANG Yong, CAI Zixing, ZHOU Yuren, et al. Constrained optimization evolutionary algorithms[J]. Journal of Software, 2009, 20(1): 11–29. |
| [18] | MEZURA-MONTES E, COELLO C A C. Constraint-handling in nature-inspired numerical optimization: past, pr e sent and future[J]. Swarm and Evolutionary Computation, 2011, 1(4): 173–194. DOI:10.1016/j.swevo.2011.10.001 |
| [19] | KRAMER O. A review of constraint-handling techniques for evolution strat egies[J]. Applied Computational Intelligence and Soft Computing, 2010(11): 1–11. |
| [20] | MONTEMURRO M, VINCENTI A, VANNUCCI P. The automatic dynamic penalisation method(ADP) for handling constraints with genetic algorithms[J]. Computer Methods in Applied Mechanics and Engineering, 2013, 256: 70–87. DOI:10.1016/j.cma.2012.12.009 |
| [21] |
林丹, 李敏强, 寇纪淞.
基于遗传算法求解约束优化问题的一种算法[J]. 软件学报, 2001, 12(4): 628–632.
LIN Dan, LI Minqiang, KOU Jisong. A GA-based method for solving constrained optimization problems[J]. Journal of Software, 2001, 12(4): 628–632. |
 2017, Vol. 49
2017, Vol. 49


