发动机的气动稳定性一直是航空发动机发展过程中一个极其重要的技术问题,直接关系到发动机的工作可靠性[1]。然而随着现代空战的日趋激烈,先进发动机追求高推重比,低耗油率,高压比等,使得航空发动机压缩部件(风扇和压气机,下文统称为压气机)的稳定性问题更加突出[2-3]。而战斗机高机动性和隐身设计等又带来进气道出口流场畸变的问题,对发动机尤其是风扇、压气机等压缩部件的影响很大,甚至会导致其发生失速或喘振。在超声速条件下,航空发动机压缩部件工作在高压比、高流量、高效率的极限工作状态,其稳定裕度的保障受到严重挑战[4]。引起发动机不稳定的因素有很多,可以被分为内部因子和外部因子两类。内部因子是由发动机内部变量引起的稳定裕度损失的因子,如发动机的控制容差、部件老化等。外部因子是由发动机外部环境造成发动机稳定裕度损失的因子,如雷诺数、平面波、冲击波、进气畸变等[5-6]。降稳因子通过使共同工作线上移或稳定边界线降低导致稳定裕度下降。目前的研究表明,进气畸变是影响发动机稳定裕度的主要因素[7],主要通过使发动机的稳定边界下移造成稳定裕度下降,还会影响压气机的流量、压比和效率以及其他部件的性能,使发动机整体性能下降[8-10]。
在20世纪60年代的越南战争中,美军投入的F-111战斗机由于发动机进口畸变导致频频失稳而被迫提前退役,并花费了十年时间解决相应的发动机稳定性问题[8]。随后美国机动车工程师学会的S-16技术委员会发布了推荐性标准:《燃气涡轮发动机进口流场畸变指南》和《燃气涡轮发动机进气总压畸变评审方法》等并被美国航空发动机通用规则所采用[2]。而国内稳定性研究起步较晚,在20世纪90年代中期才编写发布了国家军用标准《涡喷和涡扇发动机进口总压畸变评定指南》,但受限于国内的试验条件和设计经验,一直未受到相关部门的广泛采纳。于2005年发布的《航空燃气涡轮发动机稳定性设计与评定指南》,已经成为我国当前航空发动机气动稳定性设计和评定的重要依据[11]。
当发动机进入旋转失速或者喘振状态时,由于发动机各项参数会发生明显的变化,监测旋转失速和喘振的发生并不困难,然而即便是短暂的失稳状态也会在瞬间对发动机造成较大的损失。因此若能够对发动机失稳做出准确而及时的预测,在发动机将要失稳时稍微调整发动机的工作点就避免其进入喘振状态,这对发动机失稳问题的解决具有重要意义[12]。国内外对此已经做了大量的研究工作,其中基于相关系数的失速预测算法,通过对压气机转子叶片上方高频压力信号的分析和处理能够对发动机真实稳定裕度做出准确的预估,并且经过了压气机部件及发动机整机的试验验证,具有较好的普适性[13]。本文在此算法的基础上进行了改进,考虑到了试验时传感器采样周期固定,而叶片转动经过传感器时与传感器在此时间段内初次采样时间不固定的情况,可以有效防止信号交错。同时,由于鲜有研究对如何获取压气机工作状态的压气机稳定观测点进行讨论,因此在压气机进口、出口以及压气机首级转子叶尖各位置分别布置了压力传感器,探究最适宜作为压气机失速预测观测位置。
正是基于以上原因,本文针对低速双级轴流式压气机,开展了均匀进气及畸变条件下不同转速近喘失速试验,实时动态测量压气机由正常工作到失速工况下的压力信号,并在时域提出了一种压气机失速预测算法,对进口、出口以及压气机首级转子叶尖各位置压力信号预测分析,得出距叶片前端20%处叶尖位置最适宜作为压气机失速预测观测位置,此时压气机叶尖压力系数自相关性数据与压气机喘振裕度具有明显的单调相关性。
1 压气机失速近喘试验方案本试验的基本思路为:当压气机处于正常工作状态时, 通过控制压气机流量使得压气机向近喘失速状态逼近,同时记录下压气机不同观测点的压力信号,以探究压气机由正常工作状态向近喘失速工作状态的相关性规律。
1.1 试验目的及试验内容为寻找可以通过压力信号分析判断出压气机工作状态的压气机稳定观测点,建立压气机近喘失速工作状态与压气机信号的相关关系,尤其是探索在进气畸变情况下压气机信号与压气机稳定性关系,文中设计了如下试验内容。
(1) 开展压气机喘振边界获取试验(包括压气机在进口畸变条件下的喘振边界)。通过测量在不同转速下压气机进出口稳态总压,进行诱喘试验来捕捉压气机稳定边界,并通过进口截面安装总压畸变发生器进行轴向畸变诱喘。采用的畸变发生器有两种畸变网形式:周向90°单畸变区和周向90°对称双畸变区。诱喘手段为通过控制排气段电磁节流阀,不断减小压气机空气流量,从而改变压气机工作状态。
(2) 研究压气机动态压力信号与压气机工作状态的相关关系,记录在不同进气条件以及不同转速下压气机的压力动态数据。其中,进气条件分为3种,即无进气畸变,进气单畸变和进气双畸变;选取的动态压力信号采集试验转速分别为600,800,1 000 r/min。同时由于考虑到进气畸变和压气机叶尖形状等影响因素,因此需要在压气机进口周向及叶尖轴向均布动态压力传感器。
1.2 试验设施在低速双级轴流式压气机(Low speed compressor,LSC)上进行,试验系统简图如图 1所示,其主要装置为双级轴流式压气机、进排气系统、辅助动力系统和控制及信号测量系统。压气机为双级轴流式压气机,其主要设计参数为:外径0.9 m,轮毂比0.6,设计点的转速为1 500 r/min,压比为1.035,效率为0.88,流量为25 kg/s。进气系统主要由喇叭口、整流罩、进气管道和畸变模拟器(包含单畸变及对称双畸变模拟器,如图 2所示)组成。排气系统包含蜗壳、排气道、节流阀和消声室。动力系统为直流电机及其控制部件。信号测量系统包含传感器、信号处理器和存储器。

|
图 1 低速双级轴流式压气机试验系统简图 Figure 1 Schematic diagram of low speed two-stage axial flow compressor test system |

|
图 2 畸变模拟器 Figure 2 Distortion simulators |
1.3 信号测量系统
本试验中信号测量系统包含稳态测量系统及动态测量系统。稳态测量系统包含转速测量仪、压力测量系统、稳态压力探针和信号存储处理器,主要用于获得压气机在不同进气条件下的稳态总压信号,其中在进口布置周向均匀分布的36个稳态总压测点以及在压气机出口设置周向均匀分布48个稳态总压测点;动态测量系统由动态压力测量仪、动态压力传感器及信号存储处理器组成,主要用于压气机近喘失速判断及获取动态总压信号。其中,在进口周向均匀分布6个动态总压测点,压气机出口1个动态总压测点,压气机第一级转子叶尖部分6个动态总压测点(传感器分别在转子轴向离叶片前缘0%, 20%, 44%, 61%, 88%, 100%处分布)。
2 压气机压力信号时域分析为了消除环境等因素对试验数据的影响,提高数据的准确度,使得到的压气机压力信号试验规律更具一般性,选取压力系数Cp作为分析的主要对象,其定义如下
| $ {C_p} = \left( {p{\rm{ - }}{p_0}} \right)/{p_0} $ | (1) |
式中:p为压气机压力传感器采集数据,p0为压气机进口大气平均压力。
在压气机近喘试验中,可以借助喘振裕度来定量地评价压气机工作状态
| $ {S_{\rm{m}}} = \frac{{{\pi _{\rm{s}}}}}{{{\pi _{\rm{o}}}}}\frac{{{m_{\rm{o}}}}}{{{m_{\rm{s}}}}} - 1 $ | (2) |
式中:Sm为喘振裕度;π为压比; m为流量;下标中s为喘振边界上的值,o为工作线上的值。在此强调压气机近喘失速并非是发生喘振,失速状态是压气机喘振的前提以及必经之路。进行压气机压力系数时域分析的目的在于希望通过观测压气机的压力信号,实时分析出压气机的工作状态。由此必须要建立压气机失速预测算法,用于实时估计压气机工作状态。下文将具体介绍失速预测算法及其效果仿真验证。
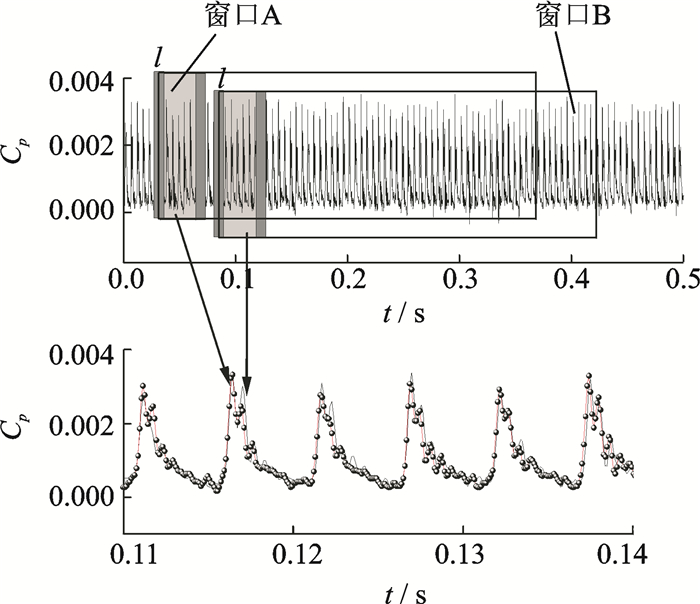
2.1 失速预测算法本文的失速预测算法是以压气机叶尖压力系数为例进行分析的,典型压气机叶尖压力系数在正常工作状态和近喘失速工作状态下脉动图如图 3, 4所示。
|
图 3 叶尖压力系数在正常工作状态的脉动图 Figure 3 Fluctuation diagram of blade tip pressure coefficient in normal working condition |

|
图 4 叶尖压力系数在近喘失速工作状态的脉动图 Figure 4 Fluctuation diagram of blade tip pressure coefficient in near surge stall state |
由图 3可知,在正常工作状态下,不同采样周期下的压气机压力系数曲线吻合程度较高,压气机压力系数的周期性和脉动规律良好。
由图 4可知,在近喘失速工作状态时,压气机压力系数在失速时其周期性及幅值均变化较大,失速团旋转周期明显为转子转动周期3~5倍,压力信号在失速团旋转周期内重复度较差,压力系数自相关性与时间序列相关性较差。
基于以上分析,提出压气机失速预测算法的基础思想:定义压气机压力系数自相关系数Ct,用于描述压力系数周期性重复度
| $ \begin{array}{l} {C_t} = \\ \frac{{\sum\limits_{i = n - {\rm{wnd}}}^n {|\left( {{C_{p, i}} - {C_{p, {\rm{ave}}}}} \right) \cdot \left( {{C_{p, i - N}} - {C_{p, {\rm{ave}}}}} \right)|} }}{{\sqrt {\left( {\sum\limits_{i = n - {\rm{wnd}}}^n {{{\left( {{C_{p, i}} - {C_{p, {\rm{ave}}}}} \right)}^2}} } \right) \cdot \left( {\sum\limits_{i = n - {\rm{wnd}}}^n {{{\left( {{C_{p, i - N}} - {C_{p, {\rm{ave}}}}} \right)}^2}} } \right)} }} \end{array} $ | (3) |
其中
| $ i = \left\{ {i|{C_t}\left( i \right) = {\rm{max}}{C_t}\left( {{i_1}, {i_2}, \ldots, {i_l}} \right)} \right\} $ |
式中:n为采样周期序列长度;wnd为自相关系数分析窗口长度;Cp, i为当前压力系数;Cp, ave为窗口内压力系数平均值;N为窗口A,B间隔序列信号长度。由于传感器采样周期固定,而叶片转动经过传感器时与传感器在此时间段内初次采样时间不固定,因此通过式(3)确定自相关系数在窗口A,B间保持对应,防止出现信号交错;其原理为先确定在叶片转动经过传感器时间段内的最大采样次数l,然后通过前后移动初始计算序列点i,对比选取出l段内使得Ct最大值的i值。
分析式(3)后可知,若失速预测算法计算得到的自相关系数Ct值接近1时,预示着压力信号脉动规律良好,则压气机工作状态良好,远离喘振区域;相反,若计算得到的自相关系数Ct值远离1,则说明压力系数脉动规律较差,压气机靠近喘振边界,发生近喘失速工况。
2.2 压力系数失速预测分析压气机压力系数近喘失速试验分别在无进气畸变、单进气畸变以及对称进气畸变情况下进行,下文将进行这3种进气情况下的压气机压力系数时域分析。
2.2.1 压气机工作特性曲线及喘振边界通过试验测量得到的压气机在进口无畸变情况下的工作特性图如图 5所示。由图可知,转速一定时,随着压气机流量(mc)的减小,压气机压比(πc)先增大后减少,其工作效率无法保持原有状态,呈直线下降。图 6, 7分别为压气机在进口单畸变情况和进口双畸变情况下的工作特性曲线图。当压气机工作在进口单畸变情况下,由于进口受到畸变气流的影响,理论上压气机喘振边界应该向右下方移动,然而由于本文压气机进口总压测点位于畸变模拟装置后方,导致捕捉得到的喘振边界与进口无畸变情况下差别不大,但其影响效果依然可以从压气机近喘时工作流量可以看出,压气机在进口畸变情况下其失速流量明显不同于压气机进口无畸变情况,因此这并不影响试验目的。其次,随着压气机流量减小,压比一定程度上升,使得压气机工作效率增大,随后压气机压比下降,压气机效率继续随着流量降低而降低。

|
图 5 压气机进口无畸变情况特性曲线 Figure 5 Characteristic curve of compressor inlet without distortion |

|
图 6 压气机进口单畸变情况特性曲线 Figure 6 Characteristic curve of compressor inlet under single distortion |

|
图 7 压气机进口双畸变情况特性曲线 Figure 7 Characteristic curve of compressor inlet under double distortion |
为了进一步说明试验中进气畸变对压力系数及压气机性能的影响,在此引入流量系数和压升系数,欲通过低速双级轴流式压气机在不同进气条件和不同转子转速(600, 800, 1 000 r/min)下的压升系数特效线变化趋势来说明进气条件的影响。
流量系数定义为
| $ \varphi = \frac{{{C_a}}}{{{U_m}}} $ | (4) |
式中:Ca为压气机进口轴向速度,Um为压气机转子中径处线速度。
压升系数表达式为
| $ \psi = \frac{{{p_{{\rm{out}}}} - {p_{{\rm{AIP}}}}}}{{\frac{1}{2}{\rho _0}U_m^2}} $ | (5) |
式中:pout为压气机出口总压,pAIP为气动界面(Aerodynamic interface plane, AIP)总压, ρ0为压气机进口气流密度。
图 8为压气机转速分别处于600, 800, 1 000 r/min下的压气机压升特性曲线。由图可知,在3种不同转速条件下,压气机压升特性曲线变化趋势类似,即ψ随着流量系数φ减小先增大,随着流量系数继续减小,压升系数不再增大转而开始下降,并在下降过程中出现失速。由此可以确定该试验研究的失速扰动现象为模态波扰动,其定义为随着压气机流量的减小,压气机压升系数的顶点处于压气机中所有转子叶片失速极限攻角之前,出现失速先兆,反之则为spike波扰动。

|
图 8 压气机压升特性曲线 Figure 8 Pressure characteristic curve of compressor |
由图 8可知,在转速一定和流量系数相同时,进气畸变使压气机失速先兆比无进气畸变时提前,但均在压气机压升特性顶点之后;同时进气畸变还影响了压气机的压升系数,相同流量系数时,压气机在无进气畸变下的压升系数大于进气畸变情况下压升系数,且大致上压气机进气畸变越大,压气机压比受到的影响就越大,压比损失也越多。
2.2.2 失速预测算法应用与分析分别在压气机进口、叶尖以及出口测点,探究通过式(3)计算得到的压力系数的自相关系数Ct与喘振裕度变化的相关性。
(1) 压气机进口位置
上文在介绍试验的动态信号测量系统时已经提到,压气机进口周向均匀布置了6个动态压力测点。由于压气机进口存在周向对称性,而进气气流在畸变进气的情况下,AIP界面空气流场不对称,因此下面将首先介绍在压气机进口存在单畸变进气模拟装置情况下进口测点失速预测分析。
图 9为压气机进口在单畸变进气情况下失速预测效果图。图中可以看出,除“进口传感器2#及4#”外,其他传感器在600, 800, 1 000 r/min转速下均呈现不规则相关性,即随着压气机流量减小,喘振裕度逐渐降低,而失速预测算法经过计算得到的自相关系数Ct随喘振裕度变化不具备规律性;对于2#, 4#传感器,其在喘振裕度较大或者非失速状态下,总体呈现出较高的自相关系数,但此期间自相关系数随喘振裕度变化震荡较大,且无明显上升或下降趋势;而在压气机发生失速时自相关系数突然下降,虽然这体现了失速气流形成的失速团对这两个传感器影响,但通过2#、4#传感器计算得到的自相关系数显然与喘振裕度不具有线性相关性。

|
图 9 单畸变进气情况下失速预测效果图 Figure 9 Stall prediction effect under single distortion inlet |
图 10为压气机进口传感器在单畸变进气情况下自相关系数的标准差计算结果图。由图可以看出,在时域范围内,通过自适应失速预测算法实时计算得到的自相关系数Ct均具有较小的标准差,说明本文提出的失速预测算法可准确地计算压气机压力系数自相关性;同时可以注意到,压气机进口5#传感器在800, 1 000 r/min转速下标准差较高,这说明压气机在单畸变进气情况下5#传感器位置处的压气机流场变化较大,失速预测算法并不适用于此种情况下的失速预测。

|
图 10 单畸变进气情况下自相关系数标准差效果图 Figure 10 Effect of standard deviation of autocorrelation coefficient under single distortion inlet |
综上,经过失速预测算法得到的自相关系数与压气机喘振裕度不具有明显的线性相关性,因此压气机进口位置不适宜作为基于失速预测算法的压气机失速预测观测位置。
(2) 压气机出口位置
在气流经过压气机压缩后,流经畸变模拟装置后的流场不均匀性会得到一定程度的改善,本试验在压气机出口与叶尖压力传感器同轴向位置布置了压气机出口压力传感器,下面将分别介绍基于失速预测算法压气机出口压力系数在均匀进气、单畸变进气与对称双畸变进气情况下的自相关系数与压气机喘振裕度相关性效果。
图 11为压气机出口失速预测效果图。对比均匀进气与单、双进气畸变显然可以发现,压气机出口位置受畸变影响较小,自相关系数在喘振裕度较大时即压气机流量有一定保证时震荡扰动较小;而在邻近失速阶段或失速阶段,压气机自相关系数与喘振裕度具有一定的正相关性,可以看出,随着压气机喘振裕度减小,压气机自相关系数降低。并且,压气机转速对出口位置压力系数计算得到的自相关系数影响有限。图 12为压气机出口相关系数标准差效果图,在3种进气条件下压气机不同喘振裕度下的自相关系数标准差基本小于0.025,说明在此时域内,压气机计算得到的自相关系数扰动小,具有稳定的估计能力。

|
图 11 压气机出口失速预测效果图 Figure 11 Stall prediction effect of compressor outlet |

|
图 12 压气机出口相关系数标准差效果图 Figure 12 Effect of standard deviation of compressor outlet correlation coefficient |
综上,在邻近失速或失速状态下,压气机出口位置在基于压力系数的失速预测方面具有一定的参考价值,可作为失速预测所需压力系数的测点之一。
(3) 压气机叶尖位置
由图 1的低速双级轴流式压气机试验系统图不难发现,压气机的首级转子叶片尤其是叶尖位置,在运行过程中既会受到进气畸变装置的影响,同时还会在失速发展及失速阶段中被自身所产生的失速团影响,因此压气机首级转子叶尖处压力系数脉动规律不仅在一定程度上能体现出压气机所受外界畸变气流影响还能反映出其本身的工作状态。因此,在压气机首级转子的叶尖处,按轴向分布安装了6个动态压力传感器,具体安装位置为距压气机首级转子前端0%, 20%, 44%, 61%, 88%和100%处,分别标记为1#~6#,即轴向覆盖压气机首级转子。下面将根据压气机3种不同的进气条件分别进行分析。
图 13, 14分别为压气机均匀进气条件下叶尖失速预测效果及自相关系数标准差效果图。由失速预测效果图可以看出,3#、6#传感器由失速预测算法得到的自相关系数Ct与压气机喘振裕度没有明显相关性关系,尤其3#传感器不仅受转速影响较大并且其自相关系数具有更大的标准差,由此可以说明该压气机在首级转子前端44%, 100%位置处的压气机叶尖压力系数脉动规律并不规则,基于失速预测算法的自相关系数无法反映压气机喘振裕度的变化,不宜作为基于压气机叶尖压力系数的失速预测测点。这是由于压气机首级转子44%位置极为接近叶尖顶点,压力系数受叶尖振动以及压气机转速影响脉动幅度较大;而首级转子100%处是转子与定子交界位置,压气机叶尖气流受到压气机定子导向作用,气流较为稳定,因此压气机叶尖压力系数受压气机工作状态尤其是喘振裕度影响并不大。与之相反,在压气机2#、4#、5#传感器中,压气机叶尖压力自相关系数与喘振裕度具有明显的线性相关关系,尤其在叶尖20%位置(压气机2#传感器),压气机自相关系数随喘振裕度线性变化范围大,在邻近失速与正常工作阶段均具有明显的相关关系。而压气机1#传感器由于其自相关系数脉动规律与压气机出口位置较为相似,不具有明显优势,因此不再做讨论。

|
图 13 压气机叶尖在均匀进气情况下失速预测效果图 Figure 13 Stall prediction of compressor blade tip under uniform inlet condition |

|
图 14 压气机叶尖在均匀进气情况下自相关系数标准差效果图 Figure 14 Effect of autocorrelation coefficient standard deviation of compressor blade tip under uniform inlet condition |
由上文对压气机叶尖在均匀进气条件下的失速预测分析可知,压气机叶尖位置在20%、61%以及88%处具有作为失速预测观测点的潜质,因此下面将重点介绍这3个位置在进气单畸变以及对称双畸变进气下压气机失速预测效果,叶尖位置其他传感器不再进行讨论。
图 15~17分别为压气机叶尖20%、61%以及88%处在均匀进气以及单畸变进气与对称双畸变进气条件下失速预测效果图。由图 15可知,压气机叶尖压力系数在单畸变进气与对称双畸变进气情况下均可以保持均匀进气情况下的失速预测能力,压力系数自相关系数在压气机喘振裕度下降时会随之下降,尽管转速会影响自相关系数的分布但是并不影响自相关系数与喘振裕度的线性相关趋势,因此可以认为畸变进气对压气机首级转子叶尖20%位置处压力系数失速脉动规律影响不大,可作为失速预测观测点。

|
图 15 压气机叶尖20%失速预测效果 Figure 15 Stall prediction effect at 20% blade tip of compressor |

|
图 16 压气机叶尖61%失速预测效果 Figure 16 Stall prediction effect at 61% blade tip of compressor |

|
图 17 压气机叶尖88%失速预测效果 Figure 17 Stall prediction effect at 88% blade tip of compressor |
对比图 16, 17后不难发现,两者具有一定的相似性。首先,它们的安装位置类似,均在压气机叶尖顶点气流方向后方;其次,两者压力系数自相关系数与压气机喘振裕度具有正相关性关系。然而在畸变进气压气机不同转速情况下,压气机自相关系数呈现不规律分布,压气机自相关系数变化幅度较大,即自相关系数安全阈值受进气畸变扰动,由此对安全阈值的设定带来了极大的困难。此外,图 15~17中自相关系数对应的标准差均在0.05以内,Ct在观测范围内扰动较小。
综上所述,所提的失速预测算法具有一定失速预测能力,同时在压气机首级转子叶尖20%位置处,最适合作为失速预测压力系数观测点,此时得到的自相关系数与压气机喘振裕度具有良好的线性相关性,因此可以以此传感器位置测得的压力信号代表压气机叶尖压力。
3 结论本文进行了压气机在均匀进气及畸变进气条件下不同转速近喘失速试验,并在时域内提出失速预测算法,对进口、出口以及压气机首级转子叶尖位置压力信号预测分析,得到了以下结论;
(1) 压气机各位置在3种进气条件下自相关系数的标准差计算结果图显示,自相关系数对应的标准差基本小于0.05,表明压气机计算得到的自相关系数扰动小,提出的失速预测算法具有良好的失速预测能力。
(2) 试验结果表明,在该低速双级轴流式压气机上布置的测点中,叶尖处离叶片前缘20%的位置最适宜作为压气机失速预测观测位置,此时压气机叶尖压力自相关性数据与喘振裕度具有明显的单调相关性。
| [1] |
王春利. 风扇/压气机气动稳定性的数值模拟研究[D]. 西安: 西北工业大学, 2007.
WANG Chunli. Numerical simulation of aerodynamic stability of fan/compressor[D]. Xi'an: Northwestern Polytechnical University, 2007. |
| [2] |
刘永泉, 施磊, 梁彩云.
某航空发动机全包线气动稳定性设计方法[J]. 航空动力学报, 2012, 27(11): 2462–2467.
LIU Yongquan, SHI Lei, LIANG Caiyun. Aerodynamic stability design method for certain aero-engine in whole engine's flight operating envelope[J]. Journal of Aeronautics, 2012, 27(11): 2462–2467. |
| [3] | RYU K J, LIM S, SONG D J. A computational study of the effect of angles of attack on a double-cone type supersonic inlet with a bleeding system[J]. Computers & Fluids, 2011, 50(1): 72–80. |
| [4] | GARG S. Aircraft turbine engine control research at NASA glenn research center[J]. Journal of Aerospace Engineering, 2013, 26(2): 422–438. DOI:10.1061/(ASCE)AS.1943-5525.0000296 |
| [5] |
王鹏. 某型涡扇发动机气动稳定性模拟[D]. 西安: 西北工业大学, 2006.
WANG Peng. Aerodynamic stability simulation of turbofan engine[D]. Xi'an: Northwestern Polytechnical University, 2006. |
| [6] | MANWARING S R, LORENCE C B, WADIA A R, et al. Inlet distortion generated forced response of a low-aspect-ratio transonic fan[J]. Journal of Turbomachinery, 1996, 119(4): V005T14A039. |
| [7] | HAH C, RABE D C, SULLIVAN T J, et al. Effects of inlet distortion on the flow field in a transonic compressor rotor[J]. Journal of Turbomachinery, 1996, 120(2): V001T01A135. |
| [8] |
赵运生. 航空发动机气动稳定性分析系统研究[D]. 南京: 南京航空航天大学, 2013.
ZHAO Yunsheng.Research on aero engine aerodynamic stability analysis system[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2013. |
| [9] | KURZKE J. Effects of inlet flow distortion on the performance of aircraft gas turbines[J]. Journal of Engineering for Gas Turbines & Power, 2006, 130(4): 117–125. |
| [10] | YAO Z H, BAO W, CHANG J, et al. Modelling for couplings of an airframe-propulsion integrated hypersonic vehicle with engine safety boundaries[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2010, 224(1): 43–55. DOI:10.1243/09544100JAERO618 |
| [11] |
代冰, 叶巍.
美、俄航空发动机稳定性标准对比分析[J]. 航空标准化与质量, 2009(2): 44–48.
DAI BING, YE Wei. Comparison and analysis of the stability standards of American and Russian aircraft engines[J]. Aeronautic Standardization & Quality, 2009(2): 44–48. |
| [12] |
黄伟. 航空发动机高稳定性控制及其在加速控制中的应用[D]. 南京: 南京航空航天大学, 2013.
HUANG Wei.Research on high stability control of aero-engine and their application in acceleration control[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2013. |
| [13] |
高坤华. 基于混沌理论的压气机失速预测及分析[D]. 西安: 西北工业大学, 2007.
GAO Kunhua.Predicet and analysis for compressor stall based on chaos theory[D]. Xi'an: Northwestern Polytechnical University, 2007. |
 2017, Vol. 49
2017, Vol. 49


