随着经济的快速发展,中国已成为能源消耗大国,而因制冷供热消耗掉的能源占全部能耗的30%左右[1]。在材料内部真空度低于100 Pa时,纤维的热阻最大,隔热效果最好[2]。表 1为不同骨架材料的导热系数,微纤维玻璃棉的导热系数最低,是目前真空绝热板中普遍采用的芯材[3]。
| 表 1 不同骨架材料的导热系数 Table 1 Thermal conductivity of different matrix materials |
纤维内部排列方位角、纤维长度、纤维直径以及接触热阻等使纤维传热过程具有典型的尺度效应,其中有效导热系数是表征材料隔热性能的重要参数,与纤维相和空气相的体积分数、纤维排列方式等有关[4]。目前在微尺度传热领域用到的格子波尔兹曼方法(Lattice Boltzmann method,LBM)[5]是基于概率学原理对分散粒子的平衡态分布函数进行统计,是连接宏观-微观、连续-离散的桥梁。与传统流体力学方法相比,LBM具有以下独特的优势[6]:(1) 能够处理复杂的边界条件;(2) 在迭代过程中, 粒子只是向周围邻近点迁移并碰撞, 所有粒子可同时进行运算,并行性高;(3) 能够直接模拟多孔介质等连通域流场,无须划分网格, 计算结果稳定;(4) 可以将复杂的非线性算子进行线性简化。
本文基于随机参数生成法(Quartet structure generation set,QSGS)原理构造纤维模型,将纤维视为生长相, 气体视为非生长相, 之后用格子波尔兹曼方程来求解导热系数,最后分析纤维直径、纤维长度、孔隙率等对于有效导热系数的影响。
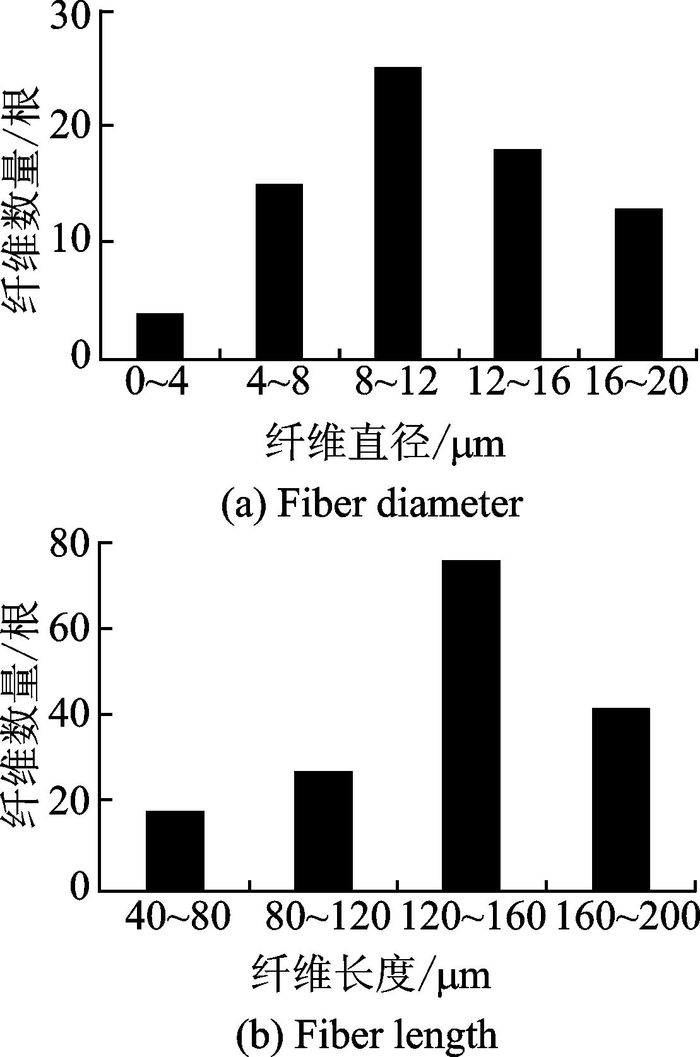
1 纤维模型 1.1 模型参数确定及构造原理通过KYKY-EM6000型电镜扫描仪可以观察到纤维排列有很大的随机性,选取放大500倍和1 000倍的电镜扫描图,如图 1所示。对其数量进行直方图统计后,加权平均后确定平均直径、平均长度,如图 2所示,可以看到纤维直径、纤维长度近似呈正态分布。

|
图 1 纤维放大500倍和放大1 000倍的电镜扫描图 Figure 1 Scanning electron microscope of fiber amplified 500 times and 1 000 times |
|
图 2 纤维直径和纤维长度直方图 Figure 2 Histogram of fiber diameter and fiber length |
在大气压环境下使用的纤维接触热阻很小,故不考虑接触热阻引起的热桥效应。纤维内部分布情况可以用相函数Z(x)来表示,通过统计气体相占全部相函数的比例, 即可得到纤维孔隙率。
| $Z\left( x \right) = \left\{ {\begin{array}{*{20}{l}} 1 & {x位于纤维骨架}\\ 0 & {x位于气体孔隙} \end{array}} \right.$ | (1) |
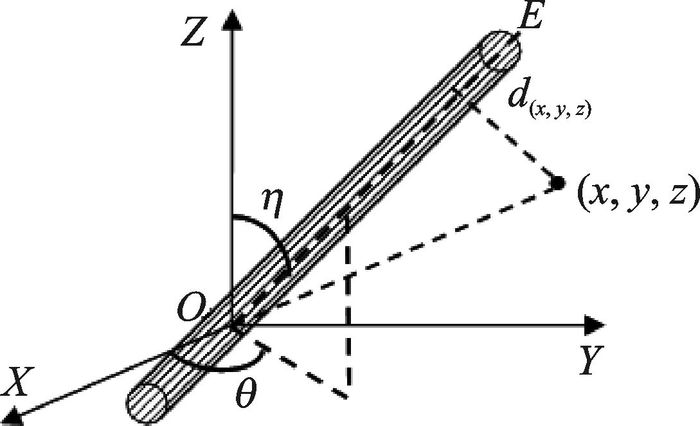
将纤维看作圆柱体,且纤维无交叉现象[7],构造模型参数如图 3所示, 其步骤如下:
|
图 3 纤维生长模型示意图 Figure 3 Diagrammatic sketch of fiber growth model |
(1) 划分网格100×100×100,将网格值初始化置0,代表孔隙气体非生长相。
(2) 给定纤维点生长概率Cd,产生一组随机坐标(X0, Y0, Z0)作为纤维生长点;产生一组角度(η,θ)来控制纤维生长方向,向周围15个方向生长, 得到单位长度纤维在3个坐标轴上的投影,得到其方向余弦分别为sinηcosθ, sinηsinθ, cosη。
(3) 以(X0, Y0, Z0)为中心,判断空间中的点(X, Y, Z)到纤维轴线的距离是否满足小于纤维半径的要求,空间点(X, Y, Z)到纤维生长轴线方向OE的距离为d(x, y, z)=||(sin ηcos θ, sinηsinθ, cosη)×(x-x0, y-y0, z-z0)||。若
(4) 当OE达到了纤维长度lf或达到了设定的纤维体积分数φf则停止运算,统计并输出数据文件。
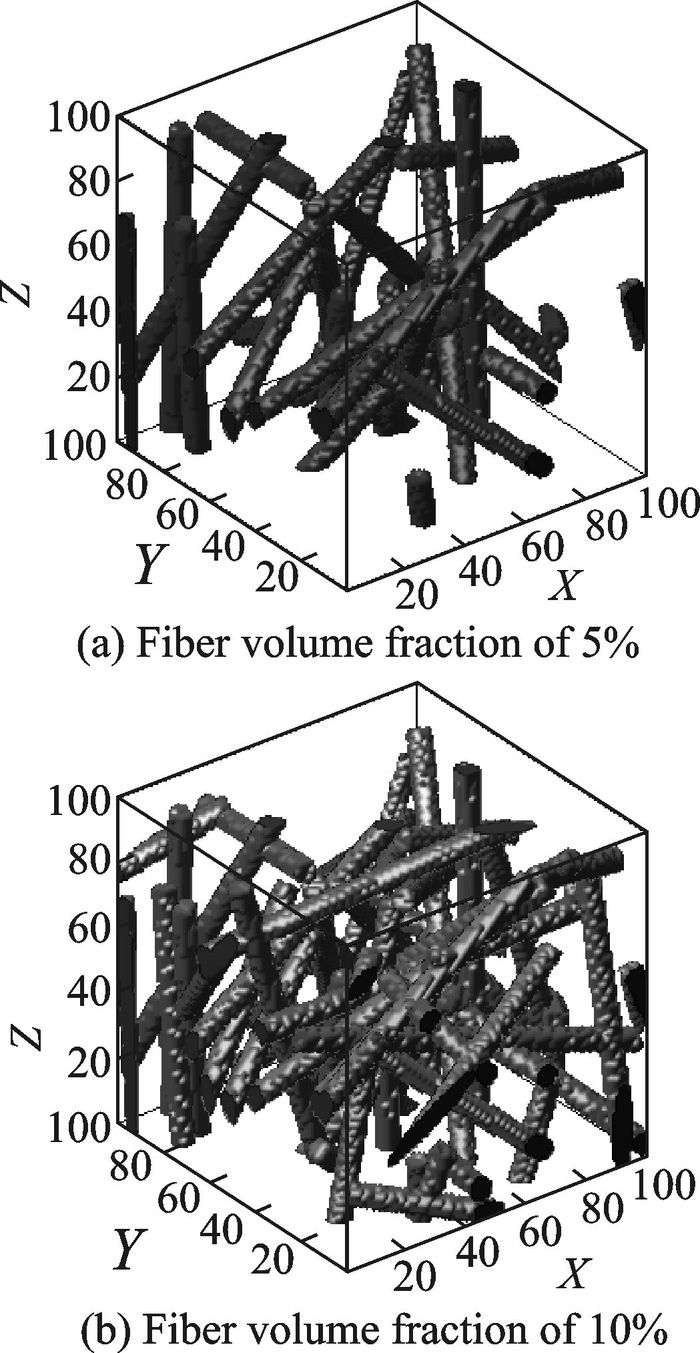
1.2 纤维物理模型构造实例纤维生长率Cd可以反映出纤维和空气的分布特征[8],例如通过电镜扫描得到100×100的区域内有10根完整纤维,则Cd=10÷100×100=0.001,表示在初始时每个节点有0.001的概率成为纤维生长点,而纤维长度(lf)、纤维半径(rf)以及孔隙率(1-φf)都可以通过电镜扫描得到,这里划分格子步长为δx=δy=δz=2 μm。由于模拟耗时较长,因此选取纤维体积分数为5%和10%的两种模型,图 4为结构模型。
|
图 4 纤维体积分数为5%和10%的结构模型(df=δx, lf=20 δx) Figure 4 Structure models with fiber volume fraction of 5% and 10% (df=δx, lf=20δx) |
2 格子波尔兹曼方程 2.1 离散速度矢量及方程
为了准确求解纤维的有效导热系数,必须正确得到其温度场分布及热流密度的能量输运方程,在无辐射热流及忽略纤维接触热阻的情况下,得到无内热源的能量方程为[9]
| ${\left( {\rho {c_{\rm{p}}}} \right)_{\rm{f}}}\left( {\frac{{\partial T}}{{\partial t}}} \right) = {k_{\rm{f}}}{\nabla ^2}T$ | (2) |
| ${\left( {\rho {c_{\rm{p}}}} \right)_{\rm{s}}}\left( {\frac{{\partial T}}{{\partial t}}} \right) = {k_{\rm{s}}}{\nabla ^2}T$ | (3) |
考虑温度及热流密度的连续性变化[10],在纤维相与气体相的接触处满足
| ${T_{\rm{f}}} = {T_{\rm{s}}}$ | (4) |
| ${k_{\rm{f}}}{\left. {\frac{{\partial T}}{{\partial \mathit{\boldsymbol{n}}}}} \right|_{{\rm{int}}}} = {k_{\rm{s}}}{\left. {\frac{{\partial T}}{{\partial \mathit{\boldsymbol{n}}}}} \right|_{{\rm{int}}}}$ | (5) |
| ${\left( {\rho {c_{\rm{p}}}} \right)_{\rm{f}}} = {\left( {\rho {c_{\rm{p}}}} \right)_{\rm{s}}}$ | (6) |
式中:下标s表示气相;f表示纤维相;int表示相接触面;n表示相接触面的单位法向量;气相有效导热系数ks=0.026 W/(m·K);纤维相有效导热系数kf=1.46 W/(m·K)。
纤维相和气体相的能量格子波尔兹曼方程为[11]
| $\begin{array}{l} {f_\alpha }(r + {\mathit{\boldsymbol{e}}_\alpha }{\delta _t},t + {\delta _t}) - {f_\alpha }\left( {r,t} \right) = \\ \quad \quad - \frac{{[{f_\alpha }\left( {r,t} \right) - f_\alpha ^{{\rm{eq}}}\left( {r,t} \right)]}}{{{\tau _n}}} \end{array}$ | (7) |
式中:fα为能量分布函数;fαeq为平衡态能量分布函数;r代表粒子在空间网格中的位置;eα为粒子迁移速度矢量;t为时间;δt为时间步长;τn为不同相的量纲一弛豫时间,为保证数值结果的稳定性,其值需要满足τn∈(0.5, 2)[12],表达式为
| ${\tau _n} = \frac{9}{5}\frac{{{k_n}}}{{{{\left( {\rho {c_{\rm{p}}}} \right)}_n}}}\frac{1}{{{c^2}{\delta _t}}} + 0.5$ | (8) |
式中
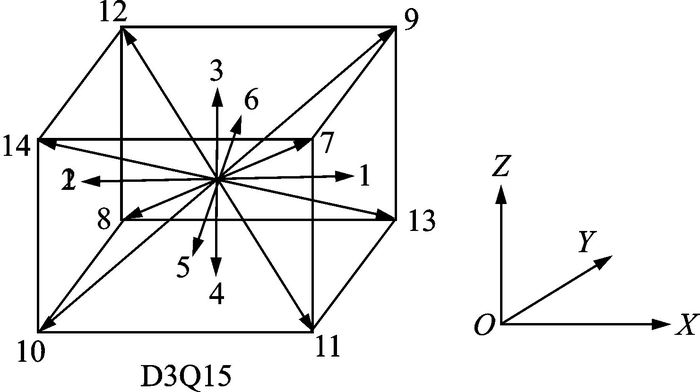
为了保证模拟结果的准确性,粒子离散速度矢量需要和三维模型中纤维向周围15个方向生长保持一致, 因此速度矢量选取D3Q15, 这样可以保证纤维各向同性的性质[13]。平衡态分布函数、宏观温度以及热流密度可表示为
| ${\mathit{\boldsymbol{e}}_\alpha } = \left\{ {\begin{array}{*{20}{c}} {\left( {0,0,0} \right)c} & {a = 0}\\ {\left( { \pm 1,0,0} \right)c,\left( {0, \pm 1,0} \right)c,} & {}\\ {\left( {0,0, \pm 1} \right)c} & {a = 1 \sim 6}\\ {\left( { \pm 1, \pm 1, \pm 1} \right)c} & {a = 7 \sim 14} \end{array}} \right.$ | (9) |
| $f_\alpha ^{{\rm{eq}}} = \left\{ {\begin{array}{*{20}{l}} 0 & {a = 0}\\ {\frac{T}{2}} & {a = 1 \sim 6}\\ {\frac{T}{{24}}} & {a = 7 \sim 14} \end{array}} \right.$ | (10) |
| $T = \sum\limits_\alpha {{f_\alpha },q = } \left( {\sum\limits_\alpha {{f_\alpha }{\mathit{\boldsymbol{e}}_\alpha }} } \right)\frac{{{\tau _n} - 0.5}}{{{\tau _n}}}$ | (11) |
当达到平衡态时,可以计算得到有效导热系数为
| ${k_{{\rm{eff}}}}{\rm{ = }}\frac{{L\int {q{\rm{d}}A} }}{{\Delta T\int {{\rm{d}}A} }}$ | (12) |
三维物理模型生成以及粒子迁移碰撞所耗费的时间较长,对于计算机硬件要求较高,为节约计算资源,设置上下表面为恒温面,上表面温度为35 ℃,下表面温度为15 ℃,周围4个表面为绝热面。对于绝热面,采用对称边界处理条件[14];对于恒温面,采用Zou和He提出的非平衡态反弹处理条件[15]
| ${f_\alpha } - f_\alpha ^{{\rm{eq}}} = - \left( {{f_\beta } - f_\beta ^{{\rm{eq}}}} \right)$ | (13) |
式中:α和β分别代表相反的两个方向;平衡态分布函数feq可以由局部温度边界条件得到。图 5, 6分别为粒子速度迁移矢量和边界处理格式。
|
图 5 D3Q15离散速度矢量 Figure 5 D3Q15 discrete velocity vectors |
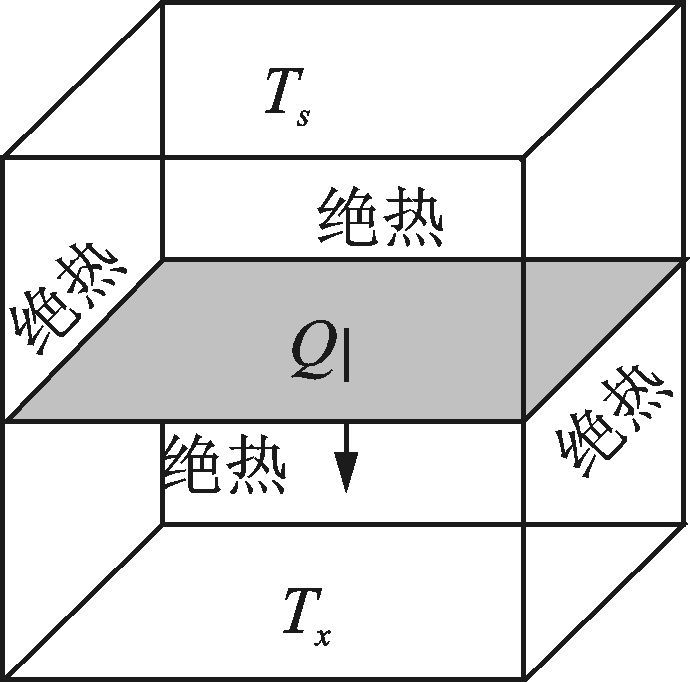
|
图 6 边界条件设置 Figure 6 Boundary condition setting |
2.3 模型验证
为了验证所采用方法的正确性, 采用天津英贝尔测控设备有限责任公司研发的智能平板导热系数测定仪,该仪器的型号为IMDRY3001-Ⅱ, 测试标准按照GB/T10294—2008进行, 其中测试用到的纤维板规格为300 mm×300 mm×10 mm, 如图 7所示。测试得到不同样品的有效导热系数实验结果和模拟得到的结果对比如表 2所示, 其中纤维孔隙率与密度的关系[16]表达式

|
图 7 测试用纤维板与平板导热系数测量仪 Figure 7 Test fiber plate and plate thermal conductivity measuring instrument |
| 表 2 纤维有效导热系数实验值与模拟值对比 Table 2 Comparison of experimental and simulation values of effective thermal conductivity of fiber |
| $\varphi {\rm{ = }}1 - \frac{\rho }{{{\rho _{\rm{f}}}}}$ | (14) |
式中:ρ为纤维板的表观密度;ρf为纤维密度[17],取2.5 g/cm3。
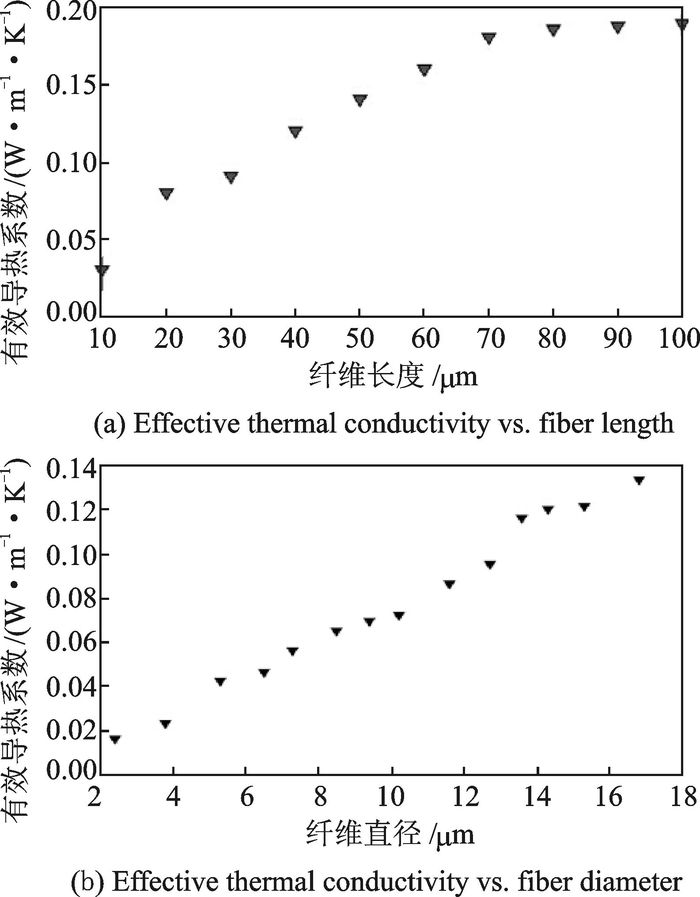
3 结果分析本文基于QSGS原理构造三维物理模型,结合格子波尔兹曼方法来求解有效导热系数,纤维的有效导热系数与纤维分布密切相关。图 8为有效导热系数随纤维直径、纤维长度的变化情况。从图 8可以看出,当纤维长度达到80δx以后,有效导热系数趋于平缓,在40δx~80δx间有效导热系数成线性增大,因此在生产纤维板时要预先对其进行蓬松、剪切处理,使用短布纤维。相比于纤维直径,纤维长度对有效导热系数的影响更大,只有当纤维直径与长度近似相等时,才会对有效导热系数造成比较大的影响,有效导热系数随着纤维直径的增大而变大,在生产工艺中尽量使用微细玻璃纤维。
|
图 8 有效导热系数与纤维长度和纤维直径的关系 Figure 8 Relationships between effective thermal conductivity and fiber length and fiber diameter |
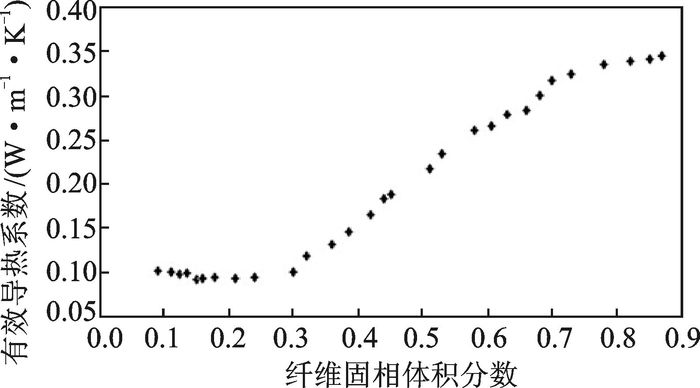
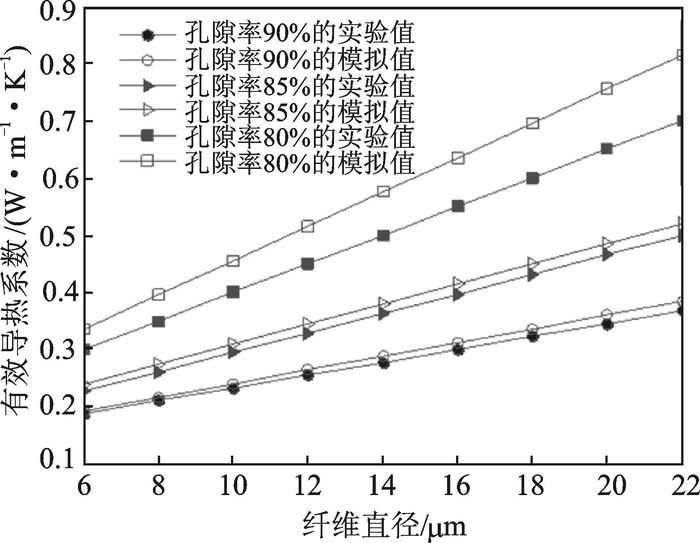
图 9为有效导热系数随纤维体积分数的变化规律,图 10为有效导热系数与孔隙率、纤维直径的关系。从图 9可以看出,当纤维体积分数0.2~0.3范围内,有效导热系数变化平缓,随着纤维体积分数的增大,有效导热系数成线性快速增加,纤维体积分数小于0.2并继续减小时,有效导热系数有增大的趋势,为保证纤维材料的低有效导热系数,一般纤维体积分数在20%~30%。在实验时采用了多种纤维长度的样品,对其纤维直径和孔隙率进行了直方图统计,为方便统计,将孔隙率80%±2%的样品的孔隙率记为80%,其余同理。从图 10可以看出,在同一孔隙率时,导热系数会随着纤维直径的增加而上升;在同一纤维直径下,导热系数会随着孔隙的增加而下降,并且孔隙率对有效导热系数的影响更大,在孔隙率较高时(>90%)可以通过使用微细纤维来进一步降低有效导热系数。
|
图 9 纤维体积分数与有效导热系数的关系 Figure 9 Relationship between fiber volume fraction and effective thermal conductivity |
|
图 10 有效导热系数与纤维直径和孔隙率的关系 Figure 10 Relationships between effective thermal conductivity and fiber diameter and porosity |
4 结论
(1) 基于随机参数生成法原理构造得到了纤维模型,并结合格子波尔兹曼方法来对模型进行有效导热系数求解,模拟求解得到的有效导热系数与实验测试值误差在10%左右,表明该方法可以用来预测纤维材料有效导热系数。
(2) 有效导热系数在纤维体积分数为20%~30%以内时有效导热系数最小,在0.09 W/(m·K)左右,当纤维体积分数>30%后有效导热系数近似成线性快速增加。
(3) 纤维长度在80~160 μm内有效导热系数从0.12 W/(m·K)线性增加到0.19 W/(m·K),当纤维长度进一步增加时,有效导热系数趋于平缓;纤维直径在4~36 μm内有效导热系数从0.018 W/(m·K)增加到0.14 W/(m·K),纤维长度比纤维直径对有效导热系数的影响更大。
(4) 相比于纤维直径,导热系数受孔隙率的影响更大,在孔隙率>90%后可以通过减小纤维直径来降低有效导热系数。
| [1] |
杨利明.
绿色建筑能耗评价方法及能耗降低新技术探讨[J]. 制冷技术, 2012, 32(2): 48–51.
YANG Liming. Green building energy consumption evaluation method and building efficiency new technology review[J]. Chinese Journal of Refrigeration Technology, 2012, 32(2): 48–51. |
| [2] |
陈照峰, 李承东, 陈清, 等.
真空绝热板芯材研究进展[J]. 科技导报, 2014, 32(9): 59–62.
DOI:10.3981/j.issn.1000-7857.2014.09.008 CHEN Zhaofeng, LI Chengdong, CHEN Qing, et al. Research progress of vacuum insulation panel core materials[J]. Science & Technology Review, 2014, 32(9): 59–62. DOI:10.3981/j.issn.1000-7857.2014.09.008 |
| [3] | DULLIEN F A L. Structure of porous media[J]. Transport Processes in Porous Media, 1991, 202: 3–41. |
| [4] |
何雅玲, 谢涛.
气凝胶纳米多孔材料传热计算模型研究进展[J]. 科学通报, 2015, 60(2): 137–163.
HE Yaling, XIE Tao. A review of heat transfer models of nanoporous silica aerogel insulation material[J]. Chinese Science Bulletin, 2015, 60(2): 137–163. |
| [5] |
马强, 陈俊, 陈振乾, 等.
分形多孔介质传热传质过程的格子Boltzmann模拟[J]. 化工学报, 2014, 65(S1): 180–187.
MA Qiang, CHEN Jun, CHEN Zhenqian, et al. Lattice Boltzmann simulation for heat and mass transfer in fractal porous media[J]. CIESC Journal, 2014, 65(S1): 180–187. |
| [6] |
阚安康, 张婷婷, 楼海军.
基于分形理论的玻璃纤维真空绝热热工特性研究[J]. 真空科学与技术学报, 2013, 33(7): 654–660.
KAN Ankang, ZHANG Tingting, LOU Haijun. Fractal study of effective thermal conductivity of fiber glass materials[J]. Chinese Journal of Vacuum Science and Technology, 2013, 33(7): 654–660. |
| [7] |
钱吉裕, 李强, 宣益民, 等.
确定复杂多孔材料有效导热系数的新方法[J]. 中国科学, 2004, 34(11): 1247–1255.
DOI:10.3969/j.issn.1674-7259.2004.11.005 QIAN Jiyu, LI Qiang, XUAN Yimin, et al. A new method to determine the effective thermal conductivity of complex porous materials[J]. Engineering & Materials Science, 2004, 34(11): 1247–1255. DOI:10.3969/j.issn.1674-7259.2004.11.005 |
| [8] |
栾辉宝, 徐辉, 陈黎, 等.
有限容积法与格子Boltzmann方法耦合模拟传热流动问题[J]. 科学通报, 2010, 55(32): 3128–3140.
LUAN Huibao, XU Hui, CHEN Li, et al. Coupling between FVM and LBM for heat transfer and fluid flow problems[J]. Chinese Science Bulletin, 2010, 55(32): 3128–3140. |
| [9] | PAEK J W, KANG B H, KIM S Y, et al. Effective thermal conductivity and permeability of aluminum foam materials[J]. Thermophys, 2000, 21(2): 453–464. DOI:10.1023/A:1006643815323 |
| [10] | CHEN X, HAN P. A note on the solution of conjugate heat transfer problems using SIMPLE-like algorithms[J]. International Journal of Heat and Fluid Flow, 2002, 21(4): 463–467. |
| [11] | WANG M, WANG J, PAN N, et al. Mesoscopic predictions of the effective thermal conductivity for microscale random porous media[J]. Physical Review: E, 2007, 75(3): 1256–1258. |
| [12] | XUAN Y M, ZHAO K, LI Q. Investigation on mass diffusion process in porous media based on Lattice Boltzmann method[J]. Heat and Mass Transfer, 2010, 46(10): 1039–1051. DOI:10.1007/s00231-010-0687-2 |
| [13] |
杨建明, 吴会军, 王沫然.
预测纤维增强气凝胶复合材料有效导热系数的研究进展[J]. 材料导报, 2015, 29(11): 124–128.
YANG Jianming, WU Huijun, WANG Moran. Advances in prediction of thermal conductivity of fiber reinforced airgel composites[J]. Materials Herald, 2015, 29(11): 124–128. |
| [14] | FREED D M. Lattice-Boltzmann method for macroscopic porous media modeling[J]. Int J Mod Phys C, 1998(9): 1494–1503. |
| [15] | ZOU Q, He X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model[J]. Physics of Fluids, 1997, 9(6): 1591–1598. DOI:10.1063/1.869307 |
| [16] |
张辑洲, 朱宝娟, 余其铮.
超细玻璃纤维的有限导热系数计算式[J]. 哈尔滨工业大学学报, 1993, 25(1): 22–23.
ZHANG Jizhou, ZHU Baojuan, YU Qizheng. Calculating formula of finite thermal conductivity of superfine glass fiber[J]. Journal of Harbin Institute of Technology, 1993, 25(1): 22–23. |
| [17] | WANG Moran, KANG Qinjun, PAN Ning. Thermal conductivity enhancement of carbon fiber composites[J]. Applied Thermal Engineering, 2009, 29: 418–421. DOI:10.1016/j.applthermaleng.2008.03.004 |
 2017, Vol. 49
2017, Vol. 49


