地基剪切波为横波,其传播方向与土颗粒振动方向垂直,剪切波速与土体剪切刚度有关,波速大小可直观反映土体的剪切性能[1]。因此剪切波速测试被广泛应用于工程地基压实质量及力学性能的评估测试中。而且由于波速测试的区域性,与传统的灌水法、灌砂法相比,剪切波速测试方法场地代表性更强,成本更低[2]。目前成熟的剪切波速测试方法主要是基于密实度、含水率等土体物性参数建立剪切波速相关性模型,工程应用时通过剪切波速反推土体压实程度,以达到评价地基强度及承载能力的技术目的。
土基剪切波速与土的颗粒大小、密实程度、含水率、应力状态等因素有关,直接反应土基抗剪能力的大小。当土层其他性能保持不变,表面受到压应力增大时,土体本身内摩擦角、粘聚力等物性参数基本保持不变,依据土力学莫尔库伦强度理论,土体抗剪强度增大,则反映土体抗剪能力的剪切波速也随之增大[3-6]。如土体剪切波速测试在地基施工过程中进行,且测试按照土基分层填筑均在薄层土填筑压实之后进行,则此时土基薄层表面为自由面,将土层作为一个整体考虑,其受到的压应力为零,此时土基剪切波速与应力状态无关,而只与压实度、含水率相关,应用已有剪切波速相关计算模型可实现较精确的测试评价。但当土层较厚、剪切波速测试对象为已填筑完毕土基或自然地基时,对位于地层深处地基,其剪切波速不仅受压实度、含水率影响,且受土层表面压应力影响较大[7-10],但目前对土层剪切波速与土基应力相关性的研究较少,传统的剪切波速计算模型均未考虑应力因素的影响,此时用传统剪切波速模型计算结果误差较大,造成土层承载能力评估失真[11-13],对受大荷载飞机作用的机场地基尤其如此。随着近年来剪切波速在地基承载评价、地基深层勘探等工程中的应用日渐广泛,对现有剪切波速模型进行地基应力影响修正、建立适用于地基深层的剪切波速评价模型已成为亟待解决的热点问题。
鉴于此,本文对粘土、砂土两种土基开展剪切波速测试研究,实际应用中剪切波速测试多针对压实度为95%以上的地基,确定室内试验对象为95%压实度土样,试验条件为变应力状态,采集参数为剪切波速。设计变应力剪切波速测试仪,分析最佳含水率状态下压实土体应力与剪切波速的相关关系。在土层应力分布均匀及土体应力传递分散损失的前提下,建立土层应力与剪切波速的相关性模型。对同压实度、同含水率理想土层,分析土体自重应力及附加应力条件下剪切波速随地基深度的变化规律,并对模型计算结果与现场实测数据进行对比分析,验证模型的有效性。该研究成果将大幅提升深层地基剪切波速测试试验及物探试验的评估准确性,对大应力、高深度地基土剪切波速特性及抗剪性能研究与分析有重要参考价值。
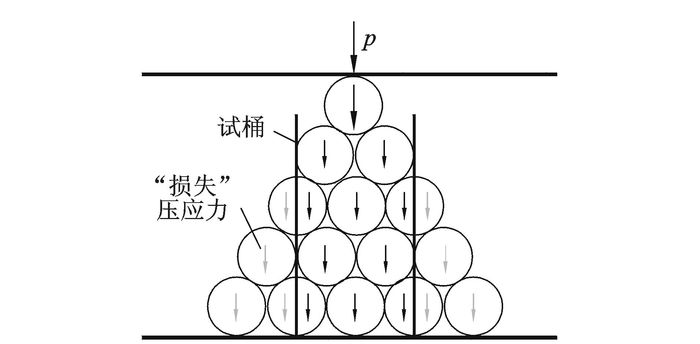
1 基于应力损失的剪切波速理论模型 1.1 土中应力基本假设依据土力学相关理论,土中应力传播主要是通过土颗粒间应力传递实现的,其随土层深度增加有应力扩散的特点,如图 1所示,应力随颗粒向下传播,随土层深度的增加土层应力不断变小,应力分布范围不断变大,但以无限远平面为限,每层的总压力为定值p。此时如在土体中加一试桶,如图 1所示,试桶将土颗粒分为桶内颗粒及桶外颗粒两部分,而上部压应力在随土颗粒传播时会受到试桶限制的影响,假设土层固定深度处的应力大小不发生改变,则原桶外颗粒受到的压应力被试桶分担。
|
图 1 土中应力扩散及应力损失示意图 Figure 1 Stress diffusion and stress loss in soil |
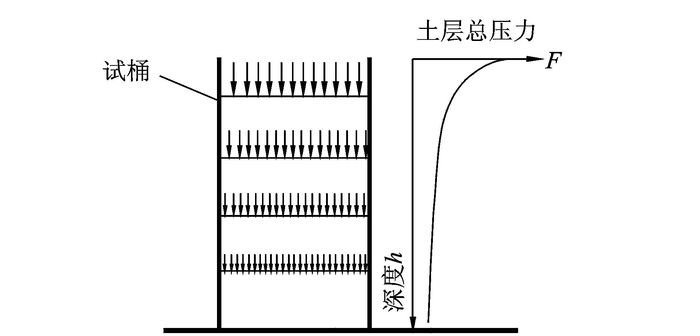
如图 1所示,固定土层处的总压力仍然为p,但其中一部分由土颗粒承担,另一部分由试桶分担。以土为研究对象,土中应力分布如图 2所示,则试桶中土体随深度增加,应力受到损失,且依据应力扩散理论,深度越深应力损失越大,图 2右侧示出了土层总压力F随深度增加而损失的示意图。在对试桶内土颗粒进行应力研究时,为方便计算,假设土层任意深度处受到的压应力为均匀分布,如图 2所示,则基于应力扩散及应力损失的固定深度土层压应力计算符合布辛尼斯克公式计算法则。
|
图 2 土中应力分布示意图 Figure 2 Stress distribution in soil |
1.2 应力-剪切波速理论模型
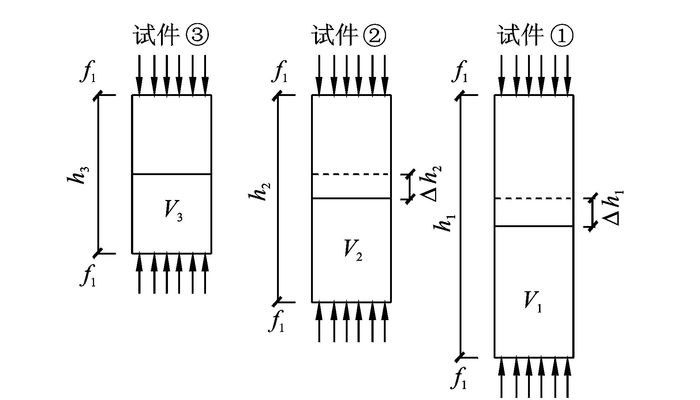
依据莫尔库伦强度理论,土中应力越小,土的抗剪强度越低,而作为反映土抗剪能力的剪切波速也随之减小。为在试验中真实反映土体应力扩散及应力损失的效应,排除土体自重应力的影响,试验时采用圆柱形试件,在试件两端加载应力并测试其剪切波速时,圆柱试件处于水平状态,且施加应力测试过程中试件长度不能发生明显变形,避免试件密实程度发生改变造成土颗粒结构重组,具体试验过程及试验设计详见第2节。应力-剪切波试验设计示意图如图 3所示,采取3个不同长度的圆柱形土样试件,高度为h,试件土质种类、含水率、密实度相同,在试件两端对称施加应力为f1,在该应力状态下,3个试件的剪切波速测得为V1,V2,V3。图 3中各试件中间的黑实线为试件中线,因试件两端受应力大小相等、方向相反,则试件中应力分布以中线为界呈对称分布,具体计算分析时仅考虑h/2的土样中应力状态即可,各试件中h/2范围内土体整体剪切波速分别为V1,V2,V3。
|
图 3 应力-剪切波试验设计示意图 Figure 3 Stress-shear wave velocity test design |
从图 3中可看出因② 号试件与① 号试件表面受压应力相等,则① 号试件虚线位置以上的土体应力状态与② 号试件h2/2范围内土体应力状态相同,该段试件整体剪切波速相同,则剪切波速V2与V1的差异可看做由于Δh1范围内土体剪切波速发生变化而引发,其原因为由于应力传递的扩散与损失,Δh1范围内土体应力降低,剪切波速随之降低。试验过程中② 号试件与① 号试件的长度可进行控制,使Δh1范围内土层高度较低呈薄饼状,由于Δh1较小,可近似认为Δh1上下表面应力相同,应力损失为零,即Δh1土层内应力分布均匀且传递无损失,则该土层剪切波速可近似看做均匀,记为Vs1,见式(1)。
| ${V_{{\rm{s1}}}} = \frac{{\frac{{{h_1} - {h_2}}}{2}}}{{\frac{{{h_1}}}{{2{V_1}}} - \frac{{{h_2}}}{{2{V_2}}}}}$ | (1) |
Δh1土层上表面压应力记为σ1,可由圆形地基均布荷载布辛尼斯克公式计算,即
| ${\sigma _1} = {f_1}\left[ {1 - {{\left( {\frac{1}{{1 + {{\left( {2r/{h_2}} \right)}^2}}}} \right)}^{3/2}}} \right]$ | (2) |
式中r为试件表面受圆形均布荷载半径。通过② 号试件与① 号试件的相关数据处理可得出:该土在最佳含水率、95%压实度、Δh1厚度的土层受应力为σ1状态下,平均剪切波速为Vs1。将此数据记录在土中应力σ、剪切波速Vs与土基深度h的三向坐标图中,如图 4所示。其中该组数据的土基深度h定位时,为坐标图中靠下方的坐标轴上自行选择一个位置进行描点。同理对③ 号试件与② 号试件的相关数据进行处理可得Δh2厚度的土层受应力为σ2状态下,平均剪切波速为Vs2。从图 3中可看出,Δh2厚度土层位于Δh1厚度土层上方,且Δh2厚度土层底面为Δh1厚度土层顶面,则将σ2, Vs2绘入三向坐标图中,如图 4所示。
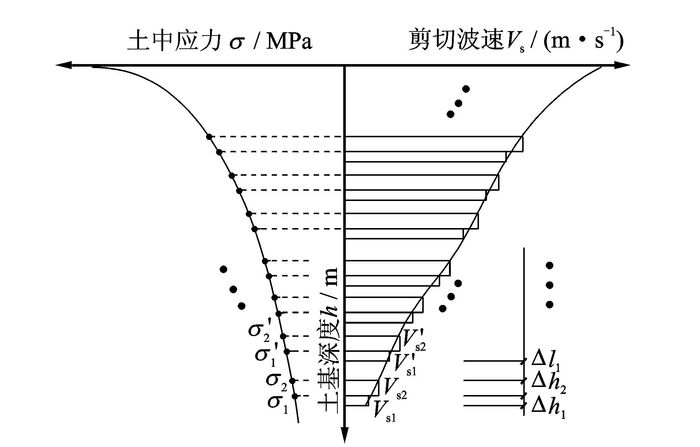
|
图 4 剪切波速与应力相关性示意图 Figure 4 Correlation of stress and shear wave velocity |
将试件表面所受压应力变为f2,且f2>f1,测试试件剪切波速为V1′,V2′,V3′。对试验数据作同样处理,Δh1土层上表面压应力记为σ1′,对应剪切波速为Vs1′;Δh2土层上表面压应力记为σ2′,对应剪切波速为Vs2′。将数据绘入三向坐标图,如图 4所示,其中定位在Vs1′所对应的土基深度位置时,需确定Δl1,Δl1定义为在应力扩散及应力损失条件下,土层受压应力为σ1′时的深度位置与土层受压应力为σ2时的深度位置之差,可由式(3) 求出。
| ${\sigma _2} = \sigma _1^\prime \left[ {1 - {{\left( {\frac{1}{{1 + {{\left( {r/\Delta {l_1}} \right)}^2}}}} \right)}^{3/2}}} \right]$ | (3) |
依此类推,不断改变土样试件表面受到的压应力fi,进行剪切波速测试试验,经处理可得出一系列数据,将其绘入三向坐标图如图 4所示,可以得出该土样在最佳含水率、95%压实度时,考虑土颗粒应力传递特性的土中应力与剪切波速的相关关系。
2 试验设计及方案为消除土体应力传递、扩散及损失过程中自重应力的影响,剪切波速测试过程中圆柱形试件保持水平放置。剪切波采用自触发的方式进行激发,测试方法为首至波时间测试法。在试件表面施加压力时,必须保证试件长度在压应力作用下不发生明显改变,以避免试件内土颗粒排布结构发生变化,剪切波速测试时信号发射及信号接收传感器必须紧贴试件表面,保障充分接触。施加的应力通过千分表进行读数。依据此原理设计变应力剪切波速测试仪,如图 5,6所示。
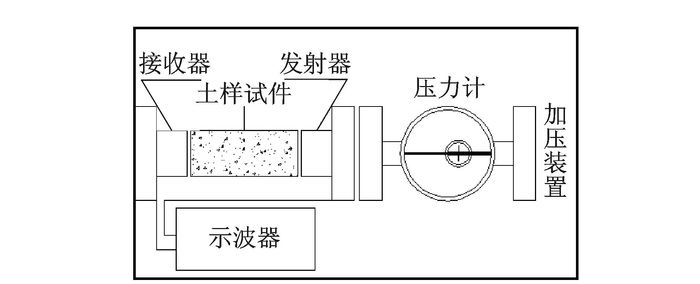
|
图 5 试验仪器设计图 Figure 5 Design of test instrument |

|
图 6 变应力剪切波速测试仪器 Figure 6 Test instrument of shear wave velocity under changing stress |
由图 5,6可见,试验试件制备为圆柱形,制备试件采用直径5 cm圆柱形试桶进行击实,试件压实度为95%,含水率为最佳含水率,将制备好的试件水平放置于测试仪内,通过加压装置对试件施加压应力,并通过压力计控制应力大小,同时采用GJY-1工程测试仪对试件在固定应力下的剪切波速进行测试。
当试件受到任何压应力时,其本身就会发生变形,但试验认为当该变形较小时,基本认为试件的变形可忽略,在土力学分层总和法计算最终沉降量中设定附加应力等于0.2倍自重应力下方的地基变形不予计算。以此为依据,经过土体变形换算,可大致得出(试件长度/可忽略变形)值近似为:1 000:1~500:1。本实验中的试件长度为10 cm以上,兼顾考虑测试设备的精度,设置土体变形在0.2 mm以下时,认为试件无体积变化,实验室测试长度可通过游标卡尺得到。
试验用粘土液限含水率为21.6%,塑性指数Ip=15.4,为粉质粘土,最佳含水率19%,最大干密度1.94 g/cm3;试验用砂土为粉砂,大于0.075 mm颗粒含量为93.80%,其中0.075~0.25 mm含量64.8%,0.25~0.5 mm含量13.8%,0.5~2 mm含量7.1%,大于2 mm含量8.1%,最佳含水率17%,最大干密度1.74 g/cm3。试验制备试件在单个应力状态下为3个长度规格,分别为5,8,11 cm。
3 数据分析与建模砂土、粘土的试验中应力采用15个应力状态,分别为37.89,75.79,113.68,151.58,189.47,227.37,265.26,303.16,341.05,378.95,416.84,454.74,492.63,530.53,568.42 kPa,在每个应力状态下,对①~③ 号试件分别进行剪切波速的测试。各应力下不同长度试件的整体剪切波速与试件表面应力关系如图 7,8所示。
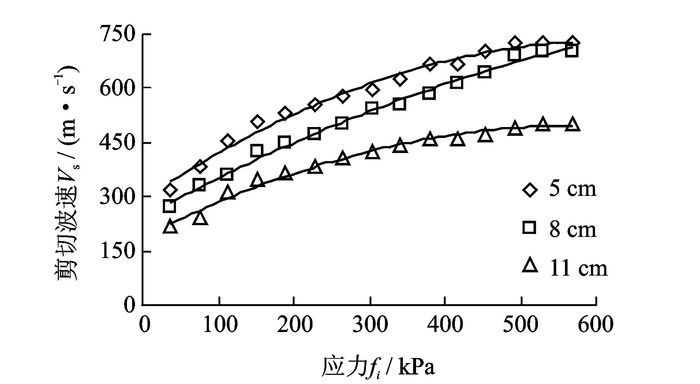
|
图 7 砂土试件整体应力-剪切波速曲线 Figure 7 Overall stress-shear wave velocity curve in sandy soil |
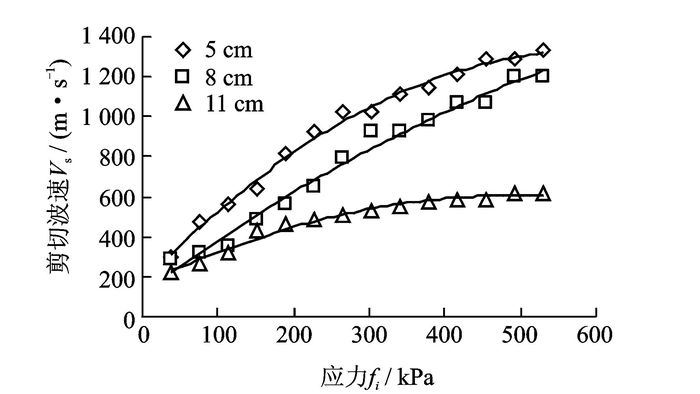
|
图 8 粘土试件整体应力-剪切波速曲线 Figure 8 Overall stress-shear wave velocity curve in clay |
从图 7,8中可看出,砂土、粘土的应力-剪切波速曲线变化趋势基本一致,剪切波速随应力的增大总体呈增大趋势,因为依据土体强度理论,土中应力增大引发土体抗剪强度增大,土体剪切刚度增大,剪切波速也随之增大。依据试验数据可看出,同等应力条件下,土体剪切波速随试件长度的增大而有所下降,这主要是因为土中应力在土颗粒间传播时会发生应力扩散及应力损失的现象。试验中剪切波沿圆柱体试件长度方向传播,当土体沿剪切波速传播方向仅受到附加应力作用影响时,随剪切波传播深度的增加,土体应力逐渐变小,对应土层所处位置处剪切波速变小。则说明试件越长,剪切波传播路径越长,土柱体应力损失越大,剪切波速减小也越发严重,这是造成长度较长的土柱体剪切波速测试结果较小的根本原因。
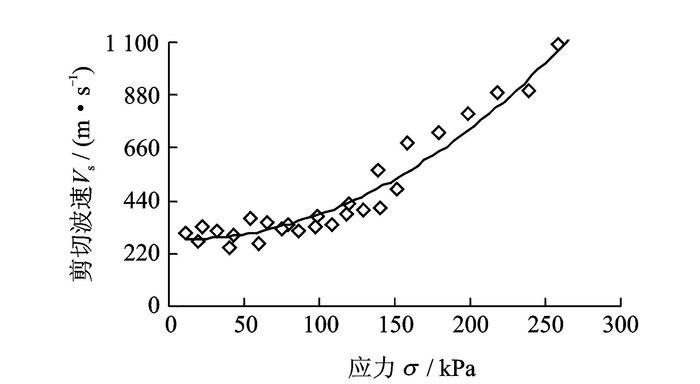
采用第1节中论述的应力-剪切波速理论建模方法对试验数据进行处理,可得到试验砂土及粘土在仅受附加应力作用下的应力-剪切波速曲线,如图 9,10所示。
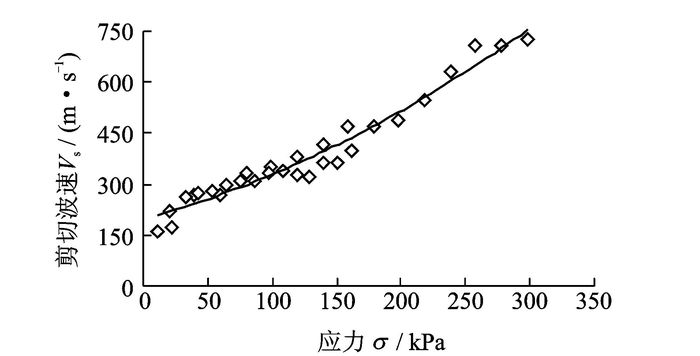
|
图 9 砂土应力-剪切波速曲线 Figure 9 Curve of stress-shear wave velocity in sandy soil |
|
图 10 粘土应力-剪切波速曲线 Figure 10 Curve of stress-shear wave velocity in clay |
从图 9,10中可看出其他条件固定的前提下,土基应力对土基剪切波速的影响显著,土样同密实度条件下,剪切波速随应力的变化幅度可达5倍以上,工程中必须考虑应力对剪切波速的影响。对图 9,10中所示的试验土体应力-剪切波速数据进行数据拟合分析,选取相关系数最高的二次多项式进行曲线趋势描述。砂土见式(4),相关系数为0.959;粘土见式(5),相关系数为0.955。
| ${V_{\rm{s}}} = 0.003{\sigma ^2} + 1.002\sigma + 199.5$ | (4) |
| ${V_{\rm{s}}} = 0.013{\sigma ^2} - 0.251\sigma + 281.5$ | (5) |
式(4,5) 反映的是试验土样的剪切波速与自身所受应力的相关关系,σ为测试土层的应力,该应力为总应力,包括土体自重应力及附加应力。利用该模型可对试验地基土任意深度的95%地基压实度进行准确测试评估,如测试剪切波速小于模型计算结果,则可判定该地基承载能力及抗剪强度已发生降低,可能造成后期地基沉陷。
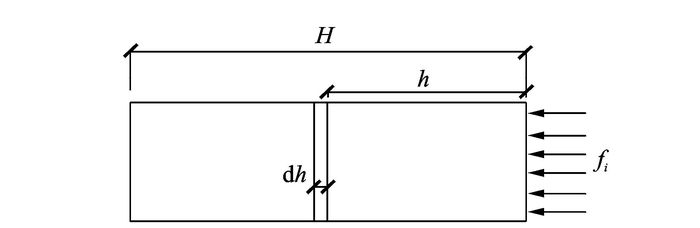
为验证该模型测试精确性,设计验证试验(图 11),试验土样为砂土,其物理参数与建模土样一致,压实度95%,含水率为最佳含水率状态,试件直径5 cm,长度为14 cm。试件保持水平状态下,表面随机施加10组不同压应力fi,读取压应力数值并测试试件整体剪切波速。
|
图 11 验证试验示意图 Figure 11 Verification test |
如图 11所示,沿应力传播方向取一微土层厚度为dh,该土层位置距离试件表面为h,微土层剪切波速为v,计算公式为
| $\begin{array}{l} v = 0.003{\left[ {{f_i}\left( {1 - {{\left( {\frac{1}{{1 + {{\left( {r/h} \right)}^2}}}} \right)}^{3/2}}} \right)} \right]^2} + \\ \quad 1.002\left[ {{f_i}\left( {1 - {{\left( {\frac{1}{{1 + {{\left( {r/h} \right)}^2}}}} \right)}^{3/2}}} \right)} \right] + 199.5 \end{array}$ | (6) |
式中r为试件表面受力面半径。则剪切波速通过dh微土层的时间dt为
| ${\rm{d}}t = \frac{{{\rm{d}}h}}{v}$ | (7) |
将式(6) 代入式(7),并对试件长度取积分可得剪切波速通过整个试件长度所需时间T,即
| $\begin{array}{l} T = \int_0^H {{\rm{d}}h} /\left\{ {0.003{{\left[ {{f_{\rm{i}}}\left( {1 - {{\left( {\frac{1}{{1 + {{\left( {r/h} \right)}^2}}}} \right)}^{3/2}}} \right)} \right]}^2}} \right. + \\ \left. {\quad \quad 1.002\left[ {{f_{\rm{i}}}\left( {1 - {{\left( {\frac{1}{{1 + {{\left( {r/h} \right)}^2}}}} \right)}^{3/2}}} \right)} \right] + 199.5} \right\} \end{array}$ | (8) |
则试件整体剪切波速计算值Vs为
| ${V_{\rm{s}}} = \frac{H}{T}$ | (9) |
将式(8) 代入式(9) 可求出试件整体剪切波速理论计算值,此处H为14 cm,r为5 cm。将每个fi作用下试件整体剪切波速的理论计算值与实测值进行对比分析,结果如表 1所示。
| 表 1 数据验证对比表 Table 1 Verification and contrast of data |
表 1中Vt为试件整体剪切波速的理论计算值,Va为试件整体剪切波速的实测值,平均相对误差指整体剪切波速的理论计算值与实测值的相对误差平均值,其值为0.04,表明模型计算精度相对较高。
4 结论本文设计了变应力剪切波速测试仪器,对粘土、砂土两种土样分别进行变应力状态下剪切波速测试试验。在考虑土颗粒应力传播扩散及损失特点的前提下,对试验数据进行分析研究,建立土基应力与剪切波速理论模型,在此基础上设计验证实验,对比分析理论及实测数据,验证模型的有效性,得出如下结论。
(1) 土基剪切波速随应力的增大总体呈增大趋势。但因土颗粒应力传播扩散特性,应力相等条件下,土体剪切波速随测试土层厚度的增大而下降。
(2) 在外界其他条件固定的前提下,土基应力对土基剪切波速的影响显著。同密实度条件下,剪切波速随应力的变化幅度可达5倍以上,工程中必须考虑应力对剪切波速的影响。
(3) 在试验建模过程中,土中应力排除了土体自重应力对剪切波速的影响,建立的应力-剪切波速模型基于土颗粒应力扩散特点,可准确反映土层所受应力与剪切波速的相关性规律,其中应力作用方向与剪切波速传播方向相同。通过实测数据验证,模型计算相对误差为0.04,表明模型计算精度相对较高。
(4) 本文研究成果将大幅提升深层地基剪切波速测试试验及物探试验的评估准确性,对大应力、高深度地基土剪切波速特性及抗剪性能研究与分析有重要参考价值。同时也存在不足,建模及试验环节尚可继续改进,减小测试误差,模型的实用性也需要大量试验及实测数据进一步完善。
| [1] |
张宇辉, 张献民, 程国勇.
土石混合介质中石料间隙土压实度剪切波速评价研究[J]. 岩土工程学报, 2011, 33(6): 909–915.
ZHANG Yuhui, ZHANG Xianmin, CHENG Guoyong. The study on interval soil compactness evaluation by the shear-wave velocity of soil-stone mixture[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(6): 909–915. |
| [2] |
王平, 王强, 王峻, 等.
黄土场地剪切波速影响因素模糊灰关联分析研究[J]. 岩石力学与工程学报, 2014, 33(S2): 4299–4304.
WANG Ping, WANG Qiang, WANG Jun. Research on loess sites shear wave velocity influencing factor based on fuzzy-gray relational analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(S2): 4299–4304. |
| [3] |
吴玉辉, 侯晋芳, 闫澍旺.
软土地基稳定性计算中抗剪强度指标的相关分析[J]. 水利学报, 2011, 42(1): 76–80.
WU Yuhui, HOU Jinfang, YANG Shuwang. Analysis of shear strength parameters in soft clay ground stability calculation[J]. Journal of Hydraulic Engineering, 2011, 42(1): 76–80. |
| [4] |
徐金, 张宇辉.
土石地基剪切波测试实验建模[J]. 南京航空航天大学学报, 2015, 47(4): 539–546.
XU jin, ZHANG Yuhui. The study of laboratory model on shear-wave test of soil-stone mixture[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(4): 539–546. |
| [5] | KAYEN R, MOSS R E S, THOMPSON E M, et al. Shear-wave velocity-based probabilistic and deterministic assessment of seismic soil liquefaction potential[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(3): 407–419. DOI:10.1061/(ASCE)GT.1943-5606.0000743 |
| [6] |
孔梦云, 陈国兴, 李小军, 等.
以剪切波速与地表峰值加速度为依据的地震液化确定性及概率判别法[J]. 岩土力学, 2015, 36(5): 1239–1252.
KONG Mengyun, CHEN Guoxing, LI Xiaojun, et al. Shear wave velocity and peak ground acceleration based deterministic and probabilistic assessment of seismic soil liquefaction potential[J]. Rock and Soil Mechanics, 2015, 36(5): 1239–1252. |
| [7] |
曹海莹, 窦远明.
上硬下软型双层路基应力扩散特征及工程应用[J]. 公路交通科技, 2012, 29(2): 29–34.
CAO Haiying, DOU Yuanming. Characteristics of dry crust's stress dispersion in two-layer roadbed and its engineering application[J]. Journal of Highway and Transportation Research and Development, 2012, 29(2): 29–34. |
| [8] |
王奎华, 吕述晖, 吴文兵, 等.
考虑应力扩散时桩端土性对单桩沉降影响分析方法[J]. 岩土力学, 2013, 34(3): 621–630.
WANG Kuihua, LV Shuhui, WU Wenbing, et al. A new method for analyzing influence of pile tip soil properties on single pile settlement considering stress dispersion[J]. Rock and Soil Mechanics, 2013, 34(3): 621–630. |
| [9] |
王奎华, 吕述晖, 吴文兵, 等.
层状地基中考虑桩端应力扩散的单桩沉降计算[J]. 浙江大学学报(工学版), 2013, 47(3): 472–479.
WANG Kuihua, LV Shuhui, WU Wenbing, et al. Calculation method for settlement of single pile considering stress dispersion of pile end soil[J]. Journal of Zhejiang University(Engineering Science), 2013, 47(3): 472–479. |
| [10] |
于旭, 宰金珉, 庄海洋.
SSI效应对隔震结构地震响应的影响分析[J]. 南京航空航天大学学报, 2011, 44(6): 846–851.
YU Xu, ZAI Jinmin, ZHUANG Haiyang. Effects of soil-structure interaction on earthquake response of isolated structure system[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2011, 44(6): 846–851. |
| [11] |
刘远, 孙进忠, 赵体.
强夯地基处理效果的多道瞬态瑞雷波检测[J]. 地球物理学进展, 2014, 29(6): 32–37.
LIU Yuan, SUN Jinzhong, ZHAO Ti. Quantitative evaluation of dynamic consolidation effect of foundation based on multi-channel transient Rayleigh wave method[J]. Progress in Geophysics, 2014, 29(6): 32–37. |
| [12] |
徐琛, 戚承志, 叶飞, 等.
纵向剪切波作用下长型地下结构与地基动力相互作用研究[J]. 世界地震工程, 2015, 31(1): 204–211.
XU Chen, QI Chengzhi, YE Fei, et al. Research on dynamic interaction between long-type underground structure and foundation under action of longitudinal shear wave[J]. World Earthquake Engineering, 2015, 31(1): 204–211. |
| [13] |
付代光, 刘江平, 周黎明, 等.
基于贝叶斯理论的软夹层多模式瑞雷波频散曲线反演研究[J]. 岩土工程学报, 2015, 37(2): 321–329.
DOI:10.11779/CJGE201502016 FU Daiguang, LIU Jiangping, ZHOU Liming, et al. Inversion of multimode Rayleigh-wave dispersion curves of soft interlayer based on Bayesian theory[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(2): 321–329. DOI:10.11779/CJGE201502016 |
 2017, Vol. 49
2017, Vol. 49


