混凝土是由骨料、水、水泥及掺合料等原料混合而成的多相复合材料,被广泛应用于建筑、桥梁及一些基础设施的建造中。随着混凝土的老化及腐蚀,其结构安全状况越来越受到人们的关注。超声检测技术作为无损检测技术的主要技术之一,在混凝土无损检测中获得较为广泛的应用[1]。由于混凝土中超声波传播的强衰减作用、多路径散射作用以及大扩散角作用的影响,超声成像的分辨率往往受到很大的限制。为了克服扩散角对横向分辨率的影响,雷达系统中的合成孔径聚焦技术(Synthetic aperture focusing technique, SAFT)被引入超声无损检测中,极大改善了成像效果。2005年,德国学者Schickert对混凝土的超声无损检测成像方法研究进展进行了回顾,并重点对合成孔径成像算法及其改进方法进行了介绍[2];2008年,石立华团队[3]将波包分解技术与合成孔径方法进行结合,可对多路径反射信号进行特征提取,增强了信噪比,进一步提高了超声成像分辨率;针对成像过程中的波包变形、多路径反射等问题,该团队又提出了一系列改进方法[4-5];2012年,Ganguli等[6]利用超声波传播过程中的模态转换特性,提取特征信息,改进了现有的超声合成孔径方法,并在仿真实验中验证了该方法对混凝土中的空洞、钢筋等缺陷的成像效果。2013年,密士文等[7]采用合成孔径聚焦方法对T梁预应力波纹管压浆密实度进行超声检测研究,其成像结果与实际相符;2014年,朱自强团队利用超声相控阵技术对预应力管道附近区域进行重点聚集,进一步提高了检测分辨率[8]。
由于混凝土的强衰减作用,大深度混凝土下的缺陷反射信号比较微弱,导致超声成像效果不佳。针对混凝土的超声衰减测量问题,国内外学者进行了大量研究。2009年,Kim等[9]对不同含水量的混凝土进行了衰减测量实验,结果表明在65%粗骨粒含量的混凝土中,主频100 kHz的激励信号的衰减系数为0.04 dB/mm左右;2010年,周正干等[10]对超声衰减的影响因素进行研究,并采用时域有限差分法进行数值仿真,研究了换能器脉冲声场特性及扩散衰减特性;2014年,朱自强等[11]利用时域有限差分方法建立了基于细观结构的混凝土数值模型,研究了骨料、孔隙和钢筋对超声波衰减的影响;针对传统衰减系数测量中耗时费力的问题,Genovés等[12]提出一种宽频测量的方法,极大地提高了衰减系数测量的效率。在实际检测中,各类混凝土结构的配比构成及施工方法不一致,文献中的衰减系数差别很大,不能很好地对现有数据进行补偿。为此,本文采用同侧一发一收方法测量混凝土的相对衰减系数,提出一种基于幅度补偿的合成孔径成像方法。其中,超声波的相对衰减系数由直达波与一次底面回波的幅度衰减来测定。通过引入幅度补偿技术,微弱反射信号得到增强,然后再经过合成孔径成像处理,超声成像结果的分辨率得到进一步提高。
1 基于幅度补偿的SAFT成像方法基于幅度补偿的合成孔径成像方法由幅度补偿技术与超声合成孔径成像技术两者组成,可看作是经过信号预处理后的超声合成孔径成像方法。针对混凝土内超声回波信号衰减严重的问题,首先对信号进行幅度补偿预处理,然后在此基础上进行超声合成孔径成像处理,最后通过分析成像结果识别得到目标缺陷。
1.1 幅度补偿技术大深度混凝土检测时,超声波衰减严重,反射信号十分微弱,导致传统B扫描及SAFT的成像结果效果不佳。为此,本文依据超声波在混凝土中按指数衰减的基本规律,提出一种基于幅度补偿的SAFT成像方法,增强大深度混凝土情况下缺陷反射强度。在相对侧一收一发方法(透射法)测量中,由于混凝土表面的粗糙程度以及换能器与混凝土表面贴合情况差异较大,一致准确的衰减系数在实地测量中很难获得。考虑到超声成像效果不佳的一个重要原因是采集得到的表面直达波信号与底面回波信号在幅值上存在巨大差异,直接导致混凝土深处的反射信号被淹没。为了减小直达波与底面回波间的差异,提高混凝土的超声成像质量,本文在文献[9]的基础上建立了表面直达波与底面回波间的联系。这里为了与传统衰减系数有所区分,本文将表面直达波与底面回波间的联系定义为相对衰减系数。本文采用同侧一收一发法(反射法)测量得到直达波与反射波的幅度大小,然后依据文献[9]的公式来测定混凝土的相对衰减系数,其表达式为
| $\alpha = - \frac{{20}}{x}{\rm{log}}\left( {\frac{{{A_x}}}{{{A_0}}}} \right)$ | (1) |
式中:α为相对衰减系数;A0为直达波的峰值;Ax为底面反射波的峰值;x为超声波的传播距离。
相对衰减系数表征了混凝土内部各反射回波相对于表面直达波的衰减程度。在实验中,将相隔2 mm的两个超声探头并排放置,同时将超声探头紧贴涂有耦合剂的混凝土表面,使其充分接触;然后通过超声成像实验系统进行收发操作,可采集得到多组超声回波信号。超声回波信号由400 V的放电脉冲激励50 kHz超声探头得到。对于厚度为30 cm的混凝土块,其来回传播距离为60 cm,则采集得到的超声回波信号如图 1所示。从图中看出,波形最左侧的波包信号幅值最大,是表面的直达波信号,而其他各处的波包幅度较小,杂乱无章,而且混叠严重,主要由混凝土内部缺陷及骨料的反射引起。为了去除杂散噪声,本文将采集得到的超声回波信号与50 kHz窄带信号进行卷积,然后对卷积结果进行Hilbert变换可得到信号的包络,包络的归一化结果如图 2所示。
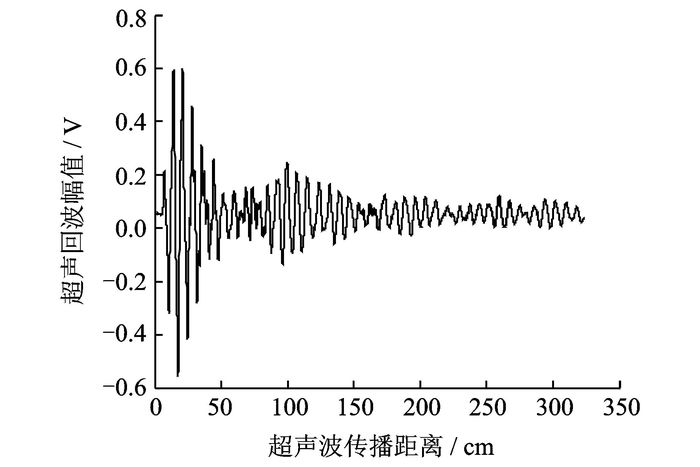
|
图 1 混凝土超声回波信号(30 cm) Figure 1 Ultrasonic echo signal of concrete (30cm) |
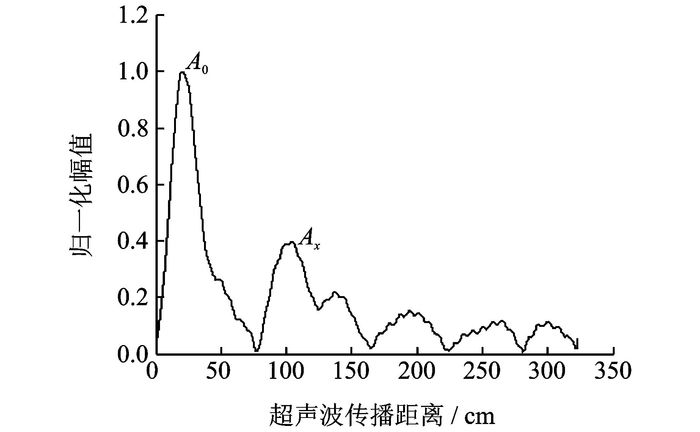
|
图 2 超声回波信号包络 Figure 2 Envelope of ultrasonic echo signal |
从图 2可知,第二大波峰值(Ax)所代表波包的起始位置与底面回波的传播距离相近,同时其包络幅度较大,可判定为混凝土的底面回波信号。通过提取包络图中的最大波峰值与第二大波峰值(即图 2中的A0与Ax),就可以得到直达波与30 cm处底面反射回波的幅度,然后采用式(1) 计算得到50 kHz超声波所对应的相对衰减系数。考虑到混凝土材料的非均匀特性,本文在厚度为30 cm的混凝土表面随机选取10个位置,然后分别测量混凝土的相对衰减系数,最后通过求取平均值的方法减少材料非均匀性带来的影响,10次测量结果如图 3所示。
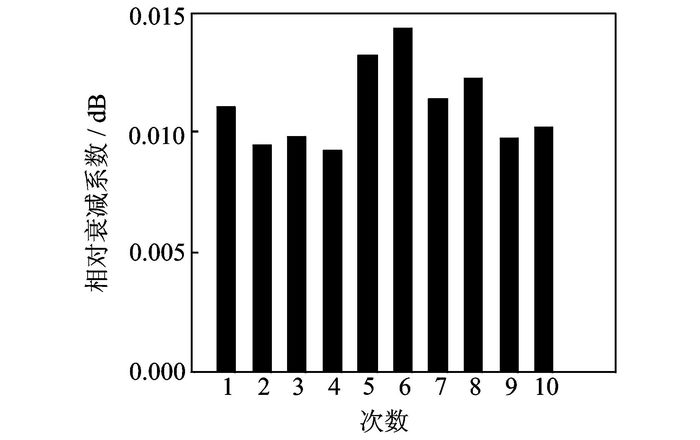
|
图 3 10次相对衰减系数测量值 Figure 3 Ten measurements of relative attenuation coefficients |
10次测量结果的平均值为
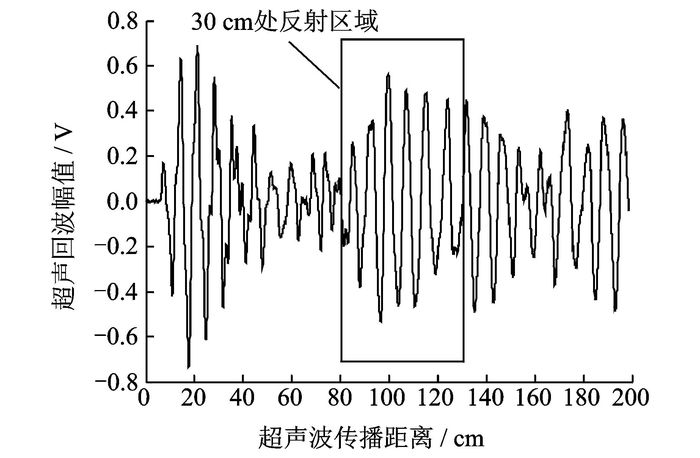
|
图 4 幅度补偿后的超声回波信号 Figure 4 Ultrasonic echo signal after compensation |
1.2 超声SAFT成像原理
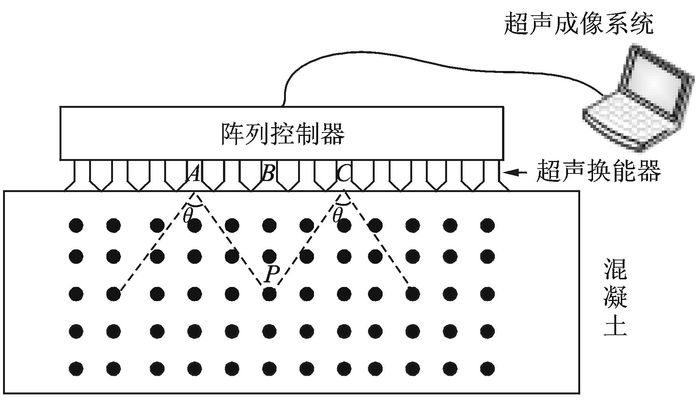
由于超声换能器扩散角θ的存在,超声成像的横向分辨率受到很大的限制。合成孔径方法可以等效为用多个小孔径换能器去模拟一个大孔径换能器,可以提高横向分辨率。通过依次收发信号,超声探头发射声束并照射内部异常介质,异常介质的反射信号被相邻探头接收;根据虚拟反射点的位置,对各通道的接收信号引入与虚拟反射距离相关的时间延迟,并将延时后的信号进行叠加及平均处理,并将处理结果作为当前通道数据;最后综合各虚拟反射点的数值可以得到聚集成像图。图 5为混凝土的超声SAFT成像原理图,图中黑点为虚拟反射点。
|
图 5 混凝土超声成像系统示意图 Figure 5 Schematic diagram of concrete ultrasonic imaging system |
如图 1所示,假设P(xi, yi)为虚拟反射点,A, B和C代表阵列中的超声换能器。由于扩散角θ的存在,当扫描采集过程进入A—C中间区域时,P点的反射信息被接收并储存;当离开A—C区域时,P点反射信息消失。此时,若利用A—C区域内对应换能器的接收信号对P点进行重建,则P点的信息将更加完整。令A—C区域内某一发射换能器的位置为(xm, ym),接收换能器位置(xm+d, ym),则P点反射信息被接收的延迟时间为
| $\begin{array}{l} {t_{mi}} = \frac{1}{c}\left( {\sqrt {{{({x_m} - {x_i})}^2} + {{({y_m} - {y_i})}^2}} + } \right.\\ \left. {\quad \quad \quad \sqrt {{{({x_m} + d - {x_i})}^2} + {{({y_m} - {y_i})}^2}} } \right)\\ \quad \quad \quad \quad m = 1,2, \ldots ,M \end{array}$ | (2) |
式中:d为收发换能器间距;c为声速;m为孔径数目。通过延时叠加,超声成像中各像素点上的值可表示为
| $S({x_i},{y_i}) = \frac{1}{M}\sum\limits_{m = 1}^M {{F_m}} ({t_{mi}})$ | (3) |
式中:Fm(t)为第m个孔径采集到的信号;S(xi, yi)就是点P的重建信号。上述分析表明,只有当虚拟反射点在扩散角区域内重建,重建信号才能被增强。
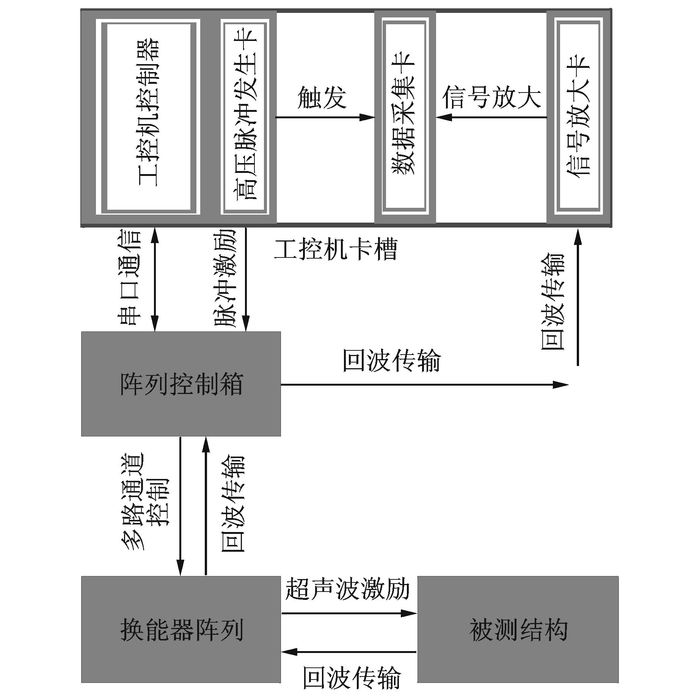
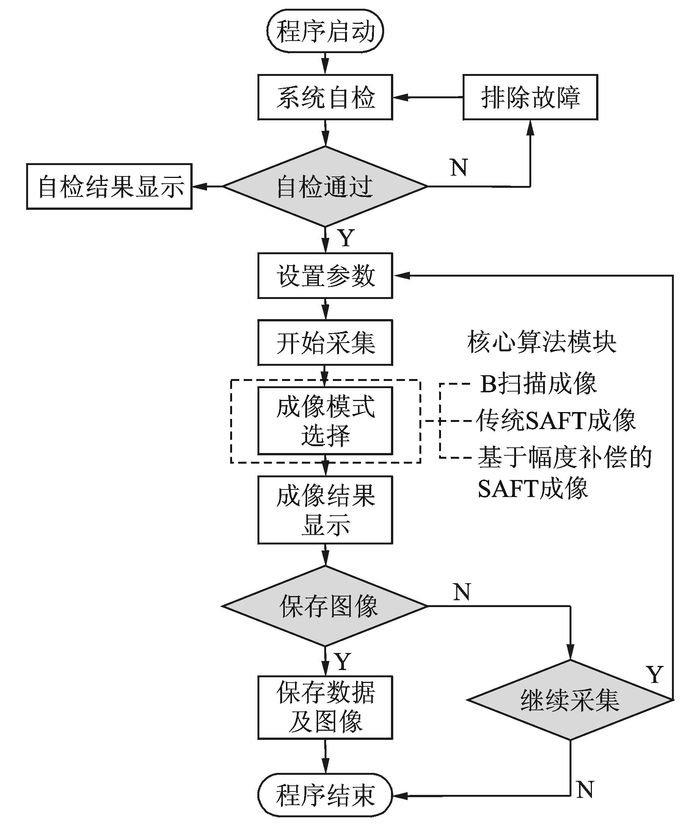
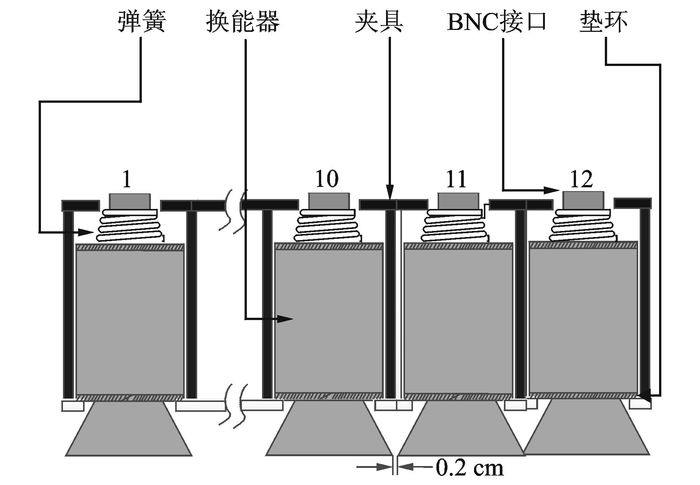
2 混凝土超声成像实验 2.1 混凝土超声成像系统考虑到超声成像系统的便捷性及可扩展性,本文选用了基于面向仪器系统的PCI扩展(PCI extensions for instrumentation,PXI)总线的插槽式模块结构来搭建超声成像系统。系统中包含3类具有PXI接口的板卡:高压脉冲发生卡、信号放大卡及数据采集卡。其中,高压脉冲发生卡由继电器触发电路和高压脉冲发生电路组成,能起到快速切换高压脉冲的作用;数据采集模块采用了具有PXI接口的高速采集卡,最高采样速率可达10MHz/s。同时,为进一步满足成像分辨率及检测效率方面的要求,本文设计了适合本系统的换能器阵列及其控制系统,工控机可通过阵列控制箱对换能器阵列任意单元发射信号和接收信号。超声成像系统的总体硬件框架如图 6所示,系统软件的运行流程图如图 7所示。混凝土超声成像系统的核心算法模块为成像模式选择模块,其中有3种成像方式可选择,分别为B扫描成像方式、传统SAFT成像方式以及本文提出的基于幅度补偿的SAFT成像方式。在实际检测成像过程中,为满足高效可靠的需求,本文设计一组由12个低频超声探头组成的线性阵列,并选取聚胺脂作为隔开低频超声探头的绝缘材料,从而消除各超声探头间的信号串扰。各超声探头等间距固定在聚胺脂夹具中,相邻超声探头之间间隔2 mm。由于检测成像时需要在阵列探头和被测结构之间加耦合剂,在操作阵列探头时,为了保证超声探头与被测结构接触良好,排干净探头与被测结构之间的空气,提高激励信号入射率,需要对阵列探头轻压。为了适应粗糙的混凝土表面,夹具与换能器上表面之间设计有弹簧卡槽,同时在夹具与下表面之间放置垫环,待放入压缩弹簧后可构成柔性阵列,其结构如图 8所示,实物的俯视图及平视图如图 9所示。图 9的俯视图中红色箭头表示检测时低频超声探头顺序收发信号的方向;序号标注圆口区域表示阵列探头单元与扫描控制装置的信号接口,平视图中阵列底部的金属区域是探头与混凝土表面的接触区域。
|
图 6 超声成像系统的硬件结构图 Figure 6 Hardware structure of ultrasonic imaging system |
|
图 7 超声成像系统的软件运行流程图 Figure 7 Software flow chart of ultrasonic imaging system |
|
图 8 阵列探头结构示意图 Figure 8 Structure of ultrasonic array probe |

|
图 9 超声阵列探头实物图 Figure 9 Object of ultrasonic array probe |
阵列控制箱通过SMA反级性公头(Sub-miniature-A,SMA)接口的屏蔽同轴线与换能器阵列连接,最多可实现24路换能器单元的控制,同时其片内倍频电路可使得复杂算法高速运行并输出控制继电器动作。超声成像检测时,阵列控制箱中ARM控制器通过串口接收上位工控机的指令,通过通用输入/输出(General purpose input output, GPIO)口控制继电器将高压脉冲施加于阵列换能器上。
2.2 混凝土超声成像结果实验验证中,本文分别对内嵌方形铁管及内嵌方形木块进行超声成像实验,主要是基于以下两点:(1) 通过对不同类形的目标缺陷进行超声成像实验,可验证本文所提方法的有效性及适用性;(2) 通过对不同深度的目标缺陷进行成像实验,可验证本文所提方法对各深度的目标缺陷均有补偿效果,而不是只针对混凝土深处的回波信号具有补偿效果。
2.2.1 内嵌方形铁管检测本文首先对内嵌方形铁管的混凝土块进行超声成像实验。被测混凝土块的大小为长100 cm×宽60 cm×高60 cm,两根内嵌铁管的大小分别为长60 cm×宽10 cm×高10 cm,中间为镂空结构,位置在混凝土块中部40 cm及30 cm处,具体设置如图 10所示。实验测量中,50 kHz的低频超声探头沿着混凝土表面进行扫描,扫描方向由A至B。在整个扫描过程中,甘油作为超声检测的耦合剂,共采集得到82组超声回波数据。
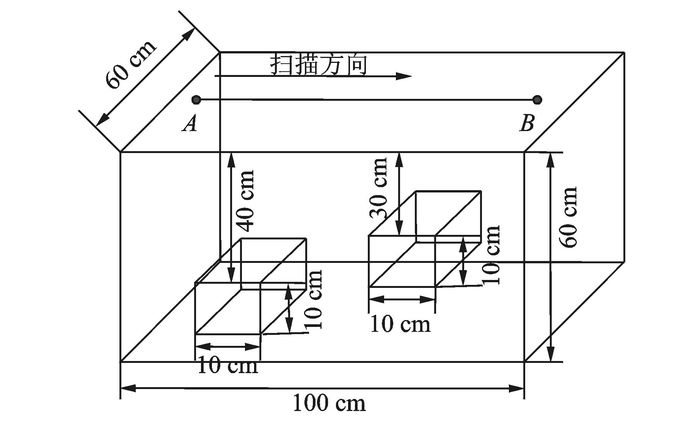
|
图 10 内嵌铁管的混凝土设置图 Figure 10 Concrete setting diagram with embedded iron pipe |
采用超声成像系统采集回波数据后,在系统的成像模式选择模块中分别用B扫描、传统SAFT以及基于幅度补偿的SAFT成像方法进行成像处理,图 11~13为3种成像处理方法的成像结果。从3种成像结果来看,每张成像图中深度0~10 cm之间都存在一条红线,该红线是由发射端与接收端之间的表面直达波引起的,基本成一直线,颜色较深且易于识别,可近似看作混凝土的上表面。
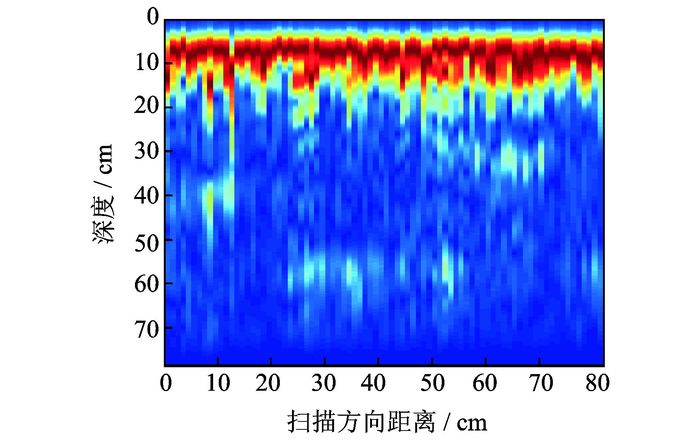
|
图 11 B扫描成像结果 Figure 11 Imaging result of B-scan method |
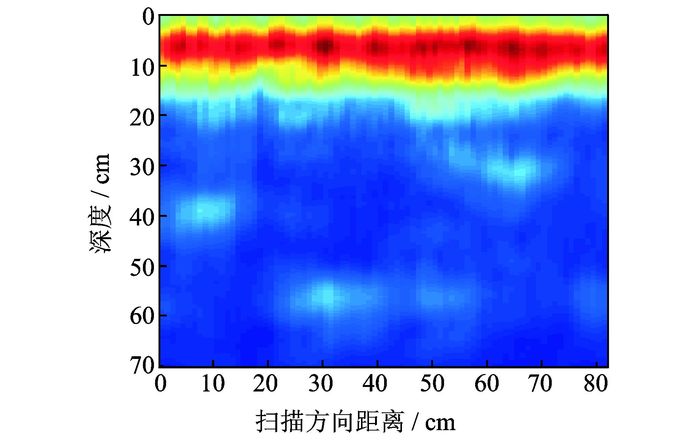
|
图 12 传统SAFT成像结果 Figure 12 Imaging result of traditional SAFT method |
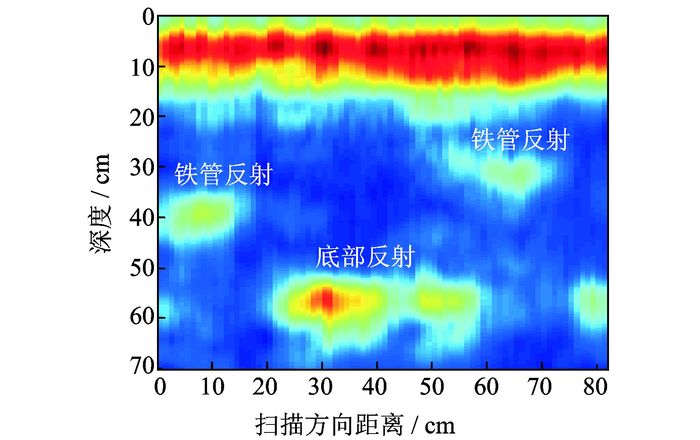
|
图 13 本文方法的成像结果 Figure 13 Imaging result of the proposed method |
对比图 11~13可知,3种成像方式都能分辨出40 cm处铁管、30 cm处铁管及60 cm底面的反射。其中B扫描成像结果最差,局部噪声较大,表面直达波会严重影响近表面目标缺陷的识别,如深度30 cm处的铁管;图 12显示的传统SAFT成像结果中,超声回波信号经过合成孔径成像处理后,各通道间信号的一致性明显好于B扫描结果,从而使得分界面区域与附近区域的区别更加明显,分辨效果要好于B扫描结果,但是图中混凝土表面以下目标缺陷的反射较弱,不利于现场检测识别;图 13是基于幅度补偿的SAFT成像结果,由于采用了基于幅度补偿的SAFT方法,使得缺陷处的反射信号明显得到增强,图像的分辨率要远远高于传统SAFT成像结果及B扫描结果,方便了混凝土内部缺陷的现场识别。另外,图 13中对深处反射信号的细节展现得更为详细,便于后续研究的分析处理,并且图中成像位置与人工混凝土块中缺陷位置保持一致。
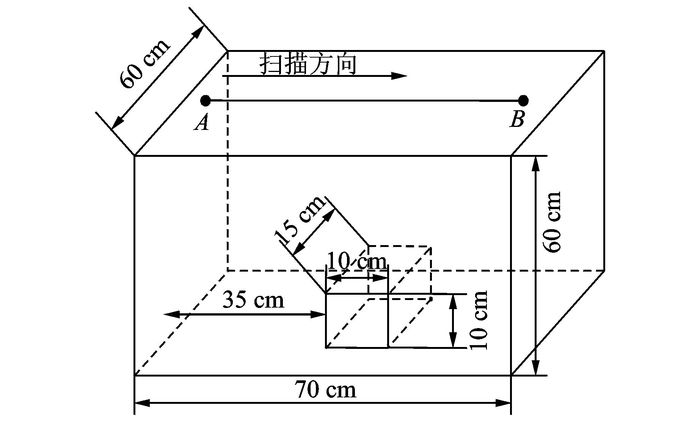
2.2.2 内嵌方形木块检测为了进一步验证本文所提方法的有效性,本文替换了内嵌缺陷的材质并增加了缺陷位置的深度,对深度为50 cm内嵌木块进行超声成像实验。被测混凝土块的大小为长70 cm×宽60 cm×高60 cm,内嵌木块的大小为长15 cm×宽10 cm×高10 cm,位置是在混凝土块底部偏中间区域,具体设置如图 14所示。实验测量中,50 kHz的超声换能器沿着混凝土表面进行扫描,扫描方向由A至B,共采集得到61组超声回波数据。
|
图 14 内嵌木块的混凝土设置图 Figure 14 Concrete setting diagram with embedded wooden block |
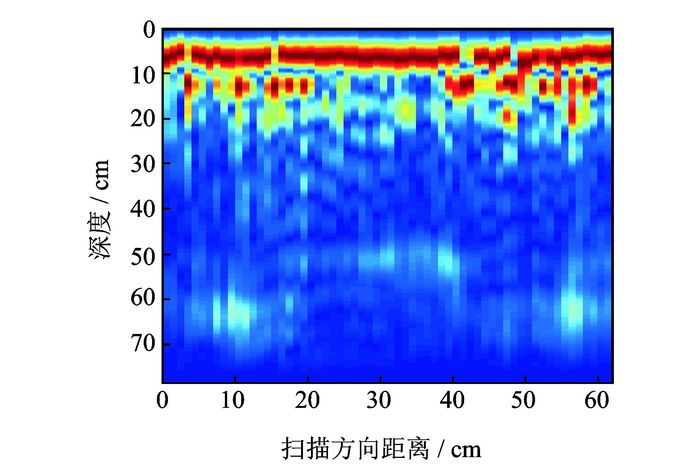
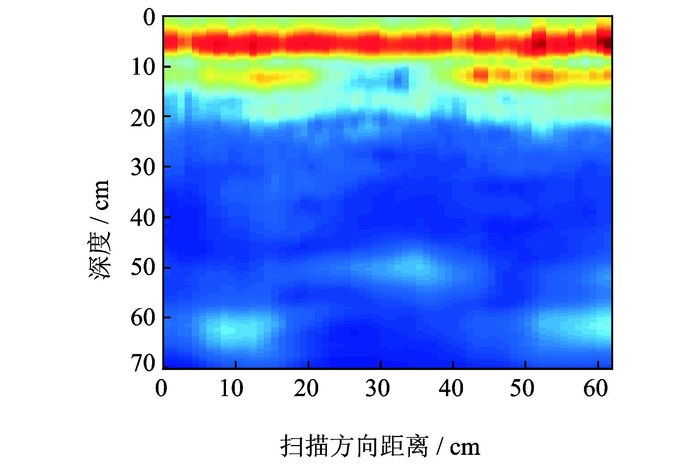
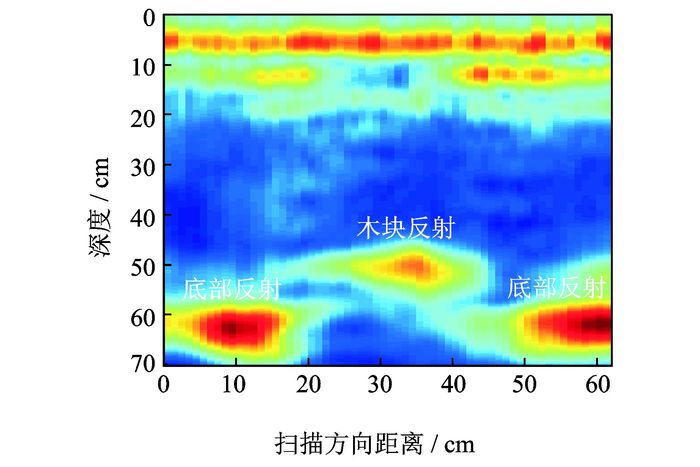
采用超声成像系统采集回波数据后,在系统的成像模式选择模块中分别用B扫描、传统SAFT以及基于幅度补偿的SAFT成像方法进行成像处理,图 15~17为3种成像处理方法的成像结果。从3种成像结果来看,每张成像图中深度0~10 cm之间都存在一条红线,与上节处理方式一样,可近似看作混凝土的上表面。但是在直线正下方10 cm处有两条未知缺陷,初步判断为混凝土内部的裂纹引起,而产生裂纹的原因可能是施工时操作不当。
|
图 15 B扫描成像结果 Figure 15 Imaging result of B-scan method |
|
图 16 传统SAFT成像结果 Figure 16 Imaging result of traditional SAFT method |
|
图 17 本文方法的成像结果 Figure 17 Imaging result of the proposed method |
对比图 15,16可知,两者都能在深度50 cm与60 cm处发现木块引起的异常界面反射,由于图 16中的超声信号经过合成孔径处理,各通道间信号的一致性明显好于B扫描结果,从而使得分界面区域与附近区域的区别更加明显,分辨效果要好于B扫描结果。而对图 17中的结果,由于采用了基于幅度补偿的SAFT方法,使得缺陷处的反射信号明显得到增强,图像的分辨率要远远好于传统SAFT成像结果及B扫描结果,方便了混凝土内部缺陷的现场识别。另外,图 17中对深处反射信号的细节展现得更为详细,便于后续研究的分析处理。
3 结束语针对大深度混凝土检测中超声成像效果不佳的问题,本文在研究超声波衰减规律的基础上,建立了表面直达波及一次底面回波间的联系,采用同侧一收一发方法测量了混凝土中超声波传播的相对衰减系数,并提出一种基于幅度补偿的超声SAFT成像方法。依据测量得到的相对衰减系数,引入幅度补偿技术对大深度超声回波信号进行补偿处理,增强了深处反射信号的幅度,经合成孔径处理后进一步增强了超声成像效果。人工混凝土块实验表明,本文所提方法比B扫描成像方法及传统SAFT成像方法具有更高的成像分辨率,底部缺陷反射更加清晰,信号细节方面展现得更加详细,内嵌铁管及木块的实验均验证了本文方法的有效性。
| [1] | MCCANN D M, FORDE M C. Review of NDT methods in the assessment of concrete and masonry structures[J]. NDT & E International, 2001, 34(2): 71–84. |
| [2] | SCHICKERT M. Progress in ultrasonic imaging of concrete[J]. Materials and Structures, 2005, 38(283): 807–815. DOI:10.1617/14298 |
| [3] | SHAO Zhixue, SHI Lihua, CAI Jian. Wavelet modeling of signals for non-destructive testing of concretes[J]. Measurement Science and Technology, 2011, 22(5): 055702. DOI:10.1088/0957-0233/22/5/055702 |
| [4] |
李秋锋, 石立华, 梁大开, 等.
混凝土检测中基于数字滤波的传感器补偿方法[J]. 南京航空航天大学学报, 2008, 40(1): 55–59.
LI Qiufeng, SHI Lihua, LIANG Dakai, et al. Compensating method for transducers based on digital filtering in concrete test[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008, 40(1): 55–59. |
| [5] |
李秋锋, 石立华, 邬冠华, 等.
提高混凝土结构成像质量的技术研究[J]. 仪器仪表学报, 2008, 29(11): 2441–2445.
DOI:10.3321/j.issn:0254-3087.2008.11.038 LI Qiufeng, SHI Lihua, WU Guanhua, et al. Reasearch on improving imaging quality of concrete stucture[J]. Chinese Journal of Scientific Instrument, 2008, 29(11): 2441–2445. DOI:10.3321/j.issn:0254-3087.2008.11.038 |
| [6] | GANGULI A, RAPPAPORT C M, ABRAMO D, et al. Synthetic aperture imaging for flaw detection in a concrete medium[J]. NDT & E International, 2012, 45(1): 79–90. |
| [7] |
密士文, 朱自强, 彭凌星, 等.
T梁预应力波纹管压浆密实度超声检测试验研究[J]. 中南大学学报(自然科学版), 2013, 44(6): 2378–2384.
MI Shiwen, ZHU Ziqiang, PENG Lingxing, et al. Experimental study of detecting grouting density of prestressed tendon ducts through ultrasonic[J]. Journal of Central South University (Science and Technology), 2013, 44(6): 2378–2384. |
| [8] |
朱自强, 喻波, 密士文, 等.
预应力管道压浆质量的超声波相控阵检测方法[J]. 中南大学学报:自然科学版, 2014, 45(10): 3521–3530.
ZHU Ziqiang, YU Bo, MI Shiwen, et al. Detection of grouting quality in posttensioned tendon duct by phased array ultrasonic[J]. Journal of Central South University (Science and Technology), 2014, 45(10): 3521–3530. |
| [9] | KIM Byeong-Chan, KIM Jin-Yeon. Characterization of ultrasonic properties of concrete[J]. Mechanics Research Communications, 2009, 36(2): 207–214. DOI:10.1016/j.mechrescom.2008.07.003 |
| [10] |
周正干, 魏东, 向上.
空气耦合超声检测中衰减因素的研究[J]. 中国机械工程, 2010(19): 2350–2354.
ZHOU Zhenggan, WEI Dong, XIANG Shang. Research on attenuation factor of air-coupled ultrasonic testing[J]. China Mechanical Engineering, 2010(19): 2350–2354. |
| [11] |
朱自强, 喻波, 密士文, 等.
超声波在混凝土中的衰减特征[J]. 中南大学学报(自然科学版), 2014, 45(11): 3900–3907.
ZHU Ziqiang, YU Bo, MI Shiwen, et al. Ultrasonic attenuation characteristics of ultrasonic in concrete[J]. Journal of Central South University (Science and Technology), 2014, 45(11): 3900–3907. |
| [12] | GENOVÉS V, GOSÁLBEZ J, CARRIóN A, et al. Optimized ultrasonic attenuation measures for non-homogeneous materials[J]. Ultrasonics, 2015, 65: 345–352. |
 2017, Vol. 49
2017, Vol. 49


