民航告警主要是指民用航空器在发生不安全事件之前,根据以往总结的规律或观测得到的可能性前兆,最大程度地减少不安全事件所造成的损失。飞行品质监控(Flight operational quality assurance, FOQA)是民航告警和安全管理的有效手段之一,它首先通过机载记录器收集飞机的飞行数据,然后采用数据分析方法对收集到的数据进行分析,最终给出不安全事件的发生数量和发展趋势。目前FOQA被广泛应用于提高飞行机组操作品质,改进标准操作程序,完善飞行训练大纲和减少运行、维护成本等多个方面[1]。在分析数据的过程中,经常会出现这样的现象:在一组数据中会出现少数几个偏差特别大的数据,这类数据称为异常值。异常值的产生主要有以下两个原因:
(1) 飞机运行环境的复杂性和随机性导致了数据的波动性,这类异常值和其他数据属于同一总体,是正确数据,本文称这类异常值为正确异常值。
(2) 数据在记录和译码的过程中,记录器或译码工具异常和人为操作错误等原因,这类异常值是错误数据,和正确异常值不属于同一总体,本文称这类异常值为错误异常值。
在数据分析的过程中,无论是正确异常值还是错误异常值,都会对分析结果产生影响,尤其需要排除错误异常值对分析结果产生的不利影响[2-3]。本文的研究重点在于如何使用异常值检测方法实现民航告警。
1 民航告警问题与数据集描述 1.1 民航告警问题本节介绍的民航告警,主要是指通过分析快速存取记录器(Quick access recorder, QAR)所记录的数据而发出的告警信息。QAR是一套可方便快速获取飞机运行数据的系统,它记录了飞机整个飞行阶段的位置、运动、操纵和告警等多项参数。由于QAR数据中的参数彼此间是相互独立的,且均不具有特殊性。因此,本文选择QAR数据中的“着陆法向加速度”和“200-50英尺(ft)进近滚转角”这两个参数为研究对象。
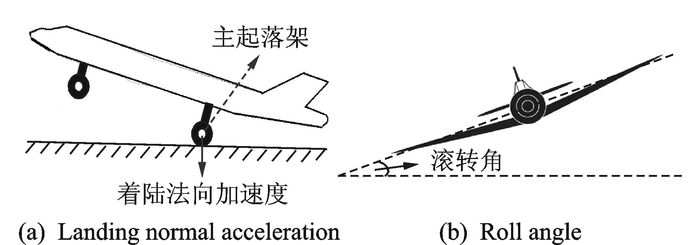
所谓着陆法向加速度是指飞机接地着陆瞬间主起落架的垂直加速度。在飞机着陆时,最理想的状况是升力等于飞机的重力,法向加速度为1,但在实际着陆中,这种理想状况难以达到[4-5]。所谓200-50 ft进近滚转角是指飞机在下降对准跑道(进近)时,当高度处于200-50 ft时飞机绕纵轴(从机头到机尾的轴)旋转的角度[6]。示意图如图 1所示。
|
图 1 飞机着陆法向加速度和滚转角示意图 Figure 1 Diagram of landing normal acceleration and roll angle of aircraft |
在中国民用航空局飞行标准司发布的咨询通告《飞行品质监控(FOQA)实施与管理》[7]中,根据记录器中的参数分别制定了空客系列飞机和波音系列飞机的59项和60项监控项目,然后通过偏差限定值的设定达到“轻度偏差告警”和“严重偏差告警”的目的。图 2以“着陆法向加速度”为例给出了采用“偏差限定值法”实现民航告警的流程图。

|
图 2 民航告警流程图——偏差限定值法 Figure 2 Flow chart of civil aviation alarm—Deviation limit method |
除了“偏差限定值法”外,“标准差法”也在民航告警中具有非常广泛的应用,但两种方法应用于民航告警仍存在以下弊端:
(1) 偏差限定值多为依靠个人经验而人为设定的,具有很强的人为主观性,与实际的飞行数据脱离;
(2) 偏差限定值的一成不变性,导致了“偏差限定值法”缺乏灵活性,告警结果无法体现飞行数据集之间存在的差异性;
(3)“标准差法”的告警结果不但依赖于数据集的正态性,而且对异常值也有比较强的敏感性,这些缺点限制了“标准差法”对数据集的适用性。
1.2 数据集描述本节主要从数据的采集、数据集规模和异常值这3个角度来介绍本文使用的数据集——“着陆法向加速度”和“200-50 ft进近滚转角”。
“着陆法向加速度”取自从飞机接地前2 s到接地后5 s所记录的所有法向加速度的最大值,该值不会小于1;“200-50 ft进近滚转角”取自飞机从200 ft高度降至50 ft高度所记录的所有滚转角的最大值,该值不会小于0。
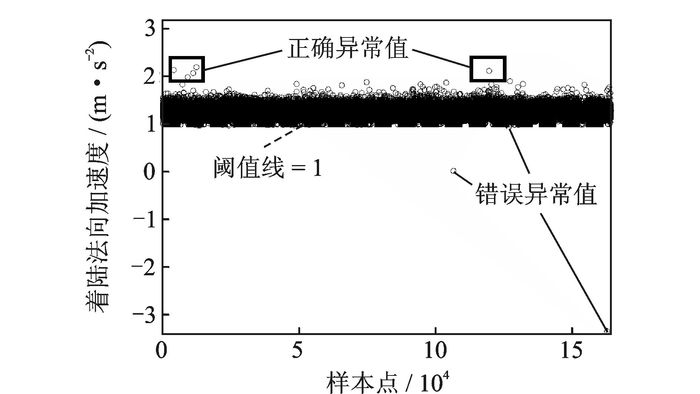
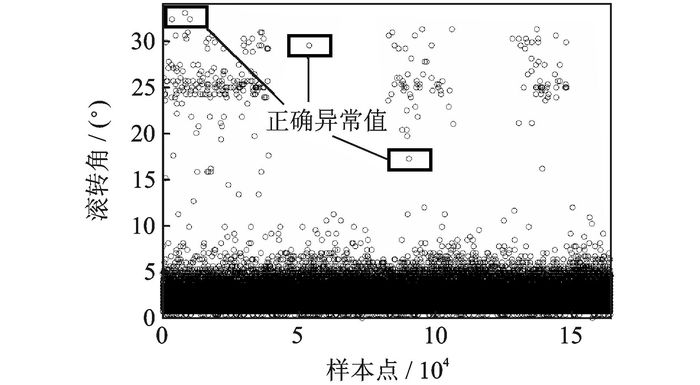
本文中的两个数据集均由164 397条数据构成,包含了正常值、正确异常值和错误异常值3类数值。“着陆法向加速度”数据集具有187条小于1的错误异常值,其散点图如图 3所示,由于受图表空间的制约,2个“-9 999”错误异常值未在图 3中标出。“200-50 ft进近滚转角”数据集的散点图如图 4所示,图中标注的点包含了正常值和正确异常值两类数值,174个“9 999”错误异常值未能在图 4中标出。
|
图 3 着陆法向加速度数据集散点图 Figure 3 Scatter plot of data of landing normal acceleration |
|
图 4 200-50 ft进近滚转角数据集散点图 Figure 4 Scatter plot of data of 200-50 ft approach roll angle |
2 标准差法
标准差法的思想来源于对标准正态分布的分析,当随机变量满足正态分布时,在[μ-σ, μ+σ],[μ-2σ, μ+2σ]和[μ-3σ, μ+3σ]这3个区间上,概率密度曲线之下的面积分别占总面积的68.3%,95.4%和99.7%,即
| $P\left\{ { - 1 \le X \le 1} \right\} = 0.683$ | (1) |
| $P\left\{ { - 2 \le X \le 2} \right\} = 0.954$ | (2) |
| $P\left\{ { - 3 \le X \le 3} \right\} = 0.997$ | (3) |
式中:μ为正态分布的均值,它决定了数据集中的位置;σ为正态分布的标准差,它决定了数据分布的幅度[8-9]。需要指出,在实际生活中,“三倍标准差(3σ)原则”,也被称为拉依达准则,应用最为广泛,常被运用在异常值诊断上[10]。
标准差法在民航告警中有着非常广泛的应用,其主要思想来自于正态分布的一倍标准差原则、二倍标准差原则和三倍标准差原则。采用“标准差法”实现民航告警的算法如下:
第1步:数据筛选。根据参数的意义和经验取值范围,排除数据集中的错误异常值。
第2步:计算标准差线。通过式(4, 5) 得到数据集的均值和标准差,进而得一倍标准差线μ±σ,二倍标准差线μ±2σ和三倍标准差线μ±3σ
| $\mu = \frac{{\sum\limits_{i = 1}^N {{x_i}} }}{N}$ | (4) |
| $\sigma = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{\left( {x - \mu } \right)}^2}} }}{N}} $ | (5) |
第3步:告警。利用标准差线μ+σ,μ+2σ和μ+3σ实现“轻度-严重”二级告警或“一级超限-二级超限-三级超限”三级告警。
下面以“着陆法向加速度”数据集为例,采用上述“标准差法”来展示民用飞机着陆法向加速度的告警流程。
第1步:数据筛选。根据着陆法向加速度的采集方式、意义和经验值,其正常值和正确异常值的取值范围为[1, 4],在此范围之外的为错误异常值,据此排除了187条小于1的错误异常值。
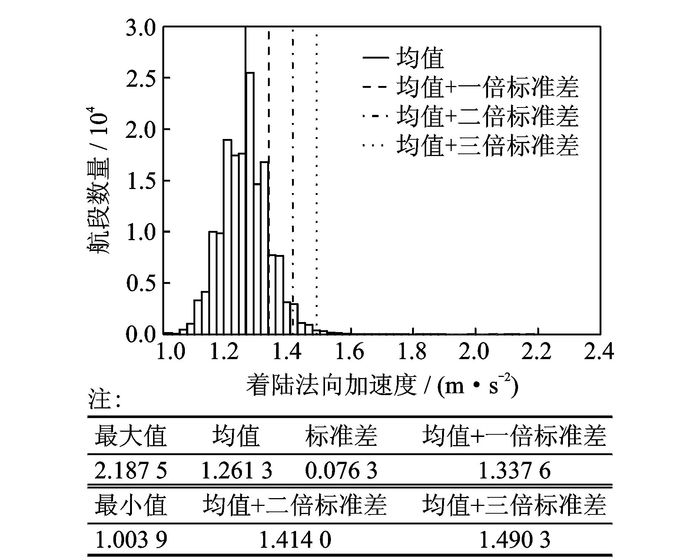
第2步:计算标准差线。由式(4,5) 得:均值μ=1.261 3,标准差σ=0.076 3,由此μ+σ=1.337 6,μ+2σ=1.414 0和μ+3σ=1.490 3。数据的柱状分布图如图 5所示。
|
图 5 着陆法向加速度直方图与告警线 Figure 5 Histogram and alarm lines of landing normal acceleration |
第3步:告警。方式1:选取1.337 6,1.414 0和1.490 3中的两条作为轻度告警线和严重告警线;方式2:分别取1.337 6,1.414 0和1.490 3为一级、二级和三级超限告警线。
3 四分位法四分位法可视为标准差法的一种改进,它使用中位数和标准四分位间距分别代替传统统计方法中的均值和标准差作为对数据总体的估计[11]。
四分位法的统计参数包括[12]:数据量N、下四分位Q1、上四分位Q3、中位数M、四分位间距(Inter quartile range, IQR)、最大值MAX和最小值MIN。四分位数是指将全部数据按大小顺序排列后,将数据集分成相等的四部分,其中每部分包含25%的数据,处于各分位点的数值就是四分位数,也就是说,Q3和Q1各有75%和25%小于它。IQR为上四分位Q3与下四分位Q1的差,即IQR=Q3-Q1,IQR中的数据占了全部数据的50%,它几乎不受异常值的影响,能够反映数据的离散程度;IQR越大,数据的离散程度越大;反之离散程度越小。当异常值比较多时,为了消除异常值的影响(重心偏移),可以采用标准四分位间距(Standard inter quartile range, SIQR)[13],表达式为
| ${\rm{SIQR}} = 0.741{\rm{ }}3 \times {\rm{IQR}}$ | (6) |
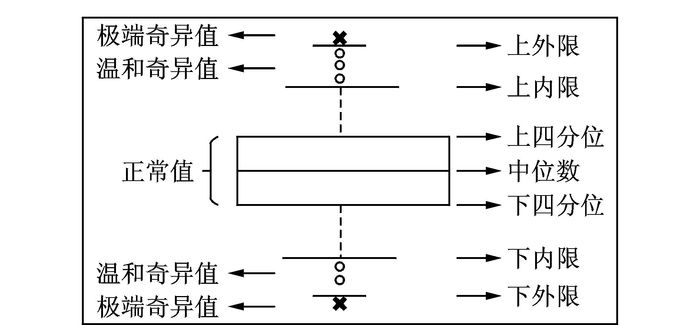
在实际数据中总是存在各式各样的异常值,而这些异常值会影响最终的分析结果。因此,确定异常值是提高分析能力的有力手段,而四分位法为确定异常值提供了可能。根据异常值对分析结果的影响程度,四分位法将异常值分成温和异常值(Mild outliers)和极端异常值(Extreme outliers)两类,其中温和奇异值分布在区间[Q1-3×IQR, Q1-1.5×IQR]和[Q3+1.5×IQR, Q3+3×IQR];极端异常值分布在区间(-∞, Q1-3×IQR]和[Q3+3×IQR, +∞),分别称Q3+3×IQR,Q1-3×IQR,Q3+1.5×IQR和Q1-1.5×IQR为上外限、下外限、上内限和下内限。四分位法的可视化可以通过箱线图(盒图)实现,如图 6所示。
|
图 6 箱线图 Figure 6 Box plot |
“四分位法”在数据统计分析方面的应用十分广泛,其优势主要集中在以下5点[14-15]:
(1) 能够直观明了地识别数据中的奇异值,为发现问题从而提出改进策略提供契机。
(2) “标准差法”是基于正态分布的,以假定数据服从正态分布为前提,但实际数据往往并不严格服从正态分布,因此“标准差法”并不适合非正态分布数据的分析,而“四分位法”依靠实际数据,不需要事先假定数据服从特定的分布形式,没有对数据作任何限制性要求,它只是真实直观地表现数据的本来面貌。
(3) “标准差法”给出异常值的标准以数据的均值和标准差为基础,而均值和标准差的耐抗性极小,异常值本身会对它们产生较大影响,这样产生的异常值个数不会多于总数的0.7%,显然应用这种方法来判断非正态分布数据中的异常值,其有效性是有限的。“四分位法”判别异常值以四分位数和四分位间距为基础,四分位数具有一定的耐抗性,多达25%的数据可以变得任意远而不会很大地扰动四分位数,所以异常值不能对这个标准施加影响。“四分位法”识别异常值的结果比较客观,具有一定的优越性。
(4) 通过分析中位数和异常值、上下四分位的位置,可以估计数据的偏态和尾重。
(5) “四分位法”具有极佳的可视化效果图(箱线图),通过对箱线图的观察,可以很直观地了解数据的特征。例如:在数据集中,哪些数据出类拔萃、哪些数据表现不及一般、以及某些数据处于整个数据集中的什么位置等。
4 数据试验与分析本节基于1.2节中的数据集,从大规模数据和小规模数据两个角度,分别采用“标准差法”和“四分位法”对数据集进行统计分析,然后基于“标准差法”的一/二/三倍标准偏差值和“四分位法”上外限、上内限、上四分位,对“标准差法”和“四分位法”进行了抗扰动性分析,从告警的角度给出与这两种方法相适应的数据集类型,以及“四分位法”在民航告警上的优越性。
4.1 大规模数据试验与分析基于未经过筛选错误异常值的数据集和经过筛选错误异常值的数据集,分别采用“标准差法”和“四分位法”对数据集进行统计分析,得到的分析结果如表 1所示。
| 表 1 “标准差法”与“四分位法”的统计参数比较 Table 1 Comparison of statistical parameters between standard deviation method and quartile method |
从表 1中容易看出,由于均值和标准差非常容易受到错误异常值,特别是-9 999和9 999这类离群错误异常值的影响。因此,在未对错误异常值进行筛选时,标准差法的抗扰动性很弱,很容易受到错误异常值的影响,得到的“均值+一/二/三倍标准差线”也失去了告警的意义;而四分位法中的上四分位、中位数和下四分位在筛选错误异常值前后均没有发生数值上的变化,从而其他统计参数也未发生变化,这就意味着四分位法完全没有受到错误异常值的影响,采用上外限、上内限和上四分位仍然具有告警的意义。需要指出,在筛选错误异常值前后,上四分位、中位数和下四分位只是在数值上不变,其在数据集中的位置实际上发生了变化,只是由于在数据集中同一数值会出现多次,因此才会出现数值不变这种情况。
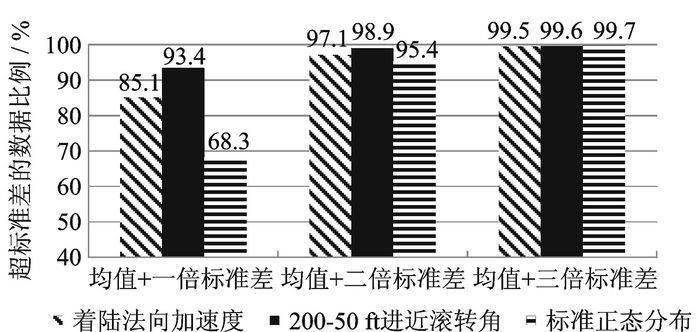
当数据集不满足正态分布时,即使对错误异常值进行了筛选,采用“标准差法”进行告警是否存在统计上的理论支持,这是一个值得研究的问题。图 7基于筛选错误异常值后的数据集,从“均值+一/二/三倍标准差”的角度,分别与标准正态分布进行了比较。这两个数据集的“均值+一倍标准差”与正态分布的68.3%差别较大,而“均值+二倍标准差”和“均值+三倍标准差”则与正态分布的95.4%和99.7%比较接近。因此,在采用“标准差法”进行告警时,采用告警线“均值+二/三倍标准差”具有统计上的理论支持,但“均值+一倍标准差”则缺乏理论依据。
通过表 1和图 7的数据比较,虽然筛选错误异常值后的数据集并不满足正态分布,但采用“标准差法”在一定程度上也能够实现告警,这主要归因于“中心极限定理”[16-17]。根据中心极限定理,大规模数据基本上服从正态分布。
|
图 7 一/二/三倍标准偏差值的比较 Figure 7 Comparison of standard deviation values |
4.2 小规模数据试验与分析
在4.1节中,对于大规模数据集,“四分位法”具有排除异常值的能力,且不受数据分布的影响,上外限、上内限、上四分位为告警提供了理论支持;而“标准差法”在经过异常值筛选后,其统计参数均值和标准差不会出现很大的扰动,采用“均值+一/二/三倍标准差”进行告警,也具有一定的理论依据。本节主要的研究对象是小规模数据,主要从“异常值比例”这个角度来研究“四分位法”和“标准差法”的统计意义和告警机制。
本节采用的数据是国内两个机场的部分航班数据,分别来自于1.2节中的“着陆法向加速度”数据集和“200-50 ft进近滚转角”数据集,详情如表 2所示。
| 表 2 数据集详情 Table 2 Details of datasets |
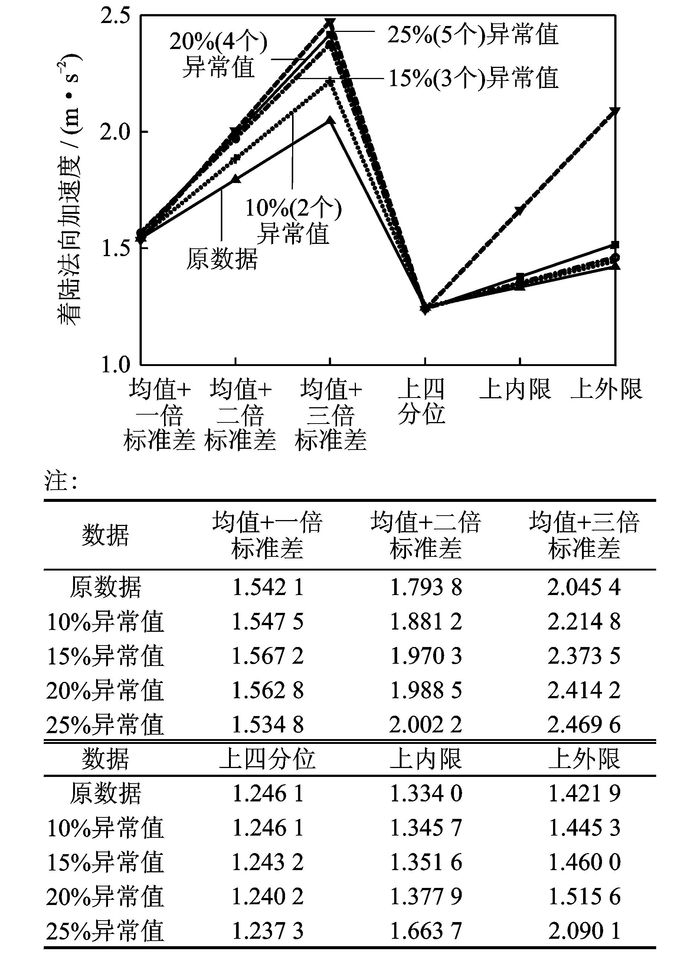
针对A机场,首先在区间(0, 1) 分别随机地生成2个、3个、4个和5个异常值,异常值数量分别占总数据量的10%,15%,20%和25%。然后基于这4组数据(原数据+随机异常数据)和原数据(未添加随机异常值),分别采用“标准差法”和“四分位法”求其主要的统计参数,如图 8所示。
|
图 8 A机场在着陆法向加速度上的主要统计参数比较 Figure 8 Comparison of main statistic parameters of landing acceleration of airport A |
由于随机添加的数据为异常值,因此在统计分析的过程中,应当排除掉这些数据对统计参数的影响,从而使得分析结果不出现较大的扰动。从图 8的曲线图容易看出,当异常值的比例不超过20%时,“四分位法”的统计参数最大偏差为0.093 7,而“标准差法”的统计参数最大偏差为0.368 8。因此,“四分位法”的抗扰动性要明显优于“标准差法”,从告警的角度来说,由于受到数据扰动的影响,由“标准差法”得到的“均值+二/三倍标准差”的取值明显偏大,失去了告警的参考价值;当异常值的比例达到25%时,由于四分位距的变化,使得“四分位法”出了较大的扰动,虽然“标准差法”受到的影响要小于“四分位法”,但得到的“均值+二/三倍标准差”同样失去了告警的价值。
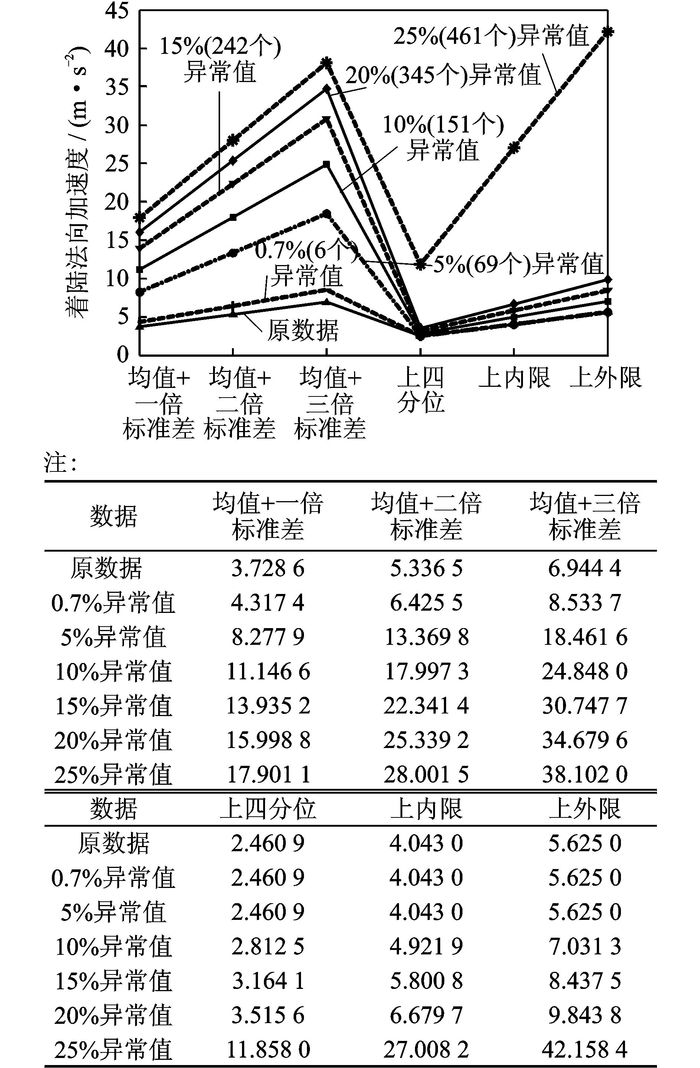
对B机场的统计分析类似于上述分析过程。首先在区间(20, 30) 分别随机地生成6个、69个、151个、242个、345个和461个异常值,异常值数量分别占总数据量的0.7%,5%,10%,15%,20%和25%。然后基于这6组数据和原数据,分别采用“标准差法”和“四分位法”求其主要的统计参数,如图 9所示。
|
图 9 B机场在200-50 ft进近滚转角上的主要统计参数比较 Figure 9 Comparison of main statistic parameters of 200-50 ft approach roll angle of airport B |
在异常值的比例不超过20%时,“四分位法”仍然具有比较好的抗扰动性,统计参数最大偏差为4.218 8,而“标准差法”的统计参数在5%时就出现了比较大的波动,在10%~20%时,“标准差法”已经失去了告警的价值。当异常值的比例达到25%时,这两种方法都出现了比较大的扰动,自然也失去了告警的意义。
5 结论在异常值的比例不超过20%时,“四分位法”仍然具有比较好的抗扰动性,统计参数最大偏差为4.218 8,而“标准差法”的统计参数在5%时就出现了比较大的波动,在10%~20%时,“标准差法”已经失去了告警的价值。当异常值的比例达到25%时,这两种方法都出现了比较大的扰动,自然也失去了告警的意义。
本文围绕“四分位法”和“标准差法”这两大经典的异常值检测方法展开讨论。首先从理论方面和如何实现民航告警这两个角度对“标准差法”进行了介绍;然后给出了“四分位法”的统计意义和可视化表示,并且结合“标准差法”给出了这两种方法的使用环境,以及“四分位法”在民航告警方面的独特优越性;最后通过数值实验,将“四分位法”和“标准差法”进行了比较,并且分析了异常值比例对这两种方法的影响。本文得到的基本结论概括如下:
(1) “四分位法”不受数据分布的限制,而“标准差法”的使用只限于服从正态分布的数据集;
(2) 基于“标准差法”对正态分布的依赖性,其异常值的检测能力要远远低于“四分位法”;
(3) “四分位法”的抗扰动性要优于“标准差法”:“四分位法”能承受20%左右的异常值扰动,而“标准差法”的承受比例不超过10%;
(4) 针对经过异常值筛选的大规模数据集,也可采用“标准差法”来进行告警;
(5) “四分位法”的统计分析结果比“标准差法”更客观,更能反映数据的特性;
(6) 在统计分析结果的可视化方面,“四分位法”也优于“标准差法”。
随着民航业的不断发展,产生的数据量越来越大,民航业已经进入了大数据时代,大数据时代的到来对数据分析的速度和结果准确性提出了很大挑战。“脏数据”(异常数据)的产生也贯穿于整个过程,“脏数据”的产生不但对数据分析的结果产生影响,也占用了大量的数据分析资源。本文对民航告警的展望主要包括:
(1) 取缔目前使用的“标准差法”,采用抗扰动性更强的“四分位法”。
(2) 对现有的“四分位法”进行改进,根据实际的告警需求采用“α分位法”。例如,取α=10,采用“十分位法”的90%和10%来替代“四分位法”的75%和25%。
(3) 将告警线的设置由数值改为比例。例如,在《飞行品质监控(FOQA)实施与管理》中,空客系列飞机的200 ft-50 ft进近滚转角的轻度偏差线和严重偏差线分别是8°和10°,这两种偏差线的设置是固定的,与数据集无关;为了体现不同数据集之间的差异性,可通过统计分析方法采用轻度偏差和严重偏差在整个数据集的比例来实现告警。
| [1] | MAILLE N. On the use of data-mining algorithms to improve FOQA tolls for airlines [C]// IEEE Aerospace Conference Proceedings. Big Sky, MT: IEEE, 2013. |
| [2] |
王洁宁, 周沅, 黄俊祥.
基于本体的陆空通讯风险识别与分析方法[J]. 南京航空航天大学学报, 2015, 47(4): 508–516.
WANG Jiening, ZHOU Yuan, HUANG Junxiang. Air-ground communication risk identification and analysis method based on ontology[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(4): 508–516. |
| [3] | CLEOPHAS T J. Machine learning in therapeutic research: The hard work of outlier detection in large data[J]. American Journal of Therapeutics, 2016, 23(3): 837–843. DOI:10.1097/MJT.0b013e31827ab4a0 |
| [4] |
舒平, 王旭辉, 黄圣国, 等.
民用飞机重着陆响应及诊断研究[J]. 中国制造业信息化, 2009, 38(15): 68–72.
DOI:10.3969/j.issn.1672-1616.2009.15.019 SHU Ping, WANG Xuhui, HUANG Shengguo, et al. Research on reaction and diagnose of civil aircraft landing[J]. Manufacture Information Engineering of China, 2009, 38(15): 68–72. DOI:10.3969/j.issn.1672-1616.2009.15.019 |
| [5] | SARTOR P, BOND D A, STASZEWSKI W J, et al. Value of an overload indication system assessed through analysis of aviation occurrences[J]. Journal of Aircraft, 2009, 46(5): 1692–1750. DOI:10.2514/1.42424 |
| [6] |
刘得一, 张兆宁, 杨新湦.
民航概论[M]. 第三版.北京: 中国民航出版社, 2011: 44-46.
LIU Deyi, ZHANG Zhaoning, YANG Xinsheng. An introduction to civil aviation[M]. Third edition. Beijing: China Civil Aviation Press, 2011: 44-46. |
| [7] |
中国民用航空局飞行标准司. 飞行品质监(FOQA)实施与管理[S]. AC-121/135-FS-2012-45R1. 北京: 中国民用航空局, 2015.
Flight Standards Division Civil Aviation Administration of China. The implementation and management flight operational quality assurance (FOQA) [S]. AC-121/135-FS-2012-45R1. Beijing: Civil Aviation Administration of China, 2015. |
| [8] | LEE N, CHOI H, KIM S H. Bayes shrinkage estimation for high-dimensional VAR models with scale mixture of normal distributions for noise[J]. Computational Statistics & Data Analysis, 2016, 101: 250–276. |
| [9] | PINKUS J L, AMATO A A, TAYLOR J P, et al. Abnormal distribution of heterogeneous nuclear ribonucleoproteins in sporadic inclusion body myositis[J]. Neuromuscular Disorders, 2014, 24(7): 611–616. DOI:10.1016/j.nmd.2014.04.012 |
| [10] |
茆诗松, 程依明, 濮晓龙.
概率论与数理统计教程[M]. 北京: 高等教育出版社, 2004: 102-107.
MAO Shisong, CHENG Yiming, PU Xiaolong. Probability and statistics tutorial[M]. Beijing: Higher Education Press, 2004: 102-107. |
| [11] |
王晓娟, 黄首先, 姜峰, 等.
四分位数及迭代稳健统计法在实验室能力验证中的应用[J]. 现代测量与实验室管理, 2016(3): 42–45.
WANG Xiaojuan, HUANG Shouxian, JIANG Feng, et al. The application of quartileand iterations of robust statistics in the laboratory proficiency testing[J]. Advanced Measurement and Laboratory Management, 2016(3): 42–45. |
| [12] | WITHERS C S, NACIARAJAH S. The distribution and quantiles of the range of a Wiener process[J]. Applied Mathematics and Computation, 2014, 232: 766–770. DOI:10.1016/j.amc.2014.01.147 |
| [13] | SINGH H P, PAL S K. An efficient class of estimators of finite population variance using quartiles[J]. Journal of Applied Statistics, 2016, 43(10): 1945–1958. DOI:10.1080/02664763.2015.1125865 |
| [14] |
钟振宇, 蒋佩英.
中位值和稳健四分位数间距的直观应用[J]. 中国科技投资, 2013(7): 123–124.
ZHONG Zhenyu, JIANG Peiying. Intuitive application of median and interquartile range in robust statistical techniques[J]. China Venture Capital, 2013(7): 123–124. |
| [15] |
李倩星.
R语言实战[M]. 北京: 电子工业出版社, 2016: 37-40.
LI Qianxing. R practical language[M]. Beijing: Publishing House of Electronics Industry, 2016: 37-40. |
| [16] | NOWAK P, HRYNIEWICZ O. On generalized versions of center limit theorems for IF-events[J]. Information Sciences, 2016, 355: 299–313. |
| [17] | DE A, BERNARDO B, GEYER C J. Nonstandard central limit theorems for Markov chains[J]. International Journal of Uncertainty Fuzziness and Knowledge-based Systems, 2011, 19(2): 251–274. DOI:10.1142/S021848851100699X |
 2017, Vol. 49
2017, Vol. 49


