固体燃料火箭发动机(Solid rocket motor,SRM)是火箭、导弹和宇航飞船等航空航天飞行器的常用动力装置。燃烧室是SRM的主体结构,主要由壳体、绝热层和固体推进剂等组成。绝热层的主要作用是防止高温燃气烧坏壳体,防止过热降低壳体强度和危及结构的完整性,同时还可以缓冲壳体与推进剂药柱之间的应力传递[1]。绝热层与壳体的良好粘接是保证发动机正常工作的重要条件。然而在实际生产中,由于壳体清洗不干净、胶接固化控制不佳或搬运不当等原因,有可能引起绝热层的脱粘[2]。脱粘的存在会缩短发动机的寿命,甚至导致航天器飞行失败[3],对绝热层的粘接质量进行无损检测十分必要。近年来,随着红外热像法的发展和日趋成熟,SRM装药包覆层、绝热层脱粘的红外热像检测法受到了一定的重视,其中闪光灯激励的脉冲热像法的可行性已被精心设计的SRM模拟试件实验所证实[4-5]。光激励的红外热像无损检测法具有单次成像面积大、非接触、可单面检测、速度快、对人体安全等优点,近10多年来在国内外得到了快速发展,已经在航空航天材料和结构的无损检测中得到了广泛应用[6-8],然而在SRM多界面脱粘检测中的实际应用还基本为空白。在SRM绝热层脱粘的脉冲热像(Pulsed thermography,PT)检测研究方面,作者已从实验和数值模拟两方面证明了检测的可行性和可靠性,并提出了用于缺陷信号增强和尺寸测量的热像数据处理方法[9-10],但对脉冲激励条件和试件结构参数对缺陷信号和检测极限的定量影响规律还不太清楚。
为了弥补当前关于SRM绝热层脱粘红外热像检测研究的不足,推进PT法在绝热层脱粘检测中的应用,本文将对SRM绝热层脱粘的脉冲热像检测的基本规律进行分析。首先建立SRM绝热层结构脉冲热像检测的三维瞬态传热模型,利用有限元分析软件ANSYS进行数值模拟,研究脱粘缺陷大小、绝热层厚度等结构参数对缺陷最大温差、最大对比度等信息参数的影响规律;然后利用预置脱粘缺陷的三层结构试件对理论研究结果进行部分实验验证,并进一步讨论脱粘的检测极限问题和尺寸测量方法;最后归纳出绝热层脱粘PT检测的基本规律和应用准则。
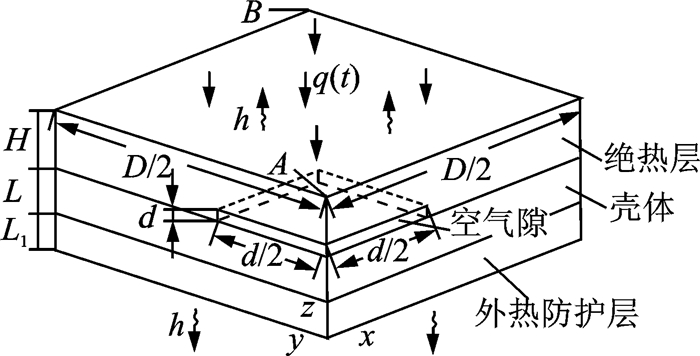
1 绝热层脱粘脉冲热像检测的有限元仿真 1.1 仿真模型和参数设定设SRM壳体由钢壳体、绝热层和外热防护层构成,绝热层为丁腈橡胶(Nitrile-butadiene rubber, NBR),考虑到试件制作的简便性,外热防护层也用丁腈橡胶代替。忽略胶粘剂的影响或假定胶粘剂的热物性参数与绝热层近似。在绝热层和壳体之间存在脱粘缺陷,脱粘处以纯空气隙代替。不考虑实际壳体的弧度,忽略各缺陷之间的相互影响,对每一个尺寸的缺陷进行单独建模仿真。设所关注的壳体区域范围为三层结构组成的大正四棱柱,上表面受均匀热流加热,下表面为自然对流换热边界,其余边界绝热。脱粘区(空气隙)是高度为δ的小正四棱柱,位于大正四棱柱的中心。以正四棱柱的中心线为z轴,底面的两条中线分别为x轴和y轴,建立三维坐标系,则传热结构关于正四棱柱的两个中心纵截面xoz和yoz具有镜像对称性,在对称面上没有法向热流通过,故可把对称面看作绝热面,只取整体结构的四分之一建立其三维瞬态传热仿真模型,如图 1所示。其中绝热层、壳体和外防护层厚度分别为H,L,L1;模型和脱粘区在xy面上的投影均为正方形,边长分别为D和d;脱粘形成的空气隙内嵌在绝热层的底部;气隙厚度为δ。关于脱粘和人工缺陷(聚四氟乙烯夹片)在仿真模型中的模拟方法及计算精度问题在前期工作中已有所论证[10]。材料的热物性参数见表 1。
|
图 1 仿真模型 Figure 1 Simulation model |
| 表 1 材料的热物性参数 Table 1 Thermal properties of materials |
考虑到SRM实际结构和试件制造尺寸,仿真模型的尺寸参数选取如下:D=20 mm,H=1.55 mm,L=2 mm,L1=1 mm,δ=0.05 mm。
设试件初始温度为T0=0 ℃,试件上下表面与环境有对流换热,换热系数为h=10 W·m-2·K-1,其他表面绝热。采用从绝热层一侧的单面检测法。根据实验室具备的脉冲热激励装置的能量,设脉冲激励的热流密度为
| $ q\left( t \right) = \left\{ \begin{array}{l} {q_0}\;\;0 \le t \le {t_h}\\ 0\;\;\;t>{t_h} \end{array} \right. $ | (1) |
式中:幅值q0=1.9×106 W·m-2;加热时长th=0.01 s。
利用有限元分析软件ANSYS进行传热计算。单元类型选用8节点三维六面体单元SOLID70;单元为长方体,在xy面内是边长为0.5 mm的正方形,在厚度方向上将对缺陷信号影响较大的操作侧表层单元尺寸设为0.15 mm,其余各层单元尺寸为0.2 mm;单元总数为12 000。仿真步长的设置是:在加热阶段,初始步长为5×10-5 s,最大步长为5×10-4 s;在散热阶段,初始步长为0.02 s,最大步长为0.1 s;总仿真时长为20 s。计算结束后,以模型表面点A和B分别代表缺陷区和无缺陷区计算缺陷信息参数。
缺陷信息参数主要有:(1) 温差(ΔT),ΔT(t)=Td(t)-Tnd(t),其中Td为缺陷处的温度,Tnd为无缺陷区的温度;(2) 最大温差(ΔTm),即ΔT(t)的最大温值;(3) 最大温差时间(tdm),即ΔTm发生的时刻;(4) 动态对比度(C),C(t)=ΔT(t)/Tnd(t);(5) 最大对比度(Cm),即C(t)的最大值;(6) 最大对比度时间(tm),即Cm发生的时刻;(7) 信噪比(S(t)),S(t)=ΔT(t)/σnd(t),σnd表示无缺陷区温度信号的标准差。由于仿真结果无噪声,故信噪比只在实验数据分析时采用。
1.2 仿真精度的验证为了验证仿真模型与计算方案的合理性,在特定条件下,用有限厚无限大平板的解析解[11]对有限元计算的精度进行校验。设仿真模型缺陷边长d=10 mm。当将各层材料(包括空气隙)的热物性参数统一按丁腈橡胶的热物性参数设定、且所有外表面绝热时,此时仿真模型等效于有限厚度无限大表面绝热的丁腈橡胶平板。有限厚无限大平板在两面绝热条件下,当前表面施加的热流密度为式(1) 时,前表面温度的精确解为[11]
| $ \theta \left( t \right) = \left\{ \begin{array}{l} \frac{{{q_0}t}}{{\rho Cl}} + \frac{{{q_0}l}}{\lambda }\left[ {\frac{1}{3} - \frac{2}{{{\pi ^2}}}\sum\limits_{n = 1}^\infty {\frac{1}{{{n^2}}}} \exp \left( { - \frac{{\alpha {n^2}{\pi ^2}t}}{{{l^2}}}} \right)} \right]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \le {t_h}\\ \frac{{{q_0}{t_h}}}{{\rho Cl}} + \frac{{2{q_0}l}}{{{\pi ^2}\lambda }}\sum\limits_{n = 1}^\infty {\frac{1}{{{n^2}}}} \exp( - \frac{{\alpha {n^2}{\pi ^2}t}}{{{l^2}}}) \cdot \left[ {\exp(\frac{{\alpha {n^2}{\pi ^2}{t_h}}}{{{l^2}}}) - 1} \right]\;\;\;t > {t_h} \end{array} \right. $ | (2) |
式中:α为热扩散系数;l为平板厚度。该解可用于校验有限元计算的正确性。
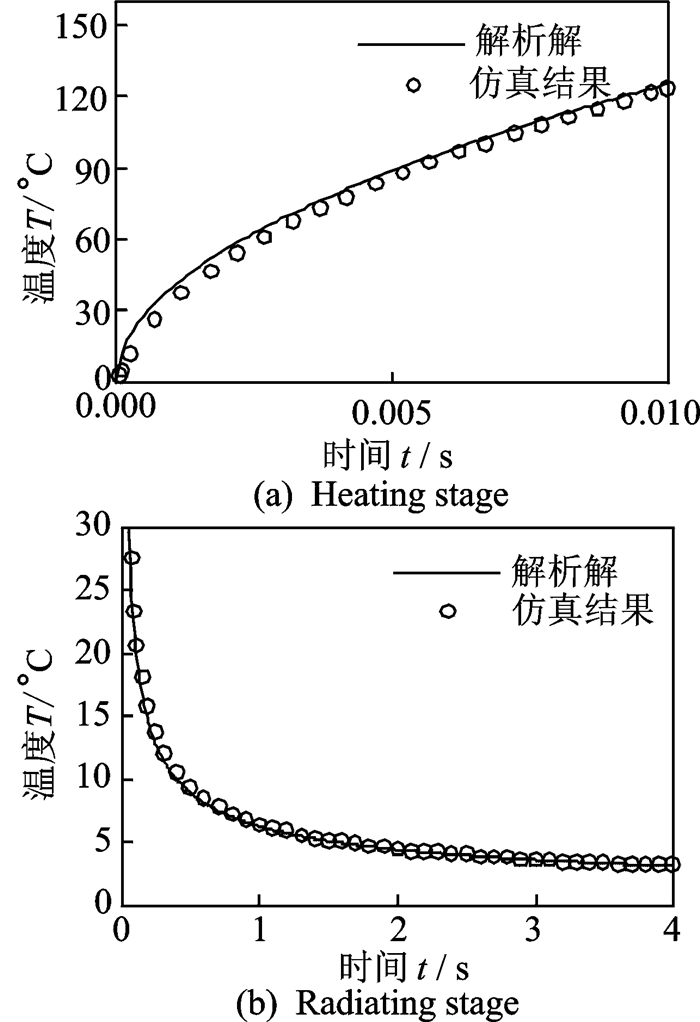
在散热阶段模型表面A点温升的仿真解与解析解的对比如图 2所示,二者基本一致,由此可知仿真的建模、单元选择、网格划分、仿真步长等参数设定是合理的。
|
图 2 表面温升的仿真解与解析解的对比 Figure 2 Excess temperature evolution of simulation result vs analytical solution |
1.3 脱粘大小对信息参数的影响
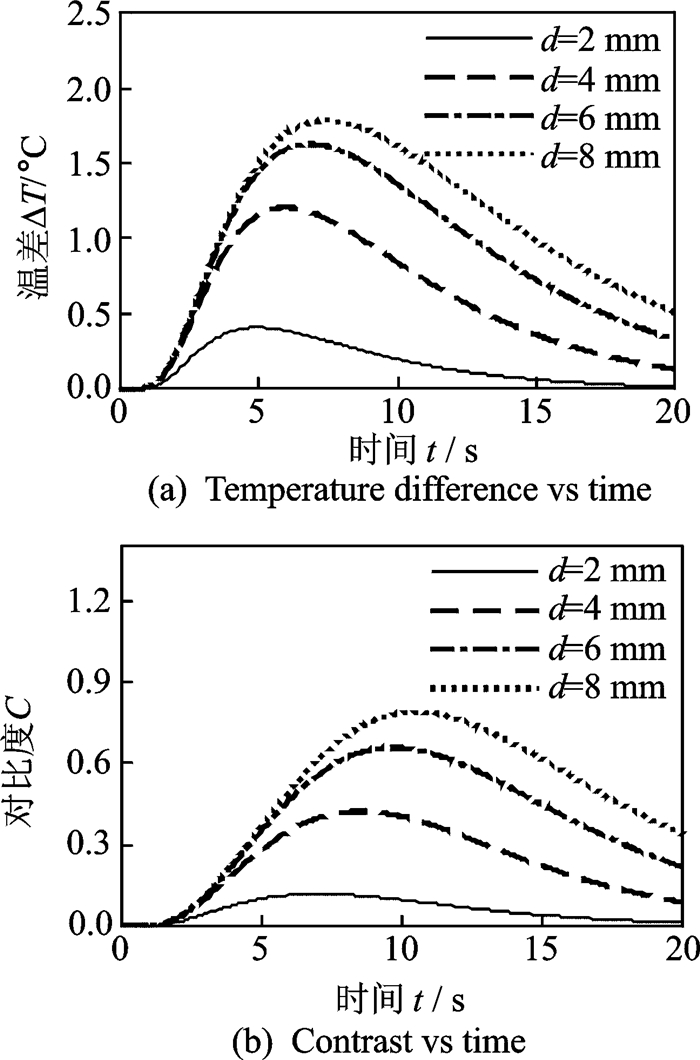
固定绝热层厚度H=1.55 mm,将脱粘缺陷边长作为变化量,取d=2,4,6,8 mm,其余参数同前述默认值。仿真得到的温差时间曲线和对比度时间曲线如图 3所示。
|
图 3 绝热层厚度H=1.55 mm,不同脱粘大小时缺陷信号的时间历程 Figure 3 Defect signal evolutions for different disbond sizes as insulator thickness H=1.55 mm |
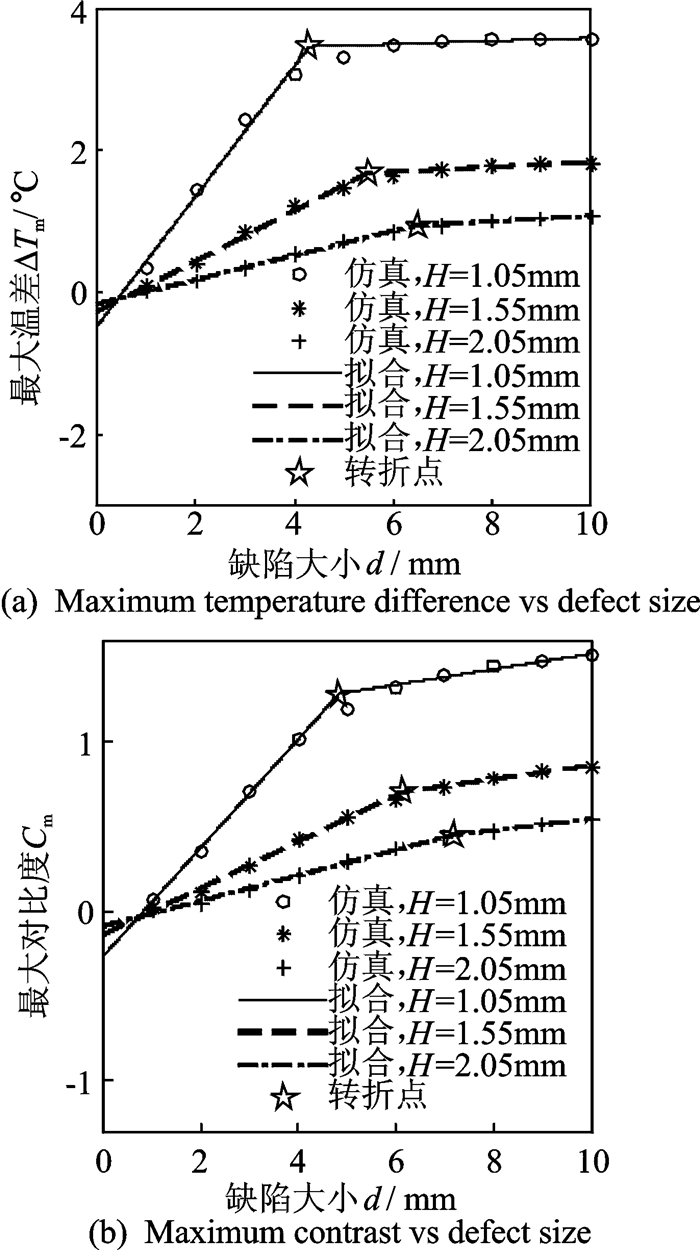
随着缺陷横向尺寸的增大,最大温差和最大对比度增大,最大温差时间和最大对比度时间也增大。设绝热层厚度H=1.05,1.55,2.05 mm,缺陷边长d=1~10 mm,间隔为1 mm,仿真得到的最大温差和最大对比度与缺陷大小的关系如图 4所示。
|
图 4 最大温差和最大对比度与脱粘缺陷大小的关系 Figure 4 Maximum temperature difference and maximum contrast vs defect size |
最大温差和最大对比度随缺陷尺寸的变化规律可用分段线性关系近似描述,有
| $ \Delta {T_{\rm m}} = \left\{ \begin{array}{l} {k_1}d + {b_1}\;\;\;d < {d_\Delta }\\ {k_2}d + {b_2}\;\;\;d > {d_\Delta } \end{array} \right. $ | (3) |
| $ {C_{\rm m}} = \left\{ \begin{array}{l} {k_1}d + {b_1}\;\;\;d < {d_{\rm C}}\\ {k_2}d + {b_2}\;\;\;d > {d_{\rm C}} \end{array} \right. $ | (4) |
式(3, 4) 中的参数如表 2所列。k2总是小于k1;超过dΔ的缺陷尺寸对最大温差的影响减弱;超过dC的缺陷尺寸对最大对比度的影响减弱,即大缺陷的易检性将不再明显增加,有趋于上限饱和值的趋势。
| 表 2 最大温差和最大对比度与缺陷大小关系的拟合方程(式(3, 4))的参数值 Table 2 Parameters in Eqs.(3, 4) for fitting curves of maximum temperature difference and maximum contrast vs defect size |
1.4 绝热层厚度对温差和对比度的影响
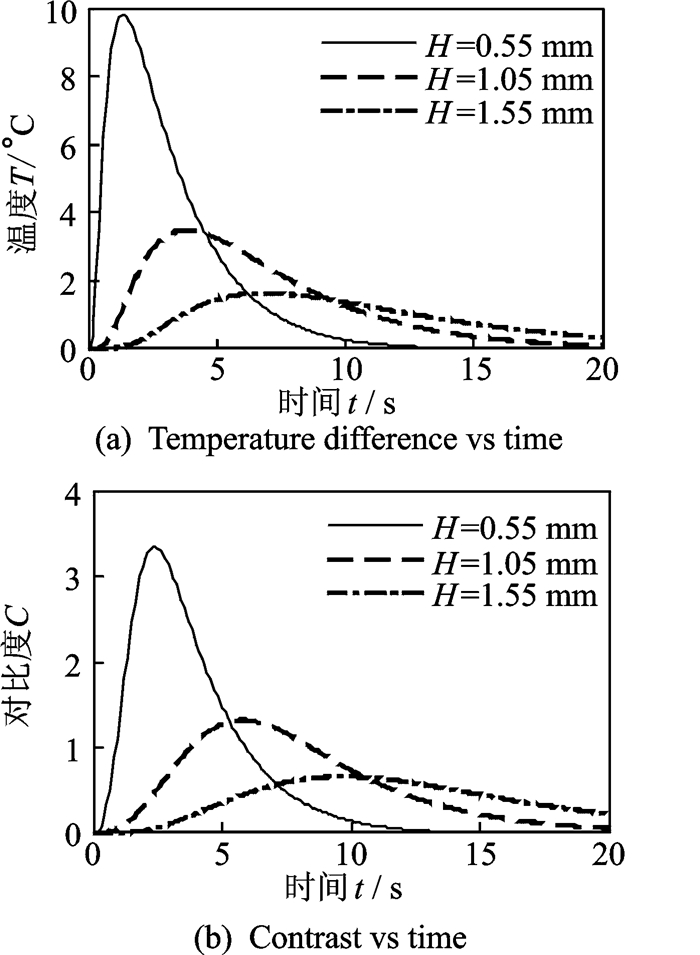
取缺陷厚度δ=0.05 mm,边长d=6 mm,绝热层厚度H分别为0.55,1.05,1.55 mm,仿真得到不同绝热层厚度的温差时间曲线和对比度时间曲线,分别如图 5(a,b)所示。随着绝热层厚度的增加,最大温差和最大对比度变小,最大温差时间和最大对比度时间变大,因此绝热层厚度越大越难检测。对d=6 mm,H=1.55 mm的缺陷,ΔTm=1.628 ℃,tdm=6.86 s,Cm=0.658,tm=9.66 s,因此对d=6 mm、H<1.55 mm的缺陷,其最佳检测时间(指最大温差时间或最大对比度时间)出现在10 s之内。
|
图 5 缺陷大小为6 mm,不同绝热层厚度时缺陷信号的时间历程 Figure 5 Defect signal evolutions for different insulator thicknesses as defect size d=6 mm |
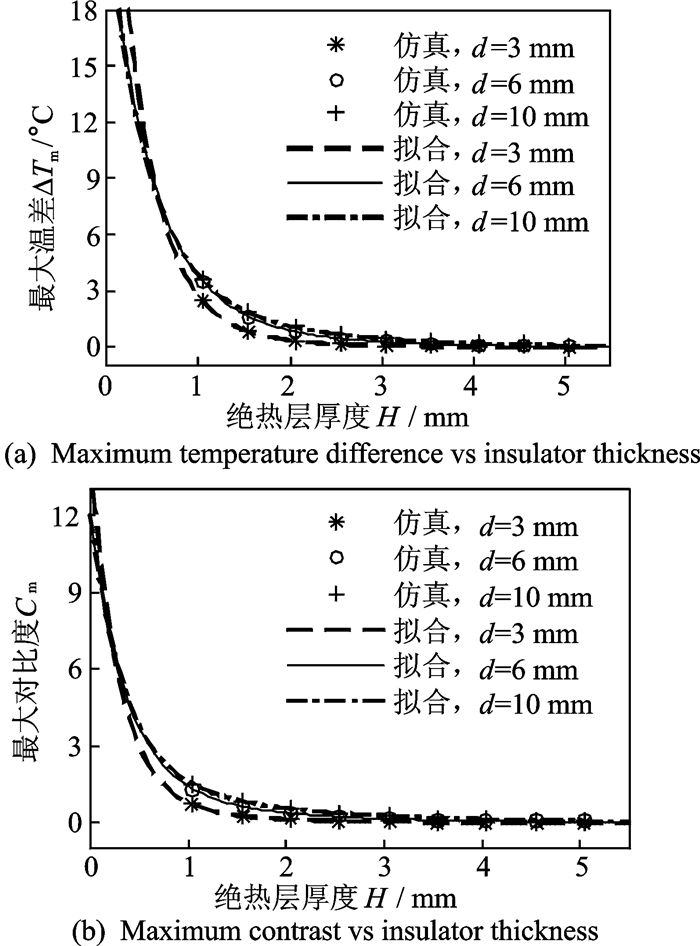
取缺陷大小d=3,6,10 mm,绝热层厚度H=1.05~5.05 mm,间隔为0.5 mm。仿真得到的最大温差和最大对比度与绝热层厚度的关系如图 6所示。
|
图 6 最大温差和最大对比度与绝热层厚度的关系 Figure 6 Maximum temperature difference and maximum contrast vs insulator thickness |
ΔTm与H之间、Cm与H之间的关系,满足拟合模型公式
| $ \Delta {T_{\rm m}} = {a_1}{{\rm{e}}^{ - {b_1}H}} + {a_2}{{\rm{e}}^{ - {b_2}H}} $ | (5) |
| $ {C_{\rm m}} = {a_1}{{\rm{e}}^{ - {b_1}H}} + {a_2}{{\rm{e}}^{ - {b_2}H}} $ | (6) |
式中H的单位为mm,对不同缺陷尺寸d求得的待定参数参见表 3。
| 表 3 最大温差和最大对比度与绝热层厚度关系的拟合方程(式(5,6))的参数值 Table 3 Parameters in Eqs.(5, 6) for fitting curves of maximum temperature difference and maximum contrast vs insulator thickness |
2 脉冲热像检测实验 2.1 实验条件
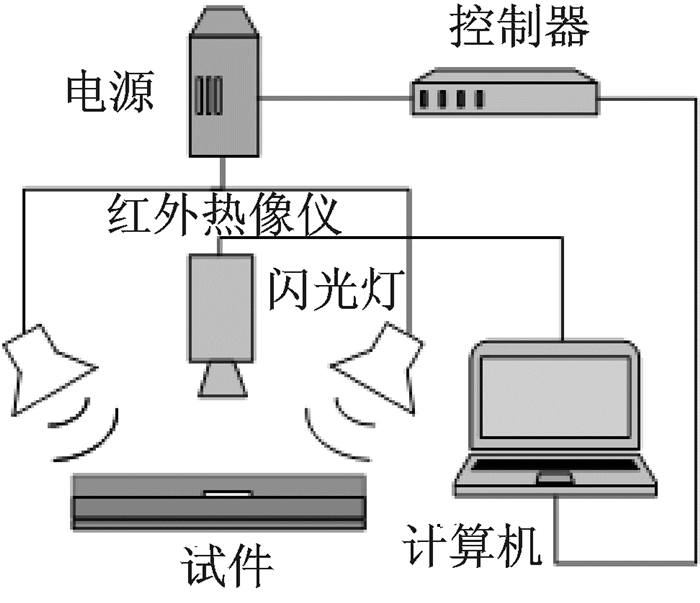
实验采用实验室自行开发的脉冲红外热像检测系统,该系统由闪光灯、红外热像仪、控制器、计算机及红外NDT应用软件组成,系统简图如图 7所示。采用从绝热层一侧检测的单面检测法。两个闪光灯的总能量为6 kJ;热像仪的像素分辨率为320×240,最高帧频为60 Hz,热灵敏度为0.1 K(在30 ℃时)。
|
图 7 脉冲红外热像检测系统 Figure 7 Pulsed infrared thermographic system |
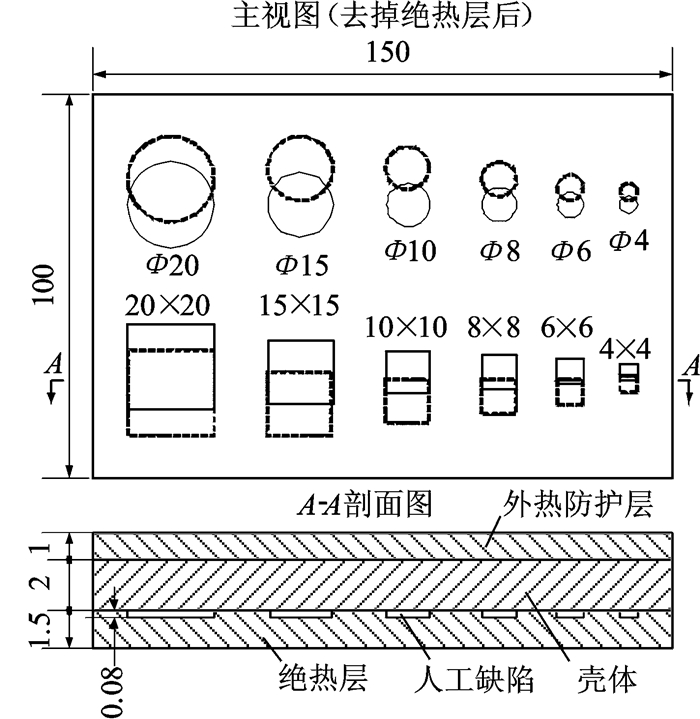
试件的结构如图 8所示,壳体材料为钢,绝热层为丁晴橡胶,为了制作方便外热防护层也用丁晴橡胶制作。在绝热层与钢壳体之间预设了两排尺寸不同的圆形和方形脱粘缺陷,以0.08 mm厚的PTFE夹片模拟脱粘,夹片与绝热层之间无胶粘剂。由于真实的脱粘难以定量制作,实践中常用PTFE夹片来模拟脱粘。图 8主视图虚线表示夹片布放的一次位置,而后又挪动到新位置。
|
图 8 试件结构图 Figure 8 Structure diagram of the sample |
实验检测时,两个闪光灯布置在试件的左右两侧,照射角(光入射角)约为45°,闪光灯距离试件中心约0.18 m;热像仪与试件的距离约0.54 m,热像采集频率设定为15 Hz,采集240帧,信号记录时长为16 s。在闪光开始前采集5帧图像,以其平均值作为试件表面初始温度。
2.2 实验结果分析典型的过余温度图如图 9所示,在一定时间范围内可以显示出所有缺陷,在t=6.0 s(图 9 (a))缺陷的温差和信噪比较高,在t=12.0 s(图 9 (b))最小缺陷信号即将消失。小尺寸缺陷信号将较早地消失。要识别是否存在更小的缺陷,只需要在目前可检测到的最小缺陷消失前的时间段内查找。图 9(a)出现的部分缺陷信号在图 9(b)消失。试件制作过程中PTFE片有挪动,在一次位置(见图 8主视图虚线)由于部分胶粘剂被带走产生了形似夹片形状的弱粘接缺陷,此处有少量空气,而在PTFE与绝热层之间存在更多空气。空气含量越少,缺陷信号消失得越早。

|
图 9 典型的过余温度图 Figure 9 Typical excess temperature images |
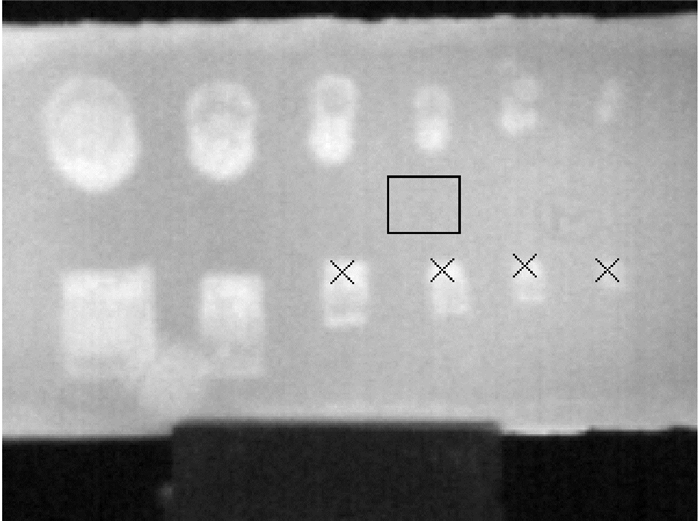
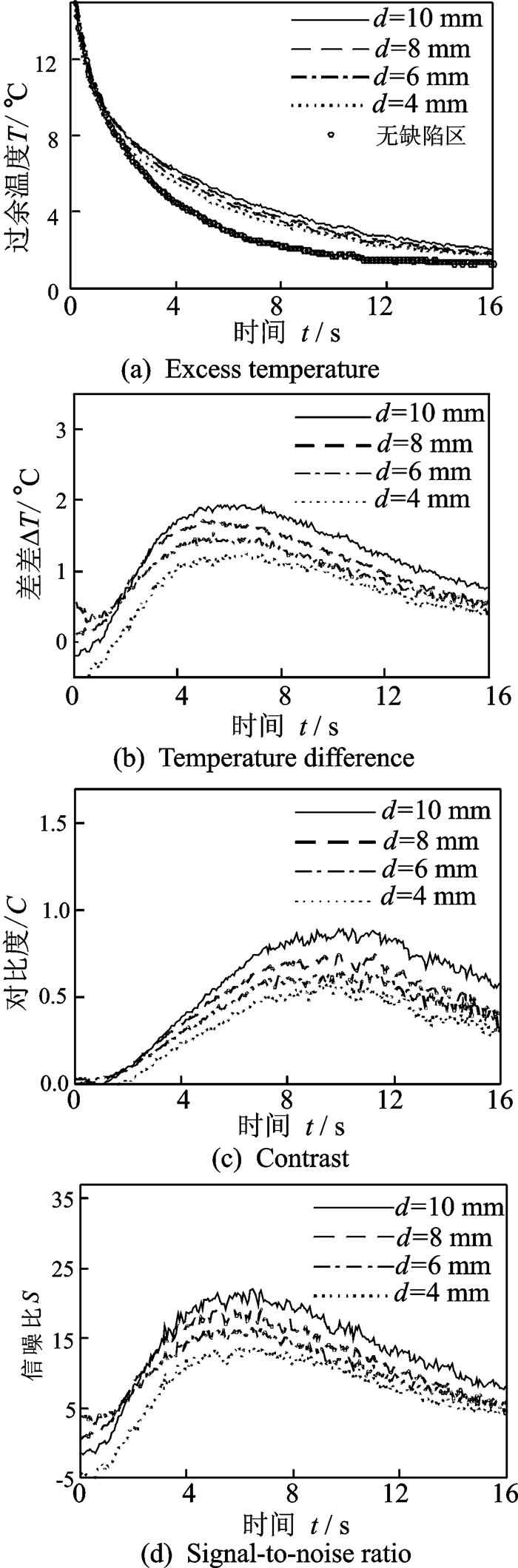
在边长d=10,8,6,4 mm的4个方形缺陷的中心分别取3×3像素为缺陷区,在附近无缺陷的地方取一个33×26像素的矩形区域作为无缺陷区,如图 10所示。相应的缺陷信息参数的时间历程曲线如图 11所示,可以看出缺陷尺寸越大,温差、对比度和信噪比越大。信噪比曲线中包含了丰富的缺陷信息,同样可以作为缺陷判别和最佳检测时间确定的依据[12]。
|
图 10 缺陷区和无缺陷区的选取 Figure 10 Choice of defect and non-defect areas |
|
图 11 缺陷信号与时间的关系曲线 Figure 11 Defect information parameters vs time |
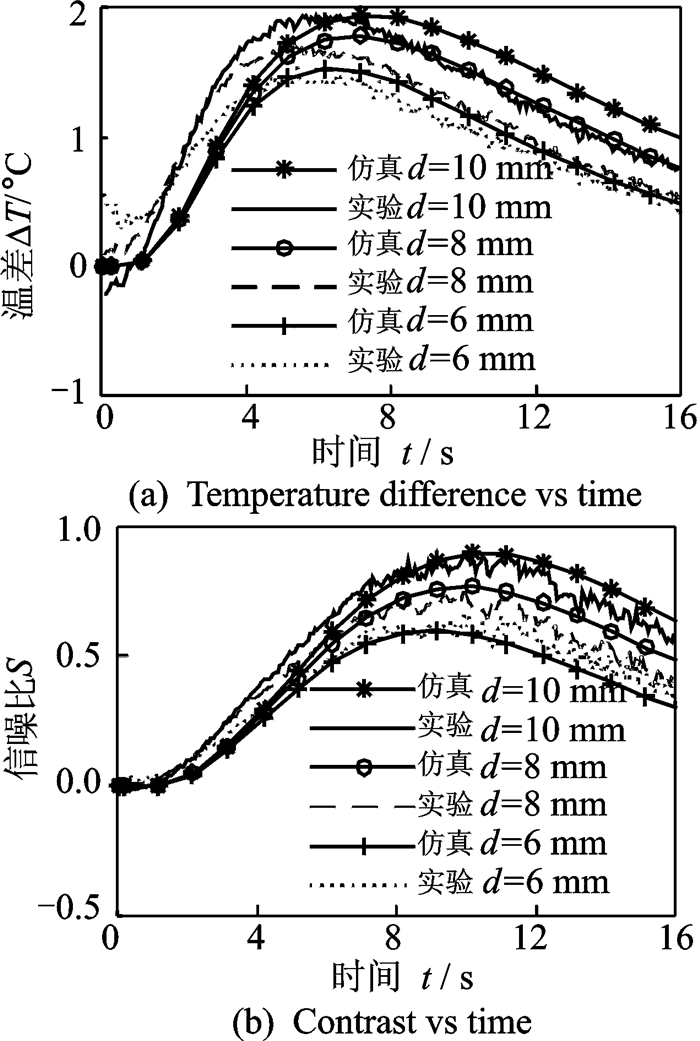
实测温差和对比度与仿真结果(设缺陷为纯空气隙,H=1.50,h=0.05 mm,d=10,8,6,4 mm,q0=1.9×106 W·m-2,th=0.01 s)的对比如图 12所示,对应的信号曲线基本相近。
|
图 12 实验与理论结果的对比 Figure 12 Comparison between experimental and theoretical results |
实验与仿真结果之间的误差来源主要有:热扩散系数的误差,混合缺陷与纯空气隙的等价转换的准确性[13],试件实际结构尺寸与设计尺寸的误差,热激励函数的差别等。实验与仿真获得的缺陷信息参数的对比如表 4所列,其中误差率的计算以理论值为参考标准。
| 表 4 缺陷信息参数的实验值与仿真值的比较 Table 4 Comparison between experimental and theoretical defect signal parameters |
表 4中多数信息参数的实测值与理论值基本相符,只有最大温差时间误差偏大,在20%以上,可能的原因有:理论计算时热扩散系数和绝热层厚度的取值与实际值有偏差;热像采集频率设定为15 Hz时,采样间隔为0.067 s,时间零点的定位有1个采样间隔的误差;实验曲线的噪声对极值点的准确定位有影响。
3 脱粘检测极限的确定为确定可检脱粘的尺寸极限和绝热层厚度极限,首先需确定可检缺陷的检测准则。缺陷可检的基本条件是信噪比大于1,即S(t)>1。从图 11(b, d)可以看出,在脉冲热像检测中,信噪比最大的时间与最大温差时间tdm一致,因此当ΔTm>σnd(tdm)时缺陷可检。考虑到一定的安全裕度,缺陷可检的准则设定为
| $ \Delta {T_{\rm m}} > \Delta {T_{{\rm{th}}}} = k{\sigma _{{\rm{nd}}}}({t_{{\rm{dm}}}}) $ | (7) |
式中:ΔTth为阈值;k为安全系数;k>1。
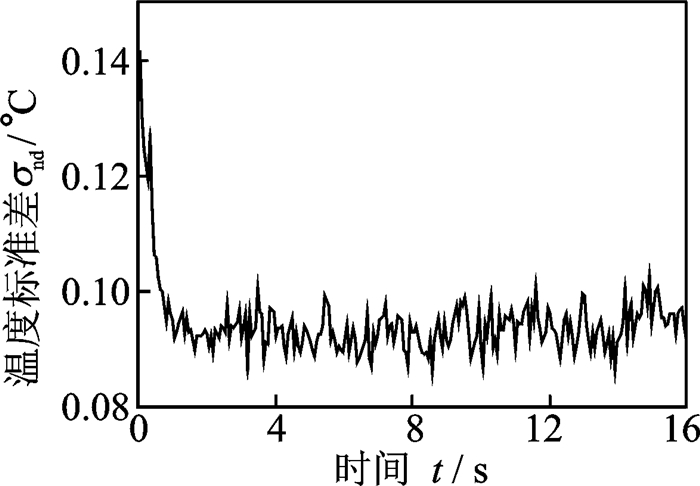
实验结果中无缺陷区的温度标准差σnd的时间曲线如图 13所示,当t≥0.8 s时,σnd≤0.1 ℃。无缺陷区的温度标准差σnd与热像仪的热灵敏度、物体结构及表面特性的均匀性、热激励光照的均匀性和外界反射干扰等多种因素有关。这里取k=1.5,则脱粘可检的准则为
|
图 13 无缺陷区温度标准差-时间曲线 Figure 13 Temperature standard deviation vs time for non-defect zone |
| $ \Delta {T_{\rm m}} > \Delta {T_{{\rm{th}}}} = 0.15\;℃;{t_{{\rm{dm}}}} > 0.8\;{\rm{s}} $ | (8) |
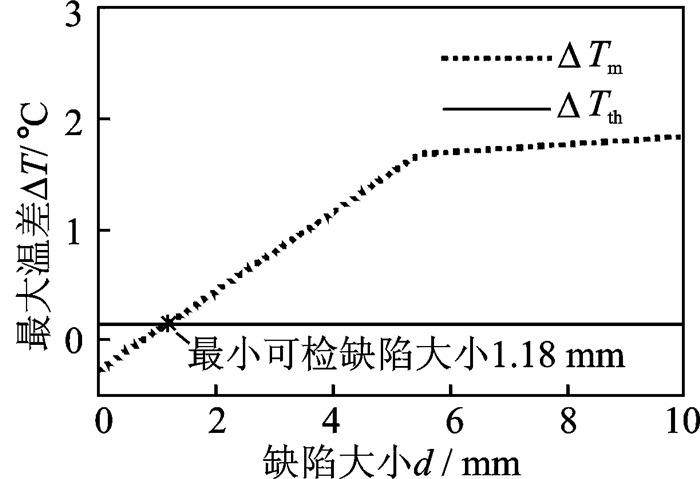
当绝热层厚度H=1.55 mm时,由式(3) 和表 2知,当d<dΔ(dΔ=5.48 mm)时,最大温差与缺陷尺寸的关系为ΔTm=0.356 9d-0.270 9,如图 14所示。假定缺陷的最大温差时间大于0.8 s,令ΔTm=ΔTth,可得到最小可检缺陷尺寸dmin=1.18 mm。同理可求得,当H=1.05,2.05 mm时,dmin分别为0.68 mm和1.82 mm。
|
图 14 绝热层厚度1.55 mm时最小可检缺陷尺寸的确定 Figure 14 Determination of the minimum size of detectable defect for insulator thickness of 1.55 mm |
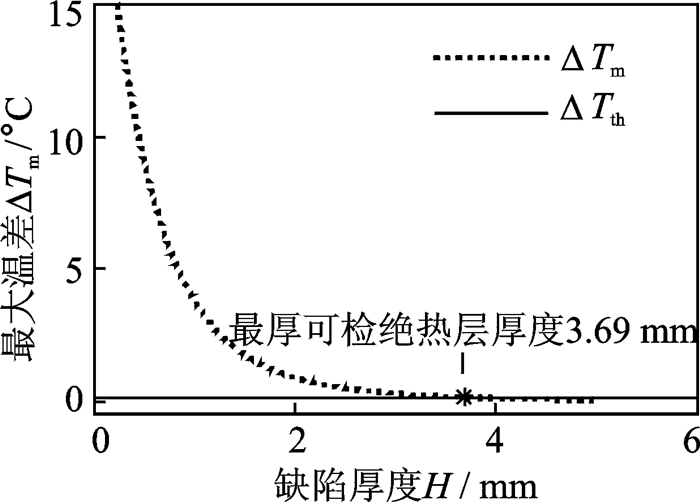
当缺陷大小d=6 mm时,根据式(5) 和表 3,最大温差与绝热层厚度的关系为ΔTm=3.698·e-0.8812H+19.39·e-2.155H,如图 15所示,令ΔTm=ΔTth,可得到最厚可检绝热层厚度Hmax=3.69 mm;同理可求得,当d=3, 10 mm时,Hmax分别为2.60, 4.45 mm。
|
图 15 缺陷大小为6 mm时最厚可检绝热层厚度的确定 Figure 15 Determination of the maximum insulator thickness for detectable defect with size of 6 mm |
4 脱粘尺寸的测量
在最大温差时刻,利用缺陷直径上的温度分布曲线可找到缺陷与非缺陷的边界,两个边界之间的部分即为缺陷区。在缺陷的最大温差时间点采集的热像上可测量该缺陷的大小。为此,需利用仿真数据研究脱粘缺陷尺寸的反求方法和误差。
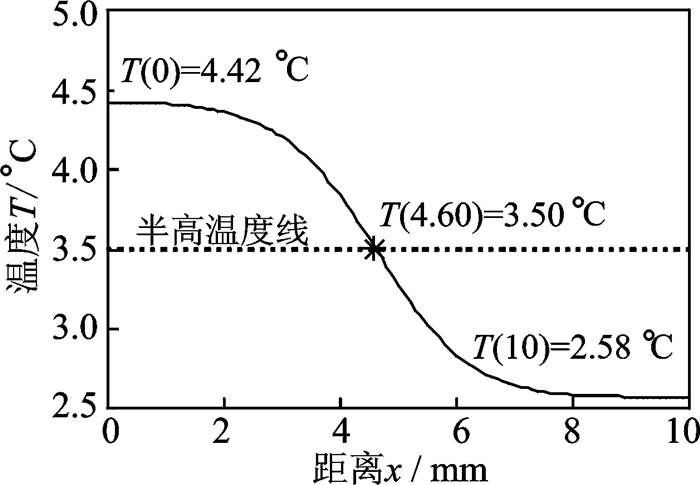
图 16是绝热层厚度为1.50 mm、大小为10 mm的缺陷在其最大温差时间tdm=7.76 s时仿真图像上的温度分布曲线,其中横坐标x沿图 1中A点所在的水平直线,x=0处为A点。采用半高法选取边界点,即选温度等于x=0和x=10两处温度的平均值的水平直线与曲线的交点为边界点。用半高宽度法测量d=10 mm的缺陷得到的半宽为4.6 mm,则测量值为d0=9.2 mm,比预设尺寸偏小。用半高宽度法测量的仿真缺陷尺寸结果如表 5所列。
|
图 16 仿真缺陷d=10 mm在最大温差时间(tdm=7.76 s)帧上的理论温度空间分布曲线 Figure 16 Spatial profile of theoretical temperature on defect with d=10 mm at its maximum temperature difference time (tdm=7.76 s) |
| 表 5 用半高法测量的缺陷尺寸与实际尺寸的对应关系(H=1.50 mm) Table 5 Defect sizes obtained using half-height measurement vs real defect sizes (H=1.50 mm) |
对表 5中的数据,可用拟合法得到实际尺寸d与测量尺寸d0的关系,即
| $ d = k \cdot {d_0} + b $ | (9) |
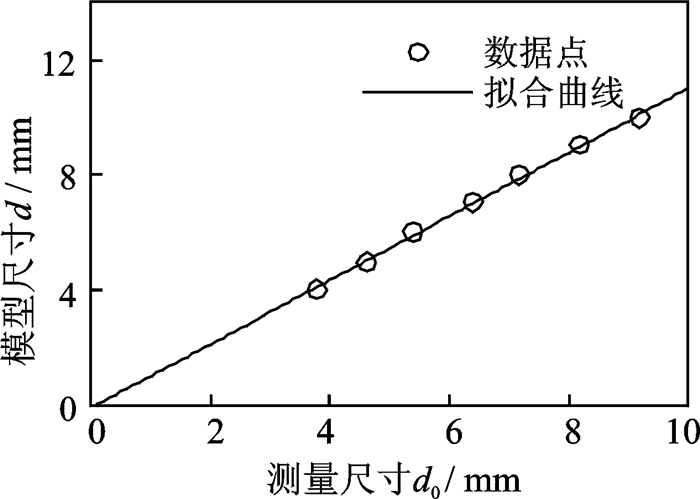
式中系数k=1.109, b=-0.098 59。拟合效果如图 17所示。
|
图 17 缺陷实际尺寸与半高法宽度测量尺寸的关系 Figure 17 Real defect size vs defect size obtained using half-height measurement |
由图 17可见半高宽度法存在确定的系统误差,可以修正,但不同的绝热层厚度对应不同的修正公式,式(9) 是H=1.50 mm时的修正公式。
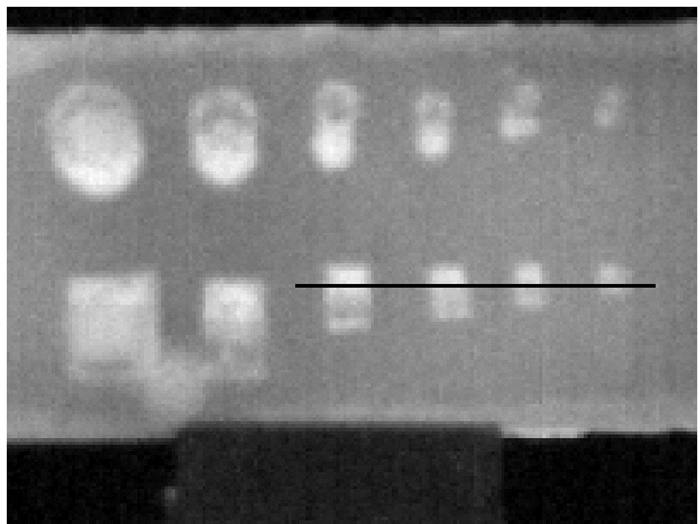
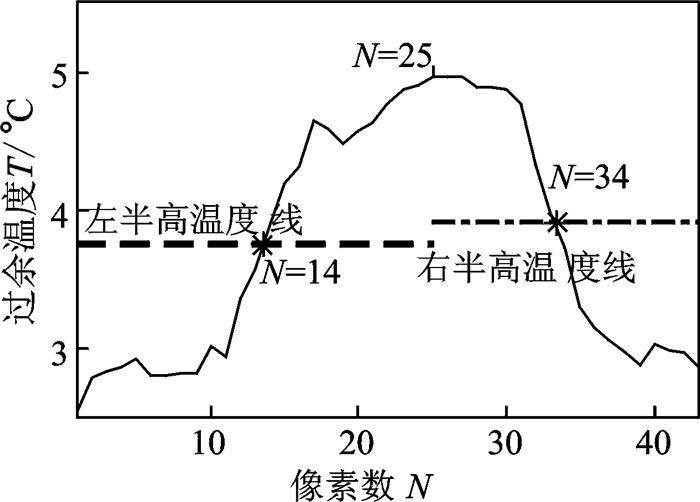
在尺寸d=10 mm的方形缺陷的最大温差帧(t=5.93 s)的热像上标记测量直线,如图 18所示,相应的温度分布曲线如图 19所示,图中标记了半高法测量的特征点,以最高温度点为中心点,分别作出左、右两侧的半高温度线,与温度-位置曲线的交点分别为左、右边界点,得到测量尺寸后再按误差修正公式(9) 进行修正。同理可测得其他3个方形缺陷(d=8,6,4 mm)的尺寸,最终测量结果如表 6所列,其中像素单位与长度单位的转换系数为p=0.528 5 mm/像素点。测量尺寸比试件图纸尺寸偏大,可能的原因是:夹片附近有弱粘接存在,缺陷制作有误差。热像仪的空间分辨率也是影响测量精度的因素,在本次实验中热像仪的尺寸分辨能力是0.528 5 mm。
|
图 18 缺陷尺寸测量标记线(t=5.93 s) Figure 18 Mark line for defect size measurement (t=5.93 s) |
|
图 19 d=10 mm的缺陷在最大温差时间帧上实测温度的空间分布曲线 Figure 19 Spatial profile of experimental excess temperature on defect with d=10 mm at its maximum temperature difference time |
| 表 6 试件缺陷尺寸的测量结果(比例尺0.528 5 mm/像素) Table 6 Measurement results of defect sizes of the sample (scale: 0.528 5 mm/pixel) |
5 结论
本文以三维有限元分析和实验,研究了固体火箭发动机绝热层脱粘的单面脉冲热像检测法的基本规律,主要得出以下结论:
(1) 最大温差和最大对比度与脱粘尺寸之间的关系可用分段线性关系近似描述(参见式(3,4)),随着脱粘尺寸的增大,最大温差和最大对比度都增加。脱粘尺寸越大越容易检测,且最佳检测时间出现的越晚。
(2) 最大温差和最大对比度与绝热层厚度(即缺陷深度)的关系是非线性函数关系(参见式(5,6)),随着绝热层厚度的增加,最大温差和最大对比度迅速下降。绝热层厚度越大越难检测,且最佳检测时间出现的越晚。
(3) 脱粘缺陷可检的准则是式(7)。
(4) 依据脱粘缺陷检测准则(7) 及绝热层厚度一定时最大温差与脱粘尺寸的关系方程(3),可确定该绝热层厚度下可检测的最小脱粘尺寸。
(5) 依据脱粘缺陷检测准则(7) 及脱粘尺寸一定时,最大温差与绝热层厚度的关系方程(5),可确定一定大小的脱粘可检测时绝热层的最大厚度。
(6) 用半高宽度法进行脱粘尺寸的测量存在系统性误差,该误差可用线性修正公式作出精确的修正。
| [1] |
王铮.
固体火箭发动机绝热层分析和设计[J]. 推进技术, 1985, 6(1): 41–46.
WANG Zheng. Analysis and design of insulators in solid rocket motors[J]. Journal of Propulsion Technology, 1985, 6(1): 41–46. |
| [2] |
王维民, 庄福康.
固体发动机燃烧室壳体/绝热层界面脱粘类型及解决的技术途径[J]. 推进技术, 1996, 15(1): 89–91.
WANG Weimin, ZHUANG Fukang. Disbond types at the shell-insulator interface in the combustion chamber of solid rocket motors and solving approaches[J]. Journal of Propulsion Technology, 1996, 15(1): 89–91. |
| [3] |
唐庆明, 张明.
固体火箭发动机的装药缺陷及检测方法[J]. 飞航导弹, 2006(7): 52–54.
TANG Qingming, ZHANG Ming. Charge flaws and their detecting methods of solid rocket motors[J]. Aerodynamic Missile Journal, 2006(7): 52–54. |
| [4] |
蒋淑芳, 郭兴旺, 沈京玲, 等.
固体火箭发动机绝热层脱粘的红外热波无损检测[J]. 激光与红外, 2005, 35(8): 584–587.
JIANG Shufang, GUO Xingwang, SHEN Jingling, et al. Infrared thermal wave NDT on the disbonds of the heat insulated layer in solid propellant rocket motors[J]. Laser & Infrared, 2005, 35(8): 584–587. |
| [5] |
杨正伟, 张炜, 田干, 等.
红外热波方法检测壳状结构脱粘缺陷[J]. 红外与激光工程, 2011, 40(2): 186–191.
YANG Zhengwei, ZHANG Wei, TIAN Gan, et al. Infrared thermography applied to detect debond defect in shell structure[J]. Infrared and Laser Engineering, 2011, 40(2): 186–191. |
| [6] | VAVILOV V P, BURLEIGH D D. Review of pulsed thermal NDT: Physical principles, theory and data processing[J]. NDT & E International, 2015, 73: 28–52. |
| [7] | VAVILOV V P. Pulsed thermal NDT of materials: Back to basics[J]. Nondestructive Testing and Evaluation, 2007, 22(2/3): 177–197. |
| [8] | IBARRA-CASTANEDO C, PIAU J M, GUILBERT S, et al. Comparative study of active thermography techniques for the nondestructive evaluation of honeycomb structures[J]. Research in Nondestructive Evaluation, 2009, 20: 1–31. DOI:10.1080/09349840802366617 |
| [9] | GUO Xingwang, VAVILOV V. Pulsed thermographic evaluation of disbonds in the insulation of solid rocket motors made of elastomers[J]. Polymer Testing, 2015, 45: 31–40. DOI:10.1016/j.polymertesting.2015.04.015 |
| [10] |
张南南, 郭兴旺.
固体火箭发动机绝热层脱粘的红外无损检测建模方法[J]. 无损检测, 2016, 36(8): 1–5.
DOI:10.11973/wsjc201608001 ZHANG Nannan, GUO Xingwang. Infrared NDT modeling of disbonds in the insulator of solid rocket motors[J]. Nondestructive Testing, 2016, 36(8): 1–5. DOI:10.11973/wsjc201608001 |
| [11] | CARSLAW H S, JAEJER J C. Conduction of heat in solids[M]. 2nd Edition. Oxford: Clarendon Press, 1986: 75-112. |
| [12] | BALAGEAS D, CHAPUIS B, DEBAN G, et al. Improvement of the detection of defects by pulse thermography thanks to the TSR approach in the case of a smart composite repair patch[J]. Quantitative InfraRed Thermography Journal, 2010, 7(2): 167–187. DOI:10.3166/qirt.7.167-187 |
| [13] | VAVILOV V P, BURLEIGH D D, KLIMOV A G. Advanced modeling of thermal NDT problems: From buried landmines to defects in composites [C] // Proc SPIE Thermosense XXIV. Bellingham, WA: SPIE, 2002, 4710: 507-521.http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=884945 |
 2017, Vol. 49
2017, Vol. 49


