2. 南京航空航天大学江苏省风力机设计高技术研究重点实验室,南京,210016
2. Jiangsu Key Laboratory of Hi-Tech Research for Wind Turbine Design, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China
目前,针对航空结构的结构健康监测(St ructural health monitoring, SHM)[1-2]研究变得日益重要。SHM由传统无损检测技术发展而来,该技术利用集成在结构中的传感/驱动元件网络对结构状态进行实时在线检测,可有效提高结构安全性并降低维护费用[3-5]。Lamb波监测方法具有监测范围广、适用于多种结构损伤形式的优点,是结构健康监测中最有效的监测方法之一。然而,由于频散效应,Lamb波波包会发生扩展,幅值下降,而且随着传播距离的增大,这种频散效应会变得更加严重,从而给信号分析和损伤特征提取带来困难,并最终影响Lamb波损伤监测结果的分辨率和准确度。实际航空结构中由于存在大量的反射体,频散问题将变得更为严重。因此,针对实际复杂航空结构的Lamb波频散补偿研究具有十分重要的意义。
为了消除频散效应,国内外研究者提出多种Lamb波频散补偿的信号处理方法。Hua和Lin[6]等采用脉冲能量演化方法来进行频散补偿。还有一种方法以时域翻转的传感信号作为优化的激励信号来进行频散补偿。Yuan[7]等提出了线性映射的Lamb波频散消除方法。Marchi [8]等提出一种基于弯折频谱的时频域转换方法。后向传播方法由Sicard等[9]提出,该方法基于后向传播函数在频域中补偿某Lamb波模式信号每个频率成份因空间传播产生的相位变化,故可以消除信号中的频散效应。时间-距离域变换方法[10]通过信号处理的方法把原始传感信号后向传播至t=0处以恢复频散扩展的波包,该方法出发点与后向传播方法类似。在实际应用中,这些补偿方法都需要相应Lamb波模式的绝对波数。然而,实际被测的航空结构含有加强筋、螺钉和孔洞,且厚度不均,结构形式复杂,波数曲线难以理论获取。相比之下,相对波数曲线则较容易测得。
本文将可利用相对测量波数曲线进行频散补偿的线性频散信号构建(Linearly-dispersive signal constructi o n, LDSC)方法[11]应用于复杂航空结构,并引入了1.5波峰正弦调制的准宽带Lamb波激励波形,可以降低多反射结构对成像结果的影响,最后在真实复杂的某型号飞机大梁结构上进行了实验验证,结果证明了基于相对测量波数的LDSC方法可以有效地消除Lamb波的频散效应,从而提高损伤成像分辨率。
1 基于相对测量波数的LDSC方法 1.1 LDSC方法Lamb波频散是指其传播速度随频率的变化而变化,其本质是由于非线性的波数关系造成的,如果将该波数关系进行线性化则能消除Lamb波频散。线性频散信号构建就是通过频域插值处理将具有非线性波数关系K0(ω)的原始频散Lamb波信号,构建为具有线性化波数关系Klin(ω)的线性频散信号,从而实现频散补偿[11]。其计算公式为
| $ {v_{{\rm{lin}}}}\left( t \right){\rm{ }} = {\rm{IFFT}}\left[{{V_0}\left( {{\mathit{\Omega} _{{\rm{lin}}}}\left( \omega \right)} \right){C_{{\rm{lin}}}}\left( \omega \right)} \right] $ | (1) |
式中:vlin(t)为线性频散信号的时域表达式;V0(ω)为原始频散信号的频域表达式;插值映射序列Ωlin(ω) = K0-1[Klin(ω)];波形补偿因子Clin(ω) = Va (ω)/Va [Ωlin(ω)];IFFT [·]表示快速逆傅里叶变换。线性化波数关系Klin(ω)=k0+k1(ω-ωc),其中k0=K0(ωc),k1=1/cg(ωc),ωc为中心频率,cg(ω)为Lamb波传播的群速度。
1.2 相对波数曲线的测量方法波数是指在波的传播方向上单位长度内波的个数,其理论表达式为
| $ K\left( \omega \right) = \mathit{\Phi} \left( \omega \right)/L $ | (2) |
式中:L为传播距离;Φ(ω)表示传感信号中激励信号波包和直达波包之间的相位差,可以计算为
| $ {\mathit{\Phi} _1}\left( \omega \right) = \left\{ \begin{array}{l} {\rm{Arctan}}\left[ {{\rm{Re}}/{\rm{Im}}} \right]\;\;\;\;\;\;\;\;{\rm{Re}} \ge 0\\ {\rm{Arctan}}\left[ {{\rm{Re}}/{\rm{Im}}} \right] + \pi \;\;\;\;{\rm{Re}} < 0,{\rm{Im}} \ge 0\\ {\rm{Arctan}}\left[ {{\rm{Re}}/{\rm{Im}}} \right] - \pi \;\;\;\;{\rm{Re}} < 0,{\rm{Im}} \le 0 \end{array} \right. $ | (3) |
式中:Re和lm分别为Va(ω)/V(ω)的实部和虚部;Arctan[·]为反正切函数;Φ1(ω)范围为-π~π,需对其进行相位展开处理,由于处理中很容易存在难以确定的2nπ(n为任意整数)误差。对Φ1(ω)进行相位展开处理后得到相对相位差Φ′(ω)=Φ(ω)+2nπ,代入式(2) 得到相对波数曲线[11]
| $ K\prime \left( \omega \right) = K\left( \omega \right) + \Delta {k_{{\rm{err}}}} $ | (4) |
式中Δkerr=2nπ/L。
2 基于LDSC的高分辨率损伤成像方法本文把LDSC用于传统延迟叠加成像方法[12-14]中以提高成像分辨率。延迟叠加成像方法中假设被测结构中每个点均为潜在的损伤散射点,对于结构中任一点O(x, y),可计算出监测信号从压电片Pm(xm, ym)经点O传播至压电片Pn(xn, yn)这一过程的传播时间为[13-14]
| $ \begin{array}{l} {t_{mn}}\left( {x,y} \right) = \sqrt {{{\left( {{x_m} - x} \right)}^2} + {{\left( {{y_m} - y} \right)}^2}} /{c_{{\rm{g}}o}} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\sqrt {{{\left( {{x_n}{\rm{ - }}x} \right)}^2} + {{\left( {{y_n} - y} \right)}^2}} /{c_{{\rm{g}}o}} \end{array} $ | (5) |
式中cgo为监测信号传播的群速度。
对于由N个压电片组成的阵列,假设smn(t)为Pm和Pn(m≠n, 1≤m, n≤N)组成的压电片对Pm-n中的损伤散射信号,则根据延迟叠加算法可把结构中任一点O(x, y)的能量值计算为
| $ E\left( {x,y} \right) = {\left[ {\frac{2}{{N\left( {N - 1} \right)}}\sum\limits_{m = 1}^N {\sum\limits_{n = m + 1}^N {{s_{mn}}\left( {{t_{mn}}\left( {x,y} \right)} \right)} } } \right]^2} $ | (6) |
计算监测区域内所有点的能量值并作为图像的像素值,得到损伤成像结果,结果中能量较大的聚焦点对应为损伤点。为了消除频散影响,LDSC被应用于损伤成像中,于是O点的像素可以通过式(7) 计算。
| $ E'\left( {x,y} \right) = {\left[ {\frac{2}{{N\left( {N - 1} \right)}}\sum\limits_{m = 1}^N {\sum\limits_{n = m + 1}^N {{{s'}_{mn}}\left( {{t_{mn}}\left( {x,y} \right)} \right)} } } \right]^2} $ | (7) |
式中s′mn(t)为smn(t)的LDSC结果。
在式(7) 中,每一个发生频散的smn(t)都经过LDSC补偿成了s′mn(t),损伤散射信号中因频散而扩展和变形的损伤散射波包得到恢复,提高了损伤散射信号的分辨率,所以损伤成像的分辨率也就得到了显著的提高。为了得到平滑的成像结果,s′mn(t)和smn(t)通常由它们的包络代替。
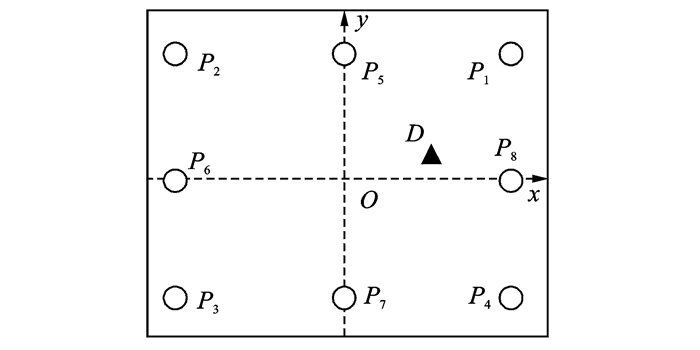
3 实验验证被测结构为某型号飞机的左翼梁(尺寸为1 300 mm×171 mm×130 mm),材料参数未知,大梁腹板部分由7个隔段组成,如图 1所示。监测区域选为大梁腹板第6个隔段,在该监测区域内布置8个圆形压电片P1~P8组成矩形阵列,如图 1中虚线框所示。初始状态下监测区域内的大梁腹板结构为未出现损伤的健康状态,为了模拟诸如裂纹、孔洞等实际损伤对Lamb波监测信号的影响,在第6个隔段的上表面粘贴一颗螺母(与大梁的接触面是外直径为8 mm的圆环)作为结构损伤状态下的模拟损伤。以被测区域中心作为原点建立直角坐标系,压电片和模拟损伤在坐标系中的分布情况和坐标分别见图 2和表 1。实验系统包括任意波形发生卡PXI5002、功率放大器、数据采集卡5105、电荷放大器和通道开关,可对传感阵列进行多通道扫查。

|
图 1 飞机翼梁 Figure 1 Beam of aircraft wing |
|
图 2 飞机翼梁腹板隔段6中传感器和损伤分布情况 Figure 2 Distribution of sensors and damage in zone 6 of beam celiac plate of aircraft wing |
| 表 1 压电片和损伤的坐标 Table 1 Coordinates of piezoelectric wafers and damage |
如图 1所示,大梁腹板是一个变厚度的结构,但由于监测区域厚度变化缓慢,可近似为等厚度。相比于铝板这种结构单一监测面积大的结构,该区域面积较小,而且由于其上下边界与多层螺钉连接结构的缘条相连,左右边界为加筋结构,Lamb波边界反射严重,再加上金属结构中信号衰减小,其多次反射信号将不可忽略。因此,Lamb波传感信号中的直达波包和反射波包将会发生严重混叠,使信号变得非常复杂,这也是将Lamb波损伤监测方法运用到实际复杂工程结构中的典型问题。
|
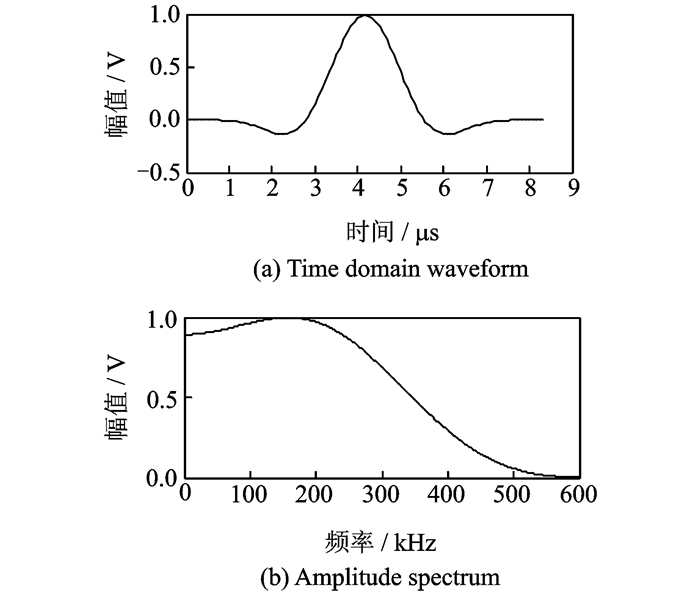
图 3 1.5波峰正弦调制激励信号 Figure 3 1.5-peak sinusoid modulated excitation signal |
为了减小Lamb波信号波包的时域宽度,提高其时域分辨率,以降低大梁多反射的复杂结构形式对成像结果的影响,本文并未选择常用的3波峰正弦调制信号,而设计出1.5波峰的正弦调制信号,如图 3所示,1.5波峰正弦调制信号的中心频率选为180 kHz,使得结构中产生A0模式为主的Lamb波监测信号,表达式为
| $ u\left( t \right) = \sin \left( {2\pi {f_{\rm{c}}}t} \right){\rm{ si}}{{\rm{n}}^5}\left( {\frac{{\pi {f_{\rm{c}}}t}}{{1.5}}} \right) $ | (8) |
式中fc为激励信号的中心频率。分别采集结构在健康和损伤状态下的传感信号,进行差运算得到损伤散射信号。信号采样率为12 MHz,采集点数为20 000个。
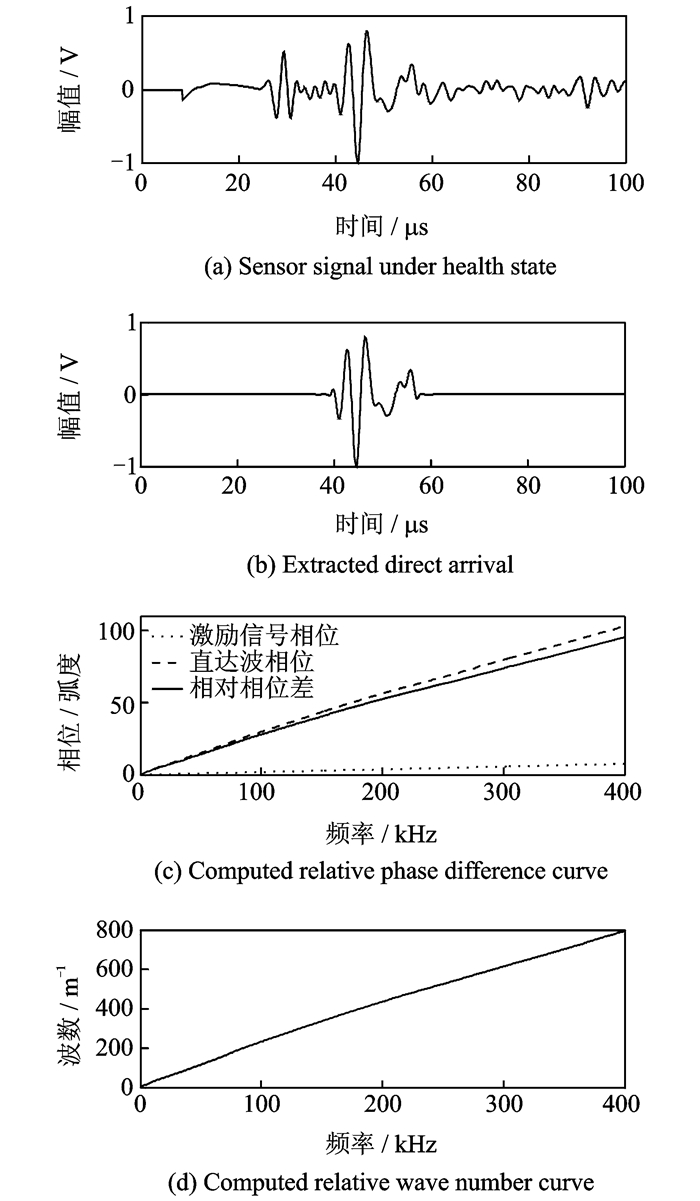
为了对散射信号进行LDSC处理,首先选择压电片对P1-2(由相距120 mm的P1和P2组成)中的传感信号测量相对波数曲线,测量过程如图 4所示。图 4(a)为健康状态下P1-2中的传感信号,其中幅值最大的波包为A0模式直达波包。从传感信号中提取直达波包,如图 4(b)所示。根据式(3) 计算出激励信号和直达波包之间的相位差并进行相位展开处理,得到不同频率下的相对相位差变化曲线,如图 4(c)所示。图 4(d)为根据式(2) 得到的相对波数曲线。
|
图 4 A0模式相对波数曲线的测量过程 Figure 4 Measurement procedure of the A0 mode relative wavenumber curve |
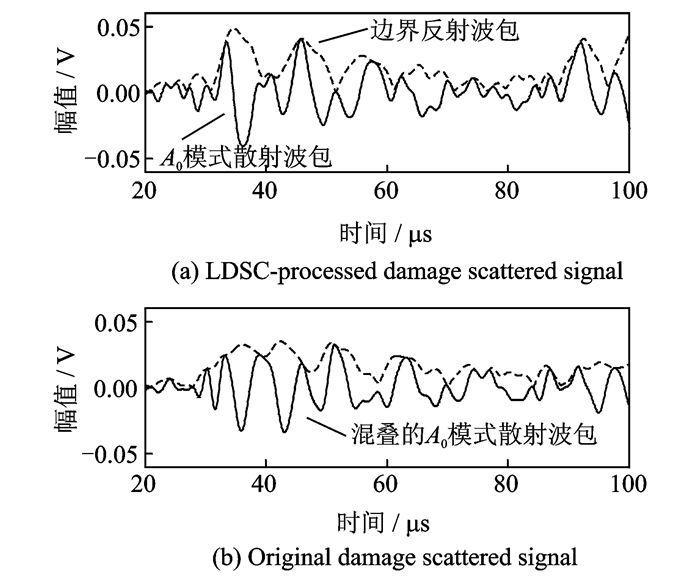
压电片对P1-5中原始和LDSC处理后的损伤散射信号如图 5所示。根据式(1) 进行LDSC的处理结果如图 5(a)所示,散射信号中各个波包再次被压缩,可明显区分出A0模式损伤散射波包。频散特性使图 5(b)中A0模式散射波包时域宽度增大到约12 μs,为原始激励波包宽度(4 μs)的3倍,这就使其与结构边界反射产生混叠而无法区分,信号变得非常复杂。这说明LDSC基于相对波数曲线能有效补偿航空复杂结构中A0模式信号的频散效应,从而提高了Lamb波的监测分辨率。
|
图 5 压电片对P1-5中原始和LDSC处理后的损伤散射信号 Figure 5 Original and LDSC-processed damage scattered signals in the PZT pair P1-5 |
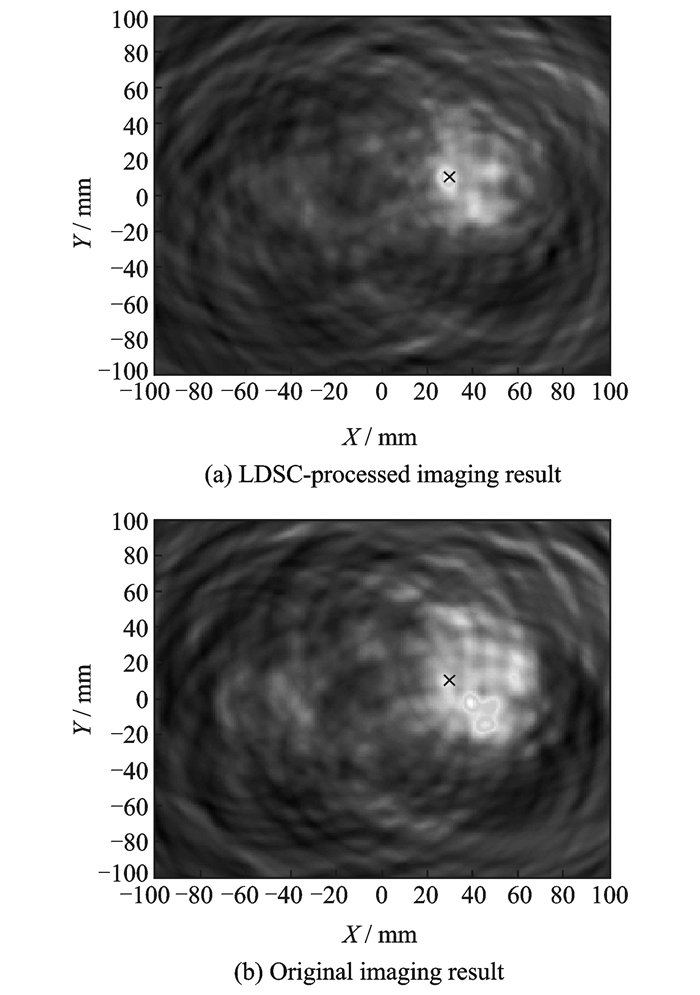
本文分别利用原始和经LDSC处理后的损伤散射信号进行延迟叠加成像,结果如图 6所示,图中“X”表示真实损伤位置。由于频散效应和腹板隔段内边界反射的存在,图 6(b)中的损伤聚集点发生了扩散,并不能显示出真实的损伤位置,而是在损伤的边上产生了伪像。与之形成对比的是,图 6(a)清晰显示出损伤聚焦点,表现出较高的分辨率和信噪比,这是因为LDSC消除了频散效应对成像结果的影响。
|
图 6 损伤成像结果 Figure 6 Damage imaging results |
4 结束语
本文将基于相对测量波数的LDSC频散补偿方法应用于复杂航空结构的损伤成像中,并引入1.5波峰正弦调制的准宽带Lamb波激励波形,从而降低了多反射的复杂航空结构形式对成像结果的影响。理论分析和实验结果表明,利用现场测得的相对波数曲线,LDSC方法能有效地实现复杂航空结构中的Lamb波频散补偿,从而增强Lamb波对复杂航空结构损伤成像的准确度和分辨率。
| [1] |
陶宝祺.
智能材料结构[M]. 北京: 国防工业出版社, 1997.
TAO Baoqi. Smart materials and structures[M]. Beijing: National Defense Industry Press, 1997. |
| [2] |
袁慎芳.
结构健康监控[M]. 北京: 国防工业出版社, 2007.
YUAN Shenfang. Structural health monitoring and damage control[M]. Beijing: National Defense Industry Press, 2007. |
| [3] | YUAN S F, LIANG D K, SHI L H, et al. Recent progress on distributed structural health monitoring research at NUAA[J]. Journal of Intelligent Material Systems and Structures, 2008, 19(3): 373–386. DOI:10.1177/1045389X07087302 |
| [4] | QING X L, BEARD S J, KUMAR A, et al. Advance in the development of built-in diagnostic system for filament wound composite structures[J]. Composites Science and Technology, 2006, 66(11/12): 1694–1702. |
| [5] | QIU L, YUAN S F. On development of a multi-channel PZT array scanning system and its evaluating application on UAV wing box[J]. Sensors and Actuators A: Physical, 2009, 151(2): 220–230. DOI:10.1016/j.sna.2009.02.032 |
| [6] | HUA J, LIN J, ZENG L, et al. Pulse energy evolution for high-resolution Lamb wave inspection[J]. Smart Materials and Structures, 2015, 24(6): 065016. DOI:10.1088/0964-1726/24/6/065016 |
| [7] | LIU L, YUAN F G. A linear mapping technique for dispersion removal of Lamb waves[J]. Structural Health Monitoring, 2010, 9(1): 75–86. DOI:10.1177/1475921709341012 |
| [8] | DE MARCHI L, MARZANI A, CAPORALE S, et al. Ultrasonic guided-waves characterization with warped frequency transforms[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56(10): 2232–2240. DOI:10.1109/TUFFC.2009.1305 |
| [9] | SICARD R, GOYETTE J, ZELLOUF D. A numerical dispersion compensation technique for time re-compression of Lamb wave signals[J]. Ultrasonics, 2002, 40(1-8): 727–732. |
| [10] | WILCOX P D. A rapid signal processing technique to remove the effect of dispersion from guided wave signals[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2003, 50(4): 419–427. DOI:10.1109/TUFFC.2003.1197965 |
| [11] | CAI J, YUAN S F, QING X L, et al. Linearly dispersive signal construction of Lamb waves with measured relative wavenumber curves[J]. Sensors and Actuators A: Physical, 2015, 221: 41–52. DOI:10.1016/j.sna.2014.10.037 |
| [12] |
蔡建, 石立华, 袁慎芳, 等.
一种基于宽带激励的虚拟时间反转方法[J]. 仪器仪表学报, 2011, 32(1): 218–224.
CAI Jian, SHI Lihua, YUAN Shenfang, et al. Virtual time reversal method based on broadband excitation[J]. Chinese Journal of Scientific Instrument, 2011, 32(1): 218–224. |
| [13] | MICHAELS J E. Detection, location and characterization of damage in plates with an in situ array of spatially distributed ultrasonic sensors[J]. Smart Materials and Structures, 2008, 17(3): 1–15. |
| [14] |
蔡建, 石立华, 袁慎芳.
一种改进的近邻多损伤"移相叠加"成像方法[J]. 振动与冲击, 2011, 30(8): 67–71.
CAI Jian, SHI Lihua, YUAN Shenfang. Improved ″delay-and-sum″ imaging method for adjacent multi-damages[J]. Journal of Vibration and Shock, 2011, 30(8): 67–71. |
 2017, Vol. 49
2017, Vol. 49


