2. 沈阳航空航天大学电子信息工程学院,沈阳,110136;
3. 航空工业上海航空测控技术研究所故障诊断与健康管理技术航空科技重点实验室,上海,201601
2. School of Electronic and Information Engineering, Shenyang Aerospace University, Shenyang, 110136, China;
3. Aviation Key Laboratory of Science and Technology on Fault Diagnosis and Health Management, Shanghai Aero Measurement & Control Technology Research Institute, Shanghai, 201601, China
为提高飞机的结构性能、减轻结构重量,性能优越的复合材料在现代飞机上得到广泛应用。但由于飞机在服役过程中其结构会出现各种损伤,致使飞机结构承载能力骤降,从而影响飞机的飞行安全。因此,及时有效地识别出飞机复合材料结构损伤已成为目前亟待解决的影响飞机飞行安全的重要问题之一。
为了实现飞机复合材料结构损伤识别,许多学者对此开展了广泛研究。华生明采用小波分析和BP神经网络对复合材料的损伤进行检测[1],但由于BP神经网络算法本身的结构问题,训练网络容易陷入局部极值,导致网络训练失败,不利于复合材料的损伤检测。王峰林等人采用RBF神经网络对复合材料脱粘缺陷进行识别[2],但在训练样本过少时,RBF神经网络的泛化能力弱,对实际应用带来不便。王明用经验模态分解和BP神经网络,较好地实现了对复合材料板的损伤识别和定位[3]。但由于经验模态分解的模态混叠现象,改变了本征模函数的物理意义,对损伤的识别准确率有较大影响。为较好地解决飞机复合材料结构损伤识别问题,本文提出采用先进的变分模态分解(Variational mode decomposition,VMD)和核独立主元分析(Kernel independent component analysis, KICA)方法进行特征提取,避免了经验模态分解固有的模态混叠现象,并结合广义回归神经网络(General regression neural network,GRNN)和极限学习机(Extreme learning machine,ELM)组合的神经网络泛化能力强、网络训练可靠等特点,对飞机复合材料结构损伤识别方法展开了研究。
1 特征提取理论 1.1 变分模态分解VMD是一种自适应和准正交的分解方法[4],通过搜寻约束变分模型的最优解以实现信号的自适应分解,可有效克服经验模态分解算法分解过程中的模态混叠,具有更强的噪声鲁棒性及较小的端点效应[5],基本理论如下[6]。
首先将每个模态重新定义为调频调幅uk(t)信号,表达式为
| $ {u_k}\left( t \right) = {A_k}\left( t \right)\cos\left( {{\varphi _k}\left( t \right)} \right)\;\;k = 1, \ldots ,K $ | (1) |
| $ {\omega _k}\left( t \right){\rm{ }} = {\rm{d}}{\varphi _{k}}\left( t \right)/{\rm{d}}t $ | (2) |
式中:φk(t)为时间t的相位函数;Ak(t)为uk(t)的瞬时幅值;k为分解的模态数量;ωk(t)为uk(t)的瞬时频率。假设每个模态uk(t)具有中心频率和有限带宽,约束条件为各模态之和等于输入信号f,且每个模态的估计带宽之和为最小,其受约束的变分模型为
| $ \begin{array}{l} \mathop {\min}\limits_{\{ {u_k}\} \{ {w_k}\} } \left\{ {\sum\limits_k {{{\left\| {{\partial _t}\left[ {\left( {\delta \left( t \right) + \frac{{\rm j}}{{\pi t}}} \right)*{u_k}\left( t \right)} \right]{{\rm e}^{ - {\rm j}{w_k}t}}} \right\|}^2}} } \right\}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{s}}{\rm{.t}}.\sum\limits_k {{u_k}} = f \end{array} $ | (3) |
式中:{uk}为分解得到的K个有限带宽基本模式分量(Intrinsic mode function, IMF){u1, …, uk};{wk}为各分量的频率中心{w1, …, wk};
引入扩展的Lagrange将约束性变分问题变为非约束性变分问题,求取式(3) 的最优解为
| $ \begin{array}{l} L\left( {\left\{ {{u_k}} \right\},\left\{ {{w_k}} \right\},\lambda } \right) = \\ \alpha \sum\limits_k {{{\left\| {{\partial _t}\left[ {\left( {\delta \left( t \right) + \frac{{\rm j}}{{\pi t}}} \right)*{u_k}\left( t \right)} \right]{{\rm e}^{ - {\rm j}{w_k}t}}} \right\|}^2}} +\\ \left\| {f\left( t \right) - \sum\limits_k {{u_k}\left( t \right)} } \right\|_2^2 + \left\langle {\lambda \left( t \right),f\left( t \right) - \sum\limits_k {{u_k}\left( t \right)} } \right\rangle \end{array} $ | (4) |
式中:α为惩罚参数;λ为Lagrange乘子。
然后采用乘法算子交替法求取式(4) 的变分约束模型,得到最优解,从而将信号分解成为K个窄带IMF分量。
1.2 奇异熵特征提取由于在不同损伤下,VMD分解得到的各阶IMF分量有所差异,计算得到的奇异值有显著不同,为了有效地提取结构损伤信息,故以VMD分解的IMF分量为基础,将奇异熵引入到复合材料结构损伤特征提取中。奇异熵可以在整体上定量衡量原始振动信号的复杂性或不确定性程度,以表征复合材料结构的不同损伤。奇异熵计算步骤[7]如下:
(1) 构建特征向量矩阵
采用VMD算法对原始信号进行自适应分解,得到m个IMF分量。提取各阶IMF分量作为初始特征向量矩阵D=[imf1, imf2, …, imfm]。
(2) 奇异值分解
由矩阵分析理论知,必然存在矩阵U,矩阵V和矩阵Λ,初始特征向量矩阵表示为
| $ \boldsymbol{D} = \boldsymbol{U} \cdot \boldsymbol{\mathit \Lambda} \cdot{\boldsymbol{V}^{\rm{T}}} $ | (5) |
对角线矩阵Λ的主对角线λj(j=1, 2, …, m)为初始特征向量矩阵的奇异值。
(3) 奇异值归一化处理
忽略残余分量,对初始特征矩阵的奇异值λj(j=1, 2, …, m)进行归一化处理,则第j个奇异值归一化的计算公式为
| $ {\sigma _j} = \lambda _j^2/\sigma $ | (6) |
式中σ为奇异值的总和,
(4) 计算奇异熵
VMD的奇异熵定义为
| $ {H_q}\left( i \right) = - \sum\limits_{i = 1}^m {{p_i}} \log({p_i}) $ | (7) |
式中:pi=σi/σ, (i=1, 2, …,m)表示第i个IMF分量的奇异值在奇异值和σ中的比重;奇异值和为
分散的单个传感器获取的特征信息难以准确表征整个复合材料结构件损伤状态,鉴于KICA方法具有能较完整保留原始数据特征信息的优点,采用KICA方法对4个光纤光栅传感器获取的特征信息进行融合,并将融合后的特征信息作为表征复合材料结构状态的特征量。
KICA的基本思想是将原始输入数据经核函数φ(·)映射到高维特征空间F中进行ICA分析,从而获取非线性独立元。具体实现过程如下[8]:
(1) 原始输入数据x1, x2, …, xn在F空间中的映射为φ(x1), φ(x2), …, φ(xn),得到核矩阵K,可表示为
| $ {K_{ij}} = \left\langle {\varphi ({x_i}),\varphi ({x_j})} \right\rangle = K({x_i},{x_j}) $ | (8) |
(2) 按式(9) 中心化, 即
| $ \tilde {\boldsymbol{K}} = \boldsymbol{K} - {\boldsymbol{E}_n} \cdot \boldsymbol{K} - \boldsymbol{K} \cdot {\boldsymbol{E}_n} + {\boldsymbol{E}_n} \cdot \boldsymbol{K}\cdot{\boldsymbol{E}_n} $ | (9) |
式中En为元素全为
(3) 按式(10) 归一化,即
| $ \tilde {\boldsymbol{K}} = \tilde {\boldsymbol{K}}/({f_{{\rm{tr}}}}(\tilde {\boldsymbol{K}})/n) $ | (10) |
式中ftr(·)为求迹运算。
(4) 求解λv=Kv的特征值问题后,得到前h个特征值λ1, λ2, …, λh和对应的特征向量[v1, v2, …, vh]。数据映射到高维特征空间,得
| $ \boldsymbol{z} = \sqrt n {\boldsymbol{\mathit \Lambda} ^{ - 1}}{\boldsymbol{v}^{\rm{T}}}\tilde {\boldsymbol{K}} $ | (11) |
式中:v=[v1, v2, …, vh];Λ=diag(λ1, λ2, …, λh)。
(5) 采用FastICA算法[9]得到分离矩阵W和特征空间中的独立主元s,建立以下关系
| $ \boldsymbol{s} = \boldsymbol{W}\cdot\boldsymbol{z} $ | (12) |
至此,通过KICA方法可以将4个光纤光栅传感器获取的4维特征信息融合为1维特征信息,实现了特征数据的降维,完成了特征向量的构建。
2 GRNN-ELM损伤识别模型GRNN网络是一种基于非线性回归理论的神经网络模型,它建立在数理统计的基础之上,具有学习速度快、网络模型稳定的特点[10]。而ELM学习机是由单隐藏层反馈神经网络发展而来,该网络可以随机初始化输入权重和偏置并得到相应的隐含层节点输出,具有训练速度快、泛化能力强、模型简单等特点[11]。本文将GRNN和ELM有效地结合,建立GRNN-ELM组合损伤识别模型。
GRNN-ELM组合神经网络可看成是由1个输入层、4个隐含层和1个输出层组成的前馈性神经网络,其网络结构如图 1所示。
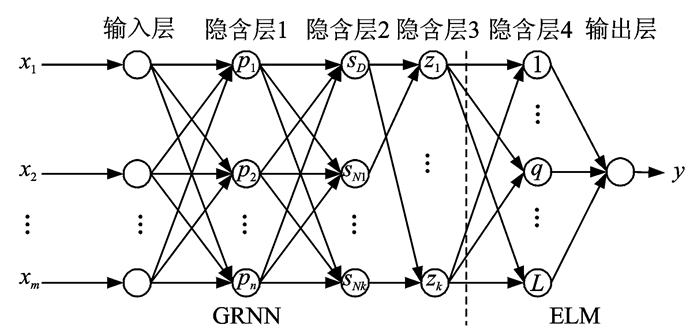
|
图 1 GRNN-ELM组合神经网络结构 Figure 1 Structure of GRNN-ELM neural networks |
GRNN子网模型构建方法如下[12]:如图 1所示,Xn×m=[x1, x2, …, xm]T为组合神经网络的输入,GRNN子网输出为Z=[z1, …, zk]T。GRNN子网的输入节点个数为m;GRNN子网的输出节点个数为k。
输入层的神经元数目等于输入样本的维数m。隐含层1的神经元数目等于输入样本的数目n,隐含层1的第i个神经元的传递函数为
| $ \begin{array}{l} {P_i} = \exp {\left[ -{\frac{{ {{\left( {\boldsymbol{X} - {\boldsymbol{X}_i}} \right)}^{\rm{T}}}\left( {\boldsymbol{X} - {\boldsymbol{X}_i}} \right)}}{{{2^{{{\rm{e}}^2}}}}}} \right]^{\rm{T}}}\\ \;\;\;\;\;\;\;\;\;\;\;i = 1,2, \ldots ,n \end{array} $ | (13) |
隐含层2包含两类神经元,传递函数分别为
| $ S_D = \sum\limits_{i = 1}^n {{P_i}} $ | (14) |
| $ {S_{{N_j}}} = \sum\limits_{i = 1}^n {{y_{ij}}{P_i}} \;\;\;\;j = 1,2, \cdots ,k $ | (15) |
式中:Pi为隐含层2第i个神经元的输入;j为GRNN子网第j个输出节点。
隐含层3中的神经元数目等于GRNN子网输出节点的个数k,隐含层3的第j个神经元输出为
| $ {z_j} = {S_{{N_j}}}/{S_D} $ | (16) |
ELM子网模型构建方法如下[13]:如图 1所示,ELM子网模型输出层的输出形式为
| $ {y_t} = \sum\limits_{q = 1}^L {{\beta _q}g({w_q} \cdot {z_t} + {b_q}){\rm{ }}} \;\;\;\;t = 1,2, \ldots ,n $ | (17) |
式中:zt为隐含层3的神经元输出,同时也是ELM子网的输入;t为隐含层3的神经元个数;g(·)为激活函数;wq为隐含层4中第q个神经元的输入权重;bq为隐含层4中第q个神经元的输出权重。
将GRNN与ELM按图 1形式进行组合,从而可完成基于GRNN-ELM飞机复合材料结构损伤识别模型的构建。
3 试验数据获取与特征提取试验件采用BA9912-G0827型号复合材料层合板,尺寸为100 mm×150 mm,多层对称层合板的一半铺层形式为[45/-45/0/-45/0/45/0/90/0/45/-45/0]s,单层铺层厚度为0.18 mm,整个层合板共24层。将4个光纤光栅传感器均布在板的表面。传感器布置见图 2,圆圈处为放置传感器的位置。
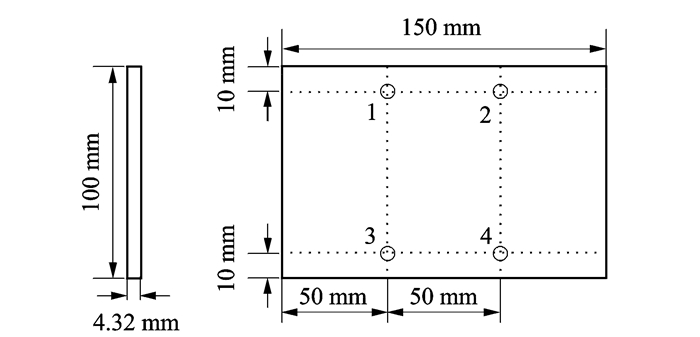
|
图 2 传感器布置示意图 Figure 2 Sensor layout diagram |
首先对试验件进行冲击,而后采用疲劳拉伸机对其进行疲劳拉伸试验直至试件损坏,如图 3所示。复合材料疲劳损伤形式有多种[14]。当试验件承受到较小的负载能量时,其损伤主要表现为分层[15]。重锤冲击后试验件出现直径为5 mm、深度为3层的圆坑,试验件处于初始损伤阶段;随着疲劳加载次数的增加,试验件上不断出现新的损伤。试验件的11~13层出现宽度2 mm、长度为6 mm的条状分层损伤时,试验件处于损伤扩展阶段;试验件的6~8层处出现直径为6.5 mm的圆形分层损伤时,试验件处于损伤失效阶段。本文将对完好、初始损伤、损伤扩展和损伤失效4种分层损伤进行研究。

|
图 3 损坏的试验件 Figure 3 Damaged test piece |
首先,对传感器网络募集到的分层损伤数据进行预处理,剔除明显干扰波动数据后,按照1.1节进行VMD分解,得到各阶IMF分量,按照1.2节特征提取步骤提取奇异熵特征,最后按照1.3节对多个传感器的奇异熵特征进行融合。具体如下:将传感器网络募集的9 000个应变值,以每10个应变值进行1次VMD分解,计算每个传感器的奇异熵后将所有传感器的奇异熵进行融合,最终得到融合后的特征,如表 1所示。
| 表 1 各传感器信息的奇异熵和融合后的特征 Table 1 Singular entropy of each sensor and fusion feature |
表 1中1~225组、226~450组、451~675组和676~900组数据分别对应完好、初始损伤、损伤扩展和损伤失效下得到的奇异熵和融合后的特征。1~200组、226~425组、451~650组和676~875组融合后的特征作为识别模型的训练数据。200~225组、426~450组、651~675组和876~900组融合后的特征作为识别模型的测试数据。
4 损伤识别模型及试验验证 4.1 损伤识别模型及模型的构建根据第2节理论,用第3节中的训练数据构建损伤识别模型。该损伤识别模型的输入层为1个节点,输出层为1个节点。结构损伤模式与对应的输出形式见表 2。
| 表 2 结构损伤模式与对应的输出形式 Table 2 Structure damage model and output form |
4.2 损伤识别试验验证
为验证所构建的GRNN-ELM损伤识别模型的准确性,本文分别设计了GRNN损伤识别模型和ELM损伤识别模型作为对比。并用第3节中未参与建模的测试数据分别对以上3个损伤识别模型的有效性进行验证,结果见表 3和图 4。
| 表 3 3种损伤识别模型验证结果 Table 3 Verification results of three models |
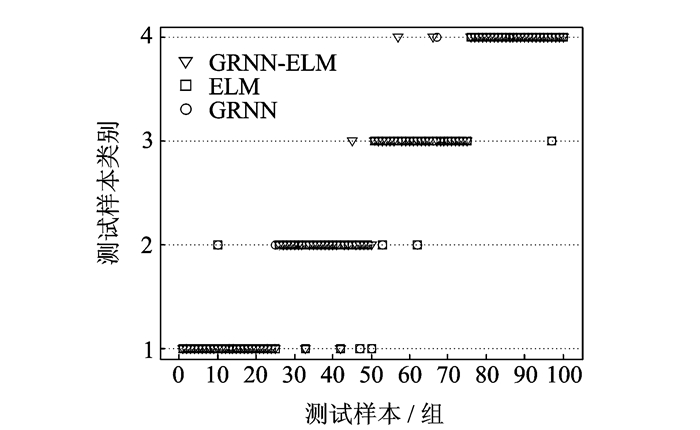
|
图 4 3种损伤识别模型验证结果 Figure 4 Verification results of three models |
由试验结果可知,飞机复合材料分层结构损伤信息经过VMD-KICA方法特征提取后,采用GRNN-ELM方法进行损伤识别,损伤识别准确率达到95%,与ELM和GRNN单一损伤识别模型相比,准确率更高,同时验证了GRNN-ELM损伤识别模型的有效性。
5 结束语本文提出了一种基于变分模式分解和GRNN-ELM组合神经网络的飞机复合材料结构损伤识别方法。以飞机复合材料层合板为具体研究对象,将光纤传感器网络募集到的应变信息通过VMD分解,得到IMF分量,提取其奇异熵特征并采用KICA方法对奇异熵特征进行融合,构建融合特征向量,分别建立基于GRNN-ELM、ELM和GRNN的飞机复合材料结构损伤识别模型,并对飞机复合材料结构损伤进行识别。试验结果表明,所提出的基于GRNN-ELM的复合材料结构损伤识别方法明显优于其他两种损伤识别方法,验证了GRNN-ELM损伤识别模型的有效性,有很好的应用前景。
| [1] |
华生明. 结合小波分析和BP神经网络的复合材料损伤检测技术研究[D]. 南京: 南京航空航天大学, 2015.
HUA Shengming. Composite material damage detection research combining wavelet analysis and BP neural network [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015.http: //d. g. wanfangdata. com. cn/Thesis_D672950. aspx |
| [2] |
王峰林, 王长龙, 胡永江.
基于改进LMS算法的复合材料超声检测缺陷识别[J]. 军械工程学院学报, 2013, 119(5): 66–69.
WANG Fenglin, WANG Changlong, HU Yongjiang. Recognition of composite materials flaws within ultrasonic testing based on improved LMS algorithm[J]. Journal of Ordnance Engineering College, 2013, 119(5): 66–69. |
| [3] |
王明. 基于光纤传感和EMD分解的复合材料损伤监测研究[D]. 武汉: 武汉理工大学, 2012.
WANG Ming. Study on damage monitoring of composite materials based on fiber optic sensor and EMD[D].Wuhan: Wuhan University of Technology, 2012.http: //cdmd. cnki. com. cn/Article/CDMD-10497-1012405661. htm |
| [4] |
岳应娟, 孙钢, 蔡艳平, 等.
变分模态分解在轴承故障诊断中的应用[J]. 轴承, 2016, 441(8): 50–54, 65.
YUE Yingjuan, SUN Gang, CAI Yanping, et al. Application of variational mode decomposition in fault diagnosis for bearings[J]. Bearing, 2016, 441(8): 50–54, 65. |
| [5] | JIANG Wanlu, WANG Zhenwei, ZHU Yong, et al. Fault recognition method for rolling bearing integrating VMD denoising and FCM clustering[J]. Journal of Information and Computational Science, 2015, 12(16): 5967–5975. DOI:10.12733/issn.1548-7741 |
| [6] |
谢平, 杨芳梅, 李欣欣, 等.
基于变分模态分解-传递熵的脑肌电信号耦合分析[J]. 物理学报, 2016, 65(11): 285–293.
XIE Ping, YANG Fangmei, LI Xinxin, et al. Functional coupling analyses of electroencephalogram and electromyogram based on variational mode decomposition-transfer entropy[J]. Acta Physica Sinica, 2016, 65(11): 285–293. |
| [7] |
王玉静, 宋立新, 康守强.
基于EMD和奇异值分解的心律失常分类方法[J]. 信号处理, 2010, 26(9): 1423–1427.
WANG Yujing, SONG Lixin, KANG Shouqiang. Arrhythmia classification based on empirical mode decomposition and singular value decomposition[J]. Signal Processing, 2010, 26(9): 1423–1427. |
| [8] |
唐勇波, 桂卫华, 彭涛, 等.
PCA和KICA特征提取的变压器故障诊断模型[J]. 高电压技术, 2014, 255(2): 557–563.
TANG Yongbo, GUI Weihua, PENG Tao, et al. Transformer fault diagnosis model based on PCA and KICA feature extraction[J]. High Voltage Engineering, 2014, 255(2): 557–563. |
| [9] |
张宵, 马洁.
数据驱动PCA、ICA和KICA故障检测仿真比较[J]. 北京信息科技大学学报, 2014, 101(5): 56–61, 66.
ZHANG Xiao, MA Jie. Simulation comparisons among PCA, ICA and KICA fault detection based on data-driven[J]. Journal of Beijing Information Science and Technology University, 2014, 101(5): 56–61, 66. |
| [10] | ZHANG J, TAN Z, LI C, et al. A novel hybrid forecasting method using GRNN combined with wavelet transform and a GARCH model[J]. Energy Sources, Part B: Economics, Planning, and Policy, 2015, 10(1/2/3/4): 418–426. |
| [11] |
甘露. 极限学习机的研究与应用[D]. 西安: 西安电子科技大学, 2014.
GAN Lu. Research and application of extreme learning machine[D]. Xi′an: Xidian University, 2014.http: //cdmd. cnki. com. cn/Article/CDMD-10701-1014330797. htm |
| [12] |
李聪. 基于GRNN网络的短期与超短期负荷预测[D]. 吉林: 东北电力大学, 2010.
LI Cong. Short-term and ultra-short-term load forecasting based on GRNN network[D]. Jilin: Northeast Electric Power University, 2010.http: //cdmd. cnki. com. cn/Article/CDMD-10188-2010156882. htm |
| [13] |
刘静雅. 基于极限学习机的航空发动机传感器故障诊断研究[D]. 天津: 中国民航大学, 2015.
LIU Jingya. Research of aero-engine sensor fault diagnosis based on extreme learning machine[D]. Tianjin: Civil Aviation University of China, 2015.http: //cdmd. cnki. com. cn/Article/CDMD-10059-1015659982. htm |
| [14] | FRUEHMANN R K, DULIEU-BARTON J M, QUINN S. Assessment of fatigue damage evolution in woven composite materials using infra-red techniques[J]. Composites Science and Technology, 2010, 70(6): 937. DOI:10.1016/j.compscitech.2010.02.009 |
| [15] |
罗武. 基于神经网络的复合材料结构的损伤监测[D]. 西安: 西北工业大学, 2004.
LUO Wu. The method based on neural network of composite structure damage monitoring[D]. Xi′an: Northwestern Polytechnical University, 2004.http: //cdmd. cnki. com. cn/Article/CDMD-10699-2004063387. htm |
 2017, Vol. 49
2017, Vol. 49


