相控阵超声检测技术是一种基于阵列换能器的多通道检测法,可通过相位控制的手段使声波在试件内部的指定区域进行偏转聚焦。与常规单通道的超声检测技术相比,相控阵超声检测技术具有更灵活的声束控制能力,以及更高的检测灵敏度、分辨率以及覆盖率,在不移动换能器的前提下便可实现被测对象内部区域的二维(采用线阵换能器)/三维(采用矩阵换能器)成像[1],是解决航空航天等领域中复杂结构检测检测问题的有效手段。上述被测对象往往具有复杂的型面轮廓或者狭小的探测空间,采用常规单探头超声难以满足检测需求[2-4]。
与此同时,相控阵超声过度灵活的声束控制能力也导致技术本身的复杂度远超常规超声,特别是检测方案的设计。在换能器方面,常规超声可采用的探头有聚焦探头和平探头,只需考虑焦距、中心频率等参数;而相控阵超声可采用的探头种类繁多,包括一维线阵、一维弧阵、二维矩阵、环阵、柔性阵列等,每种探头都有超过3个以上的参数指标,参数的数量与换能器维度呈正相关,不同参数之间还相互制约,需要结合一定的声学理论进行权衡[5-7]。在检测声束发射接收策略方面,由于常规超声换能器的焦距固定并且检测声束通道数仅为1,需要考虑的主要是换能器空间姿态、水距等因素;而在相控阵超声检测中,超声波声束的数量往往远大于1,对于每一个检测通道的声束,都需要结合被测试件的结构材料特点对激发和接收的阵列孔径、声束的偏转角度、聚焦深度(以上参数发射和接收可以不同)、阵列孔径中各阵元的延迟时间以及增益配比等参数进行考虑[8]。
在进行复杂结构试件的检测方案设计时,错误的检测参数选择将可能导致缺陷漏检、误检等问题的产生。图 1给出了一个采用一维线性阵列换能器检测铝金属结构90°圆弧区域的应用案例,由于结构的特殊性常规的相控阵超声检测方法(例如电子线性扫描或者扇形扫描)无法适用,需结合圆弧型面的几何特点对每个通道的合成声束进行定制设计,如图 2中所示。采用错误的阵列孔径和接收激发激励延时将导致声束能量无法对试件内部的指定区域进行偏转聚焦,导致严重的缺陷误检和漏检问题。

|
图 1 铝金属结构90°圆弧区域检测示意 Figure 1 Test on aluminum 90°curved structure |
|
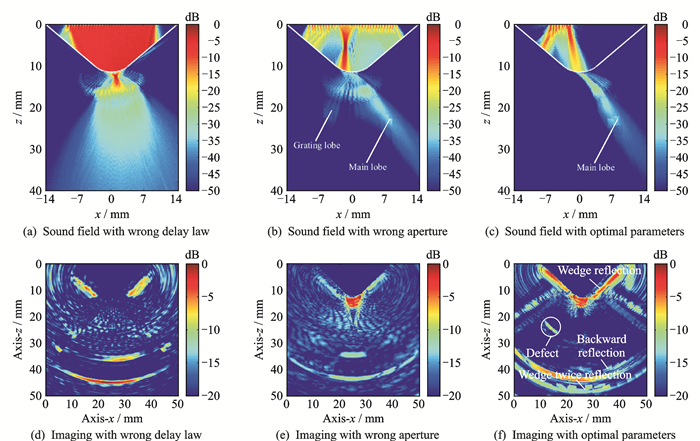
图 2 不同检测参数下的声场能量分布和检测结果图像对比 Figure 2 Acoustic field and testing results with different parameters |
产生上述误检和漏检的主要原因是,在设计相控阵超声检测方案时无法对声波的声场能量分布、是否能够与缺陷发生作用及声束能量是否能将被检测区域完全覆盖等因素进行理论量化预测分析和可视化的观测。同时检测方案的设计过程存在过多重复性的手工化操作,同样以铝金属结构90°角区域检测为例,为了保证正确的声束激发接收,可能需要对90个角度的声束发射接收策略进行逐一设计尝试,如果被测对象具有更加复杂的变曲率外形(例如航空发动机叶片),那么检测方案的设计将更加复杂。
为此,本文提出一套适用于复杂性面结构的相控阵超声检测方案设计流程,并给出5种能够有效提高检测方案设计成功率和效率的关键技术,针对某航空发动机叶片线性摩擦焊区域进行检测应用,对检测结果进行分析和讨论。
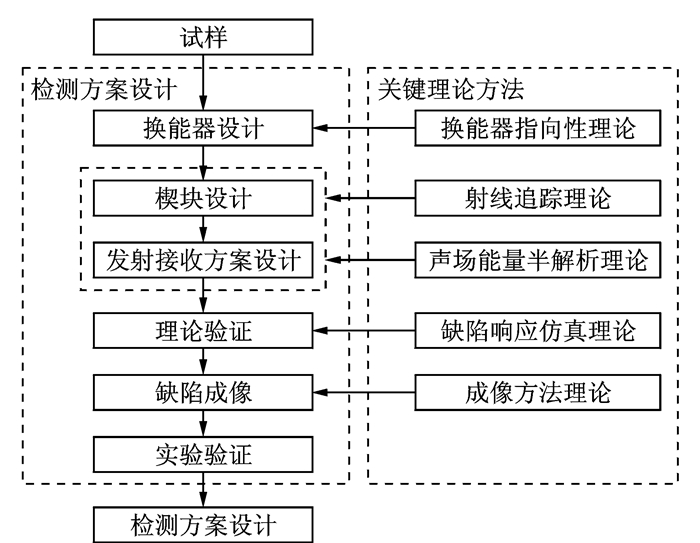
1 检测方案设计流程针对复杂型面结构的相控阵超声检测方案设计流程如图 3所示,主要包括换能器设计、楔块设计、发射接收方案设计、方案理论验证、成像算法设计以及检测实验验证6大部分。在设计的过程中,分别运用换能器指向性、射线追踪、声束能量半解析、缺陷响应仿真以及成像5大关键技术对检测方案的关键环节进行辅助支持。首先,根据缺陷的检测尺寸、被测试样的材料特性采用换能器指向性理论对阵列探头进行设计;其次,根据被测对象的几何信息采用射线追踪算法对检测所采用的楔块和每个通道的声束发射接收方案进行设计,设计时要求检测声波能将待检测区域完全覆盖;接着,基于缺陷响应仿真算法对声束发射接收全覆盖检测方案进行理论仿真,验证特定位置的缺陷能否采用特定通道的合成声束进行检测;然后,结合相控阵超声成像算法对构件的缺陷成像方法进行设计;最后,基于检测软硬件系统对预埋缺陷的试样展开检测实验,验证检测方案的正确性,如果检测结果满足预期要求,则检测方案设计完成。上述检测理论方法是能否高效、正确制定相控阵超声检测方案的关键。
|
图 3 相控阵超声检测方案设计流程 Figure 3 Design process of PAUT solution |
2 检测方案设计关键技术 2.1 换能器指向性理论
换能器指向性理论主要由Shi Chang Wooth等人[9]建立,主要应用于对阵列换能器的声场特性进行初步定量分析,为换能器参数的优化设计提供理论依据。指向性是一个以角度为自变量的函数,对于阵列换能器上的单一阵元,其指向性满足
| $ D\left( \theta \right) = \frac{{\sin\left( {\pi a\sin \left( \theta \right)/\lambda } \right)}}{{\pi a\sin \left( \theta \right)/\lambda }} $ | (1) |
式中:a为换能器阵元尺寸;λ为声波在材料内部传播时的波长;对于具有N个阵元晶片,阵元间距为d的一维线阵换能器,基于流体介质的假设,当声束偏转角度为θ0时,其指向性满足
| $ D\left( \theta \right) = \left| {\frac{{\sin\left( {\left( {\pi a\sin \theta } \right)/\lambda } \right)}}{{\pi a\sin \theta /\lambda }} \cdot \frac{{\sin \left[ {\left( {\left( {\pi d\left( {\sin {\theta _0} - \sin\theta } \right)} \right)/\lambda } \right)N} \right]}}{{N\sin \left[ {\left( {\pi d\left( {\sin {\theta _0} - \sin \theta } \right)} \right)/\lambda } \right]}}} \right| $ | (2) |
相关研究结果显示,当换能器参数不合理时,合成声束在很小的偏转角度下便可能产生极大的栅瓣能量,导致检测结果存在伪像。为了最大化声束主瓣、抑制旁瓣并消除栅瓣,在设计换能器时阵元个数应大于16个,同时要综合考虑偏转方向上的声压能量和近场长度的要求;阵元间距应大于0.5倍、小于1倍波长;阵元宽度应在小于阵元间距的情况下取尽可能大的值,声束波长应小于被检测缺陷尺寸。
2.2 射线追踪算法射线追踪算法基于高频假设,将超声波声束近似成几何声线,对声束在多层介质中的传播路径进行正反演算,是声束发射接收全覆盖方案设计的理论依据。其正演算部分,基于斯涅耳定律对由特定发射方向的声线在被测试件反射、折射路径进行自动推导,通过一定的图形绘制接口函数在屏幕上可视化显示,辅助检测工艺人员对声束角度、反射次数、波形模式等参数进行调节;其逆演算部分,基于费马原理对制定的发射和接收点之间的声传播路径以及传播试件进行计算,可用于确定激发特定合成声束时,阵列孔径上各个阵元的发射接收延迟时间。
为了对一般的复杂型面结构快速高效地进行全覆盖设计,利用UG二次开发接口函数对被测试件的CAD模型进行几何信息提取,获得被测对象界面轮廓曲线/曲面的相关信息,以便射线追踪算法进行计算和推导。
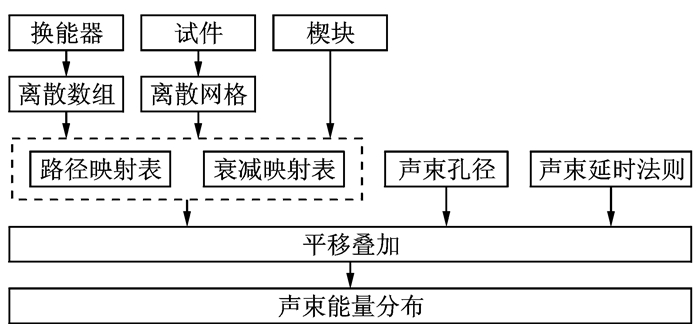
2.3 声束能量半解析算法声束能量半解析算法基于格林函数和渐进积分理论,对特定聚焦法则下的超声波声束能量场随时间的变化规律进行快速求解,是分析各个通道声束在实际检测中的主瓣、栅瓣以及旁瓣性质特点的有效手段。对于特定的换能器、楔块以及试件组合下,声束能量计算的流程如图 4所示。
|
图 4 声束能量半解析计算流程 Figure 4 Semi-analytical beam energy calculation process |
首先,将换能器各个阵元以及被测试样内部区域按一定的间距进行离散,利用费马原理计算各个阵元上的离散点到达试件内部各个离散点的传播声线路径以及传播时间;然后,根据声场的半解析公式,确定各个阵元上的离散点到达试件内部各个离散点的传播声衰减,相关公式为
| $ \left\{ \begin{array}{l} p\left( {x,z,t} \right) = \int {P\left( {x,z,\omega } \right){{\rm{e}}^{ - \omega t}}} \\ P\left( {x,z,\omega } \right) = - \frac{{{\rm j}\omega {\rho _1}}}{\pi }\sqrt {\frac{{{c_1}}}{{{\rm j}\omega }}} {V_n}\left( \omega \right)T\left( \theta \right) \cdot \sqrt {\frac{{2\pi }}{{{\rm j}\mu }}} \exp \left( { - {\rm j}\left( {{k_1}{r_1} + {k_2}{r_2}} \right)} \right)\\ \mu = {r_1} + \frac{{{c_2}{{\cos }^2}{\theta _1}}}{{{c_1}{{\cos }^2}{\theta _2}}}{r_2} - \frac{{{r_1}{r_2}}}{{\rho {{\cos }^2}{\theta _2}}}\left( {\cos {\theta _1}\frac{{{c_2}}}{{{c_1}}} - \cos{\theta _2}} \right) \end{array} \right. $ | (3) |
式中:ρ1为介质1密度;c1为介质1声速;c2为介质2声速;r1为声束在介质1中的传播路径;r2为声束在介质2中的传播路径;k1为介质1的波数;k2为介质2的波数;θ1为声束的入射角;θ2为声束的折射角;ρ为声束在介质交界处入射点的曲率半径;Vn为阵元表面的振动速度频谱;Tn为折射系数。最后,利用式(3) 对各个参与激发的阵元声能量贡献值进行计算和叠加,叠加的时候需要根据各个阵元的延时激励时间对数据进行平移操作,获得声场能量随时间变化的三维数组。通过一定的图形绘制接口函数在屏幕上可视化显示,辅助检测工艺人员对所设计合成声束的实际声场特性进行快速分析。
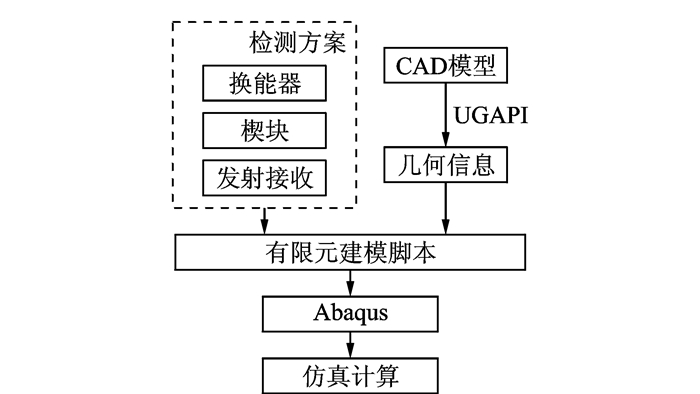
2.4 缺陷响应仿真算法缺陷响应仿真算法基于纯数值方法对声束全覆盖检测方案能否与试件内部缺陷发生作用,并将缺陷反射信号传递回换能器进行理论验证。一般可采用时域有限差分或者有限元进行仿真计算,在本文的检测方案设计之中,选择采用商业软件Abaqus的有限元模块进行仿真计算,由于相控阵超声检测技术参数复杂繁多,且被测试样可能具有不规律的变曲率型面,建立了一套基于CAD模型的缺陷响应有限元仿真半自动建模系统,该系统的工作流程如图 5所示。首先,根据利用UG二次开API提取CAD模型的轮廓信息,并基于NURBS曲线形式进行模型重构;然后,根据几何模型、检测方案的换能器、楔块、声束发射接收参数生成用于建立Abaqus仿真模型的Python格式文件;Abaqus软件导入上述生成的文件,根据文件内部的代码顺序执行模型建立、材料属性设置、力加载设置、网格划分等操作,用户无需进行任何额外的手工重复性操作便可完成仿真验证的工作。
|
图 5 基于CAD模型的有限元半自动建模流程 Figure 5 Semi-automatic finite element modeling process based on CAD model |
2.5 成像算法
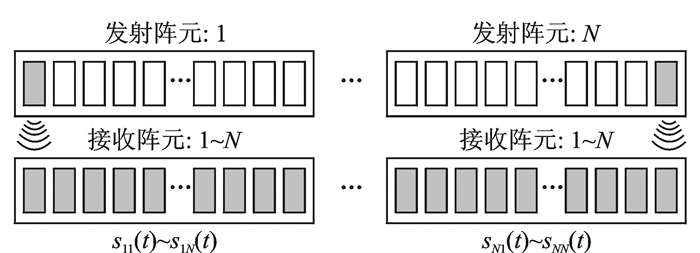
相控阵超声检测成像算法主要包括两类,一类是基于实际偏转聚焦合成声束与缺陷作用后的回波A扫信号进行检测成像,分别包括B型、电子B型、C型、D型及S型显示,若采用矩阵换能器进行体聚焦检测,还能实现实时的三维体数据成像显示;另一类是基于全矩阵数据的检测成像算法,全矩阵(Full matrix)数据是一种存储了全部发射/接收阵元组合A扫信号的特殊结构检测回波数据,如图 6所示。检测成像过程中并不实际发射偏转聚焦声束,而是通过对全矩阵数据施加特定的信号处理算法,回波数据进行虚拟聚焦,从而获得采用常规阵列超声检测方法得到的回波A扫数据,全聚焦成像方法(Total focusing method,TFM)是其中最经典的算法,该算法对被测试样内部的任意一个点都进行虚拟聚焦,利用各个点聚焦后得到的回波幅值进行成像,被誉为阵列超声检测中的“黄金标准”[10-11]。
|
图 6 全矩阵数据的定义 Figure 6 Definition of full matrix data |
3 航空航天应用案例 3.1 被测对象
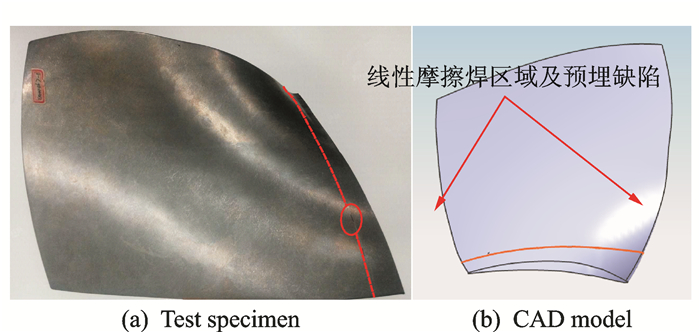
本文应用案例中的被测对象为采用线性摩擦焊工艺制备而成的航空发动机叶片,叶片结构如图 7所示。该结构的焊接区域在服役过程中可能会滋生裂纹,由于涡轮叶片之间空隙区域狭小,采用常规单探头超声检测技术难以有效实现焊接区域的全覆盖检测。为此本文结合相控阵超声检测技术的优势,研究适用于上述结构的相控阵超声现场检测方法。
|
图 7 航空发动机叶片结构 Figure 7 Aero-engine blade |
3.2 检测方案设计及验证
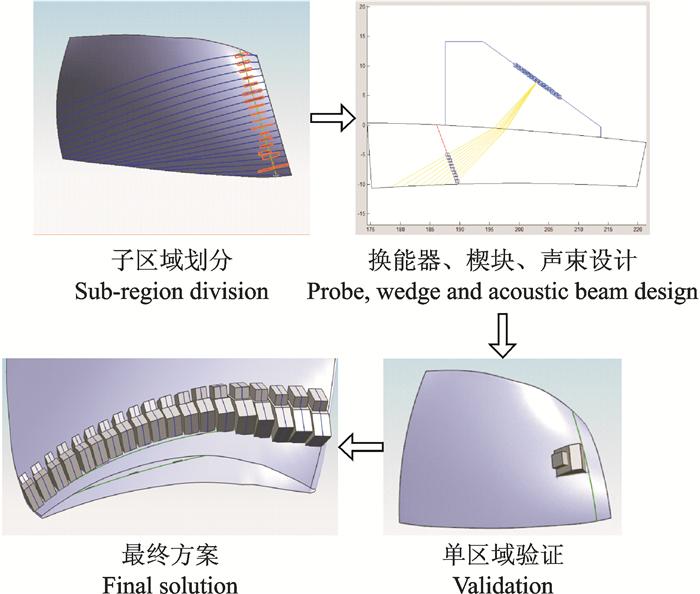
由于可探测空间的限制,在检测过程中换能器难以在叶片表面进行自由移动。为此,本文将叶片按照一定的间距划分为19个独立的子截面,针对每一个子截面按照检测方案进行检测,具体过程如图 8所示。
|
图 8 发动机叶片检测方案设计过程 Figure 8 Design process of aero-engine blade testing solution |
在换能器设计方面,考虑到检测缺陷的最小尺寸为0.8 mm,结合钛合金的材料特性以及换能器指向性理论的半波长阵元间距设计准则,采用中心频率7.5 MHz、阵元间距0.6 mm、阵元数量32的线性阵列换能器进行检测,检测采用横波波形。
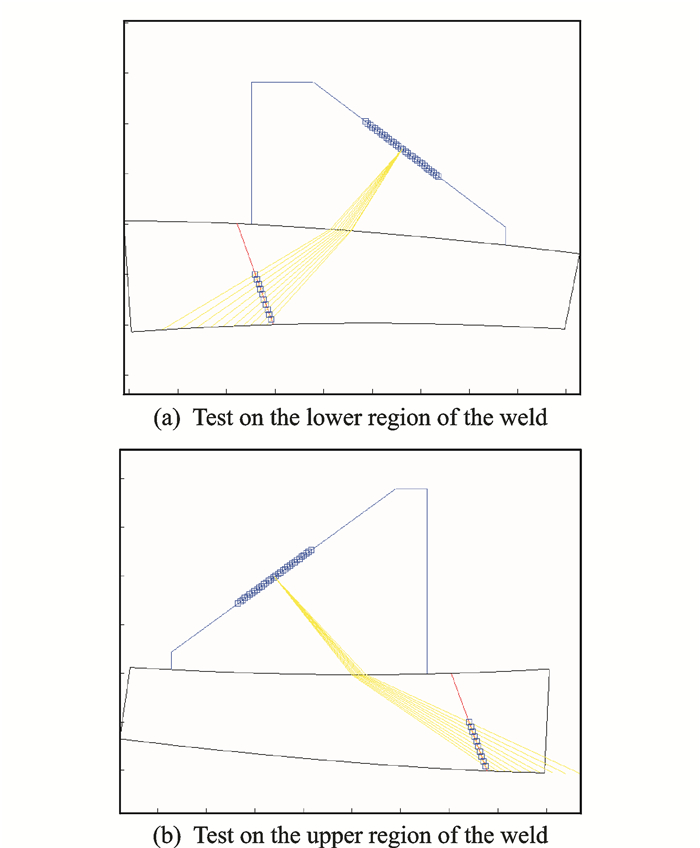
采用UG二次开发接口函数对叶片进行截面划分,并在独立开发的检测方案设计程序中以自由样条曲线形式对各个截面进行重构。考虑到叶片上下表面曲率变化均较为复杂,不适合采用一次底面反射实现检测区域的声束全覆盖,采用如图 9所示的方案,将每一个子截面划分为上下两个区域,上区域表面为凸状、下区域表面为凹状。针对上区域焊缝,设计贴合于下表面(凹面)的曲率楔块,采用直接反射的斜入射横波扇形扫描进行检测;针对下区域焊缝,设计贴合于上表面(凸面)的曲率楔块,采用直接反射的斜入射横波扇形扫描进行检测。
|
图 9 子截面检测楔块、声束发射接收全覆盖方案 Figure 9 Full beam coverage solution and testing wedge solution design of sub-region |
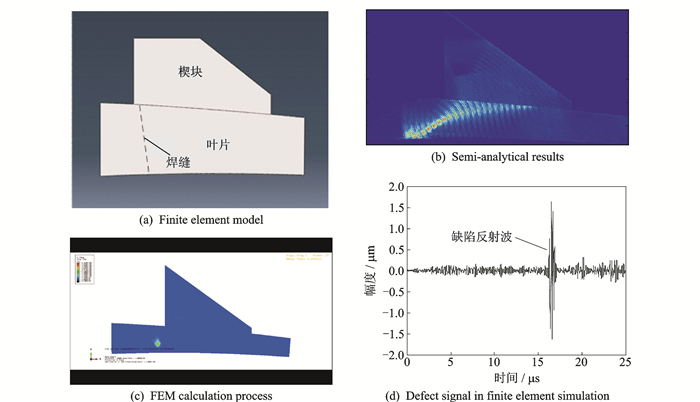
对每个子截面的检测方案分别采用声场能量半解析算法和有限元算法进行仿真验证。基于Abaqus平台,建立检测截面的叶片轮廓和楔块的二维模型。为节省计算时间、提高计算效率,本文只对靠近待检测区域两侧的区域进行计算。有限元模型如图 10(a)所示。模型上半部分为楔块,下半部分是叶片。楔块的材料密度为1 050 kg/m3,弹性模量4.007 7 GPa,泊松比为0.32,叶片的密度4 540 kg/m3,弹性模量为106.4 GPa,泊松比为0.34,裂纹的宽度为0.5 mm,深度为0.5 mm。楔块与叶片表面完全耦合,且楔块的参数是设计的楔块参数,用施加在楔块上间距为0.1 mm,长度为0.3 mm的32个线节点上的压力载荷来模拟线阵换能器的激励信号,载荷方向垂直于楔块表面。激励信号为高斯窗调制的3周期正弦信号,中心频率为5 MHz。超声波的聚焦点在待检测区域,基于延时聚焦法则对每个节点的调制信号进行相位延迟。将有缺陷的模型得到的超声信号与无缺陷模型得到的信号做差,得到缺陷的超声信号,如图 10(d)所示,其中幅度表示节点的X、Y方向的位移沿载荷施加方向的分量,且幅度是由32个节点的X、Y位移经过相位延迟之后合成的。结果表明所设计检测方案能够检测出预埋于仿真模型中的缺陷,检测声束具有较低旁瓣,无栅瓣效应的产生。
|
图 10 检测方案理论仿真结果 Figure 10 Simulation result of testing solution |
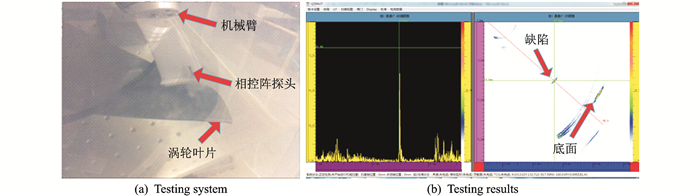
为了方便对检测方案进行实验验证,建立了一套基于六自由度机械臂的相控阵超声检测方案验证平台,如图 11(a)所示,检测时将试样和换能器浸泡于水槽当中,将换能器和试件之间的水介质当成楔块,利用机械臂调整换能器的空间姿态,模拟所设计参数的楔块进行检测。图 11(b)给了检测时的A型及S型显示结果。S型成像是通过以不同的延时聚焦法则激发阵元晶片,使声束按角度进行扫查,得到每条扫描线上的A扫数据,然后以极坐标方式对A扫数据进行重构,得到S型图像。从图中可以看出采用所设计的检测方法能够成功检测出试件内部预埋的人工裂纹缺陷。
|
图 11 检测系统及检测结果 Figure 11 Testing system and testing results |
3.3 结果分析
对每一个子截面的检测方案按照上述方法进行验证,结果表明针对航空发动机叶片线性摩擦焊区域所设计的基于多组阵列换能器的检测方案符合检测需求,根据设计结果对换能器、楔块进行制备,结果如图 12所示,每一个截面的换能器楔块采用一体化的方式进行制造,对于不同截面上的换能器及楔块,采用精心设计的机械夹持机构进行绑定形成阵列,在实际检测时,只需要将上述换能器楔块阵列贴合于叶片表面便可进行检测。

|
图 12 根据检测方案设计的换能器楔块阵列 Figure 12 Designed probe array based on testing solution |
由于采用了基于5大关键技术的检测方案设计方法,上述19个子截面的检测方案设计、理论验证、实验验证工作仅用了不到3个月的时间便得到完成,大大提高了检测方案的设计效率以及检测方案的可行性。
4 结论(1) 针对被测试样的几何结构及材料特性设计适当的检测方案是相控阵超声检测过程中最重要的一个环节,不合适的检测参数将可能导致严重的缺陷漏检和误检。
(2) 建立了一套针对复杂结构的相控阵超声检测方案设计方法,其中涉及5项关键技术,分别为换能器指向性理论、射线追踪算法、声束能量半解析算法、缺陷响应仿真算法以及成像算法。上述关键技术将对检测方案的设计效率以及检测方案的辅助验证优化提供至关重要的作用。
(3) 针对航空发动机涡轮叶片线性摩擦焊区域的检测问题,基于上述检测方案设计方法及关键技术,设计了一套基于19组阵列换能器及楔块的相控阵超声检测方法,并搭建相应软硬件系统展开实验验证,实验结果表明所设计检测方法满足航空发动机涡轮叶片线性摩擦焊区域的检测需求。
| [1] | DRINKWATER B W, WILOX P D. Ultrasonic arrays for non-destructive evaluation: A review[J]. NDT & E International, 2006, 39: 525–541. |
| [2] | LUPIEN V, HASSAN W, DUMAS P. Improved titanium billet inspection sensitivity through optimized phased array design[J]. Review of Progress in QNDE, 2006, 820: 853–860. |
| [3] | GUAN X, ZHANG J, RASSELKORDE E M. Material damage diagnosis and characterization for turbine rotors using three-dimensional adaptive ultrasonic NDE data reconstruction techniques[J]. Ultrasonics, 2014, 54: 516–525. DOI:10.1016/j.ultras.2013.07.019 |
| [4] | PUEL B, LESSELIER D, CHATILLON S. Optimization of ultrasonic arrays design and setting using a differential evolution[J]. NDT & E International, 2011, 44: 797–803. |
| [5] |
万敏, 王海涛, 程继隆, 等.
超声相控阵声束控制特性分析[J]. 无损检测, 2009, 31(11): 859–861.
WAN Min, WAN Haitao, CHENG Jilong, et al. The analysis on the features of the propagating waves control of the ultrasonic phased array[J]. Nondestructive Testing, 2009, 31(11): 859–861. |
| [6] |
白培瑞, 张丽丽, 傅颖霞.
二维超声阵列换能器声束控制技术的仿真研究[J]. 山东科技大学学报(自然科学版), 2009, 28(5): 43–48.
BAI Peirui, ZHANG Lili, FU Yingxia. The simulation study of sound-beam control techniques of two dimensional ultrasonic array transducer[J]. Journal of Shandong University of Science and Technology (Natural Science), 2009, 28(5): 43–48. |
| [7] |
赖溥祥, 张碧星, 汪承灏.
环形相控阵换能器辐射和反射声场[J]. 声学学报, 2007, 32(3): 212–220.
LAI Puxiang, ZHANG Bixing, WANG Chenghao. Radiation and reflection a coustical field of an annular phased array[J]. Acta Acustica, 2007, 32(3): 212–220. |
| [8] | SONG S J, SHIN H J, JANG Y H. Development of an ultrasonic phased array system for nondestructive tests of nuclear power plant components[J]. Nuclear Engineering and Design, 2002, 214(1): 151–161. |
| [9] | AZAR L, SHI Y, WOOH S-C. Beam focusing behavior of linear phased arrays[J]. NDT & E International, 2000, 33(3): 189–198. |
| [10] |
周正干, 彭地, 李洋, 等.
相控阵超声检测技术中的全聚焦成像算法及其校准研究[J]. 机械工程学报, 2015, 51(10): 1–7.
ZHOU Zhenggan, PENG Di, LI Yang, et al. Research on phased array ultrasonic total focusing method and its calibration[J]. Chinese Journal of Mechanical Engineering, 2015, 51(10): 1–7. |
| [11] | FAN C, CALEAP M, PAN M, et al. A comparison between ultrasonic array beamforming and super resolution imaging algorithms for non-destructive evaluation[J]. Ultrasonics, 2014, 54: 1842–1850. DOI:10.1016/j.ultras.2013.12.012 |
 2017, Vol. 49
2017, Vol. 49


