在工程结构设计及风险评估中，需要考虑输入变量的不确定性对输出响应性能不确定性的影响程度。而输出响应性能往往不止一个。传统的单个输出性能下基于方差或矩独立重要性测度可以对每个输出单独进行分析，然而由于输出之间一般具有相关性，这样单独分析每个输出的方法会造成各个指标间不同程度的信息冗余，使得分析结果难以被解释^[1-2]。因此，更好的方法是把多输出看作一个整体来对待。

Campbell等人基于对输出响应量的分解提出了一种简单实用的重要性测度方法^[1]。它通过对输出响应量进行正交分解，提取包含信息最多的几个成分，再单独进行重要性分析。Lamboni等人将其应用于农作物生长模型的分析中，并提出了一套新的综合测度^[3-4]。Gamboa等人基于协方差分解, 提出一种广义的重要性测度^[5]，该测度求解过程相比Campbell所提测度更为高效，但它们本质上是等价的^[2]。这些方法直接把输出(协)方差作为输出不确定性的唯一衡量，相比输出的完整概率分布，损失了很多信息^[6]。因此，更好的重要性测度应该考虑输出的完整概率分布。Cui等人^[7]将Borgonovo^[8]在单输出下的矩独立指标扩展到多输出条件下，定义了基于联合概率密度函数(Probability density function, PDF)的重要性测度。虽然该测度全面考虑了多个输出响应的不确定性以及输出间的相关性，但文献[7]在求解多输出的联合PDF时，采用的是直方图法，计算量大且输出的维数高时很难较准确地求得输出的联合PDF。Li等人^[9]综合前人在单输出条件下基于分布函数(Cumulative distribution function, CDF)的重要性测度方法^[10-12], 通过使用概率积分转化(Probability integral transformation, PIT)方法^[13], 提出了一种基于CDF的多输出重要性测度，该测度以联合CDF的PIT分布作为输出不确定性的度量，同Cui的测度一样包含了输出响应的完整不确定信息及其相关性信息。由于计算时需要在循环内部求解PIT变量的分布函数和条件分布函数，并在全域内进行积分，它的求解过程依旧十分繁琐。本文在文献[9]基础上，结合基于方差的重要性测度方法，提出一种新的多输出重要性测度。该测度同样利用PIT方法，在保留多输出响应不确定性和相关性信息的同时，将多维响应量化为单维。对单维PIT变量使用基于方差的重要性测度分析方法，所得测度同样能够很好地反映出输入变量不确定性对多输出响应不确定性的影响程度，且包含输出之间相关性的信息。由于无需对PIT变量再求分布函数并在全域内积分，而只需求其方差，所提测度求解过程更为简便。文献[14]提出一种基于分数矩的极大熵方法，可以高效估计输出响应的边缘概率密度函数，而联合概率密度函数可以使用文献[15]所提Nataf变换法高效估计，本文将在这两种方法的基础上，改进多输出联合分布函数的解法，提出一种高效求解方法用于计算所提测度。

令X=(X₁, …, X_n)^T表示一组独立输入变量，Y=(Y₁, …, Y_m)^T表示X通过功能函数Y_r=g_r(X₁, …, X_n)(r=1, …, m)获得的输出响应。

令F_Y (Y₁, …, Y_m)表示模型输出响应Y=(Y₁, …, Y_m)^T的联合分布函数，则Y的m维PIT可由式(1) 获得

显然变量U中已经包含了多输出响应的单维信息及多输出之间的相关性信息，且U为单维随机变量，在比较U和X_i固定U|X_i的分布差异时，可以采用U的方差V(U)和U|X_i的方差V(U|X_i)的差异，并采用绝对值的形式以保留在后续求平均差异时X_i的影响。对V(U)和V(U|X_i)的绝对值差异V(U)-V(U|X_i)求平均，可定义式(2) 所示的新指标ξ_i来衡量X_i对多个输出综合统计特征的影响

式中：f_Xi (x_i)为X_i的概率密度函数。ξ_i越大，表示固定X_i对输出响应的联合分布的变异性影响越大，X_i就越重要。特别地，当X_i和输出响应Y独立时，V(U|X_i)=V(U)在X_i的全域内恒成立，ξ_i=0。当Y的不确定性完全来自于X_i时，V(U|X_i)=0在X_i的全域内恒成立，ξ_i=1。

类似地，对任意组合的输入变量(X_i1, …, X_ir)^T(1 < r≤n, i_r∈{1, …, n})，可定义联合重要性测度指标

式中：${{f_{{X_{{i_1}}}, \cdots ,{X_{{i_r}}}}}\left( {{x_{{i_1}}}, \cdots ,{x_{{i_r}}}} \right)}$为${\left( {{X_{{i_1}}}, \cdots ,{X_{{i_r}}}} \right)^{\rm{T}}}$的联合概率密度函数。

求解ξ_i指标首先要计算输出响应的联合分布函数F_Y(Y₁, …, Y_m)以及条件联合分布函数F_Y|Xi(Y₁, …, Y_m)。由于PIT随机变量U是输出响应Y的分布函数U=F_Y(Y₁, …, Y_m)，U的样本u_k(k=1, …, N) (N为样本个数)可以通过对Y求经验分布函数，并由Y的样本y_k={y_k1, …, y_km}(k=1, …, N)来获得

式中：$F_\mathit{\boldsymbol{Y}}^m$为Y的经验分布函数；N为样本点个数；(y_k1, …, y_km)(k=1, …, N)表示第k个随机样本。ξ_i指标具体求解步骤如下：

(1) 先根据输入变量X=(X₁, …, X_n)^T的联合概率密度f_X(x)，产生N个输入变量X的随机样本x_k=(x_k1, …, x_kn)^T (k=1, …, N)，通过代入功能函数Y_r=g_r(X₁, …，X_n)(r=1, …, m)获得N个多输出随机样本y_k=(y_k1, …, y_km)^T；

(2) 通过式(4) 用经验分布函数F_Y^m(y)估计Y的联合分布函数F_Y(y₁, …, y_m)，根据U=F_Y(y₁, …, y_m)获得N个PIT变量U的样本u=(u₁, …, u_N) ^T，然后使用U的样本方差$\hat V\left( U \right)$估计无条件方差V(U)：$\hat V\left( U \right) = \sum\limits_{i = 1}^N {{{\left( {{u_i}-u} \right)}^2}} /N$；其中，$\bar u = \sum\limits_{i = 1}^N {{u_i}} /N$为U的样本均值；

(3) 对第(1) 步中X_i的每个样本x_ki(k=1, …, N; i=1, …, n)，根据条件密度f_X~i|Xi=xki (x_~i)获得N_t个条件样本x_{t, ~i}=(x_{t 1}, …, x_{t, i-1}, x_{t, i+1}, …, x_{t, n})^T (t=1, …, N_t)，代入功能函数获得N_t个多输出条件样本y_t|x_ki(t=1, …, N_t)，由y_t|x_ki (k=1, …, N; t=1, …, N_t)获得经验分布函数F_Y|xki^m(y)，并由u_t|x_ki=F_Y|xki^m(y_t|x_ki)获得X_i=x_ki情况下的N_t个条件样本u|x_ki={u₁|x_ki, …, u_Nt|x_ki}，由此可以获得X_i=x_ki时U|X_i=x_ki的条件样本方差估计$\hat V\left( {U\left| {{X_i} = {x_{ki}}} \right.} \right)$，计算差值${\Delta _{ki}} = \left| {\hat V\left( U \right)-\hat V\left( {U\left| {{X_i} = {x_{ki}}} \right.} \right)} \right|\left( {k = 1, \cdots, N} \right)$；

(4) 经过上述步骤，ξ_i可由$\frac{1}{N}\sum\limits_{k = 1}^N {\frac{{{\Delta _{ki}}}}{{\hat V\left( U \right)}}} $来估计。

2.1节Monte Carlo法简单直观，易于编程实现。可将其收敛解作为精确对照解。然而Monte Carlo法的求解过程需要双层抽样且每一层均需大量样本，内层还要对样本进行排序(求经验分布函数)，因而效率很低。为了提高求解联合分布函数的效率，本节引入一种新的计算方法：首先利用基于分数矩的极大熵法求解出各个输出的边缘概率密度函数，再使用Nataf变换法获得多输出的联合概率密度函数。由联合密度函数积分得到联合分布函数。

多输出响应Y=(Y₁, …, Y_m)^T中单个输出Y_j(j∈{1, …, m})的概率密度函数f_Yj(y_j)的熵表示如下

熵是表示混乱度的一个量，实际中认为熵最大的系统也是最稳定最能被利用的系统，因此要估计f_Yj(y_j)的值时，当某个估计${{\hat f}_{{Y_j}}}\left( {{y_j}} \right)$的熵最大时，它与真实值最接近。

基于极大熵理论，要找到${{\hat f}_{{Y_j}}}\left( {{y_j}} \right)$相当于将求解问题变成了一个优化的过程

式中${M_{{Y_j}}^{{\alpha _k}}}$为输出响应的α_k(k=0, 1, …, s)阶分数矩。文献[15]指出，采用分数矩比采用整数阶矩包含更多的样本信息，因此对输出响应的概率密度函数的拟合也就更准确。

文献[14]通过构造拉格朗日函数，求得f_Yj(y_j)的估计值${{\hat f}_{{Y_j}}}\left( {{y_j}} \right)$如下

式中：λ=[λ₀, λ₁, …, λ_s]^T为拉格朗日乘数；α=[α₁, …, α_s]为分数阶。${\alpha _0} = 0, {\lambda _0} = \ln \left[{\int_Y {\exp \left( {-\sum\limits_{k = 1}^s {{\lambda _k}{y_j}^{{\alpha _k}}} } \right){\rm{d}}{y_j}} } \right]$。具体求解过程见文献[14]，此处不再赘述。

该方法可以高效准确地估计出单个随机输出响应的边缘概率密度函数。本文使用该方法计算多输出响应的边缘概率密度函数，用以求解后面的联合分布函数。

Nataf变换是原始变量空间到标准正态空间的转换过程的一个数学模型^[15]，它根据每个随机变量的边缘概率密度函数、分布函数和随机变量之间的相关系数来求解变量之间的联合密度函数。因此为了求解多输出响应Y=(Y₁, …, Y_m)^T的联合概率密度函数f_Y(y)，须知道单个输出Y_j(j=1, …, m)的概率密度函数f_Yj(y_j)和累积分布函数F_Yj(y_j)，以及多输出响应的相关系数矩阵ρ=[ρ_ij](i, j∈{1, …, m})。Nataf变换过程如下。

使用Liu和der Kiureghian的等概率转换原则^[16]

其中引入标准正态随机向量R=(r₁, …, r_m)^T，式中Φ(·)和Φ^-1(·)分别为标准正态变量的累积分布函数和逆累积分布函数。

根据Nataf变换理论，利用隐函数求导法则，可以推导出随机向量Y的联合概率密度函数为

式中φ(·)为标准正态分布变量的概率密度函数。而

对应于均值为0、方差为1及相关系数矩阵为ρ₀的m维标准正态分布。其中det(ρ₀)表示ρ₀的行列式的值。假设多输出响应Y的相关系数矩阵ρ的各个分量为ρ_ij，则标准正态随机向量R的相关系数矩阵ρ₀的各阶分量ρ_0ij可通过式(11) 求解

式中：f_YiYj(y_i, y_j)为Y_i和Y_j的联合概率密度函数；$F_{{Y_i}}^{-1}\left( \cdot \right)、F_{{Y_j}}^{-1}\left( \cdot \right)$分别为Y_i和Y_j的逆累积分布函数。

求解上述非线性方程，即可完全确定ρ₀，f_Y(y)也可确定。本文使用Nataf变换法求解各个输出之间的联合密度函数，再积分求得联合分布函数。

本小节给出所提指标的高效求解方法，完整过程如下。

第1步：对每个输出Y_j，使用基于分数矩的极大熵方法计算每个输出的边缘概率密度函数f_Yj(y)，并积分获得其边缘分布函数F_Yj(y)(j=1, …, m)。其中，计算分数矩$M_{{Y_j}}^{{\alpha _k}}\left( {k = 0, 1, \cdots, s;j = 1, \cdots, m} \right)$时，使用文献[14]所给出的降维积分法，将每个单个输出表示如下

式中:y_j(μ)表示所有输入变量取均值时单个输出的响应值; y_j(x_i, μ_~i)表示除输入变量X_i以外其他输入变量都取均值μ_~i时单个输出的响应值。则分数矩$M_{{Y_j}}^{{\alpha _k}}$即可由式(13) 计算

该方法将求多变量函数y_j(x)的分数矩转变为求单变量函数y_j(x_i, μ_~i)的分数矩的乘积，只需少量样本点(假设为p个)即可准确估计出单个输出Y_j的各阶分数矩(例如使用Gauss七点估计，则样本点数量p=7)。

第2步：求解输出两两间的相关系数ρ_ij。根据定义

式中的期望值同样可以由降维积分法求得，该步可以确定原始空间的相关系数矩阵ρ。

第3步：由前两步所得边缘分布和相关系数矩阵ρ，使用Nataf变换法求得多输出联合概率密度f_Y(y)；并积分求得联合分布函数F_Y(y)；选取合适的数值积分方法(例如Gauss积分)用少量样本点即可获得无条件方差V(U)=V(F_Y(y))的精确估计$\hat V\left( U \right)$。

第4步：固定第1步中X_i于每个样本点x_ki (k=1, …, p; i=1, …, n)处，代入功能函数获得X_i=x_ki条件下的多输出响应函数Y_X~i|Xi=xki(x_~i)。同样使用基于分数矩的极大熵方法求得有条件边缘概率密度函数f_Yj|X_i=x_ki(y)及分布函数F_Yj|Xi=xki(y)(j=1, …, m)，再使用Nataf变换法求得联合分布函数F_Y|Xi=xki(y)。根据U|X_i=F_Y|Xi(y)计算条件方差V(U|X_i)的估计值$\hat V\left( {U\left| {{X_i} = {x_{iz}}} \right.} \right)$，然后计算差值${\Delta _{ki}} = \left| {\hat V\left( U \right)-\hat V\left( {U\left| {{X_i} = {x_{ki}}} \right.} \right)} \right|$。

第5步：ξ_i可由${{\hat \xi }_i} = \sum\limits_{k = 1}^p {\frac{{{\Delta _{ki}} \cdot {A_k}}}{{\hat V\left( U \right)}}} $来估计，其中A_k为积分点x_ki对应的权值。

考虑如下多输出功能函数

式中：X₁，X₂，X₃均为正态变量，且相互独立，均值矢量为[3, 4, 6]，标准差均为1。

3种指标计算结果如表 1所示。

表 1(Table 1)

表 1 数值算例分析结果 Table 1 Results of the numerical example Mea-sures δi ηi ξi(MC method) ξi(Proposed Method) X1 0.235(3) 0.022 5(3) 0.121 27(3) 0.127 89(3) X2 0.542(1) 0.112 7(1) 0.449 58(1) 0.468 23(1) X3 0.537(2) 0.082 5(2) 0.434 66(2) 0.427 61(2)

表 1 数值算例分析结果 Table 1 Results of the numerical example

表中：δ_i为文献[7]所提基于PDF的多输出重要性测度指标，η_i为文献[9]所提基于CDF的多输出重要性测度指标。在该算例中，ξ_i指标与δ_i指标以及η_i指标所得重要性排序结果一致。使用Monte Carlo法3个指标模型调用次数均为(nN_t+1)N。而所提方法模型调用次数为(np+1)mN_opt，其中，N_opt为使用基于分数矩的极大熵方法求解边概率缘密度时的优化次数。一般地，N_opt ≤N。上述算例中，Monte Carlo法模型调用次数为(3×50 000+1)×50 000≈7.5×10⁹，而所提方法的模型调用次数为(3×7+1)×3×25= 1 650，运算次数大大减少。

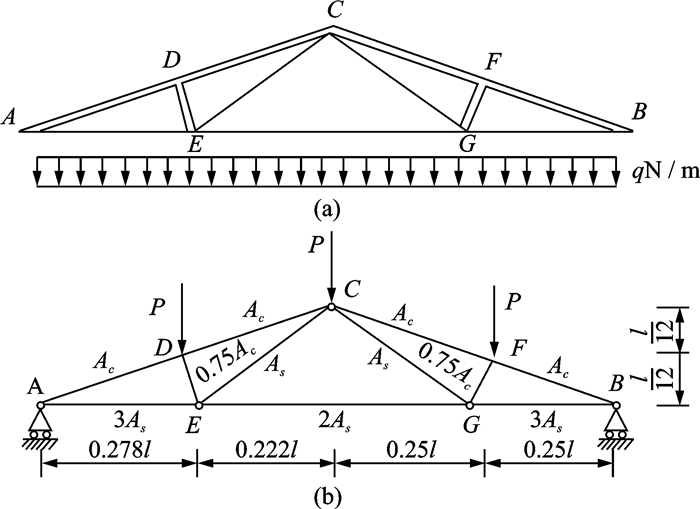
图 1所示为一屋架结构。屋架上弦杆和其他压杆为钢筋混凝土杆，下弦杆和其他拉杆为钢杆。假设屋架承受均布载荷q，A_C、E_C、A_S、E_S、l分别为CD段混凝土和CE段钢杆的横截面积、弹性模量和长度。E_D、E_E分别为AD段混凝土、AE段钢杆弹性模量。由结构力学分析可得，AD杆受压最危险，内力F_AD=-1.185ql；EC杆受压最危险，内力F_EC=0.75ql；C点沿垂直地面方向位移为$\Delta c = \frac{{q{l^2}}}{2}\left( {\frac{{3.81}}{{{A_C}{E_C}}} + \frac{{1.13}}{{{A_S}{E_S}}}} \right)$。出于安全性和适用性，以C点向下挠度不超过3 cm为约束条件。综上可得3个极限状态函数如下

图 1 屋架结构示意图 Figure 1 Sketch map of the roof truss

假设所有变量均服从独立正态分布，分布参数如表 2所示，不同指标的计算结果如表 3所示。

表 2(Table 2)

表 2 屋架结构基本随机变量分布参数 Table 2 Distribution parameters of basic random varables of the roof truss 随机变量 分布类型 均值 标准差 均布载荷q/(N·m-1) 正态 20 000 14 00 杆长l/m 正态 12 0.12 截面积AC/m2 正态 0.04 0.004 8 截面积AS/m2 正态 9.82×10-4 5.982×10-5 弹性模量ED/Pa 正态 1.34×107 2.412×106 弹性模量EE/Pa 正态 3.35×108 4.02×107 弹性模量EC/Pa 正态 2×1010 0.12×1010 弹性模量ES/Pa 正态 1×1011 0.06×1011

表 2 屋架结构基本随机变量分布参数 Table 2 Distribution parameters of basic random varables of the roof truss

表 3(Table 3)

表 3 屋架算例3种指标计算结果 Table 3 Results of three indices of the roof truss example 随机变量 δi ηi ξi(MC method) ξi(Proposed Method) q 0.508(3) 0.018(3) 0.107(3) 0.105(3) l 0.465(7) 0.003(7) 0.002(8) 0.003(8) AC 0.497(4) 0.010(4) 0.054(5) 0.054(5) AS 0.482(5) 0.008(5) 0.056(4) 0.061(4) ED 0.589(2) 0.023(2) 0.170(2) 0.177(2) EE 0.639(1) 0.039(1) 0.256(1) 0.258(1) EC 0.463(8) 0.002(8) 0.004(7) 0.003(7) ES 0.473(6) 0.006(6) 0.045(6) 0.042(6)

表 3 屋架算例3种指标计算结果 Table 3 Results of three indices of the roof truss example

从计算结果来看，本算例中ξ_i指标与δ_i指标以及η_i指标的重要性顺序基本一致。尤其是重要性排在前3位的变量，3种方法所得结果完全相同。存在微小的差异是因为δ_i指标以及η_i指标是完全基于概率分布的重要性测度指标，而ξ_i指标是包含了分布信息(CDF)的基于方差的重要性测度指标，其本质上是反映了输出响应分布函数方差与条件输出分布函数的方差之间的平均差异。这种差异一般不等同于完全使用联合密度函数或者联合分布函数产生的差异，也不等同于对每一个输出响应单独直接求方差产生的差异，而是两种不同类型指标的一种综合。

本文提出了一种结构系统多输出情况下基于概率积分转化的重要性测度新指标，用以衡量输入变量不确定性对多输出响应整体分布函数变异性的影响。所提指标可以指导工程实际对输入变量进行重要性排序。新指标一方面使用概率积分转化，包含了多个输出响应联合分布函数的信息，另一方面以方差为标准，衡量联合分布函数的变异性受输入变量的影响。因而相比基于方差的多输出重要性测度指标，它包含了前者没有考虑的输出之间相关性的信息以及多输出的整体分布函数信息。相比完全基于概率分布的多输出重要性测度指标，它以方差来衡量变异性，求解过程更为简单直观。在求解新指标时，本文同时使用了基于分数矩的极大熵方法和Nataf变换法，大大提高了求解效率。