2. 四川大学空天科学与工程学院,成都,610065;
3. 中国东方航空江苏有限公司运行控制部,南京,211113
2. School of Aeronautics & Astronautics, Sichuan University, Chengdu, 610065, China;
3. Department of Operation Control, China Eastern Airlines Jiangsu Co., Ltd, Nanjing, 211113, China
当空域扇区的流量超过容量时会造成空中交通拥堵,引发航班延误。为避免这种情况,管制员需要采取某种流量控制措施,减少将要进入本扇区的航空器数量。美国联邦航空管理局推荐管制移交间隔管理策略(Minutes in trail, MIT)作为繁忙扇区的交通流量控制方法。管制移交间隔管理是指管制员依据交通流量动态发布相邻扇区移交进入本扇区的两架飞机间可以接受的最小间隔,实质是改变在扇区边界处连续到达飞机之间的时间,从而调整后续时间的交通流密度。
管制移交间隔管理策略与扇区容量利用率密切相关。2006,Ostwald[1]分析管制移交间隔和扇区容量之间的关系,首次提出将管制移交间隔作为制约空域容量的因素,并给出了基于容量最大化的管制移交间隔的精确计算模型。2007,Sun[2]设计了一种基于改进的欧拉-拉格朗日模型,研究扇区容量与交通流之间耦合关系,指出空域拥堵与扇区不同移交点的移交间隔密切相关。2008,Avijit[3]改进了Ostwald的计算模型,通过对管制移交间隔管理策略约束条件的优化,提高了算法的收敛速度,但是并未涉及结果的稳定性和多扇区之间的耦合作用。2010,Desart[4]分析了扇区容量的动态稳定特性,指出管制移交间隔策略的稳定性和有效性对于交通流量策略的制定非常重要。2012年,申晨等[5]在研究中国管制扇区运行特点的基础上,分析多扇区之间管制移交间隔的互相影响,在Avijit计算模型的基础上建立多扇区管制间隔优化模型。2013年,Mukherjee[6]在研究管制移交间隔管理问题时不再仅关注容量提升,而是重点研究延误的分配问题,以降低延误为目标建立了一种新的间隔优化模型。2013年,Sheth[7]收集分析美国繁忙空域交通流数据,证明美国的高密度扇区,管制移交间隔管理策略是一种有效的交通流量管理策略。
然而,上述研究并未考虑空域容量的动态变化,基于动态容量的流量管理方法是目前的研究热点。2014年,温媛媛等[8]通过TAAM软件建立刻画我国空域特点的交通仿真模型,分析表明各移交点交通流量比例的变化,将导致空域容量的动态改变。2015年,Zhang[9]改进了静态空中交通流分布模式所造成的空域限制,提出了基于捕食性思想的飞机流动态调整和分配模型,提出了一种空域动态容量下的流量分配模型。2016年,Oliver[10]对扇区内航空器按照服务时间和成本进行排序,建立航空器的优先级评价方法确定服务顺序,减少航班延误。邢健[11]等通过基于航空器全飞行过程剖面生成方法,精确预测航空器的意图状态,为精确化的实时流量管理提供依据。Chang等[12]论证了受外界因素影响的扇区动态容量问题,并在此基础上建立对飞机时隙分配的流量管理模型。但是目前研究尚无涉及动态容量条件下管制移交间隔的策略和模型。
上述研究表明,因为繁忙扇区内交通流的微小改变都将造成扇区容量变化,导致将容量视为固定值的传统流量管理策略不再适用,并且动态容量条件下如果频繁更改管制移交间隔,不符合空中交通管制员的实际指挥行为,所以现有的管制移交间隔管理策略不适用于高密度扇区。因此,本文提出一种新的管制移交间隔优化方法,首先利用管制工作负荷表征容量约束和交通流量,实现对扇区流量与动态容量的解耦,提出基于管制工作负荷的扇区容量流量匹配模型;其次研究管制调配工作实际特点,基于信息熵的定义设计管制移交间隔策略稳定性表征函数,建立以策略稳定性和延误成本为目标的优化模型,并设计相应进化算法;最后依据昆明机场进近管制扇区的实际数据实施仿真分析,验证模型及方法的有效性。
1 基于扇区负荷的管制移交间隔多目标优化模型考虑空中交通管制指挥的有效性和经济性两方面因素,提出基于信息熵的管制移交间隔策略稳定性函数和航空器延误成本函数,以管制移交间隔策略的稳定性最佳和航空器延误成本最小为目标。采用管制员工作负荷值来表征扇区的容量和流量,并考虑到实际运行下的管制移交间隔限制、航空飞行特性以及最小安全间隔,然后以管制移交间隔限制、扇区容量限制、飞行特性和最小安全间隔为约束,建立基于扇区负荷的管制移交间隔多目标优化模型。
1.1 模型相关假设(1) 空域管制移交间隔的持续时间是在一个时隙窗口内;
(2) 航空器进入扇区规则是根据初始序列和先来先服务的原则安排的;
(3) 航空器预计到达扇区边界时间的预测是可靠的;
(4) 在任意一个时隙窗口内均可以用已知的交通流量函数表示扇区的容量;
(5) 该模型没有考虑空域中航空器具体的方向和高度的选择,且假设每架航空器均为匀速运行;
(6) 同一类型航空器的飞行时间在任意确定的固定点之间的飞行时间固定不变;
(7) 空域内移交间隔标准以时间为度量指标。
假设(1) 是测量运行时间的假设,假设(2~5) 是模型的确定性假设,假设(6) 是提出了简化模型,忽略由于飞行员的行为和实际管制指令导致飞机的速度不同造成的影响,假设(7) 是确定模型中的决策变量。
1.2 目标函数(1) 稳定性目标
首先,建立基于信息熵理论的策略稳定性函数,信息熵[13]是一个用于度量信息量大小的概念,从平均角度表示信息源总体包含信息多少的度量。一个系统越是有序,其信息熵就会越低,反之系统越是不稳定,信息的不确定性越大,信息熵就越大。假设某系统可能出现n种不同的状态1, 2, …, n,Pi代表状态i出现的概率,则该系统的信息熵H定义为
| $ H =-\sum\limits_{i = 1} {{P_i}{{\log }_a}{P_i}} $ | (1) |
式中:
在管制指挥场景下,管制员与飞行员构成服务系统,管制员下达管制移交间隔指令而飞行员按照指令飞行,如果管制移交间隔变动频繁,管制信息熵就会增大;而当管制移交间隔持续时间较长,则管制信息熵会越小。这意味着管制移交间隔策略的稳定性是随着持续时间递增,随着改变频率递减的函数。因此,参照信息熵的定义,提出稳定性目标函数为
| $ {\rm{Max}}\left( S \right) = \max \sum\limits_j {\frac{{-{q_j}\ln {q_j} \cdot T}}{{1 + \sqrt {\left| {\sum\limits_i {MIT_{{p_{i, j + 1}}}^2}-\sum\limits_i {MIT_{{p_{i, j}}}^2} } \right|} }}} $ | (2) |
式中:S为策略稳定值;T为当前管制移交间隔策略的持续时间;MITpi, j为入口点pi在jth时间片的管制间隔时间;qj为在jth时间片管制间隔调整的概率,且满足0≤qj≤1。
(2) 经济性目标
同时,该模型要使航班延误尽可能小,从而降低航班的延误成本。模型中的延误是指航空器的实际飞行时间与管制结束后的管制时间的差异。本文在调整管制间隔后,以最小总延误成本为优化目标函数
| $ {\rm{Min}}\left\{ {c\left( t \right)} \right\} = {\rm{Min}}\sum\limits_{p \in K} {\sum\limits_{{f_{ip}} \in {F_p}} {U_{t, p}^f} \left( {{t_{{\rm{sta}}}}^{{f_{ik}}}-{t_{{\rm{eta}}}}^{{f_{ik}}}} \right)} $ | (3) |
| $ U_{t, p}^f = \left\{ \begin{array}{l} 1\;\;\;\;\;航空器f进入扇区\\ 0\;\;\;\;\;其他 \end{array} \right. $ | (4) |
(1) 管制移交间隔约束
空域管制移交间隔管理策略的重点在于对扇区走廊口的航空器间隔进行控制,连续到达飞机的时间间隔必须大于发布的空域管制移交间隔时间。对于一个单一的扇区,从走廊口进入扇区的每一架航空器必须在控制点前满足移交间隔的限制。如果满足间隔限制,那么该航空器的飞行间隔不需要调整,否则,航空器之间的间隔必须扩大到限制要求,如式(5) 所示
| $ \left\{ \begin{array}{l} t_{{\rm{sta}}}^{{f_{i + 1, p}}} = t_{{\rm{sta}}}^{{f_{ik}}} + MI{T_p}\;\;t_{{\rm{eta}}}^{{f_{i + 1, p}}} = t_{{\rm{sta}}}^{{f_{ip}}} + MI{T_p}\\ \;\;\;\;\;t_{{\rm{sta}}}^{{f_{i + 1, p}}} = t_{{\rm{eta}}}^{{f_{i + 1, p}}}\;\;\;\;\;\;\;\;t_{{\rm{eta}}}^{{f_{i + 1, p}}} = t_{{\rm{sta}}}^{{f_{ip}}} + MI{T_p}\; \end{array} \right. $ | (5) |
式中:
(2) 飞行特性约束
航空器f从扇区中飞出时间是该航空器f进入扇区的时间与航空器f在扇区飞行的时间之和
| $ t_{{\rm{out, p}}}^f = t_{{\rm{sta}}}^f + f{t_{{f_{ip}}}} $ | (6) |
式中
(3) 基于工作负荷限制的容量约束
空中交通流量管理的目标是确保交通流量不能超过扇区容量。然而,相同数量的飞机因为不同的进离场比例可能造成不同的交通复杂度,这就会对管制员的工作造成不同的负荷,进而影响管制指挥效率,从而影响当前时段的扇区容量。因此时隙内的航空器数量无法完全反映容量约束与交通流量的关系。
本文选择管制工作负荷来表征交通流量和容量约束之间的关系。管制员工作负荷可以用管制员在单位小时内通讯行为和操作行为的时间长度之和来表示,现有空中交通管制自动化设备可以方便地提取管制员工作负荷数值。因为随着交通流量的增长,管制工作负荷也同时增加,而且工作负荷不可超过保证交通安全和顺畅所需的最大极限,所以空域最大容量可以转变为一个固定的、最大可接受的工作负荷值,因此本文提出了一种基于管制工作负荷的容量流量匹配模型
| $ {C_{{\rm{workload}}}} \ge y = \sum {{\beta _p}{x_p} + e} $ | (7) |
式中:Cworkload指管制员最大工作负荷限制的扇区容量;y为管制工作负荷;βp为pth走廊口的权重,可以通过走廊口流量比例回归分析得出,该权重系数表示不同走廊口空中交通流对管制工作负荷的影响;xp为pth走廊口的流量;e为偏置误差,为y的观测值和预测值之差。
在规定的τ时间(单位时间片)内,该扇区的航空器数量必须小于该扇区的容量,扇区容量以工作负荷值来表征,即
| $ {C_{{\rm{workload}}}} \ge \sum {{\beta _p}{x_{pj}} + e} $ | (8) |
因为目前空中交通流量管理工作通常以15 min为决策更新周期,所以设置值即单位时间片长度为15 min。因为国际民航组织9426号文件规定“空中交通管制可接受的工作负荷不可以超过工作时间的80%”,即在15 min时间片内可接受的最大工作负荷为12 min,因此表征容量的工作负荷值为720 s,是在j时间片内通过P点进入扇区的航空器数量。
(4) 最小安全间隔约束
管制移交间隔的大小必须满足一定的范围,首先不能小于规定的安全间隔,同时为了消除某一方向的特大型管制移交间隔的影响,管制移交间隔时间也不能超过允许的最大时间控制, 即
| $ sep \le MI{T_p} \le \max MIT $ | (9) |
式中sep指规定的航空器最小安全间隔。
2 扇区尾随间隔更新的算法设计多目标遗传算法(Multi-objective genetic algorithm,MOGA)是在简单遗传算法的基础上发展起来的,它可以在多个目标之间直接权衡。基于非劣解集的多目标遗传算法一次运算可得到多个均匀分布的帕累托最优解,且无须先验知识,适合在不同航路结构和航班流量不断变化的形势下快速做出决策。其中NSGA-II算法引入精英保留策略、快速非劣解排序及种群分布拥挤距离计算,在搜索效率和搜索结果上均具有一定优势,且具有较好的稳健性和鲁棒性[14],适用于本文涉及扇区多移交点的管制移交间隔优化问题。
2.1 目标函数本文模型关注的是各个控制点的管制移交间隔,而不是航班时刻,因此不选取航班作为基因。若选取航班作为基因,在较长的时间段内航班数量的累加容易导致基因群组庞大,导致计算速度会很慢,不利于算法的求解。由于实际进入扇区的航班时刻是在管制移交间隔管理之后生成的,因此在获取管制移交间隔信息之后,航班时刻可以通过计算获得。扇区的控制点是有限的,利用控制点处的管制移交间隔作为基因会减少变量,提高计算速度。
本文利用控制点处的管制移交间隔值作为基因值,对于本模型使用真值进行编码,即直接利用决策变量的实际值进行编码。将扇区各控制点的管制移交间隔值作为基因座的值,按固定的顺序排列,对应各控制点处的管制移交间隔为基因。例如,对于某一扇区,有6个控制进入点。
序号(对应扇区进入点序号):1, 2, 3, 4, 5, 6。
染色体1: 2, 6, 10, 4, 8, 5(对应各控制点的管制移交间隔值,单位min)。
染色体2: 4, 3, 2, 8, 3, 3。
2.2 目标函数计算在本模型中考虑的是管制移交间隔策略的稳定性目标和经济性目标,其中稳定性目标以时间段内尾随间隔的方差与信息熵来表征,经济性目标以航班的延误时间来表征。
(1) 管制移交间隔稳定目标
稳定性目标是各个时间片内控制点管制移交间隔的变化速率最小,即根据上述模型中的管制移交间隔稳定性目标函数确定算法稳定性适应度函数为
| $ SOF = \sum\limits_j {\frac{{-{q_j}\ln {q_j} \cdot T}}{{1 + \sqrt {\left| {\sum\limits_i {MIT_{{p_{i, j + 1}}}^2}-\sum\limits_i {MIT_{{p_{i, j}}}^2} } \right|} }}} \times \sigma $ | (10) |
(2) 最小空中延误成本目标
经济性目标是航班延误时间最小,根据上述模型中的延误成本最小目标函数,因此对于经济性目标的适应度选择函数为
| $ EOF = \frac{{1\;000}}{{\sum\limits_{p \in K} {\sum\limits_{{f_{ip}} \in {F_p}} {U_{t, p}^f} \left( {t_{cta}^{{f_{ik}}}-t_{eta}^{{f_{ck}}}} \right) + \varepsilon } }} \times \sigma $ | (11) |
式中:分子1 000是为了使适应度取值结果相对合理,以一较大正数除以延误成本;ε为非负的一个小正数,确保当延误时间为0时适应度函数有意义,本文取为1;σ为惩罚函数,在进行管制移交间隔控制之后,仍然可能会出现流量超过容量的个体,引入惩罚函数σ使得不满足约束条件的个体的适应度为0。σ表示为
| $ \sigma = \left\{ \begin{array}{l} 1\;\;\;\;流量未超过容量\\ 0\;\;\;\;流量超过容量 \end{array} \right. $ | (12) |
应用NSGA-II算法求解尾随间隔管理模型的算法流程如图 1所示。

|
图 1 多目标遗传算法流程图 Figure 1 Flow chart of multi objective genetic algorithm |
首先,生成初始尾随间隔种群。根据编码方法,通过产生随机数的方法产生一个初始种群。种群数量为50个。为了保证初始种群每个个体都是初始的可行解,即保证50个个体都要满足容量约束。通过随机编码的方法生成可行解步骤如下:
步骤1 为控制点的管制移交间隔编码。假设有k个控制点,依次随机产生k个随机数nk,若nk<sep,则重新产生随机数,直至满足所有的安全间隔;
步骤2 根据生成的nk,以及航班时刻表中每个航班的预计过点时间,生成管制移交间隔控制之后的新的航班实际过点时刻表;
步骤3 根据实际航班过移交点的时刻判断是否有超出容量的情况,若超出容量,则返回步骤1;否则,编码完毕。
然后,对种群进行非支配分类。将当前种群中所有非劣解个体划分为同一等级,并令其等级为1;而后将这些个体从种群中移出,在剩余个体中找出新的非劣解,再令其等级为2;重复上述操作,直至种群中所有个体都被设定相应的等级。
下一步,实施遗传操作。NSGA-II算法的遗传操作包括3个基本遗传算子:选择、交叉和变异。
(1) 选择
对种群Pg的选择操作:首先,根据已完成的对种群Pg的非支配分类,确定其各染色体的等级,定义个体j的等级为m(j), j=1, …, Np。然后,计算各染色体的适应度,对于个体j的适应度fGA(j)为
| $ {f_{{\rm{GA}}}}\left( j \right) = \frac{1}{{1 + m\left( j \right)}} $ | (13) |
最后,采用期望值法确定被选择的个体,选择操作后种群大小仍为Np。对种群Rg的选择操作:根据已完成的对种群Rg的非支配分类,设生成的等级序列集合分别为λ1, λ2, λ3, …。如果λ1中的个体数量大于Np,则对λ1中个体进行拥挤距离计算,按拥挤距离从大至小对个体排序,取出前Np个个体组成Pg+1;如果λ1中个体数量等于Np,则直接由λ1组成Pg+1;如果λ1中个体数量小于Np,那么就从序列集合λ2中补足,如果还不够,则从λ3中补足,依此类推,同一集合中的个体按拥挤距离从大至小排序,直至找到Np个个体组成Pg+1。其中,拥挤距离指每一个体与同级别相邻两个体间的局部拥挤距离。
(2) 交叉
采用单点交叉方式。首先对个体进行两两随机配对,然后在个体串中随机设定一个交叉点,最后依照交叉概率pc在交叉点处相互交换两个个体的部分染色体,从而产生出两个新的个体。同时,判断新生成的两个个体是否满足相应限制,若满足则进入下一步操作;否则重新进行交叉产生新的个体。
对于交叉概率pc的取值与一般遗传算法不同。一般遗传算法进化到后期时种群接近收敛,NSGA-II算法要求从始至终都要保持种群的多样性以满足对已得到的非劣解进行再度更新,因此取值通常较大,本论文选取交叉概率pc=0.8。
(3) 变异
采用基本变异操作。在满足变异概率pm的前提下,随机挑选一个个体,改变其某基因位置的编码。同时,判断新生成的个体是否满足约束条件限制,若满足则进入下一步操作;否则,实施删除操作,并重新进行变异产生新的个体。为了满足NSGA-II算法对于解的多样性的要求,此处变异概率pm=0.1。
通常遗传算法的终止条件可通过满足适应度值或最大进化代数来实现。NSGA-II算法的终止条件普遍采用设定最大进化代数来实现。其次本文算法策略中将15 min划分为一个时间片,在时间片之间进行航班时刻的调整,而且选取基于帕累托优化的多目标遗传算法进行优化模型的求解,算法中的非支配排序能够促进子代的进化,加快收敛。
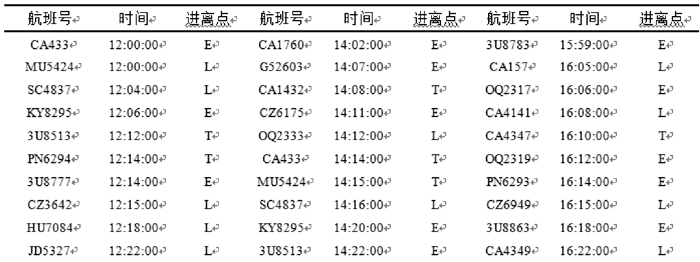
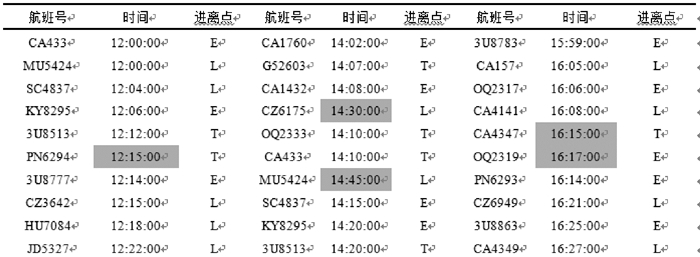
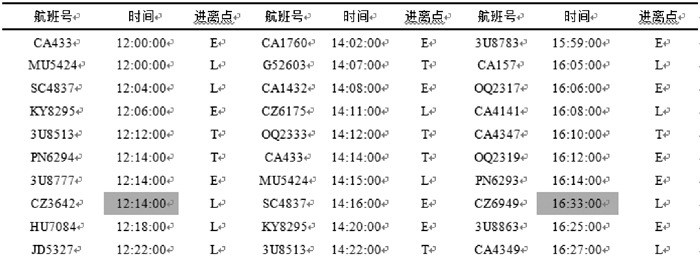
3 仿真与算例昆明机场进近04扇区有3个进离走廊口,本文中简称为O,D,G。管制员15 min最大工作负荷是720 s,选择6 h的航班时刻表并将其划分为24个时间片,每个时间片15 min。选取种群个体为50个,遗传代数300,染色体长度为3,代沟0.9,交叉率0.8,变异率0.1。通过NSGA-II算法运用MTALAB运算可以得出模型的一组帕累托最优解,分别对应模型的空中延误成本最小目标和管制移交间隔稳定目标。并且实例证明,该算法的求解能够满足策略实时性的要求。新的管制移交间隔策略是用来优化改进原始的航班时刻表,生成新的航班时刻表。图 2~5分别是部分原始航班时刻表、部分传统MIT方法优化后航班时刻表、偏向于经济性动态间隔的部分航班时刻表以及偏向于稳定性动态间隔的部分航班时刻表。图中标注部分表示航班调整后的航班时刻。根据优化前后的航班时刻表,计算管制工作负荷,空中延误成本和管制移交间隔策略的稳定性。
|
图 2 原始航班时刻表节选 Figure 2 Part of the original flight schedule |

|
图 3 MIT方法优化后航班时刻表节选 Figure 3 Part of MIT optimized flight schedule |
|
图 4 动态间隔(经济性)航班时刻表节选 Figure 4 Part of economic optimized flight schedule |
|
图 5 动态间隔(稳定性)航班时刻表节选 Figure 5 Part of stable optimized flight schedule |
图 6首先对比几种方法下的管制员工作负荷。由图 6可见,原始航班时刻表下的管制员工作负荷经常会超过15 min负荷限制720 s,当前MIT策略下的管制工作负荷也会偶尔超过。而在本文提出的新的管制间隔移交策略下,两个目标下的管制员工作负荷无一超越负荷限制,而且新的方法下管制工作负荷要比现有的MIT策略低。因此,本文提出的新的管制移交间隔策略可以有效降低管制工作负荷。

|
图 6 工作负荷对比图 Figure 6 Comparison diagram of workload |
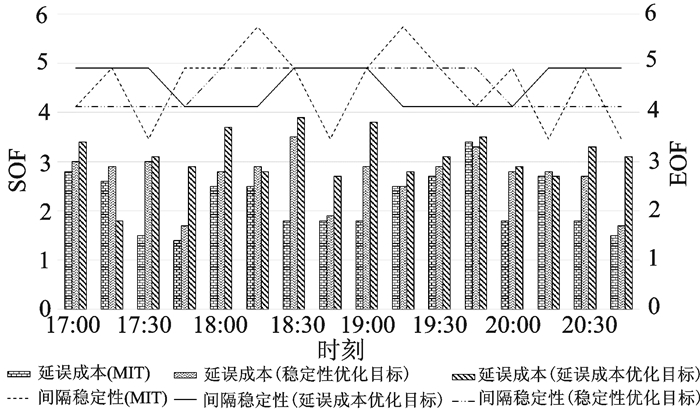
图 7中比较了3种情况下的管制移交间隔稳定性和空中延误成本,可见本文提出的新的管制移交间隔策略虽然在延误成本方面较之当前的MIT策略略有不足,但在稳定性方面却比当前MIT策略优秀很多,而当前MIT策略在管制移交间隔的稳定性方面有严重的不足,因此认为本文提出的新的管制移交间隔策略兼具良好的经济性和稳定性。
|
图 7 目标优化结果对比图 Figure 7 Comparison diagram of multi objective optimization results |
因为新的空域管制移交间隔策略在优化过程中有两个优化目标,因此着重于延误成本的优化方法虽然经济性较好,但在稳定性上略有短板,而针对管制策略稳定的优化方法则在经济性上略有欠缺,因此通常情况下空中延误成本目标与管制策略稳定性目标无法同时达到最优。在实际管制工作中,管制带班主任可以结合班组人员资质能力和当前时段内进离港航班架次的情况权衡利弊,进行科学合理的决策。当班组人员资质能力较强或当前时段内进离港航班架次较少,发布的管制移交间隔可以偏向于经济性的指标,从而降低航班的总体延误,当班组人员资质能力较弱或当前时段内进离港航班架次较多,发布的管制移交间隔可以偏向于稳定性的指标,从而降低管制调配难度,保障航班飞行安全。
4 结束语管制移交间隔管理策略是交通流管理最常用的方法,但因为繁忙扇区通常有着极其复杂的交通流,而不同交通复杂性会使扇区容量动态变化,所以在高密度交通流扇区管制移交间隔管理策略不够准确。因此本文提出一种新的管制移交间隔优化方法,首先利用管制工作负荷表征容量约束和交通流量,提出基于管制工作负荷的扇区容量流量匹配模型;其次基于信息熵的定义设计管制策略稳定性表征函数,建立以管制策略稳定性和延误成本为目标的优化模型,并设计相应进化算法;最后依据某机场终端扇区实际数据实施仿真分析,证明本方法可以获得一组帕累托最优解。
本文对昆明机场终端扇区的真实交通场景进行仿真分析后,将得出的结果与MIT策略进行对比,通过计算不同策略下的管制工作负荷、管制移交间隔稳定性和空中延误成本这3个指标,可以发现相对于MIT策略,本文提出的管制移交间隔策略虽然在延误成本上略有不足,但是可以有效地减少管制工作负荷,提升管制移交间隔稳定性。针对管制移交间隔稳定目标和空中延误成本目标的优化方法无法同时达到最优,流量管理人员可以根据实际工作偏好,选择合适的最优解。
| [1] | QSTWALD P, TOPIWALA T, DEARMON J. The miles-in-trail impact assessment capability[C]//6th AIAA Aviation Technology, Integration and Operations Conference. Wichita, USA:[s.n.], 2006. |
| [2] | SUN D, STRUB I S, BAYEN A M. Comparison of the performance of four Eulerian network flow models for strategic air traffic management[J]. Networks & Heterogeneous Media, 2007, 2(4): 569–595. |
| [3] | AVIJIT M, SHON G, BANAVAR S. Alleviating airspace restrictions through strategic control [C]//AIAA Guidance, Navigation and Control Conference and Exhibit. Hawaii, USA: [s.n.], 2008. |
| [4] | DESART B., GILLINGWATER D, JANIC M. Capacity dynamics and the formulation of the airport capacity/stability paradox: A european perspective[J]. Journal of Air Transport Management, 2010, 16(2): 81–85. DOI:10.1016/j.jairtraman.2009.10.006 |
| [5] |
申晨. 空中交通管制移交间隔管理策略研究[D]. 南京: 南京航空航天大学, 2012.
SHEN Chen. Research on minutes-in-trail policy in air traffic control [D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2012. |
| [6] | MUKHERJEE A, GRABBE S, SRIDHAR B. Alleviating airspace restriction through Strategic control[J]. Historia Critica, 2013(1): 101–146. |
| [7] | SHETH K, GUTIERREZ-NOLASCO S, PETERSEN J. Analysis and modeling of miles-in-trail restrictions in the national airspace system[C]//Aviation Technology, Integration and Operations Conference.Los Angeles, USA:[s.n.], 2013. |
| [8] |
温媛媛, 戴福清.
基于TAAM的终端区容量评估[J]. 中国民用航空飞行学院学报, 2013, 24(6): 9–14.
WEN Yuanyuan, DAI Fuqing. Terminal area capacity evaluation based on TAAM[J]. Journal of Civil Aviation Flight University of China, 2013, 24(6): 9–14. |
| [9] | ZHANG Z, HAO Z, GAO Z. A dynamic adjustment and distribution method of air traffic flow en-route[J]. Journal of Air Transport Management, 2014, 42: 15–20. |
| [10] | OLIVER R M. Delays in terminal air traffic control[J]. Journal of Aircraft, 2015, 1(3): 134–140. |
| [11] |
邢健, 汤新民, 韩松臣, 等.
一种基于航空器气象资料下传数据的飞行剖面生成方法[J]. 南京航空航天大学学报, 2015, 47(1): 64–70.
XING Jian, TANG Xinmin, HAN Songchen, et al. Method for generating flight profile based on ATMDAR data[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(1): 64–70. |
| [12] | CHANG Y H, SOLAK S, CLARKE J P B, et al. Models for single-sector stochastic air traffic flow management under reduced airspace capacity[J]. Journal of the Operational Research Society, 2016, 67(1): 54–67. DOI:10.1057/jors.2015.53 |
| [13] |
龚伟. 基于信息熵和互信息的流域水文模型不确定性分析[D]. 北京: 清华大学, 2012.
GONG Wei. Watershed model uncertainty analysis based on information entropy and mutual information [D]. Beijing: Tsinghua University, 2012. |
| [14] | SHAO Z J, HE C, PEI J H. Multi-objective optimization design of vented cylindrical airbag cushioning system for unmanned aerial vehicle[J]. Transactions of Nanjing University of Aeronautics and Astronautics, 2016, 33(2): 208–215. |
 2017, Vol. 49
2017, Vol. 49


