针对飞机金属结构损伤，20世纪70年代初期，Baker等率先提出了复合材料胶接修理方法。此后的40多年中，学术界对复合材料胶接修理损伤金属结构的疲劳寿命、应力强度因子、裂纹扩展、复合材料脱黏、残余热应力影响等进行了大量的研究^[1-2]。如Naboulsi^[3-8]和Mall^[9]等人采用有限元“三板模型”对残余热应力和预先设置的界面脱黏对修理效果的影响，以及金属结构裂纹扩展速率进行了分析。Sabelkin等人^[10]通过有限元与试验相结合的方法对复合材料胶接修理7075-T6铝合金后的若干参数进行了研究。Toudeshky等人^[11-15]利用有限元法和试验研究了复合材料单面胶接修理铝合金后疲劳裂纹的扩展以及裂纹前缘的形状。Chung等人^[16]通过三维有限元建模以及试验对复合材料单面胶接修理铝合金厚板裂纹扩展行为进行了研究。Papanikos等人^[17-18]通过三维有限元模型研究了修理结构中脱黏的萌生与扩展，以及补片参数的影响。文献[18~22]分析了修理结构的裂纹扩展以及单面修理导致的裂纹扩展纹线的变化，但都没有考虑脱黏的影响。

损伤金属结构经过复合材料胶接修理后，整个修理结构的受力特点、传力路线和应力应变场分布都发生了变化，最终导致结构的耦合失效模式。特别是复合材料的脱黏与裂纹扩展之间的相互作用不可忽略。此外，修理过程中形成的残余热应力以及单面修理导致的附加弯曲力矩等都会对修理结构的疲劳寿命产生影响。但从前文可以看出，在大多数已有的研究中，都对问题进行了简化，忽略残余热应力和弯曲变形的影响，且只考虑某一种损伤，没有分析多种损伤及其之间的相互影响。为此，本文基于有限元法和Paris裂纹扩展公式，提出了一种能够考虑残余热应力、附加弯曲力矩、单面修理导致的曲线裂纹扩展前缘以及多种失效模式相互影响的复合材料修理损伤金属结构疲劳寿命评估方法。

复合材料胶接修理损伤金属结构在疲劳载荷的作用下，主要的失效模式有：

(1) 金属结构原有裂纹的扩展直至断裂；

(2) 金属结构与复合材料之间脱黏的萌生与扩展；

(3) 复合材料的疲劳破坏。

疲劳加载时，上述失效模式相互影响，共同作用决定了修理结构的疲劳寿命。因此分析修理结构的疲劳寿命应综合考虑各种失效模式。

对于金属结构原有的裂纹，将其从初始裂纹长度a₀到临界裂纹长度a_f的整个裂纹扩展过程划分为有限个较小的裂纹长度增量Δa₁, Δa₂, …, Δa_j, Δa_j+1, …, Δa_n，则有

那么结构的疲劳寿命为结构经历每次裂纹扩展的疲劳周次之和，即

式中ΔN_i为对应于Δa_i的疲劳寿命。如果Δa_i足够小，那么可认为在此期间应力强度因子幅ΔK_i保持不变。依Paris公式，ΔN_i为

式(2) 可写为

随着裂纹的扩展，胶接修理区域应力状况恶化，当裂纹扩展到某一长度时，金属结构与复合材料之间出现脱黏或复合材料产生损伤，将同样的思路应用于脱黏及复合材料中的损伤，假设在裂纹扩展过程Δa_i中，产生的脱黏面积为ΔS_i和复合材料损伤为ΔD_i。当金属结构中裂纹长度扩展到a_m时，脱胶面积和复合材料补片损伤为

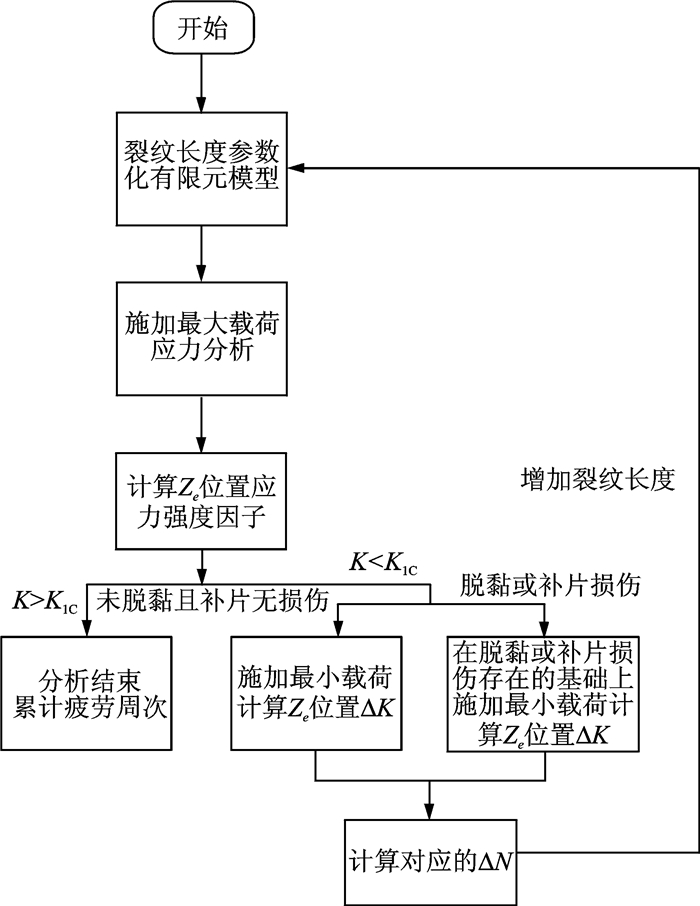
金属结构中裂纹长度、脱胶面积和复合材料补片损伤都会影响到修补区的应力应变场。因此本文的模型充分考虑这些耦合效应，提出了如图 1所示的疲劳寿命分析流程。

图 1 疲劳寿命分析模型 Figure 1 Fatigue life analysis chart

在该模型中，相关要素的处理方法如下：

(1) 胶黏剂脱黏分析采用牵引分离法。

(2) 复合材料补片的失效准则采用Hashin准则，受损材料的性能按照线性规律退化，直至损伤d=1，材料完全失效。

(3) 应力强度因子采用虚拟裂纹闭合法计算，裂纹扩展采用Paris公式。

(4) 单面修理产生局部弯曲，进而影响金属结构中裂纹的扩展。采用Toudeshky模型^[11]，用铝合金板厚度上任意一点Z_e的裂纹长度来表示修理结构的曲面裂纹长度

式中：t_p为铝合金板厚度; W为铝合金板宽度; E_Al和E_patch分别为铝合金和复合材料纤维方向的弹性模量。

LY12CZ铝合金板试验件尺寸为180 mm×120 mm×3 mm，预制10 mm中心穿透裂纹。

补片为碳纤维/环氧树脂复合材料，其尺寸为76 mm×38 mm。补片尺寸满足刚度一致的要求^[23]，即

式中：E_patch，E_plate分别为复合材料及铝合金的弹性模量；t_patch，t_plate分别为复合材料补片及铝合金板的厚度。

根据材料性能参数和铝合金板厚度，可得

由此确定铺设8层0°碳/环氧预浸料，每层厚度为0.2 mm。

在进行单面胶接修理前，对铝合金进行疲劳加载，最大应力σ_max=100 MPa，应力比R=0.1，使预制的10 mm中心穿透裂纹扩展至14 mm。

损伤区域经过表面处理后，将碳/环氧预浸料一层层铺设在修理区域，按照一定的固化工艺制度进行共固化。试验件如图 2所示。

图 2 试验件 Figure 2 Specimens

修理结构两端施加σ_max=100 MPa, R=0.1的疲劳载荷。试验过程中，记录载荷循环次数及对应的裂纹长度。裂纹扩展过程中伴随有黏接界面脱黏，采用染色技术对其进行观察。经过一定疲劳周次的试验后，将DPT-8着色渗透剂从试件的裂纹中喷入，之后将其拉断并剥离复合材料补片，由着色情况可观察到脱黏形貌。最终的疲劳试验结果如表 1所示。

表 1(Table 1)

表 1 疲劳试验结果 Table 1 Fatigue test results 试件 未修理试件 修理试件 疲劳寿命/cycle 405 020 649 129 370 467 543 313 584 396 755 013 692 381

表 1 疲劳试验结果 Table 1 Fatigue test results

试验时发现，在疲劳加载初期，由于裂纹存在，引起中心区域应力集中，使胶黏剂传递载荷时形成的剪应力较大，造成裂纹周边区域容易出现脱黏失效，且形状呈椭圆形，长轴与裂纹扩展方向一致。随着裂纹的扩展，脱黏也以椭圆形状逐渐扩展，当裂纹扩展到靠近复合材料补片边缘时，裂尖的应力集中造成胶黏剂边缘区域剪应力增大，使得补片边缘出现较大面积的脱黏，由试件中心向两边呈喇叭状。裂纹进一步扩展，超出补片宽度之后，中心区域的椭圆形脱黏和边缘的喇叭形脱黏连成一片，基本呈矩形，如图 3所示。

图 3 试验脱黏形貌 Figure 3 Debond shape in experiments

材料的性能参数见表 2~4。

表 2(Table 2)

表 2 碳纤维性能数据 Table 2 Properties of carbon fiber 参数 数值 拉伸强度/MPa 4 000 拉伸模量/MPa 240 断裂伸长率/% 1.7 纤维直径/μm 7 密度/(g·cm-3) 1.75 体积电阻率/ (Ω·cm) 1.7×10-3

表 2 碳纤维性能数据 Table 2 Properties of carbon fiber

表 3(Table 3)

表 3 环氧树脂性能数据 Table 3 Properties of epoxy 拉伸模量/GPa 拉伸强度/MPa 2.6 85

表 3 环氧树脂性能数据 Table 3 Properties of epoxy

表 4(Table 4)

表 4 单向连续碳纤维增强环氧树脂基本力学性能 Table 4 Properties of unidirectional carbon/epoxy composite 0°拉伸 强度/MPa 1 800 模量/GPa 130 90°拉伸 强度/MPa 100 模量/GPa 10 0°拉伸 强度/MPa 1 520 模量/GPa 110 0°压缩强度/MPa 1 100 90°压缩强度/MPa 167 层间剪切强度/MPa 80 剪切模量/GPa 5 泊松比 0.3 密度/(g·cm-3) 1.6 纤维重量含量/% 68

表 4 单向连续碳纤维增强环氧树脂基本力学性能 Table 4 Properties of unidirectional carbon/epoxy composite

建立三维有限元模型。铝合金板采用8节点六面体三维实体单元C3D8R进行建模，胶黏剂采用黏性单元COH3D8模拟，复合材料为各向异性，采用SC8R连续壳单元。由于对称性，建立1/4模型。

由于热膨胀系数的不同以及中性轴偏移，单面胶接修理会在结构中形成残余热应力和附加弯曲力矩，进而对结构的疲劳寿命产生影响。为计及这种影响，分析时首先根据固化制度设置温度和压力进行非线性分析，可以得到修理结构中残余热应力的分布以及弯曲变形如图 4所示。

图 4 固化形成的弯曲变形 Figure 4 Bending deformation during curing

在此基础上，设每次裂纹长度变化Δa=0.1 mm，分别在结构两端施加σ_max=100 MPa和σ_min=10 MPa进行应力分析。

分析发现，裂纹扩展初期，复合材料完全黏接在中心贯穿裂纹铝合金板上，胶黏剂通过剪切作用传递载荷，因此在中心贯穿裂纹覆盖区域应力明显较大，而边缘由于刚度突变，应力也大于其余区域，其应力分布如图 5所示。当半裂纹从初始长度a₀=7 mm扩展到a=16.4 mm时，铝合金板和复合材料之间在围绕裂纹的中心区域出现脱黏，其形状基本呈椭圆形，且长轴垂直裂纹扩展方向，随着裂纹的扩展，椭圆形脱黏区域的面积也逐渐增大，直到其长轴贯穿复合材料长度方向，根据对称性，可知整个胶黏剂中心区域都发生了脱黏，其形貌如图 6所示。但这一模拟结果与试验研究结果并不一致。

图 5 胶黏剂中应力分布 Figure 5 Stress distribution in adhesive

图 6 胶黏形貌 Figure 6 Debond shape

脱黏后，胶黏剂传递载荷的作用减弱，铝合金板承担的载荷越来越多，裂尖应力强度因子快速增加。当裂纹扩展超出补片边缘之外至a=48.7 mm时，Z_e位置应力强度因子达到铝合金的断裂韧性，裂纹快速扩展，铝合金板断裂。整个过程中，复合材料没有出现损伤。

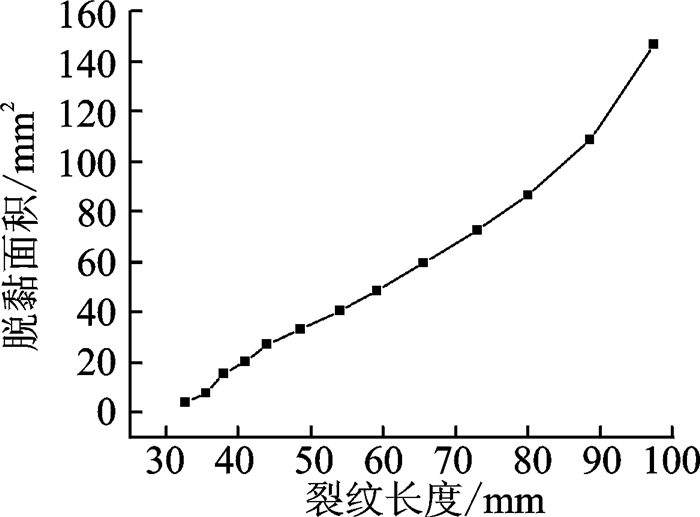
分析过程中，当胶黏剂单元中的应力满足牵引分离法时，即认为单元失效，并被删除，由此可得脱黏面积，即失效单元的数量与单元XY平面内面积的乘积，这样得到脱黏面积与裂纹长度的关系如图 7所示。

图 7 裂纹长度与脱黏面积的关系 Figure 7 Relationship between crack length and debond area

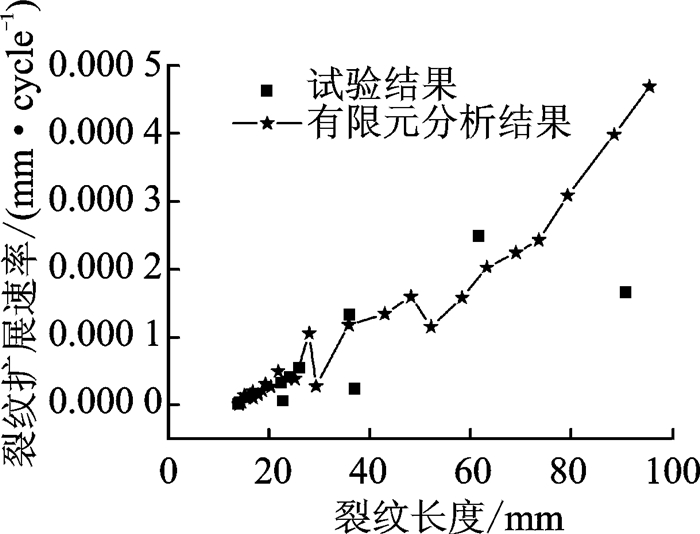
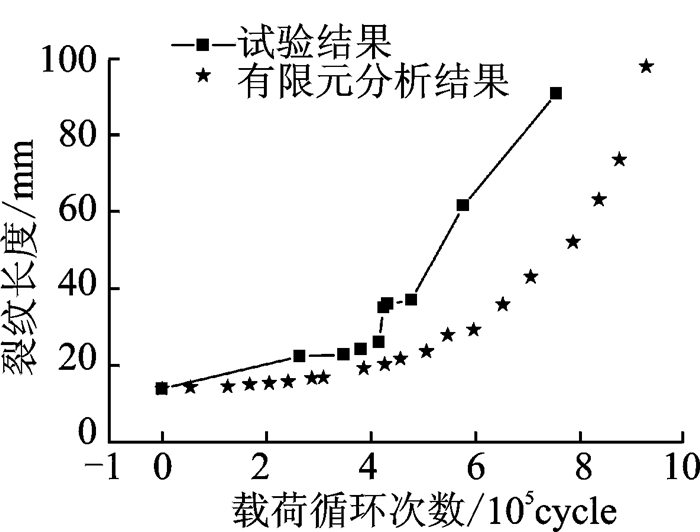
计算得到裂纹扩展过程中，裂纹扩展速率与裂纹长度的关系如图 8所示，结果见表 4。利用Paris公式计算每段Δa_j对应的ΔN_j，裂纹扩展常数C=3.51×10^-9，m=1.66，将其累加得到修理结构的疲劳寿命如图 9所示。

图 8 裂纹扩展速率与裂纹长度的关系 Figure 8 Relationship between crack length and crack propagation rate

图 9 疲劳寿命分析结果 Figure 9 Fatigue life analysis results

从图中可以看出，相同裂纹长度下，有限元分析得到的疲劳寿命分析结果与试验结果相比较大，最终计算得到的修理结构疲劳寿命为926 418次循环，与试验结果的平均值644 846次循环相比，相对误差为30.39%，偏于危险，造成误差的原因有：

(1) 有限元分析时，在每个裂纹长度增量内，认为裂纹扩展速率不变，与裂纹扩展速率越来越快的实际不符，造成最终的计算结果偏大。

(2) 分析过程中，脱黏的形貌与实际情况不符。虽然同为椭圆形，但方向不一致，其长轴垂直于裂纹扩展方向意味着，在同样情况下，裂纹扩展方向上未脱黏的胶黏剂多，这样就可以传递更多的载荷，进而铝合金板承受的载荷减小，裂尖处应力强度因子幅也会变小，最终减缓裂纹扩展，使计算结果偏大。

(3) 文献[10]中确定Z_e位置方法没有考虑修理结构中出现脱黏损伤，实际上在脱黏出现后，Z_e位置裂纹还能否代表铝合金板中的曲面裂纹有待进一步研究，这也是造成误差的可能原因之一。

本文基于有限元法和Paris公式，提出了一种复合材料胶接修理损伤金属结构疲劳寿命的评估方法。该方法通过牵引分离失效法则和Hashin准则、复合材料固化过程的模拟以及被修理结构厚度方向裂纹长度表征点的选择，能够考虑修理结构多种失效模式、残余热应力和附加弯曲力矩以及单面修理导致裂纹非均匀扩展的影响。通过算例对其可行性进行验证，表明该方法可以为复合材料单面胶接修理损伤金属结构疲劳寿命估算提供参考。但由于计算结果与试验结果相对误差偏大，且偏于危险，如何提高预测精度以应用于工程还须进一步研究。