无人机(Unmanned aerial vehicle, UAV)导航系统主要建立在惯性测量单元(Inertial measure unit, IMU)以及全球定位系统(Global position ing system, GPS)接收机的基础上[1-2]。惯性导航系统(Inertial navigation system, INS)具有隐蔽性、独立性以及抗干扰的优点[3],GPS具有全方位、全天候、全时段和高精度的优点,但其易受干扰[4]。GPS/INS复合导航具有两大优势:一方面,GPS可改善INS的误差累加现象;另一方面,INS具备短期精度高的特点,可保证GPS接收机在GPS信号弱或是受到干扰时正常工作。随着无人机的广泛应用,其导航系统的干扰问题已成为研究热点。文献[5]研究了存在GPS信号阻塞或干扰时,无人机的自主导航问题,使用多个激光传感器实现无人机的导航定位。但在实际应用中,无人机需要定期通过GPS测量值对惯性导航引起的误差进行校正,不可完全依靠非GPS导航系统。文献[6]通过产生虚假GPS信号,对采用GPS导航的民用无人机进行场地实验,干扰无人机的GPS接收机改变其定位结果。文献[7]研究了转发式欺骗干扰,通过对原始卫星信号加入时延以影响GPS接收机的定位结果,不受GPS信号加密码型限制,同时适用于民用和军用GPS。上述两种GPS欺骗干扰的方法都会引起定位结果的跳变,对于采用GPS/INS的飞行器来说,会检测到干扰并摒弃GPS测量值对定位结果的校正,导致GPS欺骗干扰失败[8-9]。
本文在研究传统GPS欺骗干扰原理的基础上,通过对无人机导航系统进行控制的方法来保证GPS欺骗干扰的隐蔽性。利用雷达系统获取无人机的位置与速度信息[10-11],由此计算出各卫星时延以及多普勒偏移信息,生成与真实GPS信号一致的欺骗信号,完成对无人机GPS接收机中跟踪环路的控制。欺骗无人机的惯性导航系统,需要控制目标无人机的状态估计量。由于无人机处于飞行状态时,经常使用GPS测量值来修正外界干扰[12-14],因此干扰机能够通过发送欺骗GPS信号的方法,使目标无人机获得错误位置及速度,导航系统输出错误的状态量,从而完成对状态估计量的控制。本文通过建模采用直接干扰和轨迹融合两种方法对导航系统进行控制,仿真结果表明轨迹融合的方法符合隐蔽性的要求,控制了无人机的导航系统实现轨迹欺骗。
1 GPS欺骗干扰原理GPS接收机利用伪距进行定位,接收4颗或4颗以上的卫星信号,根据各卫星支路信号到接收机传播时间计算得到距离信息[15]。由于卫星与接收机都存在时钟偏移,并且信号传播过程中存在对流层延迟以及电离层延迟,故称之为伪距。
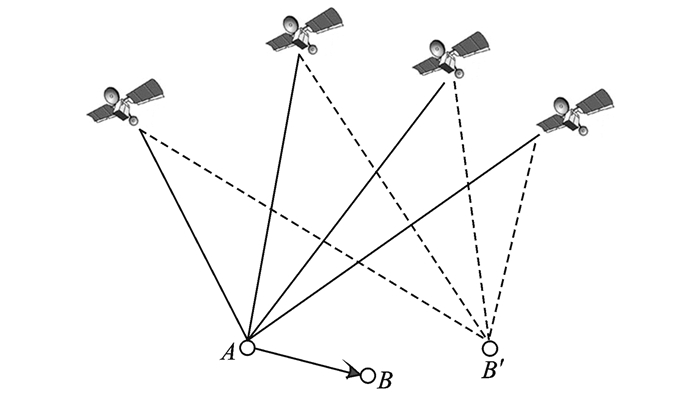
图 1中,A为欺骗设备,B为目标无人机。A接收到真实的卫星信号后,根据A与B的相对位置以及期望B被欺骗到的位置计算出各卫星支路变化的时延,随后A将调整后的卫星信号加大功率转发给B,令B定位到错误位置B′。设欺骗设备A的坐标为(xA, yA, zA),目标接收机B的坐标为(xB, yB, zB),欺骗位置B′的坐标为(xB′, yB′, zB′),第i颗卫星的坐标为(xi, yi, zi),那么第i颗卫星到A的伪距[16]可以表示为
|
图 1 GPS欺骗干扰示意图 Figure 1 Schematic of GPS deception jamming |
| $ \begin{array}{l} P_i^A = \sqrt {{{\left( {{x_i}-{x_A}} \right)}^2} + {{\left( {{y_i}-{y_A}} \right)}^2} + {{\left( {{y_i}-{y_A}} \right)}^2}} + \\ \;\;\;\;\;\;\;\;\;\;c\left( {{\rm{d}}{t_i} - {\rm{d}}{t_A}} \right) + {T_i} + {I_i} + {e_i} \end{array} $ | (1) |
式中:dti,dtA分别为卫星和欺骗设备的时钟偏移,Ti为对流层延迟,Ii为电离层延迟,ei表示伪距的观测误差。
同理,第i颗卫星到B以及预期欺骗位置B′的伪距可以表示为
| $ \begin{array}{l} P_i^B = \sqrt {{{\left( {{x_i}-{x_B}} \right)}^2} + {{\left( {{y_i}-{y_B}} \right)}^2} + {{\left( {{y_i}-{y_B}} \right)}^2}} + \\ \;\;\;\;\;\;\;\;\;\;c\left( {{\rm{d}}{t_i} - {\rm{d}}{t_B}} \right) + {T_i} + {I_i} \end{array} $ | (2) |
| $ \begin{array}{l} P_i^{B'} = \sqrt {{{\left( {{x_i}-{x_{B'}}} \right)}^2} + {{\left( {{y_i}-{y_{B'}}} \right)}^2} + {{\left( {{y_i}-{y_{B'}}} \right)}^2}} + \\ \;\;\;\;\;\;\;\;\;\;c\left( {{\rm{d}}{t_i} - {\rm{d}}{t_{B'}}} \right) + {T_i} + {I_i} \end{array} $ | (3) |
根据GPS伪距定位原理可知,改变伪距可以使GPS接收机定位到错误位置。若使B定位到B′,则通过A转发各支路卫星信号所需的时延为
| $ \begin{array}{l} \Delta {t_i} = \left( {P_i^B-P_i^{B'}-{P_{AB}}} \right)/c = \\ \;\;\;\;\;\;\;\;\left( {\sqrt {{{\left( {{x_i}-{x_B}} \right)}^2} + {{\left( {{y_i} - {y_B}} \right)}^2} + {{\left( {{y_i} - {y_B}} \right)}^2}} - } \right.\\ \;\;\;\;\;\;\;\;\sqrt {{{\left( {{x_i} - {x_{B'}}} \right)}^2} + {{\left( {{y_i} - {y_{B'}}} \right)}^2} + {{\left( {{y_i} - {y_{B'}}} \right)}^2}} - \\ \;\;\;\;\;\;\;\;\left. {\sqrt {{{\left( {{x_A} - {x_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2} + {{\left( {{y_A} - {y_B}} \right)}^2}} } \right)/\\ \;\;\;\;\;\;\;\;c - {\rm{d}}{t_B} + {\rm{d}}{t_{B'}} \end{array} $ | (4) |
式中dtB和dtB′作为各位星公共误差不对定位结果产生影响。由于实际应用中时延应为正,取tp=max(Δti),则经由A发送到B的最终信号时延为Δti=Δti+tp。
除位置欺骗之外,还需考虑对无人机的速度欺骗[17]。设真实信号的载波相位为ϕ,欺骗信号的载波相位为ϕs,则欺骗前后的速度偏差映射到多普勒频移上可以表示为
| $ \Delta {f_D} \buildrel \Delta \over = \left( {\phi-{\phi _s}} \right)/2{\rm{\pi }} $ | (5) |
设第i颗卫星速度为
| $ \begin{array}{l} {e_{ix}} = \left( {{x_i}-{x_A}} \right)/{r_{iA}}\\ {e_{iy}} = \left( {{y_i}-{y_A}} \right)/{r_{iA}}\\ {e_{iz}} = \left( {{z_i}-{z_A}} \right)/{r_{iA}} \end{array} $ | (6) |
式中riA为卫星到A的几何距离。采用高精度时钟A点接收机钟漂可忽略不计,则A点多普勒频率为
| $ f_D^{Ai} = \left[{{e_{ix}}\;\;{e_{iy}}\;\;{e_{iz}}} \right]\left[\begin{array}{l} v_x^i\\ v_y^i\\ v_z^i \end{array} \right] -{\rm{d}}{f^i} $ | (7) |
设雷达跟踪到的无人机位置为(xB, yB, zB),速度为(vBx, vBy, vBz),预期欺骗的速度变化量为(Δvx, Δvy, Δvz),则欺骗后B′相对于卫星的多普勒频率为
| $ f_D^{B'i} = \left[{{e_{ix}}'\;\;{e_{iy}}'\;\;{e_{iz}}'} \right]\left[\begin{array}{l} v_x^i-\left( {{v_{Bx}} + \Delta {v_x}} \right)\\ v_y^i-\left( {{v_{By}} + \Delta {v_y}} \right)\\ v_z^i-\left( {{v_{Bz}} + \Delta {v_z}} \right) \end{array} \right] -{\rm{d}}{f^i} $ | (8) |
则A需要调整的多普勒频率为:
通过调整欺骗信号的码相位以及载波相位使其与真实信号一致,控制无人机GPS接收机的跟踪环路[18],这是对无人机实行轨迹欺骗的第一步。接下来要在跟踪环路更新时间间隔和限定带宽下,考虑对无人机导航系统的控制。
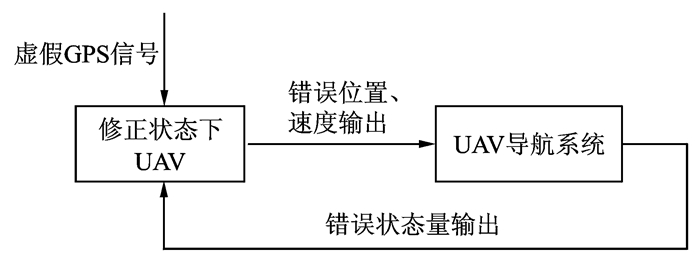
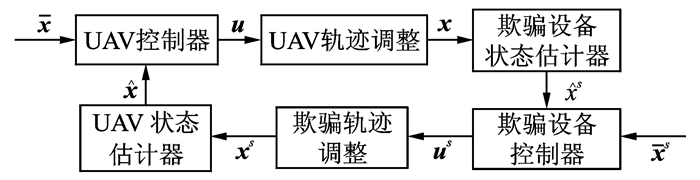
利用无人机需要GPS测量值对惯导进行修正的特点,可向目标无人机发送虚假GPS信号,使其定位到错误位置,输出错误状态量,以此实现对无人机导航系统的控制。GPS引导的导航系统控制框图见图 2。虚假GPS信号多普勒偏移和码相位偏移的调整方法已在第1节作了说明,下面主要考虑导航系统的建模分析。无人机与欺骗设备的导航系统主要由控制器和状态估计器构成。两者控制器都采用比例微分(Proportion differentiation, P D)补偿器,UAV状态估计器采用变维卡尔曼算法(Variable dimension of Kalman filtering algorithm, VD-Kalman filtering algorithm)[19]实现对航迹的跟踪,欺骗设备采用二阶伪贝叶斯估计量引导下的卡尔曼滤波实现对UAV位置速度的跟踪。控制UAV导航系统的整体框图如图 3所示。
|
图 2 导航系统控制框图 Figure 2 Block diagram of navigation system control |
|
图 3 轨迹欺骗框图 Figure 3 Overall diagram of the design |
图 3中,
UAV通常不是匀速飞行,有非机动(常速)和机动(加速)两个状态。当UAV匀速运动时,处于非机动模式下,系统模型如下
| $ \mathit{\boldsymbol{X}}\left( k \right) = \mathit{\boldsymbol{AX}}\left( {k-1} \right) + \mathit{\boldsymbol{BU}}\left( {k-1} \right) $ | (9) |
式中:X(k)=[x(k) Vx(k) y(k) Vy(k)]T,A为状态转移矩阵,B为控制矩阵,U(k)为过程噪声,U(k)=[Ux(k) Uy(k)]T,E[U(k)]=0,E[U(k)UT(j)]=Qδkj。
测量模型为
| $ \mathit{\boldsymbol{Z}}\left( k \right) = \mathit{\boldsymbol{HX}}\left( k \right) + \mathit{\boldsymbol{V}}\left( k \right) $ | (10) |
式中:
当UAV变速运动时,处于机动模式,系统模型如下
| $ {\mathit{\boldsymbol{X}}^m}\left( k \right) = {\mathit{\boldsymbol{A}}^m}{\mathit{\boldsymbol{X}}^m}\left( {k-1} \right) + {\mathit{\boldsymbol{B}}^m}{\mathit{\boldsymbol{U}}^m}\left( {k-1} \right) $ | (11) |
式中:
观测模型与非机动模式下相同,H矩阵变为Hm
| $ {\mathit{\boldsymbol{H}}^m} = \left[{\begin{array}{*{20}{l}} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 \end{array}} \right] $ |
根据UAV的运动状态,图 3中的UAV状态估计器采用VD卡尔曼算法。VD卡尔曼算法采用两种模型,即非机动模型和机动模型,无机动时滤波器工作于正常模式(低阶模型),用一机动检测器监视机动,一旦检测到机动,立即增加状态变量维数,用机动模型跟踪直至下一次判决而退回到非机动模型。
一般的卡尔曼滤波算法可以描述如下
| $ \mathit{\boldsymbol{\hat X}}\left( {k/k-1} \right) = \mathit{\boldsymbol{A\hat X}}\left( {k-1/k-1} \right) + \mathit{\boldsymbol{BU}}\left( {k - 1} \right) $ | (12a) |
| $ \mathit{\boldsymbol{P}}\left( {k/k-1} \right) = \mathit{\boldsymbol{AP}}\left( {k-1/k-1} \right){\mathit{\boldsymbol{A}}^{\rm{T}}} + \mathit{\boldsymbol{GQ}}\left( {k - 1} \right){\mathit{\boldsymbol{G}}^{\rm{T}}} $ | (12b) |
| $ \mathit{\boldsymbol{K}}\left( k \right) = \mathit{\boldsymbol{P}}\left( {k/k - 1} \right){\mathit{\boldsymbol{H}}^{\rm{T}}}{\left[ {\mathit{\boldsymbol{HP}}\left( {k/k - 1} \right){\mathit{\boldsymbol{H}}^{\rm{T}}} + \mathit{\boldsymbol{R}}} \right]^{ - 1}} $ | (12c) |
| $ \mathit{\boldsymbol{\hat X}}\left( {k/k} \right) = \mathit{\boldsymbol{\hat X}}\left( {k/k- 1} \right) + \mathit{\boldsymbol{K}}\left( k \right)\left[{\mathit{\boldsymbol{Z}}\left( k \right)-\mathit{\boldsymbol{HX}}\left( {k/k-1} \right)} \right] $ | (12d) |
| $ \mathit{\boldsymbol{P}}\left( {k/k} \right) = \mathit{\boldsymbol{P}}\left( {k/k-1} \right)-\mathit{\boldsymbol{K}}\left( k \right)\mathit{\boldsymbol{HP}}\left( {k/k-1} \right) $ | (12e) |
式(12a, 12b)为卡尔曼滤波的预测阶段,其中式(12a)为状态转移公式,表示如何从上一时刻状态推测出当前状态,式(12b)为协方差更新公式。式(12c~12e)为卡尔曼滤波的修正阶段,其中式(12c)中的K为卡尔曼系数,用来计算预测协方差占总误差(预测协方差与测量协方差之和)的比重,其值越大,表示真值接近测量值的概率越大,反之亦然。最后利用K以及式(12d, 12e)完成状态量和协方差的修正,得到卡尔曼滤波器的输出。
VD卡尔曼算法的实现流程如图 4所示。图 4涉及到的一个关键环节是机动检测问题。滤波器开始工作于正常模式,其输出的新息序列为v(k),S(k)是v(k)的协方差矩阵,令

|
图 4 VD卡尔曼滤波算法流程图 Figure 4 VD-Kalman filtering algorithm flow chart |
| $ \begin{array}{l} \mu \left( k \right) = \alpha \mu \left( {k-1} \right) + \delta \left( k \right)\\ \delta \left( k \right) = {\mathit{\boldsymbol{v}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{S}}^{-1}}\left( k \right)\mathit{\boldsymbol{v}}\left( k \right) \end{array} $ | (13) |
取Δ=(1-α)-1作为检测机动的有效窗口长度,机动检测的方法为:
如果μ(k)≥Th,则认为目标在k-Δ-1开始有一恒定的加速度加入,这时目标模型应由低阶模型转向高阶模型。引入计数量m,其初始值为0,机动模式每运行一次,m值加1,保证UAV进入机动模式后,至少运行Δ次。
由高阶机动模型退回低阶非机动模型的检测方法是检测加速度估计值是否有统计显著性意义,即一定时间范围内的加速度估计值差异是否显著。令
| $ \begin{array}{l} {\mu _a}\left( k \right) = \sum\limits_{j- \Delta- 1}^k {{\delta _a}\left( j \right)} \\ {\delta _a}\left( k \right) = {{\mathit{\boldsymbol{\hat a}}}^{\rm{T}}}\left( {k/k} \right){\left[{\mathit{\boldsymbol{P}}_a^m\left( {k/k} \right)} \right]^{ -1}}\mathit{\boldsymbol{\hat a}}\left( {k/k} \right) \end{array} $ | (14) |
式中:
μa(k) < Ta
则加速度估计无显著性意义,滤波器退出机动模型。
图 3中的欺骗设备的状态估计器采用二阶伪贝叶斯估计(Generalized pseudo-Bayesian estimator of the second order, GPB2) 引导下的卡尔曼滤波算法。欺骗设备认为UAV有两种工作模式:(1) 非机动模式,这一阶段无加速度,只存在高斯白噪声;(2) 机动模式,这一阶段由加速度激励,可视为维纳过程。GPB2使用这两种模式进行概率融合来综合反映UAV的运动情况,以完成对轨迹的正确跟踪。
对于式(9~11) 描述的线性离散系统,k时刻的似然函数为
| $ \begin{array}{l} p\left( {\mathit{\boldsymbol{z}}\left( k \right)\left| {\mathit{\boldsymbol{x}}\left( k \right)} \right.} \right) = \exp \left[{-\frac{1}{2}\left( {\mathit{\boldsymbol{z}}\left( k \right)} \right.-} \right.\\ \;\;\;\;\;\;\left. {{{\left. {\mathit{\boldsymbol{Hx}}\left( k \right)} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}}-1\left( {\mathit{\boldsymbol{z}}\left( k \right) - \mathit{\boldsymbol{H}}x\left( k \right)} \right)} \right]/\sqrt {2{\rm{ \mathsf{ π} det}}\left( \mathit{\boldsymbol{P}} \right)} \end{array} $ | (15) |
式(15) 中P为似然函数的协方差,可表示为
| $ \begin{array}{l} \mathit{\boldsymbol{P}} = Cov\left( {\mathit{\boldsymbol{z}}\left( k \right)\left| {\mathit{\boldsymbol{x}}\left( k \right)} \right.} \right) = Cov\left( {\mathit{\boldsymbol{Hx}}\left( k \right) + \mathit{\boldsymbol{v}}\left( k \right)} \right) = \\ \;\;\;\;\mathit{\boldsymbol{HP}}\left( {k\left| {k-1} \right.} \right){\mathit{\boldsymbol{H}}^{\rm{T}}} + \mathit{\boldsymbol{R}} \end{array} $ | (16) |
令非机动及机动情况下使用传统卡尔曼滤波的似然函数分别为λ11 和λ21 ,使用增维卡尔曼滤波的似然函数分别为λ12 和λ22 。采用传统卡尔曼滤波和增维卡尔曼滤波的概率分别为m1和m2 (初始值都为0.5)。由于实际情况中,卡尔曼滤波器的工作模式选择存在误差,因此令传统卡尔曼滤波对应非机动及机动情况的概率设为0.95和0.05,增维卡尔曼滤波对应非机动及机动情况的概率设为0.05和0.95。则k时刻不同情况下的后验概率分别为
| $ \begin{array}{l} p\left( {{\mathit{\boldsymbol{x}}_{11}}\left( k \right)\left| {\mathit{\boldsymbol{z}}\left( k \right)} \right.} \right) = 0.95{\lambda _{11}}{m_1}\\ p\left( {{\mathit{\boldsymbol{x}}_{21}}\left( k \right)\left| {\mathit{\boldsymbol{z}}\left( k \right)} \right.} \right) = 0.05{\lambda _{21}}{m_1} \end{array} $ | (17) |
| $ \begin{array}{l} p\left( {{\mathit{\boldsymbol{x}}_{12}}\left( k \right)\left| {\mathit{\boldsymbol{z}}\left( k \right)} \right.} \right) = 0.05{\lambda _{12}}{m_2}\\ p\left( {{\mathit{\boldsymbol{x}}_{22}}\left( k \right)\left| {\mathit{\boldsymbol{z}}\left( k \right)} \right.} \right) = 0.95{\lambda _{22}}{m_2} \end{array} $ | (18) |
进行数据融合后得到非机动以及机动模式下的状态量x(k)和xVD(k)分别为
| $ \begin{array}{l} \mathit{\boldsymbol{x}}\left( k \right) = p\left( {{\mathit{\boldsymbol{x}}_{11}}\left( k \right)\left| {\mathit{\boldsymbol{z}}\left( k \right)} \right.} \right){\mathit{\boldsymbol{x}}_{11}}\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;p\left( {{\mathit{\boldsymbol{x}}_{21}}\left( k \right)\left| {\mathit{\boldsymbol{z}}\left( k \right)} \right.} \right){\mathit{\boldsymbol{x}}_{21}}\left( k \right) \end{array} $ | (19) |
| $ \begin{array}{l} {\mathit{\boldsymbol{x}}_{VD}}\left( k \right) = p\left( {{\mathit{\boldsymbol{x}}_{12}}\left( k \right)\left| {\mathit{\boldsymbol{z}}\left( k \right)} \right.} \right){\mathit{\boldsymbol{x}}_{12}}\left( k \right) + \\ \;\;\;\;\;\;\;\;\;\;p\left( {{\mathit{\boldsymbol{x}}_{22}}\left( k \right)\left| {\mathit{\boldsymbol{z}}\left( k \right)} \right.} \right){\mathit{\boldsymbol{x}}_{22}}\left( k \right) \end{array} $ | (20) |
最后,对m1和m2进行更新,令
| $ \begin{array}{l} {c_1} = 0.95{\lambda _{11}}{m_1} + 0.05{\lambda _{21}}{m_1}\\ {c_2} = 0.05{\lambda _{12}}{m_2} + 0.95{\lambda _{22}}{m_2} \end{array} $ | (21) |
可得:m1=c1/(c1+c2),m2=c2/(c1+c2)。最终估计器的状态量输出为
| $ {\mathit{\boldsymbol{x}}_{{\rm{out}}}}\left( k \right) = {m_1}\mathit{\boldsymbol{x}}\left( k \right) + {m_2}{\mathit{\boldsymbol{x}}_{VD}}\left( k \right) $ | (12) |
根据以上分析,欺骗设备以伪贝叶斯估计为基础,可完成UAV两种运动模式下的轨迹跟踪。
此外,需要考虑欺骗的隐蔽性问题。在这里引入归一化新息平方(Normalized innovation squared, NIS)[20],定义为
| $ {\rm{NIS}}\left( k \right) = {\left( {\mathit{\boldsymbol{z}}\left( k \right)-\mathit{\boldsymbol{Hx-}}\left( k \right)} \right)^{\rm{T}}}\mathit{\boldsymbol{S}}{\left( k \right)^{-1}}\left( {\mathit{\boldsymbol{z}}\left( k \right) - \mathit{\boldsymbol{Hx}}\left( k \right)} \right) $ | (23) |
式中:z(k)为k时刻UAV的观测值;Hx(k)为卡尔曼滤波过程中根据k-1时刻及其过去时刻对k时刻观测值的预测;z(k)-Hx(k)即为k时刻观测值提供的新息;S(k)为预测误差协方差矩阵,可表示为
| $ \mathit{\boldsymbol{S}}\left( k \right) = \mathit{\boldsymbol{HP}}\left( {k\left| {k-1} \right.} \right){\mathit{\boldsymbol{H}}^{\rm{T}}} + \mathit{\boldsymbol{R}} $ | (24) |
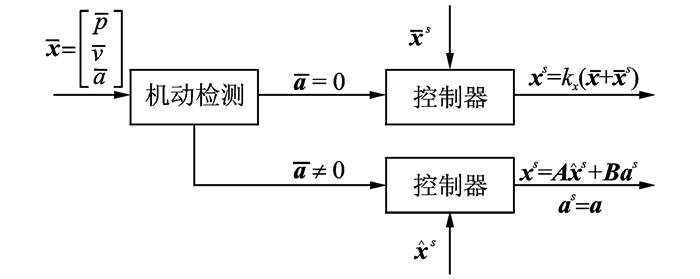
NIS用于导航系统的创新检测,当NIS大于设定的门限值时,则认为导航系统受到干扰。根据以上关于NIS的分析,考虑利用轨迹融合的方法进行欺骗干扰,其目的是令欺骗设备的加速度a与UAV加速度as达到匹配。当检测到UAV加速度为0时,欺骗设备跟踪并改变UAV轨迹的常速部分,欺骗轨迹为
|
图 5 改进后的欺骗设备控制模块 Figure 5 Improved controller of jammer |
3 仿真验证
假设目标UAV飞行起点在(0, 0) 处,在0~400 s沿y轴作匀速直线运动,此时得速度为-15 m/s;在t=400~600 s向x轴方向做90°慢转弯,加速度为ax=ay=0.075 m/s2,完成慢转弯后加速度将降为0,此时vx=15 m/s,vy=0 m/s;而后沿x轴作匀速直线运动;从t=610 s开始向y轴负方向作90°的快转弯,加速度为ax=ay=-0.3 m/s2,转弯结束后加速度降至0,此时,vx=0 m/s,vy=-15 m/s;660~800 s开始沿y轴做匀速直线运动。欺骗设备的预设轨迹为匀速运动,起点在(0, 0) 处,vx=2.5 m/s,vy=-15 m/s。设UAV与欺骗设备的x和y的观测标准差均为100 m。雷达扫描周期T=2 s,UAV控制器的参数Ku=1,轨迹调整模块参数G=0.6,欺骗设备控制器参数Ks=1,Gs=0.01。
采用直接欺骗,UAV受欺骗前后轨迹如图 6所示。
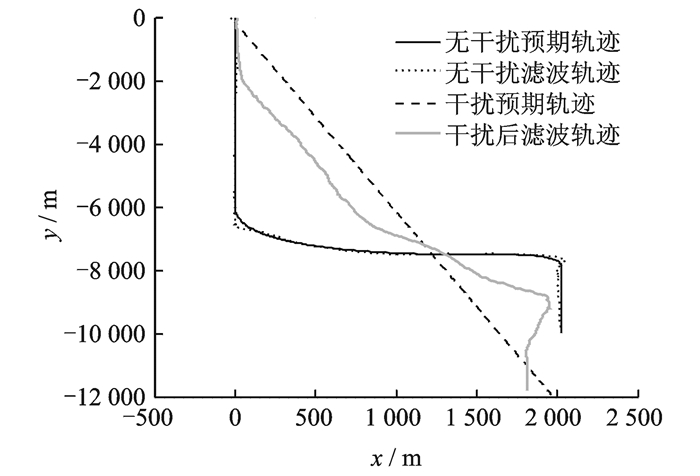
|
图 6 欺骗前后UAV轨迹图 Figure 6 UAV trajectory output with improved interference strategy |
由图 6知,欺骗设备可将UAV轨迹向预设轨迹诱导,但是UAV输出与欺骗设备预设轨迹偏差较大。可利用本文第2节的NIS分析轨迹干扰是否隐蔽。
根据仿真条件可知,NIS是一个自由度为2的χ2分布,由χ2分布表可知,自由度为2的99%(α=0.01) 的置信区间为[0, 9.21]。图 7为直接欺骗时UAV的NIS输出,以9.21为门限,由图 7可知,NIS已大于门限,UAV认为导航系统已受干扰,会触发警报导致欺骗无效。
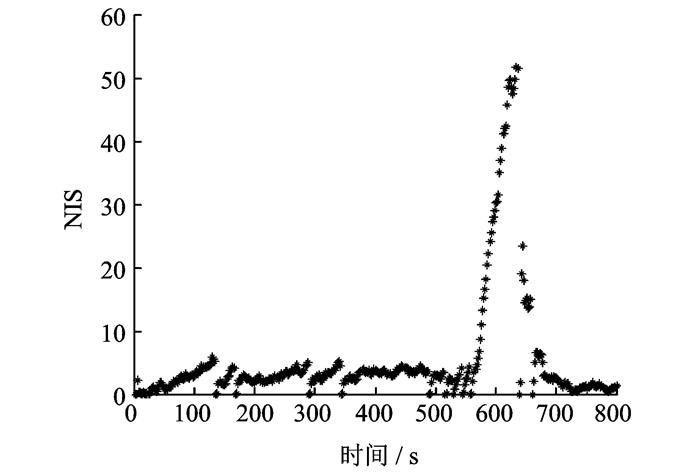
|
图 7 直接欺骗时UAV的NIS输出 Figure 7 NIS with direct track deception |
利用MATLAB画图工具中的Data Statistics对图 7中NIS进行数值分析,统计结果如表 1所示。由于NIS为归一化数值,因此数值统计结果无单位,下同。
| 表 1 直接欺骗时NIS数值统计 Table 1 Data statistics of NIS with the direct track deception |
针对直接欺骗存在的问题,利用本文第2节提出的轨迹融合进行改进。kx取0.5,UAV处于非机动模式时,欺骗轨迹为沿y轴做匀速运动,速度为-35 m/s。得到的UAV轨迹图以及NIS值如图 8,9所示。图 9中NIS的数值分析结果如表 2所示。由表 2知,NIS最大值为6.90,小于9.21,因此可躲避UAV导航系统的反干扰检测,达到轨迹欺骗的目的。
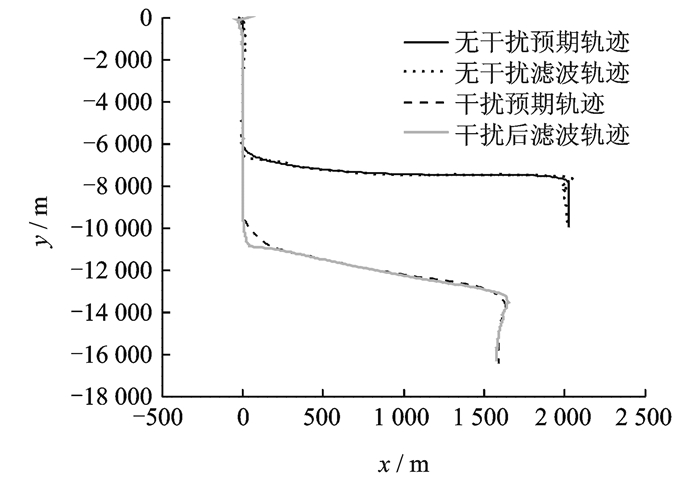
|
图 8 干扰策略改进后UAV轨迹输出 Figure 8 UAV trajectory output with improved interference strategy |
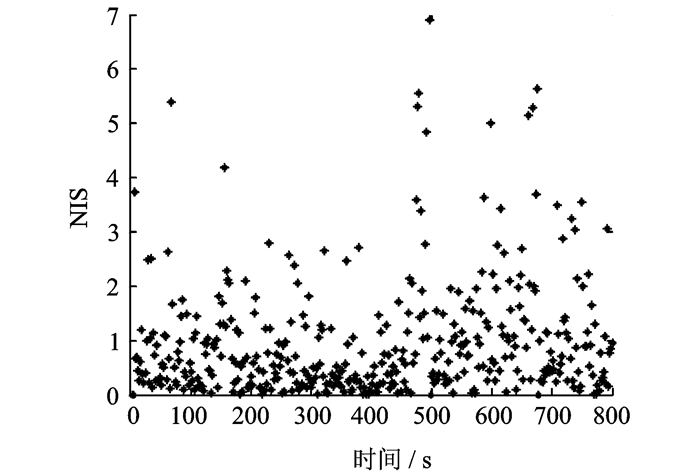
|
图 9 干扰策略改进后UAV的NIS输出 Figure 9 NIS with improved interference strategy |
| 表 2 轨迹融合欺骗时NIS数值统计 Table 2 Data statistics of NIS with the track fusion de ception |
下面考虑提高UAV的速度与加速度值,假设目标UAV起点在(0, 0) 处,在0~400 s沿y轴作匀速直线运动,速度为-50 m/s;在t=400~600 s向x轴方向做90°慢转弯,加速度为ax=ay=0.25 m/s2,完成慢转弯后加速度将降为0,此时vx=50 m/s,vy=0 m/s;而后沿x轴作匀速直线运动;从t=610 s开始向y轴负方向作90°的快转弯,加速度为ax=ay=-1 m/s2,转弯结束后加速度降至0,此时,vx=-10 m/s,vy=-50 m/s;660~800 s开始以vx =-10 m/s,vy=-50 m/s的速度做匀速直线运动。采用轨迹融合的方法,kx取0.5,UAV处于非机动模式时,欺骗轨迹为沿y轴做匀速运动,速度为-87.5 m/s。设UAV与欺骗设备的x和y的观测标准差均为100 m。雷达扫描周期T=2 s,UAV控制器的参数Ku=1,轨迹调整模块参数G=0.6,欺骗设备控制器参数Ks=1,Gs=0.01。UAV受欺骗前后轨迹图以及NIS值如图 10,11所示。图 11中NIS的数值分析结果如表 3所示。
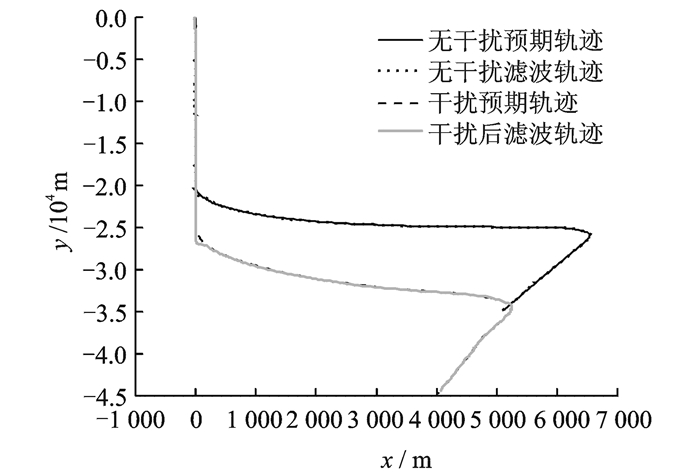
|
图 10 提高UAV速度与加速度后受干扰前后轨迹图 Figure 10 UAV trajectory output with improved velocity and acceleration |
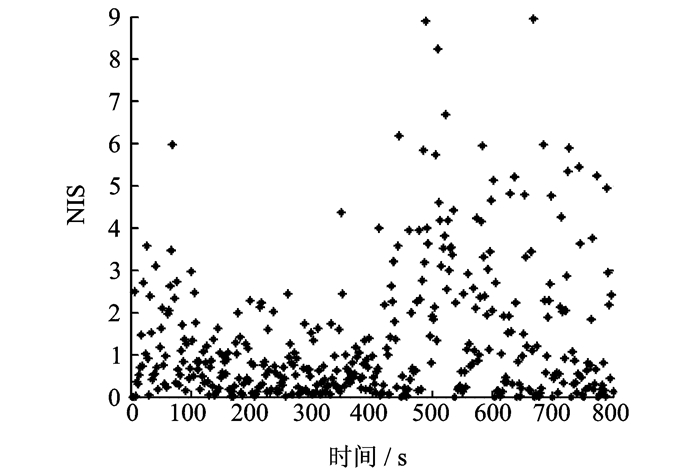
|
图 11 提高UAV速度与加速度后UAV的NIS输出 Figure 11 NIS with improved velocity and acceleration |
| 表 3 提高UAV速度与加速度后NIS数值统计 Table 3 Data statistics of NIS with improved velocity and acceleration |
由表 3知,提高UAV的速度与加速度后,NIS最大值为8.94,小于9.21,仍可实现轨迹欺骗。对比表 2,3可知,NIS最大值由6.90增加到8.94,均方差由1.06增加到1.55,NIS输出值较之前增加,稳定程度减小。
4 结束语本文提出了对无人机实行轨迹欺骗的策略。主要思路是通过调整欺骗信号的时延以及码相位与载波相位偏移使其与真实信号一致,使其控制目标无人机的跟踪环路,在环路更新间隔内,侵入无人机导航系统,配合发送对应的GPS欺骗信号,改变无人机状态估计器的输出。仿真表明,采用直接干扰以及轨迹融合策略都可以达到无人机状态输出偏离预设值的目的,其中轨迹融合策略可有效躲避无人机导航系统的反干扰检测。此外,对于真实环境中UAV速度和加速度很大以及受扰动干扰严重的情况,还需进一步的研究,可在目标跟踪滤波算法方面继续研究。
| [1] |
韩军海, 谢玲, 陈家斌.
INS/GPS组合导航方式及应用前景[J]. 火力与指挥控制, 2002, 27(4): 66–68.
HAN Junhai, XIE Ling, CHEN Jiabin. The prospect of the integration on INS and GPS and its application[J]. Fire Control & Command Control, 2002, 27(4): 66–68. |
| [2] |
刘建业, 贾文峰, 赖际舟, 等.
微小型四旋翼飞行器多信息非线性融合导航方法及实现[J]. 南京航空航天大学学报, 2013, 45(5): 575–582.
LIU Jianye, JIA Wenfeng, LAI Jizhou, et al. Multi-information nonlinear fusion technology of micro quadrotor aircraft[J]. Journal of Nanjng University of Aeronautics & Astronautics, 2013, 45(5): 575–582. |
| [3] |
秦红磊, 柴璐璐, 丛丽.
GPS/INS超紧组合抗干扰性能分析[J]. 计算机工程与设计, 2013, 34(1): 333–337.
QIM Honglei, CHAI Lulu, CONG Li. Analysis on anti-jamming of GPS/INS ultra-tight coupled system[J]. Computer Engineering and Design, 2013, 34(1): 333–337. |
| [4] | 谢钢. GPS原理与接收机设计[M]. 北京: 电子工业出版社, 2009. |
| [5] | BACHRACH A, PRENTICE S, HE R, et al. RANGE-robust autonomous navigation in GPS-denied environments[J]. Journal of Field Robotics, 2011, 28(5): 644–666. DOI:10.1002/rob.20400 |
| [6] | SHEPARD D P, BHATTI J A, HUMPHREYS T E, et al. Evaluation of smart grid and civilian UAV vulnerability to GPS spoofing attacks[C]//ION GNSS Conference. TN, USA: Institute of Navigation, 2012:3591-3605. |
| [7] |
王伟, 陶业荣, 王国玉, 等.
GPS欺骗干扰原理研究与建模仿真[J]. 火力与指挥控制, 2009, 34(6): 115–118.
WANG Wei, TAO Yerong, WANG Guoyu, et al. Study and simulation of GPS deception jamming[J]. Fire Control & Command Control, 2009, 34(6): 115–118. |
| [8] |
齐志强.
全球定位系统的抗干扰技术研究[J]. 电子设计工程, 2011, 19(19): 112–115.
DOI:10.3969/j.issn.1674-6236.2011.19.042 QI Zhiqiang. Anti-jam technique research for GPS[J]. International Electronic Elements, 2011, 19(19): 112–115. DOI:10.3969/j.issn.1674-6236.2011.19.042 |
| [9] | AKOS D M. Who′s afraid of the spoofer? GPS/GNSS spoofing detection via automatic gain control (AGC)[J]. Navigation -Journal of The Institute of Navigation, 2012, 59(4): 281–290. |
| [10] |
陈康, 嵇成新, 颜仲新.
雷达跟踪机动目标的多模型算法研究[J]. 舰船科学技术, 2004, 26(1): 53–57.
CHEN Kang, JI Chengxin, YAN Zhongxin. The research of multiple model algorithm on radar tracking maneuvering target[J]. Ship Science and Technology, 2004, 26(1): 53–57. |
| [11] | FERRANTE J. A Kalman filter-based radar track data fusion algorithm applied to a select ICBM case[C]//IEEE Radar Conference. Philadelphia, USA: IEEE, 2004:457-462. |
| [12] |
杨柳庆, 肖前贵, 牛妍, 等.
基于渐消卡尔曼滤波器的定位系统设计[J]. 南京航空航天大学学报, 2012, 44(1): 134–138.
YANG Liuqing, XIAO Qiangui, NIU Yan, et al. Design of localization system based on reducing Kalman filter[J]. Journal of Nanjng University of Aeronautics & Astronautics, 2012, 44(1): 134–138. |
| [13] | WENDEL J, MEISTER O, SCHLAILE C, et al. An integrated GPS/MEMS-IMU navigation system for an autonomous helicopter[J]. Aerospace Science & Technology, 2006, 10(6): 527–533. |
| [14] | SHEPARD D P, HUMPHREYS T E, FANSLER A A. Evaluation of the vulnerability of phasor measurement units to GPS spoofing attacks[J]. International Journal of Critical Infrastructure Protection, 2012, 5(3): 146–153. |
| [15] |
姜洋, 张和芬, 汪精华, 等.
GPS+BDS组合的实时定轨技术[J]. 南京航空航天大学学报, 2015, 47(6): 842–847.
JIANG Yang, ZHANG Hefen, WANG Jinghua, et al. Real-time orbit determination using combined GPS+BDS systems[J]. Journal of Nanjng University of Aeronautics & Astronautics, 2015, 47(6): 842–847. |
| [16] |
BORREK, AKOSD M, BERTELSENN, 等.
软件定义的GPS和伽利略接收机[M]. 北京: 国防工业出版社, 2009.
BORRE K, AKOS D M, BERTELSEN N, et al. A software-defined GPS and Galileo receiver[M]. Beijing: National Defense Industry Press, 2009. |
| [17] |
张会锁, 高关根, 寇磊, 等.
利用轨迹诱导的欺骗式GPS干扰技术研究[J]. 弹箭与制导学报, 2013, 33(3): 149–152.
ZHANG Huisuo, GAO Guangen, KOU Lei, et al. Deceptive jamming technology of GPS based on track induction method[J]. Journal of Projectiles Rockets Missiles and Guidance, 2013, 33(3): 149–152. |
| [18] | KENDOUL F. Survey of advances in guidance, navigation, and control of unmanned rotorcraft systems[J]. Journal of Field Robotics, 2012, 29(2): 315–378. DOI:10.1002/rob.20414 |
| [19] |
陈晓荣, 陈淑芬.
变维卡尔曼滤波实现运动目标的跟踪[J]. 仪器仪表学报, 2006, 27(9): 1163–1166.
CHEN Xiaorong, CHEN Shufen. Variable dimension of Kalman filter for target tracking[J]. Chinese Journal of Scientific Instrument, 2006, 27(9): 1163–1166. |
| [20] | BAR-SHALOM Y, LI X R, KIRUBARAJAN T. Estimation with applications to tracking and navigation: theory, algorithms and software[M]. NewYork: John Wiley & Sons, 2001. |
 2017, Vol. 49
2017, Vol. 49


