随着直升机的应用越来越广泛,人们不仅仅满足于其突出的悬停、低空低速性能和良好的机动性,还希望有更高的飞行速度和航程。但由于受到前行桨叶的压缩性和后行桨叶的气流分离限制,常规直升机的最大飞行速度小于350 km/h[1]。为此,国内外直升机界长期致力于探索新的技术途径,力图发展一种既保持常规直升机的性能优势又能像固定翼飞机那样具有快速巡航飞行的新型旋翼飞行器。
共轴倾转旋翼飞行器是一款新型的转换式高速旋翼飞行器,在整个飞行过程中存在直升机模式、倾转过渡模式和固定翼飞机模式。在悬停、垂直飞行和小速度前飞状态以共轴双旋翼直升机模式飞行,经过倾转过渡模式飞行器切换至共轴螺旋桨固定翼飞机模式,并进行大速度前飞,是一种能实现高速飞行的旋翼飞行器[2]。因此,共轴倾转旋翼飞行器的关键技术之一是共轴双旋翼的空气动力学问题,在直升机模式的悬停和垂直飞行以及固定翼飞机模式,共轴双旋翼处于轴向气流中,存在两副旋翼的干扰问题;在直升机模式的小速度前飞和倾转过渡模式,不仅两副旋翼的干扰问题依然存在,而且随倾转角度和飞行状态的变化而变化,使得旋翼空气动力学问题更加复杂。
共轴双旋翼的气动问题已有很多研究[3-9],但未涉及倾转状态。最近,Leishman团队针对共轴倾转旋翼飞行器的旋翼气动问题进行了研究[10-12],文献[10]运用动量叶素理论和自由尾迹探究了直升机模式悬停和轴向飞行时的旋翼特性,但只考虑上旋翼对下旋翼的气动干扰,没有考虑下旋翼对上旋翼的气动干扰。文献[11, 12]采用文献[10]的动量叶素方法研究了共轴倾转旋翼飞行器直升机模式悬停和固定翼飞机模式飞行时的旋翼性能和优化问题。而有关共轴倾转旋翼飞行器倾转过渡模式的旋翼性能研究尚未见报道。
本文建立了一种共轴倾转旋翼飞行器直升机模式、倾转过渡模式和固定翼飞机模式的旋翼性能计算方法。该方法结合能量原理并考虑了倾转过渡状态中两副旋翼的尾流重叠问题。在对计算结果与试验数据进行比对的基础上,分析了倾转过渡状态中旋翼各性能参数的变化,探究了上下旋翼诱导速度的分布,以及上下旋翼之间的干扰面积和干扰因子的变化规律。
1 数值计算模型图 1分别为共轴倾转旋翼飞行器的直升机模式、倾转过渡模式和固定翼飞机模式。

|
图 1 共轴倾转旋翼飞行器主要飞行状态 Figure 1 Flight conditions of coaxial tilt-rotor craft |
针对直升机模式悬停和垂直飞行以及固定翼飞机模式,旋翼流场呈轴对称形式,上下旋翼间存在如图 2所示的气动干扰关系。因此,数学模型简单、计算快捷方便的轴对称干扰模型适用于此种情形下的螺旋桨和旋翼的气动性能建模,是目前常见且有效的研究手段[13-17]。
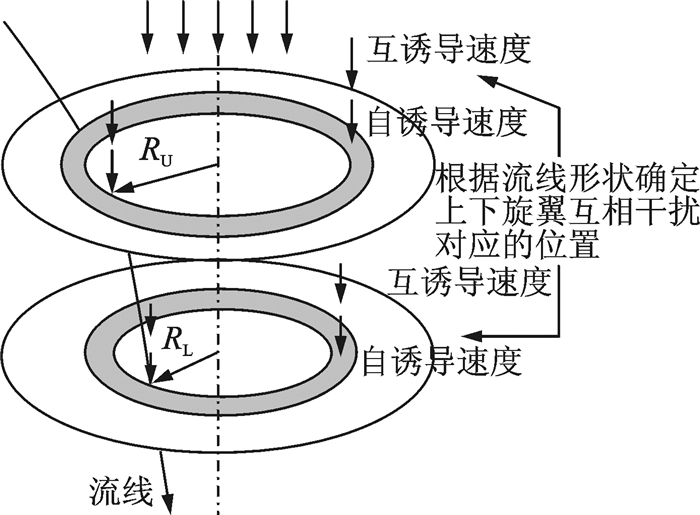
|
图 2 轴对称干扰模型 Figure 2 Axially symmetrical interference model |
但在直升机模式前飞和倾转过渡模式,来流与桨盘平面不垂直,轴对称的模型显然不再适用。如3图所示,旋翼轴倾转角δ,此时流过旋翼的气流发生倾斜,两副旋翼间的互相干扰在空间内发生变化。
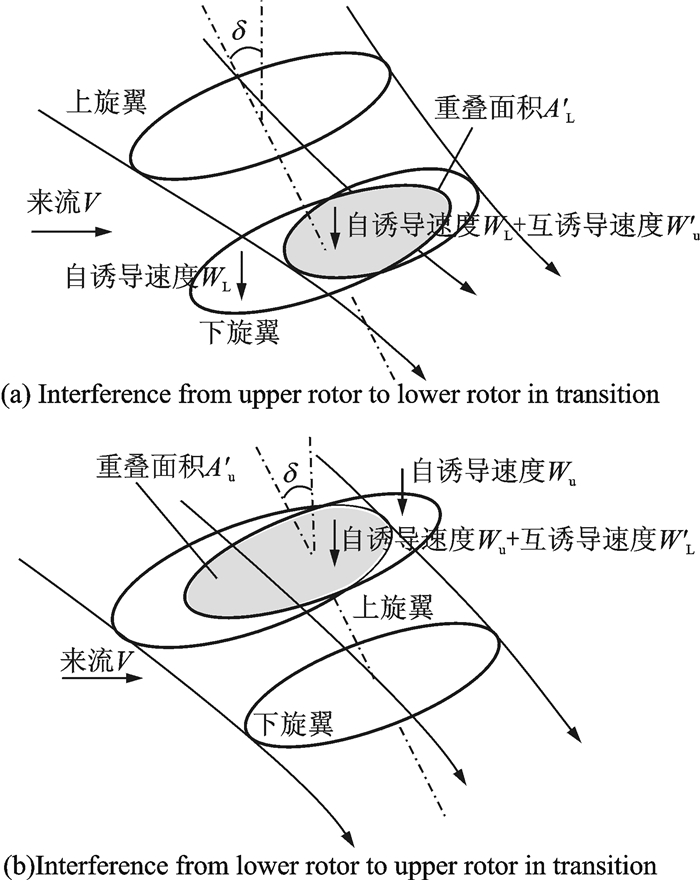
|
图 3 倾转过渡状态共轴倾转旋翼干扰模型 Figure 3 Interference model of coaxial tilt-rotors in transition |
将质量守恒定律运用到倾斜流场中,经过变形,推广得到如下能量方程
| $ {\rm{d}}\mathit{\boldsymbol{T}} = 2\rho {\rm{d}}A\left| {{\mathit{\boldsymbol{V}}_x} + {\mathit{\boldsymbol{V}}_z} + \mathit{\boldsymbol{W}}} \right|\mathit{\boldsymbol{W}} $ | (1) |
式中:T为旋翼拉力;ρ为空气密度;A为桨盘面积;Vx为自由来流平行桨盘平面的速度分量;Vz为自由来流垂直桨盘平面的速度分量;W为旋翼上的诱导速度。
因为存在尾流倾斜角χ=arctan(Vx/V⊥),使得诱导速度发生轴向变化,此时的诱导速度可表示为
| $ \mathit{\boldsymbol{W}}\left( z \right) = \mathit{\boldsymbol{W}}\left( 0 \right)\left( {1 + \frac{z}{{\sqrt {{R^2}{{\cos }^2}\chi + {z^2}} }}} \right) = \varepsilon \left( z \right)\mathit{\boldsymbol{W}}\left( 0 \right) $ | (2) |
式中:V⊥为自由来流和诱导速度在垂直桨盘平面的合速度;z为轴向位置;R为旋翼半径。
在此情况下,滑流形状会发生收缩和偏移,此时上旋翼的流线方程(用xs, ys表示)为
| $ \begin{array}{l} {x_s}\left( z \right) = {\gamma _{\rm{u}}}\left( z \right){x_{\rm{u}}} + z{\rm{tan}}{\chi _{\rm{u}}}\\ {y_s}\left( z \right) = {\gamma _{\rm{u}}}\left( z \right){y_{\rm{u}}}\\ {\gamma _{\rm{u}}}\left( z \right) = \sqrt {\frac{{{\mathit{\boldsymbol{V}}_z} + {\mathit{\boldsymbol{W}}_{\rm{u}}} + A{'_{\rm{u}}}/A\varepsilon \left( {-d} \right){\mathit{\boldsymbol{W}}_{\rm{L}}}}}{{{\mathit{\boldsymbol{V}}_z} + \varepsilon \left( z \right){\mathit{\boldsymbol{W}}_{\rm{u}}} + A{'_{\rm{u}}}/A\varepsilon \left( {z-d} \right){\mathit{\boldsymbol{W}}_{\rm{L}}}}}} \end{array} $ | (3) |
下旋翼的流线方程(用xs, ys表示)为
| $ \begin{array}{l} {x_s}\left( z \right) = {\gamma _{\rm{L}}}\left( z \right){x_{\rm{L}}} + z{\rm{tan}}{\chi _{\rm{L}}}\\ {y_s}\left( z \right) = {\gamma _{\rm{L}}}\left( z \right){y_{\rm{L}}}\\ {\gamma _{\rm{L}}}\left( z \right) = \sqrt {\frac{{{\mathit{\boldsymbol{V}}_z} + {\mathit{\boldsymbol{W}}_{\rm{L}}} + A{'_{\rm{L}}}/A\varepsilon \left( d \right){\mathit{\boldsymbol{W}}_{\rm{u}}}}}{{{\mathit{\boldsymbol{V}}_z} + \varepsilon \left( z \right){\mathit{\boldsymbol{W}}_{\rm{L}}} + A{'_{\rm{L}}}/A\varepsilon \left( {z + d} \right){\mathit{\boldsymbol{W}}_{\rm{u}}}}}} \end{array} $ | (4) |
式中:下标u, L分别表示上旋翼和下旋翼;收缩率ru(z), rL(z)由尾迹的质量守恒定律近似得到;Au,AL为上下旋翼的干扰面积,是旋翼尾流在另一副旋翼上的投影面积,可通过式(3,4) 所给出的干扰点对应关系确定,投影面积如图 3所示。
在此定义干扰因子,表征旋翼受干扰情况。既计入诱导速度发生的轴向变化,又计入尾迹收缩和偏移引起的干扰面积变化,计算公式如下
| $ \begin{array}{l} \varepsilon {'_{\rm{u}}} = A{'_{\rm{u}}}/A\varepsilon \left( {-d} \right)\\ \varepsilon {'_{\rm{L}}} = A{'_{\rm{L}}}/A\varepsilon \left( d \right) \end{array} $ | (5) |
对每副旋翼列出用平均诱导速度表示的能量方程和积分形式的叶素方程,从而求得平均诱导速度
| $ \begin{array}{l} {T_{\rm{u}}} = \frac{{N\rho }}{{4{\rm{ \mathsf{ π} }}}}\int_{{R_0}}^R {c\int_0^{2{\rm{ \mathsf{ π} }}} {U_{\rm{u}}^2{C_{\rm{L}}}\left( {{\theta _{\rm{u}}}-{\varphi _{\rm{u}}}} \right){\rm{d}}r{\rm{d}}\psi {\rm{ = }}} } \\ \;\;\;\;\;\;\;\;2\rho A{'_{\rm{u}}}\sqrt {V_x^2 + {{\left( {{\mathit{\boldsymbol{V}}_z} + {\mathit{\boldsymbol{W}}_{\rm{u}}} + \varepsilon \left( {-d} \right){\mathit{\boldsymbol{W}}_{\rm{L}}}} \right)}^2}} {\mathit{\boldsymbol{W}}_{\rm{u}}} + \\ \;\;\;\;\;\;\;\;2\rho \left( {A-A{'_{\rm{u}}}} \right)\sqrt {V_x^2 + {{\left( {{\mathit{\boldsymbol{V}}_z} + {\mathit{\boldsymbol{W}}_{\rm{u}}}} \right)}^2}} {\mathit{\boldsymbol{W}}_{\rm{u}}}\\ {T_{\rm{L}}} = \frac{{N\rho }}{{4{\rm{ \mathsf{ π} }}}}\int_{{R_0}}^R {c\int_0^{2{\rm{ \mathsf{ π} }}} {U_{\rm{L}}^2{C_{\rm{L}}}\left( {{\theta _{\rm{L}}} - {\varphi _{\rm{L}}}} \right){\rm{d}}r{\rm{d}}\psi {\rm{ = }}} } \\ \;\;\;\;\;\;\;\;2\rho A{'_{\rm{L}}}\sqrt {V_x^2 + {{\left( {{\mathit{\boldsymbol{V}}_z} + {\mathit{\boldsymbol{W}}_{\rm{L}}} + \varepsilon \left( d \right){\mathit{\boldsymbol{W}}_{\rm{u}}}} \right)}^2}} {\mathit{\boldsymbol{W}}_{\rm{L}}} + \\ \;\;\;\;\;\;\;\;2\rho \left( {A - A{'_{\rm{L}}}} \right)\sqrt {V_x^2 + {{\left( {{\mathit{\boldsymbol{V}}_z} + {\mathit{\boldsymbol{W}}_{\rm{L}}}} \right)}^2}} {\mathit{\boldsymbol{W}}_{\rm{L}}} \end{array} $ | (6) |
式中:N为桨叶片数;C为弦长;U为桨叶剖面来流速度;CL为翼型升力系数;θ为桨叶剖面安装角;φ为来流角;r为径向位置;ψ为方位角。
用迭代方法求解式(6),诱导速度分布Wu (r, φ), WL(r, φ)用平均诱导速度的谐波形式表示。诱导速度的分布可以近似用平均诱导速度变换得到[1]
| $ \begin{array}{l} {\mathit{\boldsymbol{W}}_{\rm{u}}}\left( {r, \psi } \right) = {{\bar W}_{\rm{u}}}\left( {1 + {\kappa _{X{\rm{U}}}}\hat r\cos \psi + {\kappa _{Y{\rm{U}}}}\hat r\sin \psi } \right)\\ {\mathit{\boldsymbol{W}}_{\rm{L}}}\left( {r, \psi } \right) = {{\bar W}_{\rm{L}}}\left( {1 + {\kappa _{X{\rm{L}}}}\hat r\cos \psi + {\kappa _{Y{\rm{L}}}}\hat r\sin \psi } \right) \end{array} $ | (7) |
式(7)是Drees公式,式中已经给出了诱导速度的谐波形式,其中考虑了前进比和尾迹倾斜角,对于共轴双旋翼系统,式[7]中各系数为
| $ {\kappa _{x{\rm{U}}}} = \frac{4}{3}\frac{{1-\cos {\chi _{\rm{u}}}-1.8\mu _{\rm{u}}^2}}{{\sin {\chi _{\rm{u}}}}}\;\;{\kappa _{Y{\rm{U}}}} =-2{\mu _{\rm{u}}} $ | (8) |
| $ {\kappa _{x{\rm{L}}}} = \frac{4}{3}\frac{{1-\cos {\chi _{\rm{L}}}-1.8\mu _{\rm{L}}^2}}{{\sin {\chi _{\rm{L}}}}}\;\;{\kappa _{Y{\rm{L}}}} = + 2{\mu _{\rm{L}}} $ | (9) |
式中:χ为尾迹倾斜角;μ为前进比。
经过迭代计算得到旋翼上的诱导速度,再运用式(7)计算旋翼上的载荷
| $ {T_{{\rm{u, L}}}} = \frac{N}{{2{\rm{\pi }}}}\int_0^{2{\rm{\pi }}} {\int_{{R_0}}^R {{{\left( {\frac{{{\rm{d}}L}}{{{\rm{d}}r}}\cos \varphi-\frac{{{\rm{d}}D}}{{{\rm{d}}r}}\sin \varphi } \right)}_{{\rm{u, L}}}}} } {\rm{d}}r{\rm{d}}\psi $ | (10) |
| $ {M_{{\rm{u, L}}}} = \frac{B}{{2{\rm{\pi }}}}\int_0^{2{\rm{\pi }}} {\int_{{R_0}}^R {{{\left( {\frac{{{\rm{d}}L}}{{{\rm{d}}r}}\sin \varphi-\frac{{{\rm{d}}D}}{{{\rm{d}}r}}\cos \varphi } \right)}_{{\rm{u, L}}}}} } {\rm{d}}r{\rm{d}}\psi $ | (11) |
式中:L为翼型升力;D为翼型阻力;M为扭矩。
2 结果及分析 2.1 轴流状态首先采用文献[11]的风洞试验数据检验上述方法在双旋翼轴流状态性能计算的准确性。旋翼特征参数如表 1所示[18-20]。
| 表 1 旋翼基本参数 Table 1 Basic parameter of rotor |
图 4给出了不同总距的共轴倾转旋翼轴流状态的旋翼拉力、功率及效率随着入流比的变化关系。图中的入流比高达1.0,能涵盖直升机模式垂直飞行和固定翼飞机模式的性能。由图可知,理论方法与试验结果吻合较好,表明本文的性能计算方法合理可行。
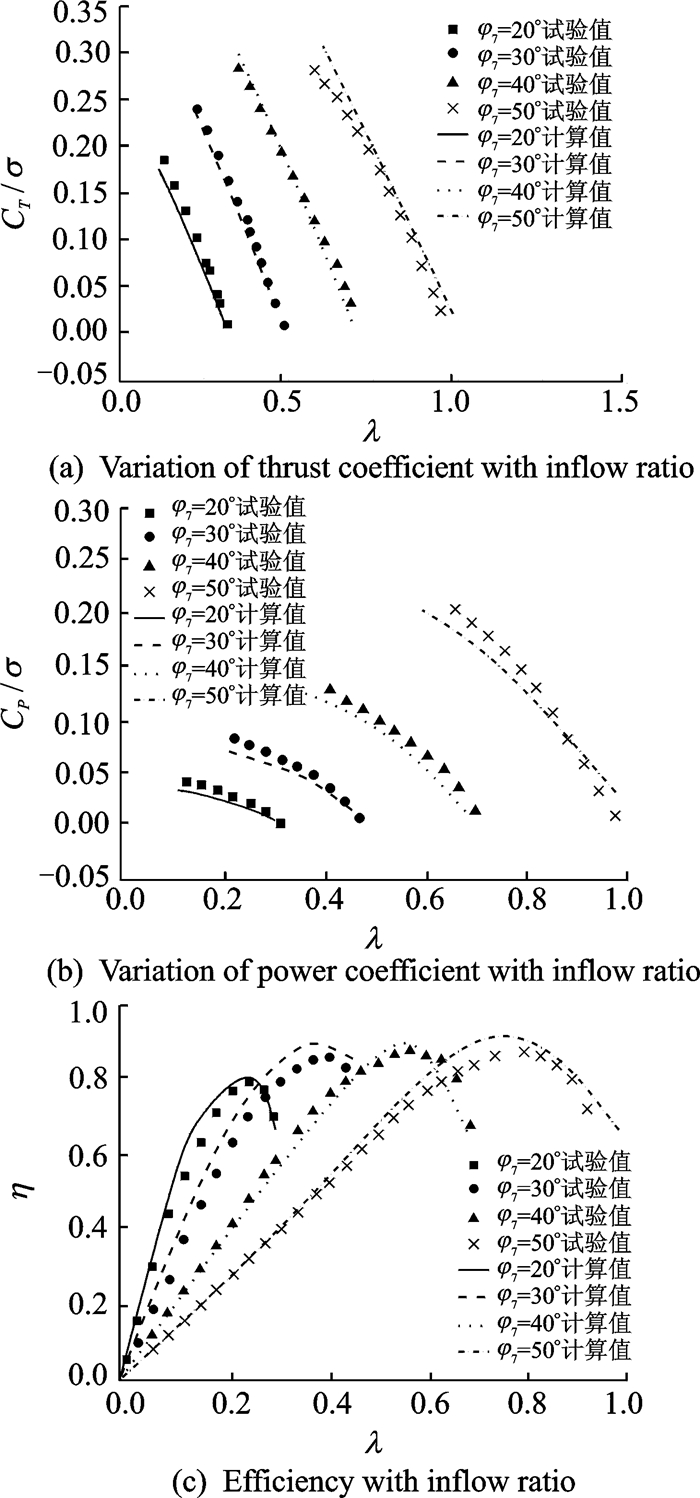
|
图 4 性能参数随入流比的变化关系 Figure 4 Variation of performance with inflow ratio |
2.2 倾转过渡状态 2.2.1 方法验证
共轴倾转旋翼在倾转过程中,桨盘平面受到与其不垂直的入流影响,两旋翼间的干扰形式和旋翼性能都会发生变化。本文假设倾转过程保持流速v不变,只改变倾转角δ,如图 5所示。
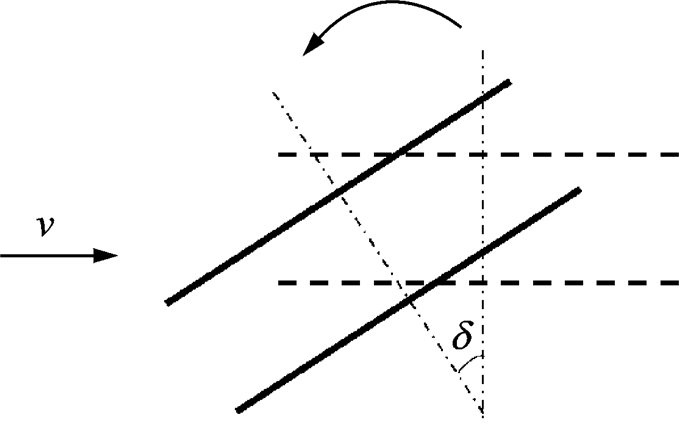
|
图 5 倾转过渡状态示意图 Figure 5 Diagram of transition condition |
由于文献[11]风洞试验并未给出有关共轴倾转旋翼飞行器倾转过渡模式的旋翼性能数据,本文采用文献[21]提供的共轴双旋翼在前飞情况下(此时入流与共轴双旋翼桨盘平面不垂直)的风洞试验数据,用于检验本文方法对于共轴倾转旋翼飞行器倾转过渡模式研究的合理性。
试验参数:半径0.38m,弦长0.06m,升力线斜率5.3,桨叶片数2~4,桨叶间距h/R=0.21,桨尖速度123.4m/s,μ=0.16。本文计算了4片及2片桨叶的单旋翼和2片桨叶的共轴双旋翼的拉力和扭矩,结果见图 6。由图可知,计算结果与试验结果吻合较好,表明本文的计算方法可用于共轴倾转旋翼飞行器倾转过渡模式的旋翼性能研究。

|
图 6 共轴双旋翼前飞状态计算结果 Figure 6 Coaxial rotor in forward flight |
2.2.2 性能
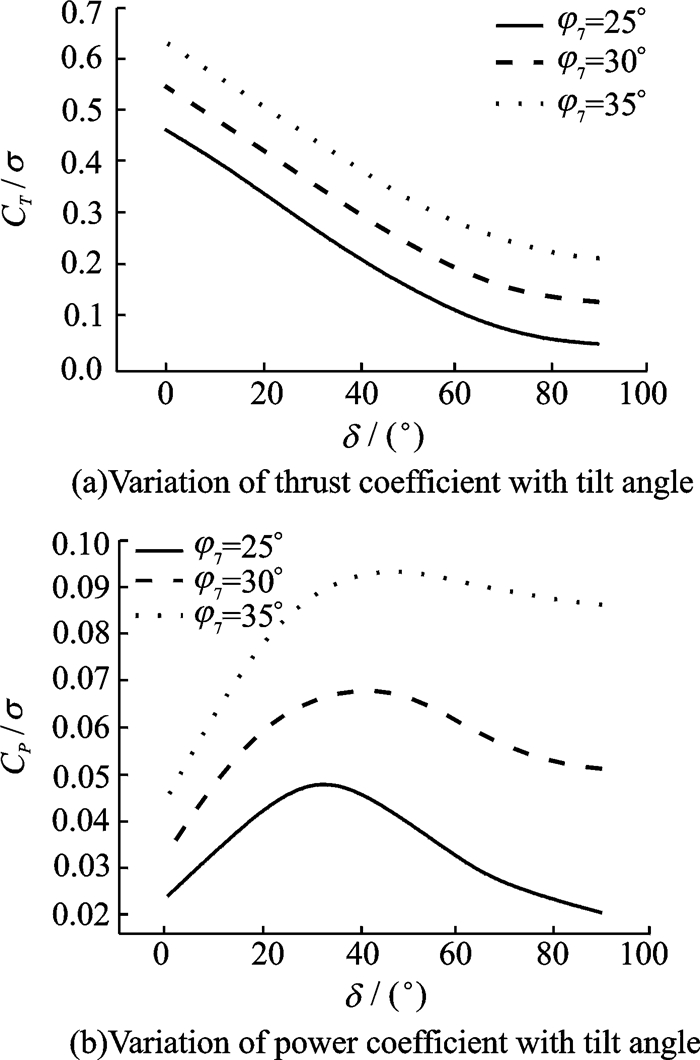
图 7给出了以表 1为例的旋翼系统流速30 m/s,总距分别为25°,30°,35°时共轴倾转旋翼的性能参数随倾转角的变化关系。可以看出,当倾转角δ增大,旋翼的拉力系数减小,功率系数先增大后减小。这是因为当倾转角增大时,桨盘的垂直速度分量增大,翼型的来流角增大,迎角减小,使得拉力系数减小。在倾转角较小时,桨盘的水平速度分量占主导,因此当倾转角增大,水平速度分量减小,旋翼诱导功率增大,导致功率系数增大。在倾转角较大时,桨盘的垂直速度分量逐渐占主导,因此随着倾转角增大,垂直速度分量增大,旋翼诱导功率减小,导致功率系数减小。
|
图 7 性能参数随倾转角的变化关系图 Figure 7 Variation of performance with tilt angle |
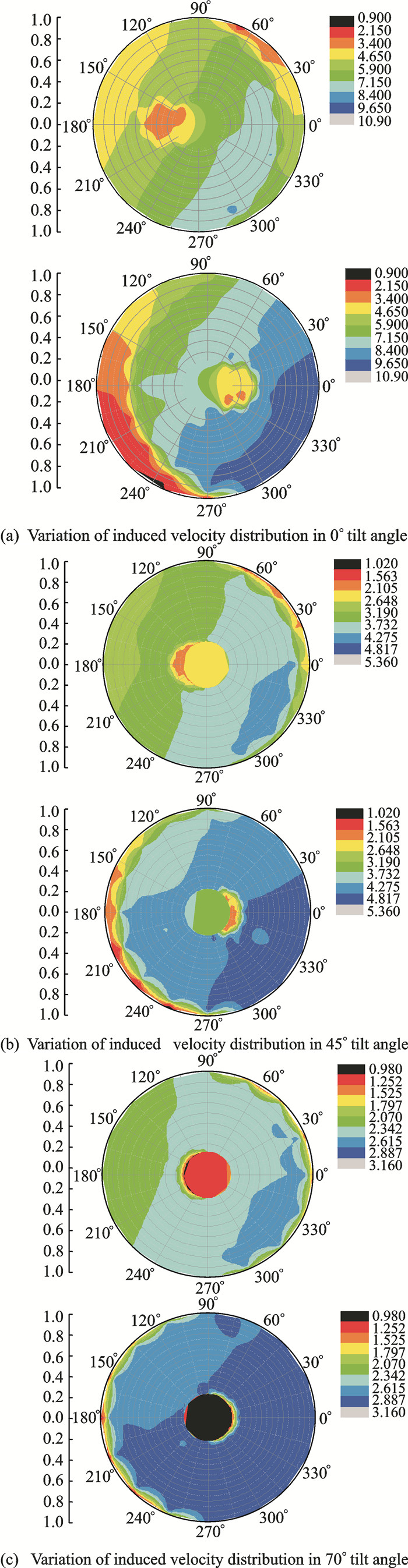
图 8给出在流速为30 m/s,总距为30°时上下旋翼的诱导速度在倾转角为0°,45°,70°时的分布情况。可以看出,在同一倾转角下,下旋翼所占大诱导速度区域面积较大,说明其受到的干扰更严重。随着倾转角增大,桨盘的水平速度分量减小,两副旋翼的诱导速度分布不均匀程度减弱;桨盘的垂直速度分量增大,两副旋翼的诱导速度减小。图中上下旋翼在圆心附近出现的诱导速度较小区域,是由于算例旋翼有根切导致的,从其变化趋势也可以看出,当倾转角增大,上旋翼的受干扰区域从180°方位角方向向圆心移动,下旋翼的受干扰区域从0°方位角方向向圆心移动。
|
图 8 双旋翼诱导速度分布随倾转角变化图 Figure 8 Variation of induced velocity distribution with tilt angle |
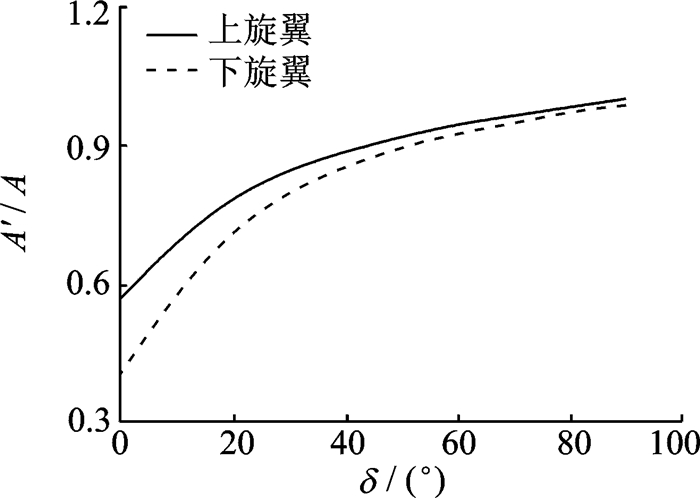
图 9给出了流速为30 m/s,总距为30°时上下旋翼受干扰面积占旋翼总面积的百分比随倾转角变化关系。可以看出,随着倾转角的增大,上下旋翼的受干扰面积都逐渐增大,且根据滑流收缩规律,下旋翼处于上旋翼尾流的收缩区,而上旋翼处于下旋翼尾流的扩张区,因此下旋翼的受干扰面积小于上旋翼。
|
图 9 干扰面积随倾转角变化关系图 Figure 9 Variation of interference area with tilt angle |
图 10给出了上下旋翼的干扰因子随倾转角变化关系。可以看出,随着倾转角增大,上下旋翼的干扰因子都增大,这说明上下旋翼之间的干扰在增强。其中,下旋翼的干扰系数始终大于上旋翼,说明下旋翼受到的干扰大于上旋翼。这是因为下旋翼处于上旋翼尾流的收缩区域,根据质量守恒定律,下旋翼的互诱导速度更大,因此虽然下旋翼受干扰的面积较小(如图 9所示),但实际上其受到的干扰更大。

|
图 10 干扰因子随倾转角变化关系图 Figure 10 Variation of interference coefficient with tilt angle |
本节用上文所述的共轴倾转旋翼性能计算模型检验了直升机模式垂直飞行和固定翼飞机模式的旋翼性能,讨论了倾转过渡状态的旋翼性能。对于直升机模式的悬停实质上是垂直飞行时速度为零的特例,直升机模式的前飞实质上是倾转过渡模式在小速度小倾转角时的特例,由于篇幅所限不再赘述。
3 结论(1) 本文建立的共轴倾转旋翼性能计算方法考虑了双旋翼间实际存在的干扰现象,适用于共轴倾转旋翼飞行器的整个飞行过程,应用该方法进行性能估算和初步参数设计是可行的;
(2) 在共轴倾转旋翼飞行器倾转的过程中,若来流速度不变,当倾转角增大,旋翼的拉力系数减小,功率系数先增大后减小;
(3) 从上下旋翼诱导速度的分布来看,下旋翼受到的干扰更大。随着倾转角的增大,旋翼诱导速度分布不均匀程度减弱且诱导速度逐渐减小。上旋翼的受干扰区域从180°方位角方向向圆心移动,下旋翼的受干扰区域从0°方向向圆心移动;
(4) 在倾转过程中,随着倾转角的增大,上下旋翼的受干扰面积都逐渐增大,下旋翼的受干扰面积小于上旋翼;上下旋翼的干扰因子逐渐增大,下旋翼的干扰因子大于上旋翼。因此,上下旋翼受干扰的程度,既与受干扰面积大小有关,还与旋翼的相对位置有关。
| [1] | WAYNE J. Helicopter theory[M]. New Jersey: Princeton University Press, 1980. |
| [2] | PREATOR R, LEISHMAN J G, BLADWIN G D.Conceptual design studies of a mono tiltrotor (MTR) architecture [C]//American Helicopter Society 60th Annual Forum Proceedings.Baltimore, MD:[ s.n.], 2004. |
| [3] |
黄水林, 李春华, 徐国华.
基于自由尾迹和升力面方法的双旋翼悬停气动干扰计算[J]. 空气动力学学报, 2007, 25(3): 390–395.
HUANG Shuilin, LI Chunhua, XU Guohua. An analytical method for aerodynamic interactions of twin rotors based upon free-vortex and lifting-surface models[J]. Journal of Aerospace Power, 2007, 25(3): 390–395. |
| [4] |
唐正飞, 李锋.
用三维激光多谱勒测速仪对共轴双旋翼悬停流场的测定[J]. 流体力学实验与测量, 1998, 12(1): 81–87.
TANG Zhengfei, LI Feng. Measurement of the coaxial-rotor flowfield in hovering using 3-D laser doppler velocimeter[J]. Experiments and Measurement in Fluid Mechanics, 1998, 12(1): 81–87. |
| [5] |
张昆. 基于CFD方法的高速直升机共轴刚性双旋翼的气动特性研究[D]. 南京: 南京航空航天大学, 2012.
ZHANG Kun.Researches on aerodynamic characteristics of rigid coaxial rotor of high-speed helicopter based on CFD method[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2012. |
| [6] |
王强, 陈铭, 王保兵, 等.
旋翼几何参数对共轴双旋翼悬停性能的影响[J]. 航空动力学报, 2014, 29(6): 1434–1443.
WANG Qiang, CHEN Ming, WANG Baobing, et al. Effect of geometric parameters of rotor on hovering performance of coaxial rotor[J]. Journey of Aerospace Power, 2014, 29(6): 1434–1443. |
| [7] |
邓彦敏, 陶然, 胡继忠.
共轴式直升机上下旋翼之间气动干扰的风洞实验研究[J]. 航空学报, 2003, 24(1): 10–14.
DENG Yanmin, TAO Ran, HU Jizhong. Experimental investigation of the aerodynamic interaction between upper and lower rotors of a coaxial helicopter[J]. Acta Aeronautica et Astronautica Sinica, 2003, 24(1): 10–14. |
| [8] | BAGAI A, LEISHMAN J G. Free-wake analysis of tandem tilt-rotor and coaxial rotor configurations[J]. Journal of the American Helicopter Society, 1996, 41(3): 196–207. DOI:10.4050/JAHS.41.196 |
| [9] | RAMASAMY M. Hover performance measurements to ward understanding aerodynamic interference in coaxial, tandem, and tilt rotors[J]. Journal of the American Helicopter Society, 2015, 60(3): 1–17. |
| [10] | LEISHMAN J G, Ananthan S.Aerodynamic optimization of a coaxial proprotor[C]//62th Annual Forum and Technology Display of the American Helicopter Society International.Phoenix, AZ:[s.n.], 2006. |
| [11] | LEISHMAN J G. Aerodynamic performance considerations in the design of a coaxial proprotor[J]. Journal of the American Helicopter Society, 2009, 54(1): 12005–12005. DOI:10.4050/JAHS.54.012005 |
| [12] | STAHLHUT C, LEISHMAN J G.Aerodynamic design optimization of proprotors for convertible-rotor concepts[C]//American Helicopter Society 68th Annual Forum Proceedings. Fort Worth, TX:[s.n.], 2012. |
| [13] | LEISHMAN J G. Principles of helicopter aerodynamics[M]. 2nd edition. Cambridge: Cambridge University Press, 2007. |
| [14] | 王适存. 直升机空气动力学[M]. 北京: 航空专业教材编审组, 1985. |
| [15] | 刘沛清. 空气螺旋桨理论及其应用[M]. 北京: 北京航空航天大学出版社, 2006. |
| [16] | VALKOV T.Aerodynamic loads computation on coaxial hingless helicopter rotors[R]. AIAA-90-0070, 1990. |
| [17] | GILLMORE K B, SCHNEIDER J J. Design considerations of the heavy lift helicopter[J]. Journal of the American Helicopter Society, 1963, 8(1): 31–37. DOI:10.4050/JAHS.8.31 |
| [18] | NAIMAN I.Method of calculating dual-rotating propellers from airfoil characteristics[R].NACA-ARR-3E24, 1943. |
| [19] | BIERMANN D, GRAY W H.Wind-tunnel tests of eightbladed single and dual rotating propellers in the tractor position[R].NACA-ARR, 1941. |
| [20] | BIERMANN D, GRAY W H, MAYNARD J D. Wind-tunnel test of single and dual rotating tract or propellers of large blade width[R].NASA-ARR, 1942. |
| [21] | SAITO S, AZUMA A.A numerical approach to coaxial rotor aerodynamics[C]//Proceedings of the 7th European Rotorcraft and Powered Lift Forum. Garmisch-Partenkirchen: Deutsche Gesellschaft für Luft-und Raumfahrt, 1981. |
 2017, Vol. 49
2017, Vol. 49


