2. 南京航空航天大学航空宇航学院,南京, 210016;
3. 南京工业大学城市建设学院,南京, 210009
2. College of Aerospace Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China;
3. College of Urban Construction, Nanjing Tech University, Nanjing, 210009, China
多股流板翅式换热器通过冷热流体资源整合,具有系统集成度高、便于管理、节约投资成本和占地面积小等优点,在航空领域有着广泛的应用前景。相比于两股流板翅式换热器,多股流板翅式换热器由于通道分配和排列不当,可能会出现温度交叉和热量内耗现象。国内外学者分别从多股流板翅式换热器传热分析、通道排列优化设计和换热性能评价等方面展开了研究。
传统的多股流板翅式换热器计算方法将所有流体分别按照吸热、放热综合,从而等效为两股流换热器。该方法将翅片效率按定值处理,忽略了翅片旁通效应可能造成的影响。Prasad[1-2]根据平行式多股流板翅式换热器翅片、隔板和流体的偏微分能量方程,探讨了多股流换热中翅片可能存在的3种温度分布形式,同时与定翅片效率的计算方法进行了对比分析,另外还提出了通道排列优化的等壁温原则。Goyal[3]基于FVM法,综合考虑了翅片横向热传导、周围环境影响因素,建立了多股流板翅式换热器二维模型,并与商业软件ASPEN MUSE计算结果对比,验证了计算方法的合理性。Ghosh[4-5]提供了一种通过轴向离散求解多股流板翅式换热器的方法,并以此模型为基础通过GA算法对3~8股流板翅式换热器进行了通道排列优化设计。Shrivastava[6-7]基于两股流换热器分析方法提出了三股流换热器6个量纲为一的参数,并建立了换热器通用数学模型,同时采用热效率的评价方法对三股流换热器的换热性能作了分析。Saeid[8]采用有限元方法分析了平行式三股流板翅式换热器的换热特性。Yuan[9]数值分析了交叉式三股流换热器3种不同通道排列方式下纵向导热对换热性能的影响。Luo[10]基于3个匹配矩阵建立了平行式流多股流板翅式换热器和换热网络的稳态数学模型,为多股流换热器和换热网络优化分析奠定了基础。Zhao[11-12]采用IMTD法建立了平行式三股流换热器数学模型,另外基于局部热负荷平衡原则和等壁温原则,采用GA算法对多股流板翅式换热器通道排列做了优化设计,Wang[13]在上述工作的基础上搭建实验台,从流体出口温度、换热量、热效率和流阻等角度分析了4种通道排列方式下的三股流换热器换热性能。Peng[14-15]以三通道子换热器为基础,采用IMTD建立了多股流板翅式换热器数学模型,通过ASPEN软件对模型进行了校核,并采用均匀、线性和半抛物线流量分配模型,以4股流36通道板翅式换热器为例,分析了物流分配不均对多股流板翅式换热器换热性能的影响。曹业玲[16]采用分布参数法对两股叉流板翅式蒸发器数学建模,获得了制冷剂两相流干度和温度场分布规律。
上述研究工作主要针对空分领域,对于多股流换热器的相变和交叉流动换热研究较少,但是机载条件下,R134a、防冻液、燃油和冲压空气是环控系统常用工质。为了匹配各股流体阻力,换热器设计布局时,常将冲压空气与其余工质交叉布置。相比于常规多股流板翅式换热器,机载多股流板翅式换热器流体间交叉流动以及R134a在换热器通道内相变流动导致其数值计算更加复杂。本文拟基于前期关于单相多股流板翅式换热器传热分析的研究成果[17],针对机载多股流板翅式换热器相变流动的特点,对其数值计算方法进行研究,并基于蒸发制冷循环试验台实验验证数值方法的合理性。
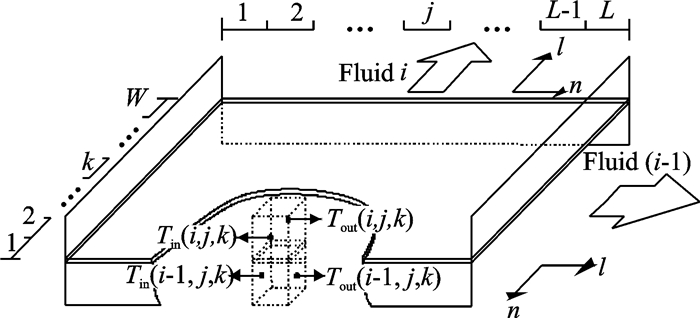
1 数值计算方法 1.1 数学模型对于多股流板翅式换热器,物理模型如图 1所示。为便于数值计算,作如下假设:(1) 通道内流体沿通道高度方向温度相等;(2) 忽略同一层流体横向热质交换以及流动方向热传导;(3) 翅片和隔板厚度方向温度相同,且翅片根部温度等于隔板温度;(4) 各股流体在通道内流量均匀分配;(5) 忽略各股流体压降对物性参数的影响;(6) 换热器与外界环境之间无热量交换。

|
图 1 板翅式换热器结构示意图 Figure 1 Structure of plate-fin heat exchanger |
多股流板翅式换热器任一通道流体温度变化受多种因素制约,翅片定性尺寸不为定值。基于上述假设,分别对流体、隔板以及翅片建立能量守恒方程,对于流体(包括相变工质),有
| $ \left\{ \begin{array}{l} {\left( {FG{c_p}} \right)_{{\rm{fluid, }}i}}{H_i}{\left( {1- f\delta } \right)_i}\frac{{{\rm{d}}{T_i}\left( l \right)}}{{{\rm{d}}l}} = {\alpha _i}{\left( {1- f\delta } \right)_i}\left[{{t_i}\left( 0 \right) + {t_i}\left( {{H_i}} \right)-2{T_i}\left( l \right)} \right] + \\ 2{f_i}{a_i}\int_0^{{H_i}} {\left[{{t_i}\left( x \right)-{T_i}\left( l \right)} \right]{\rm{d}}x\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{T_i}\left( l \right) \ne T_t^*} \\ {\left( {FG} \right)_{{\rm{fluid, }}i}}{H_i}{\left( {1 - f\delta } \right)_i}\frac{{{\rm{d}}{h_i}\left( l \right)}}{{{\rm{d}}l}} = {\alpha _i}{\left( {1 - f\delta } \right)_i}\left[{{t_i}\left( 0 \right) + {t_i}\left( {{H_i}} \right)-2{T_i}\left( l \right)} \right] + \\ 2{f_i}{a_i}\int_0^{{H_i}} {\left[{{t_i}\left( x \right)-{T_i}\left( l \right)} \right]{\rm{d}}x\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{T_i}\left( l \right) = T_t^*} \end{array} \right. $ | (1) |
式中:F表示流体间的相对流动方向(F等于1或-1);G表示质量流速;cp表示流体定压比热容;H表示翅片高度;f表示翅片密度;δ表示翅片厚度;T表示流体温度;T*表示流体相变温度;t表示翅片温度;α表示对流表面换热系数;h表示相变流体比焓;x, l分别表示流体沿翅片高度方向、流动方向的笛卡尔坐标;下标i表示通道编号,i=1, 2, …, N。
另外,式(1) 中的第1项表示流体从隔板和翅片所获得的热流量,第2项表示流体与上、下隔板之间的热流量,第3项表示流体与翅片之间的热流量。其中第3项同时等于翅片上下根部热流之差,表示为
| $ \begin{array}{l} 2{f_i}{a_i}\int_0^{{H_i}} {\left[{{t_i}\left( x \right)-{T_i}\left( l \right)} \right]{\rm{d}}x = } \\ \lambda {F_{{\rm{fin, }}i}}\frac{{{\rm{d}}{t_i}\left( {{H_i}} \right)}}{{{\rm{d}}{x_i}}} -\lambda {F_{{\rm{fin, }}i}}\frac{{{\rm{d}}{t_i}\left( 0 \right)}}{{{\rm{d}}{x_i}}} \end{array} $ | (2) |
式中:λ为换热器金属材质导热系数。对于隔板,建立能量守恒方程
| $ \begin{array}{l} - \lambda {\left( {f\delta } \right)_{{\rm{fin, }}i}}\frac{{{\rm{d}}{t_{{\rm{fin, }}i}}\left( {{H_i}} \right)}}{{{\rm{d}}x}} + \lambda {\left( {f\delta } \right)_{{\rm{fin, }}i + 1}}\frac{{{\rm{d}}{t_{{\rm{fin, }}i + 1}}\left( 0 \right)}}{{{\rm{d}}x}} + \\ \;\;{\alpha _i}{\left( {1- f\delta } \right)_{{\rm{fin, }}i}}\left[{{T_i}\left( l \right)-{t_{{\rm{fin, }}i}}\left( {{H_i}} \right)} \right] + \\ {\alpha _{i + 1}}{\left( {1 - f\delta } \right)_{{\rm{fin, }}i + 1}}\left[{{T_{i + 1}}\left( l \right)-{t_{{\rm{fin, }}i + 1}}\left( 0 \right)} \right] = 0 \end{array} $ | (3) |
式中:i=0, 1, 2, …, N,且第1, 3项分别表示第i通道翅片、流体通过隔板上端面流入隔板的热量;第2, 4项分别表示第(i+1) 通道翅片、流体通过隔板下端面流入隔板的热量。根据假设(6),换热器上下隔板绝热,上隔板(i=N)绝热时,式(3) 中第2,4项为0,下隔板(i=0) 绝热时,式(3) 中第1,3项为0。
根据假设(3),隔板上下端面温度相等,即
| $ {t_i}\left( {{H_i}} \right) = {t_{i + 1}}\left( 0 \right)\;\;\;i = 1, 2, \cdots, N-1 $ | (4) |
对于翅片,建立能量守恒方程
| $ \lambda {\delta _i}\frac{{{{\rm{d}}^2}{t_i}\left( x \right)}}{{{\rm{d}}{x^2}}} + 2{\alpha _i}\left[{{T_i}\left( l \right)-{t_i}\left( x \right)} \right] = 0 $ | (5) |
式(5) 的一般解可表示为
| $ \left\{ \begin{array}{l} {t_i} = {T_i} + {A_i}\sin {\rm{h}}\left( {{P_i}{x_i}} \right) + {B_i}\cosh \left( {{P_i}{x_i}} \right)\\ \frac{{{\rm{d}}{t_i}}}{{{\rm{d}}{x_i}}} = {P_i}\left[{{A_i}\cos {\rm{h}}\left( {{P_i}{x_i}} \right) + {B_i}\sinh \left( {{P_i}{x_i}} \right)} \right] \end{array} \right. $ | (6) |
将式(6) 代入式(1~4),将式(2) 代入式(1),经整理后式(1, 3, 4) 构成关于流体温度Ti(l)和翅片定解参数Ai, Bi共计3N个方程。将换热器划分为如图 2所示的W×L个子单元换热器,对于式(1) 中Ti(l)的一阶导数项,通过一阶中心差分离散为
|
图 2 交叉式换热器网格划分示意图 Figure 2 Subdivision of cross flow heat exchanger |
| $ \frac{{{\rm{d}}{T_i}\left( l \right)}}{{{\rm{d}}l}} = \frac{{{T_{{\rm{out}}}}\left( {i, j, k} \right)-{T_{{\rm{in}}}}\left( {i, j, k} \right)}}{{\Delta l}} $ | (7) |
当流体处于相变阶段时,假定相变流体为比热容无穷大的单相流体,则求解格式可统一为式(7),每当子单元换热器计算完毕时,通过程序设定,将下一行或列的子单元换热器的相变流体温度重置为相变温度,同时累加相变流体的热流量直至相变结束。
对于流体与隔板、翅片的对流换热定性温度,取子单元流体进出口温度的算术平均值
| $ {T_i}\left( l \right) = \frac{{{T_{{\rm{out}}}}\left( {i, j, k} \right) + {T_{{\rm{in}}}}\left( {i, j, k} \right)}}{2} $ | (8) |
综上,将各股流体的入口温度作为边界条件,可求得子单元换热器各股流体的出口温度,依次循环,采用逐行或逐列依次扫描的方式进行求解,可获得多股流板翅式换热器各层流体的温度场。当流体间逆流流动时,可假定温度初场,采用交替方向块迭代法的思想迭代计算直至逆流流体温度场收敛。
通过上述分析可知,本文所述多股流板翅式换热器数值解法尽管与传统方法相比计算效率较低,但其优点在于:充分考虑了翅片热传导的不对称性、流体物性参数变化对换热器换热性能的影响,计算精度得到提高,同时解决了流体间交叉流动和流体相变换热问题。
1.2 翅片数据库为了实现多股流板翅式换热器精确数值计算,合理的数值计算方法是关键,但是翅片的对流表面换热系数计算也是比较重要的影响因素。翅片结构的传热特性常用j因子表征。比较典型的j因子的计算公式有Weiting拟合公式[18]、Joshi拟合公式[19]、日神钢通用计算公式[20],另外商业软件ASPEN MUSE也提供了j因子的计算方法。通过对特定翅片结构型式的无相变流体j因子计算公式进行筛选,对于锯齿形翅片,最终选用Weiting拟合公式为
| $ \left\{ \begin{array}{l} j = 0.483{\left( {\frac{a}{{{d_{\rm{e}}}}}} \right)^{-0.162}}{\left( {\frac{{{s_{{\rm{fin}}}}-{\delta _{{\rm{fin}}}}}}{{{H_{{\rm{fin}}}}-{\delta _{{\rm{fin}}}}}}} \right)^{ - 0.184}}R{e^{ - 0.536}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Re \le 1\;000\\ j = 0.242{\left( {\frac{a}{{{d_{\rm{e}}}}}} \right)^{ - 0.322}}{\left( {\frac{{{\delta _{{\rm{fin}}}}}}{{{d_{\rm{e}}}}}} \right)^{0.089}}R{e^{ - 0.368}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Re \ge 2\;000 \end{array} \right. $ | (9) |
式中:a表示锯齿形翅片不间断流动长度;de表示当量直径;sfin表示翅片间距;Hfin表示翅片高度;δfin表示翅片厚度;Re表示雷诺数。式(7) 中关于过渡区的j因子通过j-Re曲线的交点确定,实际Re小于交点处Re,采用层流区公式计算,反之,采用湍流区公式。
相变流体在冷凝阶段对流表面换热系数计算公式为[20]
| $ {\alpha _c} = 4.348\;29 \times {10^{-4}}G{\left( {\frac{{{c_l}{\rho _l}{\lambda _l}}}{{2{\mu _l}{\rho _v}}}} \right)^{0.5}}Re_v^{-0.276\;2} $ | (10) |
式中:G表示平均质量流速;cl表示液相比热容;λl表示液相导热系数;μl表示液相动力黏度;Rev表示气相雷诺数;ρl, ρv分别表示液相、气相流体密度。
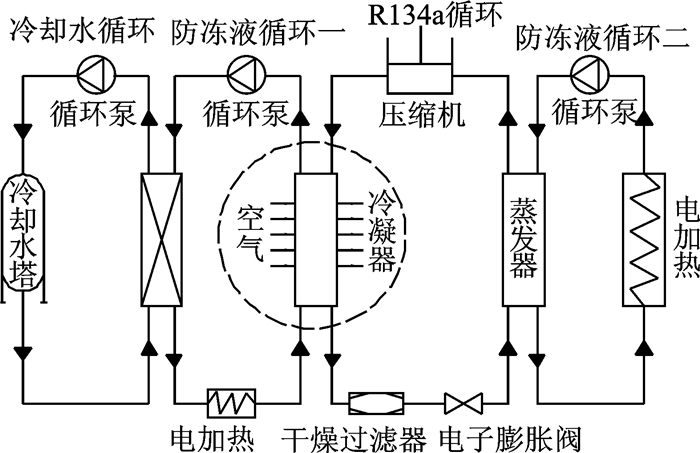
2 数值与实验 2.1 实验系统及实验流程介绍为了验证上述多股流板翅式换热器数值计算方法的合理性,基于蒸发制冷循环试验台对机载交叉式三股流板翅式冷凝器进行实验研究。实验原理如图 3所示。
|
图 3 蒸发制冷循环系统实验原理图 Figure 3 Schematic diagram of evaporative cooling circulatory system |
冷凝器三股流体分别为空气、65#防冻液和R134a。空气由中压空气源提供,65#防冻液和空气作为冷流体冷却R134a。加热后的65#防冻液通过冷却水循环进行冷却,冷却后的制冷剂R134a通过防冻液循环二进行加热。
三股流冷凝器的结构参数如表 1所示,其中芯体长度400 mm,宽度130 mm,材质为LF-21,通道排列方式为ABACABAC…A,空气沿宽度方向流动,65#防冻液和R134a相互逆流且沿长度方向流动,三股流体翅片为锯齿形结构,不间断流动长度均为3 mm。
| 表 1 三股流板翅式冷凝器结构参数 Table 1 Structure parameters of three-stream plate-fin condenser |
实验中空气通过控制阀调节其流量变化,流量变化范围1 000~1 600 kg/h,调节频率约为200 kg/(h·次);R134a流量通过控制循环系统中压缩机的转速实现,压缩机转速变化范围4 500~5 700 r/min,调节频率约为300 r/(min·次);65#防冻液在整个实验过程中保持不变。实验过程中每次调节应保证各股流体的进出口参数稳定,如此可进行多次实验,选取其中4种工况(如表 2所示)与数值计算结果对比。
| 表 2 不同工况下各股流体的进出口参数 Table 2 Inlet and outlet parameters of each stream in different operating conditions |
2.2 数值分析
采用文中所述数值计算方法,以工况1给定的各股流体入口参数为输入条件,对其进行数值计算,考虑到65#防冻液与R134a逆流流动,设定逆流迭代时前后两次温度场计算误差小于等于0.01 ℃。换热器为周期性通道排列,因此可选取各股流体的中间通道,观察各股流体温度分布如图 4所示。
|
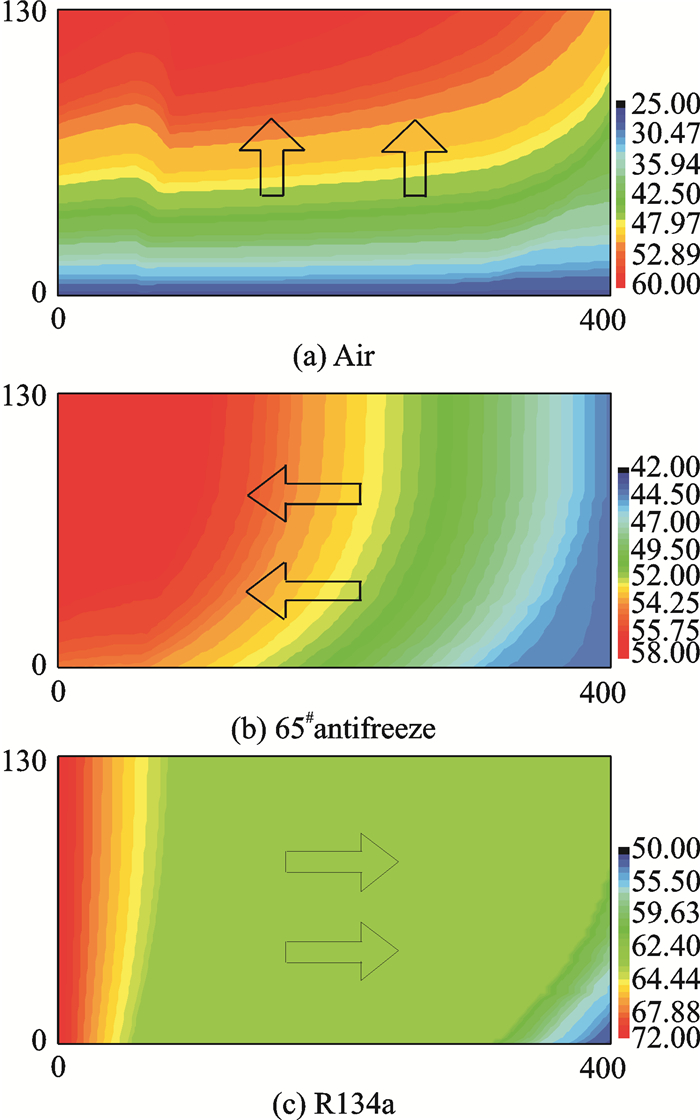
图 4 工况1条件下中间通道各股流体温度场 Figure 4 Temperature field of each fluid inside the middle passage in the first operating condition |
从图 4(a)可看出,空气与其余两股流体交叉流动换热,导致空气流动方向横向截面存在温度梯度,且在换热器左侧,横向存在非单调性温度变化。原因在于:在换热器左侧(靠近R134a进口)区域,气态R134a通过与空气、65#防冻液换热,由过热态转变为两相态,对流换热表面传热系数增大,从而导致该区域空气温升高。
另外,从图 4(a)可看出,换热器左侧区域,沿空气流动方向,有较高的温升速率。原因在于:R134a本身有较高的入口温度,65#防冻液与R134a逆流流动换热,导致其出口温度也较高,空气通道与R134a和65#防冻液通道相邻布置,此区域内空气用于冷却其余两股流体,而其余区域空气和65#防冻液作为冷流体用于冷却R134a,从中也可以看出该区域内空气和65#防冻液通道间热量内耗较为严重。
从图 4(b)可看出,沿65#防冻液流动方向的横向截面,在靠近空气进口侧存在温度梯度较大,靠近空气出口侧,温度梯度趋于0。原因在于:靠近空气进口侧的空气温度较低,空气对65#防冻液温度影响较大,但是本例中,65#防冻液热容流值约为空气的12倍,空气在流动过程中温度快速上升后温升速率降低,导致65#防冻液横向温度梯度趋于零。
从图 4(c)可看出,R134a在通道内主要处于两相态,且在靠近空气出口区域的R134a出口侧未完全相变。
2.3 实验数据分析对上述4种试验工况点进行能量平衡验证,计算公式为
| $ EB = \frac{{{q_{\rm{C}}}-\left( {{q_{\rm{B}}} + {q_{\rm{A}}}} \right)}}{{{q_{\rm{C}}}}} $ | (11) |
式中:下标A, B, C分别代表流体空气、65#防冻液和R134a。图 5展示了能量平衡验证的结果,表明对于文中所述实验数据点所计算的换热量偏差在3%以内,由此说明能量损失较少,实验准确度高。

|
图 5 不同工况热平衡计算 Figure 5 Heat balance calculation in different operating conditions |
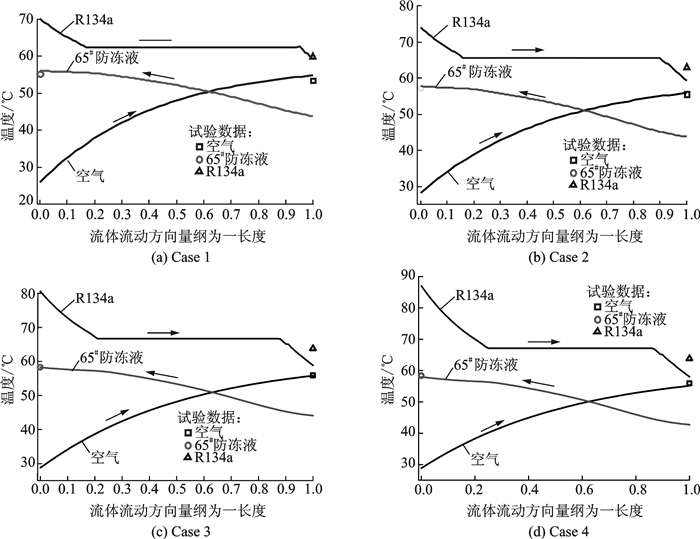
采用文中所述数值计算方法,分别对4种工况进行数值计算,数值计算与实验结果之间对比如图 6所示。
|
图 6 不同工况下数值计算与实验结果对比 Figure 6 Comparison between simulation results and experimental data in different operating conditions |
定义各股流体数值计算与实际换热量之间的相对误差为
| $ R{D_i} = \frac{{{q_{{\rm{pred, }}i}}-{q_{{\rm{exp, }}i}}}}{{{q_{{\rm{exp, }}i}}}} \times 100 $ | (12) |
式中:理论换热量qpred, i通过数值计算获得。各股流体在不同工况下RDi如表 3所示。从表 3可看出,当冷流体空气和65#防冻液相对误差较小时(工况2,3,4),热流体R134a相对误差较大,工况1条件下与之恰好相反。一般情况下在对无相变换热器误差分析时,若冷流体的相对误差较小,则热流体的相对误差也会较小,本次实验结果与此矛盾。主要原因在于:在4种工况条件下对换热器进行数值计算时,对于相变流体R134a在工作压力下单位质量相变潜热理论值与实际相变换热可能有一定的偏差,导致R134a在相同的进出口温度条件下理论换热量比实际换热量要小,这是在工况2,3,4条件下理论计算R134a出口温度偏低的原因之一。
| 表 3 不同工况下各股流体换热量相对误差 Table 3 Relative errors of heat exchange with each fluid in different operating conditions |
实验用板翅式换热器翅片为锯齿型结构形式,翅片之间存在横向流动,由于重力作用,两相流在水平换热器内有相分离趋势,当两相流干度变化时,可能导致两相流压降变化,造成两相流在流动中分配不均匀,同时换热器封头和导流片的影响会加剧流体分配的不均匀性;对于无相变流体65#防冻液,由于质量流量较大,其流量分配不均匀性也较为严重;同时由于总管布局,65#防冻液和R134a的大流量区域并不在同一位置,R134a高温大流量区域(入口侧)靠近冷流体空气出口侧。因此,65#防冻液和R134a的流量分配不均匀性会降低换热器换热效率,这也是理论计算R134a出口温度偏低的另外一个主要原因。
目前,国内外关于伴有相变及两相流的传热及流动特性的研究相对薄弱,本文关于流体冷凝时表面对流换热系数计算所采用的经验公式并不一定具有较高的准确性。空气和R134a换热时,由于空气侧的对流表面换热系数远小于R134a侧冷凝换热系数,因此R134a冷凝换热系数的计算准确性对于空气和R134a之间的换热计算影响不太大;但是65#防冻液侧对流表面换热系数与R134a侧冷凝换热系数接近,两者之间的换热受R134a侧冷凝换热系数计算的准确性影响较大;同时在数值计算时,R134a相变对流表面换热系数为定值,显然R134a在相变过程中不同的干度下对流表面换热系数存在一定的差异。采用经验公式对R134a相变换热系数的预测不确定性对换热器数值计算分析准确性造成了一定的影响。
3 结论(1) 文中所述的数值计算方法,可用于计算包含相变和交叉式在内的多股流板翅式换热器,同时可获得不同通道流体的温度分布,从而为多股流换热器换热性能分析提供依据。
(2) 通过4种工况条件下数值计算结果与实验结果的对比,流体换热量的最大相对误差为8.08%,满足工程设计计算需求,证明了数值计算方法的合理性。
(3) 对于带有相变的多股流板翅式换热器,流体流量分配不均、相变流体潜热以及相变对流表面换热系数的计算影响数值计算精度;若需进一步提高计算精度,上述问题有待进行更加深入的研究。
| [1] | PRASAD B S V. Fin efficiency and the mechanisms of heat exchange in multi-stream plate-fin heat exchangers: Formulation[J]. International Journal of Heat and Mass Transfer, 1996, 39(2): 419–428. DOI:10.1016/0017-9310(95)00125-S |
| [2] | PRASAD B S V. The performance prediction of multi-stream plate-fin heat exchangers based on stacking pattern[J]. Heat Transfer Engineering, 1991, 12(4): 58–70. DOI:10.1080/01457639108939764 |
| [3] | GOYAL M, CHAKRAVARTY A, ATREY M D. Two dimensional model for multi-stream plate fin heat exchangers[J]. Cryogenics, 2014(61): 70–80. |
| [4] | GHOSH I, SARANG S K, DAS P K. An alternate algorithm for the analysis of multi-stream plate fin heat exchangers[J]. International Journal of Heat and Mass Transfer, 2006, 49: 2889–2902. DOI:10.1016/j.ijheatmasstransfer.2005.12.022 |
| [5] | GHOSH S, GHOSH I, PRATIHAR D K, et al. Optimum stacking pattern for multi-stream plate-fin heat exchanger through a genetic algorithm[J]. International Journal of Thermal Sciences, 2011, 50: 214–224. DOI:10.1016/j.ijthermalsci.2010.07.003 |
| [6] | SHRIVASTAVA D, AMEEL T A. Three-fluid heat exchangers with three thermal communications. Part A: General mathematical model[J]. Int J Heat Mass Transfer, 2004, 47(17/18): 3855–3865. |
| [7] | SHRIVASTAVA D, AMEEL T A. Three-fluid heat exchangers with three thermal communications. Part B: Effectiveness evaluation[J]. Int J Heat Mass Transfer, 2004, 47(17/18): 3867–3875. |
| [8] | SAEID N H, SEETHARAMU K N. Finite element analysis for co-current and counter-current parallel flow three-fluid heat exchanger[J]. International Journal of Numerical Methods for Heat and Fluid Flow, 2006, 16: 324–337. DOI:10.1108/09615530610649744 |
| [9] | YUAN P, KOU H S. The comparison of longitudinal wall conduction effect on the crossflow heat exchangers including three fluid streams with different arrangements[J]. Applied Thermal Engineering, 2001(21): 1891–1907. |
| [10] | LUO X, LI M L, ROETZEL W. A general solution for one-dimensional multi stream heat exchangers and their networks[J]. Int J Heat Mass Transfer, 2002, 45(13): 2695–2705. DOI:10.1016/S0017-9310(02)00003-0 |
| [11] | ZHAO M, LI Y Z. New integral-mean temperature difference model for thermal design and simulation of parallel three-fluid heat exchanger[J]. International Journal of Thermal Sciences, 2012, 59: 203–213. DOI:10.1016/j.ijthermalsci.2012.04.019 |
| [12] | ZHAO M, LI Y Z. An effective layer pattern optimization model for multi-stream plate-fin heat exchanger using genetic algorithm[J]. International Journal of Heat and Mass Transfer, 2013(60): 480–489. |
| [13] | WANG Z, LI Y Z, ZHAO M. Experimental investigation on the thermal performance of multi-stream plate-fin heat exchanger based on genetic algorithm layer pattern design[J]. International Journal of Heat and Mass Transfer, 2015(82): 510–520. |
| [14] | PENG X, LIU Z Y, QIU C, et al. Passage arrangement design for multi-stream plate-fin heat exchanger[J]. International Journal of Heat and Mass Transfer, 2014, 77. |
| [15] | PENG X, LIU Z Y, QIU C, et al. Effect of inlet flow maldistribution on the passage arrangement design of multi-stream plate-fin heat exchanger[J]. Applied Thermal Engineering, 2016(103): 67–76. |
| [16] |
曹业玲, 郭宪民, 高晖.
机载蒸发循环制冷系统板翅式蒸发器换热特性[J]. 南京航空航天大学学报, 2006, 38(2): 170–175.
CAO Yeling, GUO Xianmin, GAO Hui. Heat transfer characteristic of plate-fin evaporator of on-board vapor cycle cool ing system[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2006, 38(2): 170–175. |
| [17] |
李俊, 蒋彦龙, 周年勇, 等.
交叉式多股流板翅式换热器数值研究[J]. 航空动力学报, 2016, 31(5): 1087–1096.
LI Jun, JIANG Yanlong, ZHOU Nianyong, et al. Numerical study on cross-type multi-stream plate-fin heat exchanger[J]. Journal of Aerospace Power, 2016, 31(5): 1087–1096. |
| [18] | WEITING A K. Empirical correlations for heat transfer and flow friction characteristics of rectangular offset-fin plate-fin heat exchangers[J]. Trans ASME, Journal of Heat Transfer, 1975, 97(Series C): 488–490. |
| [19] | JOSHI H M. Heat transfer and friction in the offset strip-fin heat exchanger[J]. Int Journal of Heat and Mass Transfer, 1987, 30(1): 69–84. DOI:10.1016/0017-9310(87)90061-5 |
| [20] | 钱颂文. 换热器设计手册[M]. 北京: 化学工业出版社, 2002. |
 2017, Vol. 49
2017, Vol. 49


