随着航空发动机矢量推进技术的发展，作动器作为矢量喷管的驱动装置，正被大量使用。伺服阀安装在作动器上，是电液伺服系统中的重要部件，因此伺服阀的可靠性变得十分重要。一般情况下，电液伺服阀的失效形式主要有堵塞、磨损、疲劳等^[1]，其最主要的失效形式为伺服阀中油液受污^[2]。而应用在航空发动机矢量喷管作动器中的伺服阀，由于受到矢量喷管夹层热环境的影响很大，因超温所导致的失效需要着重加以研究。

目前，国内外对矢量喷管伺服作动系统的研究主要集中在控制技术^[3-5]及结构设计上^[6-7]，对矢量喷管作动器热分析的研究报道很少。周松林^[8]采用热固耦合的方法分析了电液伺服阀双喷嘴挡板组件的温度场，总结出主阀在受热条件下，阀芯阀套不同部位的变形规律。关于集总参数法非稳态研究，国外Chow等^[9]利用集总参数导热模型研究两固体接触热阻的变化与接触物表面温度、接触面压力、接触面填充物之间的关系，其方程计算所得温度和测量值吻合良好。国内王为术等^[10]基于集总参数法建立了二次启动前火箭发动机泵构件的温度变化计算模型，并且考虑到管中氧化剂相变对对流换热的影响，其计算模型结果和试车数据吻合较好。赵以贤等^[11]采用集总参数法研究了坦克内燃机的传热特性，得到了其传热随大气压力和温度的变化规律。张希恒等^[12]对超高温阀的阀座建立了相应的非稳态导热数学模型，并通过理论计算和数值模拟说明了所建数学模型的合理性。王玉芝等^[13]建立了发动机活塞热冲击的集总参数模型，并且运用迭代法得到了在该模型下活塞温度场的随机解。黄小辉等^[14]将履带车辆动力装置润滑系统划分为若干个固体单元，利用集总参数法建立了相应数学模型，并利用自编程序进行迭代计算，求得润滑系统的流动方程和传热控制方程的解，其计算结果和试验值吻合较好。

某型航空发动机矢量喷管伺服阀通过螺栓连接在作动器的上部，其外环境为t_wai的高温燃气。当矢量喷管伺服阀工作在不同工况时，其工作参数也有所不同。伺服阀正常工作时，其内部工作油路和冷却油路中的介质(煤油)都处于流动状态。伺服阀不通油工况是指工作油路和冷却油路中的煤油都不流动，此时伺服阀与煤油间热传递的方式不再是对流换热而是导热。本文建立了矢量喷管伺服阀的集总参数模型，编制了伺服阀热分析FORTRAN源程序，对其进行了非稳态热分析，得到了伺服阀温度在不同参数条件下随时间的变化规律。

将阀芯、阀套、端盖、煤油组成的整体视为伺服阀部件，对于伺服阀部件，常物性、非稳态、无内热源、不考虑内部热阻的导热微分方程为

式中：ρ_sff，c_sff分别为伺服阀部件的当量密度与比热容；${{{\dot \varphi }_{{\rm{sffall}}}}}$为伺服阀的体积热源。其中ρ_sff与c_sff的乘积为

式中：V_AL表示伺服阀部件中金属的体积，伺服阀主要材料为某铝合金，其他金属的导热系数均小于某铝合金，偏安全考虑，螺栓、阀芯中各种金属均视为某铝合金的导热系数；V_o表示冷却流道中煤油的体积；V_g表示阀套内空气的体积；V_sff表示伺服阀部件的体积；ρ，c分别表示密度和比热容，不同的下标代表不同的物质。

伺服阀部件毕渥数为

式中：h_dl为空气横掠伺服阀的对流换热系数；λ为伺服阀部件导热系数；V，A分别为伺服阀部件的体积和表面积，$\frac{V}{A}$的数量级为10^-3m。计算得到的Bi=3.381 9×10^－4，满足集总参数法的适用条件，研究对象中各点过余温度的偏差小于5%。

作动器安装在矢量喷管起始段的夹层中，与喷管内的空气直接接触。伺服阀安装在作动器上部壳体外侧。对于不通油工况，煤油不流动，在非稳态时，喷管夹层高温固壁对伺服阀部件表面进行热辐射加热。矢量喷管起始段的夹层中空气的温度为T_wai，喷管夹层固壁温度视为T_wai。作动筒、伺服阀与壳体温度相近并且面积较小。喷管夹层固壁的表面积远大于伺服阀部件的表面积，且伺服阀部件为非凹表面，伺服阀部件与喷管夹层固壁辐射换热的角系数为1。

假设伺服阀部件的吸收率等于发射率，则有，伺服阀部件与喷管夹层固壁的净辐射换热量为

式中:ε_sff表示伺服阀部件的半球总发射率，伺服阀部件材料为某铝合金，其法向发射率为0.1，考虑到伺服阀部件表面较粗糙、服役环境氧化作用等，可以取其半球总发射率为0.2;A_sff表示伺服阀部件与喷管夹层固壁辐射换热的面积; σ表示Stefan Boltzmann常数；T_sff表示伺服阀部件的温度。

高温空气在喷管夹层中流动，与作动器有对流换热作用。按空气横掠作动器来计算空气与作动器的对流换热量。夹层中空气流速v_g为1 m/s，作动器的特征长度为d_dl。

空气横掠作动器流动的雷诺数为

努赛尔数^[15]

式中：C=0.102，n=0.675。

空气横掠作动器的对流换热系数

空气与作动器上部伺服阀部件的对流换热量

伺服阀的焦耳热为φ_r，此为内热源，不随时间变化。总的源项为

式中:φ_sfffs表示伺服阀的辐射换热量；φ_sffdl表示伺服阀的对流换热量。

辐射换热量和对流换热量的比值计算方法为

式中：ε_ssf，σ，T_wai，h_dl均在上文中给出，根据T_sff的取值范围，式(10) 可化为

由式(11) 可知，辐射换热量与对流换热量的比值范围从0.754变化到1.274。取极大值1.274，则有φ_sfffs=1.274φ_sffdl。

所以，可以将辐射换热量用对流换热量来表示，式(9) 可化为

将总的源项折算成伺服阀部件的体积热源

于是有

对式(13) 分离变量得

对τ从0时刻到τ积分，对应温度为t₀到t_sff，t₀为伺服阀初始时刻的温度。

于是有

首先对上式左侧温度求积分

对右侧时间求积分

于是有伺服阀温度与时间的关系式

即得

在式(15) 中，环境温度t_wai、伺服阀初始温度t₀、伺服阀的焦耳热φ_r是影响伺服阀温度t_sff的3个重要因素。根据作动器的实际工况情况设置计算模型，模型计算参数如表 1所示，实际条件下，伺服阀不通油工况有两种情况：(1) 一开始就处在不通油工况; (2) 从正常工作状态突然转变为不通油工况。两种工况所对应的初始温度t₀不同，分别为70 ℃和122.6 ℃。在数值计算中，分别研究了伺服阀初始温度，环境温度，伺服阀焦耳热3个参数对伺服阀超温时间的影响。在研究环境温度与伺服阀焦耳热的分组中，又根据不通油工况两种不同的情况将算例按初始温度分为两组。

表 1(Table 1)

表 1 模型参数 Table 1 Model parameters 参数 t0/ ℃ twai/ ℃ φr/W 实际条件 下伺服阀 工作参数 开始就不 通油工况 70 300 0.08 突然转变为 不通油工况 122.6 300 0.08 数值计算 时假定伺 服阀参数 t0对伺服阀温度随时间变化的影响 50 300 0.08 60 70 80 90 100 twai对伺服阀温度随时间变化的影响 70 200 0.08 250 300 350 400 122.6 200 0.08 250 300 350 400 φr对伺服阀温度随时间变化的影响 70 300 0.08 2 4 6 8 10 122.6 300 0.08 2 4 6 8 10

表 1 模型参数 Table 1 Model parameters

伺服阀所能耐受的最高工作温度t_max假设为200 ℃，超过此温度，伺服阀将不能正常工作。将伺服阀从开始工作至温度超过t_max的时间称为超温时间。

当伺服阀一开始就是不通油工况，初始温度t₀为70 ℃，经伺服阀热分析程序计算的伺服阀温度随时间的变化如表 2所示，表中仅给出了部分时刻的温度结果，温度随时间的变化曲线见图 1。

表 2(Table 2)

表 2 初始温度t0＝70 ℃时伺服阀温度随时间的变化 Table 2 Temperature of servo valve changing with time at t0=70 ℃ Time/min tsff/ ℃ 1 77.90 2 85.54 3 92.91 4 100.03 5 106.90 10 137.90 20 185.81 30 219.62 60 272.19 120 297.16 180 300.24 240 300.62

表 2 初始温度t0＝70 ℃时伺服阀温度随时间的变化 Table 2 Temperature of servo valve changing with time at t0=70 ℃

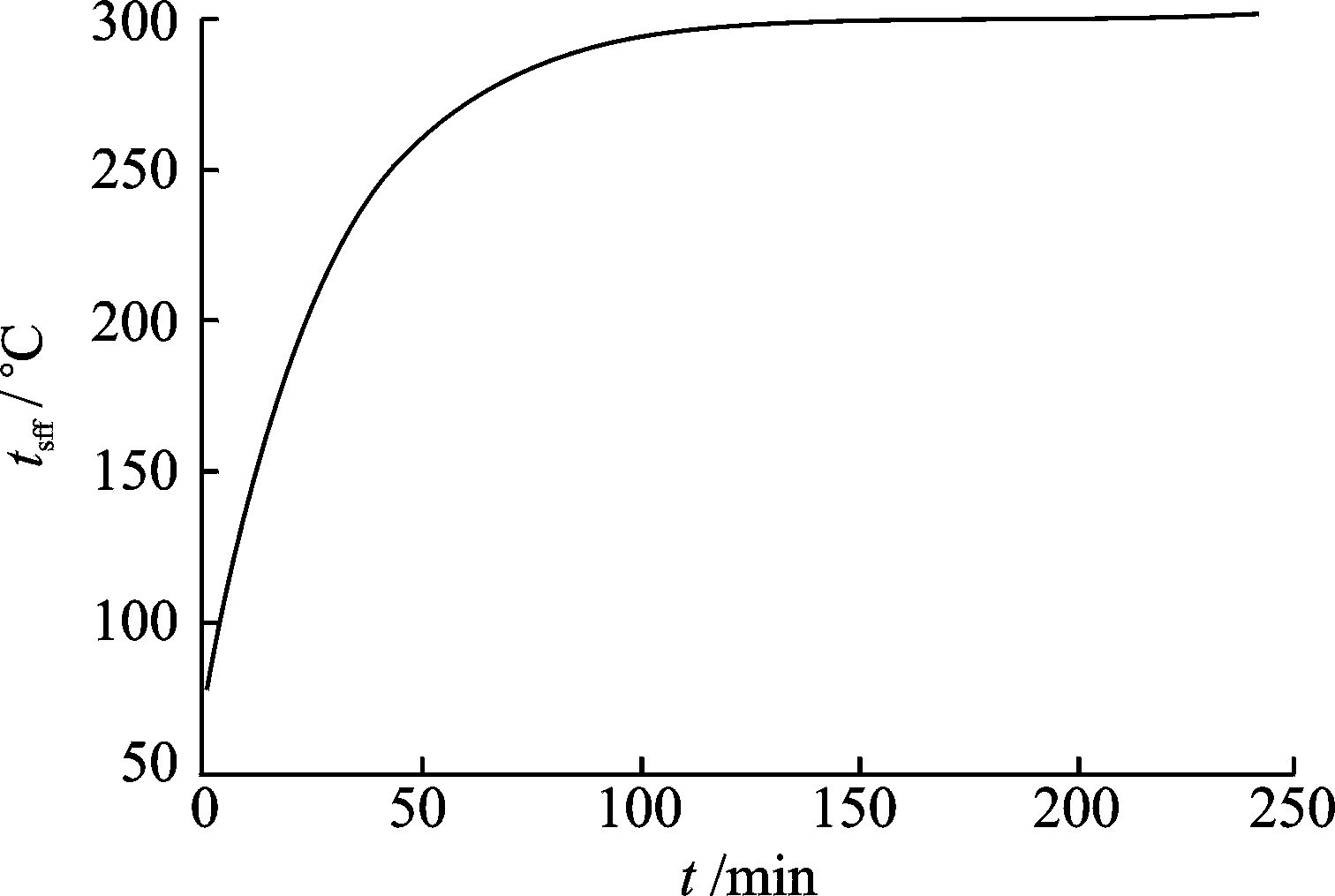
图 1 温度随时间的变化(t0=70 ℃) Figure 1 Curve of tsff changing with time under condition of t0=70 ℃

由图 1可知，当伺服阀从一开始就是不通油工况，初始温度t₀为70 ℃时，伺服阀超温的时间为24 min。

当伺服阀从正常工作状态进入不通油状态，初始温度t₀和此时煤油进口温度t_in相等，为122.6 ℃，经伺服阀热分析程序计算的伺服阀温度随时间的变化如表 3所示，表中仅给出了部分时刻的温度结果，温度随时间的变化曲线见图 2。

表 3(Table 3)

表 3 初始温度t0=122.6 ℃时伺服阀温度随时间的变化 Table 3 Temperature of servo valve changing with time at t0=122.6 ℃ Time/min tsff/ ℃ 1 128.76 2 134.65 3 140.34 4 145.83 5 151.14 10 175.06 20 212.03 30 238.12 60 278.70 120 297.96 180 300.34 240 300.63

表 3 初始温度t0=122.6 ℃时伺服阀温度随时间的变化 Table 3 Temperature of servo valve changing with time at t0=122.6 ℃

图 2 温度随时间的变化(t0=122.66 ℃) Figure 2 Curve of tsff changing with time under condition of t0=122.6 ℃

由图 2可知，当伺服阀从正常工作状态进入不通油状态，初始温度t₀为122.6 ℃的条件下，伺服阀超温的时间为16.3 min。相比初始温度t₀为70 ℃时，超温时间缩短了32.08%。

为了详细研究初始温度t₀的变化对伺服阀温度的影响规律，取环境温度t_wai为300 ℃，取伺服阀焦耳热φ_r为0.08 W，并保持不变。分别取伺服阀初始温度为50, 60, 70, 80, 90, 100 ℃，一共6组计算模型，计算所得伺服阀温度随时间的变化曲线如图 3所示。从图 3中可以看出，同一时刻下，伺服阀温度随着t₀的升高而升高。比较不同的计算模型，其超温时间随着初始温度的升高而缩短。其中初始温度为50 ℃的计算模型，超温时间最长，为26.2 min。初始温度t₀为100 ℃的计算模型，超温时间最短，超温时间为20.8 min，相比于初温50 ℃的计算模型，超温时间缩短了20.6%。

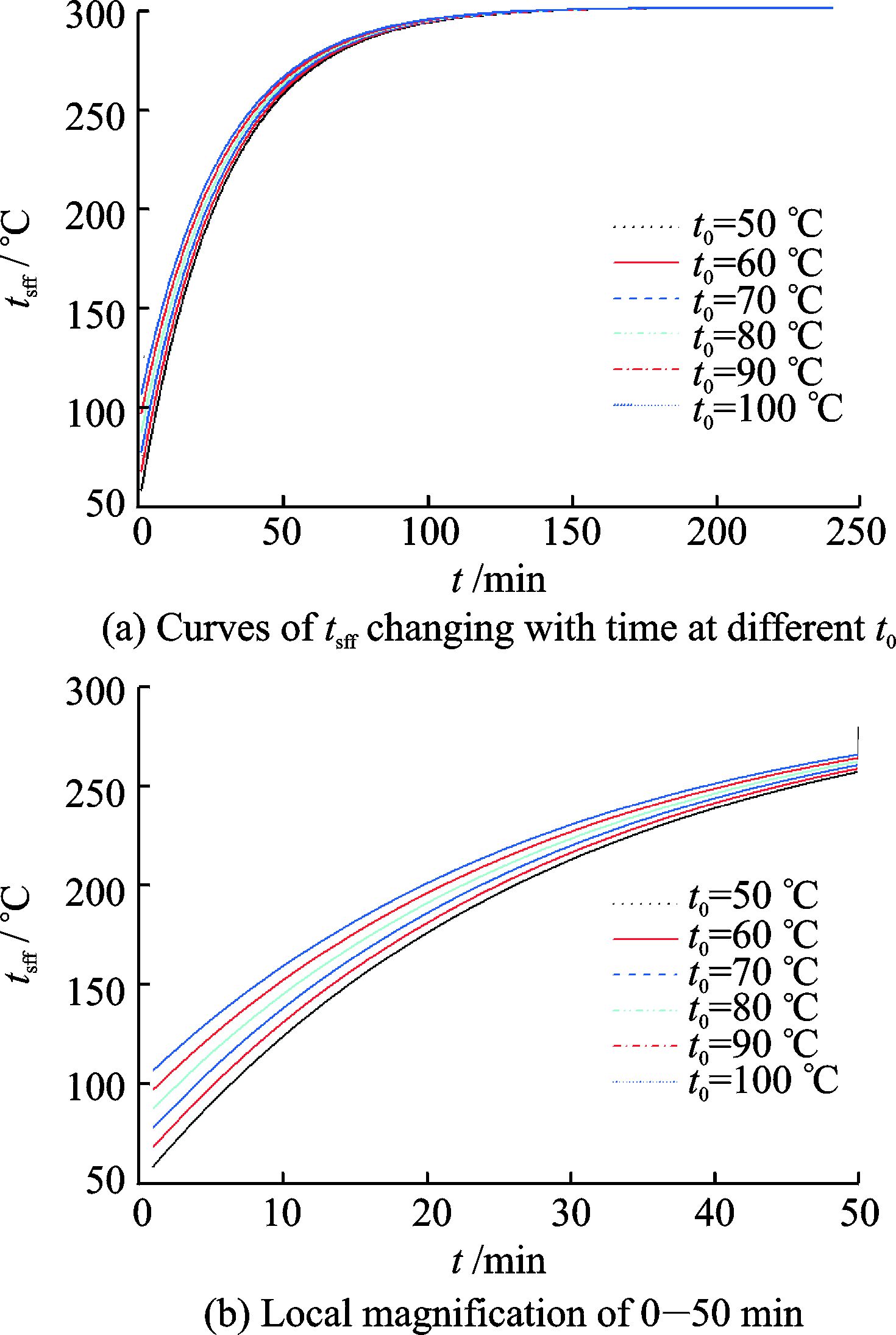
图 3 伺服阀温度随时间的变化 Figure 3 Curves of tsff changing with time at different t0

在研究环境温度对伺服阀温度随时间变化的影响时，首先取伺服阀初始温度t₀为70 ℃，伺服阀焦耳热φ_r为0.08 W，此时对应的伺服阀实际工况为开始就是不通油工况，保持伺服阀初始温度、伺服阀焦耳热这两个参数值不变，分别改变环境温度为250，300，350，400 ℃，在以上条件下，伺服阀温度随时间的变化曲线表示在图 4中。从图 4中可以看出，随着时间的增加，伺服阀的温度先匀速升高，后逐渐趋于平缓，最终达到一个和环境温度相同的稳定值。在相同时刻下，伺服阀温度随着环境温度的升高而升高。超温时间随着t_wai的升高而缩短。在环境温度为250 ℃时，超温时间在这4组计算模型中最长，为36.5 min。在环境温度为400 ℃时，超温时间在这4组计算模型中最短，为14.3 min，相比于环境温度为250 ℃的计算模型，超温时间缩短了60.8%。

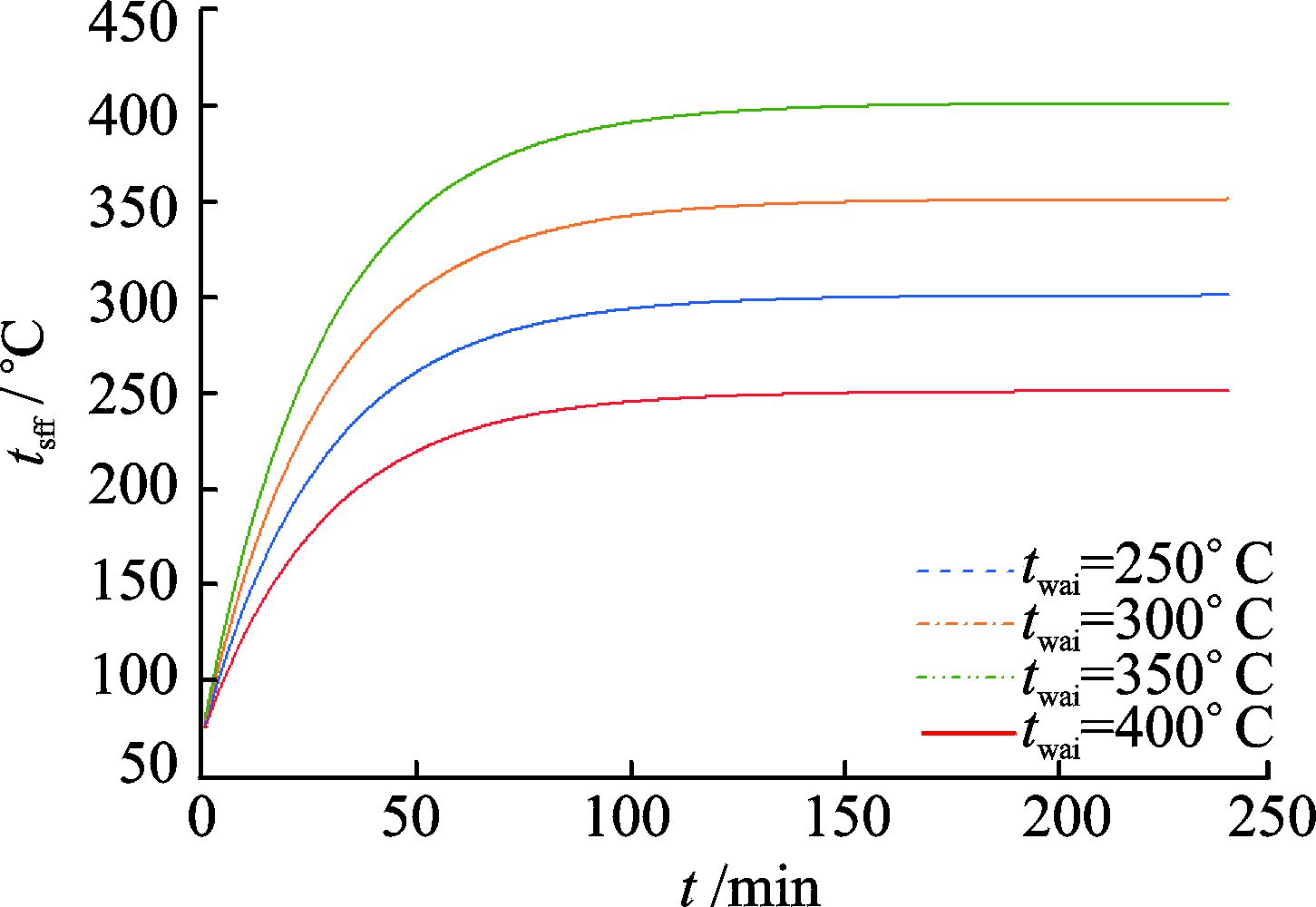
图 4 不同环境温度下伺服阀温度随时间变化(t0=70 ℃) Figure 4 Curves of tsff changing with time at different twai(t0=70 ℃)

然后取伺服阀初始温度t₀为122.6 ℃，伺服阀焦耳热φ_r为0.08 W，此时对应的伺服阀工作状态为从正常工况突然转变为不通油工况，为了研究在这种状态下环境温度的变化对伺服阀温度随时间变化的影响，分别改变环境温度为250，300，350，400 ℃，一共4组计算模型，得到伺服阀温度随时间的变化曲线见图 5。与图 4相比可以发现，在相同的环境温度条件下，图 5中的计算模型的温度更快地达到与环境温度一致，其超温时间也相应减小。其中，t_wai=250 ℃的计算模型，超温时间最长，为26.6 min；t_wai=400 ℃的计算模型，超温时间最短，超温时间为9.4 min，相比于环境温度250 ℃的计算模型，超温时间缩短了64.7%。相比伺服阀初始温度为70 ℃，伺服阀焦耳热φ_r为0.08 W时，环境温度400 ℃相比于环境温度为250 ℃超温时间缩短的比例升高了3.9%。

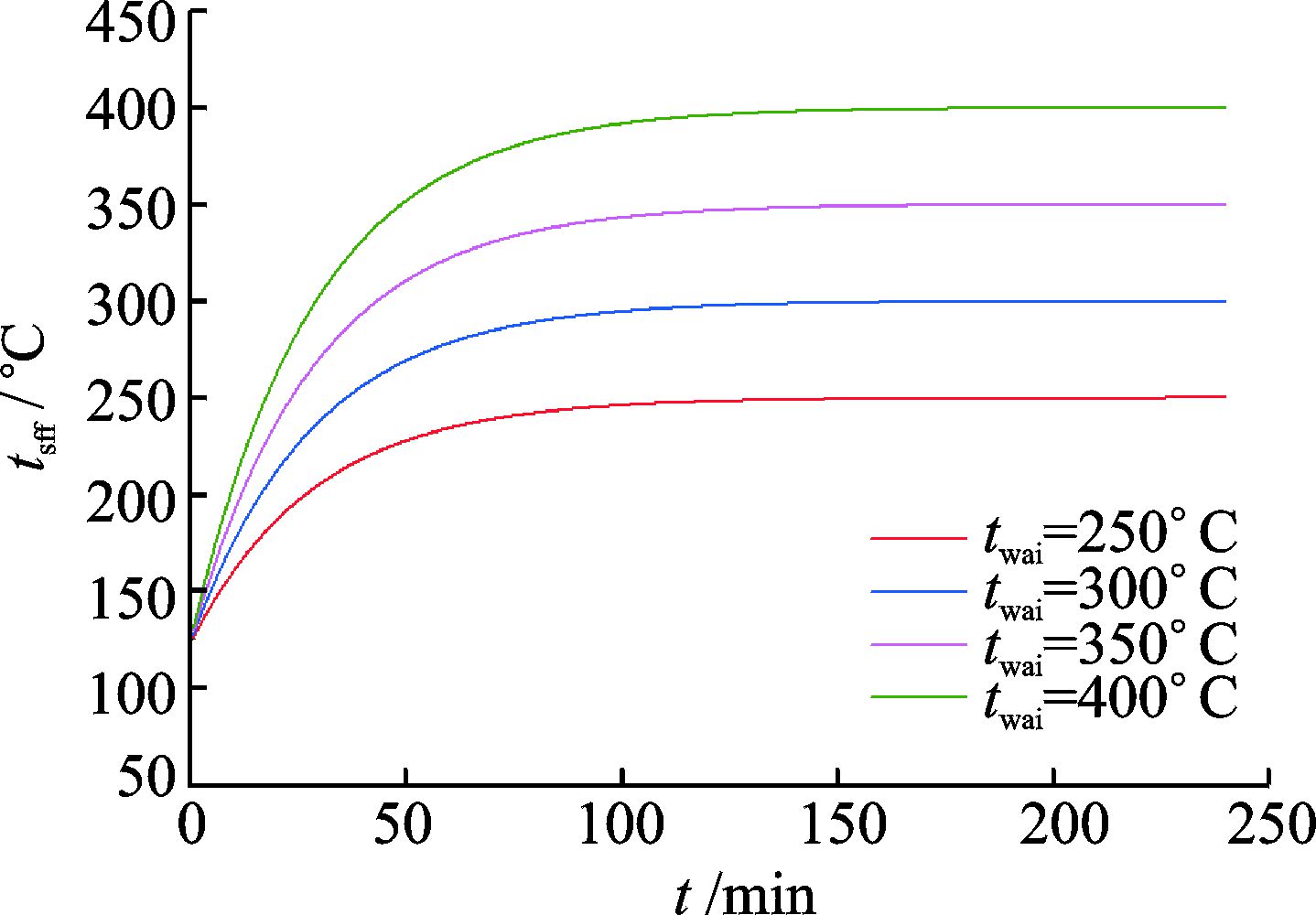
图 5 不同环境温度下伺服阀温度随时间变化(t0=122.6 ℃) Figure 5 Curves of tsff changing with time at different twai (t0=122.6 ℃)

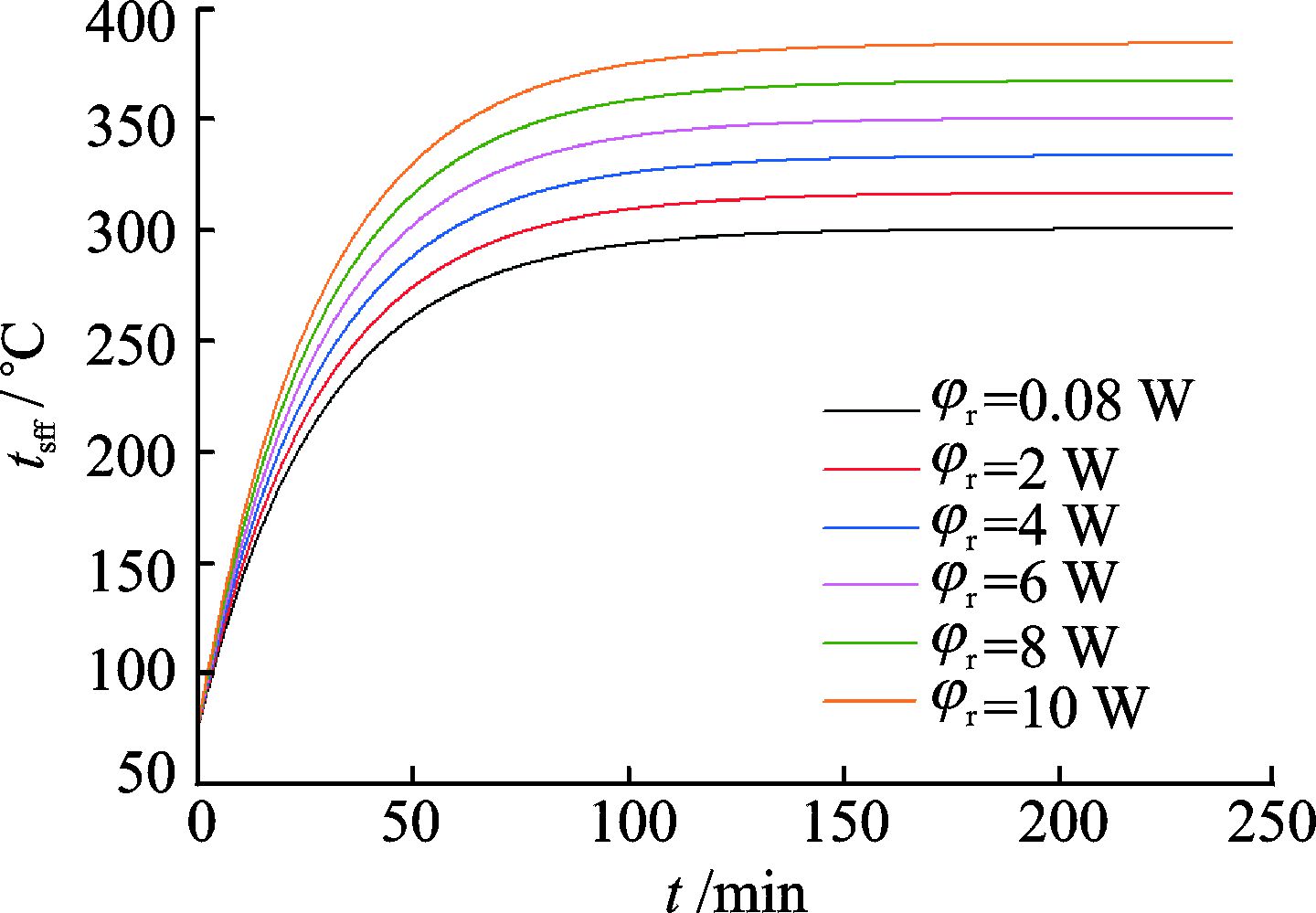
为了研究伺服阀焦耳热对伺服阀温度随时间变化的影响，首先取环境温度为300 ℃，伺服阀初始温度为70 ℃，此时对应的伺服阀工作状态为开始就不通油工况，在以上条件下，分别改变伺服阀焦耳热为0.08，2，4，6，8，10 W。这样，一共建立了6组计算模型来研究伺服阀焦耳热对伺服阀温度随时间变化的影响。从图 6可以看出，虽然每组计算模型的伺服阀焦耳热不同，但是伺服阀温度随时间的变化规律都是类似的。在伺服阀温度还未达到稳定之前，伺服阀温度的增加速度随着伺服阀焦耳热的增加而增加。比较6组计算模型可以发现，随着伺服阀焦耳热的增加，伺服阀最终达到的稳定温度也随之增加，6组模型所对应的稳定温度分别为300.6，316.8，333.7，350.6，367.4，384.3 ℃。随着伺服阀焦耳热的增加，伺服阀超温时间随之减少。φ_r=10 W的计算模型超温时间最短，超温时间为15.3 min，相比于φ_r=0.08 W的计算模型，超温时间缩短了36.3%。

图 6 伺服阀温度随时间变化(t0=70 ℃，twai＝300 ℃) Figure 6 Curves of tsff changing with time in different φr(t0=70 ℃, twai＝300 ℃)

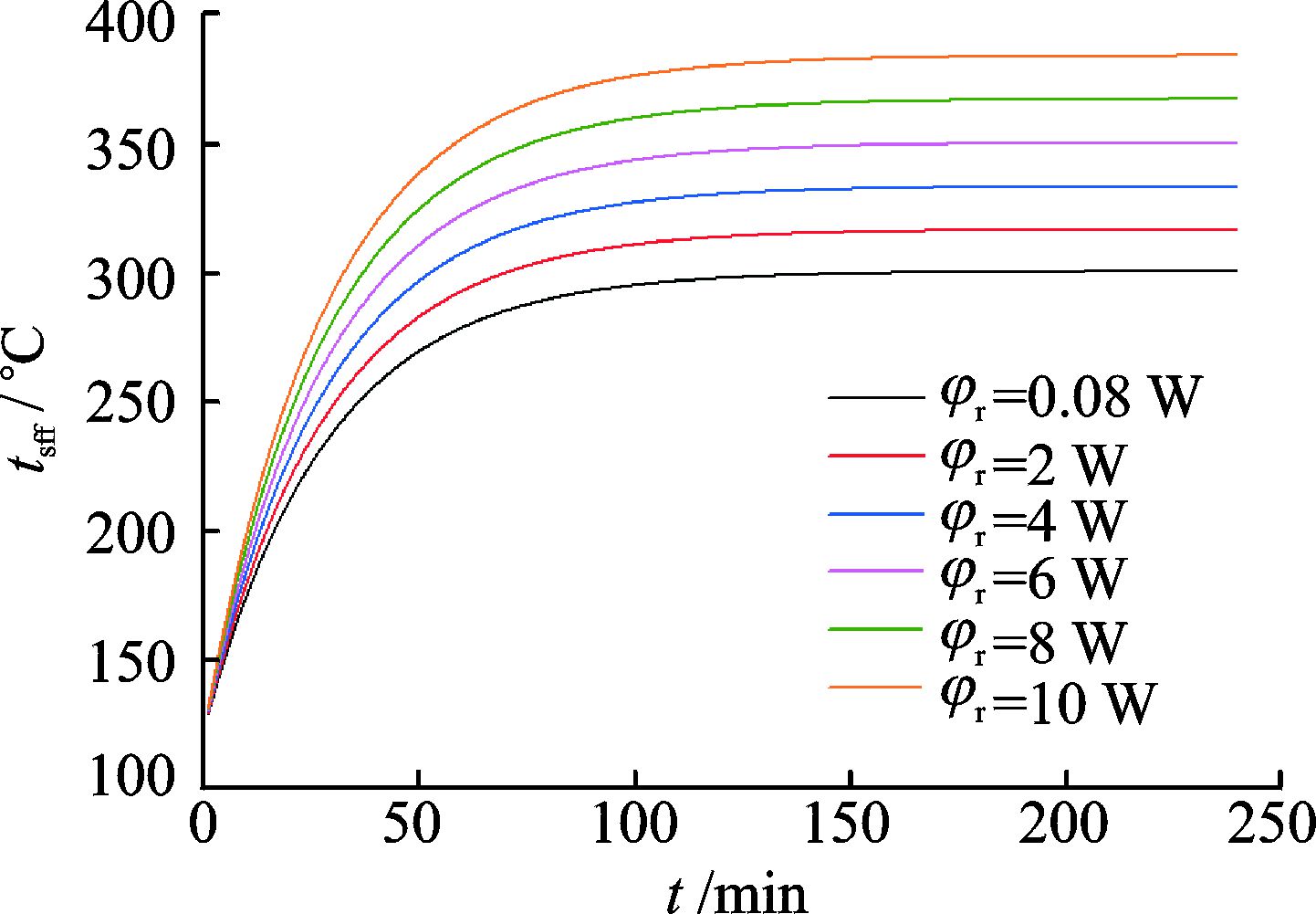
然后取伺服阀环境温度为300 ℃，初始温度为122.6 ℃，此时对应的伺服阀工作状态为正常工况突然转变为不通油工况，同样分别取伺服阀焦耳热为0.08，2，4，6，8，10 W，建立6组计算模型来研究该状态下，伺服阀焦耳热对伺服阀温度随时间变化的影响。变化规律如图 7所示，和图 6相比可以看出，伺服阀初始温度的变化对伺服阀最终达到的稳定温度没有影响。在式(15) 中，令时间τ趋于正无穷，式中第3项

图 7 伺服阀温度随时间变化(t0=122.6 ℃，twai＝300 ℃) Figure 7 Curves of tsff changing with time in different φr (t0=122.6 ℃, twai＝300 ℃)

则趋于0，此时

可见，当时间τ趋于正无穷时，伺服阀的稳定温度只与环境温度和伺服阀焦耳热有关，而与初始温度无关。对比这6组计算模型结果可以看出，随着伺服阀焦耳热的增加，伺服阀超温时间一直减小。其中，φ_r=10 W的计算模型超温时间最短，为10.1 min，相比于φ_r=0.08 W的计算模型，超温时间缩短了38.3%；与伺服阀初始温度为70 ℃时，φ_r=10W相比于φ_r=0.08W超温时间缩短的百分比相近，仅增加了2%。

本文采用集总参数法，针对航空发动机矢量喷管作动器伺服阀，在考虑导热、对流换热、辐射换热的条件下，对其进行了非稳态热分析，并建立了相应的数学模型，研究了环境温度t_wai、伺服阀初始温度t₀和伺服阀焦耳热φ_r三个参数对伺服阀温度随时间变化的影响。在本文的研究参数范围内，可以得到以下结论：

(1) 在其他参数相同时，伺服阀超温时间随着初始温度的升高而缩短。环境温度为300 ℃，伺服阀焦耳热为0.08 W时，初始温度100 ℃相比50 ℃，超温时间缩短了20.6%。

(2) 在其他参数相同时，伺服阀的超温时间随着环境温度的升高而缩短。伺服阀焦耳热为0.08 W，初始温度为70 ℃，环境温度从250 ℃上升400 ℃时，超温时间缩短了60.8%。

(3) 在其他参数相同时，伺服阀的超温时间随着伺服阀焦耳热的增大而缩短。环境温度为300 ℃，初始温度为122.6 ℃，10 W的伺服阀焦耳热相比0.08 W，超温时间缩短了38.3%。

(4) 通过物理模型简化后建立的数学模型在时间取无穷大时的分析结果与数值计算的结果都表明, 伺服阀的稳定温度只随环境温度和伺服阀焦耳热的增大而升高，与伺服阀初始温度无关，即与伺服阀如何进入不通油工况无关。