2. 先进航空发动机协同创新中心,北京, 100083
2. Collaborative Innovation Center of Advanced Aero-Engine, Beijing, 100083, China
叶轮机械作为航空发动机能量转换部件,在发动机轴向尺寸和重量上都占有较大比重,对发动机推重比、耗油率及可靠性有着重要影响。随着航空发动机推重比的不断提高,叶轮机械呈现结构紧凑、负荷攀升的趋势,这也使得其气动设计逐渐由早期的“简单设计”转向现代的“精细设计”:即从宏观气动指标的实现(效率、压比/落压比、裕度等)转向为对其内部流动细节(激波、分离流、转捩等)及其影响因素的有效控制。如吸附式叶片通过抽吸附面层来消除附面层分离[1]、叶片的掠形设计可有效控制激波的位置和强度[2],可控扩散叶型通过压力梯度的控制以防止附面层分离[3],端壁造型则通过对局部压力梯度的调控实现叶片/端壁角区的分离控制[4]等。显然,上述先进设计方法的发展很大程度上是基于对复杂内流场物理机理研究上取得的突破,其应用的效果严重依赖于对叶片表面附面层分离、激波、转捩等复杂流动现象发生的准确诊断与有效控制。然而,由于高速旋转引起的时间序列上的固有非定常性,再加上叶片通道构成的狭小流动空间,限制了实验测量技术在认识压气机复杂流动机理方面的应用,使得对高速旋转压气机复杂流场结构在准确、精细的捕捉方面尚无法达到设计者的要求。
随着计算流体力学(Computational fluid dynamic, CFD)技术的不断发展,数值模拟不仅在工程实践中发挥了重要作用,而且在探索和发现新的流动结构和相应的流动控制方法领域也发挥了积极的作用。但是,在叶轮机械中广泛应用的RANS(Reynolds averaged Navier-Stokes)方法,在高负荷分离状态的计算中性能不佳[5];而LES (Large eddy simulation)方法因其自身的原因,计算量较大,应用到叶轮机械的计算中还存在较大的困难[6],成为制约叶轮机械性能提升的关键因素。
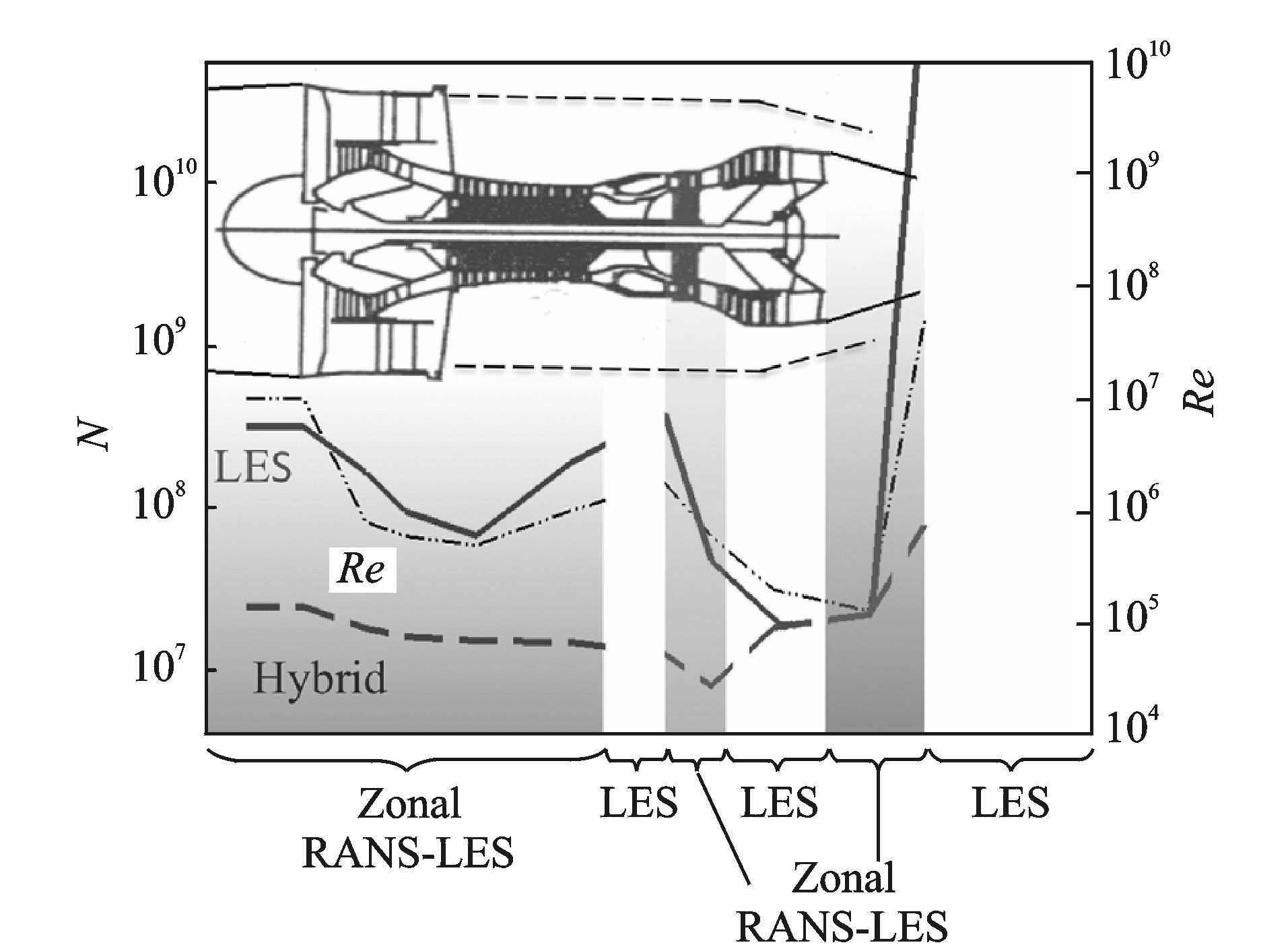
1997年Spalart[7]提出分离涡模拟方法(Detached eddy simulation, DES),属于RANS/LES耦合算法之一。如图 1所示,耦合算法(Hybrid)可以有效解决LES计算量大的问题,成为目前工程上最可能实现的高精度数值方法。此外,DES方法具有构造简单、物理意义明确、易于推广以及非固定分区的优点,自提出后得到广泛认可。由于DES兼顾RANS计算量小和LES计算精度高的特点,为压气机复杂内流场的高精度数值模拟提供新思路。
|
图 1 发动机不同部件数值方法计算量(N:网格需求量; Hybrid:RANS/LES耦合方法; Re:雷诺数) Figure 1 Numerical calculation amount of different parts of engine with different methods (N: Grid number; Hybrid: Hybrid Rans/LES; Re: Reynolds number) |
DES类方法发展近20年,受叶轮机械流场复杂性的影响,在内流场的应用还不到10年,仍存在准确性、网格、计算精度和计算量等方面的问题。本文综述DES方法的发展历程,论述DES类方法对不同物理问题预测的准确性,深入探讨其在内流场的应用现状及存在的问题,为后续的相关科研工作提供支撑和启发。
1 DES类方法发展及准确性验证1997年最早提出的DES方法又称为“DES97”,在1999年得到成功应用[8]。之后,针对DES存在的问题和缺陷展开研究,并陆续提出了多种修正方法:延迟分离涡模拟(Delay detached eddy simulation, DDES)[9]、改进延迟分离涡模拟(Improved delay detached eddy simulation, IDDES)[10]。每一种方法的提出都是针对特定问题提出的修正方法,本节将回顾DES类方法发展中遇到的关键问题及其解决方案,简要阐明以上3种方法构造思路,并论述DES类方法对复杂流动预测的准确性。
1.1 分离涡模拟方法起源RANS方法在模拟大分离流动时存在固有缺陷:RANS方法中采用的湍流模型,例如Baldwin-Lomax[11], Spalart-Allmaras[12], k-ε模型[13], k-ω模型[14]等,都是基于各项同性假设提出,可以较好地预测附着流动;但对于远离壁面剪切层的大分离流动,由于湍流存在较强的各项异性,因此这些湍流模型无法对该类问题进行准确预测。
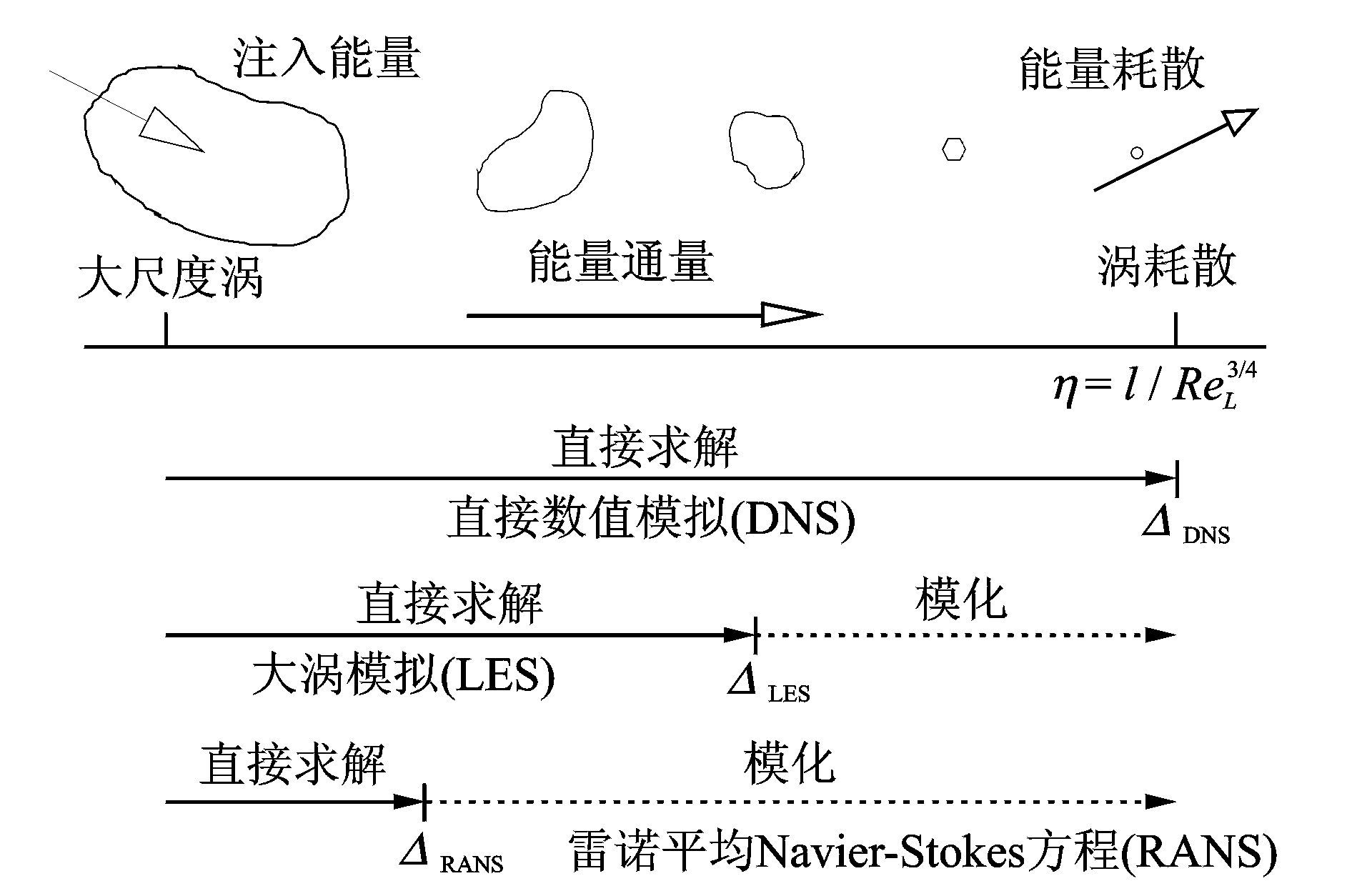
LES方法通过对更小尺度涡的直接解析而得到更为精确的流场,如图 2所示。但对很多高雷诺数问题,其计算代价现阶段工程无法承受。LES方法网格需求量的突增主要来源于壁面边界层内网格的加密[15]。然而很多时候人们更关心的是远离壁面区域流场的非定常信息,例如尾迹、涡脱落、涡破碎等。因此,如果在近壁面区域采用RANS方法对“附着涡”[16]进行模化,在远离壁面区域采用LES方法对“分离涡”直接解析,如图 3所示,即可兼顾两者优势。这即是发展DES方法的动机。
|
图 2 不同数值模拟方法解析涡尺度对比图 Figure 2 Comparison of different numerical simulation methods for resolved vortex scale |
|
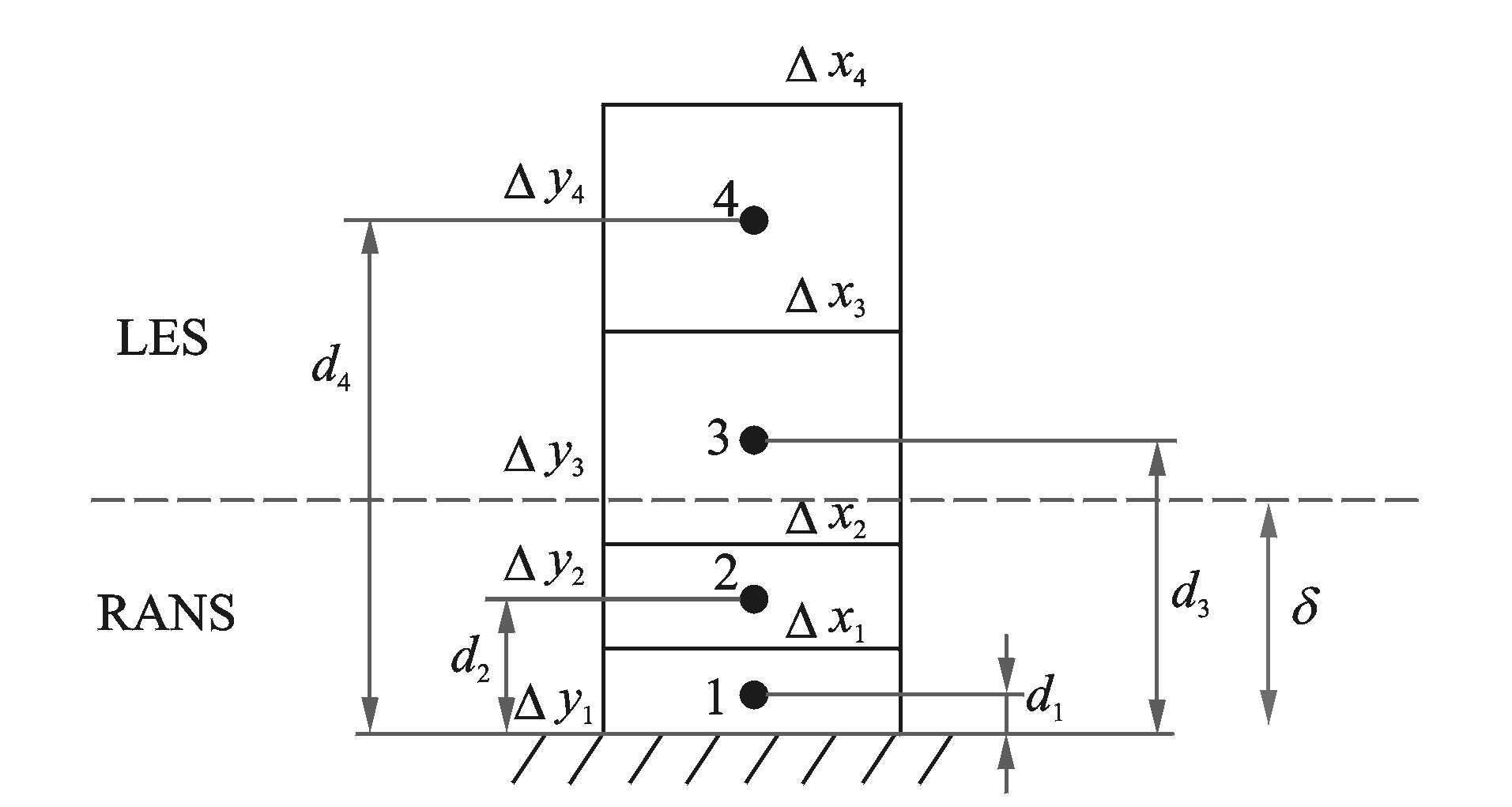
图 3 DES分区示意图(δ:附面层厚度;di:网格中心点到最近壁面距离;Δxi,Δyi:网格单元尺度) Figure 3 Sketch map of DES method (δ: boundary layer thickness; di: distance between grid center and nearest wall; Δxi, Δyi: grid scale in different directions) |
1.2 分离涡模拟方法发展 1.2.1 DES方法
DES方法的思想是对原来湍流模型中混合长度进行修改,通过嵌入模型开关来控制RANS和LES方法的求解区域。下面以基于一方程Spalart-Allmaras(S-A)模型的DES方法为例阐述DES构造方法。
守恒形式的S-A模型准运动涡黏性系数输运方程为
| $\begin{array}{l} \frac{\partial }{{\partial t}}(\rho {{\hat \upsilon }_T}) + \frac{\partial }{{\partial {x_i}}}(\rho {{\hat \upsilon }_T}{u_i}) = \\ \frac{1}{\sigma }\underbrace {\left\{ {\frac{\partial }{{\partial {x_i}}}\left[ {(\rho {\mu _l} + \rho {{\hat \upsilon }_T})\frac{{\partial {{\hat \upsilon }_T}}}{{\partial {x_i}}}} \right] + {c_{b2}}\rho \frac{{\partial {{\hat \upsilon }_T}}}{{\partial {x_i}}}\frac{{\partial {{\hat \upsilon }_T}}}{{\partial {x_i}}}} \right\} + }_{{\rm{扩散项}}}\\ \underbrace {{c_{b1}}\rho \hat S{{\hat \upsilon }_T}}_{{\rm{产生项}}} - \underbrace {{c_{w1}}{f_w}\rho {{\left( {\frac{{{{\hat \upsilon }_T}}}{d}} \right)}^2}}_{{\rm{耗散项}}} \end{array}$ | (1) |
式中:xi,t分别为空间、时间坐标;
DES方法只对S-A模型中的耗散项进行修改,即将输运方程耗散项中d改为
| ${{\tilde d}_{{\rm{DES}}}}{\rm{ = min}}(d,{C_{{\rm{DES}}}}\mathit{\Delta })$ | (2) |
式中:CDES为经验系数,通常取0.65;Δ代表着亚格子模型滤波尺度,通常指单元最大尺度,如图 3所示, 即Δi=max(Δxi, Δyi, Δzi)。假设在物面附近有d1<CDESΔ1,d2<CDESΔ2,根据式(2) 有
| ${c_{b1}}\rho \hat S{{\hat \upsilon }_T} = {c_{w1}}{f_w}\rho {\left( {\frac{{{{\hat \upsilon }_T}}}{{{C_{{\rm{DES}}}}\mathit{\Delta }}}} \right)^2}$ | (3) |
即
DES97方法对RANS和LES求解区域的判断严重依赖于当地网格尺度,即对网格有强烈的依赖性。具体来说,当沿着平行于壁面方向逐渐加密网格时,如图 3所示,会使得Δy1≤Δx1<δ,此时在附着区内开关提前打开,提前进入LES状态,但网格尺度又不足以解析附面层内的速度脉动,即网格密度不满足LES的要求,进而导致由于雷诺应力损耗(Modeled-stress depletion, MSD)[9]而引起的非物理分离现象,这就是受到广泛关注的网格诱导分离(Grid induced separation, GIS)[9]问题。
针对GIS问题,Spalart于2006年提出延迟分离涡模拟方法[9](Delay detached eddy simulation, DDES), 通过引入延迟函数来修正混合长度降低对网格密度的过分依赖。同样以基于S-A模型的DDES方法来说明其构造思想。
修正混合长度
| ${{\tilde d}_{{\rm{DES}}}} \equiv d - {f_d}{\rm{max}}(0,d - {C_{{\rm{DES}}}}\mathit{\Delta })$ | (4) |
| ${f_d} \equiv 1 - {\rm{tanh}}({[8{r_d}]^3})$ | (5) |
用rd取代式(1) 中的r,定义与r定义类似, 即
| ${r_d} = \frac{{{{\hat \upsilon }_T} + {\mu _l}}}{{\sqrt {{L_{i,j}}{L_{i,j}}} {\kappa ^2}{d^2}}}$ | (6) |
式中:Li, j为速度梯度;κ为常数。在分子中添加层流黏性系数μl,可使得rd在近壁区确保不为零。
根据式(4~6),在近壁区与主流分离区之间的过渡区,有d>CDESΔ,0<fd<1,此时
由上述分析可知,混合长度不再完全由网格尺度所决定,而是通过随时间变化的流场对速度梯度的影响而改变的。这样DES方法中RANS和LES之间的分界面并非固定,而是会随时间变化,有效减弱了方法对网格的依赖性。由于DDES方法的优秀表现,2009年Spalart建议DDES作为新的标准DES方法。
1.2.3 IDDES方法DES方法中存在的另一个问题是对数层不匹配(Log-layer mismatch, LLM)[17]。分区模拟结果给出两个对数层:内部对数层(由RANS计算得到)和外部对数层(由LES计算得到)。但是,这两个对数层并不匹配,这将导致预测的表面摩擦降低15%~20%,该误差远远超过航空工业能够容许的范围[18]。DDES方法虽然对DES方法进行了改进,但同样未能解决LLM问题。
针对LLM问题,2006年俄罗斯圣彼得堡国立工业大学Travin联合Spalart将DDES方法与耦合壁面模型的WMLES(Wall-modeled LES)方法相结合,提出了IDDES方法[18]。该方法的改进不仅体现在滤波尺度Δ,还引入了混合函数fhyb。以基于S-A模型的IDDES为例阐明构造思路,即
| $\mathit{\Delta } = {\rm{min}}\left\{ {{\rm{max}}\left[ {0.15{d_w},0.15{\mathit{\Delta }_{{\rm{max}}}},{\mathit{\Delta }_{wn}}} \right],{\mathit{\Delta }_{{\rm{max}}}}} \right\}$ | (7) |
| $\begin{array}{l} {f_{{\rm{hyb}}}} = {\rm{max}}\left\{ {\left( {1 - {f_d}} \right),{f_{{\rm{step}}}}} \right\};{\rm{ }}{f_{{\rm{step}}}} = \\ {\rm{min}}\left\{ {2{e^{ - 9{\alpha ^2}}},1.0} \right\};\alpha = 0.25 - \frac{d}{{{\mathit{\Delta }_{{\rm{max}}}}}} \end{array}$ | (8) |
式中:Δwn为垂直壁面方向的网格尺度,具体来看,新构造的滤波尺度将流场分为3个部分。远离壁面时有d=Δmax,回归到了与DES相同的形式,非常靠近壁面时Δ=0.15hmax,其他位置则是二者的一个线性混合[15]。另外,为了防止在RANS和LES区域交界面附近出现RANS雷诺应力过度损耗的问题,也就是MSD问题,引入了一个正函数
| ${f_{{\rm{restore}}}} = {\rm{max}}\left\{ {\left( {{f_{{\rm{hill}}}} - 1} \right),0} \right\}{f_{{\rm{amp}}}}$ | (9) |
| $\begin{array}{l} {f_{{\rm{hill}}}} = \left\{ {\begin{array}{*{20}{l}} {2{{\rm{e}}^{ - 11.09{\alpha ^2}}}} & {\alpha \ge 0}\\ {2{{\rm{e}}^{ - 9.0{\alpha ^2}}}} & {\alpha < 0} \end{array}} \right.\\ {f_{{\rm{amp}}}} = 1 - {\rm{max}}\left\{ {{f_t},{f_l}} \right\}\\ {f_t} = {\rm{tanh}}\left[ {{{\left( {{{3.55}^2}{r_d}} \right)}^3}} \right],{f_l} = {\rm{tanh}}\left[ {{{\left( {{{1.63}^2}{r_{dl}}} \right)}^{10}}} \right] \end{array}$ | (10) |
| $\begin{array}{l} {r_{dl}} = \frac{1}{{{\kappa ^2}{d^2}}} \cdot \frac{{{\nu _l}}}{{{\rm{max}}\left( {{L_{ij}}{L_{ij}},{{10}^{ - 10}}} \right)}}\\ {r_{dt}} = \frac{1}{{{\kappa ^2}{d^2}}} \cdot \frac{{{{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over \nu } }_t}}}{{{\rm{max}}\left( {{L_{ij}}{L_{ij}},{{10}^{ - 10}}} \right)}} \end{array}$ | (11) |
对于探测器函数rdl和rdt, 相当于把DDES当中的rd被拆成黏性底层和对数区两部分。最终混合长度定义为
| ${{\tilde d}_{{\rm{IDDES}}}} = {f_{{\rm{hyb}}}}\left( {1 + {f_{{\rm{restore}}}}} \right)d + \left( {1 - {f_{{\rm{hyb}}}}} \right){C_{{\rm{DES}}}}\mathit{\Delta }$ | (12) |
虽然DES的提出仅是基于S-A模型,但可以推广到多种RANS湍流模型。目前已发展了基于零方程[19],一方程[20],二方程[21-22]雷诺模型以及耦合转捩模型[23]的DES类方法。由于构造思路相同,这里不再赘述。目前研究中常见的还是基于S-A、k-ωSST的DES类方法。
1.3 DES类方法准确性验证方法的提出不仅需要理论基础,还需要开展多方面的测试来校核其准确性。DES方法的提出是针对高雷诺数大分离流动难以准确预测的问题,那么DES方法对大分离、层流分离、转捩等物理问题的预测能力如何?为明确这些问题,早期开展了很多基于简单物理模型的准确性验证工作。简单模型在可以反映物理现象的同时较为方便地获得实验数据,便于进行验证。
湍流分离问题是叶轮机械中常见而富有挑战的流动问题。早期开展了以简单模型为研究对象、针对高/低雷诺数大分离问题的经典测试。Travin[24]、英国南安普顿大学的Nishino[25]以及国内中国空气动力研究与发展中心程江涛[26]、南京航空航天大学邓枫[27]、中国科学技术大学Lu[28]等多家研究机构以圆柱绕流为测试对象,对Re从103~106量级的流动分离问题进行验证,包含层流分离及湍流分离问题。通过与实验及URANS方法的对比,证明了DES方法无论在涡解析的精细程度方面还是对时均参数预测能力方面均优于URANS,尤其在层流分离的情况下性能更佳。但研究中也发现一些问题:
(1) 灰区效应影响对小分离流动模拟的精度
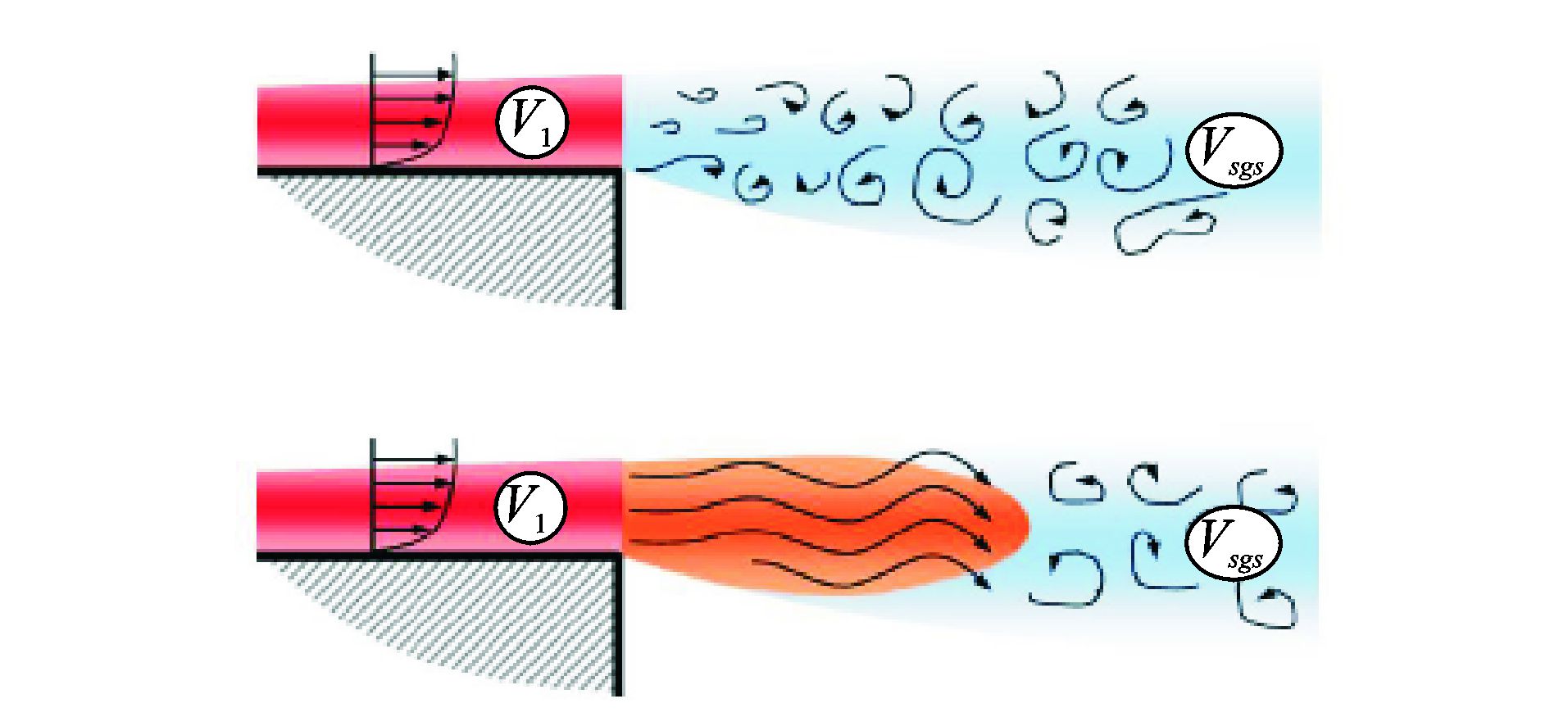
“灰区(Grey area)”指RANS到LES的过渡区域[29]。如图 4所示,当气流突然离开壁面进入自由剪切层时,由于上游RANS模化的湍流黏性系数通过对流进入LES区域,对湍流脉动的解析带来较大的抑制,使得灰区内的小尺度分离涡被抹平,引入模拟误差。
|
图 4 理想的RANS/LES混合方法模拟效果(上)与实际模拟效果(下)[29] Figure 4 Outline of ideal hybrid RANS/LES (up) and actual simulation result (down)[29] |
Travin[24]在验证工作中发现,圆柱绕流的数值模拟中,回流区的尺度和湍流应力的评估误差相对较大,尤其在湍流分离的工况下(层流分离预测的准确性相对较好)。2008年Nishino[25]也在高雷诺数情况下发现了类似的问题。对于这个现象Travin的解释是:误差的来源有很多,仅仅减小其中的一项误差并不能让求解结果区域完美[24]。本文认为是受“灰区”问题的影响。当Re较低时,流体本身的分子黏性(μmolecule)较大,数值计算中总黏性系数μtotal=μmolecule+μturbulence,发生层流分离后由于灰区效应而引入湍流黏性(μturbulence)内的误差对总黏性系数的影响较小;但当Re较大时,上游RANS区域内较大的涡黏性通过扩散方程传递到下游LES方法区域,此时μmolecule较小,μturbulence引入的误差对μtotal的影响较大,即灰区效应明显。
灰区效应是这类方法研究的难点也是热点,为了解决灰区问题有很多尝试[30-32],但是这些方法由于缺乏普适性,所以并没有得到广泛的应用。2015年,Shur[33]对原来DES方法的亚格子模型滤波尺度进行修改,加速RANS到DES的过渡,并在DDES和IDDES中测试[34], 得到较好的结果。
(2) 转捩问题的精确预测需要特殊处理
在涡轮中或压气机处于高空低雷诺数条件下,附面层转捩也成为叶轮机械中是普遍存在流态。转捩对叶轮机械气动性能有着显著影响[35],准确地预测转捩对低损失层流叶型的设计具有重要意义[36]。而Travin[24]的圆柱绕流测试、Li[37]对NACA-0012翼型的测试结果都显示,基于S-A模型的DES方法对并不能很好预测附面层转捩。为此,Li[37]在基于S-A模型的DES方法中引入转捩,即人为给定转捩位置(S-A模型的限制),模拟结果得到改善。分析原因,虽然DES方法提高了涡的解析能力,但在层流区域和分离刚开始发生的一段距离内都采用的是RANS湍流模型,对转捩问题的精确预测受限于RANS湍流模型本身,需要采用转捩模型进行修正。2011年,Niels[23]发展了耦合

|
图 5 圆柱绕流实验与数值模拟阻力对比[23] (Transitional:带转捩模型;Fully turb:全湍流模型) Figure 5 Comparison of computed drag force for fully turbulent and transitional computations with measurements[23](Transitional: DES results based on transition model; Fully turb: DES results based on fully turbulence model) |
2 DES类方法在叶轮机械内流场中的应用现状
虽然通过简单模型验证了DES类方法的有效性和相对于RANS方法的优势,但在叶轮机械的实际应用中,由于几何更为复杂,且存在多种复杂涡系的干涉作用,仍然有新的难点需要解决。由于不同类型的叶轮机械的数值模拟中存在的难点不同,例如对于叶栅的数值模拟,难点在于对三维角区分离的准确预测;对于亚声速叶轮机械而言,难点在于对大尺度分离涡的准确捕捉;对于跨声速叶轮机械而言,又引入了对激波附面层干扰问题。因此,本节以研究对象为分类依据,分别针对上述3种叶轮机械内DES方法的应用现状展开讨论。
2.1 DES类方法在直叶栅流场模拟中的应用DES类方法在叶栅流场中的应用起始于清华大学李雪松等[38-39],2007年首次将基于S-A模型的DES类方法引入压气机叶栅内流场的数值中,与实验结果对比显示,在时均性能上DES相比于RANS更接近实验结果。随后,日本名古屋大学Mahmoud等[40]采用基于S-A模型的DES和DDES方法分析涡轮叶栅尾迹能量分离机理,并指导了低损失叶型的设计[41]。西北工业大学高丽敏课题组则以高负荷压气机叶栅为研究对象,初步探讨了在内流场中格式精度对DES/DDES模拟结果的影响[42-43]。
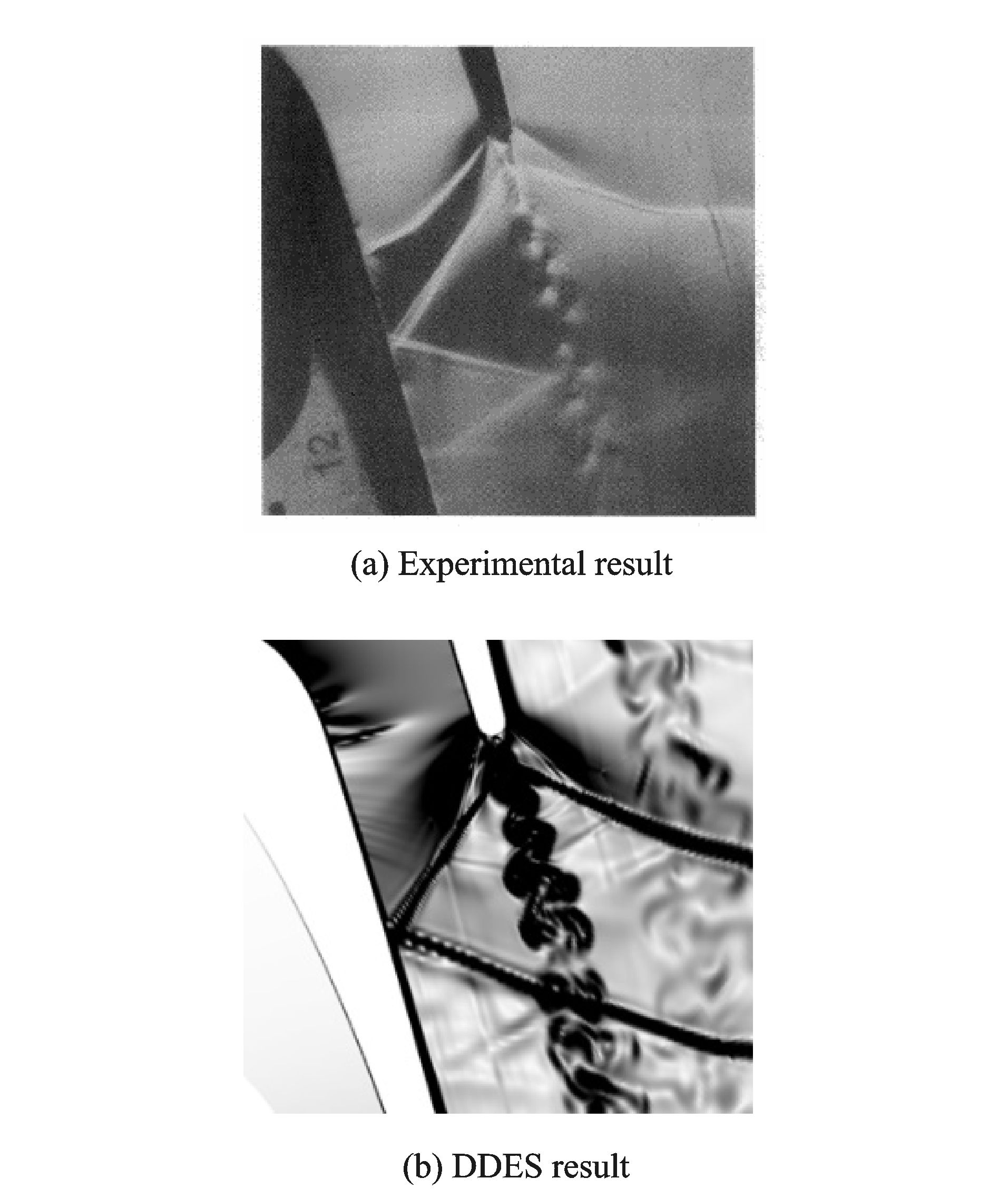
随着DES类方法的发展,研究人员逐渐尝试将其应用于激波/附面层干扰问题。2008年李雪松等将基于S-A模型的DDES方法用于跨声速涡轮叶栅数值模拟中,却发现虽然DDES能有效计算亚声速流动,但在计算跨声流动时精度下降严重[44]。李雪松认为是由于激波/尾迹干扰导致DDES中迟滞函数失效所致。然而,2015年清华大学苏欣荣等[45-46]同样采用基于S-A模型的DDES方法对跨声涡轮导叶进行数值模拟,却在激波以及激波附面层/尾迹干扰等细节的捕捉方面得到较好的结果,如图 6, 7所示,本文认为是数值格式精度的影响,具体将在第3节讨论。
随着商用软件的发展,在Fluent, NUMECA等软件当中嵌入了DES类方法,很多基于商用软件的研究工作随之展开[47-49]。2013年,上海交通大学的马威[48]则通过DDES方法成功捕捉到实验中出现的角区分离“双峰”现象,但RANS方法却无法捕捉。随后,北京航空航天大学的柳阳威[47]和侯安平[49]采用基于S-A模型的DDES方法对压气机叶栅的数值模拟,从宏观时均参数上证实了DDES方法对三维角区分离各项异性湍流模拟的准确性。
2.2 DES类方法在转子或级环境下应用揭示压气机旋转失速前流动非定常特性可以在设计中更好地预测失速边界,这也是基于失速控制的高性能压气机设计的基础。在转子和级环境条件下,存在转子与机匣以及转、静子之间的相对运动,非定常现象更为显著。
2008年,顾春伟[50]、李雪松[51]等做了DES类方法在压气机转子及单级压气机中应用的尝试,但由于没有实验数据对比,其准确性无从得知。为了验证DES类方法在亚声速叶轮机械内流场应用的准确性,2011年起,日本九州大学Yamada[52]和Kusano[53]以及华北电力大学王晓东等[54]分别从宏观性能[52]和时均流场细节[53-54]的角度将数值与实验结果进行了对比,证明了DES在低速轴流压气机中应用的准确性,并于2015年,首次对7级亚声速压气机进行全环、非设计工况数值模拟,计算量达到DES类方法在内流场应用的顶峰,每级静压比数值模拟与实验对比如图 8所示,可见DES对前面级的预测精度较高,对后面级逊于RANS。

|
图 8 非设计工况每级静压比(7级压气机)[55] Figure 8 Stage pressure ratios at off-design point (Front 7-stage simulation)[55] |
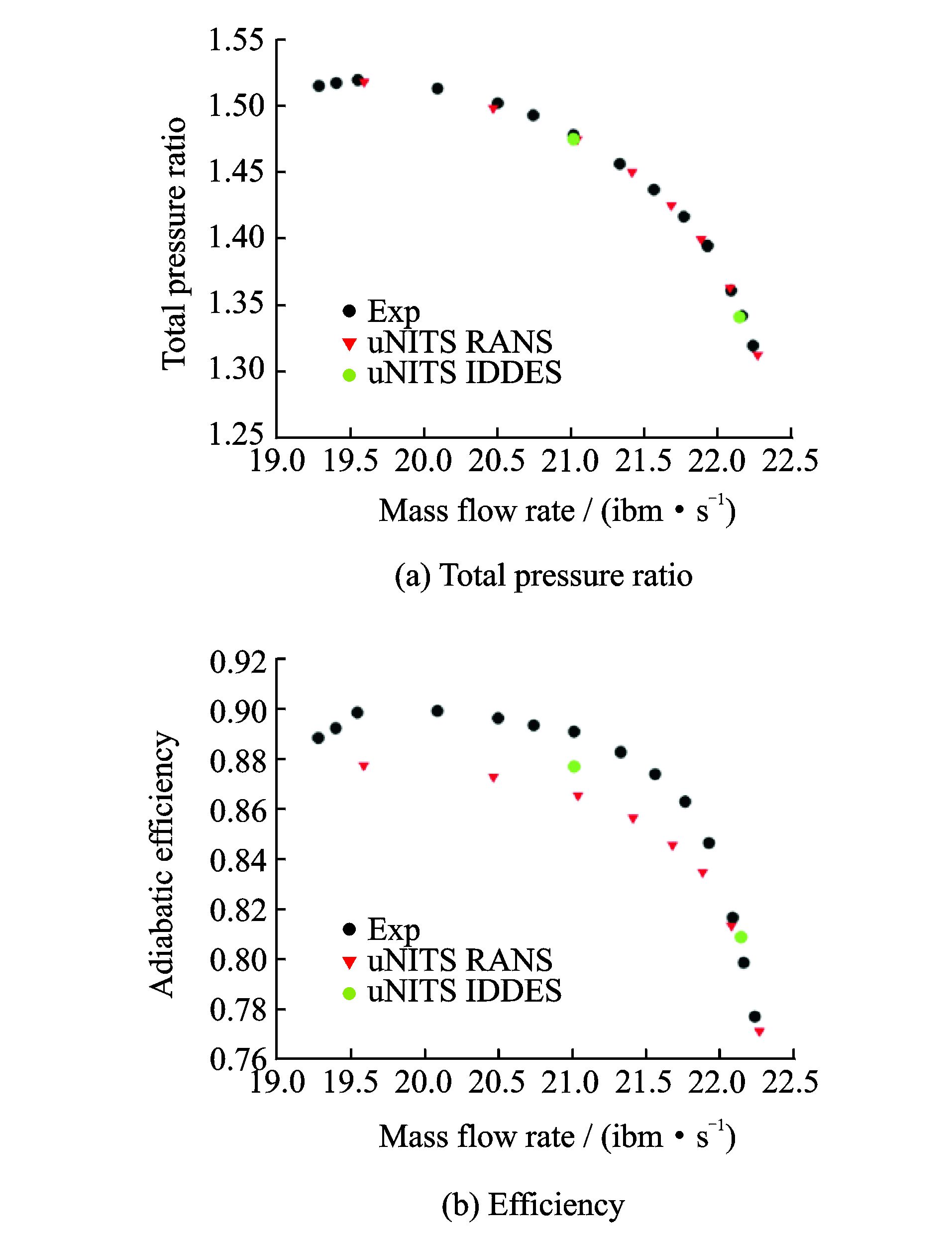
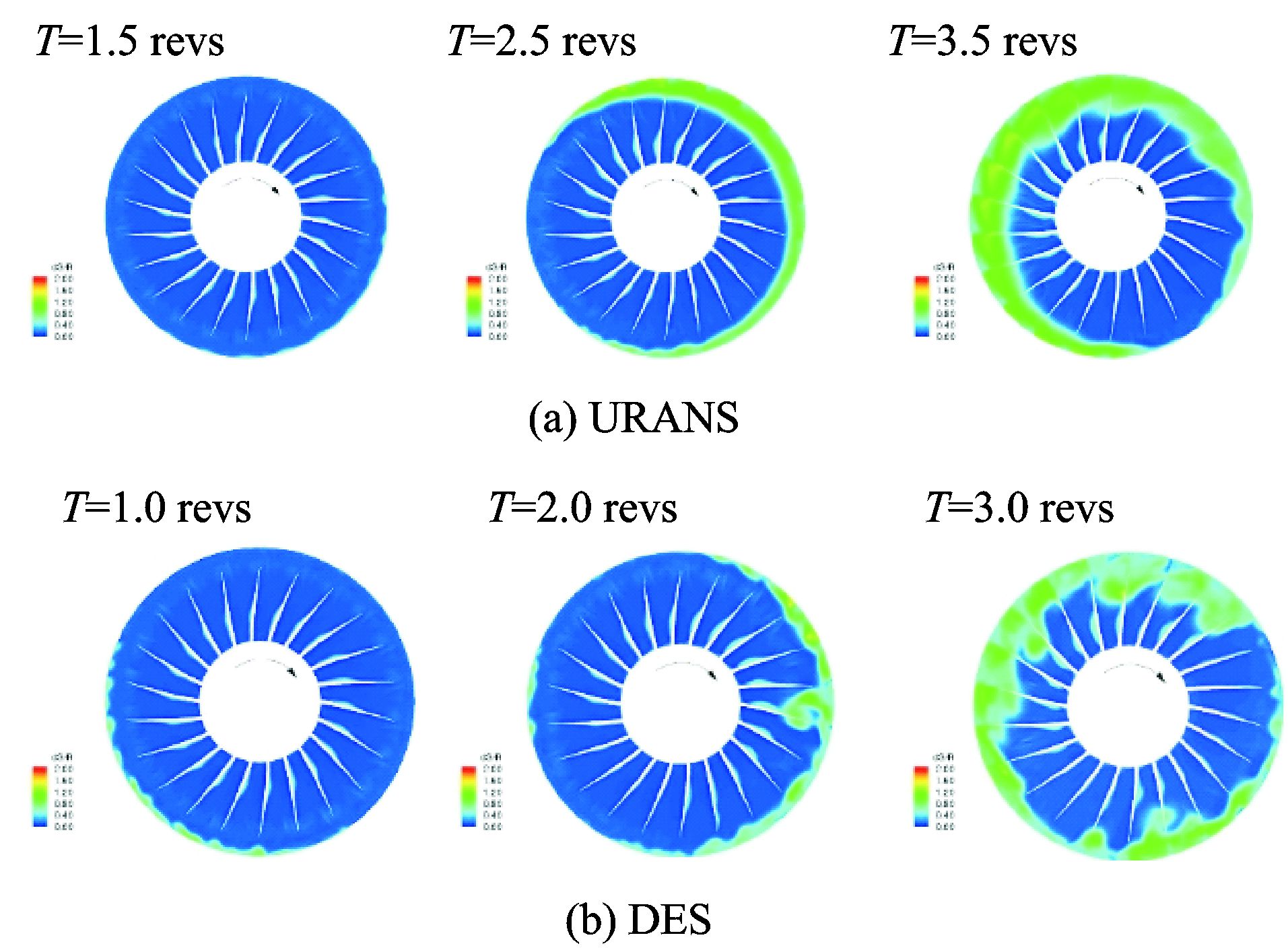
为了提高单级压气机压比,转子转速不断提高,跨声速流动成为高负荷压气机常见的流动特征。开展DES类方法在跨声速叶轮机械中应用研究的课题组主要是美国迈阿密大学的Zha以及清华大学的符松课题组。2011~2016年间,Zha课题组对DES和DDES方法在跨声速单转子[56-57]、单级跨声速压气机[58-59]中数值模拟的准确性进行校核,通过与URANS方法的对比,在近失速工况下DES类方法对宏观性能的预测更为准确,而且在对间隙泄漏流、角区分离等二次流动的捕捉更为精细(图 9),并获得了与URANS结果不同的失速特性。在国内,清华大学符松课题组采用IDDES方法对某跨声速转子的数值模拟结果也证明了IDDES方法在近失速工况对效率预测的准确程度[60-61],如图 10所示,并在失速机理方面挖掘出与URANS模拟结果不同的失速诱因。
|
图 9 Rotor67近失速工况近前缘S3流面不同时刻熵云图[56] Figure 9 Entropy change of axial plane near rotor leading edge during rotating stall in Rotor67[56] |
3 内流场应用中存在的问题及发展方向
虽然DES类方法已经在叶栅、转子及叶轮机械级中得到应用,但很多工作都是在原有RANS方法基础上直接修改混合长度完成,对DES类方法在叶轮机械中应用的精度、网格依赖性、计算量等问题还缺乏深入分析,下面着重讨论目前在叶轮机械中DES方法的应用仍然存在问题及发展方向。
(1) 格式精度对DES类方法适应性问题
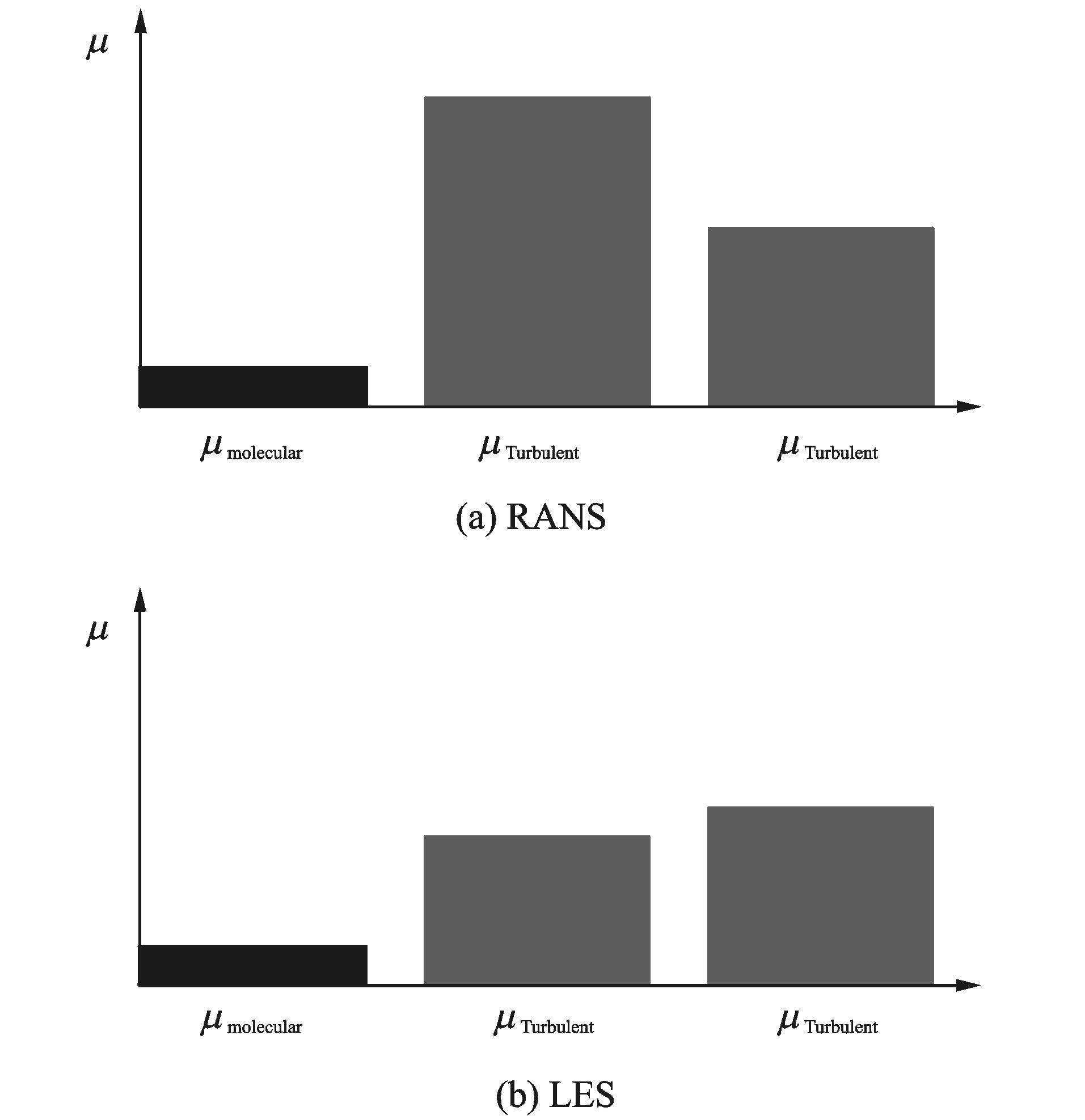
数值计算中的总黏性系数由分子黏性(μmolecular)、湍流黏性(μTubulence)和数值黏性(μNumercial)组成。其中数值黏性是由于对无黏项离散格式的数值耗散引入。在RANS方法中,无黏项离散格式一般优先考虑收敛性、复杂外形适用性等,因此通常采用数值耗散较大的低阶迎风格式。RANS方法湍流黏性本身较大,如图 11所示,纵然格式耗散较大,但对模拟结果影响较小。然而在LES当中,湍流输运方程中耗散项减小,μTubulence也相应降低,如果仍然采用相同的数值离散格式,总黏性系数中数值黏性占据主导作用,最终导致计算错误。因此在LES计算域需要采用高精度、低耗散的数值格式。但耗散和计算稳定性却是一对矛盾。因此DES类方法的准确、稳定与数值离散格式有着必然的联系。
前文2.1节所述的李雪松[39]和苏欣荣[45]对跨声速问题预测精度的差异,本文认为正是由于格式精度造成。从目前的应用来看(表 1),DES类方法在叶轮机械中应用时多采用2阶或3阶精度的格式,虽然在恶劣工况下对宏观性能的预测能力提高,但仍然存在盲目性。
| 表 1 DES类方法在叶轮机械中应用总结 Table 1 Summary of DES method used in turbomachinery |
西北工业大学高丽敏课题组[42]和法国国家航空航天中心的Marty[63]等就格式精度对DES方法数值结果的影响开展研究,发现格式精度与涡结构的解析精度息息相关,但测试算例有限,缺乏与实验的对比,目前尚没有形成系统性的结论。
另外,DES方法的LES区域,湍流输运方程中降低了耗散项,对流项的作用更加明显,因此输运方程对流项的离散精度对结果影响程度加大,但目前该问题仍未得到关注。
(2) 网格依赖性问题
RANS方法随着网格数量的增加,数值模拟结果则不再变化,达到网格无关性状态。但是对于DES而言,网格尺度与滤波尺度直接相关,加密网格则可以得到更加精细的涡结构,因此,很难找到一个无关性网格。表 1中总结了在内流场数值模拟中,DES类方法针对不同问题所需的网格数,从表中看出目前针对相同的问题所用的网格量级差异较大。例如同样针对涡轮叶栅,Mahmoud[40]和苏欣荣[45]所用网格相差3个量级。DDES方法在减弱DES97对网格依赖性问题做出贡献,较好地解决了网格诱导分离问题,但在LES区域仍然选用网格最大尺度作为滤波尺度,即Δ=max(Δx, Δy, Δz),此时网格短边信息将被浪费,划分网格的长宽比也将一定程度地决定预测结果。基于简单的物理模型,人们提出多种滤波尺度定义方法,例如Δ=(ΔxΔyΔz)1/3, 以及
目前除IDDES方法外,在叶轮机械内使用DES和DDES结果均采用最大网格尺度作为滤波尺度,IDDES方法构造复杂,无疑极大地增加了计算量,因此可以考虑采用考虑3个方向网格尺度的滤波尺度,减少对网格的依赖性。
(3) 对设计工况及小分离流动预测不准
目前DES类方法在内流场的应用主要集中在失速或堵塞等恶劣工况下,在设计工况或小分离工况下,甚至会出现DES类预测精度低于RANS的情况。例如Kim[65]在对跨声速转子叶轮的的研究中发现峰值效率工况下,DDES模拟结果没有RANS方法准确。对于流场中存在大分离的情况,漩涡的生成、发展及耗散过程发展剧烈,贯穿整个流场,形成了反馈机制,使得前文所述的灰区变得模糊不清甚至忽略不计[17];而对于小分离流动而言,较弱的流动信息传递使得这种反馈机制几乎不存在,流动分离越小,RANS对下游LES区域的影响越大,即灰区效应越明显[15]。在简单物理模型中,对灰区效应进行了丰富的研究,但是在叶轮机械中,对灰区效应的考虑几乎处于空白。然而在级环境下,由于轴向间距较小,上游尾迹、分离涡造成的流场不均匀性对下游流场性能有明显影响,因此,很有必要在叶轮机械中考虑灰区效应对小分离及无分离工况数值模拟的准确性影响。
(4) 有待发展精细化实验测量手段
为了验证DES类方法在叶轮机械领域应用的准确性,数值模拟与实验结果进行了大量的对比,但大部分都是对时间平均的宏观性能参数进行对比。DES方法在时间和空间上都有较高的分辨率,通过加密网格可以捕捉更小、更精细的涡结构,但同时也存在例如网格诱导分离等非物理现象。由于目前能够提供校核的实验数据无论是空间还是时间分辨率都很难达到高精度数值模拟的要求,所以DES类方法对精细涡结构预测精度的判断主要依赖LES计算结果,例如NTS的Garbaruk[66]对低速叶栅采用DES进行数值模拟,并与斯坦福大学You[67]对同样叶栅的LES结果进行对比来验证DES对涡系的捕捉能力。而对于这些流场细节捕捉的正确性则无从得知。
因此,在发展高精度数值模拟方法的同时,亟待发展适用于内流场的精细化实验测量方法,例如快速响应压力敏感涂料测压法(Fast-respond pressure sensitive paint)、纹影法、三维PIV测速技术等,为DES类方法准确性校核提供精细化实验数据。
(5) 如何降低计算量的问题
DES类方法作为RANS/LES耦合方法,可以在很大程度上减少LES方法对网格的需求量,表 1中总结了目前内流场DES类方法的数值模拟中针对不同问题数据量,可以看出尤其在级环境下,网格量达到千万量级;此外,时间上的非定常和复杂的空间离散格式,计算量仍然不可小觑。为此,通过分区高精度处理的方法减少计算量具有很强的工程应用价值。即在非定常性较弱以及流场结构简单的地方采用RANS方法,例如对于叶栅进口延伸段、压气机的进口导叶等,而仅在复杂流场附近采用DES类方法,网格划分也只需加密DES区域的网格。如此,可以有效减少计算量。同理,对于数值离散格式精度而言,只在存在激波、多种涡系干涉等区域采用高精度格式,也是解决高精度计算量高的方法之一。
需要注意的是,采用高/低精度混合方法时,混合界面的选择和处理方法需要相当谨慎,处理不当则会出现类似于DES方法中的“灰区效应”,使得低精度区域的数值黏性引入高精度区域而降低高精度数值方法的效果。
| [1] |
曹志远. 附面层抽吸对轴流压气机流动控制及性能影响的研究[D]. 西安: 西北工业大学, 2014.
CAO Zhiyuan. Investigation of boundary layer suction on the influence of flow control and performance of axial flow compressor[D]. Xi′an: Northwestern Polytechnical University, 2014. |
| [2] | JIN H, JIN D, ZHU F, et al. Design of a highly loaded transonic two-stage fan using swept and bowed blading[C]//ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition. [S.l.]:American Society of Mechanical Engineers, 2011: 213-224. |
| [3] |
高丽敏, 蔡宇桐, 李瑞宇, 等. 一种压气机可控扩散叶型稳健优化设计方法: 中国, CN105046041A[P]. 2015-11-11.
GAO Limin, CAI Yutong, LI Ruiyu, et al. A method for robust optimization design of compressor airfoil: China, CN105046041A[P]. 2015-11-11. |
| [4] |
张鹏, 刘波, 毛晓晨, 等.
三维造型和非轴对称端壁在跨声速压气机中的应用[J]. 推进技术, 2016, 37(2): 250–257.
ZHANG Peng, Liu Bo, MAO Xiaochen, et al. Application of 3D blading and non-axisymmetric endwall in a transonic compressor[J]. Journal of Propulsion technology, 2016, 37(2): 250–257. |
| [5] | WANG Z J. High-order computational fluid dynamics tools for aircraft design[J]. Philosophical Transactions of the Royal Society Mathematical Physical & Engineering Sciences, 2014, 372(2022): 20130318–20130318. |
| [6] | HAH C. Large eddy simulation of transonic flow field in NASA rotor 37[C]// AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. [S.l.]:AIAA, 2009. |
| [7] | SPALART P R, JOU W H, STRELETS M, et al. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach[J]. Advances in DNS/LES, 1997, 1: 4–8. |
| [8] | SHUR M, SPALART P R, STRELETS M, et al. Detached-eddy simulation of an airfoil at high angle of attack[J]. Engineering Turbulence Modelling & Experiments, 1999, 4: 669–678. |
| [9] | SPALART P R, DECK S, SHUR M L, et al. A new version of detached-eddy simulation, resistant to ambiguous grid densities[J]. Theoretical and Computational Fluid Dynamics, 2006, 20(3): 181–195. DOI:10.1007/s00162-006-0015-0 |
| [10] | GRISTSKEVICH S M, GARBARUK V A, SCHVTZE J, et al. Development of DDES and IDDES formulations for the k-ω shear stress transport model[J]. Flow Turbulence Combust, 2012, 88: 431–449. DOI:10.1007/s10494-011-9378-4 |
| [11] | BALDWIN B, LOMAX H. Thin-layer approximation and algebraic model for separated turbulentflows[C]//AIAA 16th Aerospace Sciences Meeting. [S.l.]:AIAA, 1978: 257. |
| [12] | SPALART P R, ALLMARAS S R. A one-equation turbulence model for aerodynamic flows[J]. La Recherche Aérospatiale, 2003, 439(1): 5–21. |
| [13] | LAUNDER B E, SPALDING D B. The numerical computation of turbulent flows[J]. Computer Methods in Applied Mechanics and Engineering, 1974, 3(2): 269–289. DOI:10.1016/0045-7825(74)90029-2 |
| [14] | WILCOX D C. Formulation of the k-ω turbulence model revisited[J]. AIAA Journal, 2008, 46(11): 2823–2838. DOI:10.2514/1.36541 |
| [15] |
王翔宇. RANS/LES混合方法在湍流精细数值模拟中的应用与改进[D]. 西安: 西北工业大学, 2016.
WANG Xiangyu. The application and improvement of hybrid RANS/LES method in the fine numerical simulation of turbulent flow[D]. Xi′an: Northwestern Polytechnical University, 2016. |
| [16] | JIMÉNEZ J. Near-wall turbulence[J]. Physics of Fluids, 2013, 25(10): 97–120. |
| [17] | SPALART P R. Detached eddy simulation[J]. The Annual Review of Fluid Mechanics, 2009, 41: 181–202. DOI:10.1146/annurev.fluid.010908.165130 |
| [18] | TRAVIN A K, SHUR M L, SPALART P R, et al.Improvement of delayed detached-eddy simulation for LES with wall modeling [C]// European Conference on Computational Fluid Dynamics. The Netherlands:TU Delft, 2006. |
| [19] | NIKITIN N V, NICOUD F, WASISTHO B, et al. An approach to wall modeling in large-eddy simulations[J]. Physics of Fluids, 2000, 12(7): 1629–1632. DOI:10.1063/1.870414 |
| [20] | TRAVIN A, SHUR M, STRELETS M M, et al. Physical and numerical upgrades in the detached-eddy simulation of complex turbulent flows[C]//Advances in LES of Complex Flows. Springer Netherlands: Springer, 2002: 239-254. |
| [21] | YAN J, MOCKETT C, THIELE F. Investigation of alternative length scale substitutions in detached-eddy simulation[J]. Flow Turbulence and Combustion, 2005, 74(1): 85–102. DOI:10.1007/s10494-005-6916-y |
| [22] | JEE S K, SHARIFF K. Detached-eddy simulation based on the v2-f model[J]. International Journal of Heat and Fluid Flow, 2014, 46: 84–101. DOI:10.1016/j.ijheatfluidflow.2013.12.006 |
| [23] | NIELS N S, BECHMANN A, ZAHLE F. 3D CFD computations of transitional flows using DES and a correlation based transition model[J]. Wind Energy, 2011, 14(1): 77–90. DOI:10.1002/we.v14.1 |
| [24] | TRAVIN A, SHUR M, STRELETS M, et al. Detached-eddy simulations past a circular cylinder[J]. Flow, Turbulence and Combustion, 2000, 63(1): 293–313. |
| [25] | NISHINO T, ROBERTS G T, ZHANG X L, et al. Unsteady RANS and detached-eddy simulations of flow around a circular cylinder in ground effect[J]. Journal of Fluids and Structures, 2008, 24(1): 18–33. DOI:10.1016/j.jfluidstructs.2007.06.002 |
| [26] |
陈江涛, 张培红, 周乃春, 等.
基于SA湍流模型的DES方法应用[J]. 北京航空航天大学学报, 2012, 38(7): 905–909.
CHEN Jiangtao, ZHANG Peihong, ZHOU Naichun, et al. Application of detached-eddy simulation based on spalart-allmaras turbulence model[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(7): 905–909. |
| [27] |
邓枫, 伍贻兆, 刘学强.
用DES数值模拟分离绕流中的旋涡运动[J]. 计算物理, 2008, 25(6): 683–688.
DENG Feng, WU Yizhao, LIU Xueqiang. Simulation of vortex in separated flows with DES[J]. Chinese Journal of Computational Physics, 2008, 25(6): 683–688. |
| [28] | XU Changyue, CHEN Liwei, LU Xiyun. Large-eddy and detached-eddy simulations of the separated flow around a circular cylinder[J]. Journal of Hydrodynamics, 2007, 19(5): 559–563. DOI:10.1016/S1001-6058(07)60153-X |
| [29] | MICHEL U, ESCHRICHT D, GRESCHNER B, et al. Advanced DES methods and their application to aeroacoustics[C]//Progress in Hybrid RANS-LES Modelling.Berlin Heidelberg:Springer, 2010: 59-76. |
| [30] | DECK S. Recent improvements in the Zonal Detached Eddy Simulation (ZDES) formulation[J]. Theoretical and Computational Fluid Dynamic, 2012, 26: 523–550. DOI:10.1007/s00162-011-0240-z |
| [31] | KOK J C, van der VEN H. Destabilizing free shear layers in X-LES using a stochastic subgrid-scale model[C]// Progress in Hybrid RANS-LES Modelling. Berlin Heidelberg: Springer, 2010:179-189. |
| [32] | KOK J C, van der VEN H. Capturing free shear layers in hybrid RANS-LES simulations of separated flow[R]. Second Symposium "Simulation of Wing and Nacelle Stall" NLR-TP-2012-333. Germany: National Aerospace Laboratory, 2012. |
| [33] | SHUR M L, SPALART P R, STRELETS M K, et al. An enhanced version of DES with rapid transition from RANS to LES in separated flows[J]. Flow, Turbulence and Combustion, 2015, 95(4): 709–737. DOI:10.1007/s10494-015-9618-0 |
| [34] | EKATERINA K G, ANDREY V G, MIKHAIL K S. Assessment of delayed DES and improved delayed des combined with a shear-layer-adapted subgrid length-scale in separated flows[J]. Flow, Turbulence and Combustion, 2017, 98(2): 481–502. DOI:10.1007/s10494-016-9769-7 |
| [35] | Hodson H P, HOWELL R J. Bladerow interactions, transition, and high-lift aerofoils in low-pressure turbines[J]. Annu Rev Fluid Mech, 2005, 37: 71–98. DOI:10.1146/annurev.fluid.37.061903.175511 |
| [36] |
高丽敏, 曾瑞慧, 杨冠华, 等. 层流叶片在压气机中的应用研究[R]. 编号162064. 无锡: 中国工程热物理学会, 2016.
GAO Limin, ZENG Ruiyu, YANG Guanhua. Application research of laminar blade in compressor[R] Paper No.162064. Wuxi: Chinese Society of Engineering Thermophysics, 2016. |
| [37] | LI D, MEN'SHOV I, NAKAMURA Y. Detached-eddy simulation of three airfoils with different stall onset mechanisms[J]. Journal of Aircraft, 2006, 4(43): 1014–1021. |
| [38] |
陈美兰, 李雪松, 顾春伟. DES和RANS模型在压气机叶栅流动中的研究[R]. 深圳: 大型飞机关键技术高层论坛暨中国航空学会2007年学术年会, 2007.
CHEN Meilan, LI Xuesong, GU Chunwei. Study on DES and RANS model in compressor cascade flow[R]. Shenzhen: Key Technology of Large Aircraft Forum and the 2007 Annual Meeting of Chinese Society of Aeronautics and Astronautics, 2007. |
| [39] |
李雪松, 顾春伟.
有大分离的压气机高压级静叶分离涡模拟研究[J]. 工程热物理学报, 2009, 30(1): 31–34.
LI Xuesong, GU Chunwei. Detached eddy simulation for the compressor stator of high-pressure cascade with massive separation[J]. Journal of Engineering Thermophysics, 2009, 30(1): 31–34. |
| [40] | ELGENDI M M, LBRAHIM M K, MORI K, et al. Energy separation in high subsonic turbine cascade[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2010, 52(178): 206–212. DOI:10.2322/tjsass.52.206 |
| [41] | ELGENDI M M, LBRAHIM M K, MORI K, et al. Novel flow control method for vortex shedding of turbine blade[J]. Transactions of the Japan Society for Aeronautical and Space Sciences, 2010, 53(180): 122–129. DOI:10.2322/tjsass.53.122 |
| [42] |
杨泽宇. 基于S-A模型的DDES方法在压气机平面叶栅中的应用研究[D]. 西安: 西北工业大学, 2016.
YANG Zeyu. Applied research of DDES based on S-A turbulence model in a compressor cascade [D]. Xi′an: Northwestern Polytechnical University, 2016. |
| [43] |
陈璇. 叶轮机械非定常数值模拟方法研究[D]. 西安: 西北工业大学, 2014.
CHEN Xuan. Study of unsteady numerical simulation in turbomachinery stage[D]. Xi′an: Northwestern Polytechnical University, 2014. |
| [44] |
李艳, 李雪松, 顾春伟.
涡轮叶栅流动分离涡模拟验证研究[J]. 工程热物理学报, 2010, 31(1): 40–43.
LI Yan, LI Xuesong, GU Chunwei. Evaluation of a detached eddy simulation in turbine cascades[J]. Journal of Engineering Thermophysics, 2010, 31(1): 40–43. |
| [45] |
林敦, 苏欣荣, 袁新.
高压透平导叶的DDES模拟[J]. 工程热物理学报, 2016, 37(10): 2084–2088.
LIN Dun, SU Xinrong, YUAN Xin. DDES simulations of a high-pressure turbine guide vane[J]. Journal of Engineering Thermophysics, 2016, 37(10): 2084–2088. |
| [46] |
卞修涛, 林敦, 苏欣荣, 等.
跨音透平中激波与边界层、尾迹干涉机理研究[J]. 工程热物理学报, 2017, 38(5): 965–969.
BIAN Xiutao, LIN Dun, SU Xinrong, et al. Study on interaction mechanism of shock wave and boundary layer, wake in transonic turbine[J]. Journal of Engineering Thermophysics, 2017, 38(5): 965–969. |
| [47] | LIU Y, YAN H, LU L. Numerical study of the effect of secondary vortex on three-dimensional corner separation in a compressor cascade[J]. International Journal of Turbo & Jet-Engines, 2016, 33(1): 9–18. |
| [48] | MA W, OTTAVY X, LU L, et al. Intermittent corner separation in a linear compressor cascade[J]. Experiments in Fluids, 2013, 54(6): 1–17. |
| [49] |
刘若阳, 侯安平, 单树军, 等.
基于DDES方法的叶栅分离旋涡的非定常流动数值研究[J]. 推进技术, 2017, 38(1): 16–26.
LIU Ruoyang, HOU Anping, SHAN Shujun, et al. Unsteady numerical investigation on cascade separation vortex flow based on delayed detached-eddy simulation[J]. Journal of Propulsion Technology, 2017, 38(1): 16–26. |
| [50] |
顾春伟, 奉凡, 李雪松, 等.
DES模型在压气机亚音转子中的应用探讨[J]. 工程热物理学报, 2008, 29(6): 951–956.
GU Chunwei, FENG Fan, LI Xuesong, et al. Application of detached eddy simulation in subsonic compressor rotor[J]. Journal of Engineering Theromophysics, 2008, 29(6): 951–956. |
| [51] |
李雪松, 奉凡, 顾春伟.
静动干涉流动的分离涡模拟研究[J]. 工程热物理学报, 2009, 30(6): 953–956.
LI Xuesong, FENG Fan, GU Chunwei. Detached eddy simulation for the stator-rotor interaction[J]. Journal of Engineering Thermophysics, 2009, 30(6): 953–956. |
| [52] | YAMADA K, KIKUTA H, IWAKIRI K, et al. An explanation for flow features of spike-type stall inception in an axial compressor rotor[J]. Journal of Turbomachinery-Transactions of the ASME, 2013, 135: 0210232. |
| [53] | KUSANO K, JEONG J H, YAMADA K, et al. Detached eddy simulation of unsteady flow field and prediction of aerodynamic sound in a half-ducted propeller fan[C]//ASME-JSME-KSME 2011 Joint Fluids Engineering Conference. [S.l.]:ASME, 2011: 713-722. |
| [54] | WANG X, LIANG L, KANG S. Numerical simulations on flow separation within an axial turbine at very low reynolds number[C]//ASME Turbo Expo 2015: Turbine Technical Conference and Exposition. [S.l.]:ASME, 2015: V02CT44A018-V02CT44A018. |
| [55] | YAMADA K, FURUKAWA M, NAKAKIDO S, et al. Large-scale DES analysis of unsteady flow field in a multi-stage axial flow compressor at off-design condition using k computer[C]//ASME Turbo Expo 2015: Turbine Technical Conference and Exposition. [S.l.]:American Society of Mechanical Engineers, 2015: V02CT44A011-V02CT44A011. |
| [56] | IIM H, CHEN X Y, ZHA G. Detached-eddy simulation of rotating stall inception for a full-annulus transonic rotor[J]. Journal of Propulsion and Power, 2012, 28(4): 782–798. DOI:10.2514/1.B34395 |
| [57] | IM H, CHEN X, ZHA G. Detached eddy simulation of transonic rotor stall flutter using a fully coupled fluid-structure interaction[C]//ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition. [S.l.]:ASME, 2011: 1217-1230. |
| [58] | GAN J Y, IM H S, ZHA G C. Simulation of stall inception of a high speed axial compressor with rotor-stator interaction[C]//51st AIAA/SAE/ASEE Joint Propulsion Conference. [S.l.]:AIAA, 2015: 3932. |
| [59] | GAN J Y, IM H S, ZHA G C.Delayed detached eddy simulation of rotating stall for a full annulus transonic axial compressor stage[C]//ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition. [S.l.]:ASME, 2016: V02AT37A051-V02AT37A051. |
| [60] | SHI K, FU S. Study of shock/blade tip leakage vortex/boundary layer interaction in a transonic rotor with IDDES method[C]//ASME Turbo Expo 2013: Turbine Technical Conference and Exposition. [S.l.]:ASME, 2013:V06CT42A028-V06CT42A028. |
| [61] | SHI K, FU S, MORRIS S C. IDDES study of the shock induced flow separation in a transonic compressor rotor at near stall condition[C]//ASME Turbo Expo 2014: Turbine Technical Conference and Exposition. [S.l.]:ASME, 2014: V02DT44A043-V02DT44A043. |
| [62] | BOERSMA B J, van DER HOEVEN S. Low dissipative methods for turbulent reacting flows[C]//ECCOMAS CFD 2006: Proceedings of the European Conference on Computational Fluid Dynamics. The Netherlands:[s.n.], 2006. |
| [63] | MARTY J, LANTOS N, MICHEL B, et al. LES and hybrid RANS/LES simulations of turbomachinery flows using high order methods[C]//ASME Turbo Expo 2015: Turbine Technical Conference and Exposition. [S.l.]:ASME, 2015: V02CT44A003-V02CT44A003. |
| [64] | CHAUVET N, DECK S, JACQUIN L. Zonal detached eddy simulation of a controlled propulsive jet[J]. AIAA Journal, 2007, 45(10): 2458–2473. DOI:10.2514/1.28562 |
| [65] | KIM D, KIM K, JEONGYEOL C, et al. A comparative study of numerical methods on aerodynamic characteristics of a compressor rotor at near-stall condition[J]. International Journal of Aeronautical and Space Sciences, 2015, 16(2): 157–164. DOI:10.5139/IJASS.2015.16.2.157 |
| [66] | GARBARUK A, SHUR M, STRELETS M, et al. Detached-eddy simulation of a linear compressor cascade with tip gap and moving wall[R].Stockholm: Symposium on Hybrid RANS-LES Methods, 2005. |
| [67] | YOU D, MITTLE R, WANG M, et al. Computational methodology for large-eddy simulation of tip-clearance flows[J]. AIAA Journal, 2004, 42(2): 271–279. DOI:10.2514/1.2626 |
 2017, Vol. 49
2017, Vol. 49