目前,单一的导航系统很难满足高精度导航的要求,结合多种传感器,建成组合导航系统,利用滤波技术,将导航信息有机结合,能够有效提高系统可靠性和精度[1-3]。惯性导航系统/合成孔径雷达(Inertial navigation system/synthetic aperture radar,INS/SAR)组合导航系统因其自主性强、体积小、成本低、不易受电磁干扰等优点,在航空航天飞行器导航领域具有广泛应用[4]。该系统主要依靠图像匹配技术[5-6], 将SAR图像[7]与存储在机载存储器中的数字地图进行空间上对准,从而获得飞行器的位置、航向信息。
在组合导航系统中,不同的量测系统获得信息是不同步的。INS一般具有比较小的积分时间。数字图像处理往往伴随大量的运算,因此图像匹配定位[8]和测速会有较大的量测间隔,而且动态的拍摄图像具有不同的特征信息,不同飞行位置的SAR定位和测速的量测时间也不相同。图像匹配定位测速的输出会产生信息不同步,如果不对这些信息进行修正会对组合滤波精度产生负面影响,甚至导致滤波发散。
针对量测信息滞后的问题,文献[9]利用数组记录下量测开始到量测结束时间段内的所有INS状态信息,当量测结束,将量测信息与量测开始对应时刻的INS状态进行组合滤波,获得过去时刻对应的状态估计和误差均方误差阵。再次利用状态转移矩阵进行时间更新,将状态估计和均方误差阵递推到当前时刻,从而实现对INS误差的修正。这种方法在滤波点进行了两次时间更新,计算量大[10],在状态方程与真实系统具有较大偏差时,会在递推过程中引入一定的偏差。文献[11]提出利用曲线拟合进行滞后信息补偿的方法,该方法利用前几个时刻的卫星数据输出值和滞后时间,通过二次或三次曲线拟合,获得当前时刻卫星导航系统的真实输出值从而解决卫星数据量测滞后问题。但是该方法主要用于卫星量测滞后信息的修正,由于卫星导航系统延迟滞后时间相对于图像匹配时间较短,利用曲线拟合能取得比较好的效果,但是SAR定位和测速涉及大量的数据运算,滞后时间长,曲线拟合的离散间隔较大,会产生误差。文献[12]利用INS增量补偿量测滞后量,取得良好效果,但是,以上方法都假设量测起始和结束时刻都在滤波离散间隔或INS周期间隔上。
近年来,利用连续两帧图像进行动态分析也得到研究人员关注[13], 文献[14]将序列图像匹配用于无人机自测速,经试验验证,能够得到良好效果。因此,本文将在INS/SAR组合导航中引入图像匹配测速信息,对INS进行速度修正。为了防止导航信息在高度通道的发散,本文还引入了气压高度表的测高信息。同时,针对量测在非离散间隔的情况,本文也将利用INS在离散间隔内信息增量进行修正。
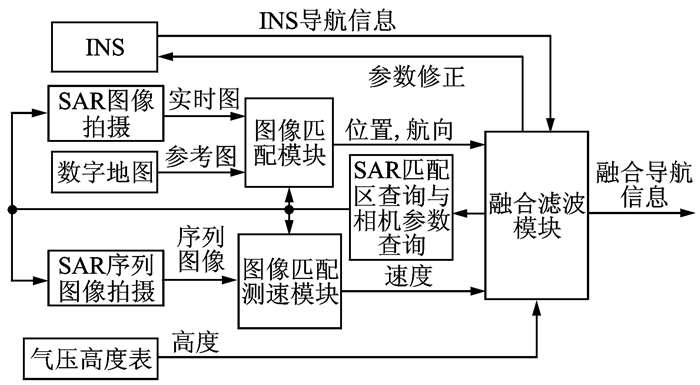
1 INS/SAR组合导航数学模型将SAR图像与机载数字地图数据库匹配,可以获得高精度的位置(经度、纬度)和航向角信息,将连续序列图像进行图像匹配可以获得速度信息[14],本文还引入气压高度计抑制INS信息在高度通道的发散。将SAR与气压高度计信息与INS信息偏差作为观测值传入卡尔曼滤波器,修正INS信息, 其原理如图 1所示。
|
图 1 组合导航系统原理图 Figure 1 Schematic diagram of integrated navigation system |
1.1 INS/SAR组合导航系统的状态方程
采用卡尔曼滤波进行信息融合,滤波方式采用间接法[15],系统的状态方程为惯导系统的误差方程,导航坐标系为东北天地理坐标系,建立状态方程
| $\boldsymbol{\dot X}\left( t \right) = \boldsymbol{F}\left( t \right)\boldsymbol{X}\left( t \right) + \boldsymbol{G}\left( t \right)\boldsymbol{W}\left( t \right)$ | (1) |
式中:F(t)为状态转移阵;G(t)为噪声系数阵;W(t)为噪声矩阵。具体参数说明请参见文献[16]。
系统共有9个误差参数:3个姿态角误差,3个方向的速度误差和3个方向的位置误差。再将9个噪声相关参数加入状态变量,合成18维的状态向量X(t)
| $\begin{array}{l} \boldsymbol{X = }\left[{{\varphi _E}, {\varphi _N}, {\varphi _U}, {\delta _E}, {\delta _N}, {\delta _U}, \delta L, \delta \lambda, \delta h, {\varepsilon _{bx}}, {\varepsilon _{by}}, } \right.\\ {\left. {\;\;\;\;\;\;\;{\varepsilon _{bz}}, {\varepsilon _{rx}}, {\varepsilon _{ry}}, {\varepsilon _{rz}}, {\nabla _x}, {\nabla _y}, {\nabla _z}} \right]^{\rm{T}}} \end{array}$ |
式中:φE,φN,φU为姿态角误差;δE,δN,δU为东向、北向、天向速度误差;δL,δλ,δh为纬度、经度、高度误差;εbx,εby,εbz为陀螺常值漂移误差;εrx,εry,εrz为陀螺仪一阶马尔可夫漂移误差;∇x,∇y,∇z为加速度计零偏。
1.2 INS/SAR组合导航系统的量测方程量测量Z为6维向量,如式(3) 所示,Z1为INS与图像匹配量测航向角之差;Z2, Z3为INS与序列图像匹配量测东向、北向速度之差;Z4,Z5为INS与图像匹配量测纬度、经度位置之差;Z6为INS与气压高度表高度之差
| $\boldsymbol{Z}\left( t \right) = \boldsymbol{H}\left( t \right)\boldsymbol{X}\left( t \right) + \boldsymbol{V}\left( t \right)$ | (2) |
| $\boldsymbol{Z = }\left[\begin{array}{l} {Z_1}\\ {Z_2}\\ {Z_3}\\ {Z_4}\\ {Z_5}\\ {Z_6} \end{array} \right] = \left[{\begin{array}{*{20}{c}} {}&1&{}&{}&{}&{}&{}&{}\\ {}&{}&1&{}&{}&{}&0&{}\\ {}&{}&{}&1&{}&{}&{}&{}\\ {{{\bf{0}}_{6 \times 2}}}&{}&{}&{}&{}&{}&{}&{{{\bf{0}}_{6 \times 9}}}\\ {}&{}&{}&{}&0&{{R_M}}&{}&{}\\ {}&{}&{}&0&{}&{}&{{R_N}\cos L}&{}\\ {}&{}&{}&{}&{}&{}&{}&{} \end{array}} \right]\boldsymbol{X + }\left[\begin{array}{l} {V_1}\\ {V_2}\\ {V_3}\\ {V_4}\\ {V_5}\\ {V_6} \end{array} \right]$ | (3) |
式中:H(t)即为t时刻量测矩阵;RM, RN为地球曲率半径;L为纬度;V1为图像匹配输出的航向角误差,其大小依赖图像匹配定位精度;V2,V3分别为序列图像匹配输出的东向、北向速度误差,其大小依赖序列图像匹配测速精度;V4,V5为图像匹配纬度、经度方向位置误差,其大小依赖图像匹配定位精度;V6为气压高度表高度误差,其大小依赖气压高度表测高精度。
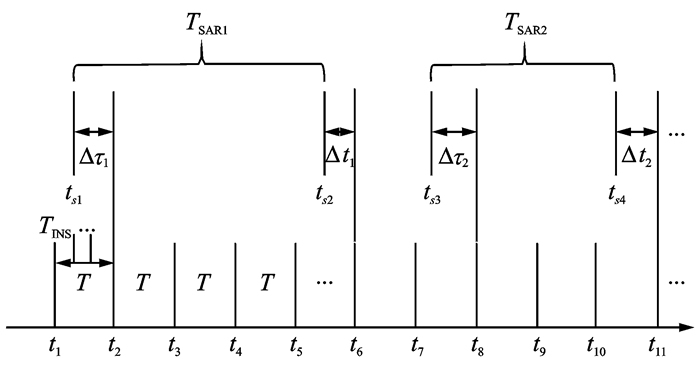
2 解决量测不同步和信息滞后算法在INS/SAR组合导航中,由于不同导航信息的不同步,图像匹配耗时较大,而且每次耗时间隔具有随机性。量测不同步和信息滞后的时序关系如图 2所示。图中, TINS为INS的计算周期,状态方程的离散化周期为T,设T=NTINS, N为正整数,t1,t2,t3, …为滤波输出时刻;TSAR1,TSAR2为SAR定位从开始定位到图像匹配算法运行结束的时间间隔,每次SAR定位的TSARi的时间间隔不一定相同,本算法不假设SAR定位开始时刻和匹配算法结束时刻在状态方程的离散间隔上,因为SAR定位是另一个独立的系统,时序上具有独立性,如图 2中,ts1,ts2为SAR定位开始与结束时刻,在时序上不与离散时间点t1, t2, t3, …对齐。Δτ为SAR定位开始时刻到紧邻的后一个状态方程离散间隔的时间间隔,Δt为图像匹配算法运行结束到紧邻的后一个状态方程离散间隔的时间间隔。图像匹配测速与SAR定位具有相似的时序。
|
图 2 组合导航信息时序图 Figure 2 Timing diagram of integrated navigation information |
针对量测不同步的问题,本文采取文献[9]的方法,如图 2所示,在T离散间隔点t1, t2, t3, …到来时,判断是否有除INS以外的量测输出,如果没有,则利用状态转移矩阵,只进行卡尔曼滤波的时间更新
| $\begin{array}{c} {{\mathit{\boldsymbol{\hat X}}}_{k/k}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k-1}}{{\mathit{\boldsymbol{\hat X}}}_{k-1/k-1}}\\ {\mathit{\boldsymbol{P}}_{k/k}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}{\mathit{\boldsymbol{P}}_{k - 1/k - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}^{\rm{T}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k, k - 1}}{\mathit{\boldsymbol{Q}}_{k - 1}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k, k - 1}^{\rm{T}} \end{array}$ | (4) |
式中:Φk, k-1为k-1时刻到k时刻的离散化状态转移矩阵;Γk, k-1为k-1时刻到k时刻离散化系统噪声驱动阵;时间间隔为状态方程的滤波离散化周期T,具体的离散过程可以参考文献[15];
当其他传感器产生量测输出时,如果量测输出不在状态方程离散间隔上,则延迟至紧邻的后一个状态方程离散间隔上进行组合滤波,并同时进行卡尔曼滤波的时间更新和量测更新,其方程为
| $\begin{array}{l} {{\mathit{\boldsymbol{\hat X}}}_{k/k-1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k-1}}{{\mathit{\boldsymbol{\hat X}}}_{k-1/k - 1}}\\ {\mathit{\boldsymbol{P}}_{k/k - 1}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}}{\mathit{\boldsymbol{P}}_{k - 1/k - 1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{k, k - 1}^{\rm{T}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k, k - 1}}{\mathit{\boldsymbol{Q}}_{k - 1}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{k, k - 1}^{\rm{T}}\\ {{\mathit{\boldsymbol{\hat X}}}_{k/k}} = {{\mathit{\boldsymbol{\hat X}}}_{k/k - 1}} + {\mathit{\boldsymbol{K}}_k}\left( {{\mathit{\boldsymbol{Z}}_k} - {\mathit{\boldsymbol{H}}_k}{{\mathit{\boldsymbol{\hat X}}}_{k, k - 1}}} \right)\\ {\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{k/k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}{\left( {{H_k}{\mathit{\boldsymbol{P}}_{k/k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}} \right)^{ - 1}}\\ {\mathit{\boldsymbol{P}}_{k/k}} = \left( {I - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{H}}_k}} \right){\mathit{\boldsymbol{P}}_{k/k - 1}}{\left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{H}}_k}} \right)^{\rm{T}}} + {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{R}}_k}\mathit{\boldsymbol{K}}_k^{\rm{T}} \end{array}$ | (5) |
式中:
量测矩阵H在全部传感器有量测输出时的矩阵形式如式(3) 所示,但INS、图像匹配定位、图像匹配测速、高度计的信息输出是独立的,在滤波时,量测矩阵H、噪声方差阵R需要根据量测传感器输出进行选择。如图 2的t6,t11有SAR定位的量测输出,此时应判断是否有其他传感器的量测输出,如有SAR图像测速输出,则进行两者组合,如果还有高度计测高输出,则进行三者组合,因此共有7种组合方式。设SAR定位的量测矩阵为Hposi,噪声方差阵为Rposi;SAR图像测速的量测矩阵为Hvelo,噪声方差阵为Rvelo;气压高度计测高的量测矩阵为Hheight,噪声方差阵为Rheight。那么两者组合的量测矩阵和噪声方差阵分别为:
通过这种方式可以解决量测信息不同步的问题,可以发现,不同传感器的量测可以是并行的,当传感器出现故障或数据发生异常时,可以屏蔽该传感器数据,系统仍然可以工作。
由于INS具有短期精度高的优点,本文利用INS信息增量将其他传感器量测信息递推到当前时刻,利用该信息直接在当前时刻进行组合滤波,然后利用状态估计修正INS信息。以图 2第一次SAR定位修正时序为例,在ts1时刻SAR开始定位,记录下与后一个滤波离散间隔时间点t2的时间差Δτ1=t2-ts1,并记录t2,t3时刻的位置状态量Xins_t2,Xins_t3,直到ts2SAR匹配结束,因为图像是ts1时刻获取的,所以输出在ts2输出ts1时刻的量测值Zposi,如果ts2在状态方程离散间隔上,则记录该时间点的状态量,如果不在间隔上,则记录后一个离散间隔点t6的位置状态量Xins_t6。t6时刻的SAR匹配定位量测修正值Zposi_modi为
| $\begin{array}{l} {Z_{{\rm{posi\_modi}}}} = {Z_{{\rm{posi}}}} + \frac{{\Delta {\tau _1}}}{T}\left( {{X_{{\rm{in}}\;{\rm{s\_}}t3}}-{X_{{\rm{in}}\;{\rm{s\_}}t2}}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{X_{{\rm{in}}\;{\rm{s\_}}t6}}-{X_{{\rm{in}}\;{\rm{s\_}}t2}} \end{array}$ | (6) |
式中:
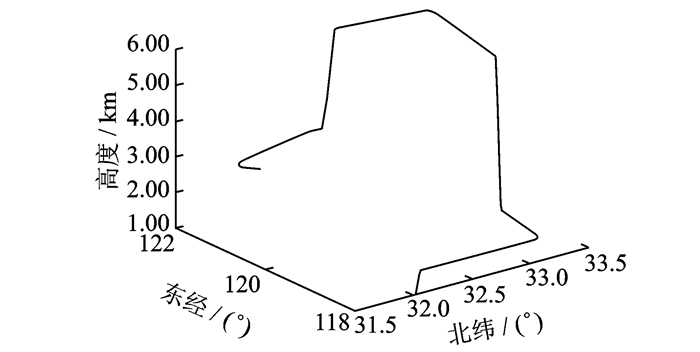
飞行器的初始位置为北纬32°,东经118°,初始高度为1 000 m,初始速度为200 m/s, 航向为正北。导航路径由仿真系统航迹发生器产生,模拟飞行器加速、减速、爬升、下降、转弯等飞行状态。INS的积分时间为20 ms,初始误差忽略,等效陀螺漂移为0.1(°)/h,陀螺仪一阶马尔可夫过程相关时间为3 600 s,等效加速度零偏为10-4g,加速度计一阶马尔可夫过程相关时间为1 800 s,INS的数据是通过航迹发生器数据进行加速度计与陀螺仪仿真,解算得到。图像匹配定位匹配时间为1~6s之间的随机数[9-10],位置量测精度为10 m,航向量测精度为1°;序列图像匹配速度计算时间为1~4 s之间的随机数[17-18],速度量测精度为5 m/s; 气压高度计量测间隔为1 s,高度量测精度为20 m[9]。图像匹配定位,序列图像匹配测速,气压高度计数据是通过航迹发生器数据加入均值为零,标准差为相应精度的正态分布的噪声产生的。
本仿真的总时间为1 500 s,误差为组合滤波后导航信息与航迹发生器的真实信息之差,由于本文算法只对航向角、位置、速度、高度修正,图 3~8给出了这组数据的误差曲线,同时与二次曲线拟合法对比。表 1, 2分别为本文算法与其他算法的误差及误差统计对比。
|
图 3 三维飞行航迹 Figure 3 Three-dimensional flight path |
|
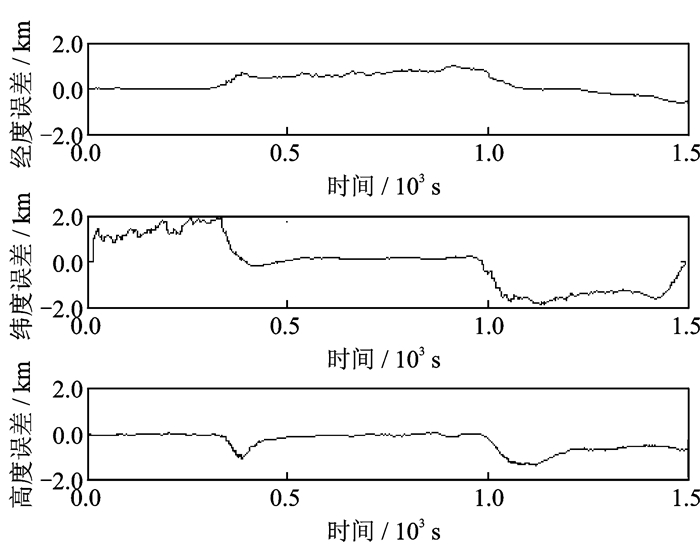
图 4 滞后未修正算法的位置误差 Figure 4 Position error of unmodified algorithm |

|
图 5 滞后未修正算法的航向与速度误差 Figure 5 Heading and velocity error of unmodified algorithm |
|
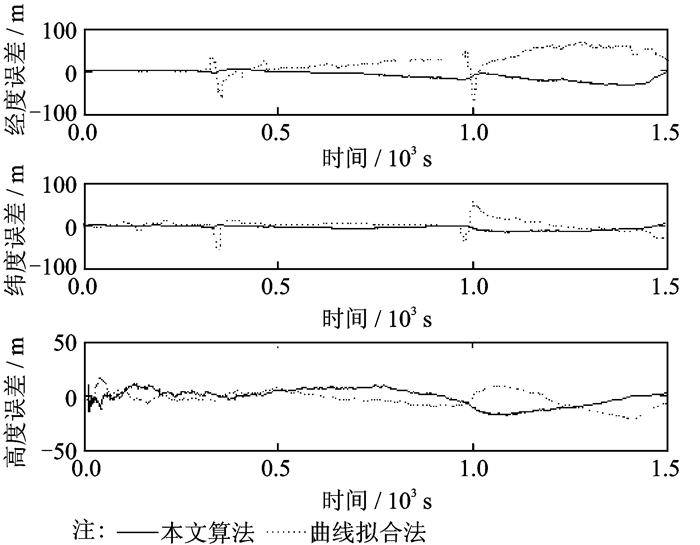
图 6 滞后修正算法位置误差对比 Figure 6 Position error comparison between modified algorithm and curve fitting method |
|
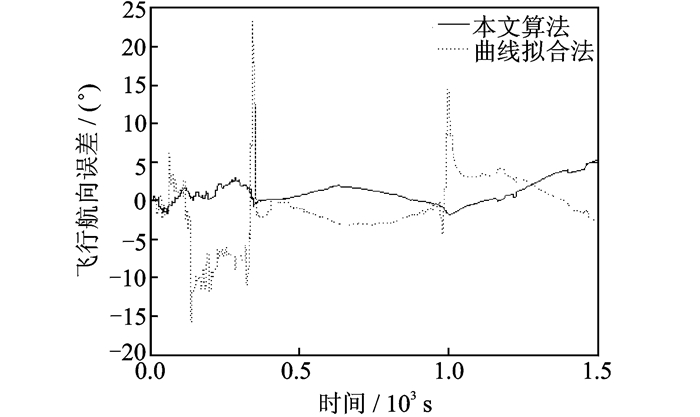
图 7 滞后修正算法航向角误差对比 Figure 7 Heading error comparison between modified algorithm and curve fitting method |
|
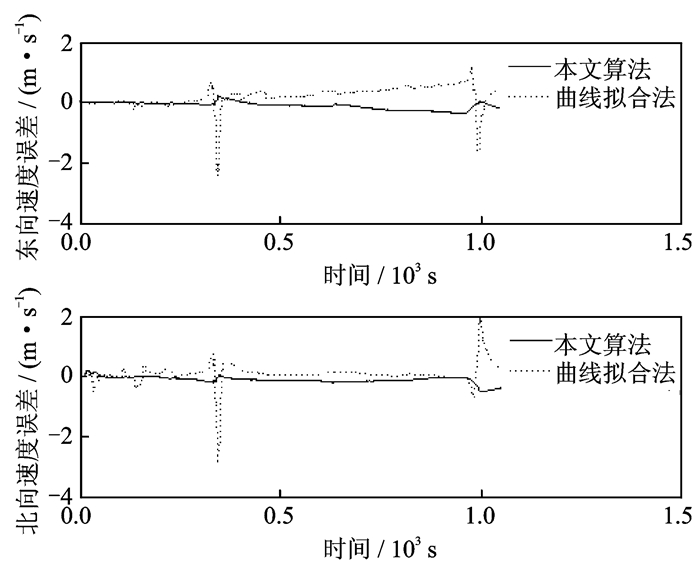
图 8 滞后修正算法速度误差对比 Figure 8 Velocity error comparison between modified algorithm and curve fitting method |
| 表 1 导航算法滤波后误差范围对比 Table 1 Error range comparison of navigation algorithms |
| 表 2 导航算法滤波后误差统计对比 Table 2 Error statistical comparison of navigation algorithms |
仿真结果表明,在模拟飞行器多种飞行状态以后,经过1 500 s仿真,在采用本文算法的情况下,导航信息没有出现明显的发散。在误差绝对值方面,滞后未修正算法产生了相当大的误差,其经纬度误差绝对值达到了2 000 m左右,高度误差绝对值也达到334.13 m,东北向速度误差绝对值达到26.88 m/s, 航向角误差绝对值达到147.72′,与经过滞后修正的算法存在很大差距,这也说明在INS/SAR组合导航系统中,对图像匹配信息滞后问题的处理是非常必要的。
在滞后修正算法中,两种算法都能有效修正信息延迟引起的误差,从滞后修正算法误差对比(图 6~8)可见,在经纬度误差、航向误差和速度误差方面,本文算法相对于二次曲线拟合算法更具优势。飞行器出现加速、爬升、转弯等机动时,如在本仿真300 s和1 000 s左右,位置、速度、航向角的滤波曲线会出现较大的波动,而本文算法更加平滑。这表现在误差绝对值上,本文算法经纬度误差绝对值为36.77 m,航向误差绝对值为5.27′,速度误差绝对值为0.50 m/s,而曲线拟合算法经纬度误差绝对值达到74.32 m,航向误差绝对值达到23.27′,速度误差绝对值达到2.87 m/s。其原因如本文引言所述,图像匹配耗时较大,两次信息输出时间间隔较大,特别在高机动点拟合效果不佳。
表 2的误差统计对比结果也符合实验结果图的预期,滞后未修正算法误差相对于两个修正算法具有较大的差距。本文算法的经纬度误差标准差、航向误差标准差、速度误差标准差只有曲线拟合算法的1/2左右。在高度误差方面差距不大,原因在于本文仿真的信息延迟问题存在于图像匹配模块,与气压高度表无关。总体而言,不论是在误差范围还是误差标准差方面本文的延迟修正方法都优于曲线拟合算法,使导航精度进一步提高。
4 结束语本文在INS/SAR组合系统中引入气压高度计抑制高度通道的发散,并引入图像匹配测速系统,使系统在原有图像匹配定位速度基础上获得了速度信息,在延迟滞后补偿方面,利用INS增量进行信息补偿,同时对SAR定位,SAR测速在非INS离散间隔上的信息增量也进行了补偿修正,利用系统仿真验证了算法的有效性。对比曲线拟合算法,本文算法在误差,稳定性上都具有一定优势。本文利用的滤波融合算法在其他组合导航中,如INS/GPS(Global positioning system),也有适用性,因此具有良好的工程应用前景。
| [1] | HU G, GAO S, ZHONG Y. A derivative UKF for tightly coupled INS/GPS integrated navigation[J]. ISA Transactions, 2014, 56: 135–144. |
| [2] | ZHAO L, QIU H, FENG Y. Analysis of a robust Kalman filter in loosely coupled GPS/INS navigation system[J]. Measurement, 2016, 80: 138–147. DOI:10.1016/j.measurement.2015.11.008 |
| [3] |
熊智, 潘加亮, 林爱军, 等.
发射系下SINS/GPS/CNS组合导航系统联邦粒子滤波算法[J]. 南京航空航天大学学报, 2015, 47(3): 319–323.
XIONG Zhi, PAN Jialiang, LIN Aijun, et al. SINS/GPS/CNS integrated navigation system federal PF algorithm in launch inertial coordinate system[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(3): 319–323. |
| [4] | SAMCZYNSKI P, MALANOWSKI M, GROMEK D, et al. Effective SAR image creation using low cost INS/GPS[C]// 2014 15th International Radar Symposium (IRS). Poland: Warsaw University of Technology, 2014:1-4. |
| [5] |
李想, 朱遵尚, 尚洋, 等.
方向矩异源图像匹配算法[J]. 国防科技大学学报, 2015, 37(1): 153–158.
DOI:10.11887/j.cn.201501026 LI Xiang, ZHU Zunshang, SHANG Yang, et al. Multimodal image registration based on orientation-moment[J]. Journal of National University of Defense Technology, 2015, 37(1): 153–158. DOI:10.11887/j.cn.201501026 |
| [6] | SEDAGHAT A, EBADI H. Very high resolution image matching based on local features and k-means clustering[J]. Photogrammetric Record, 2015, 30(150): 166–186. DOI:10.1111/phor.2015.30.issue-150 |
| [7] |
田宵骏, 梁媚蓉, 毛新华.
超高分辨率机载SAR成像算法及GPU实现[J]. 南京航空航天大学学报, 2015, 47(3): 384–391.
TIAN Xiaojun, LIANG Meirong, MAO Xinhua. Imaging algorithm and its implementation on GPU for ultra-high resolution airborne SAR[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(3): 384–391. |
| [8] | SHENG Qinghong, FEI Lijia, LIU Jianfeng, et al. Accuracy analysis on bundle adjustment of remote sensing images based on dual quaternion[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2015, 32(5): 523–529. |
| [9] |
冷雪飞, 刘建业, 熊智.
SAR/INS/TAN组合导航系统中的滤波算法研究[J]. 系统工程与电子技术, 2006, 28(1): 23–25.
LENG Xuefei, LIU Jianye, XIONG Zhi. Study of filtering algorithm for SAR/INS/TAN integrated navigation systems[J]. Systems Engineering & Electronics, 2006, 28(1): 23–25. |
| [10] |
崔曼曼, 刘思伟, 高社生.
SINS/SAR组合导航系统中量测滞后补偿方法研究[J]. 测控技术, 2014, 33(6): 20–23.
CUI Manman, LIU Siwei, GAO Shesheng, et al. Study on measuring delay compensation method for SINS/SAR integrated navigation system[J]. Measurement & Control Technology, 2014, 33(6): 20–23. |
| [11] |
杨波, 王跃钢, 徐洪涛.
高速飞行环境下卫星导航信息滞后补偿方法[J]. 中国惯性技术学报, 2011, 19(3): 293–297.
YANG Bo, WANG Yuegang, XU Hongtao. Compensation method for satellite navigation information delay in high-speed flight environment[J]. Journal of Chinese Inertial Technology, 2011, 19(3): 293–297. |
| [12] |
熊智, 冷雪飞, 刘建业.
基于北斗双星定位辅助的SAR/INS组合导航系统研究[J]. 宇航学报, 2007, 28(1): 88–93.
XIONG Zhi, LENG Xuefei, LIU Jianye. Research of SAR/INS integrated navigation system aided by BeiDou double star position[J]. Journal of Astronautics, 2007, 28(1): 88–93. |
| [13] | TU Z, POPPE R, VELTKAMP R C. Weighted local intensity fusion method for variational optical flow estimation[J]. Pattern Recognition, 2016, 50: 223–232. DOI:10.1016/j.patcog.2015.09.002 |
| [14] |
李鑫. SAR图像导航定位测速技术研究[D]. 长沙: 国防科学技术大学, 2010.
LI Xin. Research on SAR image navigation position and speed measuring technology [D]. Changsha: National University of Defense Technology, 2010. |
| [15] |
刘建业, 曾庆化, 赵伟, 等.
导航系统理论与应用[M]. 西安: 西北工业大学出版社, 2010.
LIU Jianye, ZENG Qinghua, ZHAO Wei, et al. Navigation system theory and application[M]. Xi′an: Northwestern Polytechnical University Press, 2010. |
| [16] |
高社生.
组合导航原理及应用[M]. 西安: 西北工业大学出版社, 2012.
GAO Shesheng. Principle and application of integrated navigation[M]. Xi′an: Northwestern Polytechnical University Press, 2012. |
| [17] |
朱婧, 焦淑红.
基于光流场的序列图像分析[J]. 弹箭与制导学报, 2006, 26(S2): 443–445.
ZHU Jing, JIAO Shuhong. Approach to image sequences analysis based on optical flow field[J]. Journal of Projectiles Rockets Missiles and Guidance, 2006, 26(S2): 443–445. |
| [18] |
李耀军, 潘泉, 赵春晖, 等.
基于动态关键帧的自然地标景象匹配视觉导航[J]. 光电工程, 2010, 37(9): 32–38.
LI Yaojun, PAN Quan, ZHAO Chunhui, et al. Natural-landmark scene matching vision navigation based on dynamic key frame[J]. Opto-Electronic Engineering, 2010, 37(9): 32–38. |
 2017, Vol. 49
2017, Vol. 49


