多旋翼无人机经过多年的发展,作用越来越重要。不管在军用还是民用方面,都已经取得了重大的成果。由于小型无人机的自身因素,要使无人机具有良好的飞行品质, 良好的飞行控制系统必不可少,而控制系统中的控制器参数调节也成为重中之重。
常见的现代飞行控制律的设计方法有线性二次型最优控制、非线性动态逆控制、滑模变结构控制、自适应控制、神经网络控制和模糊逻辑控制等[1-2]。
多旋翼无人机飞行控制系统是一个非线性系统,目前针对非线性系统控制多采用非线性模型线性化,然后再代入线性模型得到参数,最后再把参数代入非线性系统中。这种方法设计的控制器在文献[3]中分为两种:定常控制器和增益调度控制器。这样虽然得到了一组非线性系统参数,但是由于非线性系统飞行包线大,选取的状态点多,就不得不面对反复调参问题。
针对参数整定问题,已有的自动优化算法有模糊算法、神经网络算法与粒子群算法等。文献[4]概述了粒子群优化算法(Particle swarm optimization, PSO)的特点,并针对典型被控对象模型进行了模拟仿真验证。文献[5, 6]分别将PSO算法与神经网络算法和蚁群算法做出了比较,PSO算法具有的记忆机制主要应用于连续问题[7]。文献[6]进一步阐述了PSO算法的优点,用经典Z-N公式进行整定说明。文献[8]将PSO算法应用到船舶航向PID控制,并取得成果。本文以变距变转速四旋翼飞行器为研究对象,基于PSO算法对系统控制器进行参数整定,相比其他多旋翼无人机变距变转速四旋翼飞行器还需进行变距控制和转速控制,对控制器设计要求更高,因此对其飞行控制进行自动调参具有重要意义。
1 自动调参飞行模式 1.1 自动调参工作原理如果一个飞行控制系统工作状态发生了变化,可以自动地改变控制器参数,使其回到最优工作状态。可以根据系统响应输出,利用负反馈思想,将控制器参数和系统响应性能之间的关系看作一个未知的传递关系,控制器自动调参过程可视为寻找控制器参数和系统响应性能之间的最佳对应关系的寻优过程。在利用自动优化算法时,先确定优化的目标和优化的约束条件。对无人机的自动调参设计既要保证飞行的稳定性又要考虑反应速率,在约束条件内,根据反馈查看系统响应是否满足优化目标。设计中在确保稳定性的前提下,通过调节内环控制器参数要求无人机保持一个较高角速率响应控制,且在角速率允许的浮动范围内,调节外环控制器使控制系统调节时间短,无超调,无稳态误差,并且无震荡。
1.2 自动调参算法研究PSO具有待调参数少、收敛速度快及算法结构简单等特点[9-10]。PSO算法初始化一群粒子,然后通过迭代寻找最优解。每一个粒子都是优化问题的可行解,粒子的坐标就是待优化参数变量,文中粒子坐标指的是控制器需要调节的参数。粒子的优劣性由一个适应度函数来判断,所有的粒子都会计算出一个适应值。粒子在可行解空间中飞行,由一个速度决定它的方向和距离,在每一次迭代优化中, 粒子通过跟随两个极值来更新自身在空间中的飞行速度和位置。一个极值是粒子本身所寻找的最优解,称为个体极值,记作pl; 另一个极值是粒子群在全局中寻找的最优解,称为全局极值,记作pg。若n维第i个粒子在T时刻时速度记作Vi=(V1i, V2i, …, Vni)T,位置记作Xi=(x1i, x2i, …, xni)T。每次迭代都通过以下公式更新位置和速度量
| $\begin{array}{c} {\boldsymbol{V}^i}\left( {t + 1} \right) = w{\boldsymbol{V}^i}\left( t \right) + {c_1}{r_1}\left( {p_1^i\left( t \right)-{\boldsymbol{X}^i}\left( t \right)} \right) + \\ {c_2}{r_2}\left( {p_{\rm{g}}^i\left( t \right)-{\boldsymbol{X}^i}\left( t \right)} \right) \end{array}$ | (1) |
| ${\boldsymbol{X}^i}\left( {t + 1} \right) = {\boldsymbol{X}^i}\left( t \right) + {\boldsymbol{V}^i}\left( {t + 1} \right)$ | (2) |
式中:t表示时刻,即迭代次数;w为惯性权重,表示t+1时刻速度对t时刻速度影响;c1,c2为学习因子;r1,r2为在(0, 1) 的随机数。每一个粒子的位置都限定在搜索空间里,即Xmin≤X≤Xmax,Xmax,Xmin为搜索空间上限、下限;速度也要限定在一定范围内,即Vmin≤V≤Vmax,Vmax,Vmin为最大、最小速度。
PSO算法流程图如图 1所示。

|
图 1 粒子群算法流程图 Figure 1 Particle swarm optimization flowchart |
PSO算法实现步骤如下:
步骤1 初始化粒子群参数,确定惯性权重w,学习因子c1,c2以及r1,r2和迭代次数T。规定搜索上下限Xmax,Xmin;最大速度与最小速度Vmax,Vmin。
步骤2 计算粒子适应值判断粒子的优劣性,更新极值pl,pg。如果当前所计算的pl(t+1) 优于pl(t)值,则pl(t)=pl(t+1),反之pl(t)=pl(t);同理,如果当前所计算的pg(t+1) 优于pg(t)值,则pg(t)=pg(t+1),反之pg(t)=pg(t)。
步骤3 更新粒子状态,根据式(1,2) 更新粒子的速度和位置。
步骤4 判断循环条件是否达到设计要求,达到则停止计算,反之循环步骤2。
最后,根据优化目标,判断计算结果是否满足约束条件,剔除不满足条件的计算结果。
1.3 目标函数的建立根据适应度函数和约束条件设计目标函数。要使得系统性能各方面都是最优,目前还无法实现,因为系统各个方面性能都相互联系,相互影响。多旋翼无人机是非线性多耦合系统,以横向操纵为例,改变滚转角速率不但会引起滚转角变化还会使侧向速度和偏航角速率发生改变。要使得一方面的最优只能是在牺牲另一方面性能前提下才能实现。为了实现系统综合性能的最优化,需要采用一些能体现综合性能的指标,现阶段常用的综合性能评价标准主要是基于系统的偏差e(t)= r(t) -y (t)(r(t)为输入信号,y(t)为输出信号)与时间的关系[3, 6]。
文中以图 2所示模型为基础,在约束条件下,以被控对象所选定状态点的数据经过运算并仿真出来的输出信号与输入的指令信号偏差绝对值量与时间的积分作为目标函数,选定时间绝对偏差积分(Integral time absolute error,ITAE)作为适应度函数
| ${\rm{ITAE = }}\int_0^\infty {t\left| {e\left( t \right)} \right|{\rm{d}}t} $ | (3) |
在自动调参过程中ITAE值越小越好。约束条件可以是自动调参时间、超调量或者稳态误差大小。

|
图 2 系统流程框图 Figure 2 System flowchart |
2 自动调参仿真模型 2.1 控制器设计
本文采用的控制律是PID控制器,此控制律具有结构简单、易操作、鲁棒性能高及可实现性能强等优点[11]。PID控制器是一种基于系统稳定偏差e(t)= r(t)-y(t),通过对误差信号进行比例、积分和微分线性组合运算来构成系统的控制信号,对被控对象进行控制的算法。
算法表达式为
| $u\left( t \right) = {K_p}\left[{e\left( t \right) + \frac{1}{{{T_i}}}\int {e\left( t \right){\rm{d}}t} + {T_d}\frac{{{\rm{d}}e\left( t \right)}}{{{\rm{d}}t}}} \right]$ | (4) |
式中:Kp代表比例环节的比例系数;Ti代表积分环节的积分时间常数;Td代表微分环节的微分时间函数;u(t)代表控制器输出量。传递函数可写成如下形式
| $G\left( s \right) = {K_p} + {K_i}\frac{1}{s} + {K_d}\frac{s}{{1 + \frac{s}{N}}}$ | (5) |
式中:Kp,Ki,Kd分别为PID控制器的比例增益,积分增益,微分增益,也是文中自动调参的待优化量;N在程序设计中取50。控制器设计如图 3所示。角速率采取PID控制,rll_Ki值设计为rll_Kp值的0.1倍,外环采取P控制。

|
图 3 基于PID的滚转差动通道控制结构图 Figure 3 Roll differential channel control based on PID |
2.2 自动调参模型
本文被控对象是变距变转速四旋翼飞行器[12],飞行器的质量和尺寸如表 1所示。变距变转速四旋翼飞行器采用了轴对称的基本布局,电机和旋翼组件相对机身左右对称分布,4个旋翼均匀分布且处于同一高度平面,中心机舱布置电源、飞控系统等机载设备。通过调整4个电机转速和旋翼总距的大小,可实现该无人机各个方向的运动。
| 表 1 变距变转速四旋翼飞行器质量和尺寸 Table 1 Mass and size of variable-pitch and variable rotational-speed four-rotor aircraft |
针对变距变转速四旋翼飞行器进行非线性动力学建模,可以得到4个操纵量U和9个状态量X的变距变转速四旋翼三维空间动力学方程[11-12]
| $\boldsymbol{\dot X} = f\left( {\boldsymbol{X}, \boldsymbol{U}, t} \right)$ | (6) |
操纵量U和状态量X分别如下所示
| $\boldsymbol{U = }\left[{{\boldsymbol{\delta }_{{\rm{rll}}}}, {\delta _{{\rm{pit}}}}, {\delta _{{\rm{yaw}}}}, {\delta _{{\rm{col}}}}} \right]$ | (7) |
| $\boldsymbol{X = }\left[{u, v, w, p, q, r, \varphi, \theta, \psi } \right]$ | (8) |
根据建模理论分析,在Matlab/Simulink仿真环境中,建立变距变转速四旋翼仿真模型,如图 4所示,模型包括机身气动力模型,旋翼气动力模型、6自由度方程模型与外部环境模型。在输入模块中,采取上述控制器设计方法,如图 5所示。

|
图 4 基于Matlab/Simulink的变距变转速四旋翼无人机仿真模型 Figure 4 Matlab/Simulink simulation model of variable-pitch and variable rotational-speed four-rotor aircraft |

|
图 5 输入模块仿真图 Figure 5 Simulation diagram of input module |
2.3 模型仿真结果
在输入模块中,无人机初始状态为悬停状态,输入指令为20°滚转角阶跃指令信号,目标是使无人机滚转角动态跟随滚转指令。姿态角控制律调参只考虑无人机滚转运动,其他通道输入指令为0°。根据临界比例法和工程实践试凑法[13]确定控制器参数大致范围。为了避免出现0值则最小值设置为0.01,最大值设置为20。在提高系统控制精度和灵敏度条件下,确保系统不震荡,超调量小且无稳态误差[14-15]。保持滚转角速度响应最大速率为90 (°)/s,且在20%范围内整定,则内环PID控制器参数rll_Kp进一步限幅为[3, 8]。响应角度最大误差不超过2°。根据系统模型特征设计rll_Kd限幅为[0.01, 2]。按照上述算法流程编写出粒子群算法程序,结合调参目标与约束条件,进行在线自动调整控制律参数的软件设计。通过仿真得到的粒子群自动整定控制器PID参数得到变距变转速四旋翼滚转差动通道响应曲线(图 6,7)。对比图 6,7可知,粒子在自动整定参数过程中,逐步收敛于最优解,符合设计理念。运行自动调参软件优化出一组PID参数:Kp=8,Ki=0.8,Kd=0.059。

|
图 6 初始粒子分布图 Figure 6 Initial particle distribution |

|
图 7 优化后粒子分布图 Figure 7 Optimized particle distribution |
图 8,9给出了滚转角速率和滚转角调参前后的对比曲线。由图 8可知,自动调参结果符合设计要求。滚转角速率最大值近90(°)/s,相比于无调参情况既提高了四旋翼无人机飞行控制的灵敏度,最后收敛又确保了系统的稳定性。在内环角速率的调参基础上,对外环角度参数stb_P进行调节, 由于内外环控制的联系,设计期望角度为20°,角速率为90(°)/s,stb_P值为4.5。如图 9所示,滚转角自动调参响应,调节时间约为1 s,且无超调,满足设计指标。整个通道控制器参数调节由程序自动运行完成,实现了自动调参功能。

|
图 8 滚转角速率对比图 Figure 8 Comparison of roll angle rate |

|
图 9 滚转角对比图 Figure 9 Comparison chart of roll angle |
2.4 悬停跟踪响应
悬停跟踪响应是利用上述控制器测试悬停状态下的控制效果。其任务是,多旋翼无人机从地面坐标系原点起飞至目标位置并保持悬停,通过系统输出的曲线进行分析研究。具体步骤为,从坐标(0, 0, 0) 飞至点(5, 2, 10)。通过仿真可以得到粒子群整定参数在PID控制器下多旋翼无人机6组输出状态响应曲线,如图 10~15所示。

|
图 10 X坐标仿真效果图 Figure 10 X axis simulation result |

|
图 11 Y坐标仿真效果图 Figure 11 Y axis simulation result |

|
图 12 Z坐标仿真效果图 Figure 12 Z axis simulation result |
|
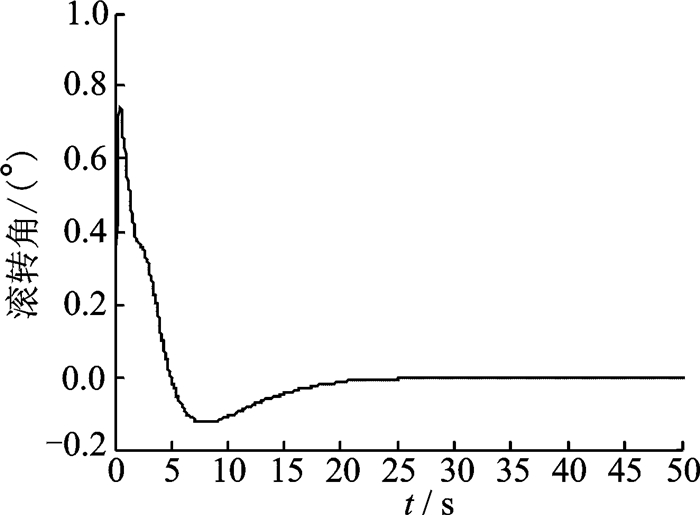
图 13 滚转角仿真效果图 Figure 13 Roll angle simulation result |

|
图 14 俯仰角仿真效果图 Figure 14 Pitch angle simulation result |

|
图 15 偏航角仿真效果图 Figure 15 Yaw angle simulation result |
由仿真图 10~12可以看出:基于粒子群自动调参设计的PID控制器具有良好的控制效果,可以对多旋翼无人机悬停快速响应跟踪指令。从起始点飞到目标点经过10 s左右时间,3个坐标数值从开始保持稳定直至仿真结束。另外,三轴角速率中,滚转角和俯仰角经过20 s后数值变为0,而偏航角则在30 s开始收敛。
3 结束语文中设计的自动调参软件针对内环角速率PID控制器参数先给定取值范围,在此范围内,通过粒子算法不断地迭代计算寻找满足设计要求的最优控制器参数。在整定内环基础上再对外环角度进行控制器参数整定,在设计目标和约束条件下不断地调整比例系数,寻找符合系统响应要求的参数,从而完成了本次自动调参任务。从仿真效果上分析,自动调参比手动调参时间短,大大地减少了调参工作量,提高了控制器调参水平,使得调参工作更加科学。自动调参技术为飞行控制器寻找最优控制参数,使飞行器悬停或是前飞状态下达到最优结果完成自稳飞行。且基于Matlab/Simulink的编程和仿真平台,被控对象模型易修改,结果易查看。根据设计要求的不同,可以编写不同的软件程序,结构简单,操作方便且可以在其他环境下进行移植。
| [1] |
吴文海, 高丽, 周胜明.
飞行器控制系统设计方法现状与发展[J]. 海军航空工程学院学报, 2010, 25(4): 421–426.
WU Wenhai, GAO Li, ZHOU Shengming. Present research and development of FCS design methods[J]. Journal of Naval Aeronautical and Astronautical University, 2010, 25(4): 421–426. |
| [2] | ASTROM K J. Adaptive control[M]. New York: Addison-Wesley, 1989. |
| [3] |
熊治国, 懂新民.
程序调参飞行控制律的研究与展望[J]. 飞行力学, 2013, 21(4): 9–13.
XIONG Zhiguo, DONG Xinmin. Study and outlook of gain scheduling flight control law[J]. Flight Dynamics, 2013, 21(4): 9–13. |
| [4] |
刘道. 基于改进粒子群优化算法的PID参数整定研究[D]. 衡阳: 南华大学, 2012.
LIU Dao. Research on PID parameters tuning based on improved PSO algorithm [D]. Hengyang: University of South China, 2012.http://cdmd.cnki.com.cn/Article/CDMD-10555-1012458473.htm |
| [5] | 张顶学. 遗传算法与粒子群算法的改进及应用[D]. 武汉: 华中科技大学, 2007. |
| [6] | XUE Dingyu, CHEN Yangquan, ATHERTON D P. Linear feedback control analysis and design with MATLAB[J]. International Journal of Systems Science, 2007, 19(6): 979–984. |
| [7] |
雷开友. 粒子群算法及其应用研究[D]. 重庆: 西南大学, 2004.
LEI Kaiyou. Research on particle swarm optimization and its application [D]. Chongqing: Southwest University, 2004.http://cdmd.cnki.com.cn/Article/CDMD-10635-2006192807.htm |
| [8] |
沈锡. 基于粒子群优化算法的船舶航向PID控制[D]. 大连: 大连海事大学, 2011.
SHEN Xi. PID control for ship steering based on particle swarm optimization[D].Dalian: Dalian Maritime University, 2011. |
| [9] | KENNEDY J. Particle swarm optimization [C] //Encydopedia of machine learning.[S.l.]: Springer US, 2010. |
| [10] | REYNOLDS C W. Flocks, herds and schools: A distributed behavioral model[J]. Computer Graphics, 1987, 21(4): 25–34. DOI:10.1145/37402 |
| [11] |
宋述锡. 四旋翼无人直升机控制算法研究[D]. 沈阳: 沈阳航空航天大学, 2012.
SONG Shuxi, Research on control algorithm for quadrotor unmanned helicopter [D].Shenyang: Shenyang Aerospace University, 2012.http://cdmd.cnki.com.cn/Article/CDMD-10143-1013174291.htm |
| [12] |
林子国. 变总距变转速四旋翼无人机设计技术研究[D]. 南京: 南京航空航天大学, 2015.
LIN Ziguo. Research on variable collective pitch and rotor RPM quadrotor UAV design [D].Nanjing: Nanjing University of Aeronautics & Astronautics, 2015.http://cdmd.cnki.com.cn/Article/CDMD-10287-1016925507.htm |
| [13] | 刘春生, 吴庆宪. 现代控制工程基础[M]. 北京: 科学出版社, 2011: 86-91. |
| [14] | KAMEN E W. On the control of linear systems whose coefficients are functions of parameters[J]. IEEE Transactions on Automatic Control, 1984, 29(1): 25–33. DOI:10.1109/TAC.1984.1103374 |
| [15] | HAHRUZ S M. Design of controllers for linear parameter-varying systems by the gain scheduling technique[J]. Journal of Mathematical Analysis and Applications, 1992, 168(1): 195–217. DOI:10.1016/0022-247X(92)90199-N |
 2017, Vol. 49
2017, Vol. 49


