刚性旋翼系统相比传统的柔软旋翼系统有着突出的优点,它结构简单、易于设计、维修量小,并且使直升机大过载机动成为可能。更重要的是,刚性旋翼系统比传统的柔软旋翼系统在挥舞方向有更大的基频比 (一阶挥舞频率与旋翼速度的比值),这可以有效避免直升机在某些状态下易发生地面共振和空中共振等动力学不稳定的问题,现已在很多无轴承旋翼系统的直升机上得到应用[1-2]。但采用刚性旋翼系统的桨叶由于刚度较大会带来桨叶根部交变载荷过大的问题,进而会引起桨叶根端的疲劳问题和机体振动等一系列不稳定问题。为抑制桨根处挥舞方向的二阶交变弯曲荷载,较为直接有效的措施就是在旋翼系统上安装动力吸振振器,产生反向惯性力,抵消其需抑制的载荷。
动力吸振技术已经历了一个多世纪的发展, 最早是于1909年被德国的Frahm[3]提出,并且成功应用在邮船的防摇水箱上,这是吸振器在工程实践振动控制中的最早应用。Ormondroyd[4]等人于1928年推导出动力吸振原理,并指出在有阻尼动力吸振器的优化设计中存在最优阻尼。但直到1946年才由Brock[5]推导出最优阻尼的关系,动力吸振器理论才算逐渐发展完善。20世纪60年代以来,动力吸振器随生产技术的提高和新型智能材料的出现而不断发展,特别是磁流变技术的大力发展,半主动式动力吸振器的研究已经取得丰富的成果,本文所提到的粘弹吸振器和液弹吸振器都属于半主动式动力吸振器的一种。McGuire[6]于1994年成功设计并制造出液弹阻尼器和隔振器模型构件,并通过对模型构件的试验测试证实了液弹技术的可行性和性能的优越性。1996年,Panda[7]等人对嵌入式液弹阻尼器和粘弹阻尼器进行对比实验分析,结果表明液弹阻尼器具有更大的耗散因子且更加平稳。2005年,Petrie[8-9]等人对安装有弦向阻尼器的旋翼系统进行了动力学分析,结果显示液弹阻尼器能为直升机的气弹稳定提供足够的阻尼。2006年,Byers[10]提出在桨叶径向嵌入动力吸振器的柯氏耦合系统,并和弦向阻尼器增大阻尼的效果进行对比,证明了径向吸振器能更有效地把阻尼转移到旋翼桨叶的摆振模态,并且不容易受气动弹性不稳定和动态变距拉杆荷载的影响,但径向吸振器容易受大的离心力作用而产生静态位移。2009年,Han[11-13]等人提出在旋翼桨叶弦向嵌入弹性吸振器来减少刚性旋翼桨叶的摆振载荷,并通过相关参数分析来探讨该方法的可行性,结果显示,在桨叶弦向嵌入的弹性吸振器大荷载状态下能够减少桨根处90%的摆振弯曲荷载。
1 旋翼桨叶与液弹吸振器耦合系统模型在讨论嵌入式液弹吸振器对旋翼桨叶桨根挥舞载荷的影响时,为了简化运算,不考虑旋翼桨叶的摆振和扭转运动。二自由度耦合系统模型分别为桨叶的挥舞运动和液弹吸振器质量块在旋翼桨叶内挥舞方向的振动。
采用挥舞铰偏置量e并且挥舞铰内安装有弹簧的刚性旋翼模型如图 1所示,方位角为Ψ,挥舞角为β,挥舞角刚度为Kβ。假定旋翼的质量沿桨叶径向均匀分布,直升机在飞行过程中旋转速度Ω不变。液弹吸振器安装在桨叶内部顶端,沿桨叶挥舞方向运动。

|
图 1 嵌有液弹吸振器的旋转桨叶挥舞模型 Figure 1 Blade flapwise model with fluidlastic absorber |
液弹吸振器主质量块质量为mρ,流体基元质量为mt,Ka为弹簧静刚度,apo和ato为液弹吸振器主质量块和流体质量块相对桨叶羽轴的起始位移,ap和at为主质量块和流体质量块在桨叶内部沿挥舞方向的位移,调谐口面积比为G,G=b/a。液弹吸振器由两个质量块组成,其主质量块和流体质量块运动方向相反,并且它们间的关系为
| $ {a_t}(t) =-(G-1){a_\rho }(t) $ | (1) |
根据建立的嵌有液弹吸振器的桨叶挥舞模型,取地面为参考系,桨叶径向任一微段的坐标为 (xb, yb, zb),主质量块和流体质量块的坐标分别为 (xρ, yρ, zρ),(xt, yt, zt)。根据上述坐标表达式,可求出耦合系统的动能T和势能V,利用拉格朗日方程
| $ \frac{{{\rm{d}}q}}{{{\rm{d}}t}}\frac{{\partial L}}{{\partial {{\dot q}_j}}}-\frac{{\partial L}}{{\partial {q_j}}} = {Q_j} $ | (2) |
式中:qj为每个自由度的位移;Qj为qj相应的外激励力。把得到的动能T和势能V的表达式代入式 (2),即可得到耦合系统的运动微分方程,其矩阵形式如下
| $ \boldsymbol{M}\left\{ \begin{array}{l} {\dot \beta }\\ {{\ddot a}_\rho } \end{array} \right\} + \boldsymbol{C}\left\{ \begin{array}{l} {\dot \beta }\\ {{\dot a}_\rho } \end{array} \right\} + \boldsymbol{K}\left\{ \begin{array}{l} \beta \\ {a_\rho } \end{array} \right\} = \boldsymbol{F} $ | (3) |
式中
| $ \begin{array}{l} \mathit{\boldsymbol{M}} = \left[\begin{array}{l} \int_e^R {m{{\left( {r- e} \right)}^2}} {\rm{d}}r + ({m_\rho } + {m_t}){(R- e)^2}\;\;[{m_\rho }- {m_t}(G- 1)(R- e)\\ \;\;\;\;\;\;\;[{m_\rho }-{m_t}(G-1)]({r_a} -e)\;\;\;\;\;\;\;\;\;{m_\rho } + {m_t}{(G -1)^2} \end{array} \right]\\ \mathit{\boldsymbol{C}} = \left[{\begin{array}{*{20}{c}} {{c_\xi }} & 0\\ 0 & {{c_a}} \end{array}} \right]\\ \mathit{\boldsymbol{K}} = \left[\begin{array}{l} {K_\beta } + \int_e^R {{\mathit{\Omega }^2}} r\left( {r- e} \right)mdr + ({m_\rho } + {m_t}){\mathit{\Omega }^2}R\left( {R- e} \right)\;\;\;[{m_\rho }-{m_t}\left( {G-1} \right)]{\mathit{\Omega }^2}R\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;[{m_\rho }-{m_t}\left( {G-1} \right)]{\mathit{\Omega }^2}R\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{K_a} \end{array} \right]\\ \mathit{\boldsymbol{F}} = \left[{\begin{array}{*{20}{c}} {{F_\beta }-{m_\rho }{\mathit{\Omega }^2}R{a_{\rho 0}}-{m_t}{\mathit{\Omega }^2}R{a_{t0}}}\\ 0 \end{array}} \right] \end{array} $ |
由式 (3) 中旋翼桨叶挥舞运动微分方程,得到桨叶挥舞的固有频率为
| $ \omega _\beta ^2 = \int_e^R {\frac{{mr(r-e){\mathit{\Omega }^2}{\rm{d}}r + {K_\beta }}}{{\int_e^R {m{{\left( {r-e} \right)}^2}{\rm{d}}r} }}} $ | (4) |
令
| $ \omega _{\beta 0}^2 = \frac{{{K_\beta }}}{{\int_e^R {m{{(r-e)}^2}{\rm{d}}r} }} $ | (5) |
式中:ωβ0表示转速为零时桨叶挥舞的固有频率。从式 (4) 可以看出,调节挥舞铰的刚度,即可改变旋翼桨叶挥舞的固有频率。
由式 (3) 中液弹吸振器在桨叶挥舞方向振动的微分方程,可得液弹吸振器的固有频率为
| $ \omega _a^2 = \frac{{{K_a}}}{{{m_\rho } + {m_t}{{\left( {G-1} \right)}^2}}} $ | (6) |
液弹吸振器的调谐频率f表示为
| $ {f^2} = \frac{{{K_a}}}{{{m_\rho } + {m_t}{{\left( {G-1} \right)}^2}}} $ | (7) |
由式 (4,6) 可知,旋翼桨叶挥舞的固有频率随桨叶旋转速度的增加而增大;而液弹吸振器的固有频率则不受离心力的影响,它等于挥舞吸振器的调谐频率。另外,调谐频率可根据液弹吸振器的结构参数的改变而变化,从而能使液弹吸振器抑制一定频率范围内的激励力。
2 吸振器响应分析算例为研究吸振器在旋转状态时的动力学特性和吸振器对桨根处低阶挥舞载荷的吸振效果,本文采用典型的无铰旋翼系统,利用反共振原理,下面用具体的算例进行说明。桨叶和液弹吸振器的参数表如表 1,2所示。
| 表 1 桨叶参数 Table 1 Blade parameters |
| 表 2 液弹吸振器参数 Table 2 Fluidlastic absorber parameters |
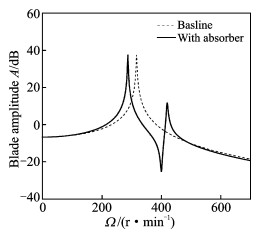
根据表 1, 2,将液弹吸振器的调谐频率设置为f2=13.33 Hz。图 2为液弹吸振器二阶幅频响应曲线。由图 2可知,当旋翼达到正常工作转速时,桨根处挥舞载荷确实减小很多。经计算嵌入式挥舞液弹吸振器可减少
|
图 2 液弹吸振器二阶幅频响应曲线 Figure 2 Second-order amplitude response curve of fluidelastic absorber |
弹性吸振器模型跟液弹吸振器等效模型相比少了液体单元。因此,只要令mt=0,G=1,代入前面得到的旋翼桨叶/液弹吸振器耦合系统运动微分方程,即可获得旋翼桨叶/弹性吸振器耦合系统的运动微分方程。进而可以得到桨叶挥舞的固有频率和弹性吸振器的固有频率等重要物理参数。弹性吸振器的参数如表 3所示。
| 表 3 弹性吸振器参数 Table 3 Elastic absorber parameters |
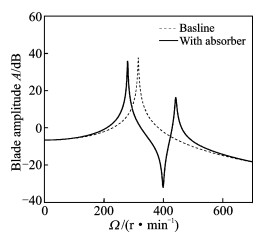
根据表 3将弹性吸振器的调谐频率设置为f2=13.33 Hz。图 3为弹性吸振器二阶幅频响应曲线。由图 3可知,当旋翼桨叶达到正常工作转速时,桨根处挥舞载荷确实减小。经计算嵌入式弹性吸振器可减少
|
图 3 弹性吸振器二阶幅频响应曲线 Figure 3 Second-order amplitude response curve of elastic absorber |
3 吸振器结构参数分析
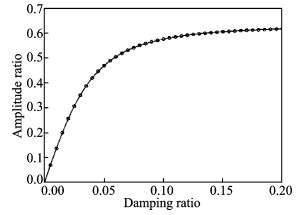
从频响函数Hij(ω) 的表达式可以知道,吸振器的结构参数对挥舞吸振器的吸振效果有很大影响。图 4给出了液弹吸振器阻尼比与旋翼桨叶挥舞幅值比关系图 (桨叶挥舞幅值比是指嵌有吸振器的桨叶挥舞幅值与不含吸振器的桨叶挥舞幅值的比值)。从图中可以看出,挥舞幅值比随吸振器阻尼比的增加而增大,即小的吸振器阻尼比对二阶外激励力会有较好的抑制作用。
|
图 4 液弹吸振器阻尼比与桨叶挥舞幅值比关系图 Figure 4 Fluidelastic absorber damping ratio VS blade flapping amplitude ratio |
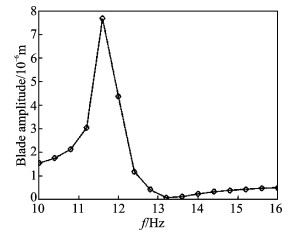
图 5给出了嵌有弹性吸振器的二阶桨叶挥舞幅值随调谐频率变化的关系图,当调谐频率达到二阶调谐频率f2=13.3 Hz时,旋翼桨根处的挥舞荷载降到最小。
|
图 5 弹性吸振器调谐频率与二阶桨叶挥舞幅值关系曲线 Figure 5 Relationship between tuning frequency and second-order blade flapping amplitude of elastic absorber |
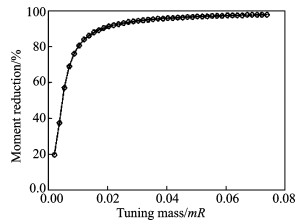
图 6为液弹吸振器的吸振效果与调谐质量的关系图。如图所示,当给定调谐口面积比G=20时,液弹吸振器对桨根处的二阶挥舞荷载的吸振效果随调谐质量的增加而增大;但当调谐质量增加到一定程度时,吸振效果增加的就不再明显。从而可知,适当地增加流体质量有助于减小桨根的二阶挥舞载荷。
|
图 6 调谐质量与吸振效率关系图 (G=20) Figure 6 Tuning mass VS vibration-absorbing efficiency (G=20) |
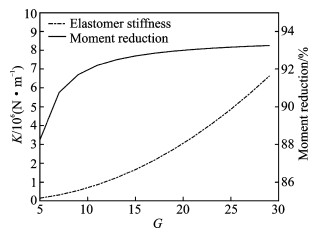
图 7给出了给出了液弹吸振器吸振效果和弹性体刚度随调谐口面积比的变化关系。由图可知,在给定的调谐质量和二阶调谐频率条件下,液弹吸振器的弹性体刚度和吸振效果都随调谐口面积比的增大而显著增加,但调谐口面积G对吸振效果的影响非常小。
|
图 7 调谐口面积比对吸振器刚度和吸振效果关系图 Figure 7 Tuning port area ratio VS absorber stiffness & vibration absorption effect |
由于吸振器安装在桨叶内部,吸振器的动态行程受桨叶的剖面尺寸限制,较小的动态行程对直升机飞行是比较有利的,因此对影响吸振器动态行程的结构参数分析也是必要的。
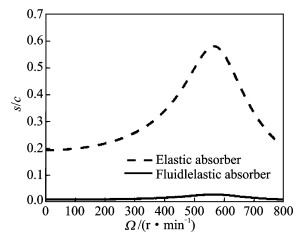
图 8给出了嵌入式液弹吸振器和弹性吸振器动态行程 (s) 与旋翼速度关系图,由图可知,在吸振器质量相等,调谐口面积一定的条件下,液弹吸振器的动态行程比弹性吸振器的动态行程小得多。
|
图 8 吸振器动态行程与旋翼速度关系图 Figure 8 Absorber dynamic stroke VS rotor speed |
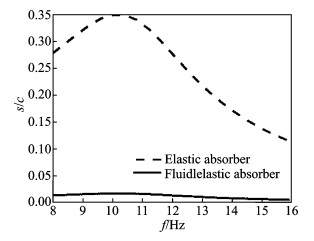
吸振器的动态行程与调谐频率的关系如图 9所示,当旋翼到达正常工作转速400 r/min时,吸振器的行程随调谐频率先增大后减小,但液弹吸振器的动态行程同样小得多。
|
图 9 吸振器动态行程与调谐频率关系图 Figure 9 Absorber dynamic stroke VS tuning frequency |
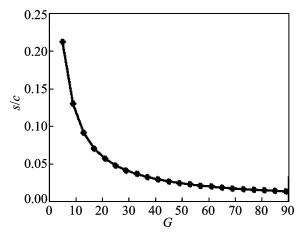
液弹吸振器动态行程与调谐口面积比G关系如图 10所示,吸振器的动态行程随调谐口面积的增大而显著减小。调谐口面积相当于放大了吸振器的等效质量,因此可以用来减小吸振器的质量和尺寸。
|
图 10 液弹吸振器动态行程与调谐口面积比关系图 Figure 10 Dynamic stroke VS tuning port area ratio of fuluidelastic absorber |
图 11为液弹吸振器挥舞方向的动态行程与吸振器主质量关系图。吸振器在桨叶挥舞方向的动态行程随吸振器质量的增加而减小。因此,增加吸振器质量是一个可以减小吸振器动态行程的有效方法。

|
图 11 动态行程与吸振器主质量关系图 Figure 11 Dynamic stroke VS primary mass of fluidelastic absorber |
4 结论
为了抑制刚性旋翼桨叶的二阶挥舞弯曲载荷,在桨叶挥舞方向嵌入动力吸振器。比较了弹性吸振器与液弹吸振器对挥舞方向二阶载荷的抑制效果,并且对影响吸振器吸振性能的结构参数和挥舞吸振器的动态特性进行分析。通过本文的研究可得到以下结论:
(1) 旋翼桨根处的低阶挥舞荷载可以通过在桨叶内部挥舞方向嵌入动力吸振器来抑制,挥舞吸振器的固有频率不受离心力的影响,与旋翼转速Ω无关。
(2) 在给定相同条件下,如不考虑吸振器在桨叶内挥舞方向的动态行程,弹性吸振器比液弹吸振器的吸振效果更好,然而桨叶内部实际对弹性吸振器的动态行程的限制大大限制了弹性吸振器的性能。
(3) 减小液弹吸振器阻尼ξa,可以增强吸振器的吸振效果,但同时也增大了吸振器挥舞方向的动态行程。因此,为了保证对桨叶挥舞交变荷载较好的吸振效果,采用轻阻尼吸振器。
(4) 随调谐口面积G的增加,对液弹吸振器吸振效果的增强很小,但能显著减小吸振器的动态行程,可以用来减小吸振器的质量和尺寸。
(5) 增加液弹吸振器的质量,既可以增强吸振效果,也可以减小吸振器挥舞方向的动态行程,但同时也以增加重量为代价。
总之,相对于弹性吸振器,液弹吸振器提供了一种可行有效的方法来抑制刚性旋翼桨叶的二阶挥舞荷载,因为它比弹性吸振器具有更小的有效质量和动态行程但却有相当的吸振效率。
| [1] |
陈俊伟, 张勇刚, 韩东.
基于嵌入式吸振器的旋翼桨叶摆振载荷抑制研究[J]. 振动工程学报, 2014, 27(s2): 13–17.
CHEN Junwei, ZHANG Yonggang, HAN Dong. Lagwise loads reduction of rotor blades by fluidlastic absorbers[J]. Journal of Vibration Engineering, 2014, 27(s2): 13–17. |
| [2] |
陈俊伟, 吴世杰, 韩东. 基于桨叶吸振器的旋翼摆振载荷抑制试验方案设计[C]//第三十届直升机年会. 黑龙江: 中国航空学会, 2014.
CHEN Junwei, WU Shijie, HAN Dong. The experimental design on lagwise loads reduction of rotor blades by fluidlastic absorbers[C]//The 30th National Helicopter Annual Meeting. Harbin, China: China Aviation Society, 2014. |
| [3] | FRAHM H. Device for damping vibrations of bodies[P]. U.S: Patent No.0/989, 958, 1909-10-30. |
| [4] | ORMONDROYD J, HARTOG J P D. The theory of dynamic vibration absorber[J]. Journal of Applied Mechanics, 1928, 50: 9–22. |
| [5] | BROCK J E. A note on the damped vibration absorber[J]. Journal of Applied Mechanics, 1946, 13(4): A-284. |
| [6] | MCGUIRE D P. Fluidelastic dampers and isolators for vibration control in helicopters[C]//American Helicopter Society 50th Annual Forum. Washington, DC: American Helicopter Society, 1994:295. |
| [7] | PANDA B, MYCHALOWYCZ E, TARZANIN F J. Application of passive dampers to modern helicopters[J]. Smart Materials & Structures, 1996, 5(5): 509–516. |
| [8] | PETRIE J S, LESIEUTRE G A, SMITH E C. Helicopter blade lag damping using embedded fluid elastic inertial dampers[C]//Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics & Materials Conference. California, USA : American Institute of Aeronautics and Astronautics, 2004. |
| [9] | PETRIE J S, LESIEUTRE G A, SMITH E C. Design and model testing of helicopter rotor blade lag fluid elastic embedded chordwise inertial dampers[C] //Annual Forum Proceedings-American Helicopter Society. USA : American Helicopter Society, 2005, 61(1): 994. |
| [10] | BYERS L K. Helicopter rotor lag damping augmentation based on radial absorber and coriolis coupling[D]. Pennsylvania: The Pennsylvania State University, 2006. |
| [11] | HAN D, SMITH E C. Lagwise loads analysis of a rotor blade with an embedded chordwise absorber[J]. Journal of Aircraft, 2009, 46(4): 1280–1290. DOI:10.2514/1.40569 |
| [12] | HAN D, WANG J, SMITH E C, et al. Transient loads control of a variable speed rotor during lagwise resonance crossing[J]. AIAA Journal, 2012, 51(1): 20–29. |
| [13] | HAN D. Flapwise loads reduction of rotor blades by embedded flapwise absorbers[J]. The Aeronautical Journal, 2016, 120(1230): 1215–1229. DOI:10.1017/aer.2016.53 |
 2017, Vol. 49
2017, Vol. 49


