无人直升机具有垂直起降、定点悬停、灵活机动、自主飞行等独特的飞行特性,在军民领域应用广泛。随着复合材料、动力系统、传感器等新技术的发展,无人直升机得到迅速发展。其中,飞行动力学建模与仿真技术是其研制过程中的核心内容之一。
国内外直升机飞行动力学建模手段经历了由简单到复杂的过程。根据建模机理,大致可划为以下几类:(1) 动量滑流理论建模,如德国DLR实验室搭建的BO-105直升机飞行动力学模型[1]。该方法计算效率高,但模型精度较低,仅限用于初步模型验证与仿真。(2) 叶素理论建模,其中以GENHEL模型[2]为典型代表。该方法建模过程复杂,置信度高,Ballin曾利用UH-60A直升机的飞行测试数据对GENHEL模型进行了系统的验证[3]。验证结果表明该模型在大速度配平特性及异轴响应预测方面精度有待提高。(3) 仿射非线性建模。如北京航空航天大学的杨超等人搭建了UH-60直升机飞行动力学模型[4],其通过与国外试飞数据对比验证了理论模型的准确性,该方法置信度高,仿真效果较好,但建模难度大,不易执行。(4) 计入旋翼非定常气动特性、弹性桨叶动力学模型及旋翼/机体耦合的建模[5]。目前对该建模方法的研究较多,该方法计算精度较高,可提高机动飞行仿真的准确性,但由于缺乏公开的大机动飞行测试数据,多数仅对单一通道的小幅操纵机动飞行进行验证,而且其计算效率偏低,不能满足实时仿真的需求。(5) 扫频辨识建模[6-7],基于合理的辨识方法可得到能够反映直升机动力学特性的模型,再基于相同飞行状态的试验数据对模型进行校验。由于该方法基于试验数据,不宜应用于新研制无人直升机飞行控制律设计。
在无人直升机仿真技术方面,目前主要有3种形式[8]:(1) 数字仿真。采用数值方法模拟整个无人直升机系统,是完全基于数学模型的,无需模拟真实环境的各种物理设备,主要用于控制律参数初步设计。(2) 半物理仿真。在仿真系统中接入部分实物,采用真实的机上设备或等效设备实时运行,仿真系统置信度得到提高。(3) 人在回路仿真。接入外控设备,形成人/机飞行环境的动态特性,可以更加直观地反馈飞控系统性能,对于无人直升机来说,其主要适用于起飞或回收阶段仿真。
基于无人直升机实时飞行仿真需要,本文建立了实用的直升机非线性飞行动力学模型,并针对某型无人直升机完成飞行控制系统设计;为验证理论模型的准确性,开展了半物理仿真和飞行试验研究。
1 直升机飞行动力学模型无人直升机是多变量、强耦合的非线性系统。本节分别建立主旋翼、尾桨、机身、垂尾及平尾气动力模型,之后基于各部件气动力和力矩构建机体运动微分方程和姿态微分方程,完成无人直升机非线性飞行动力学建模。
无人直升机非线性运动方程可表示为状态空间格式[9]
| $ \boldsymbol{\dot y} = f(\boldsymbol{y}, \boldsymbol{u}, t) $ | (1) |
式中:t为时间;u为操纵输入;y为直升机状态向量,表示为
| $ \boldsymbol{y} = [{y_B}\;\;{y_R}] $ | (2) |
式中:yR为旋翼挥舞运动状态量和入流状态量;yB为机体运动状态量。
1.1 旋翼气动力模型为准确地考虑马赫数对翼型气动力的影响以及桨叶失速后的气动力非线性变化,本文基于翼型气动试验数据插值计算不同马赫数和迎角下的翼型气动力,作为后续计算分析的基础。
基于Petes-He有限状态尾迹模型[10],本文建立旋翼非均匀入流计算模型。为保证足够的计算精度,周向谐波阶数取至3阶,径向形函数取至4阶,共13个入流状态量,其中与旋翼入流谐波分量αjr和βjr有关的微分方程组为
| $ {\boldsymbol{M}^c}{\{ \alpha _j^r\} ^*} + {\boldsymbol{L}^{c-1}}\{ \alpha _j^r\} = \frac{1}{2}\{ \boldsymbol{\tau} _j^{rc}\} \\ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {\boldsymbol{M}^s}{\{ \beta _j^r\} ^*} + {\boldsymbol{L}^{s - 1}}\{ \beta _j^r\} = \frac{1}{2}\{\boldsymbol{ \tau} _j^{rs}\} \end{array} $ | (3) |
式中:M为质量矩阵,反映了空气惯性的影响;L为影响系数矩阵,与来流和尾迹倾角有关;τ为广义力矩阵;上标c, s分别表示余弦谐波和正弦谐波。
根据桨叶惯性力、离心力、气动力对挥舞铰的力矩平衡,同时考虑机体俯仰、滚转运动引起的随动挥舞[11], 可建立带挥舞铰偏置量的铰接式刚体桨叶挥舞运动方程组
| $ \begin{array}{l} {{\ddot \beta }_0} = [{({\mathit{\boldsymbol{M}}_T})_0}-{\mathit{\Omega }^2}({\mathit{\boldsymbol{I}}_b} + e{\mathit{\boldsymbol{M}}_s}){\beta _0}-{\mathit{\boldsymbol{M}}_s}({{\dot u}_y} + {u_x}{\omega _z}-\\ \;\;\;\;\;\;\;{u_z}{\omega _x}) - {\mathit{\boldsymbol{M}}_s}g] = /{\mathit{\boldsymbol{I}}_b}\\ {{\ddot \beta }_{1s}} = [{({\mathit{\boldsymbol{M}}_T})_{1s}} -e{\mathit{\boldsymbol{M}}_s}{\mathit{\Omega }^2}{\beta _{1s}} + 2\mathit{\Omega }{\mathit{\boldsymbol{I}}_b}{{\dot \beta }_{1c}} -2({\mathit{\boldsymbol{I}}_b} + \\ \;\;\;\;\;\;\;\;\;e{\mathit{\boldsymbol{M}}_s}){\omega _z}\mathit{\Omega } + {\mathit{\boldsymbol{I}}_b}{{\dot \omega }_x}]/{\mathit{\boldsymbol{I}}_b}\\ {{\ddot \beta }_{1c}} = [{({\mathit{\boldsymbol{M}}_T})_{1c}} -e{\mathit{\boldsymbol{M}}_s}{\mathit{\Omega }^2}{\beta _{1c}} -2\mathit{\Omega }{\mathit{\boldsymbol{I}}_b}{{\dot \beta }_{1s}} -2({\mathit{\boldsymbol{I}}_b} + \\ \;\;\;\;\;\;\;\;\;e{\mathit{\boldsymbol{M}}_s}){\omega _x}\mathit{\Omega } + {\mathit{\boldsymbol{I}}_b}{{\dot \omega }_z}]/{\mathit{\boldsymbol{I}}_b} \end{array} $ | (4) |
式中:MT为桨叶气动力对挥舞铰的力矩;Ω为旋翼转速;Ib为桨叶对挥舞铰的挥舞惯性矩;Ms为桨叶对挥舞铰的质量静矩;e为挥舞铰偏置量;u, ω分别为桨轴系下的线速度和角速度。
1.2 机体运动方程在机体坐标系下,单旋翼带尾桨无人直升机非线性运动微分方程组如下
| $ \begin{array}{l} m{{\dot V}_x} = m({V_y}{\omega _z}-{V_z}{\omega _y})-mg{\rm{sin}}\mathit{\Theta } + {F_x}\\ m{{\dot V}_y} = m({V_z}{\omega _x}-{V_x}{\omega _z}) - mg{\rm{cos}}\mathit{\Theta }{\rm{cos}}\mathit{\Phi } + {F_y}\\ {m_z} = m({V_x}{\omega _y} - {V_y}{\omega _x}) + mg{\rm{cos}}\mathit{\Theta }{\rm{sin}}\mathit{\Phi } + {F_z}\\ {I_x}{\omega _x} = ({I_y} - {I_z}){\omega _y}{\omega _z} + {I_{xy}}({{\dot \omega }_y} - {\omega _z}{\omega _x}) + {M_x}\\ {I_y}{{\dot \omega }_y} = ({I_z} - {I_x}){\omega _z}{\omega _x} + {\rm{ }}{I_{xy}}({{\dot \omega }_x} + {\omega _y}{\omega _z}) + {M_y}\\ {I_z}{{\dot \omega }_z} = ({I_{x}} - {I_y}){\omega _{x}}{\omega _{y}} + {\rm{ }}{I_{xy}}(\omega _x^2 - \omega _y^2) + {M_z} \end{array} $ | (5) |
式中:m为无人直升机重量;Vi,ωi(i=x,y,z) 分别为无人直升机在机体坐标系下的运动线速度和角速度;Fi,Mi分别为直升机各部件气动力作用在直升机重心处的合力和合力矩。其中旋翼气动力基于1.1节计算得到,尾桨气动力采用相对简单且具有较好精度的修正贝利模型计算,根据经验值考虑悬停及低速下垂尾对尾桨的阻塞效应;机体气动力基于风洞试验结果通过插值获得,旋翼下洗对机身升力的影响以垂直增重系数表示;垂尾和平尾的气动力采用薄翼型升力线理论计算获得。
机体姿态微分方程组如下
| $ \begin{array}{l} \mathit{\dot \Phi } = {\omega _x}-{\rm{tan}}\mathit{\Theta }({\omega _y}{\rm{cos}}\mathit{\Phi }-{\omega _z}{\rm{sin}}\mathit{\Phi })\\ \mathit{\dot \Theta } = {\omega _y}{\rm{sin}}\mathit{\Phi } + {\omega _z}{\rm{cos}}\mathit{\Phi }\\ \dot \psi = \frac{1}{{{\rm{cos}}\mathit{\Theta }}}({\omega _y}{\rm{cos}}\mathit{\Phi }-{\omega _z}{\rm{sin}}\mathit{\Phi }) \end{array} $ | (6) |
式中:Θ为俯仰角;Φ为滚转角;Ψ为偏航角。
基于本节所建立的无人直升机非线性飞行动力学模型,可实现从操纵输入至直升机状态量输出的飞行特性模拟。用C语言进行代码编译,可满足实时仿真要求。
2 飞行控制系统设计基于前文所建立的无人直升机非线性飞行动力学模型,本节针对某型无人直升机开展飞行控制律设计,实现飞行控制系统的功能和性能指标要求。
对于飞行控制系统来说,飞行控制律是实现各类控制策略的基础。本文采用文献[12]中成熟的控制算法。飞行控制律设计分3步进行:
(1) 无人直升机模型分析。将非线性飞行动力学模型进行小扰动线化,对操纵线系、舵回路时延和死区、输出反馈滤波、舵面偏转速率限幅等非线性环节进行模拟。
(2) 基本控制律设计。该过程不考虑轴间耦合因素,简化各通道模型,用单回路根轨迹法计算出各个控制器的基本参数。首先进行内回路基本控制律设计,包括姿态保持、航向保持、垂速保持,内回路是底层控制,用于实现无人直升机的稳定性、动态特性等性能指标;其次进行外回路基本控制律设计,包括速度保持、位置保持、高度保持、航迹角保持,用于实现与飞行任务相关的速度、高度以及航迹指标。
(3) 飞行控制参数优化。该过程考虑轴间耦合因素,对基本控制律进行修正。针对4个控制通道,依次进行姿态角、速度、位置联合控制律设计,并通过仿真测试对控制参数进行微调。
整体控制框架如图 1所示。
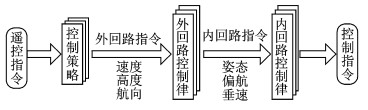
|
图 1 飞行控制框架图 Figure 1 Scheme of flight control system |
3 算例与分析
为验证本文所建立的直升机非线性飞行动力学模型和飞行控制律设计方法,本节以某型无人直升机为例开展了半物理仿真和飞行试验。以期通过分析仿真模型姿态角和速度的闭环控制效果,评估飞控系统性能;通过对比飞行试验数据和仿真数据的差异,评估直升机非线性飞行动力学模型的准确性及飞控系统性能。
3.1 半物理仿真验证将样例无人直升机飞行动力学模型嵌入仿真机内部,飞控计算机实物接入控制回路,舵机、传感器采用数值模拟,进行了悬停机动飞行和小速度飞行仿真。嵌入式仿真系统原理如图 2所示。
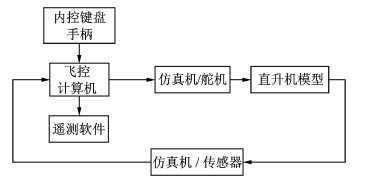
|
图 2 嵌入式仿真系统原理图 Figure 2 Scheme of embedded simulation system |
(1) 悬停机动飞行仿真
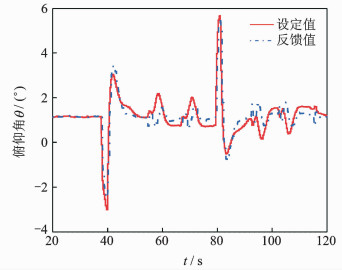
在本次仿真中共进行6次悬停机动飞行,依次为“前移”、“左移”2次、“后移”、“右移”2次,最终回到起始点。每次机动飞行的位移设定值为10 m,仿真过程共持续约80 s。为准确评估仿真模型的控制效果,图 3,4分别给出了仿真过程中模型俯仰角和滚转角变化。
|
图 3 悬停机动飞行仿真俯仰角变化 Figure 3 Variation of pitch angle in hover maneuver simulation |

|
图 4 悬停机动飞行仿真滚转角变化 Figure 4 Variation of roll angle in hover maneuver simulation |
从图 3,4可以看出,每次控制指令发出后,模型姿态响应正确,约10 s后模型位置控制满足要求。机动飞行过程中,姿态角反馈值能够较好地跟踪其设定值且存在一定时延,如前/后移时俯仰角响应 (同轴) 峰值的反馈与设定差值小于±0.5°,滚转角响应 (异轴) 峰值的反馈与设定差值小于±2°,已满足姿态保持±2°的精度要求。
(2) 小速度飞行仿真
在本次仿真中,进行了由悬停转入3 m/s飞行,再加速至10 m/s飞行,稳定后再转入3 m/s飞行,最终刹车悬停的飞行过程。图 5,6分别给出了能够体现控制效果的内环姿态角变化以及机体前向速度变化。
|
图 5 小速度飞行仿真俯仰角变化 Figure 5 Variation of pitch angle in low speed flight simulation |

|
图 6 小速度飞行仿真机体前向速度变化 Figure 6 Variation of forward speed in low speed flight simulation |
从姿态角变化可以看出,在前飞过程中,每次发送加/减速指令后,姿态角反馈值能够较好地跟踪其设定值且存在一定时延,俯仰角峰值的反馈与设定差值约±1°,已满足姿态保持±2°的精度要求。从机体前向速度变化可以看出,模型速度反馈能够较好地跟踪其设定值且存在小幅超调,超调量小于1 m/s。
3.2 飞行试验验证开展与仿真科目对应的飞行试验,其中,飞行控制系统结构和控制参数与半物理仿真中相同。提取关键遥测数据,以期通过将相同状态下的姿态角和速度反馈值与仿真数据对比,验证直升机非线性飞行动力学模型的准确性;通过分析飞行试验中姿态角和速度的控制效果,进一步评估飞控系统性能。
(1) 悬停机动飞行试验
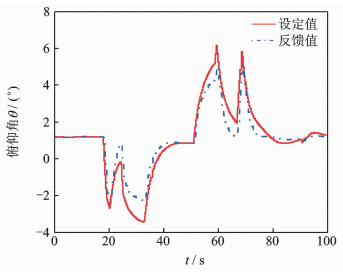
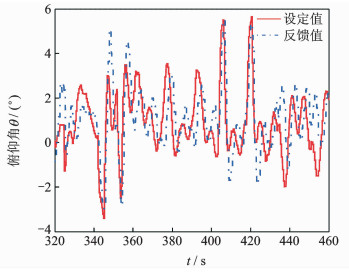
在本次试验中共进行8次悬停机动飞行,依次为“前移”2次、“左移”2次、“后移”2次、“右移”2次,最终回到起始点。图 7,8分别给出了试验过程中直升机俯仰角和滚转角变化。
|
图 7 悬停机动飞行试验俯仰角变化 Figure 7 Variation of pitch angle in hover maneuver test |
|
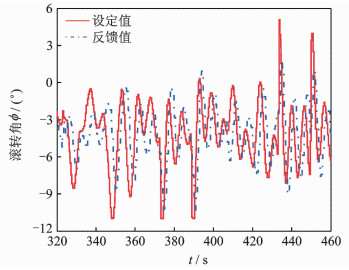
图 8 悬停机动飞行试验滚转角变化 Figure 8 Variation of roll angle in hover maneuver test |
从姿态角变化趋势可以看出,直升机姿态响应反馈值能够较好地跟踪其设定值,进一步验证了飞控系统设计的合理性。
机动飞行过程中,前移时直升机低头反馈峰值约-3°,后移时直升机抬头反馈峰值约5.5°,左移时直升机左滚反馈峰值约-10.5°,右移时直升机右滚反馈峰值约2°。通过与图 3,4的仿真数据对比,可以看出俯仰角响应试验值与仿真值基本一致,误差小于0.5°,滚转角响应试验值与仿真值存在一定差异,最大误差接近3°。分析认为,滚转响应差异与试验时直升机横向重心偏左以及右侧风干扰有关,导致直升机稳态悬停时左滚角度偏大。
另外,对比飞行试验数据和仿真数据可以看出,实际飞行试验时直升机姿态始终处于波动状态,与仿真时的平滑曲线有所差异,且反馈值与设定值之间的时延更加明显。这与无人直升机高度非线性耦合特性密切相关,如试飞时直升机易受到外部环境扰动的影响,仿真模型中传感器时延、舵机时延及死区仅能够根据工程经验模拟等。
(2) 小速度飞行试验
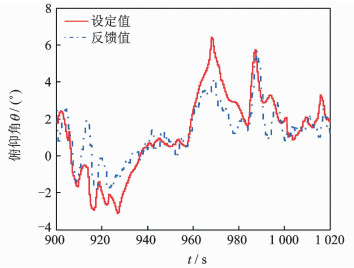
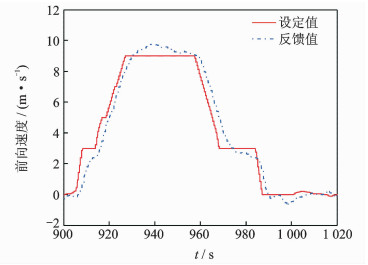
图 9,10分别给出了小速度飞行试验中直升机姿态角和机体前向速度变化。为保证试验安全,试验中采用相对保守的策略,即通过内控键盘逐次发送加速指令,每次将速度设定值提高2 m/s,直至达到8 m/s。
|
图 9 小速度飞行试验俯仰角变化 Figure 9 Variation of pitch angle in low speed flight test |
|
图 10 小速度飞行试验机体前向速度变化 Figure 10 Variation of forward speed in low speed flight test |
从飞行试验数据可以看出,直升机俯仰角和前向速度反馈值均能够较好地跟踪其设定值且存在一定时延,稳态飞行时俯仰角反馈与设定差值小于±2°,前向速度反馈与设定差值小于±1 m/s,与仿真结果基本一致,进一步验证了飞控系统设计的合理性。
直升机俯仰和速度变化与仿真值趋势一致,加速过程中直升机低头反馈峰值约-1.8°,与仿真值之间的误差约0.5°,分析认为,这与飞行试验中采取了更加平缓的加速策略有关。
4 结论本文建立了无人直升机非线性飞行动力学模型,完成样例无人直升机的飞行控制律设计,并进行了飞行仿真和飞行试验验证。
(1) 对比仿真和试验结果发现,俯仰角响应试验值与仿真值误差约0.5 °,受重心位置和外界扰动影响,滚转角响应试验值与仿真值误差约3°,验证了无人直升机非线性飞行动力学模型的准确性。
(2) 仿真和试验过程中,直升机姿态、速度反馈值均能够较好地跟踪各自的设定值,已满足姿态保持±2°的精度要求,速度反馈超调量小于1 m /s,验证了飞行控制参数的合理性。
受试验条件限制,本文仅开展了悬停机动和小速度飞行的模型验证,后续将进行盘旋和大速度飞行的模型验证。
| [1] |
宋于波. 基于Flightlab的无人直升机建模与仿真技术研究[D]. 南京: 南京航空航天大学, 2011.
SONG Yubo. Modeling and simulation technology based on Flightlab for unmanned helicopter[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2011. |
| [2] | HOWLETT JJ. UH-60 Black Hawk engineering simulation program: Volume I-Mathematical model[R]. NASA CR-166309, 1981. |
| [3] | BALLIN MG. Validation of a real-time engineering simulation of the UH-60A helicopter[R]. NASA-TM-88360, 1987. |
| [4] |
杨超, 洪冠新, 宋寿峰.
直升机飞行动力学仿射非线性系统建模[J]. 北京航空航天大学学报, 1997, 23(4): 471–476.
YANG Chao, HONG Guanxin, SONG Shoufeng. Affine nonlinear mathematical model for helicopter flight dynamics[J]. Journal of Beijing University of Aeronautics and Astronautics, 1997, 23(4): 471–476. |
| [5] | RIBERA M. Helicopter flight dynamics simulation with a time-accurate free-vortex wake model[D]. College Park, Maryland: University of Maryland, 2007. |
| [6] |
顾冬雷, 高正, 孙传伟.
无人直升机控制动态特性的频域辨识建模方法[J]. 南京航空航天大学学报, 2004, 36(6): 688–692.
GU Donglei, GAO Zheng, SUN Chuanwei. Frequency domain identification for unmanned helicopter[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2004, 36(6): 688–692. |
| [7] | KUMAR R, GANGULI R, OMKAR SN. Rotorcraft parameter identification from real time flight data[J]. JournalofAircraft, 2008, 45(1): 333–341. DOI:10.2514/1.32024 |
| [8] |
张登建. 无人直升机飞行仿真系统软件设计与开发[D]. 南京: 南京航空航天大学, 2012.
ZHANG Dengjian. Research on simulation software of flight control system for unmanned helicopter[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2012. |
| [9] |
李攀, 陈仁良.
直升机急拉杆机动飞行仿真建模与验证[J]. 航空学报, 2010, 31(12): 2315–2323.
LI Pan, CHEN Renliang. Formulation and validation of a helicopter model for pull-up maneuver simulation[J]. Chinese Journal of Aeronautics, 2010, 31(12): 2315–2323. |
| [10] | HE CJ. Development and application of a generalized dynamic wake theory for lifting rotors[D]. Atlanta: Georgia Institute of Technology, 1989. |
| [11] | CHEN R T N. Effects of primary rotor parameters on flapping dynamics[R]. NASA Technical Paper 1431, 1980. |
| [12] |
王小青. 无人直升机建模与控制技术研究[D]. 南京: 南京航空航天大学, 2010.
WANG Xiaoqing. Research on technology for unmanned helicopter modeling and control system design[D]. Nanjing: University of Aeronautics & Astronautics, 2010. |
 2017, Vol. 49
2017, Vol. 49


