直升机改进改型是当今世界主要直升机公司研制新型直升机的一种常用策略。由于只是重新设计原机型的部分结构件,其余的结构件仍可在新机型上继续使用,这种研制策略有效降低了新机型的设计、生产和维护成本。
直升机机身动特性设计是直升机设计的基础领域之一[1-3],而直升机机身动特性的参数影响分析是直升机机身动特性设计中的一个关键环节。根据参数影响分析的结果选择新机型动特性的设计参数,可尽量少地改变机身结构以达到机身动特性设计要求,充分发挥直升机改进改型的设计优势。针对直升机动特性的参数影响分析,中国国内研究起步较晚,目前多采用灵敏度法[4-5],该方法通过求解刚度矩阵和质量矩阵对参数的导数确定参数变化对动特性的影响。国外研究人员在早期多采用Vincent圆法[6]和模态应变能法[7]。Vincent圆法通过Vincent圆的中心位置和半径大小确定参数变化对动特性的影响,其适用于简单结构。而模态应变能法通过结构的应变能密度确定参数变化对动特性的影响,其适用于复杂结构。之后在模态应变能法的基础上发展出的灵敏度法[8-9]慢慢成为主流分析方法。
本文利用直11型直升机机身有限元模型,对有限元模型进行灵敏度分析,研究在直升机改进改型设计中机身改动对机身动态特性的影响,为直升机改进改型的设计提供依据。
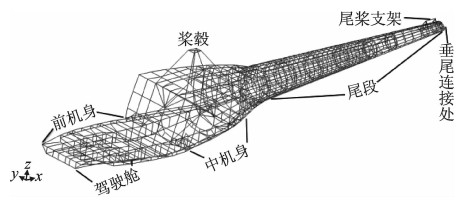
1 机身有限元模型本文以直11型直升机机身有限元模型 (如图 1所示) 为研究对象,模型包含1 632个节点,3 731个结构单元。该模型由机身段、尾段和难建模部件3个部分组成。
|
图 1 直11机身有限元模型 Figure 1 Finite element model of Z11 helicopter fuselage |
机身段包括前机身和中机身,这部分结构非常复杂,几乎直升机的全部装载质量都集中在机身段,难建模结构 (如舱门、舱罩、仪表板和操纵机构等) 及部件 (把装载质量当部件处理) 多。机身段的承力结构在建模中依据受力情况,桁条简化为两节点梁或杆,蒙皮和地板简化为四边形正应力板或剪应力板,框和腹板简化为二力杆和四边形正应力板及三角形正应力板组成的杆板结构[4]。
尾段结构细长且主要由承力结构组成,主要传递直升机尾桨、平尾以及垂尾的载荷。尾段的蒙皮、腹板简化为四边形壳单元,长桁、框和橼条简化为两节点梁单元。
难建模部件主要为客舱门、驾驶舱门、整流罩等非承力件和次要结构,提供一定的刚度和惯量,对机体动力学特性有较明显的影响。通过选取位移协调单元和集中质量单元可对这些部件进行有效准确的建模。
2 机身模态分析利用自编的接口程序将直11机身NASTRAN模型导入有限元分析软件FEMtools中,利用其中的模态分析模块求得机身的模态频率和振型。该软件的模态分析方法为Lanczos方法。
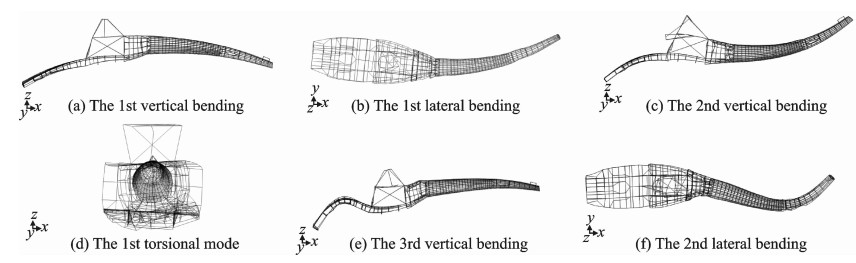
从计算结果中选取机身前六阶整体模态。其中,一阶垂向弯曲的固有频率为8.474 Hz;一阶横向弯曲的固有频率为9.812 Hz;二阶垂向弯曲的固有频率为14.564 Hz;一阶扭转的固有频率为23.694 Hz;三阶垂向弯曲的固有频率为27.898 Hz;二阶横向弯曲的固有频率为39.469 Hz。相应的振型图如图 2所示。
|
图 2 直11机身前六阶振型图 Figure 2 First six mode shapes of Z11 helicopter fuselage |
3 灵敏度分析
灵敏度分析是一种计算因设计变量或参数 (如边界条件、材料刚度、几何属性等) 的改变而引起结构特征量 (如质心、固有频率、振型等) 变化率的方法。参数和特征量的选择是灵敏度分析过程中的重要步骤,选择依据取决于分析目的。由于本文旨在研究直升机改进改型过程中机身的结构参数改变对机身动态特性的影响,结构特征量选为直升机机身的前六阶固有频率,模型的参数选为机身不同部件处的质量、弹性模量以及板、壳、杆和梁单元的几何属性。
基于模态参数的灵敏度分析需要考虑两个重要的约束方程:特征方程和加权正交方程[10-11]
| $ (\boldsymbol{K}-{\lambda _i}\boldsymbol{M}){\boldsymbol{\varphi} _i} = 0 $ | (1) |
| $ \boldsymbol{\varphi} _i^{\rm{T}}\boldsymbol{M}{\boldsymbol{\varphi} _i} = 1 $ | (2) |
式中:K,M分别为结构的刚度和质量矩阵;λi为第i阶特征值;φi为第i阶振型。
将式 (1,2) 分别对结构的第j个参数Pj求微分,得
| $ (\frac{{\partial \boldsymbol{K}}}{{\partial {P_j}}}-\frac{{\partial {\lambda _i}}}{{\partial {P_j}}}\boldsymbol{M}-{\lambda _i}\frac{{\partial \boldsymbol{M}}}{{\partial {P_j}}}){\boldsymbol{\varphi} _i} + (\boldsymbol{K}-{\lambda _i}\boldsymbol{M})\frac{{\partial {\boldsymbol{\varphi} _i}}}{{\partial {P_j}}} = 0 $ | (3) |
| $ 2\boldsymbol{\varphi} _i^{\rm{T}}\boldsymbol{M}\frac{{\partial {\boldsymbol{\varphi} _i}}}{{\partial {P_j}}} + \boldsymbol{\varphi} _i^{\rm{T}}\frac{{\partial \boldsymbol{M}}}{{\partial {P_j}}}{\boldsymbol{\varphi} _i} = 0 $ | (4) |
整理得到结构第i阶特征值对结构的第j个参数的导数
| $ \frac{{\partial {\lambda _i}}}{{\partial {P_j}}} = \boldsymbol{\varphi} _i^{\rm{T}}(\frac{{\partial \boldsymbol{K}}}{{\partial {P_j}}}-{\lambda _i}\frac{{\partial \boldsymbol{M}}}{{\partial {P_j}}}){\boldsymbol{\varphi} _i} $ | (5) |
式中:
| $ \frac{{\partial \boldsymbol{K}}}{{\partial {P_j}}} = \frac{{\boldsymbol{K}({P_j} + \Delta {P_j})-\boldsymbol{K}({P_j})}}{{\Delta {P_j}}} $ | (6) |
| $ \frac{{\partial \boldsymbol{M}}}{{\partial {P_j}}} = \frac{{\boldsymbol{M}({P_j} + \Delta {P_j})-\boldsymbol{M}({P_j})}}{{\Delta {P_j}}} $ | (7) |
在直升机的改进改型设计中,增减设备、加强承力结构等措施通常会导致机身的质量变化。本文使用的直升机机身有限元模型采用集中质量单元建立结构的质量模型。在分析不同位置处质量变化对机身固有频率的影响时,本文将模型中的所有393个集中质量单元的质量作为参数,利用FEMtools中的灵敏度分析模块求出机身前六阶固有频率对这些参数的灵敏度。
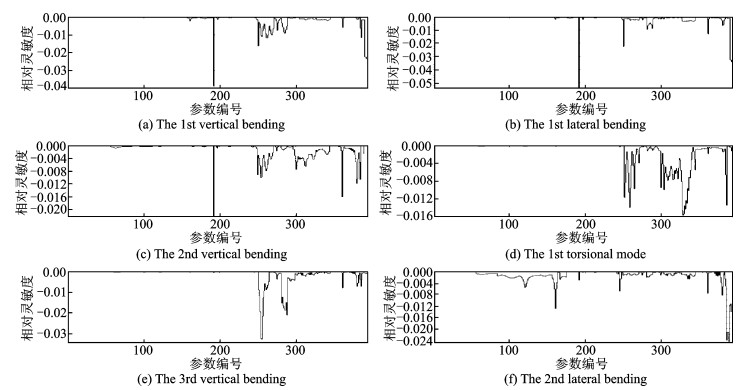
图 3给出了前六阶固有频率对质量的灵敏度曲线。其中,横轴表示质量单元质量参数的编号,纵轴表示固有频率对质量变化的相对灵敏度值。可以看出,固有频率对质量的灵敏度是负值,即无论何处质量增加,固有频率都会出现不同程度的降低。结合各质量参数所在的机身位置,发现振型位移越大,质量越大的质量单元对固有频率的影响越大。如对于8.474 Hz的机身垂向一阶弯曲模态,驾驶舱 (对应参数编号251~270)、尾桨支架处 (对应参数编号192, 250) 以及尾段与垂尾连接处 (对应参数编号390~393) 的质量对其影响最大,灵敏度值均在-0.01以下;对于9.812 Hz的机身横向一阶弯曲模态,尾桨支架以及尾段与垂尾连接处的质量对其影响最大,灵敏度值均在-0.02以下;对于23.694 Hz的机身一阶扭转模态,驾驶舱、中机身 (对应参数编号300~340) 以及桨毂处 (对应参数编号385) 的质量对其影响最大,灵敏度值均在-0.01以下。
|
图 3 前六阶固有频率关于质量的灵敏度曲线 Figure 3 Sensitivity of mass on first six modal frequencies |
3.2 材料弹性模量影响
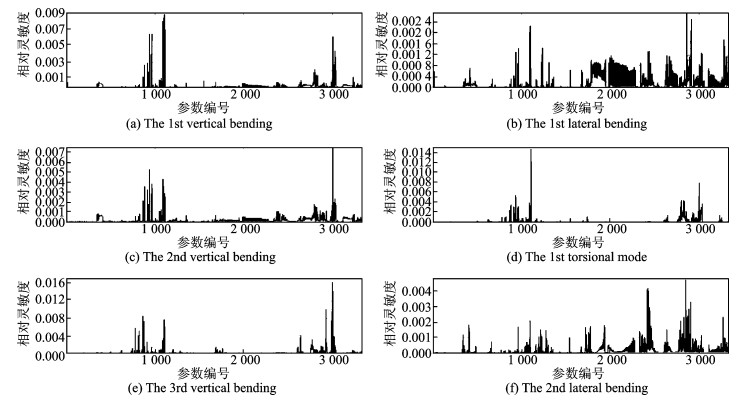
随着新型材料的发展,直升机机身所使用的材料也在不断变化,更换结构件原先使用的材料通常会导致机身的刚度变化。分析不同位置处单元的弹性模量变化对机身固有频率的影响时,本文将模型中的3 334个单元的弹性模量作为参数,利用FEMtools中的灵敏度分析模块求出机身前六阶固有频率对这些参数的灵敏度。图 4给出了前六阶固有频率对单元弹性模量的灵敏度曲线。其中,横轴表示单元弹性模量参数的编号,纵轴表示固有频率对弹性模量变化的相对灵敏度值。可以看出,固有频率对单元弹性模量的灵敏度是正值,即任意单元弹性模量增加,固有频率都会出现不同程度的升高。横向弯曲模态频率对弹性模量参数的灵敏度值均在0.004以下,相对其他模态频率较低。结合各参数所处的机身位置,发现机身底部的两根主承力梁 (对应参数编号911~931, 3 000~3 020) 和中机身处的两对交叉杆 (对应参数编号1 104~1 111) 对各阶频率的影响最为明显。
|
图 4 前六阶固有频率关于材料弹性模量的灵敏度曲线 Figure 4 Sensitivity of Young′s modulus on first six modal frequencies |
3.3 单元几何属性影响
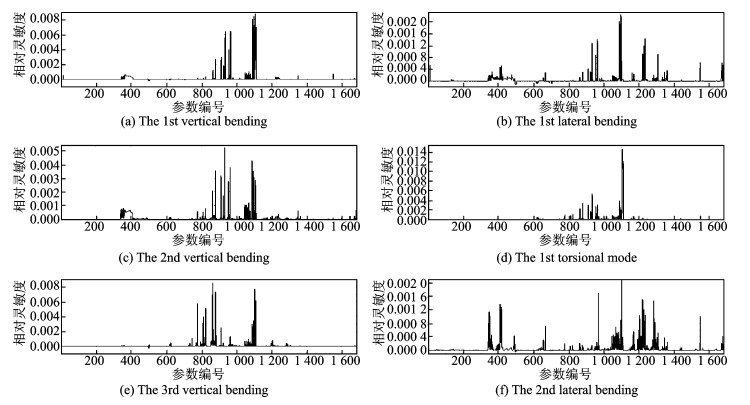
机身的承力结构的加强与减弱通常是通过修改杆、梁的截面属性或者改变蒙皮、腹板的厚横截面积作为参数进行灵敏度计算。为了分析结构的几何属性对固有频率的影响,本文将模型中的1 683个杆、梁单元的横截面作为参数进行灵敏度计算。图 5给出了前六阶固有频率对单元横截面积的灵敏度曲线。其中,横轴表示单元的横截面积参数的编号,纵轴表示固有频率对单元的横截面积变化的相对灵敏度值。可以看出,单元的横截面积增加可提高机身频率,固有频率对其的灵敏度为正值。横向弯曲模态频率对单元横截面积参数的灵敏度值均在0.002以下,相对其他模态频率较低。结合各参数所处的机身位置,发现机身底部两根主承力梁处 (对应参数编号911~931) 和中机身处的两对交叉杆 (对应参数编号1 104~1 111) 的单元横截面积对固有频率的影响最明显。
|
图 5 前六阶固有频率关于杆、梁横截面积的灵敏度曲线 Figure 5 Sensitivity of cross-sectional area of bars and beams on first six modal frequencies |
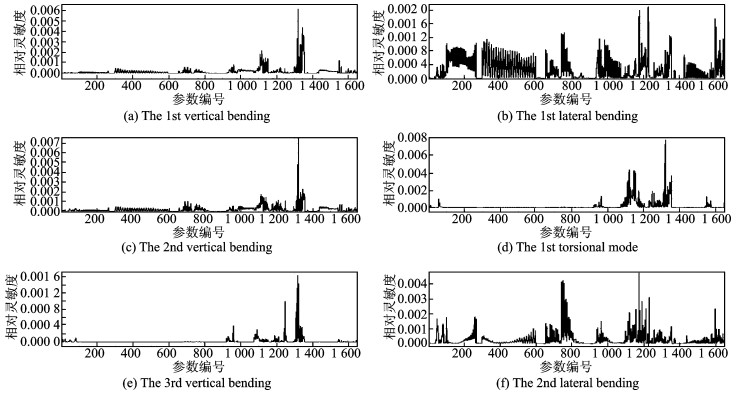
本文将模型中的1 649个三边形、四边形单元的厚度作为参数进行灵敏度计算。图 6给出了前六阶固有频率对单元厚度的灵敏度曲线。其中,横轴表示单元厚度参数的编号,纵轴表示固有频率对单元厚度变化的相对灵敏度值。可以看出,单元厚度增加可提高机身频率。一阶横向弯曲与三阶垂向弯曲模态频率对单元厚度参数灵敏度值均在0.002以下,相对其他模态频率较低。结合各参数所处的机身位置,发现前机身地板 (对应参数编号1 073~1 120) 和底部的两根主承力梁腹板处 (对应参数编号1 316~1 355) 的单元厚度对除机身横向一阶弯曲以外的各阶固有频率造成明显影响,对于机身横向一阶弯曲,尾段上 (对应参数编号98~990) 的蒙皮厚度对机身横向一阶弯曲模态影响最为明显。
|
图 6 前六阶固有频率关于蒙皮、腹板厚度的灵敏度曲线 Figure 6 Sensitivity of thickness of skins on first six modal frequencies |
4 结论
本文研究了直11机身有限元模型的建模方法,计算分析了前六阶模态的固有频率和振型,并对机身模态关于质量,材料弹性模量以及结构几何属性等参数进行灵敏度分析,结果表明:
(1) 固有频率对质量的灵敏度是负值,对材料弹性模量的灵敏度是正值,对几何属性的灵敏度有正有负。
(2) 驾驶舱、尾桨支架处以及尾段与垂尾连接处的质量对固有频率负影响最明显;机身底部的两根主承力梁和中机身处的两对交叉杆的材料弹性模量和横截面积,前机身地板和两根主承力梁腹板的厚度对固有频率的正影响最明显。
(3) 结构质量对垂向弯曲和横向弯曲固有频率的影响比结构材料弹性模量和几何属性参数的影响至少大两倍,而这些参数对扭转固有频率的影响却相近。
在直升机改进改型的机身动特性设计中,应当针对动特性设计要求,优先考虑将这些机身结构件的材料和几何参数作为新机型机身的设计参数。同时,在进行新机型静强度、气动外形、操稳性等方面的设计时,应慎重修改这些机身结构。
| [1] |
张晓谷.
直升机动力学设计[M]. 北京: 航空工业出版社, 1995.
ZHANG Xiaogu. Dynamic design of helicopter[M]. Beijing: Aviation Industry Press, 1995. |
| [2] | RAYMOND G K. The NASA/Industry design analysis methods for vibrations (DAMVIBS) program—A government overview[R]. AIAA-92-2200-CP, 1992. |
| [3] |
张令弥.
直升机全机振动分析与控制[J]. 南京航空学院学报, 1979, 11(3): 22–32.
ZHANG Lingmi. The analysis and control of rotor induced vibration of helicopter[J]. Journal of Nanjing Aeronautical Institute, 1979, 11(3): 22–32. |
| [4] |
凌爱民, 韩普祥, 李五洲.
直升机结构动特性建模技术研究[J]. 应用力学学报, 2001(S1): 131–136.
LING Aimin, HAN Puxiang, LI Wuzhou. Investigation of modeling techniques for helicopter structure dynamic behaviour[J]. Chinese Journal of Applied Mechanics, 2001(S1): 131–136. |
| [5] |
李明强. 直升机机体动力学相似模型设计与结构响应主动控制[D]. 南京: 南京航空航天大学, 2009.
LI Mingqiang. Dynamic design and active control of structural response of helicopter airframe analogous model[D]. Nanjing: Nanjing University of Aeronautics & Astronautics, 2009. |
| [6] | VINCENT A H. A note on the properties of the variation of structural response with respect to a single structural parameter when plotted in the complex plane[R]. Westland Helicopters Limited Report GEN/DYN/RES/010R, 1973. |
| [7] | HANSON H W. Investigation of vibration reduction through structural optimization[R]. Bell Helicopter Textron Report USAAVRADCOM-TR-80-D-13, 1980. |
| [8] | MURTHY T S. Optimization of helicopter airframe structures for vibration reduction considerations, formulations, and applications[J]. Journal of Aircraft, 1991, 28(1): 66–73. DOI:10.2514/3.45993 |
| [9] | MOTTERSHEAD J E, LINK M, FRISWELL M I. The sensitivity method in finite element model updating: A tutorial[J]. Mechanical System and Signal Processing, 2011, 25(7): 2275–2296. DOI:10.1016/j.ymssp.2010.10.012 |
| [10] |
黄海燕, 王德禹.
基于灵敏度多学科优化设计变量的模糊分析[J]. 上海交通大学学报, 2009, 43(8): 1327–1331.
HUANG Haiyan, WANG Deyu. Fuzzy comprehensive analysis of design variables for multidisciplinary design optimization based on sensitivity analysis[J]. Journal of Shanghai Jiaotong University, 2009, 43(8): 1327–1331. |
| [11] |
夏品奇, BROWNJ M W.
斜拉桥有限元建模与模型修正[J]. 振动工程学报, 2003, 16(2): 220–223.
XIA Pinqi, BROWN J M W. Finite element modeling and model updating of a cable-stayed bridge[J]. Journal of Vibration Engineering, 2003, 16(2): 220–223. |
 2017, Vol. 49
2017, Vol. 49


