直升机减振是襟翼主动控制 (Active controlled flap, ACF) 旋翼技术应用的主要方向。通过自适应控制器控制襟翼高频偏转产生高阶气动力谐波,这些谐波载荷作用在桨叶上能够有效抵消桨叶的振动载荷,其机理是通过额外的能量输入抵消旋翼振动能量,从源头上抑制直升机振动。
在ACF旋翼建模与振动控制方面,美国高校的相关学者基于Hamilton能量原理建立了带后缘襟翼的旋翼桨叶运动方程,采用多周控制器对旋翼振动载荷控制进行了数值仿真[1-5]。Spencer研究了具有在线训练功能的神经模拟器,并将其应用到全尺寸ACF旋翼上进行了振动控制仿真研究[6]。中国国内,南京航空航天大学的李春明在智能旋翼气动-控制-结构动力学模型的基础上,利用正交样本训练得到了能够映射襟翼偏角与桨毂振动载荷的频域神经网络模拟器,并将其与神经控制器相结合,进行半物理仿真研究[7]。王荣、夏品奇基于线性梁理论建立了带后缘小翼的柔性桨叶动力学模型,采用频域算法对旋翼振动载荷优化控制进行了数值分析[8]。
以上研究大多基于自建的ACF旋翼气弹分析模型,振动载荷的计算精确度尚达不到工程应用的要求,为了提高控制迭代效率,通常要对被控模型进行线性化假设,在一定程度上降低了控制迭代的精度。为此,本文采用直升机行业内成熟的综合分析平台CA MRAD Ⅱ软件进行了ACF旋翼建模以及样本计算,利用径向基函数 (Radial basis function, RBF) 网络对非线性系统的映射能力[9], 构建了适用于ACF旋翼振动控制研究的RBF网络模拟器。在样本选择方法上借鉴了生物、化工领域常见的正交试验法[10],该方法能够有效避免样本冗余、矛盾等不利因素的影响,大幅降低样本数量。最后采用多周控制方法,以RBF网络模型为被控对象,对智能旋翼进行了减振分析。
1 ACF旋翼被控模型ACF旋翼的关键是对襟翼施加恰当的控制,从而达到降低旋翼振动载荷的目的,ACF旋翼桨叶如图 1所示。

|
图 1 ACF旋翼桨叶 Figure 1 ACF rotor blade |
本文建立的襟翼主动控制模型是以襟翼偏角为输入,以桨毂振动载荷为输出的非线性多输入多输出 (Multiple input multiple output,MIMO) 被控系统, 如图 2所示。

|
图 2 ACF旋翼减振分析模型 Figure 2 Analytic model of ACF rotor |
对于桨叶片数为N的ACF旋翼,旋翼振动载荷以频率为NΩ的谐波量为主,是由频率为 (N-1)Ω,NΩ以及 (N+1)Ω的桨叶载荷在桨毂中心的集成而来。后缘襟翼作N-1, N以及N+1阶谐波偏转运动, 对桨毂振动载荷影响较为明显,因此本文建立的ACF旋翼被控模型以桨毂N阶振动载荷为输出,对应的输入为后缘襟翼N-1, N以及N+1阶谐波偏转角度。
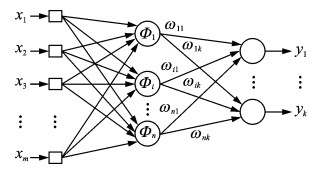
1.1 RBF神经网络模型RBF网络是由3个神经层构成的前馈网络, 其结构如图 3所示。第一层为输入层,节点个数等于输入维数;第二层为隐含层,节点的个数视问题的复杂程度而定;第三层为输出层,节点个数等于输出数据的维数。RBF网络的各层功能不同,隐含层是非线性的,采用RBF作为基函数,从而将输入向量空间转换到隐含层空间,使原来线性不可分的问题变得线性可分,输出层是线性的,其功能是将隐含层的输出进行线性变换,最终得到网络的输出。
|
图 3 RBF网络结构 Figure 3 Architecture of RBF network |
图 3中, X为网络输入,Y为网络输出,Φ为基函数,ω为权值矩阵。本文令
| $ \begin{array}{l} \boldsymbol{X} = {\rm{ }}{[{\delta _{\left( {N-1} \right)c}}\;{\delta _{\left( {{\rm{ }}N-1} \right)s}}\;{\delta _{Nc}}\;{\delta _{Ns}}\;{\delta _{\left( {N + 1} \right)c}}\;{\delta _{\left( {N + 1} \right)s}}]^{\rm{T}}}\\ \boldsymbol{Y} = {[{F_{Nx}}\;{F_{Ny}}\;{F_{Nz}}\;{M_{Nx}}\;{M_{Ny}}]^{\rm{T}}}\\ \phi = G(\left\| {\boldsymbol{X} -{X_i}} \right\|) = {\rm{exp}}( -\frac{1}{{2{\sigma ^2}}}\left\| {\boldsymbol{X} -{X_i}} \right\|) \end{array} $ | (1) |
式中:N为桨叶片数; 下标c, s分别代表小翼偏转角谐波量的余弦和正弦项;FNx, FNy, FNz代表桨毂中心N阶航向、侧向以及垂向力;MNx, MNy代表桨毂N阶滚转、俯仰力矩;Φ选用Green函数;Xi为基函数的中心;σ为基函数的标准差;‖*‖代表欧几里得范数。RBF网络的输出可表示为
| $ {y_j} = \sum\limits_{i = 1}^n {{\omega _{ij}}\phi (\boldsymbol{X}, {X_i})} \;\;\;\;j = 1, 2, \cdots, k $ | (2) |
RBF网络需要训练的参数为Xi, σ, ω,训练中随机选取一个固定的基函数中心,基函数的标准差为
| $ \sigma = \frac{{{d_{\max }}}}{{\sqrt {2n} }} $ | (3) |
式中:dmax为所选取中心之间的最大距离; n为隐含层节点数。权值ω的训练采用伪逆法,令网络的期望输出为d={dkj}, dkj为第k个输入向量在第j个输出节点的期望输出值,对应训练样本的输出,权值可表示为
| $ {\omega _{ij}} = {\boldsymbol{G}^ + }\;d $ | (4) |
式中:G=[gki], gki=Φ(Xk-Xi2),k=1, 2, …, K; i=1, 2, …, n。ωij代表从第i个隐含节点到第j个输出节点的权值;k为训练样本的个数;G+为G的伪逆,可通过奇异值分解获得。
1.2 训练样本的选取令后缘襟翼的偏转角为谐波形式, 即
| $ \delta = \sum\limits_{i = N-1}^{N + 1} {{\delta _i}{\rm{sin(}}i\Omega t + {\varphi _i})} $ | (5) |
式 (5) 由δN-1,φ N-1,δN,φN,δN+1,φN+1这6个独立变量确定,分别代表各个阶次下的幅值和初相。幅值的取值范围应由襟翼的实际偏转能力确定,如对于偏转角度在±10°之间的襟翼,可令-3°≤δN-1≤3°, -4° ≤δN≤4°, -3°≤δN+1≤3°。初相位取值范围为0°~360°。
采用正交法选取训练样本,将式 (5) 中6个变量在最小值到最大值区间内取16个均分点,则训练样本的选取可描述为6因素16水平正交试验。通过6个16阶正交拉丁方阵构建正交表L162(167), 表达式为
| $ {L_{{{16}^2}}}({16^6}) = \left[{\begin{array}{*{20}{c}} 1&1&{{A_{1, 1}}}&{{B_{1, 1}}}&{{C_{1, 1}}}&{{D_{1, 1}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1&{16}&{{A_{1, 16}}}&{{B_{1, 16}}}&{{C_{1, 16}}}&{{D_{1, 16}}}\\ 2&1&{{A_{2, 1}}}&{{B_{2, 1}}}&{{C_{2, 1}}}&{{D_{2, 1}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 2&{16}&{{A_{2, 16}}}&{{B_{2, 16}}}&{{C_{2, 16}}}&{{D_{2, 16}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {16}&1&{{A_{16, 1}}}&{{B_{16, 1}}}&{{C_{16, 1}}}&{{D_{16, 1}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ {16}&{16}&{{A_{16, 16}}}&{{B_{16, 16}}}&{{C_{16, 16}}}&{{D_{16, 16}}} \end{array}} \right] $ | (6) |
式中:正交表的前两列给出了两个1~16之间整数的所有组合,即前两列的每一行为一组互不相同的整数对;A, B, C, D为4个相互正交的拉丁方阵,将各自元素按照上式连成一列即可构成正交表的后4列。
式 (6) 中包含6个因素的256个组合,ACF旋翼模型的训练样本输入由正交表L162 (167) 进行线性变换得到,加上0输入样本,共有257个训练样本。为了得到样本输入对应的输出,采用CAMRAD Ⅱ软件计算前飞配平状态下的旋翼桨毂振动载荷,提取桨毂N阶振动载荷FNx, FNy, FNz, MNx, MNy作为训练样本的输出。
2 ACF旋翼振动控制方法ACF旋翼振动控制采用与文献[1]中类似的多周控制算法。该方法适用于准静态频域控制,被控系统需要在当前步控制输入条件下达到稳定状态以后,才可施加下一步控制量,对于旋翼而言,通常需要旋转数周才能达到稳定状态。多周控制的本质是一种针对离散系统的优化算法,通过梯度下降原理不断修正控制量,使目标函数达到极小值。
多周控制算法的目标函数可表示为
| $ \boldsymbol{J} = {\rm{ }}\boldsymbol{z}_i^{\rm{T}}\cdot{\boldsymbol{W}_z}\cdot{\boldsymbol{z}_i} + \boldsymbol{u}_i^{\rm{T}}\cdot{\boldsymbol{W}_u}\cdot{\boldsymbol{u}_i} $ | (7) |
式中:ui, zi为第i个控制步的输入和输出,在本文中分别对应襟翼偏角输入和桨毂N阶振动载荷输出
ui=[δ(N-1)c δ(N-1)s δNc δNs δ(N + 1)c δ(N + 1)s]iT, zi= [FNx FNy FNz MNx MNy]iT; Wz,Wu为对角阵,分别代表桨毂振动载荷、襟翼偏角所对应的权重矩阵。
当目标函数达到极小值时,有
| $ \frac{{\partial J}}{{\partial {\boldsymbol{u}_i}}} = 0 $ |
由此可得到最优控制输入
| $ \begin{array}{l} \boldsymbol{u}_i^{{\rm{opt}}} =-\boldsymbol{D}_{i-1}^{-1}(\boldsymbol{T}_{i - 1}^T \cdot {\boldsymbol{W}_z} \cdot {\boldsymbol{z}_{i - 1}} - \boldsymbol{T}_{i - 1}^T \cdot {\boldsymbol{W}_z} \cdot \\ \;\;\;\;\;\;\;\;\;{\boldsymbol{T}_{i - 1}} \cdot {\boldsymbol{u}_{i - 1}}) \end{array} $ | (8) |
式中:Di-1=Ti-1T·Wz·Ti-1+Wu, Ti-1为传递矩阵,由桨毂振动载荷相对于襟翼控制输入的偏导数构成, 即
| $ {\boldsymbol{T}_{i-1}} = {\left. {\frac{{\partial z}}{{\partial \boldsymbol{u}}}} \right|_{{\boldsymbol{u}_{i-1}}}} $ |
在线性化假设下,传递矩阵可用向前差分法计算,即
| $ {\boldsymbol{T}_{i-1}} = \frac{{\boldsymbol{z}({\boldsymbol{u}_{i-1}} + \Delta \boldsymbol{u})-\boldsymbol{z}({\boldsymbol{u}_{i - 1}})}}{{\Delta \boldsymbol{u}}} $ | (9) |
式中Δu为ui-1附近的扰动增量。
计算传递矩阵是该方法的关键,控制量每更新一次都要重新计算传递矩阵,而计算一次传递矩阵要求解两次被控模型,这对于复杂的旋翼气弹动力学模型而言,计算量太大。为了解决这一问题,可将传递矩阵在整个控制进程中视为固定值,只在控制初始位置计算一次,这样达到相同的控制效果通常需要更多的控制步数。本文所建立的神经网络模型能够快速求解,可在每步更新传递矩阵,从而解决了计算量与控制效率之间的矛盾。
3 结果与分析计算模型采用2桨叶铰接式旋翼,半径2 m,桨叶翼型为OA312,前进比为μ=0.25,升力系数CL/σ=0.064的前飞状态进行神经网络建模与振动控制分析。旋翼主要参数见表 1。
| 表 1 模型旋翼参数 Table 1 Basic parameters of mo del rotor |
3.1 神经网络模型训练与校验
为了充分利用训练样本,在257组正交样本空间内进行插值,将样本数量扩展到600组,输入RBF网络进行离线训练,经过600步训练后达到收敛,误差性能曲线见图 4。

|
图 4 RBF网络训练的误差性能曲线 Figure 4 Training performance of RBF network |
为了检验训练后的网络模型能否精确映射智能旋翼襟翼偏角与桨毂振动载荷的关系,选取一定规模的测试样本对网络进行检验。测试样本的选取应满足以下两个条件:(1) 与训练样本不重复;(2) 具有一定的代表性,能反映出输出随输入的变化趋势。
按表 2选取25组测试样本,检验襟翼偏角的幅值和相位对桨毂振动载荷的影响。
| 表 2 RBF网络测试样本输入 Table 2 Training inputs of RBF network |
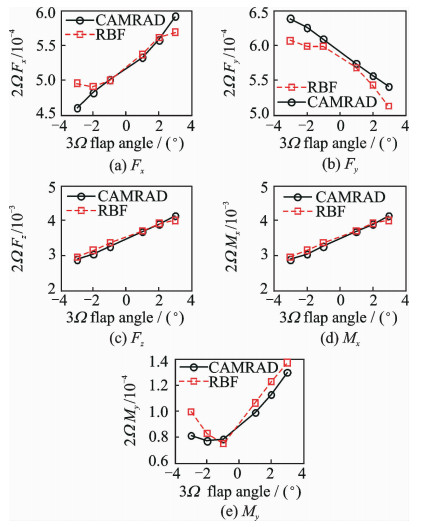
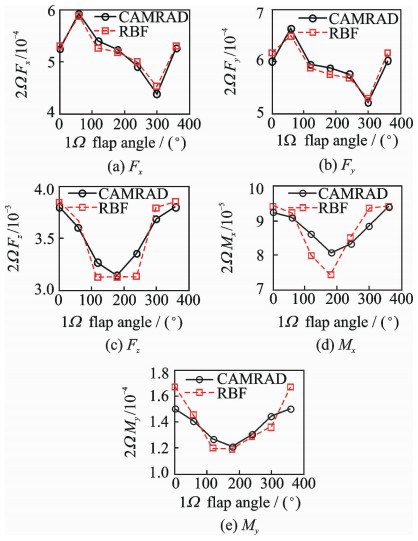
利用CAMRAD Ⅱ和已训练的RBF网络模型分别计算以上测试样本的输出。襟翼偏角输入以3Ω幅值变化和1Ω相位变化为例,桨毂振动载荷各分量随幅值和相位的变化如图 5, 6所示。
|
图 5 振动载荷与各参数关系曲线 (δ=δ3sin (3Ωt+φ3)) Figure 5 Variation of vibration loads with flap parameters (δ=δ3sin (3Ωt+φ3)) |
|
图 6 振动载荷与各参数关系曲线 (δ=δ1sin (Ωt+φ1)) Figure 6 Variation of vibration loads with flap parameters (δ=δ1sin (Ωt+φ1)) |
图 5为在形如δ=δ3 sin (3Ωt+φ3) 的襟翼输入下,2Ω无量纲桨毂载荷随φ3的变化曲线。图 6为形如δ=δ1sin (Ωt+φ1) 的襟翼输入下,2Ω无量纲桨毂载荷随φ1的变化曲线。可见,在上述测试样本下,CAMRAD计算的桨毂振动载荷与RBF网络输出结果具有较高的吻合度,两者相对误差在10%以内。说明经过正交样本训练的RBF神经网络模型能够有效映射后缘襟翼偏角与ACF旋翼桨毂振动载荷的关系。
3.2 旋翼减振分析将已训练好的网络模型作为多周控制器的被控对象,建立智能旋翼振动控制仿真模型。襟翼的控制迭代从0输入开始,分别研究权重矩阵Wz和Wu对减振效果的影响。
3.2.1 Wz对减振的影响Wz的主对角元素对应各个振动载荷分量的权重系数,令Wz的取值依次如表 3所示,分别对应5种减振状态。
| 表 3 Wz的5种取值 Table 3 Parameter values of Wz |
Wu取固定值
| $ {\boldsymbol{W}_u} = \left[{\begin{array}{*{20}{c}} {0.1}&{}&{}&{}&{}&{}\\ {}&{0.1}&{}&{}&{}&{}\\ {}&{}&{0.1}&{}&{}&{}\\ {}&{}&{}&{0.1}&{}&{}\\ {}&{}&{}&{}&{0.1}&{}\\ {}&{}&{}&{}&{}&{0.1} \end{array}} \right] $ |
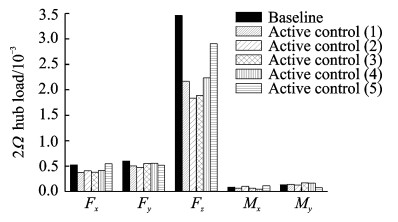
经过控制迭代,得到襟翼静止与上述5个受控状态下旋翼桨毂2Ω振动载荷 (无量纲) 的变化示意图,见图 7。
|
图 7 旋翼桨毂振动载荷随Wz变化示意图 Figure 7 Variation of vibrational loads with Wz |
从图 7中可看出,控制器在5个状态下均能取得较好的减振效果,尤其是垂向振动载荷Fz,最大降低接近50%。桨毂振动载荷每个分量在不同状态下的减振幅度不同。Fx在状态 (1) 减振幅度最大,为28%;Fy在状态 (2) 减振幅度最大,为20.7%;Fz在状态 (2) 减振幅度最大,为47%;Mx在状态 (4) 减振幅度最大,为44.3%;My在状态 (5) 减振幅度最大,为41.8%。
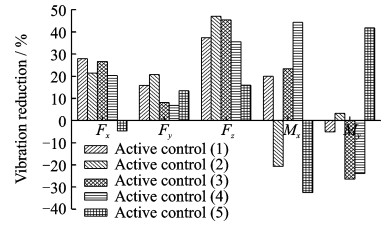
振动载荷降低幅度随Wz变化如图 8所示。
|
图 8 振振动载荷降低幅度随Wz变化示意图 Figure 8 Variation of vibration reduction with Wz |
从图 8中可看出,振动载荷各分量的降低幅度基本上与其权重系数所占的比例直接相关,比例越高,减振效果越好。于此同时,其他分量的减振效果下降,甚至会出现振动加大的情况。
3.2.2 Wu对减振的影响Wu的主对角元素对应襟翼偏转谐波量的权重系数,令其依次取表 4中的3个值。
| 表 4 Wu的3种取值 Table 4 Parameter values of Wu |
Wz取固定值
| $ {\boldsymbol{W}_z} = \left[ {\begin{array}{*{20}{c}} {0.2}&{}&{}&{}&{}\\ {}&{0.2}&{}&{}&{}\\ {}&{}&{0.2}&{}&{}\\ {}&{}&{}&{0.2}&{}\\ {}&{}&{}&{}&{0.2} \end{array}} \right] $ |
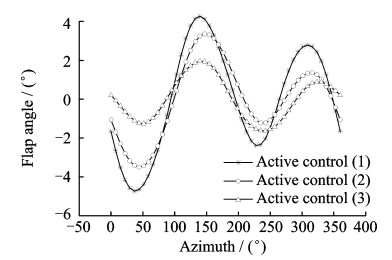
经过控制迭代,得到以上3种Wu取值对应的受控旋翼振动载荷,如图 9所示。3种控制状态下,襟翼最优控制输入的时域信号如图 10所示。

|
图 9 旋翼桨毂振动载荷随Wu变化示意图 Figure 9 Variation of vibrational loads with Wu |
|
图 10 襟翼最优控制输入信号时域曲线 Figure 10 Time-domain curves of optimized flap angle |
由图 9,10可见,随着Wu主对角元素的增大,襟翼偏角谐波量在目标函数J中所占的比例上升,J达到最小值时,所需的襟翼偏角越来越小,而控制器对桨毂振动载荷的控制能力逐渐被削弱。
4 结论本文利用RBF网络建立了ACF旋翼振动载荷预测模型,结合多周控制方法,对基于后缘襟翼主动控制的旋翼减振进行了分析,结果表明:
(1) 本文所建立的RBF神经网络模型能够精确地映射襟翼偏角与旋翼振动载荷之间的非线性关系。
(2) 正交方法是一种高效的样本选取方法,能够大幅降低训练所需的样本数量。
(3) 采用多周控制器能有效对旋翼桨毂振动载荷实施控制,其中垂向振动载荷可降低接近50%。
(4) 在数值计算中,可将Wu设为0,但在实际情况下,后缘襟翼的偏转能力有限,振动载荷控制的目标应当是使用最小的襟翼偏角达到最好的减振效果,因此合理设置Wu至关重要。
| [1] | MILLOTT T A, FRIEDMANN P P. Vibration Reduction in Helicopter Rotors U sing an Active Control Surface Located on the Blade [C]// 33rd Structures, Str uctural Dynamics and Materials Conference. Dallas, TX, USA: AIAA, 1992: 1975-1988. |
| [2] | SHEN Jinwei. Comprehensive aeroelastic analysis of helicopter rotor with trailing-edge flap for primary control and vibration control [D]. Maryland: University of Maryland, 2002. |
| [3] | MYRTLE T F, FRIEDMANN P P. Vibration reduction in rotorcraft using the actively controlled trailing edge flap and issues related to practical implementation[J]. AHS 54th Annual Forum, 1998. |
| [4] | LIU Li, FRIEDMANN P P, KIM I, et al. Vibration reduction and performance enhancement in rotorcraft using active flaps at high advance ratios[C]//47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Newport, Rhode Island: AIAA, 2006. |
| [5] | ZHANG Jianhua, SMITH E C, WANG K W. Active-passive hybrid optimization of rotor blades with trailing edge flaps [C]//40th Structures, Structural Dynamics, and Materials Conference and Exhibit. St. Louis, MO, USA: AIAA, 1999. |
| [6] | SPENCER M G, SANNER R M. Neurocontrol of simulated full scale rotor vibrations using trailing edge flaps [C]//40th Structures, Structural Dynamics, and Materials Conference and Exhibit. [S.l.]:AIAA, 1999: 2744-2752. |
| [7] |
李春明. 智能旋翼的振动控制研究[D]. 南京: 南京航空航天大学, 2001.
LI Chunming. Research on vibration control for smart rotor[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2001. |
| [8] |
王荣, 夏品奇.
利用桨叶后缘小翼运动的旋翼桨毂振动载荷优化控制[J]. 振动工程学报, 2013, 26(4): 574–582.
WANG Rong, XIA Pinqi. Optimal control of rotor hub vibration loads by using motion of trailing edge flap[J]. Journal of Vibration Engineering, 2013, 26(4): 574–582. |
| [9] |
董长虹.
Matlab神经网络与应用[M]. 第二版. 北京: 国防工业出版社, 2007: 122-129.
DONG Changhong. Application of the Matlab neural networks[M]. The second edition. Beijing: The National Defence Industries Press, 2007: 122-129. |
| [10] |
成岳.
工程试验设计方法[M]. 第二版. 武汉: 武汉理工大学出版社, 2010: 51-60.
CHENG Yue. Engineering experimental methods[M]. The second edition. Wuhan: Wuhan University of Technology Press, 2010: 51-60. |
 2017, Vol. 49
2017, Vol. 49


