2. 中国空气动力研究与发展中心低速空气动力研究所, 绵阳, 621000
2. Low Speed Aerodynamics Institute, China Aerodynamics Research & Development Center, Mianyang, 621000, China
旋翼翼型设计技术是直升机设计中的一项核心技术[1], 而翼型设计中的一个重要环节是风洞性能验证,新设计的旋翼翼型大部分静态特性数据依赖0.6 m量级的跨声速风洞获取[2],由于受洞壁等因素干扰,当前国内此类风洞试验准度欠佳。以国内多座跨声速风洞的OA309旋翼翼型试验数据为例,其升力线斜率、最大升力系数等都明显小于国外试验得到的性能数据,这轻则拖慢了旋翼翼型的设计进程,重则误导旋翼翼型优化设计方向。针对此问题,一是可以建设“自修正风洞”[3],尽量减小风洞洞壁干扰;二是可以进行相应的洞壁干扰修正[4-6]。对于已建成的跨声速风洞,第二种方法较为现实可靠。
对于跨声速风洞,其洞壁附近区域的局部流动很不均匀,基于扰动速度势的洞壁边界条件十分复杂,洞壁干扰修正十分困难。目前,用于洞壁干扰修正的方法大致有试验修正法、映像法、Maskell法、涡格法、面元法、数值计算法和壁压信息法等[7-10]。其中,壁压信息法不需要额外知晓洞壁通气参数,仅需在试验的同时实时测量洞壁附近的气流参数,不需提出种种近似假设,精准度高、耗资少,故国外Mokry [11-12]和国内范召林等[13]均采用壁压信息法进行透气壁干扰修正。而旋翼翼型与常规翼型相比,其升力效应更大,洞壁干扰更为明显,故本文基于已有的单线性壁压信息法,在做相应简化改动后,使用MATLAB软件编制了相应的修正程序,并成功应用在OA 309旋翼翼型高速风洞试验中,其修正结果证明该方法简单合理,可用于高升力旋翼翼型的通气壁干扰修正。
1 旋翼翼型壁压测量试验 1.1 试验装置试验在中国空气动力研究与发展中心的FL-21风洞中进行 (图 1)。该风洞为试验段长1.775 m、横截面0.6 m×0.6 m的暂冲式跨、超声速风洞。跨声速时,试验段上下壁板由60°斜孔壁组成,两侧均为实壁。

|
图 1 旋翼翼型FL-21风洞试验图 Figure 1 Rotor airfoil FL-21 wind tunnel test |
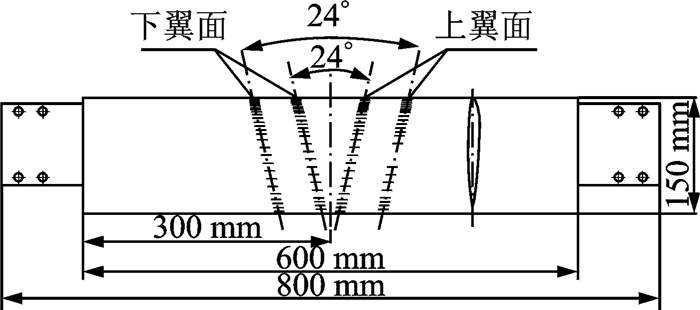
试验模型为OA309旋翼翼型,翼型模型展长800 mm (其中翼型段600 mm),弦长c=150 mm。为增加翼型上测压孔数量,同时避免相邻测压孔之间的干扰,上、下型面均分别布置两列测压孔,同一型面的两列测压孔交替组成一个测压序列;上型面布置53个测压孔,下型面布置51个测压孔 (图 2)。在风洞中采取横跨方式水平安装在左、右转窗上,回避了支架对试验准确度的干扰。
|
图 2 旋翼翼型测压点分布图 Figure 2 Pressure measuring point layout at rotor airfoil |
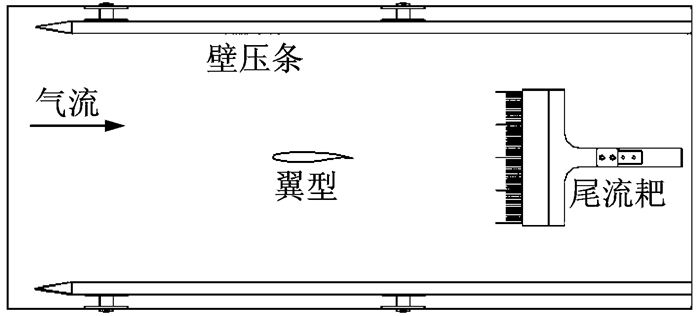
尾流耙设计有48个总压管和5个静压管,安装在风洞的大攻角机构上,安装后静压管端部的基准位置距离翼型后缘262 mm (1.75倍模型弦长),此处翼型尾流已得到充分发展。
壁压条共使用两根,分别安装于上、下透气壁处,每根壁压条上沿风洞流线方向布置40个壁压孔。为避免壁压条长度影响迎角修正量和速度修正量的准确度,壁压条最前端的壁压测量点应位于风洞轴向压力梯度接近于零的位置,最后端的壁压测量点应延续到模型后缘约两倍弦长处。另外,测压孔距离壁面的距离为53 mm,避开了通气孔附近的强烈不均匀流动区。翼型0°迎角时堵塞度为2.25%。试验模型、尾流耙和壁压条的相对安装位置如图 3所示。
|
图 3 试验模型相对安装位置 Figure 3 Installation position of test model |
翼型表面、壁压信息条静压以及尾流测压耙总、静压由PSI9016电子扫描阀系统采集,该电子扫描阀具有数字温度补偿功能,稳定性好,其系统精度达到±0.05%FS (满量程)。
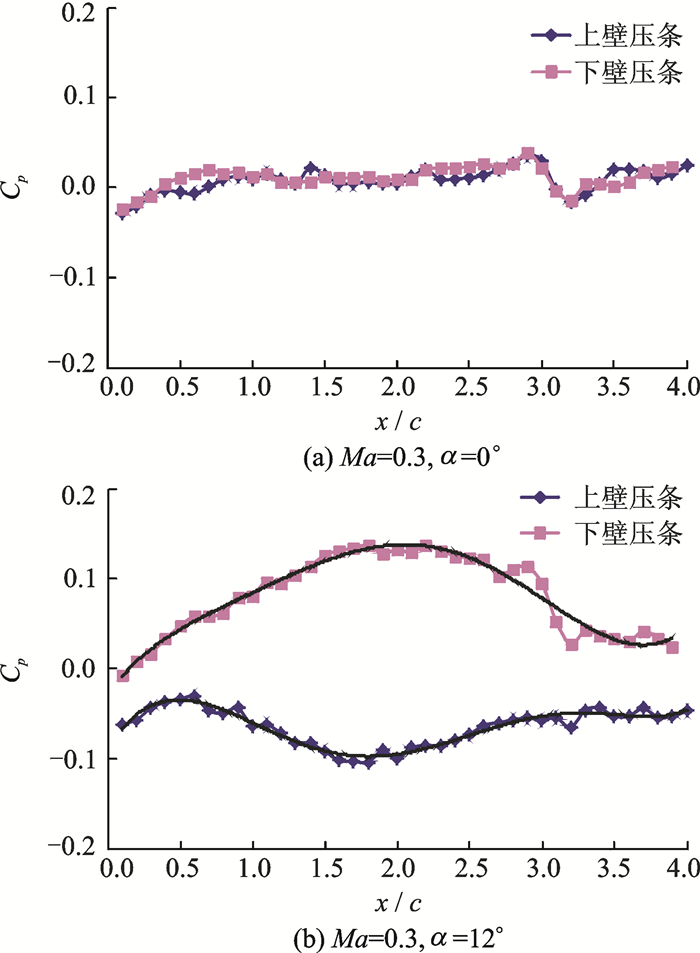
1.2 试验结果图 4为马赫数Ma=0.3以及迎角α=0°, 12°时OA309模型壁压分布。其纵坐标为压力系数Cp,横坐标为壁压条长度 (x/c)。图 4(a)中,由于翼型迎角为0°,翼型产生升力较小,对上、下壁压力分布干扰较小,故上、下壁压条压力系数值基本重合。图 4(b)中,当翼型迎角为12 °时,翼型产生较大升力,对上、下壁压力分布干扰较大,故上、下壁压条测得的压力数据不重合,前、后端压力差异较小,翼型区压力差异较大。此处需说明,壁压条测压的结果出现不规则的波动,这与壁压条的加工精度等因素有关,试验数据处理时可通过减去相同条件下空风洞的壁压条测量值给予扣除,同时可采用样条曲线对其进行光顺。
|
图 4 试验壁压分布 Figure 4 Test wall pressure distribution |
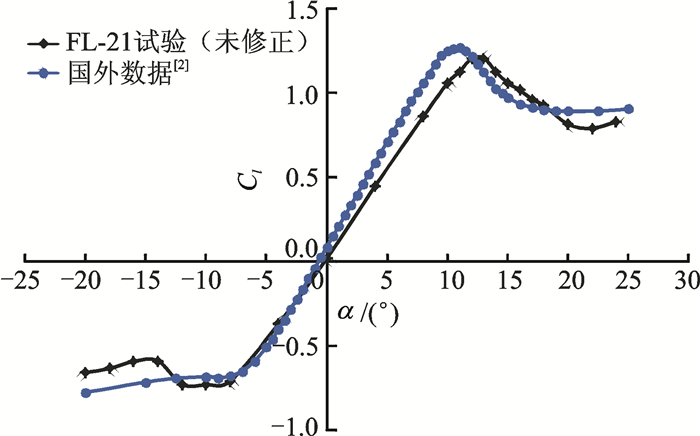
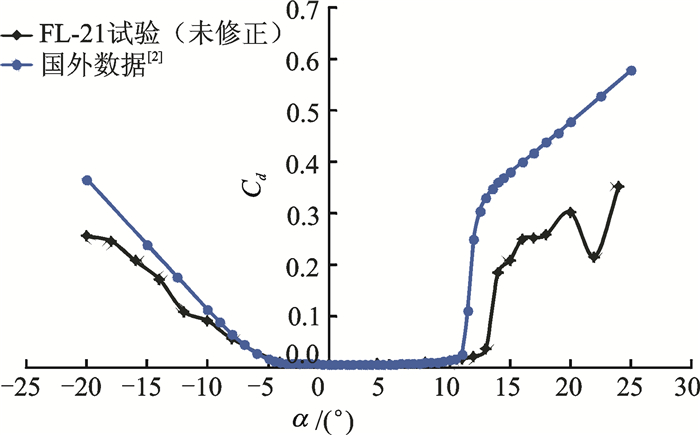
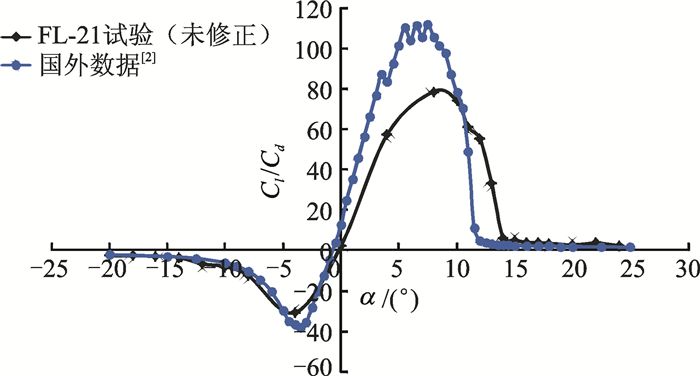
通过对翼型表面上各点的压力系数Cpi进行积分,得到翼型的升力系数Cl;通过对尾流动量损失的积分得到翼型阻力系数Cd;升力系数与阻力系数之比为翼型升阻比。图 5~7为Ma=0.4时未经壁压法修正的OA309旋翼翼型试验结果,由图可见,其升力线斜率、最大升力系数所对应迎角、最大升阻比等均与国外数据[2]有较大差异。
|
图 5 OA309旋翼翼型升力系数曲线对比 Figure 5 Cl curve comparison of OA309 rotor airfoil between FL-21 test and Ref.[2] results |
|
图 6 OA309旋翼翼型阻力系数曲线对比 Figure 6 Cd curve comparison of OA309 rotor airfoil between FL-21 test and Ref.[2] results |
|
图 7 OA309旋翼翼型升阻比曲线对比 Figure 7 Cl/Cd curve comparison of OA309 rotor airfoil between FL-21 test and Ref.[2] results |
2 简化的单线性壁压信息法 2.1 方法概述
扰动速势φm在透气壁附近区域满足亚声速小扰动线化速势方程[7]
| ${\beta ^2}\frac{{{\partial ^2}\varphi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\varphi }}{{\partial {y^2}}} = 0$ | (1) |
式中:β=
翼型试验中将翼型沿弦线分为数块,每块上分别布置一个涡、源、偶极子 (合称为奇点),这些奇点的φm满足[14]
| $\begin{array}{l} {\varphi _m} = - \frac{1}{{2{\rm{ \mathsf{ π} }}}}\sum\limits_K {{G_K}\arctan \left[{\frac{{\beta \left( {y - {y_K}} \right)}}{{x - {x_K}}}} \right]} + \\ \frac{1}{{2{\rm{ \mathsf{ π} }}\beta }}\sum\limits_K {{V_K}\frac{{x - {x_K}}}{{R_K^2}}} + \frac{1}{{2{\rm{ \mathsf{ π} }}\beta }}\sum\limits_K {{Q_K}\log {R_K}} \end{array}$ | (2) |
RK满足
| ${R_K} = \sqrt {{{\left( {x - {x_K}} \right)}^2} + {\beta ^2}{{\left( {y - {y_K}} \right)}^2}} $ | (3) |
涡强度GK满足
| $\sum\limits_K {{G_K}} = 0.5{b_a}{C_{Lu}}$ | (4) |
源强度QK满足
| $\sum\limits_K {{Q_K}} = 0.5{b_a}{C_{Du}}$ | (5) |
偶极子强度VK满足
| $\sum\limits_K {{V_K}} = V$ | (6) |
式中:CLu和CDu为试验所得升力系数和阻力系数;下标K表示第K个奇点值;ba为翼型弦长;V为模型的横截面积。
二维翼型试验中,各分块上偶极子和源强度由各分块的面积决定,涡强度沿翼弦的分布由翼型上、下表面压力分布规律确定。经验表明,旋翼翼型高速风洞的修正结果受奇点强度分布规律的影响较小,故可根据实际需要进行奇点强度分配,只要总强度满足GK,QK,VK即可。
此外,由于壁压条测得的数据有一定程度的跳动散布,在使用这些数据之前应采用三次样条光顺法对每根壁压条的壁压数据进行光顺处理。为消除系统误差,一般用带模型的壁压值减去相同条件下空风洞的壁压值,所得数据应用于式 (2)。
根据调和函数的性质,由式 (1) 可推导出,透气壁干扰产生的轴向速度分量u=∂φb/∂x满足
| ${\beta ^2}\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} = 0$ | (7) |
由上、下壁压条测出的压力系数Cp,可得到控制边界上的u值
| $u = - 0.5{C_p} - \frac{{\partial {\varphi _m}}}{{\partial x}}$ | (8) |
式 (7, 8) 一起构成了一个Dirichlet问题,可以采用有限差分法求解该问题,从而求出模型区各处的u值。再根据式 (9~12) 进行马赫数以及迎角修正
| $\Delta Ma = \left( {1 + 0.2Ma_{\rm{u}}^2} \right)M{a_{\rm{u}}} \times u$ | (9) |
| $\Delta \alpha = \frac{1}{\beta }\int\limits_{{x_0}}^{{x_{\rm{e}}}} {\frac{{\partial u\left( {x,y} \right)}}{{\partial y}}} {\rm{d}}x - \frac{{\partial {\varphi _m}}}{{\partial y}}$ | (10) |
| $M{a_{\rm{c}}} = M{a_{\rm{u}}} + \Delta Ma$ | (11) |
| ${\alpha _{\rm{c}}} = {\alpha _{\rm{u}}} + \Delta \alpha $ | (12) |
式中:Mau和αu为修正前的马赫数和迎角; Mac和αc为修正后的量; ∂φm/∂y可由式 (2) 求解。
试验通常希望得到在Mau和αu状态下的无洞壁干扰气动力系数值,可以使用测量的气动力系数对马赫数或迎角的导数值等,通过适当的工程计算方法得到Mau和αu状态下的修正气动力系数值。例如,翼型试验数据可使用式 (13~15) 进行修正
| ${C_{lc}} = {C_{lu}} + \frac{{\partial {C_{lu}}}}{{\partial \alpha }}\Delta \alpha + \frac{{\partial {C_{lu}}}}{{\partial Ma}}\Delta Ma$ | (13) |
| ${C_{mc}} = {C_{mu}} + \frac{{\partial {C_{mu}}}}{{\partial \alpha }}\Delta \alpha + \frac{{\partial {C_{mu}}}}{{\partial Ma}}\Delta Ma$ | (14) |
| ${C_{dc}} = {C_{du}} + \frac{{\partial {C_{du}}}}{{\partial \alpha }}\Delta \alpha + \frac{{\partial {C_{du}}}}{{\partial Ma}}\Delta Ma$ | (15) |
式中:Clc, Cmc, Cdc为修正后的系数;Clu, Cmu, Cdu为修正前的系数。
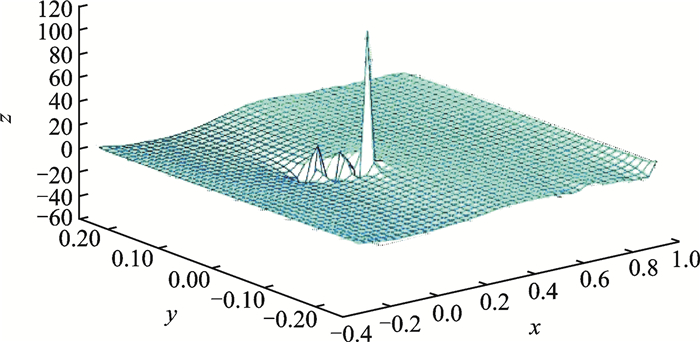
图 8为二元旋翼翼型试验迎角修正量,由图可见,由于式 (2) 中分母是修正位置坐标与所布置奇点坐标之差,若奇点位置布置不合理,必将造成迎角修正量畸变,马赫数修正量亦是如此。故需根据壁压条上测压孔的位置 (即修正位置坐标) 对奇点位置进行调整,使奇点的轴向位置 (x方向) 与相邻两个壁压条测压孔中点的轴向位置相等,避免奇点太过接近测压孔而引起修正量畸变;当翼型模型迎角变化时奇点的轴向位置亦要与相邻两个壁压条测压孔中点轴向位置保持相等。
|
图 8 二元旋翼翼型试验迎角修正量 Figure 8 α correction of 2-D rotor airfoil test |
2.2 修正结果
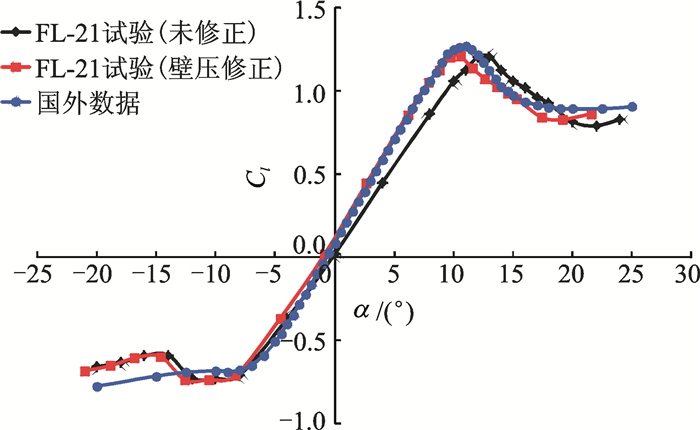
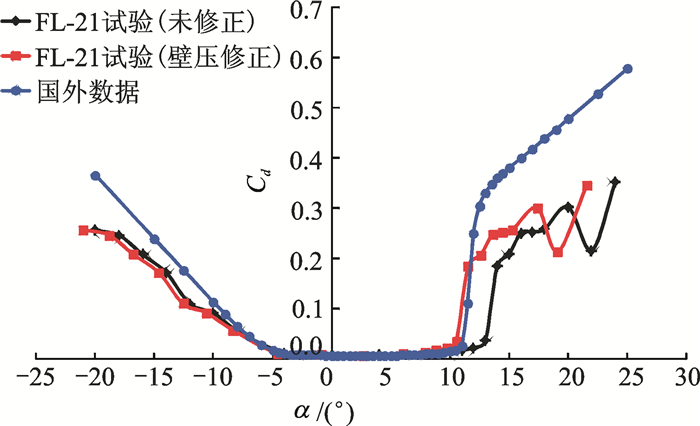
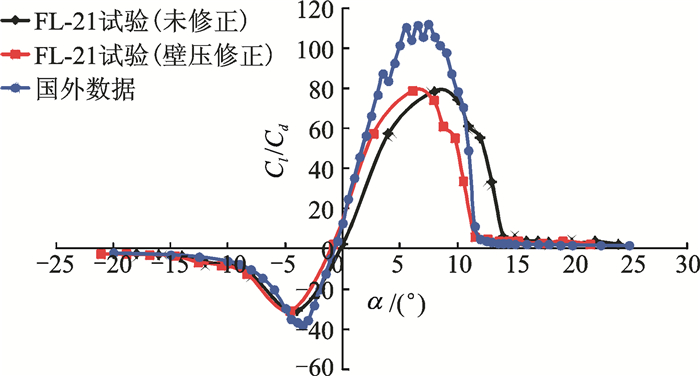
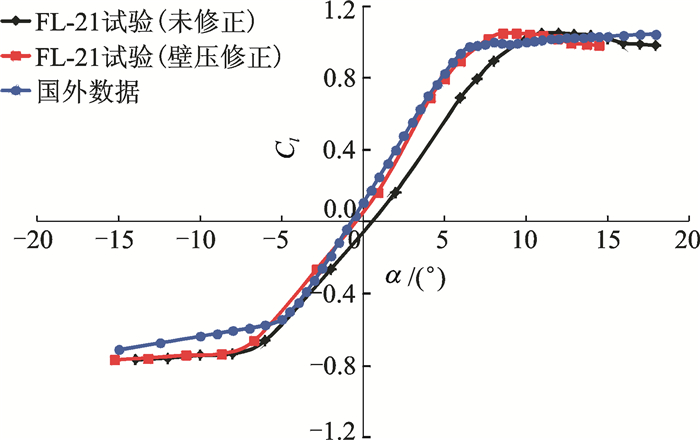
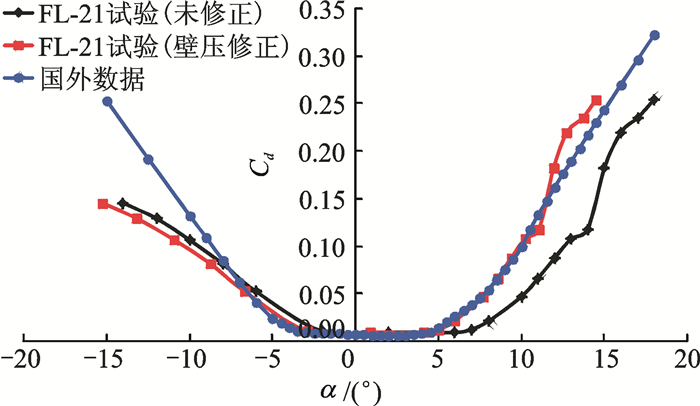
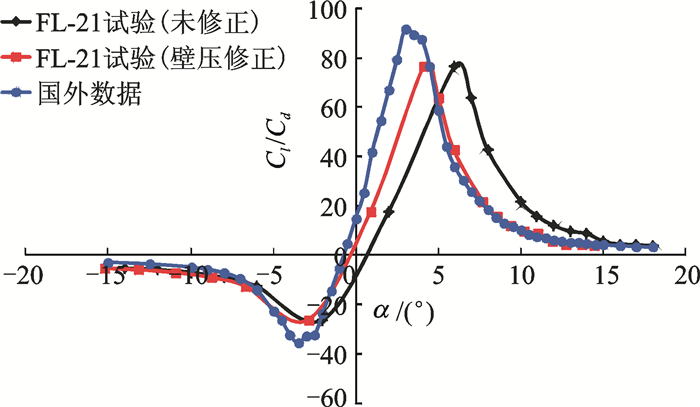
采用2.1节中简化改进的单参数线化壁压信息法,对FL-21高速风洞中OA309旋翼翼型典型马赫数 (Ma=0.4,0.6) 下的试验数据进行修正,其修正结果如图 9~14所示。图中黑线代表未修正的试验数据,蓝线代表国外OA309翼型性能数据,红线代表修正后的数据。由图 9, 12可明显看出,修正后的升力曲线在线性段与国外数据极为吻合,二者差别约为2%(升力线斜率修正量约为10%), 且最大升力系数所对应的迎角十分接近。由图 10, 13可看出,修正后的阻力发散迎角与国外数据极为吻合,迎角α=-4°~11°时,阻力系数重合较好。由图 11, 14可看出,修正后较修正前,升阻比曲线亦有了较大改善。所以该方法能有效修正OA309旋翼翼型试验数据,特别是模型迎角,而对马赫数 (修正量小于0.1%)、升力系数、阻力系数和俯仰力矩系数的修正量不大。
|
图 9 OA309旋翼翼型升力系数曲线修正前后对比 (Ma=0.4) Figure 9 Cl curve comparison of OA309 rotor airfoil before and after correction (Ma=0.4) |
|
图 10 旋翼翼型阻力系数曲线修正前后对比 (Ma=0.4) Figure 10 Cd curve comparison of OA309 rotor airfoil before and after correction (Ma=0.4) |
|
图 11 旋翼翼型升阻比曲线修正前后对比 (Ma=0.4) Figure 11 Cl/Cd curve comparison of OA309 rotor airfoil before and after correction (Ma=0.4) |
|
图 12 旋翼翼型升力系数曲线修正前后对比 (Ma=0.6) Figure 12 Cl curve comparison of OA309 rotor airfoil before and after correction (Ma=0.6) |
|
图 13 旋翼翼型阻力系数曲线修正前后对比 (Ma=0.6) Figure 13 Cd curve comparison of OA309 rotor airfoil before and after correction (Ma=0.6) |
|
图 14 旋翼翼型升阻比曲线修正前后对比 (Ma=0.6) Figure 14 Cl/Cd curve comparison of OA309 rotor airfoil before and after correction (Ma=0.6) |
从修正后的数据还可以看出,修正后的最大升力系数和最大升阻比较国外数据偏小,本文认为这与试验雷诺数有关。国外部分风洞采用增压方式进行翼型试验,雷诺数高于国内风洞,而从雷诺数对试验数据影响规律可以知道,雷诺数越大,最大升力系数越大,阻力系数越小。所以,由于本文试验雷诺数偏低,修正后的最大升力系数偏小,阻力系数偏大,致使最大升阻比明显小于国外数据。该问题可通过增加试验雷诺数或雷诺数外插修正等方法解决。
3 结论(1) 本文采用的简化改进单参数线化壁压信息法能快速对旋翼翼型进行洞壁干扰修正,且修正效果明显。
(2) 本文方法主要用于修正旋翼翼型的来流迎角,而对试验马赫数、升力系数和阻力系数等的修正量不大。
(3) 修正后的翼型最大升力系数和最大升阻比仍偏小,后期可采用改进尾流积分区域判定方法、增加试验雷诺数等方法予以解决。
| [1] | 李萍, 庄开莲, 李静. 国外直升机旋翼翼型研究综述[J]. 直升机技术, 2007(3): 103–109. |
| [2] |
袁红刚, 杨永东, 杨炯, 等.
典型直升机旋翼翼型气动特性试验研究[J]. 实验流体力学, 2013, 27(1): 20–24.
YUAN Honggang, YANG Yongdong, YANG Jiong, et al. Experimental investigation on aerodynamic performance of one typical helicopter rotor airfoil[J]. Journal of Experiments in Fluid Mechanics, 2013, 27(1): 20–24. |
| [3] | 卢勇. 自适应壁风洞原理应用于洞壁干扰修正的研究[D]. 西安: 西北工业大学, 2007. |
| [4] |
张其威.
适用于任意壁的二维亚跨音速洞壁干扰修正法[J]. 空气动力学学报, 1987, 5(2): 132–140.
ZHANG Qiwei. Two-dimensional subsonic and transo nic wind tunnel wall interference corrections for varied walls[J]. Acta Aerody namica Sinica, 1987, 5(2): 132–140. |
| [5] |
张其威.
壁压法用于高速风洞洞壁干扰修正[J]. 南京航空航天大学学报, 1992, 24(5): 496–505.
ZHANG Qiwei. Wall-signature methods for high speed wind tunnel wall interference corrections[J]. Journal of Nan jing University of Aeronautics & Astronautics, 1992, 24(5): 496–505. |
| [6] | ULBRIC H N, BOONE A R. Validation of a wall interference correction system for a transo nic wind tunnel[R]. AIAA 2004-605, 2004. |
| [7] |
范洁川.
风洞试验手册[M]. 北京: 航空工业出版社, 2002: 663-684.
FAN Jiechuan. Handbook of wind tunnel test[M]. Beijing: Aviation Industry Press, 2002: 663-684. |
| [8] |
钟世东, 李巍, 苏继川, 等.
三种跨声速洞壁干扰修正方法及其在小展弦比飞翼标模试验中的应用[J]. 空气动力学学报, 2016, 34(1): 113–118.
ZHONG Shidong, LI Wei, SU Jichuan, et al. Three type s of transonic wind tunnel wall interference correction method and their applica tion on low aspect ratio flying wing calibration model[J]. Acta Aerodynamica Sinica, 2016, 34(1): 113–118. |
| [9] | AKIKO H, SHIGERU K I, TOSHIMI F, et al. Wall interference correction by the panel method for the jaxa low speed wind tunnel[R]. JAXA-RR-07-026, 2008. |
| [10] |
范召林, 张玉伦, 贺中.
跨音速飞机模型实验洞壁干扰数值模拟的初步研究[J]. 航空学报, 1997, 18(2): 210–214.
FAN Zhaolin, ZHANG Yulun, HE Zhong. Preliminary research on numerical simulation of transonic wall interference foe aircraft model tests[J]. Acta Aeronauticaet Astronautica Sinica, 1997, 18(2): 210–214. |
| [11] | MOKRY M, OHMAN L H. Application of the fast f ourier transform to two dimensional wind tunnel wall interference[J]. Aircraft, 1980, 17(6): 402–408. DOI:10.2514/3.44666 |
| [12] | MOKRY M, DIGNEY J R, POOLET R J D. Doublet panel method for half model wind tunnel corrections[J]. Aircraft, 1987, 24(5): 322–327. DOI:10.2514/3.45448 |
| [13] |
范召林, 崔乃明, 恽起麟.
壁压法应用于高速风洞大迎角实验洞壁干扰的修正[J]. 空气动力学学报, 1991, 9(2): 243–250.
FAN Zhaolin, CUI Naiming, YUN Qil in. Application of the wall pressure method to wall interference correctons for model tests at high angle of attack in high speed wind tunnel[J]. Acta Aerodyn amica Sinica, 1991, 9(2): 243–250. |
| [14] | MOKRY M, CHAN Y Y, JONES D J. Two-dimensional wind tunnel wall interference[R]. AGARD AG-281, 1990. |
 2017, Vol. 49
2017, Vol. 49


