Improvement of Radial Point Interpolation Method in Computational Efficiency
1. Jiangsu Province Key Laboratory of Aerospace Power System, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China;
2. Collaborative Innovation Center of Advanced Aero-Engine, Nanjing, 210016, China
无网格法的近似函数是基于节点的近似,相比于有限元法,无网格方法降低了对网格的依赖性。无网格法的主要近似方案有:移动最小二乘近似[1]、点插值法[2](Point interpolation method, PIM)、重构核力子法[3](Reproducing kernel particle method, RKPM)、径向基点插值法 (Radial basis point interpolation method, RPIM)[4, 5]、单位分解法[6](Partition of unity method, PUM) 和自然邻接点插值[7](Natural neighbor interpolation,NNR) 等。考虑到移动最小二乘法得到的形函数不满足Kronecker delta函数性质,导致本质边界条件难以施加[8]。为此,Liu等给出点插值方法[9-10],将其用于伽辽金全局弱势方案。但是点插值法采用多项式作为基函数,当节点按一定规律排布时,在计算过程中有时会出现矩阵奇异的状况。基函数采用径向基函数时,可克服这一缺点,但纯粹的径向基函数插值不具有一阶一致性,为此可在径向基函数插值时引入多项式基[11],同时为了提高求解效率,一般采用局部形式的插值方法[12]。相比于其他近似方案,径向基函数插值的优点在于它没有矩阵奇异性的问题,同时满足Kronecker delt a函数性质以及一阶一致性。
相比于移动最小二乘法,RPIM采用的基函数较为复杂,同时在使用RPIM近似时需要的节点数量较多,导致RPIM无网格法计算速度较慢。为了提高RP IM无网格法的求解效率,Hu等[13]将求解域分解为任意形状的子域,各子域之间的节点没有联系,减少了求解自由度。Afsari等[14]引入小波框架下的多尺度无网格技术,去除RPIM近似时的求逆步骤,减少了计算时间。张琰等[15]提出了RPIM无网格法与有限元法耦合计算方法,但新方法已不是纯粹的无网格法,失去了一些无网格法的一些优势。因此,Cao等[16]将RPIM无网格法与无网格伽辽金法耦合,在一定程度上提高了计算精度,同样降低了一定的计算时间。本文在使用网格积分的RPIM方法中,提出在同一网格中的积分点的插值计算采用同一组节点,减少了插值过程中部分矩阵的计算次数,可降低RPIM无网格法的计算时间。然而,改变了插值计算方案可能降低RPIM无网格法的计算精度。在有限元法中,最初的单元都是基于位移求解的,称为位移元。位移元广泛应用后,计算精度低的问题逐渐显现,为了提高计算精度,一些杂交应力单元[17-22]被提出来,表现出很好的计算精度。本文将基于Hellinger-Reissner (H-R) 变分原理推出的求解方程应用于RPIM无网格法中,以提高计算求解精度。
1 径向基函数插值
1.1 径向基函数 径向基 (Radial basis function, RBF) 是一类以计算点和节点之间的距离为自变量的函数。在二维平面问题和三维问题中,计算点X(坐标为 (x, y) 或 (x, y, z)) 和节点Xi(坐标为 (xi, yi) 或 (xi, yi, zi)) 之间的距离分别为
|
$
{r_i} = \sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2}}
$
|
(1) |
|
$
{r_i} = \sqrt {{{\left( {x - {x_i}} \right)}^2} + {{\left( {y - {y_i}} \right)}^2} + {{\left( {z - {z_i}} \right)}^2}}
$
|
(2) |
径向基函数有很多种类,常见的有4种,分别为复合二次 (Multiquadrics) 函数、高斯 (Gaussians) 函数、逆复合二次 (Reciprocal multiquadrics) 函数和薄板样条 (Thin-plate splines) 函数,见表 1。
表 1(Table 1)
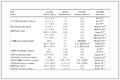
表 1 径向基函数
Table 1 Radial basis functions
| 名称 |
公式 |
| Multiquadrics |
$ {R_i}(\mathit{\boldsymbol{x}}) = {({c^2} + r_i^2)^{\frac{1}{2}}}\ $ |
| Gaussians |
Ri(x)=exp(-cri2) |
| Reciprocal multiquadrics |
$ {R_i}(\mathit{\boldsymbol{x}}) = {({c^2} + r_i^2)^{\frac{{ - 1}}{2}}}\ $ |
| Thin-plate splines |
Ri(x)=ri2βlogri |
|
表 1 径向基函数
Table 1 Radial basis functions
|
表 1中:c为大于零的常数;β为整数。另外复合二次函数和逆复合二次函数都属于广义复合二次函数,即
|
$
{R_i}\left( \mathit{\boldsymbol{x}} \right) = {\left( {\alpha {d_c} + r_i^2} \right)^q}
$
|
(3) |
式中:dc为计算点在其局部支持域中与所有节点间距相关的特征长度,通常为支持域的节点平均间距;α和q为2个形状参数。一般情况下,在二维固体力学问题中,α=1,q=1.03为MQ函数的最优参数。本文的算例采用这两个值。
1.2 径向基函数插值 域Ω中共有n个数据对 (x1, u1), (x2, u2), …, (xn, un),采用添加多项式基的径向基点插值方法,函数u(x) 在域Ω中的近似函数uh(x) 可以表示为
|
$
\begin{array}{*{20}{c}}
{{u^h}\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^n {{R_i}\left( \mathit{\boldsymbol{x}} \right){a_i}} + \sum\limits_{i = 1}^m {{p_i}\left( \mathit{\boldsymbol{x}} \right){b_i}} = }\\
{{\mathit{\boldsymbol{R}}^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{a + }}{\mathit{\boldsymbol{p}}^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right)\mathit{\boldsymbol{b}}}
\end{array}
$
|
(4) |
式中:m为多项式基函数的个数;ai和bi为待定常数。式中有n+m个未知数,令近似函数uh(x) 在节点xi处的值等于函数u(x) 在该节点处的值ui,可得n个线性方程,写成矩阵的形式有
|
$
{\mathit{\boldsymbol{R}}_0}\mathit{\boldsymbol{a}} + {\mathit{\boldsymbol{P}}_m}\mathit{\boldsymbol{b}} = {\mathit{\boldsymbol{u}}_s}
$
|
(5) |
式中
|
$
\begin{array}{l}
{\mathit{\boldsymbol{R}}_0} = \left[ {\begin{array}{*{20}{c}}
{{R_1}\left( {{r_1}} \right)}&{{R_2}\left( {{r_2}} \right)}& \cdots &{{R_n}\left( {{r_1}} \right)}\\
{{R_1}\left( {{r_2}} \right)}&{{R_2}\left( {{r_2}} \right)}& \cdots &{{R_n}\left( {{r_2}} \right)}\\
\vdots & \vdots & \ddots & \vdots \\
{{R_1}\left( {{r_n}} \right)}&{{R_2}\left( {{r_n}} \right)}& \cdots &{{R_n}\left( {{r_n}} \right)}
\end{array}} \right]\\
{\mathit{\boldsymbol{P}}_m} = \left[ {\begin{array}{*{20}{c}}
1&{{x_1}}& \cdots &{{p_m}\left( {{x_1}} \right)}\\
1&{{x_2}}& \cdots &{{p_m}\left( {{x_2}} \right)}\\
\vdots & \vdots & \ddots & \vdots \\
1&{{x_n}}& \cdots &{{p_m}\left( {{x_n}} \right)}
\end{array}} \right]
\end{array}
$
|
(6) |
|
$
\begin{array}{*{20}{c}}
{{\mathit{\boldsymbol{a}}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}}
{{a_1}}&{{a_2}}& \cdots &{{a_n}}
\end{array}} \right],{\mathit{\boldsymbol{b}}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}}
{{b_1}}&{{b_2}}& \cdots &{{b_n}}
\end{array}} \right]}\\
{\mathit{\boldsymbol{u}}_s^{\rm{T}} = \left[ {\begin{array}{*{20}{c}}
{{u_1}}&{{u_2}}& \cdots &{{u_n}}
\end{array}} \right]}
\end{array}
$
|
(7) |
再引入m个约束方程
|
$
\sum\limits_{i = 1}^n {{p_j}\left( {{\mathit{\boldsymbol{x}}_i}} \right){a_i}} = \mathit{\boldsymbol{P}}_m^Ta = 0\;\;\;\;\;\;j = 1,2, \cdots ,m
$
|
(8) |
由式 (5) 得
|
$
\mathit{\boldsymbol{a}} = \mathit{\boldsymbol{R}}_0^{ - 1}{\mathit{\boldsymbol{u}}_s} - \mathit{\boldsymbol{R}}_0^{ - 1}{\mathit{\boldsymbol{P}}_m}\mathit{\boldsymbol{b}}
$
|
(9) |
将式 (9) 代入式 (8) 得
|
$
\mathit{\boldsymbol{b = }}{\left( {\mathit{\boldsymbol{P}}_m^T\mathit{\boldsymbol{R}}_0^{ - 1}{\mathit{\boldsymbol{P}}_m}} \right)^{ - 1}}\mathit{\boldsymbol{P}}_m^T\mathit{\boldsymbol{R}}_0^{ - 1}{\mathit{\boldsymbol{u}}_s}
$
|
(10) |
再将式 (10) 回代到式 (9) 得
|
$
\mathit{\boldsymbol{a = }}\left[ {\mathit{\boldsymbol{R}}_0^{ - 1} - \mathit{\boldsymbol{R}}_0^{ - 1}{\mathit{\boldsymbol{P}}_m}{{\left( {\mathit{\boldsymbol{P}}_m^T\mathit{\boldsymbol{R}}_0^{ - 1}{\mathit{\boldsymbol{P}}_m}} \right)}^{ - 1}}\mathit{\boldsymbol{P}}_m^T\mathit{\boldsymbol{R}}_0^{ - 1}} \right]{\mathit{\boldsymbol{u}}_s}
$
|
(11) |
令
|
$
{\mathit{\boldsymbol{C}}_a} = \left[ {\mathit{\boldsymbol{R}}_0^{ - 1} - \mathit{\boldsymbol{R}}_0^{ - 1}{\mathit{\boldsymbol{P}}_m}{{\left( {\mathit{\boldsymbol{P}}_m^T\mathit{\boldsymbol{R}}_0^{ - 1}{\mathit{\boldsymbol{P}}_m}} \right)}^{ - 1}}\mathit{\boldsymbol{P}}_m^T\mathit{\boldsymbol{R}}_0^{ - 1}} \right]
$
|
(12) |
|
$
{\mathit{\boldsymbol{C}}_b} = {\left( {\mathit{\boldsymbol{P}}_m^T\mathit{\boldsymbol{R}}_0^{ - 1}{\mathit{\boldsymbol{P}}_m}} \right)^{ - 1}}\mathit{\boldsymbol{P}}_m^T\mathit{\boldsymbol{R}}_0^{ - 1}
$
|
(13) |
则RPIM方法的插值表达式为
|
$
\mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{R}}^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right){\mathit{\boldsymbol{C}}_a} + {\mathit{\boldsymbol{p}}^{\rm{T}}}\left( \mathit{\boldsymbol{x}} \right){\mathit{\boldsymbol{C}}_b}
$
|
(14) |
形函数的导数为
|
$
{\mathit{\boldsymbol{N}}_{,k}} = \mathit{\boldsymbol{R}}_{,k}^{\rm{T}}\left( \mathit{\boldsymbol{x}} \right){\mathit{\boldsymbol{C}}_a} + \mathit{\boldsymbol{p}}_{,k}^{\rm{T}}\left( \mathit{\boldsymbol{x}} \right){\mathit{\boldsymbol{C}}_b}
$
|
(15) |
1.3 基于网格定义域的RPIM方法 在RPIM方法中,点x的近似函数由其定义域Ωx中的节点构造。对点x插值计算有贡献的节点确定方法有两种,以二维问题为例:
(1) 先定义节点的定义域。如图 1(a)所示,节点xi定义域一般取半径为di=scale×dci的圆形或长宽分别为dxi=scalex×dci和dyi=scaley×dci的矩形区域,其中,dci为节点xi处的节点平均距离,scale,scalex和scaley是大于1的乘子,定义域覆盖计算点的节点即为点x定义域Ωx中的节点。
(2) 直接定义计算点x的定义域Ωx。如图 1(b)所示,如以点x为中心的矩形域,矩形的长和宽分别取为dx=scalex×dc和dy=scaley×dc,dc为计算点x处的节点平均距离。本文参考的是第2种方法。
在有限元方法中,通过划分网格,将求解域离散成一系列单元,对全域的积分可等价于对各单元的积分之和。而伽辽金型无网格方法中,域是通过节点离散的,因此积分方案有所不同,常见的积分方案有:节点积分、有限元网格积分、背景网格积分和移动最小二乘积分。本文采用了有网格的积分方案,此方法是对每个网格采用高斯积分的方案。
一般的RPIM无网格法研究中,对于积分网格内的每个高斯积分点,都要分别搜索该积分点对应的定义域内的节点,而本文定义每个网格内的积分点采用同一组节点计算形函数及其导数。
因此定义了网格的定义域,如图 2所示,以网格中点为中心的矩形域,矩形的长和宽分别取为dx=scale1
×dc和dy=scale2×dc。在对网格内的积分点进行插值时,由于式 (14, 15) 中的矩阵Ca和Cb是由矩阵Pm和R0通过运算得到的,而由式 (6) 可知,当节点相同时,矩阵Pm和R0相同,因此采用网格定义域作为该网格内所有积分点的定义域方法可以减少计算矩阵Ca和Cb的次数,由此可降低计算量。
2 伽辽金型无网格法 以二维线弹性力学问题为例,二维平面力学问题的控制方程为
|
$
\left\{ \begin{array}{l}
平衡方程\;\;\;\;\;{\sigma _{ij,j}} + {F_i} = 0\;\;\;\;\;\;域\mathit{\Omega }内\\
力边界条件\;\;\;\;\;{\sigma _{ij}}{n_j} - {{\bar T}_i} = 0\;\;\;\;\;\;面力边界{\mathit{\Gamma }_t}上\\
位移边界条件\;\;\;\;\;{u_i} - {{\bar u}_i} = 0\;\;\;\;\;\;\;\;\;\;位移边界{\mathit{\Gamma }_u}上\\
几何方程\;\;\;\;\;{\varepsilon _{ij}} = \frac{1}{2}\left( {{u_{i,j}} + {u_{j,i}}} \right)\;域\mathit{\Omega }内\\
物理方程\;\;\;\;\;\;\;{\sigma _{ij}} = {\mathit{\boldsymbol{D}}_{ijkl}}{\varepsilon _{kl}}\;\;\;\;\;\;\;域\mathit{\Omega }内
\end{array} \right.
$
|
(16) |
式中:T为力边界上的表面力;u为位移边界上的已知位移;Dijkl为本构张量。
原始的RPIM无网格法采用最小势能原理进行推导。根据最小势能原理,伽辽金全局弱形式的变分方程为
|
$
\begin{array}{l}
\delta \prod = \int_\mathit{\Omega } {\delta {u_i}\left( {{\sigma _{ij,j}} + {F_i}} \right){\rm{d}}\mathit{\Omega }} - \\
\;\;\;\int_\mathit{\Omega } {\delta {u_i}\left( {{\sigma _{ij}}{n_j} - {{\bar T}_i}} \right){\rm{d}}\mathit{\Gamma }} = 0
\end{array}
$
|
(17) |
对式 (17) 第1项分部积分得
|
$
\begin{array}{l}
\delta \prod = \int_\mathit{\Omega } {\left( { - \delta {u_{ij}}{\sigma _{ij}} + \delta {u_i}{F_i}} \right){\rm{d}}\mathit{\Omega }} + \\
\;\;\;\;\int_{{\mathit{\Gamma }_u}} {\delta {u_i}{\sigma _{ij}}{n_j}{\rm{d}}\mathit{\Gamma }} + \int_{{\mathit{\Gamma }_t}} {\delta {u_i}{{\bar T}_i}{\rm{d}}\mathit{\Gamma }} = 0
\end{array}
$
|
(18) |
如果位移边界条件自动满足,则式 (18) 可简化为
|
$
\delta \prod = \int_\mathit{\Omega } {\left( { - \delta {u_{ij}}{\sigma _{ij}} + \delta {u_i}{F_i}} \right){\rm{d}}\mathit{\Omega }} + \int_{{\mathit{\Gamma }_t}} {\delta {u_i}{{\bar T}_i}{\rm{d}}\mathit{\Gamma }} = 0
$
|
(19) |
考虑到应力张量的对称性有
|
$
\delta \prod = \int_\mathit{\Omega } {\left( { - \delta {\mathit{\boldsymbol{\varepsilon }}^{\rm{T}}}\mathit{\boldsymbol{\sigma + }}\delta {\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{F}}} \right){\rm{d}}\mathit{\Omega }} + \int_{{\mathit{\Gamma }_t}} {\delta {\mathit{\boldsymbol{u}}^{\rm{T}}}{{\mathit{\boldsymbol{\bar T}}}_i}{\rm{d}}\mathit{\Gamma }} = 0
$
|
(20) |
位移插值为
|
$
\mathit{\boldsymbol{u}} = \mathit{\boldsymbol{Nd}}
$
|
(21) |
式中
|
$
\mathit{\boldsymbol{d = }}{\left[ {\begin{array}{*{20}{c}}
{u_x^1}&{u_y^1}&{u_x^2}&{u_y^2}& \cdots &{u_x^n}&{u_y^n}
\end{array}} \right]^{\rm{T}}}
$
|
(22) |
|
$
\mathit{\boldsymbol{N}} = {\left[ {\begin{array}{*{20}{c}}
{{N_1}}&0&{{N_2}}&0& \cdots &{{N_n}}&0\\
0&{{N_1}}&0&{{N_2}}& \cdots &0&{{N_n}}
\end{array}} \right]^{\rm{T}}}
$
|
(23) |
因此应变为
|
$
\mathit{\boldsymbol{\varepsilon = Bd}}
$
|
(24) |
式中
|
$
\mathit{\boldsymbol{B = }}\left[ {\begin{array}{*{20}{c}}
{{B_1}}&{{B_2}}& \cdots &{{B_n}}
\end{array}} \right]
$
|
(25) |
|
$
\mathit{\boldsymbol{B}}_k^{\rm{T}} = \left[ {\begin{array}{*{20}{c}}
{{N_{k,x}}}&0&{{N_{k,y}}}\\
0&{{N_{k,y}}}&{{N_{k,x}}}
\end{array}} \right]
$
|
(26) |
将式 (21,2, 4) 和物理方程σ=Dε代入式 (20),有
|
$
\begin{array}{l}
\delta \prod = \delta {\mathit{\boldsymbol{d}}^{\rm{T}}}\left[ { - \mathit{\boldsymbol{d}}\int_\mathit{\Omega } {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{DB}}{\rm{d}}\mathit{\Omega }} } \right. + \\
\left. {\int_\mathit{\Omega } {{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{F}}{\rm{d}}\mathit{\Omega }} + \int_{{\mathit{\Gamma }_t}} {{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{\bar T}}{\rm{d}}\mathit{\Gamma }} } \right] = 0
\end{array}
$
|
(27) |
其中,对于平面应力问题有
|
$
\mathit{\boldsymbol{D = }}\frac{E}{{1 - {v^2}}}\left[ {\begin{array}{*{20}{c}}
1&v&0\\
v&1&0\\
0&0&{\frac{{1 - v}}{2}}
\end{array}} \right]
$
|
(28) |
式中:E为弹性模量;υ为泊松比。考虑到δd的任意性,有
|
$
\mathit{\boldsymbol{Kd}} = \mathit{\boldsymbol{Q}}
$
|
(29) |
|
$
\mathit{\boldsymbol{K = }}\int_\mathit{\Omega } {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{DB}}{\rm{d}}\mathit{\Omega }}
$
|
(30) |
|
$
\mathit{\boldsymbol{Q}} = \int_\mathit{\Omega } {{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{F}}{\rm{d}}\mathit{\Omega }} + \int_{{\mathit{\Gamma }_t}} {{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{\bar T}}{\rm{d}}\mathit{\Gamma }}
$
|
(31) |
以上方程是通过最小势能原理推导而得。
采用H-R变分原理来推导线弹性力学问题,推导过程如下,变分泛函为
|
$
\begin{array}{*{20}{c}}
{{\prod _{{\rm{HR}}}} = \int_\mathit{\Omega } {\left[ { - \frac{1}{2}{\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\mathit{\boldsymbol{S\sigma }} + {\mathit{\boldsymbol{\sigma }}^{\rm{T}}}\left( {\mathit{\boldsymbol{Du}}} \right) - {\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{\bar F}}} \right]} {\rm{d}}V - }\\
{\int_{{\mathit{\Gamma }_t}} {{{\mathit{\boldsymbol{\bar T}}}^{\rm{T}}}\mathit{\boldsymbol{u}}{\rm{d}}S} - \int_{{\mathit{\Gamma }_t}} {{\mathit{\boldsymbol{T}}^{\rm{T}}}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{\bar u}}} \right){\rm{d}}S} }
\end{array}
$
|
(32) |
求解域中任意计算点的应力,由此计算点的定义域内的节点应力进行插值计算求得
|
$
\mathit{\boldsymbol{\sigma }}{\rm{ = }}\mathit{\boldsymbol{P\beta }}
$
|
(33) |
式中
|
$
\mathit{\boldsymbol{P = }}{\left[ {\begin{array}{*{20}{c}}
{{N_1}}&0&0&{{N_2}}&0&0&{}&{{N_n}}&0&0\\
0&{{N_1}}&0&0&{{N_2}}&0& \cdots &0&{{N_n}}&0\\
0&0&{{N_1}}&0&0&{{N_2}}&{}&0&0&{{N_n}}
\end{array}} \right]^{\rm{T}}}
$
|
(34) |
设位移边界条件自动满足,并将式 (21,33) 代入式 (32) 得
|
$
{\prod _{{\rm{HR}}}} = - \frac{1}{2}{\mathit{\boldsymbol{\beta }}^{\rm{T}}}\mathit{\boldsymbol{H\beta + }}{\mathit{\boldsymbol{\beta }}^{\rm{T}}}\mathit{\boldsymbol{Gd}} - {\mathit{\boldsymbol{Q}}^{\rm{T}}}\mathit{\boldsymbol{d}}
$
|
(35) |
|
$
\mathit{\boldsymbol{H = }}\int_\mathit{\Omega } {{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{SP}}{\rm{d}}V}
$
|
(36) |
|
$
\mathit{\boldsymbol{G = }}\int_\mathit{\Omega } {{\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{B}}{\rm{d}}V}
$
|
(37) |
缩掉参数β,有
|
$
\frac{{\partial {\prod _{{\rm{HR}}}}}}{{\partial \mathit{\boldsymbol{\beta }}}} = 0\;\;\; \Rightarrow \;\;\;\mathit{\boldsymbol{\beta }} = {\mathit{\boldsymbol{H}}^{ - 1}}\mathit{\boldsymbol{Gd}}
$
|
(38) |
代回式 (35),有
|
$
{\prod _{{\rm{HR}}}} = \frac{1}{2}{\mathit{\boldsymbol{d}}^{\rm{T}}}\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{H}}^{ - 1}}\mathit{\boldsymbol{Gd}} - {\mathit{\boldsymbol{Q}}^{\rm{T}}}\mathit{\boldsymbol{d}}
$
|
(39) |
由式 (39) 可得到待解方程
|
$
\frac{{\partial {\prod _{{\rm{HR}}}}}}{{\partial \mathit{\boldsymbol{d}}}} = 0\;\;\; \Rightarrow \;\;\;\left( {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{H}}^{ - 1}}\mathit{\boldsymbol{G}}} \right)\mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Q}}
$
|
(40) |
由上述推导可以看出,最小势能原理求解的推导中消除了应力项,而H-R变分原理的求解推导中保留了应力项,这两种方法求解的效果将在下文的算例中进行比较。
3 算例
3.1 悬臂梁 如图 3所示悬臂梁,受端部载荷作用的悬臂梁的解析解为
|
$
{u_x} = \frac{{Py}}{{6EI}}\left[ {\left( {6L - 3x} \right)x + \left( {2 + v} \right)\left( {{y^2} - \frac{{{D^2}}}{4}} \right)} \right]
$
|
(41) |
|
$
\begin{array}{*{20}{c}}
{{u_y} = - \frac{P}{{6EI}}\left[ {3v{y^2}\left( {L - x} \right) + } \right.}\\
{\left. {\frac{1}{4}\left( {4 + 5v} \right){D^2}x + {x^2}\left( {3L - x} \right)} \right]}
\end{array}
$
|
(42) |
|
$
{\sigma _x} = \frac{{P\left( {L - x} \right)y}}{I}
$
|
(43) |
|
$
{\tau _{xy}} = - \frac{P}{{2I}}\left( {\frac{{{D^2}}}{4} - {y^2}} \right)
$
|
(45) |
式中:E为弹性模量;υ为泊松比;I为悬臂梁截面惯性矩;P为端部载荷。
计算中,相关参数取为E=1 000 Pa,υ=0.3,P=6 N,D=12 m,L=4 8 m。节点分布方案如图 4所示。
采用3种方案进行求解计算。方案1:基于节点定义域的RP IM方法 (原始RPIM方法);方案2:基于网格定义域的RPIM方法;方案3:基于网格定义域的RPIM方法,同时使用HR变分原理推导的求解方程对问题进行求解。悬臂梁的积分网格如图 5所示,对于每个网格都采用4×4的高斯积分方案。
本文影响域采用矩形区域,scale1=scale2=3,梁左边界和右边界的边界条件按照精确解 (式 (41~45)) 施加。为了进行误差分析,定义如下两个误差范数
|
$
{L_u} = \frac{{\sqrt {\sum\limits_{i = 1}^N {{{\left( {\mathit{\boldsymbol{u}}_i^h - {\mathit{\boldsymbol{u}}_i}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{u}}_i^h - {\mathit{\boldsymbol{u}}_i}} \right)} } }}{{\sqrt {\sum\nolimits_{i = 1}^N {\mathit{\boldsymbol{u}}_i^{\rm{T}}{\mathit{\boldsymbol{u}}_i}} } }} \times 100\%
$
|
(46) |
|
$
{L_\sigma } = \frac{{\sqrt {\sum\limits_{i = 1}^N {{{\left( {\mathit{\boldsymbol{\sigma }}_i^h - {\mathit{\boldsymbol{\sigma }}_i}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{\sigma }}_i^h - {\mathit{\boldsymbol{\sigma }}_i}} \right)} } }}{{\sqrt {\sum\limits_{i = 1}^N {\mathit{\boldsymbol{\sigma }}_i^{\rm{T}}{\mathit{\boldsymbol{\sigma }}_i}} } }} \times 100\%
$
|
(47) |
方案1沿着y=0处,y方向的位移求解结果,以及沿着$x = \frac{L}{2} $处,x方向的应力结果分别如图 6(a, b) 所示。
影响半径r=scalex=scaley从1.5~3.0变化时3种方案的计算误差和计算时间如表 2所示。计算结果表明,除了少量数据有偏差,位移与应力的计算误差随着影响半径的增大而减小。在r=1.5,r=2.0和r=3.0时,方案3的位移误差最小;r=1.5时,方案3的应力误差最小;r=2.0和r=3.0时,3种方案的计算误差几乎相同。计算时间随着影响半径的增大而增长,整体看来方案2的计算时间最短,方案1的计算时间最长,方案3的计算时间与方案2的计算时间相近,方案3的计算误差整体上低于其余两个方案。
表 2(Table 2)

表 2 悬臂梁算例3种方案计算结果的比较
Table 2 Comparison of three plans for cantilever beam
| 影响半径 |
方案 |
Lu/% |
Lσ/% |
计算时间/s |
| r=1.5 |
方案1 |
2.83 |
5.85 |
0.52 |
| 方案2 |
1.70 |
4.01 |
0.27 |
| 方案3 |
0.19 |
3.11 |
0.27 |
| r=2.0 |
方案1 |
1.76 |
4.07 |
0.64 |
| 方案2 |
1.76 |
4.07 |
0.31 |
| 方案3 |
1.64 |
4.08 |
0.33 |
| r=2.5 |
方案1 |
0.99 |
1.05 |
0.88 |
| 方案2 |
1.76 |
4.07 |
0.31 |
| 方案3 |
1.64 |
4.08 |
0.33 |
| r=3.0 |
方案1 |
0.47 |
2.64 |
1.22 |
| 方案2 |
0.47 |
2.64 |
0.42 |
| 方案3 |
0.41 |
2.72 |
0.54 |
|
表 2 悬臂梁算例3种方案计算结果的比较
Table 2 Comparison of three plans for cantilever beam
|
考虑节点不规则分布情况,不规则节点分布悬臂梁如图 7所示。当影响半径r=3时,计算位移与应力的误差结果,如表 3所示。
表 3(Table 3)

表 3 不规则节点分布时的计算结果
Table 3 Computational results for irregularly node distribution
| 方案 |
Lu/% |
Lσ/% |
计算时间/s |
| 方案1 |
0.54 |
3.15 |
1.29 |
| 方案2 |
0.54 |
3.19 |
0.42 |
| 方案3 |
0.48 |
3.16 |
0.56 |
|
表 3 不规则节点分布时的计算结果
Table 3 Computational results for irregularly node distribution
|
计算结果表明,不规则节点分布时方案3的位移误差最小,3种方案的应力计算误差接近;方案2的计算时间最短,方案1的计算时间最长,方案3的计算时间和方案2的接近。另外,不规则节点分布比规则节点分布的计算精度低。
3.2 具有中心圆孔的无限大平板 在x方向受均匀拉伸σ0,具有半径为a的中心圆孔的无限大平板,其解析解为
|
$
\begin{array}{*{20}{c}}
{{u_r} = \frac{{{\sigma _0}}}{{4G}}\left[ {r\left( {\frac{{\kappa - 1}}{2} + \cos 2\theta } \right) + } \right.}\\
{\left. {\frac{{{a^2}}}{r}\left[ {1 + \left( {1 + \kappa } \right)\cos 2\theta } \right] - \frac{{{a^4}}}{{{r^3}}}\cos 2\theta } \right]}
\end{array}
$
|
(48) |
|
$
{u_\theta } = \frac{{{\sigma _0}}}{{4G}}\left[ {\left( {1 - \kappa } \right)\frac{{{a^2}}}{r} - r - \frac{{{a^4}}}{{{r^3}}}} \right]\sin 2\theta
$
|
(49) |
|
$
{\sigma _x} = {\sigma _0}\left[ {1 - \frac{{{a^2}}}{r}\left( {\frac{3}{2}\cos 2\theta + \cos 4\theta } \right) + \frac{{3{a^4}}}{{2{r^4}}}\cos 4\theta } \right]
$
|
(50) |
|
$
{\sigma _y} = - {\sigma _0}\left[ {\frac{{{a^2}}}{r}\left( {\frac{1}{2}\cos 2\theta - \cos 4\theta } \right) - \frac{{3{a^4}}}{{2{r^4}}}\cos 4\theta } \right]
$
|
(51) |
|
$
{\tau _{xy}} = - {\sigma _0}\left[ {\frac{{{a^2}}}{r}\left( {\frac{1}{2}\sin 2\theta + \sin 4\theta } \right) + \frac{{3{a^4}}}{{2{r^4}}}\sin 4\theta } \right]
$
|
(52) |
式中:(r, θ) 为极坐标, 其坐标原点位于圆孔中心;G,κ表达式为
|
$
G = \frac{E}{{2\left( {1 + v} \right)}}
$
|
(53) |
|
$
\kappa = 3 - 4v\left( {平面应变} \right)
$
|
(54) |
|
$
\kappa = \frac{{3 - v}}{{1 + v}}\left( {平面应力} \right)
$
|
(55) |
考虑到对称性,取模型的右上部分按平面应力问题进行分析。需要将相关参数取为E=1 000 Pa,υ=0.3,σ0=1 Pa,a=1 m。节点分布方案即离散点的无网格模型如图 8所示,积分网格如图 9所示,对于每个网格采用4×4的高斯积分方案。在平板的下边界和左边界分别施加对称的边界条件,在中心圆孔边界r=a处施加自由边界条件。在板的右边界和上边界按式 (50~52) 给出的应力施加边界条件。
图 10比较了不同方法得到的板左边界上各点的正应力σx(图 10(a)) 和板下边界上各点的正应力σy(图 10(b))。不同方法的误差和计算时间如表 4所示。由表 4可见,对于两种计算误差,方案3的计算精度都处于中等水平,但方案1和方案2都有某个应力的计算精度处于最差。另外方案1的计算时间较长,后两个方案的计算时间接近。
表 4(Table 4)

表 4 平板算例3种方案计算结果的比较
Table 4 Comparison of three plans for flat
| 方案 |
Lσx/% |
Lσy/% |
计算时间/s |
| 方案1 |
7.87 |
31.33 |
0.57 |
| 方案2 |
9.09 |
27.03 |
0.27 |
| 方案3 |
8.36 |
27.92 |
0.28 |
|
表 4 平板算例3种方案计算结果的比较
Table 4 Comparison of three plans for flat
|
4 结束语 本文在研究RPIM无网格法计算效率时发现,在使用有网格计算积分时,传统的方法在每个积分点都需要进行重新搜索节点,再进行插值,这一过程增大了计算量。本文通过将同一网格中的积分点用同一组节点插值,降低了RPIM无网格法的计算时间,另外将H-R变分原理推导的求解方程引入RPIM方法。由算例结果可以看出,该方法可提高改变积分方式后的RPIM无网格法的计算精度,同时对计算时间只产生很小的影响。










 2017, Vol. 49
2017, Vol. 49


