2. 中航工业成都飞机设计研究所,成都,610091
2. AVIC Chengdu Aircraft Design & Research Institute, Chengdu, 610091, China
飞机机翼、尾翼和机身上的薄壁加筋结构承受压缩、剪切等载荷作用时,最常见的失效模式是丧失稳定性,又称“失稳”或者“屈曲”。结构稳定性主要取决于结构自身的刚度和边界条件。典型的边界条件有简支和固支两种,在实际情况中,筋条/桁条对于板壳的支持介于简支和固支之间。对于这类结构进行稳定性分析,解析方法很难求得精确解,通常需要对结构进行简化分析,采用近似分析方法,如能量法、数值法和有限元素法等。目前有限元法是应用最为广泛的一种方法。有限元法结果精确,但是建模复杂,计算时间长。作为解析法的一种近似分析方法,能量法计算效率快,并且也能取得较好的计算精度,适合初步设计。采用能量法分析平板/加筋平板结构的稳定性在国内外已进行了数量可观的研究。Qiao和Shan采用里兹能量法建立特征值方程,对受到均匀面内压缩载荷作用下的矩形正交各向异性平板在两加载边简支、两非加载边扭转弹性约束或者一侧自由一侧扭转弹性约束下进行了局部屈曲分析,给出了与扭转支持刚度k有关的平板局部屈曲应力封闭解,并讨论了侧边为板约束时扭转支持刚度k的计算方法[1]。Chen,Xu等人在Qiao的研究基础上发展了一般面内载荷下的各向异性平板的屈曲计算方法[2]。Kollar总结了以往长板和一般各向异性矩形层合板在各种边界条件下的轴压以及剪切屈曲公式,并将之运用到复合材料开剖面/闭剖面型材的局部屈曲分析上,提出扭转杆和扭转弹簧两种模拟扭转弹性支持的方法[3]。Stamatelos等考虑筋条对于蒙皮的弹性支持,将筋条等效成变剪切刚度系数和变扭转刚度系数的弹簧,采用里兹能量法求解轴压各向同性/各向异性加筋板蒙皮局部屈曲问题[4]。Bisagni和Vescovini将轴压加筋板结构中的筋条简化为圣维南扭转杆,采用Kantorovich法和里兹能量法分别建立加筋板蒙皮局部屈曲应力公式,最重要的贡献是利用里兹法得到了屈曲应力的显式解[5]。另外,Bisagni和Vescovini还以帽形加筋板为例研究了复合材料加筋板轴压以及剪切情况下的屈曲以及后屈曲解析方法,在屈曲计算中,将蒙皮和筋条离散成板元并考虑所有板元的能量,采用能量变分原理建立整个加筋板系统的特征值方程[6]。
上述文献虽然给出了能量法分析加筋板结构稳定性的一般方法,但是研究层压板与型材居多,仅仅针对I形 (Blade-shape) 加筋板有显式的轴压屈曲计算公式;没有考虑到筋条下缘条对蒙皮局部屈曲的影响,缺乏针对任意筋条形式的加筋板的显式轴压屈曲计算公式,不能满足工程需要。本文采用能量方法,考虑筋条的扭转弹性支持作用以及筋条下缘条对于蒙皮局部屈曲的影响,提出改进的工程实用的复合材料加筋板轴压屈曲载荷计算方法,结果表明精度大大提高。本文方法能够运用到任意筋条形式的复合材料加筋板局部稳定性初步设计与分析中。
1 模型以及分析方法 1.1 分析模型加筋板结构主要屈曲形式有蒙皮局部屈曲、筋条局部屈曲和整体屈曲等。工程中常用的加筋板结构多为中等长度的加筋板结构,筋条先于蒙皮发生局部屈曲将会显著降低加筋板的承载能力,是不合理的设计。因此本文主要讨论筋条间蒙皮的局部屈曲。
图 1(a)为加筋蒙皮结构示意图。加筋板总宽度为B,总长度为a。对加筋板局部屈曲的研究通常简化为对宽度为bs(筋条腹板之间的距离) 的蒙皮板元以及蒙皮板元两侧的筋条 (图中灰色部分) 所组成部分的研究。考虑筋条对于蒙皮的扭转弹性支持,将筋条简化为圣维南扭转杆 (De Saint Venant torsion bar),同时本文指出筋条下缘条对于蒙皮局部屈曲有一定影响,反映在理论模型中即蒙皮板元宽度应为b而不是bs,b的取法与加筋板的横截面特性有关。因此轴压加筋板蒙皮局部屈曲分析模型最终简化为长度为a,宽度为b,两加载边受到均匀轴压且支持条件为简支,两侧边弹性支持的平板屈曲分析模型,如图 1(b)所示, 其中kL和kR分别定义为y=0和y=b两侧边扭转杆的扭转支持刚度。
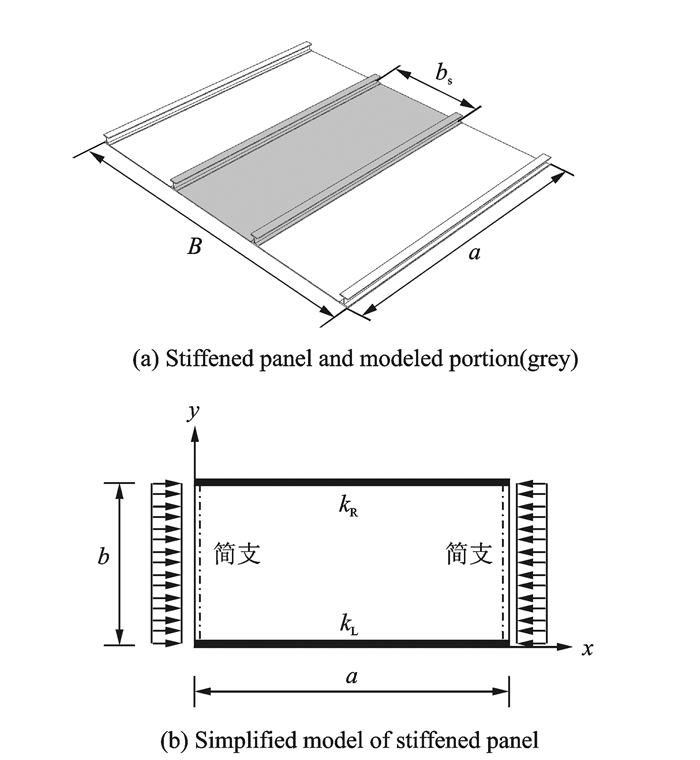
|
图 1 轴压复合材料加筋板蒙皮稳定性分析模型 Figure 1 Analytical model of stiffened composite panel |
1.2 总势能及其变分
图 1(b)所示的平板系统的总势能 (Π) 包含3个部分:蒙皮板元的弹性应变能 (Up)、筋条的扭转应变能 (Us) 和外力所做的功 (W),则总势能表达为
| $ \mathit{\prod} = {U_{\rm{p}}} + {U_{\rm{s}}} - W $ | (1) |
蒙皮板元有以下两个假设:(1) 铺层均衡对称;(2) 材料完全弹性且板元变形微小。此时板元屈曲分析中平面问题和弯曲问题是解耦的,板元应变能只需考虑板的弯曲应变能并且表达为[2]
| $ \begin{gathered} {U_{\rm{p}}} = \frac{1}{2}\iint\limits_\mathit{\Omega } {\left[ {{D_{11}}{{\left( {\frac{{{\partial ^2}w}}{{\partial {x^2}}}} \right)}^2} + {D_{22}}{{\left( {\frac{{{\partial ^2}w}}{{\partial {y^2}}}} \right)}^2} + } \right.} \hfill \\ \left. {\;\;2{D_{12}}\frac{{{\partial ^2}w}}{{\partial {x^2}}}\frac{{{\partial ^2}w}}{{\partial {y^2}}} + 4{D_{66}}{{\left( {\frac{{{\partial ^2}w}}{{\partial x\partial y}}} \right)}^2}} \right]{\rm{d}}x{\rm{d}}y \hfill \\ \end{gathered} $ | (2) |
式中:Ω为蒙皮中面的面积;w为蒙皮面外位移函数;Dij(i,j=1,2或6) 是板元弯曲刚度矩阵分量。坐标系与图 1(b)相同。
筋条的扭转应变能表达为
| $ \begin{array}{l} {U_{\rm{s}}} = \frac{1}{2}\int_0^a {{k_{\rm{L}}}{{\left( {\frac{{{\partial ^2}w}}{{\partial y\partial x}}} \right)}^2}{\rm{d}}x\left| {_{y = 0}} \right.} + \\ \;\;\;\;\;\;\;\frac{1}{2}\int_0^a {{k_{\rm{R}}}{{\left( {\frac{{{\partial ^2}w}}{{\partial y\partial x}}} \right)}^2}{\rm{d}}x\left| {_{y = b}} \right.} \end{array} $ | (3) |
扭转支持刚度除了与筋条截面自由扭转刚度有关之外,还与筋条受压[1]、筋条限制扭转[7]等因素有关。本文对加筋板做出以下假设:(1) 筋条数量很多、构型相同且等距分布;(2) 筋条相对刚硬。满足以上假设的情况下扭转杆的扭转支持刚度表达为
| $ {k_{\rm{L}}} = {k_{\rm{R}}} = GJ/2 $ | (4) |
式中GJ为筋条截面自由扭转刚度,可参考材料力学方法计算。
外力功仅包含轴力做的功,表达为
| $ W = - \frac{1}{2}\iint\limits_\mathit{\Omega } {\left[ {{{\bar N}_x}{{\left( {\frac{{\partial w}}{{\partial x}}} \right)}^2}} \right]{\rm{d}}x{\rm{d}}y} $ | (5) |
式中Nx为沿着x方向单位宽度的轴力,压力为负,拉力为正。
根据最小势能原理,在满足位移边界条件的所有容许位移中,真实位移应使总势能有驻值。系统的平衡方程等价于系统总势能一阶变分为0,即
| $ \delta \mathit{\prod} = \delta {U_{\text{p}}} + \delta {U_{\text{s}}} - \delta W = 0 $ | (6) |
选择满足位移边界条件和满足力的边界条件的面外位移函数代入到式 (2,3,5) 中并将结果代入到式 (6) 中,建立屈曲特征值方程求解屈曲载荷。
1.3 里兹法及屈曲应力封闭解里兹法要求面外位移函数应精确满足位移边界条件而近似满足力边界条件。蒙皮板元两加载边为简支,边界条件为
| $ \left\{ \begin{gathered} w\left( {0,y} \right) = 0,{M_x}\left( {0,y} \right) \approx - {D_{11}}\frac{{{\partial ^2}w}}{{\partial {x^2}}} = 0 \hfill \\ w\left( {a,y} \right) = 0,{M_x}\left( {a,y} \right) \approx - {D_{11}}\frac{{{\partial ^2}w}}{{\partial {x^2}}} = 0 \hfill \\ \end{gathered} \right. $ | (7) |
板元两侧边为弹性支持边界条件,抗弯弯矩由筋条提供。由于假设筋条为圣维南扭转杆,因此筋条只有扭转变形而无挠曲变形,其边界条件为
| $ \left\{ \begin{array}{l} w\left( {x,0} \right) = 0\\ w\left( {x,b} \right) = 0\\ {M_y}\left( {x,0} \right) \approx - {D_{22}}{\left( {\frac{{{\partial ^2}w}}{{\partial {y^2}}}} \right)_{y = 0}} = {k_{\rm{L}}}{\left( {\frac{{{\partial ^3}w}}{{\partial {x^2}\partial y}}} \right)_{y = 0}}\\ {M_y}\left( {x,b} \right) \approx - {D_{22}}{\left( {\frac{{{\partial ^2}w}}{{\partial {y^2}}}} \right)_{y = b}} = - {k_{\rm{R}}}{\left( {\frac{{{\partial ^3}w}}{{\partial {x^2}\partial y}}} \right)_{y = b}} \end{array} \right. $ | (8) |
本文选择面外位移函数为多项式与正弦函数复合的形式,则
| $ w = \left( {{A_1}y + {A_2}{y^2} + {A_3}{y^3} + {A_4}{y^4}} \right)\sin \left( {\frac{{m{\rm{ \mathsf{ π} }}x}}{a}} \right) $ | (9) |
式中:A1~A4为未知系数;m为板元沿着长轴方向的屈曲半波数。将式 (9) 代入式 (7,8) 中,可消去未知数A2~A4,仅A1未知。此时位移函数精确满足位移边界条件,近似满足力的边界条件,满足里兹法要求。将满足边界条件的位移函数代入式 (2,3,5) 中并将结果代入式 (6) 中,可得平衡方程
| $ \frac{{\partial \mathit{\prod} }}{{\partial {A_1}}}\delta {A_1} = 0 $ | (10) |
解平衡方程 (10),即得到平板压缩屈曲载荷Nx。分别令m=1,2,3,…,取其中最小值 (不含符号) 作为板的临界压缩屈曲载荷Nxcr。
2 考虑筋条下缘条的改进方法复合材料加筋平板由于筋条下缘条和蒙皮连接,因此理论模型中蒙皮板宽度未必是bs,而是随着筋条的强弱介于筋条下缘条自由端之间距离b1到筋条间距bs之间的b,如图 2所示。如何正确地选择b值,目前在国内外没有任何相关研究。笔者对常见开/闭剖面筋条截面形式的金属以及复合材料加筋板进行了有限元与试验对比分析,分析结果表明蒙皮板宽度b与加筋板典型单元的弯曲刚度比和扭转刚度比有关。在此基础上笔者构造了几种蒙皮板元宽度的近似计算方法并进行了大量的算例分析,本文所提出的蒙皮板元宽度的近似计算方法是其中准确性最好的一种计算方法。
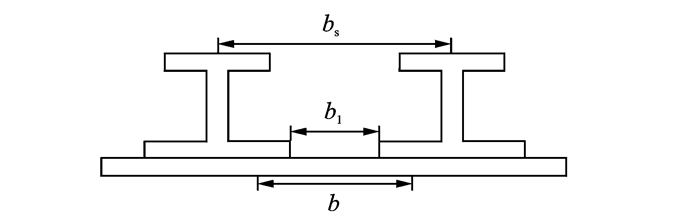
|
图 2 复合材料加筋板蒙皮间距 (板宽度) 选取示意图 Figure 2 Skin spacing dimension (plate breadth) of stiffened composite panel |
2.1 结构横截面特性
本节从刚度特性角度定义加筋板结构典型单元的弯曲刚度比W和扭转刚度比N,利用这两种无量纲参数可以考察任意加筋板的横截面特性,为蒙皮板宽度b的改进取法奠定基础。
忽略非加载边边缘筋条的影响,将加筋板看成带有单个筋条的板单元的重复排列。单个筋条以及相邻的板单元定义为典型单元,如图 3所示,其中bbflange为下缘条宽度。
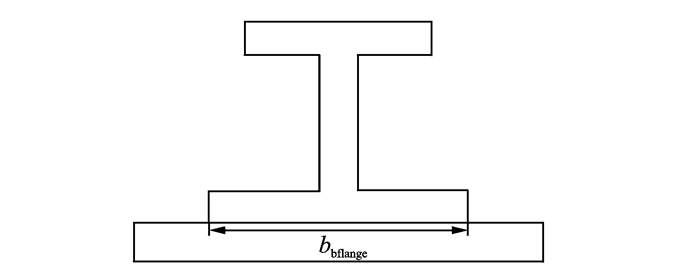
|
图 3 加筋板结构中的典型单元 Figure 3 Typical unit of stiffened panel |
典型单元的弯曲刚度比定义为W=(EI)sti/(EI)skin,其中(EI)sti为单根筋条相对于典型单元中性轴的弯曲刚度,(EI)skin为典型单元蒙皮相对于中性轴的弯曲刚度。弯曲刚度比反映加筋板筋条和蒙皮之间抗弯强弱关系。弯曲刚度比越大,越由筋条承弯。
典型单元扭转刚度比定义为
如果加筋形式为Ⅰ形筋条,由于Ⅰ形筋条没有下缘条,因此蒙皮板元宽度取为相邻两个筋条腹板之间的距离bs。
如果加筋形式为工字形,T形等筋条腹板位于下缘条对称轴位置上的筋条形式,建议采用式 (11) 作为蒙皮板宽度的近似值,即
| $ \begin{array}{l} b = {b_{{\rm{bflange}}}}\left\{ {\frac{1}{2} + \sqrt {\left[ {{{\left( {\frac{1}{{1 + W}}} \right)}^2} + {{\left( {\frac{1}{{1 + N}}} \right)}^2}} \right]/8} } \right. - \\ \left. {\;\;\;\;\;\;\sqrt {\left[ {{{\left( {\frac{W}{{1 + W}}} \right)}^2} + {{\left( {\frac{N}{{1 + N}}} \right)}^2}} \right]/8} } \right\} + {b_1} \end{array} $ | (11) |
可以证明,当W→∞,N→∞时,b→b1;当W→0,N→0时,b→bs。
如果筋条形式为L形、Z形等筋条腹板位于下缘条一侧端部的筋条形式,蒙皮板宽度的近似计算公式建议采用式 (12) 计算,即
| $ \begin{array}{l} b = \frac{{{b_{{\rm{bflange}}}}}}{2}\left\{ {\frac{1}{2} + \sqrt {\left[ {{{\left( {\frac{1}{{1 + W}}} \right)}^2} + {{\left( {\frac{1}{{1 + N}}} \right)}^2}} \right]/8} } \right. - \\ \left. {\;\;\;\;\;\;\sqrt {\left[ {{{\left( {\frac{W}{{1 + W}}} \right)}^2} + {{\left( {\frac{N}{{1 + N}}} \right)}^2}} \right]/8} } \right\} + {b_1} \end{array} $ | (12) |
常见闭剖面筋条形式如图 4所示。对于第1种闭剖面筋条形式,所研究的筋条间蒙皮局部屈曲实质上是蒙皮与下缘条的复合体的局部屈曲。根据结构的不同,蒙皮局部屈曲可能发生在闭室中,这不在本文的讨论范围内。当研究筋间蒙皮屈曲时,蒙皮板元宽度取为两个相邻筋条帽腰与蒙皮交点之间的距离。对于第2种闭剖面形式,如果筋条排列稀疏、下缘条刚度较弱时,由于闭剖面筋条自由扭转刚度一般较大,可以忽略下缘条对于蒙皮屈曲的影响,蒙皮板元宽度选取与第1种加筋形式相同。如果筋条排列密集、下缘条刚度较强,则不能忽略下缘条对于蒙皮屈曲的影响,建议采用式 (13) 作为蒙皮板宽度的近似值。式中b1定义与图 2相同,bbflange定义为帽形筋条一侧下缘条宽度。另外,由于扭转刚度比N与屈曲半波数m有关,因此运用式 (11~13) 计算蒙皮板宽度是一个迭代的过程。
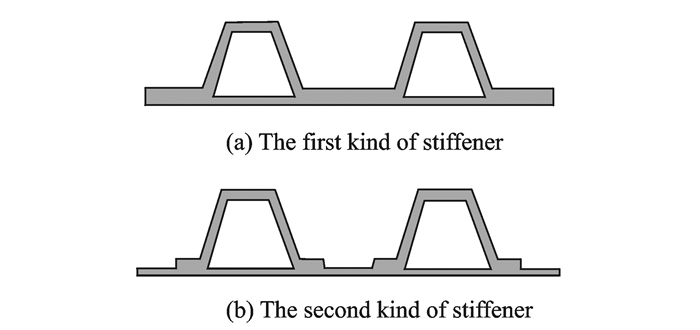
|
图 4 两种闭剖面筋条形式 Figure 4 Two kinds of closed section stiffener |
| $ \begin{array}{l} b = 2{b_{{\rm{bflange}}}}\left\{ {\frac{1}{2} + \sqrt {\left[ {{{\left( {\frac{1}{{1 + W}}} \right)}^2} + {{\left( {\frac{1}{{1 + N}}} \right)}^2}} \right]/8} } \right. - \\ \left. {\;\;\;\;\;\;\sqrt {\left[ {{{\left( {\frac{W}{{1 + W}}} \right)}^2} + {{\left( {\frac{N}{{1 + N}}} \right)}^2}} \right]/8} } \right\} + {b_1} \end{array} $ | (13) |
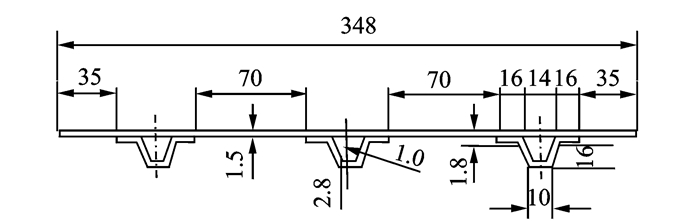
对复合材料帽形加筋板、Z形加筋板和T形加筋板进行了轴压稳定性分析计算。帽形加筋板剖面结构简图如图 5所示,加筋层压板长300 mm,宽348 mm。2个受压边取简支,2个侧边取固支。
|
图 5 帽形加筋板剖面尺寸 Figure 5 Section size of omega-shaped stiffened panel |
铺层情况:(1) 蒙皮:[0/90/0/90/0/90/0/90]s,15层,厚度1.5 mm;(2) 帽顶:[09/-45/452/-452]s,28层,厚度2.8 mm;(3) 帽腰:[-45/452/-452]s,10层,厚度1 mm;(4) 帽缘:[04/-45/452/-452]s,18层,厚度1.8 mm。
单层材料性能:单层厚度0.1 mm,E11=98 GPa,E22=10.78 GPa,G12=5.194 GPa,ν12=0.31。
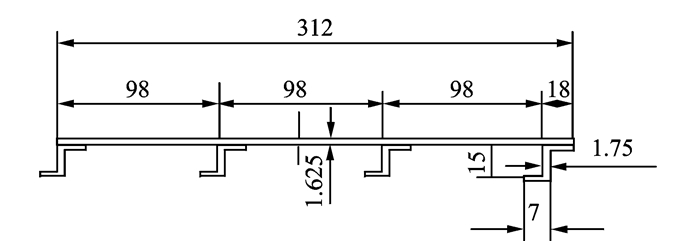
Z形加筋板剖面结构简图如图 6所示,加筋板长度290 mm,宽312 mm。2个受压端取简支,2个侧边取自由。
|
图 6 Z形加筋板剖面尺寸 Figure 6 Section size of Z-shaped stiffened panel |
铺层情况:(1) 蒙皮:[45/0/-452/45/-45/0]s,13层,厚度1.625 mm; (2) Z形桁条:[45/0/-45/0/45/0/-45]s,14层,厚度1.75 mm。
单层材料性能:单层厚度0.125 mm,E11=118 GPa,E22=8.11 GPa,G12=3.75 GPa,ν12=0.31。
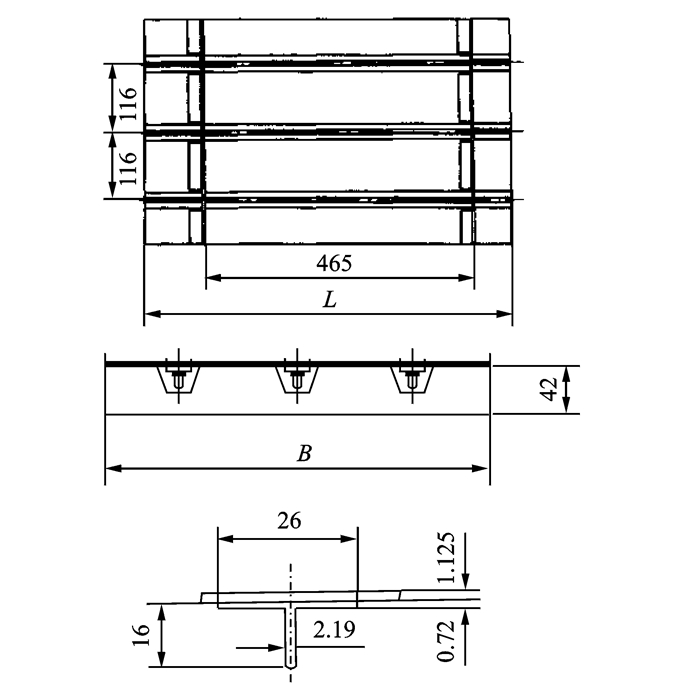
T形加筋板结构简图如图 7所示。加筋板总长度720 mm,总宽度450 mm。
|
图 7 T形加筋板剖面尺寸 Figure 7 Section size of T-shaped stiffened panel |
铺层情况:(1) 蒙皮:[45/-45/0/45/ 90]s,9层,厚度1.125 mm;(2) 水平缘条:[45*/-45*],2层,厚度0.72 mm;(3) 竖直缘条:[45*/-45*/
单层材料性能:3种单层材料包括织物、单向带和加厚单向带,其中织物 (带“ * ”) 单层厚度0.36 mm,性能Ex=50 GPa,Ey=50 GPa,Gxy=4.8 GPa,νxy=0.3;加厚单向带 (带“ · ”) 单层厚度0.25 mm;普通单向带 (不带“ · ”) 单层厚度0.125 mm。两种单向带性能为E11=115.2 GPa,E22=7.72 GPa,G12=4.7 GPa,ν12=0.3。
有限元建模采用S4R常规壳单元,单元尺寸10 mm×10 mm。帽形加筋板加载边简支约束,侧边固支约束;T形加筋板四边简支约束;Z形加筋板加载边简支约束,侧边自由。采用buckle分析步对模型进行屈曲分析。图 8为3种加筋板的有限元网格划分。

|
图 8 3种加筋板有限元模型 Figure 8 Three FEM models of different stiffened panels |
3.2 理论计算
首先对3种加筋板采用工程简化分析方法进行计算,筋条简化为简支或者固支。简支情况按照四边简支正交各向异性矩形层合板轴压屈曲公式计算[8],即
| $ \begin{array}{l} {{\bar N}_x} = \frac{{{{\rm{\pi }}^2}{D_{22}}}}{{{b^2}}}\left[ {\frac{{{D_{11}}}}{{{D_{22}}}}{{\left( {\frac{b}{a}} \right)}^2}{m^2}} \right. + \\ \left. {2\left( {\frac{{{D_{12}} + 2{D_{66}}}}{{{D_{22}}}}} \right) + {{\left( {\frac{a}{b}} \right)}^2}\frac{1}{{{m^2}}}} \right] \end{array} $ | (14) |
计算时分别令m=1,2,3,…,取其中最小值作为板的临界压缩屈曲载荷Nxcr,对应的m值为屈曲半波数。a取加筋板长度或者肋之间的长度,b取筋条 (帽腰) 间距。
固支情况按照两加载边简支两侧边固支正交各向异性矩形层压板轴压屈曲公式计算[8]为
| $ {{\bar N}_{xcr}} = \frac{{{{\rm{\pi }}^2}\sqrt {{D_{11}}{D_{22}}} }}{{{b^2}}}\left[ {K - 2.40\left( {1 - \frac{{{D_{12}} + 2{D_{66}}}}{{\sqrt {{D_{11}}{D_{22}}} }}} \right)} \right] $ | (15) |
式中K以及屈曲半波数按照文献[8]中2.2.1节图 2-3查取。
然后考虑筋条的扭转弹性支持,筋条简化为圣维南扭转杆,采用能量法计算加筋板的蒙皮局部屈曲载荷和屈曲半波数。蒙皮板元宽度分别按照筋条腹板之间的距离 (帽形加筋板取帽腰之间的距离) 以及本文提出的蒙皮板元宽度近似计算方法计算,以进行对比分析。
3.3 结果对比图 9为3种加筋板的屈曲模态图。表 1给出了3种加筋板的试验结果[8]、有限元结果、工程简化分析方法计算结果以及两种蒙皮板元宽度取法下的能量法结果。

|
图 9 3种加筋板有限元屈曲模态 Figure 9 Buckling modes of three stiffened panels |
| 表 1 3种加筋板试验结果、有限元结果、工程方法结果以及能量方法结果对比 Table 1 Comparison of results by experiment, FEM, engineering method and energy method |
按照工程简化分析方法,开剖面筋条一般简化为简支,闭剖面筋条一般简化为固支。则帽形加筋板分析值与试验值误差40.1%,Z形加筋板分析值与试验值误差42.3%,T形加筋板分析值与试验值误差48.9%。进一步对比简/固支结果,可以看出Z形加筋板和T形加筋板按固支计算误差小于按简支计算误差,表明按工程经验将开剖面筋条简化为简支、闭剖面筋条简化为固支在某些情况下是不合适的。因此,考虑筋条弹性支持更为合理且很有必要。
对比3种加筋板考虑筋条弹性支持的能量法计算结果,按照筋条 (帽腰) 间距计算结果误差分别为41.4%,29.6%和30.8%。结果表明,对T形加筋板和Z形加筋板,考虑筋条的扭转弹性支持能够明显提高计算精度,但与试验值仍有一定误差;对帽形加筋板,由于闭剖面筋条扭转刚度大,扭转弹性支持作用与固支近似,因此考虑筋条的转弹性支持的计算精度与固支计算精度相差不大。
上述结果表明,仅仅考虑筋条的扭转弹性支持作用是不够的,筋条下缘条对于蒙皮屈曲的影响不可忽略。而按照本文提出的蒙皮板元宽度近似取法计算,其计算结果与试验值误差仅为7.9%,3.4%和8.0%,表明考虑下缘条对于蒙皮屈曲的影响,按照本文提出的方法可以大大提高能量法的计算精度。
4 结论(1) 传统的工程简化分析方法存在较大误差。原因有两点:一是没有考虑到下缘条对于蒙皮屈曲的影响,蒙皮板元宽度取值不当,二是简/固支简化与真实支持存在差异。另外,按照以往工程经验将开剖面筋条简化为简支,闭剖面筋条简化为固支的做法在某些情况下不合适。因此考虑筋条弹性支持更为合理且很有必要。
(2) 采用能量方法,考虑筋条的弹性扭转支持可以提高屈曲载荷的计算精度,但是如果忽略了筋条下缘条对于蒙皮屈曲的影响而导致蒙皮板元宽度取值不当,则计算精度提高程度有限。
(3) 采用本文提出的蒙皮板元宽度近似计算方法可以大大提高能量法的计算精度,计算结果与试验结果误差在10%以内,验证了本文方法的合理性。
| [1] | QIAO Pizhong, SHAN Luyang. Explicit local buckling analysis and design of fiber-reinforced plastic composite structural shapes[J]. Composite Structures, 2005, 70(4): 468–483. DOI:10.1016/j.compstruct.2004.09.005 |
| [2] | QIAO Pizhong, CHEN Fangliang, XU Jifeng, et al. Local buckling analysis of restrained orthotropic plates under generic in-plane loading[J]. American Society of Civil Engineers, 2013, 139(8): 936–951. |
| [3] | KOLLAR L P. Local buckling of fiber reinforced plastic composite structural members with open and closed cross sections[J]. Journal of Structural Engineering, 2003, 129(11): 1503–1513. DOI:10.1061/(ASCE)0733-9445(2003)129:11(1503) |
| [4] | STAMATELOS D G, LABEAS G N, TSERPES K I. Analytical calculation of local buckling and post-buckling behavior of isotropic and orthotropic stiffened panels[J]. Thin-Walled Structures, 2011, 49(3): 422–430. DOI:10.1016/j.tws.2010.11.008 |
| [5] | BISAGNI C, VESCOVINI R. Analytical formulation for local buckling and post-buckling analysis of stiffened laminated panels[J]. Thin-Walled Structures, 2009, 47(3): 318–334. DOI:10.1016/j.tws.2008.07.006 |
| [6] | BISAGNI C, VESCOVINI R. Two-step procedure for fast post-buckling analysis of composite stiffened panels[J]. Computers and Structures, 2013, 128(5): 38–47. |
| [7] |
崔德刚.
结构稳定性设计手册[M]. 北京: 航空工业出版社, 2006.
CUI Degang. Handbook of structure stability[M]. Beijing: Aviation Industry Press, 2006. |
| [8] |
中国航空研究院.
复合材料结构稳定性分析指南[M]. 北京: 航空工业出版社, 2002.
Chinese Aeronautical Establishment. Analysis manual of composite structure stability[M]. Beijing: Aviation Industry Press, 2002. |
 2017, Vol. 49
2017, Vol. 49


