2. 上海航天控制技术研究所,上海,200233
2. Shanghai Aerospace Control Technology Institute, Shanghai, 200233, China
硬质合金球广泛应用于轴承、球形电机[1]中,其球形误差、表面粗糙度直接影响设备的精准性、可靠性以及使用寿命。球体零件的加工方法主要为研磨和抛光,加工过程产生的接触轨迹是影响球体零件精度、表面质量的关键。球体加工方式的研究多以研磨轨迹作为出发点,研究不同研磨方式的优劣性。聂兰芳等人[2]研究了球体成球条件,总结为:球面上每个点被加工的概率都是相同的(切削等概率性);加工过程中,选择性研磨大球、长轴方向(尺寸选择性)。朱晨[3]对同轴两转盘和同轴三转盘两种研磨方式进行了力学分析,分析了两者的研磨轨迹,得出了同轴三转盘研磨方式的力学特性;王军等人[4]研究了锥形研磨方法的研磨轨迹,得出其研磨效率比V形槽研磨法更高的结论;Zhang等人[5]通过分析磁流体研磨方法的研磨轨迹,得出结论:磁流体研磨过程中研磨轨迹是一组固定的圆环,其成球需要有系统自身的影响;Zhang和Nakajima[6]对实际研磨轨迹和研磨仿真轨迹进行了对比,发现偏心研磨和双转盘研磨是加工高精密球体的有效方法。
然而,以上研磨轨迹研究只是单纯的几何研究,没有考虑研磨过程中的研磨压力和球体表面原始形貌的影响。这种几何研究法只能对研磨过程的轨迹均匀性进行定性评价,评价准确性低。
1 硬质合金球体材料去除方程推导双转盘偏心V形槽研磨方式结构图如图 1所示,球体与上、下研磨盘三点接触,研磨过程中球体

|
图 1 双转盘偏心V形槽研磨方式结构示意图 Figure 1 Structure diagram of eccentric lapping method with two rotatable lapping plates |
和研磨盘发生滚动摩擦,由此在球体表面产生3条研磨轨迹。由于摩擦方式为滚动摩擦,硬质合金材料去除方程将以滚动摩擦去除实验为基准。类似于单转盘偏心V形槽研磨方法,双转盘偏心V形槽研磨的材料去除主要影响因素为研磨压力和研磨盘转速[7-9]。在其他实验条件确定的情况下,本文考虑研磨压力和上、下研磨盘转速对材料去除率的影响。研磨实验条件如表 1所示。
| 表 1 研磨实验条件 Table 1 Lapp ing test conditions |
实验中,保持磨料浓度、磨粒粒度不变,采用单因素实验,分别分析研磨压力和上、下研磨盘转速对硬质合金材料去除率的影响。研磨压力变化范围为5~26 N/ball,上研磨盘转速变化范围为0~64 r/min,下研磨盘转速变化范围为30~135 r/min。采用材料去除率和平均半径变动率(单位时间半径减小值)作为评价指标。材料去除率用MRR表示,使用精密分析天平(BS224S,德国Sartorius,精度0.1 mg),测量研磨前后每组球的质量变化,计算每组中单个球体的材料去除质量的平均值,作为材料去除率。平均半径变动率用Δr表示,由式(1)获得。实验结果见表 2。
| $MRR=\left[ \frac{3}{4}\pi {{R}^{3}}-\frac{4}{3}\pi {{(R-\Delta ~r)}^{3}}) \right]\text{ }\rho $ | (1) |
式中:R=6.35 mm为硬质合金球原始半径;ρ=6.4 mg/mm3为硬质合金材料密度。
材料去除主要与球体-研磨盘相对速度和研磨压力相关,将研磨盘转速通过式(2)转化为接触点的线速度,则可以得出材料去除率与上下接触点线速度的关系。
| $V=\frac{n\times 2\pi }{60}\cdot {{R}_{0}}$ | (2) |
式中:n为研磨盘转速;R0为V形槽圆形半径。
| 表 2 材料去除实验结果 Table 2 Materi als removal test results |
实验中平均半径变动率的影响因素有3个:研磨压力p,上接触点线速度VU,下接触点线速度VL。为得出材料去除率方程,本文利用多元线性回归分析法[10],构建四者之间的多元线性回归模型。由Preston[11]方程可知,材料去除率与研磨相对速度和研磨压力成正比关系,故多元线性回归方程表示如下
| $\Delta r=K{{p}^{x}}V{{~}^{y}}_{U}{{V}^{z}}_{L}$ | (3) |
结合表 2和式(2),使用最小二乘法求解线性回归方则得出K,x,y,z分别为0.930,0.554,-0.082,0.676,即硬质合金球在双转盘偏心V形槽研磨方式中的平均半径变动率方程为
| $\Delta r=0.930{{p}^{0.554}}{{V}^{-0.082}}_{U}{{V}^{0.676}}_{L}$ | (4) |
文献[12]中提出了球体研磨均匀性的纯几何评价方法。将球面分为100个区域后,通过计算研磨接触点轨迹离散后在各区域的分布情况,衡量研磨均匀性。这种评价方法主要考虑了研磨过程的运动规律,考察接触点的分布情况,不考虑球体表面原有的表面形貌和研磨过程中材料去除对表面的影响,只能定性评价研磨轨迹的均匀性。本文结合硬质合金材料去除方程,对球体表面各个划分区域进行赋值(模拟原始形貌),计算仿真后球体表面各区域值,将仿真后各区域差值最大值作为球体球度[13],衡量研磨均匀性。
为方便分析,作如下假设:(1)球体与研磨盘在研磨过程中无弹塑性变形;(2)球体与研磨盘接触各点在圆周运动中线速度相同;(3)各球体之间无相互摩擦、撞击作用;(4)不考虑研磨液对研磨过程的影响。
硬质合金球坯的球度为4μm,因此,赋值区间选择0~4μm。采用MATLAB产生10×10的随机分布矩将其赋值到按经纬度划分的100个球面区域,赋值结果是在球体表面产生随机的表面形使得球体各区域原始形貌值(区域赋值)各不相同。
定义硬质合金球体接触点处去除规则:接触点发生材料去除时,材料去除量是该点形貌值(该点发生材料去除前的值)、取样时间和单位时间材料去除比例(平均半径变动率与去除实验球度误差H的比值)的乘积,则某区域经n个接触点切除材料后的形貌值Hn
| $~{{H}_{n}}={{H}_{0}}{{(1-\frac{\Delta t\Delta r}{3\text{ }600H})}^{n}}$ | (5) |
式中:Δt=0.05s为取样时间,H=4μm为去除实验的原始球度误差。
仿真模型是采用MATLAB建立的数学模型。对研磨轨迹离散、球体表面区域划分[12]、区域表面赋值后,结合硬质合金材料去除方程和去除规则,可以计算出一定研磨时间后,球体表面各区域形貌值(各区域高度),各区域形貌值差值的最大值即为球体球度。最大形貌值差值越大,则研磨均匀性越差;最大形貌值差值越小,则研磨均匀性越好,以此来判断双转盘偏心V形槽研磨方法的均匀性。
3 仿真与研磨实验在得出双转盘偏心V形槽研磨均匀性定量评价方法的基础上,结合该评价方开展仿真与研磨实验研究。通过正交实验研究研磨压力、上研磨盘转速和下研磨盘转速对球体球度的影响。仿真采用标准的4因素、3水平L9(34)正交表,加工水平及参数如表 3所示。仿真条件为球坯半径6.35mm,V形槽圆弧半径55mm,偏心距8mm,仿真时间为3 600s,取样时间间隔Δt =0.05s。
| 表 3 加工参数及水平 Table 3 Parameters a nd their levels |
将仿真后的形貌高度值差值作为评价指标,实验结果如表 4所示。
| 表 4 仿真实验结果 Table 4 Simulation results |
使用SPQMJ-350双转盘偏心V形槽研磨机(南京航空航天大学与上海航天控制技术研究所联合研制)进行研磨实验,研究实际加工中,研磨压力、上研磨盘转速和下研磨盘转速3个参数对球体球度的影响。研磨实验以球体球度做评价标准,使用Talyrond-250圆度仪进行测量。研磨条件同表 1,加工参数及水平同表 3,研磨结果如表 5所示。
| 表 5 研磨实验结果 Table 5 Lapping results |
4 分析与讨论
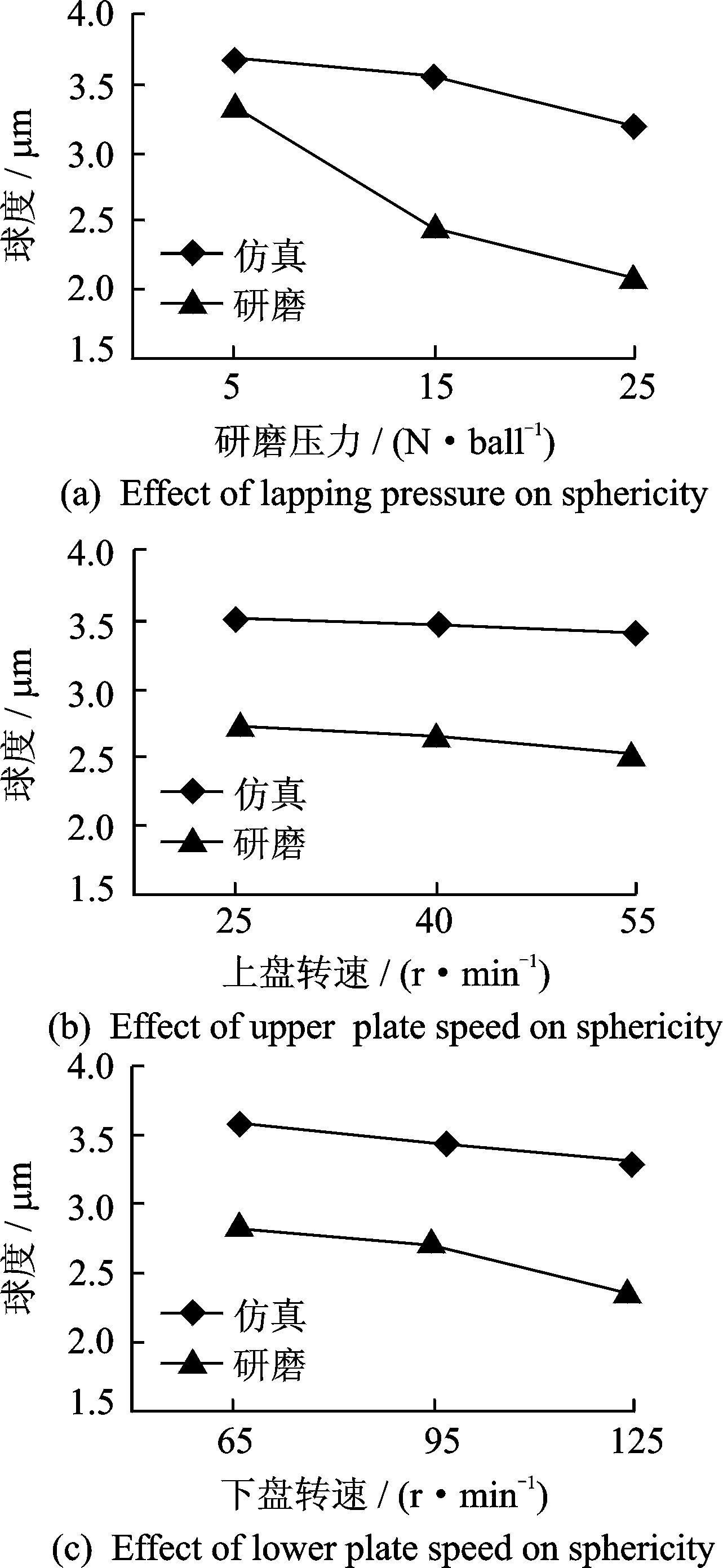
为了方便分析不同研磨参数对球体球度的影响,将表 4和表 5中,各参数水平对应下的平均值如图 2所示。
|
图 2 各研磨参数对球体球度的影响 Figure 2 Effects of lapping parameters on sphericity |
由图 2可以看出,虽然仿真值与研磨实验值有一定的差值,但在球度值变化趋势上,仿真结果与实验结果有很好的相似性。
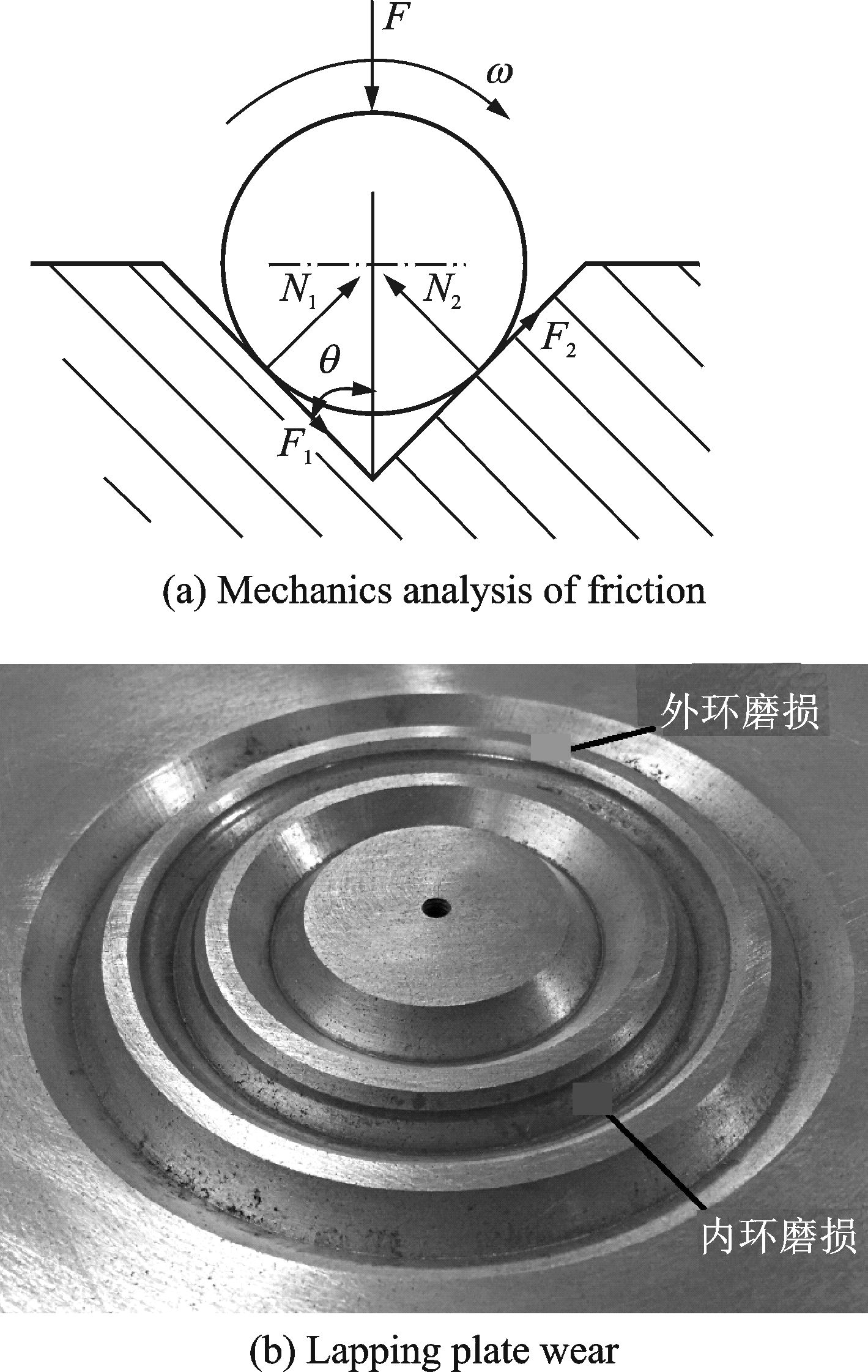
对于研磨压力而言,随着研磨压力的增加,仿真与实验的球度值差值由0.35 μm增加到1.08 μm,再到1.10 μm,球度值差值增加趋势变缓。研磨压力导致仿真结果差异变化的主要原因在于研磨压力的变化导致研磨过程中下盘磨损不同。如图 3(a)所示,摩擦力F1和F2可以由式(6)获得,其大小与研磨压力成正比关系。随着压力增大,摩擦力增大,球体材料去除增加,同时下研磨盘磨损量也会增加。下研磨盘磨损,会出现图 3(b)所示的沟槽。在一定范围内,这种沟槽能够使得下研磨盘表面质量提高,有利于球体与研磨盘充分接触,从而减小球体球度值[7, 10]。因此,在压力为15 N/ball时,实验球度值更小,与仿真值差值较大;在实验过程中,发现磨损沟槽的进一步增加会导致研磨系统不稳定。长时间、大压力的研磨实验后,下研磨盘出现部分区域磨损严重。区域严重磨损会导致球体在研磨过程中受力变化增大,发生直径变动量增大[14],降低球体精度。实验中,研磨时间较短,并没有出现严重磨损的情况,但仍影响到了球体球度,尤其在研磨压力为25 N/ball磨损沟槽较大,研磨稳定性变差,球体球度改善变慢,球体球度值虽然有所减小,但减小趋势变缓,与仿真值差值变小。
|
图 3 旋转摩擦分析 Figure 3 Analysis of rotating friction |
| $\left\{ \begin{matrix} {{F}_{1}}=\frac{u\left( 1-u \right)}{\sqrt{2}(1+{{u}^{2}})}F \\ {{F}_{2}}=\frac{u\left( 1-u \right)}{\sqrt{2}(1+{{u}^{2}})}F \\ \end{matrix} \right.$ | (7) |
式中u为摩擦因数。
对于下盘转速而言,随着下盘转速增加,仿真与实验的球度值差值由0.81 μm增加到0.82 μm,再到0.91 μm,球度值差值变化很小。从图中曲线可以看出,当下盘转速增加时,在实验与仿真中,球体球度值都呈下降趋势,且下降趋势基本相同。
对于上盘转速而言,随着上盘转速增加,仿真与实验的球度值差值由0.77 μm增加到0.78 μm,再到0.98 μm。仿真所得球度值与实验所得球度值差值变化较小,在转速增加过程中,球度值差值基本保持0.77~1.00之间。从研磨球度值下降趋势而言,随着上盘转速的增大,研磨球度值降低。
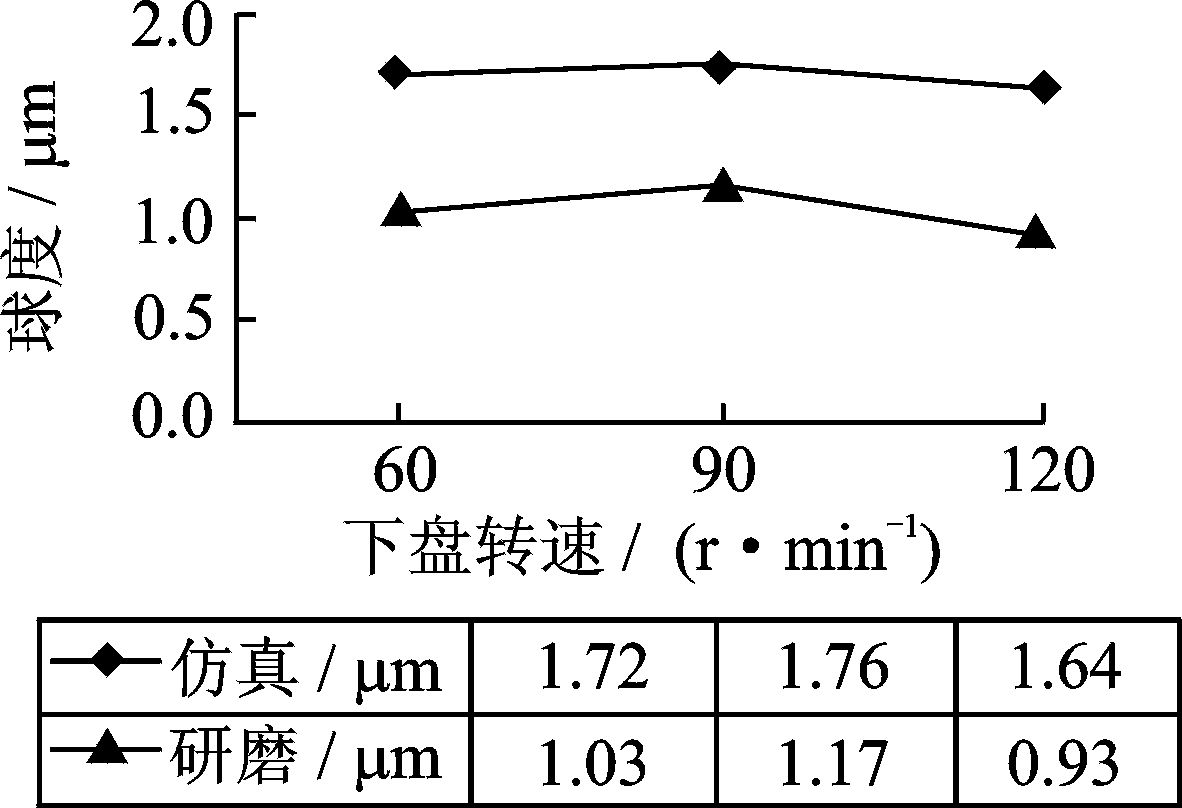
对比文献[12]中的数据,发现下盘转动对球体球度影响不尽相同。通过仿真与研磨实验发现,主要影响因素为球体原始球度不同。将本文中仿真模型进行修改,随机数由0~4修改为0~2,即修改球体原始球度值。虽然仿真与实验的球体球度仍不一样,但是球度随下盘转速的变化的趋势相同(如图 4所示)。因此,球体原始形貌对研磨结果也有着很大的影响。
|
图 4 原始球度为2 μm 时,下盘转速对球度的影响 Figure 4 Effect of lower lapping plate on sphericity with original sphericity of 2 μm |
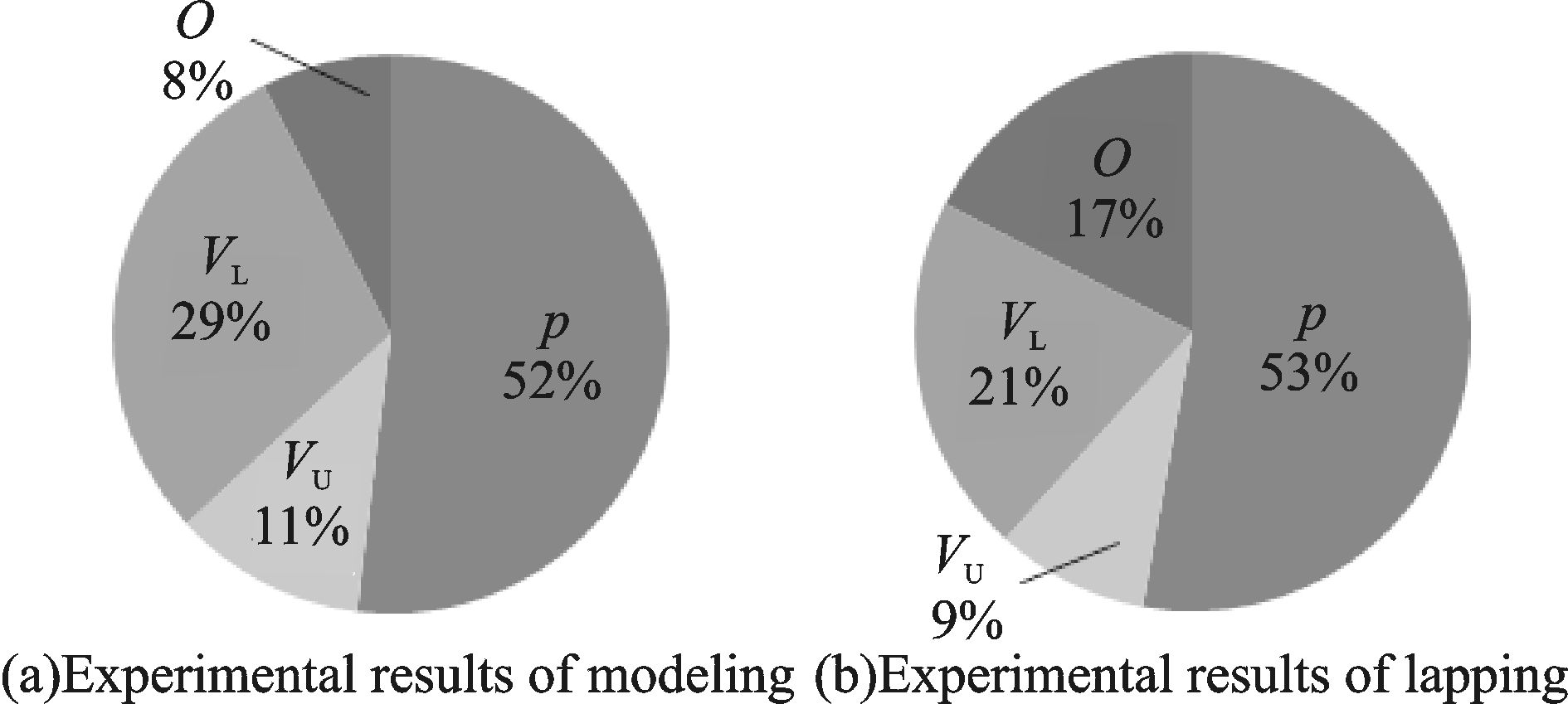
根据仿真实验与研磨实验的极差分析,将极差值比例作为各研磨参数对球体球度的影响比例,如图 5所示。在研磨实验中,研磨压力所占影响比例为53%,上盘转速影响比例为9%,下盘转速影响比例为21%,实验中其他因素所占比例为17%;在仿真结果中,研磨压力、上盘转速、下盘转速和其他因素所占比例分别为52%,11%,29%,8%。在仿真与研磨实验中,3个研磨参数影响比例虽然不相同,但由大到小依次均为研磨压力、下盘转速和上盘转速。影响比例主要差别在于其他因素方面。在仿真中,由于不考虑研磨实验中球体滑动现象和受力不均匀现象,其他因素影响比例很小;而实验中,这两种现象对球体球度的影响较大,所以其他因素影响较大,以后需要进一步研究。
|
图 5 各研磨参数对球体球度的影响比例 Figure 5 Percentage contributions for parameters |
本文只对研磨压力、研磨盘转速进行了仿真,研磨加工中还有很多加工参数对研磨结果产生很大的影响,例如磨粒大小、磨料流量和研磨时间等。在完善仿真模型过程中,这些参数都应包含在内,需要在这些方面进行大量的实验。
5 结束语本文通过实验推导了双转盘偏心V形槽球体研磨材料去除公式,并提出了双转盘偏心V形槽研磨方式研磨均匀性定量评价的方法。 研磨均匀性定量评价方法既能考虑研磨中材料去除的影响,又能将球体原始表面质量影响包含在内。本文使用正交实验对仿真实验与研磨实验对比,发现研磨均匀性定量评价方法可以有效预测各个研磨参数对研磨结果的影响。
实验表明,在研究的3个加工参数中,研磨压力对球体球度的影响最大,其次是下盘转速,上盘转速的影响最小,其他因素对球体球度也有着很大的影响。同时研磨表面粗糙度和研磨材料去除对研磨都有着很大的影响。
| [1] |
过希文, 王群京, 李国丽, 等.
永磁球形电机的自适应反演滑模控制[J]. 南京航空航天大学学报, 2014, 46(1): 59–64.
Guo Xiwen, Wang Qunjing, Li Guoli, et al. Adaptive backstepping sliding mode control in permanent magnet spherical motor[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(1): 59–64. |
| [2] |
聂兰芳, 赵学军.
钢球加工成圆条件及其影响因素探讨[J]. 轴承, 2001(1): 16–18.
Nie Lanfang, Zhao Xuejun. Forming circle condition and affecting factors in steel ball process[J]. Bearing, 2001(1): 16–18. |
| [3] |
朱晨.
两种钢球研磨方式的力学分析[J]. 轴承, 2000(9): 11–13.
Zhu Chen. Mechanics analysis on two kinds of lapping mode of steel balls[J]. Bearing, 2000(9): 11–13. |
| [4] |
王军, 张淳, 吴玉厚.
精密陶瓷球研磨加工技术研究[J]. 制造技术与机床, 1998(9): 34–36.
Wang Jun, Zhang Chun, Wu Yuhou. Research on lapping processing technology of precision ceramic balls[J]. Manufacturing Technology & Machine Tool, 1998(9): 34–36. |
| [5] | Zhang B, Uematsu T, Nakajima A. High efficiency and precision grinding of Si3N4 ceramic balls aided by magnetic fluid support using diamond wheels[J]. JSME International Journal, Series C, 1998, 41(3): 499–505. DOI:10.1299/jsmec.41.499 |
| [6] | Zhang B, Nakajima A. Spherical surface generation mechanism in the grinding of balls for ultra-precision ball bearings[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2000, 214(4): 351–357. DOI:10.1243/1350650001543241 |
| [7] | Kang J, Hadfield M. A novel eccentric lapping machine for finishing advanced ceramic balls[J]. Proc Inst Mech Eng, Part B, 2001, 215(6): 781–795. DOI:10.1243/0954405011518728 |
| [8] | Kang J, Hadfield M. Parameter optimization by Taguchi methods for finishing advanced ceramic balls using a novel eccentric lapping machine[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2001, 215: 69–78. DOI:10.1243/0954405011515145 |
| [9] | Kang J, Hadfield M. The polishing process of advanced ceramic balls using a novel eccentric lapping machine[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2001, 219: 493–504. |
| [10] | Steven C C. Applied numerical method with MATLAB[M]. Beijing: Tsinghua University Press, 2009. |
| [11] | Preston F W. Glass technology[J]. Journal of the Society of Glass Technology, 1927(11): 277–281. |
| [12] | Lv C C, Sun Y L, Zuo D W. A novel eccentric lapping method with two rotatable lapping plates for finishing cemented carbide balls[J]. International Journal of Mechanical, Aerospace, Industrial and Mechatronics Engineering, 2015, 9(5): 464–471. |
| [13] |
何改云, 宋占杰.
球度误差评定方法的研究[J]. 计量技术, 1999(3): 16–19.
He Gaiyun, Song Zhanjie. Study of sphericity error evaluation method[J]. Measurement Technique, 1999(3): 16–19. |
| [14] | Ren Chengzu, Xu Yanshan, Lin Bin, et al. The eccentric circular groove lapping technique for ceramic balls[J]. Chinese Journal of Mechanical Engineering, 1995, 11(4): 21–24. |
 2016, Vol. 48
2016, Vol. 48


