工业机器人是一种集机械、电子、控制、计算机、传感器和人工智能等跨学科先进技术于一体的高端制造业的重要智能装备,近年来一直是国内外研究的热点[1-3]。降低机器人本体质量,提高其负载能力是工业机器人领域中的重要研究方向。而如何快速准确地获得带负载机器人模型是解决负载机器人高精度控制的关键。
根据获取关节力矩测量数据方法的不同可将机器人负载辨识方法分为基于机器人反作用力传感器的外部模型法与基于内部测量装置的内部模型法。例如Atkeson等[4]通过力/力矩传感器来测量负载施加到机器人末端执行器的力矩,但这种方法需要特殊的传感器,在工程中不宜推行;Gautier等[5]将已知负载模型添加到预先获得的空载机器人本体动力学模型中,从而得到整个带负载机器人模型,但并不是所有负载模型可直接获得。国内外很多学者把负载当作机器人本体的一部分进行参数辨识[6],但由于负载类型不同,辨识实验得重新实施,故这种方法费时耗力。
针对上述问题,本文提出了一种基于带负载机器人本体动力学模型的参数辨识方法。笔者已经完成了机器人本体动力学模型的辨识[7],根据Newton-Euler法推导出负载的可辨识模型,并将负载模型补偿到机器人本体模型中,然后利用加权最小二乘法对整个完整机器人模型进行辨识。最后,通过实验对本文所提辨识方法的有效性进行了验证。
1 动力学建模对于n自由度空载机器人动力学方程一般可由含关节位置、速度、加速度及连杆动力学参数的非线性函数描述[8]为
| ${{\tau }_{robotlinks}}=F(q,\dot{q},\ddot{q},{{\theta }_{full}})$ | (1) |
式中:τrobotlinks为各关节力矩;θfull为各连杆动力学参数集,包含最小惯性参数集及各关节的摩擦因数;q为各关节转角。式(1)所示的动力学方程包含了关节间摩擦对机器人动力学的影响,经典的库伦-粘性摩擦模型具有关于未知参数线性的形式,因此本文采用这一摩擦模型。
当机器人末端加上负载后,所需的力矩就会改变,产生的额外驱动力矩τpayload可表示为
| ${{\tau }_{payload}}={{J}^{T}}\left( q \right)w$ | (2) |
式中:w为负载施加的力与力矩;JT(q)为Rn×n的雅可比矩阵。
联立式(1,2)可得整个带负载机器人的动力学模型为
| $\tau ={{\tau }_{robotlinks}}+{{\tau }_{payload}}=F(q,\dot{q},\ddot{q},{{\theta }_{fu\text{ }ll}})+{{J}^{T}}\left( q \right)w$ | (3) |
从式(3)可看出,机器人本体和负载对于关节力矩的贡献并不耦合。这表明对于同一台机器人,换了新负载,无需再辨识机器人本体模型。
把负载惯性参数转换到机器人末端连杆坐标系中,得到修正的惯性参数为
| ${{\theta }_{L}}={{[m,{{s}_{x}},{{s}_{y}},{{s}_{z}},{{I}_{xx}},{{I}_{yy}},{{I}_{zz~}},{{I}_{xy}},{{I}_{xz}},{{I}_{~yz}}]}^{T}}$ | (4) |
式中:s,I分别为负载相对于末端连杆坐标系的一阶惯量与转动惯量。
根据文献[9, 10],使用改进的Newton-Euler参数或质心参数将式(2)通过参数变换写成动力学参数的线性形式
| ${{\tau }_{payload}}={{\phi }_{L}}\left( q,\dot{q},\ddot{q} \right){{\theta }_{L}}$ | (5) |
式中ΦL为仅基于机器人运动学观测矩阵。
2 参数辨识机器人的参数辨识一般包含5个步骤:动力学建模、激励轨迹设计、数据采集及预处理、参数估计和模型验证。机器人动力学辨识过程可表示为:给定机器人关节激励轨迹,采集关节力矩与角位移数据,数据预处理后代入到辨识方程中,便可得到待辨识的未知参数。具体的流程见图 1。
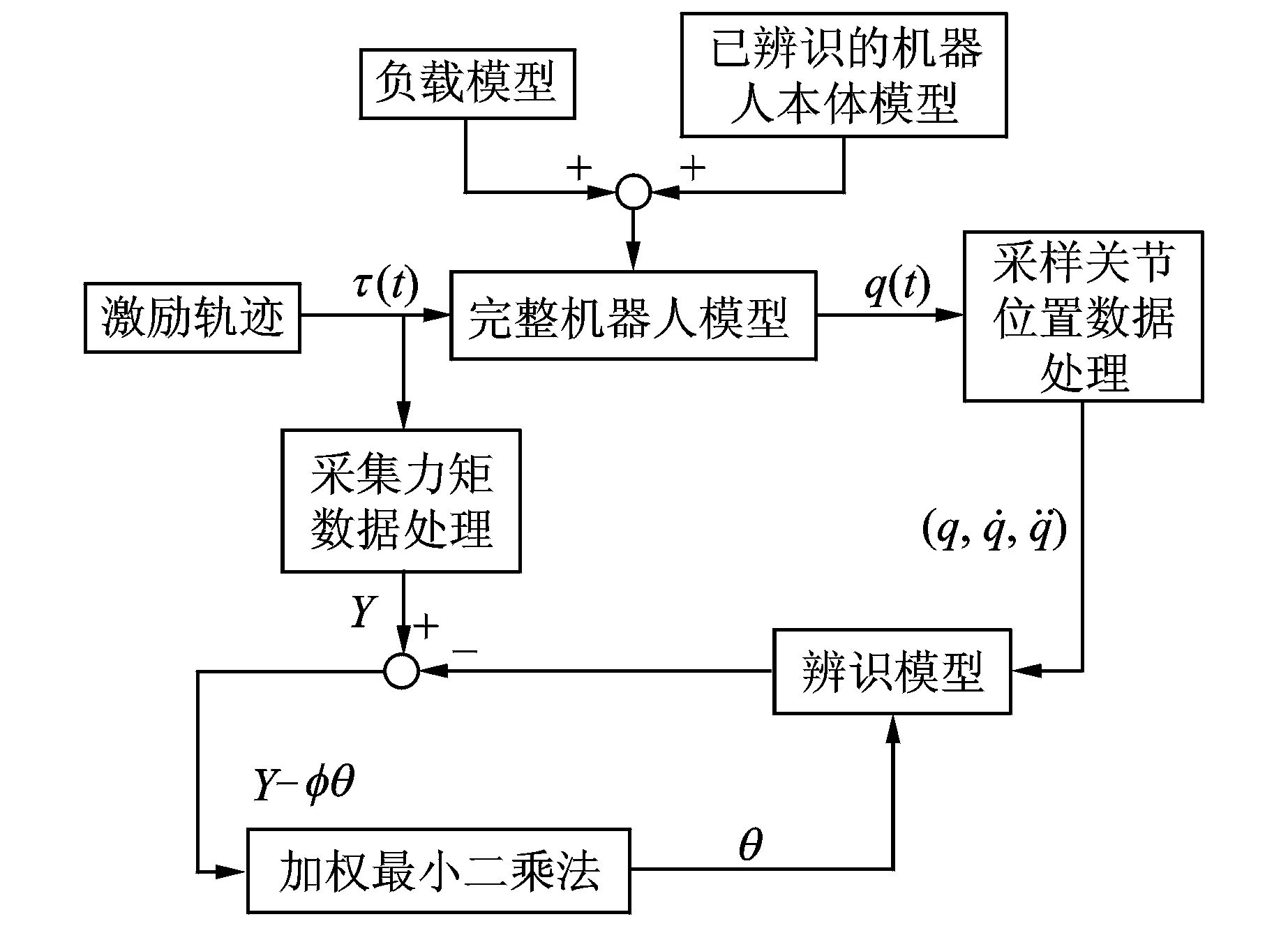
|
图 1 带负载机器人的参数辨识流程图 Figure 1 Flowchart of parameter identification of robot with payload |
2.1 激励轨迹的设计
机器人负载辨识相对于本体辨识而言,只在可辨识模型建立方面具有较大差异,而具体的辨识流程可以通过适当修改本体辨识流程得到。
与本体辨识类似,本文采用有限项周期性傅里叶级数作为激励轨迹[11],表达式为
| ${{q}_{i}}\left( t \right)={{q}_{i,0}}+\sum\limits_{k=1}^{N}{{{a}_{i,k}}sin(k{{\omega }_{f}}t)+\sum\limits_{k=1}^{N}{{{b}_{i,k}}cos(k{{\omega }_{f}}t)}}$ | (6) |
式中:qi,0为关节位置补偿量;ωf为基频;N为傅里叶级数的谐波项数每个傅里叶级数含有2N+1个参数;ai,k与bi,k分别为正弦与余弦函数的幅值。
由于激励轨迹受到电机力矩、关节位置、关节速度、关节加速度和工作空间等条件约束,故设计的轨迹需满足以下条件
| $\left\{ \begin{align} & \begin{matrix} mincond\left( \Phi \right) \\ {{q}_{min}}\le q\left( \beta \right)\le {{q}_{max}},\dot{q}\left| \left( \beta \right) \right|\le {{{\dot{q}}}_{max}} \\ \ddot{q}\left( \beta \right)\le {{{\ddot{q}}}_{max}} \\ w\left( q\left( \beta \right) \right)\subset {{W}_{o}} \\ \end{matrix} \\ & \Phi \left( q\left( \beta \right),\dot{q}\left( \text{ }\beta \right),\ddot{q}\left( \beta \right) \right)\theta \le {{\tau }_{max}} \\ \end{align} \right.$ | (7) |
式中:qmin与qmax分别为最小和最大关节位置;$\dot q$max为最大关节速度;$\ddot q$max为最大关节加速度;β为轨迹参数;w(q(β))为末端位置轨迹;Wo为工作空间;τmax为最大关节力矩。
2.2 数据预处理机器人跟踪激励轨迹时,对关节位置与电机电流进行数据采电机电流通过转矩常数转换为电机力矩。由于原始数据存在测量噪声干扰,在辨识实验之前需对采集到的数据进行去噪和平滑处理。本文采用五点三次平滑法[12]对原始数据进行滤波处理,具体表达为
| $\left\{ \begin{array}{*{35}{l}} {{y}_{1}}=\frac{1}{70}\text{ }[69{{y}_{1}}+4({{y}_{2}}+{{y}_{4}})-6{{y}_{3}}-{{y}_{5}}] \\ {{y}_{2}}=\frac{1}{35}[\text{ }2({{y}_{1}}+{{y}_{5}})+27{{y}_{2}}+12{{y}_{3}}-8{{y}_{4}}] \\ {{y}_{i}}=\frac{1}{35}[-3({{y}_{i-2}}+{{y}_{i+2}})+12({{y}_{i-1}}+{{y}_{i+1}})+17\text{ }{{y}_{i}}] \\ {{y}_{m-1}}=\frac{1}{35}\text{ }[2({{y}_{m-4}}+{{y}_{m}})-8{{y}_{m-3}}+12{{y}_{m-2}}+27{{y}_{m-1}}] \\ {{y}_{m}}=\frac{1}{70}[-{{y}_{m-4}}+4({{y}_{m-3}}+{{y}_{m-1}})-6y{{~}_{m-2}}+69{{y}_{m}}] \\ \end{array} \right.$ | (8) |
式中:Y=[y1,y2,…,ym]为原始数据样本;=1,2,…,m为经过预处理后的数据。
这里需指出,对于数据序列反复使用式(8)可得到更加平滑的曲线,但是过多的平滑也会导致原始数据信息的丢失,且越往后重复平滑,改善的效果也不大。预处理后的数据信息损失率一般不应超过10%,故本实验中重复平滑5次[13]。图 2为任意采集的输出力矩滤波前后的对比。
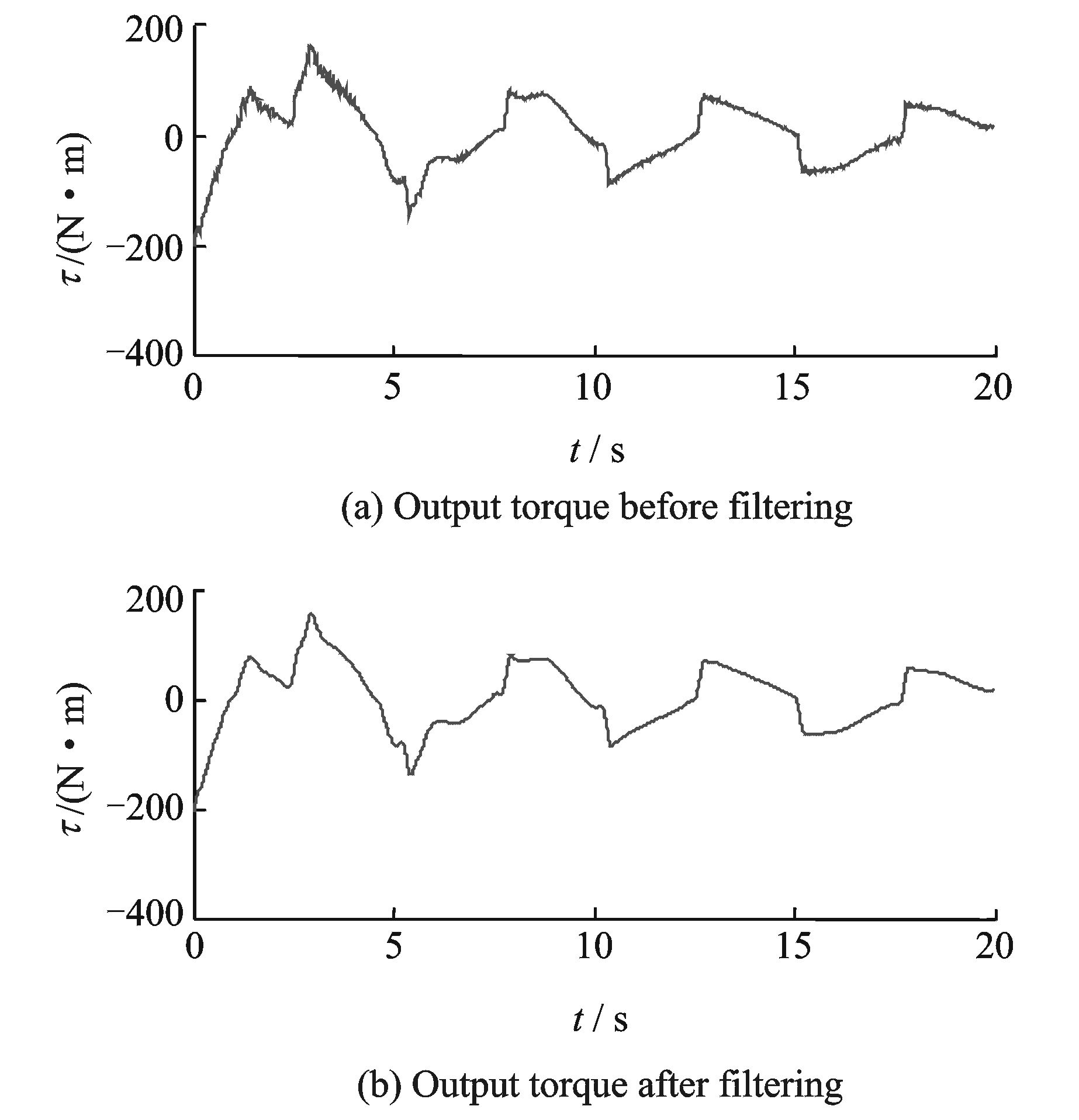
|
图 2 输出力矩滤波前后对比 Figure 2 Comparison of output torque before and after filtering |
机器人跟踪激励轨迹时对关节位置和电机电流进行采集,电机的电流通过转矩常数转换为电机力矩[14]。 由于本文采用的傅里叶级数轨迹具有周期性,因此可以通过对采集的数据进行平均化来提高信噪比,改善数据的质量,即
| $x~\left( k \right)=\frac{1}{M}\sum\limits_{m=1}^{M}{{{x}_{m}}\left( k \right)}$ | (9) |
式中:xm(k)表示第m个周期的第k次采集数据,该数据既可以是关节位置,也可以是关节力矩;(k)表示x的平均化;M为轨迹的采样周期数。对于机器人参数辨识来说,x对应于采集的关节力矩。关节速度和加速度可以采用解析法得到[9]。
2.3 辨识算法机器人重复跟踪激励轨迹时,在N个时间点t1,t2,t3,…,tN(nN>10)对关节位置和电机的力矩进行采样得到超静定线性方程
| ${{\tau }_{N}}\left| \begin{matrix} \tau ({{t}_{1}}) \\ \tau ({{t}_{2}}) \\ \vdots \\ \tau ({{t}_{N}}) \\ \end{matrix} \right|=\left| \begin{matrix} \Phi {{~}_{L}}({{q}_{{{t}_{1}}}},{{{\dot{q}}}_{{{t}_{1}}}},{{{\ddot{q}}}_{{{t}_{1}}}}) \\ {{\Phi }_{L}}({{q}_{{{t}_{2}}}},{{{\dot{q}}}_{{{t}_{2}}}},{{{\ddot{q}}}_{{{t}_{2}}}}) \\ \vdots \\ {{\Phi }_{L}}({{q}_{{{t}_{N}}}},{{{\dot{q}}}_{{{t}_{N}}}},{{{\ddot{q}}}_{t{{~}_{N}}~}}) \\ \end{matrix} \right|{{\theta }_{L}}={{\Phi }_{NL}}{{\theta }_{L}}$ | (10) |
式中:ΦNL为(nN×10)的观测矩阵;τN为(nN×1)的力矩向量,θL为(10×1)的负载惯性参数向量;N为数据采样点个数。
方程(10)是超静定线性方程,本文采用加权最小二乘法来求解该方程,通过对测量力矩噪声协方差的逆矩阵进行加权,从而区分准确和不准确的数据来提高辨识精度。惯性参数θ的加权最小二乘法估计为[15]
| ${{\hat{\theta }}_{L}}={{({{\Phi }^{~}}{{^{T}}_{NL}}{{\Sigma }^{-1}}{{\Phi }_{~}}_{NL})}^{-1}}{{\Phi }^{T}}_{NL}{{\Sigma }^{-1}}{{\tau }_{~}}_{N}$ | (11) |
式中:$\hat{\theta }$L为惯性参数向量的估计值;Σ为(N×N)的力矩协方差矩阵,即加权矩阵。
一般地,通过对比关节力矩的测量值和预测值来验证辨识出的动力学参数的正确性[16]。本文采用力矩测量值与预测值的残差均方根(RMS)来评定参数辨识的精度。
| $RMS=\sqrt{\frac{1}{K}\sum\limits_{k=1}^{K}{{{(\tau \left( k \right)-{{\tau }_{~}}pre\left( k \right))}^{2}}}}$ | (12) |
式中:τ(k)为验证轨迹第k个点的采样力矩;τpre(k) 为第k个点的预测力矩。
3 实验设计与结果分析本实验所用的ER-50六自由度串联机器人如图 3所示。表 1给出了前三关节的D-H参数。这种机器人的最大负载为16 kg,本实验使用10 kg的负载,负载的10个惯性参数可从CAD模型中得到,如图 4所示。

|
图 3 ER-50工业机器人 Figure 3 Industrial robot ER-50 |
| 表 1 ER-50前三关节的D-H参数 Table 1 D-H parameters of joints 1,2,3 of ER-50 |
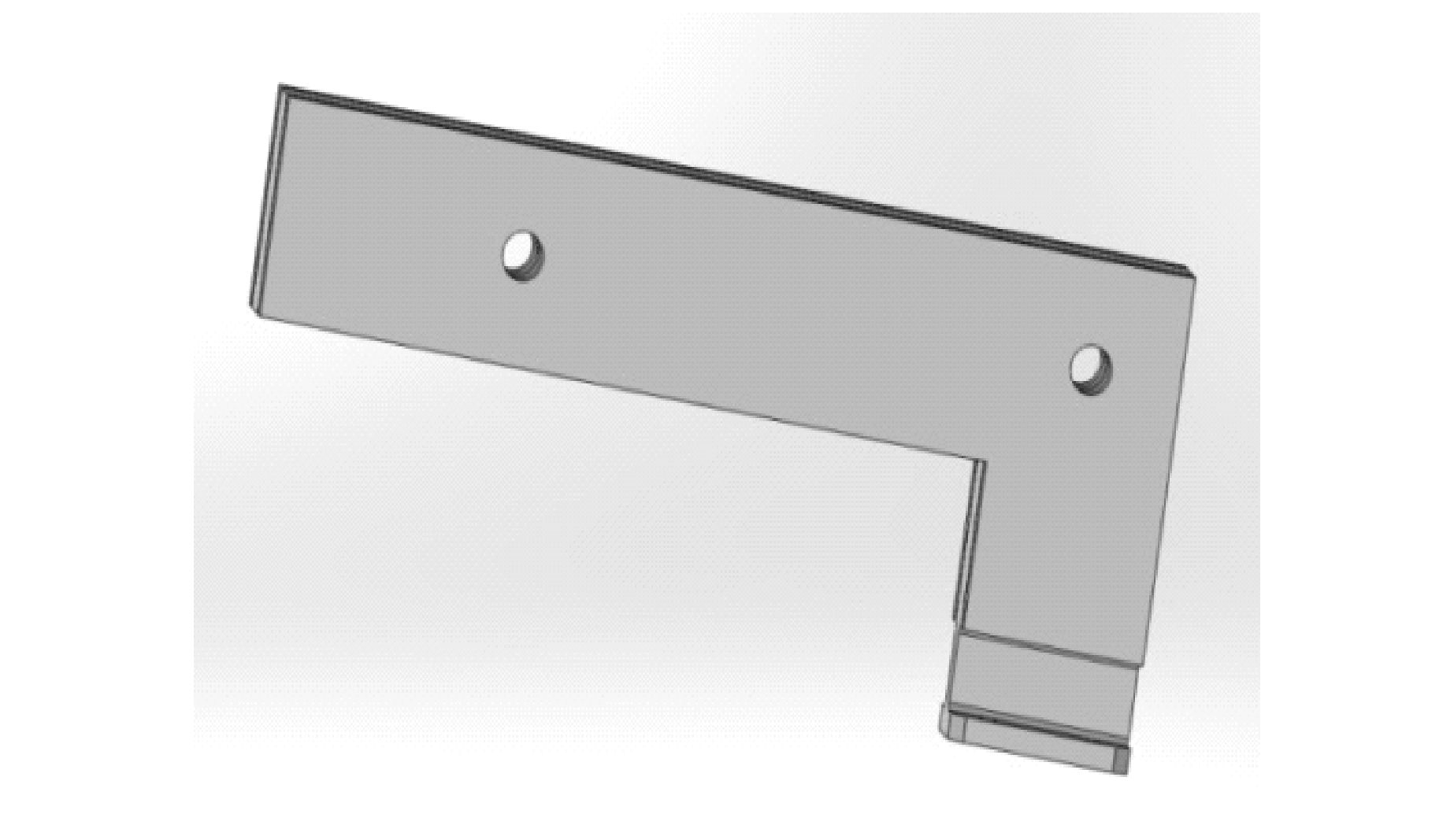
|
图 4 负载的CAD模型 Figure 4 CAD model of payload |
通常,使用腕关节运动来实现负载辨识,但是由于本文所使用6自由度串联机器人后3个关节有较明显的耦合,且力矩测量值有很大的波动,后3个关节在实验过程中相对连杆3静止,故选用前3个关节来辨识负载惯性参数值。前3个关节的激励轨迹是基频为0.05 Hz,带宽为0.25 Hz的5阶傅里叶级数,如图 5所示。机器人连续跟踪50个周期的激励轨迹,整个实验的采样频率为1 kHz,在一个周期(T=20 s)内每10个采样点记录1组关节位置与电机电流,共计2 000组信号作为辨识所需的原始数据。
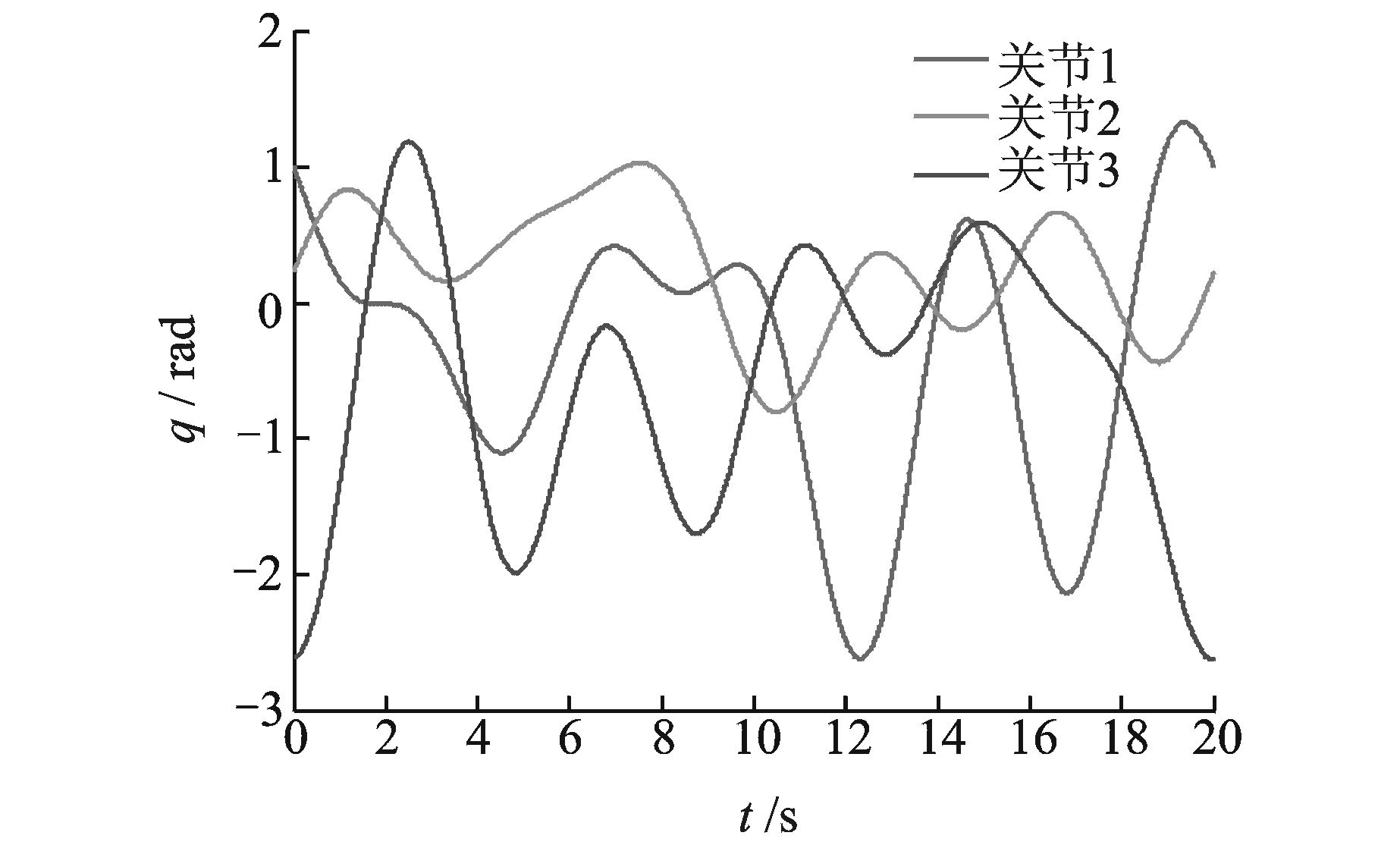
|
图 5 前3个关节的激励轨迹 Figure 5 Exciting trajectory of joints 1,2,3 |
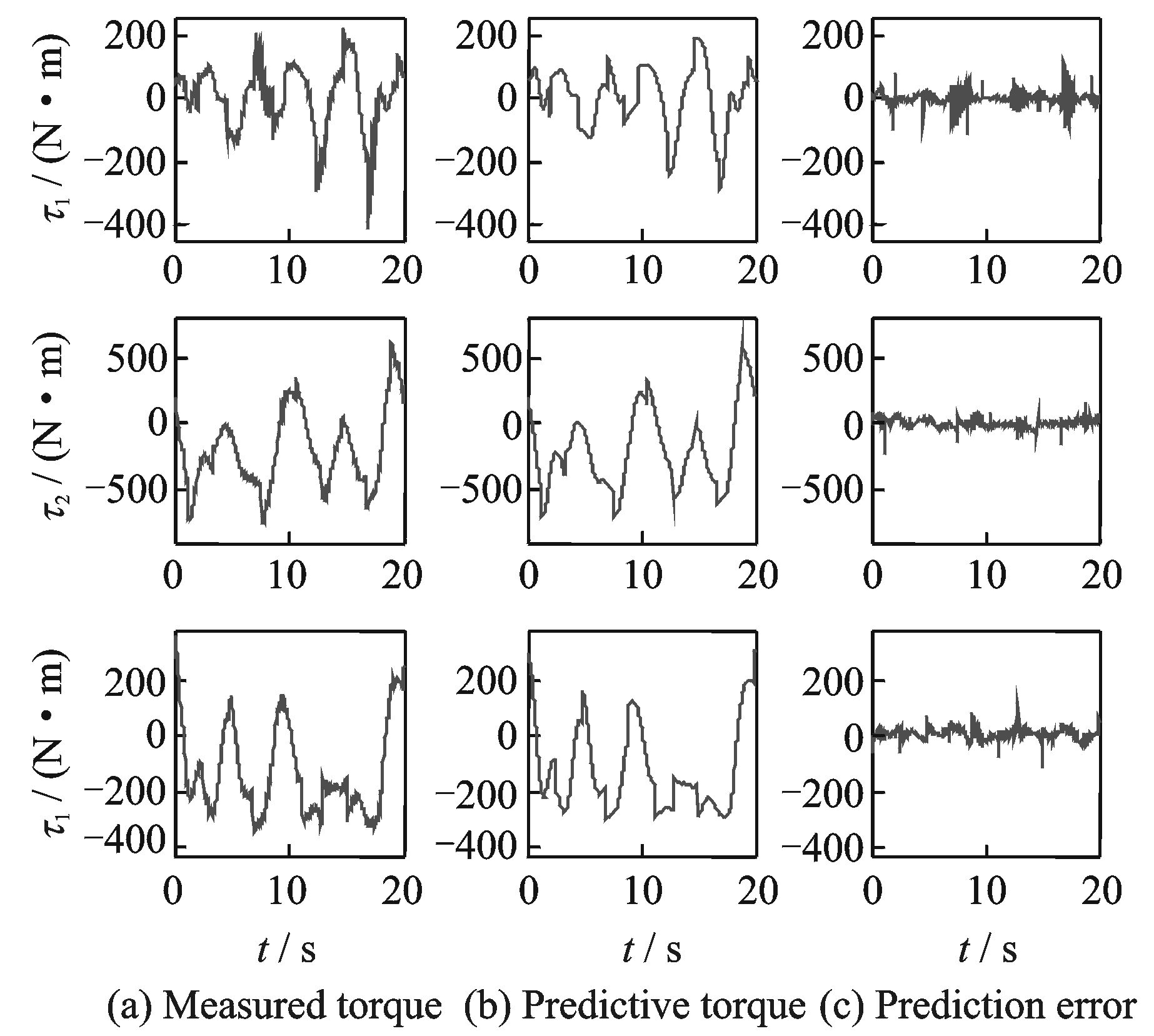
图 6为带负载的前3 个关节的测量力矩、预测力矩和力矩预测误差。从图 6中可以看出,每个关节的预测力矩对测量力矩均有较好的跟随性,且误差维持在±50 N·m内,说明所辨识的模型有较高的精度。
|
图 6 前3关节的测量值与预测值 Figure 6 Measured and predicted torque of joints 1,2,3 |
表 2给出了通过测量补偿方法所得的负载模型中惯性参数值的真实值Xreal、辨识值Xident及相对误差er 。相对误差er定义为
| ${{e}_{r}}=\frac{\left| {{X}_{real}}-{{X}_{ident}} \right|}{{{X}_{real}}}\times 100%$ | (13) |
| 表 2 负载惯性参数的真实值与辨识值 Table 2 Real and identification inertia parameters of payload |
表 3给出了前3个关节力矩残差均方根(RMS1)和噪声均方根(RMS2)。可以看由于采用了线性摩擦模型,故在关节换向附近会导致高频振动,从而出现误差峰值,这降低了一个周期内机器人辨识的整体精度。除此之外,两项指标相对于关节力矩均较小,这说明辨识的模型能够准确地预测带负载机器人运动所需力矩。
| 表 3 前3个关节RMS1与RMS2 Table 3 RMS1 and RMS2 of joints 1,2,3 |
影响带负载机器人模型辨识精度的因素有:(1)驱动器力矩常数的不准确。测量电流通过力矩常数转换为力矩,但是这个常数可能不准确;(2)测量中存在噪声误差。虽然用傅里叶级数来设计激励轨迹,但是对于负载来这种降噪效果并不明显;(3)建模误差。建模过程中忽略了电机转子、关节摩擦等;(4 )连杆的选择。本文只选用前3个关节来完成辨识实验,忽略了后3个关节的影响,可能会导致辨识精度的下降。
4 结束语针对工业机器人负载和本体消耗力矩解耦的特性,提出了一种基于完整机器人本体动力学模型辨识的负载辨识方法。通过对已辨识模型进行补偿,并结合加权最小二乘法辨识得到了负载模型。该方法大大简化了辨识模型,降低了辨识难度,更具有针对性。使用该负载辨识方法完成了10 kg负载的辨识实验,实验结果表明:(1)基于辨识结果的力矩预测精度较高,能够很好地反映重载机器人执行运动轨迹时的实时力矩;(2)辨识结果和负载的CAD模型值相符合,个别参数误差偏大,但对力矩预测影响不大,预测精度符合工程应用要求。
| [1] |
申浩宇, 吴洪涛, 丁力, 等.
基于主从任务转化的冗余度机器人避障算法[J]. 机器人, 2014, 36(4): 425–429.
Shen Haoyu, Wu Hongtao, Ding Li, et al. Obstacle avoidance algorithm for redundant robots based on transitioning between the primary and the secondary task[J]. Robot, 2014, 36(4): 425–429. |
| [2] |
耿令波, 陈柏, 吴洪涛.
基于连接组合体方法的关节机器人动力学参数辨识[J]. 中国机械工程, 2014, 25(5): 581–587.
Geng Lingbo, Chen Bai, Wu Hongtao. Identification of articulated robots' dynamics parameters based on linkage-assemblies method[J]. Chinese Journal of Mechanical Engineering, 2014, 25(5): 581–587. |
| [3] | Ranjbar B, Mahmoodi J, Karbasi H, et al. Robot manipulator path planning based on intelligent multi-resolution potential field[J]. International Journal of u-and e-Service, Science and Technology, 2015, 8(1): 11–26. DOI:10.14257/ijunesst |
| [4] | Atkeson C, An C H, Hollerbach J M. Estimation of inertial parameters of manipulator loads and links[J]. The International Journal of Robotics Research, 1986, 5(3): 101–119. DOI:10.1177/027836498600500306 |
| [5] | Gautier M, Khalil W, Restrepo P P. Identification of dynamic parameters of a closed loop robot[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Nagoya: IEEE, 1995:3045-3050. |
| [6] | Kozlowski K R, Dutkiewicz P. Experimental identification of robot and load dynamics[C]//IFAC 13th Triennial World Congress. [S.l.]:IEEE, 1996:397-402. |
| [7] |
丁亚东, 陈柏, 吴洪涛, 等.
一种工业机器人动力学参数的辨识方法[J]. 华南理工大学学报, 2015, 3(43): 49–56.
Ding Yadong, Chen Bai, Wu Hongtao, et al. An identification method of industrial robot's dynamical parameters[J]. Journal of South China University of Technology, 2015, 3(43): 49–56. |
| [8] | Swevers J, Ganseman C, Tukel D B, et al. Optimal robot excitation and identification[J]. IEEE Transactions on Robotics and Automation, 1997, 13(5): 730–740. DOI:10.1109/70.631234 |
| [9] | Calanca A, Capisani L M, Ferrara A, et al. MIMO closed loop identification of an industrial robot[J]. Control Systems Technology, IEEE Transactions on, 2011, 19(5): 1214–1224. DOI:10.1109/TCST.2010.2077294 |
| [10] | Vuong N D, Ang M H. Dynamic model identification for industrial robots[J]. Acta Plolytechnica Hungarica, 2009, 6(5): 51–68. |
| [11] | Qin Z K, Baron L, Birglen L. A new approach to the dynamic parameter identification of robotic manipulators[J]. Robotica, 2010, 28: 539–547. DOI:10.1017/S0263574709990233 |
| [12] | Ding L, Wu H T, Yao Y. Chaotic artificial bee colony algorithm for system identification of a small-scale unmanned helicopter[J]. International Journal of Aerospace Engineering, 2015(1956): 1–11. |
| [13] | Ding L, Wu H, Yao Y, et al. Dynamic model identification for 6-DOF industrial robats[J]. Journal of Robotics, 2015(11): 1–9. |
| [14] | Gautier M. Dynamic identification of robots with power model[C]//Proceedings of the IEEE International Conference on Robotics and Automation. Albuquerque: IEEE, 1997:1922-1927. |
| [15] | Kinsheel A, Taha Z, Deboucha A, et al. Robust least square estimation of the CRS A465 robot arm's dynamic model parameters[J]. Journal of Mechanical Engineering Research, 2012, 4(3): 89–99. |
| [16] | Wu J, Wang J, You Z. An overview of dynamic parameter identification of robots[J]. Robotics and Computer-Integrated Manufacturing, 2010, 26(5): 414–419. DOI:10.1016/j.rcim.2010.03.013 |
 2016, Vol. 48
2016, Vol. 48


