直升机尾传动轴系用于将主减速器输出的功率和运动传递给中间减速器、尾减速器和尾桨,是直升机上最长的传动链,其动力学性能的优劣将对直升机传动系统的整体性能产生重要影响。有害振动特别是共振会加速零部件的损坏,严重时将导致灾难性事故发生。为确保直升机的安全,设计时应保证尾传动轴系的各阶临界转速与其所有工作转速之间留有足够的裕度(一般至少10%以上)。因此,尾传动轴系临界转速的计算与分析是其动力学设计的关键内容之一。
传递矩阵法非常适合分析具有链状结构的系统的振动特性。由于各基本单元的传递矩阵仅由其力学特性所决定,使得其具有矩阵阶次低、计算工作量小的特点[1],且便于考虑各种复杂结构和因素的影响。因此,本文选用传递矩阵法分析尾传动轴系的临界转速。丛家勇等人采用传递矩阵法对尾传动轴系的横向振动固有特性进行了研究[2-4],但是他们均将传动轴等效为多个集中质量与无质量弹簧的组合体。为提高计算精度,哪怕是等截面轴,仍需细分为多个轴段后再进行计算,所以其累积误差较大[5-7]。尾传动轴系中没有大圆盘结构,尾传动轴具有质量连续均匀分布的特点,更适合采用分布质量模型。采用分布质量模型进行临界转速计算时,仅需在轴截面尺寸或单元类型发生变化时进行分段,而无需对等截面轴进行分段[8],简化了建立系统分析模型的过程,减小了计算工作量和累积误差。
本文首先以更具代表性的直升机尾斜轴为研究对象,推导了可以考虑弯矩、横向位移、剪切变形、转动惯量、陀螺力矩和轴向力等因素综合影响的尾传动轴的分布质量传递矩阵;然后,分别推导了膜片联轴器和弹性支承的传递矩阵;紧接着,给出了尾传动轴系临界转速的计算方法;最后,通过实例验证了本文传递矩阵法的正确性和有效性。
1 尾传动轴系主要部件的传递矩阵采用传递矩阵法分析临界转速的核心工作在于建立分析对象的传递矩阵。直升机尾传动轴系由传动轴、法兰盘、联轴器和支承等典型部件组成,故可将其等效为传动轴单元、集中质量单元、圆盘单元、联轴器单元和支承单元等构成的链状结构模型。
1.1 传动轴大多数单旋翼直升机尾传动轴系包含水平轴和尾斜轴。尾斜轴的横向运动可用如图 1所示的坐标系Obxbybzb描述,水平轴的横向运动可用坐标系O1x1y1z1描述。其中,yb与y1重合,xb与x1及zb与z1之间的夹角φ为尾斜轴相对水平轴的倾角。当φ=0时尾斜轴转化为水平轴,即水平轴是尾斜轴的一种特例。

|
图 1 尾传动轴的参考坐标系 Figure 1 Reference coordinated system of tail drive shaft |
考虑弯矩、横向位移、剪切变形、转动惯量、陀螺力矩和轴向力等因素的综合影响时,传动轴的横向振动微分方程为[9]
| $\left\{ \begin{align} & \rho A\frac{{{\partial }^{2}}{{u}_{zb}}}{\partial {{t}^{2}}}-{{F}_{a0}}\frac{{{\partial }^{2}}{{u}_{zb}}}{\partial {{z}_{b}}^{2}}+\kappa \prime GA\left( \frac{\partial {{\theta }_{yb}}}{\partial {{z}_{b}}}-\frac{{{\partial }^{2}}{{u}_{zb}}}{\partial {{z}_{b}}^{2}} \right)=0 \\ & \rho I\frac{{{\partial }^{2}}{{\theta }_{yb}}}{\partial {{t}^{2}}}-2\rho I{{\omega }_{\Phi }}\frac{\partial {{\theta }_{xb}}}{\partial t}-EI\frac{{{\partial }^{2}}{{\theta }_{yb}}}{\partial {{z}_{b}}^{2}}+ \\ & \kappa \prime GA\left( {{\theta }_{yb}}-\frac{\partial {{u}_{zb}}}{\partial {{z}_{b}}} \right)=0 \\ & \rho A\frac{{{\partial }^{2}}{{v}_{zb}}}{\partial {{t}^{2}}}-{{F}_{a0}}\frac{{{\partial }^{2}}{{v}_{zb}}}{\partial {{z}_{b}}^{2}}+\kappa \prime GA\left( \frac{\partial {{\theta }_{yb}}}{\partial {{z}_{b}}}-\frac{{{\partial }^{2}}{{v}_{zb}}}{\partial {{z}_{b}}^{2}} \right)=0 \\ & \rho I\frac{{{\partial }^{2}}{{\theta }_{xb}}}{\partial {{t}^{2}}}-2\rho I{{\omega }_{\Phi }}\frac{\partial {{\theta }_{yb}}}{\partial t}-EI\frac{{{\partial }^{2}}{{\theta }_{yb}}}{\partial {{z}_{b}}^{2}}+ \\ & \kappa \prime GA\left( {{\theta }_{xb}}-\frac{\partial {{v}_{zb}}}{\partial {{z}_{b}}} \right)=0 \\ \end{align} \right.$ | (1) |
式中:ρ,A,ωΦ分别为传动轴的密度、截面积和转速;I为轴截面关于中性轴的惯性矩;E,G分别为材料的弹性模量和剪切弹性模量;uzb,vzb分别为距传动轴左端面zb处的轴截面几何中心沿坐标轴xb,yb的位移;θyb,θxb分别为传动轴在平面xbOzb和ybOzb内的转角;t为时间;Fa0为轴向力;κ′为轴截面的剪切形状系数。对于空心轴,κ′的计算公式为[10]
| $\kappa \prime =\frac{6\left( 1+{{\upsilon }^{2}} \right){{\left( 1+{{a}^{2}} \right)}^{2}}}{\left( 7+12\upsilon +4{{\upsilon }^{2}} \right){{\left( 1+{{a}^{2}} \right)}^{2}}+4{{a}^{2}}\left( 5+6\upsilon +2{{\upsilon }^{2}} \right)}$ | (2) |
式中:υ为材料的泊松比;a为传动轴内外半径之比。
从式(1) 中消去θxb和θyb后,得到关于uzb和vzb的耦合方程;同样,消去uzb和vzb后,可得到关于θxb和θyb的耦合方程;然后令w=uzb+ivzb和$\vartheta $=θyb-iθxb(i为虚数单位),得到传动轴的横向弯曲自由振动控制方程为
| $\left\{ \begin{align} & \rho A\frac{{{\partial }^{2}}w}{\partial {{t}^{2}}}-{{F}_{a0}}\frac{{{\partial }^{2}}w}{\partial z_{b}^{2}}+EI\left( 1+\frac{{{F}_{a0}}}{\kappa \prime GA} \right)\frac{{{\partial }^{4}}w}{\partial z_{b}^{4}}- \\ & \rho I\left( 1+\frac{E}{\kappa \prime G}+\frac{{{F}_{a0}}}{\kappa \prime GA} \right)\frac{{{\partial }^{4}}w}{\partial z_{b}^{2}\partial {{t}^{2}}}+ \\ & \frac{{{\rho }^{2}}I}{\kappa \prime G}\frac{{{\partial }^{4}}w}{\partial {{t}^{4}}}+i2\rho I{{\omega }_{\Phi }}\left( 1+\frac{{{F}_{a0}}}{\kappa \prime GA} \right)\frac{{{\partial }^{3}}w}{\partial z_{b}^{2}\partial t}- \\ & i\frac{2{{\rho }^{2}}I{{\omega }_{\Phi }}}{\kappa \prime G}\frac{{{\partial }^{3}}w}{\partial {{t}^{3}}}=0 \\ & \rho A\frac{{{\partial }^{2}}\vartheta }{\partial {{t}^{2}}}-{{F}_{a0}}\frac{{{\partial }^{2}}\vartheta }{\partial z_{b}^{2}}+EI\left( 1+\frac{{{F}_{a0}}}{\kappa \prime GA} \right)\frac{{{\partial }^{4}}\vartheta }{\partial z_{b}^{4}}- \\ & \rho I\left( 1+\frac{E}{\kappa \prime G}+\frac{{{F}_{a0}}}{\kappa \prime GA} \right)\frac{{{\partial }^{4}}\vartheta }{\partial z_{b}^{2}\partial {{t}^{2}}}+ \\ & \frac{{{\rho }^{2}}I}{\kappa \prime G}\frac{{{\partial }^{4}}\vartheta }{\partial {{t}^{4}}}+i2\rho I{{\omega }_{\Phi }}\left( 1+\frac{{{F}_{a0}}}{\kappa \prime GA} \right)\frac{{{\partial }^{3}}\vartheta }{\partial z_{b}^{2}\partial t}- \\ & i\frac{2{{\rho }^{2}}I{{\omega }_{\Phi }}}{\kappa \prime G}\frac{{{\partial }^{3}}\vartheta }{\partial {{t}^{3}}}=0 \\ \end{align} \right.$ | (3) |
利用分离变量法[11]求得式(3) 中位移w和转角$\vartheta $的解后,代入弯矩Mzb=Myb-iMxb和剪力Qzb=Qxb+iQyb中,根据传动轴起始端(zb=0) 的状态向量,即可推导出传动轴左右两端状态向量之间的关系为
| $\begin{align} & \left[ \begin{matrix} w\left( {{z}_{b}} \right) \\ \vartheta \left( {{z}_{b}} \right) \\ {{M}_{zb}}\left( {{z}_{b}} \right) \\ {{Q}_{zb}}\left( {{z}_{b}} \right) \\ \end{matrix} \right]=\left[ \begin{matrix} {{t}_{11}} & {{t}_{12}} & {{t}_{13}} & {{t}_{14}} \\ {{t}_{21}} & {{t}_{22}} & {{t}_{23}} & {{t}_{24}} \\ {{t}_{31}} & {{t}_{32}} & {{t}_{33}} & {{t}_{34}} \\ {{t}_{41}} & {{t}_{42}} & {{t}_{43}} & {{t}_{44}} \\ \end{matrix} \right]\left[ \begin{matrix} w\left( 0 \right) \\ \vartheta \left( 0 \right) \\ {{M}_{zb}}\left( 0 \right) \\ {{Q}_{zb}}\left( 0 \right) \\ \end{matrix} \right]= \\ & T\left[ \begin{matrix} w\left( 0 \right) \\ \vartheta \left( 0 \right) \\ {{M}_{zb}}\left( 0 \right) \\ {{Q}_{zb}}\left( 0 \right) \\ \end{matrix} \right] \\ \end{align}$ | (4) |
式(4) 中的方阵T为传动轴任意截面位置zb相对于其初始截面位置的传递矩阵,其表达式为
| $\begin{align} & T= \\ & \left[ \begin{matrix} cos{{\beta }_{1}}{{z}_{b}} & sin{{\beta }_{1}}{{z}_{b}} & cosh{{\beta }_{2}}{{z}_{b}} & sinh{{\beta }_{2}}{{z}_{b}} \\ {{b}_{0}}sin{{\beta }_{1}}{{z}_{b}} & -{{b}_{0}}cos{{\beta }_{1}}{{z}_{b}} & {{a}_{0}}sinh{{\beta }_{2}}{{z}_{b}} & {{a}_{0}}cosh{{\beta }_{2}}{{z}_{b}} \\ EI{{b}_{0}}{{\beta }_{1}}cos{{\beta }_{1}}{{z}_{b}} & EI{{b}_{0}}{{\beta }_{1}}sin{{\beta }_{1}}{{z}_{b}} & EI{{a}_{0}}{{\beta }_{2}}cosh{{\beta }_{2}}{{z}_{b}} & EI{{a}_{0}}{{\beta }_{2}}sinh{{\beta }_{2}}{{z}_{b}} \\ \kappa \prime GA{{B}_{0}}sin{{\beta }_{1}}{{z}_{b}} & -\kappa \prime GA{{B}_{0}}cos{{\beta }_{1}}{{z}_{b}} & \kappa \prime GA{{A}_{0}}sinh{{\beta }_{2}}{{z}_{b}} & \kappa \prime GA{{A}_{0}}cosh{{\beta }_{2}}{{z}_{b}} \\ \end{matrix} \right] \\ & \left[ \begin{matrix} {{A}_{1}} \\ {{A}_{2}} \\ {{A}_{3}} \\ {{A}_{4}} \\ \end{matrix} \right] \\ \end{align}$ | (5) |
式中
| $\begin{align} & \left[ \begin{matrix} {{A}_{1}} \\ {{A}_{2}} \\ {{A}_{3}} \\ {{A}_{4}} \\ \end{matrix} \right]=\left[ \begin{matrix} \frac{{{a}_{0}}{{\beta }_{2}}}{B} & 0 & \frac{1}{EIB} & 0 \\ 0 & \frac{{{A}_{0}}}{D} & 0 & -\frac{{{a}_{0}}}{\kappa \prime GAD} \\ -\frac{{{b}_{0}}{{\beta }_{1}}}{B} & 0 & \frac{1}{EIB} & 0 \\ 0 & \frac{{{B}_{0}}}{D} & 0 & -\frac{{{b}_{0}}}{\kappa \prime GAD} \\ \end{matrix} \right] \\ & {{A}_{0}}={{a}_{0}}-{{\beta }_{2}},{{B}_{0}}={{b}_{0}}+{{\beta }_{1}},B={{a}_{0}}{{\beta }_{2}}-{{b}_{0}}{{\beta }_{1}}, \\ & D={{a}_{0}}{{\beta }_{1}}+{{b}_{0}}{{\beta }_{2}},{{a}_{0}}=\frac{\rho {{\omega }^{2}}}{\kappa \prime G{{\beta }_{2}}}+{{\beta }_{2}}+\frac{{{F}_{a0}}}{\kappa \prime GA}{{\beta }_{2}}, \\ & {{b}_{0}}=\frac{\rho {{\omega }^{2}}}{\kappa \prime G{{\beta }_{1}}}-{{\beta }_{1}}-\frac{{{F}_{a0}}}{\kappa \prime GA{{\beta }_{1}}},{{\beta }_{1}}=\sqrt{\frac{F+\sqrt{{{F}^{2}}-4H}}{2}}, \\ & {{\beta }_{2}}=\sqrt{\frac{F-\sqrt{{{F}^{2}}-4H}}{2}} \\ \end{align}$ |
设任意一段轴的长度和传递矩阵分别为lj和Tsj(j=1,2,…,n),则只需将式(5) 中T的zb替换成lj即可。
1.2 联轴器尾传动轴之间通过膜片联轴器相连,联轴器通过螺栓固定在两端的连接法兰上。可将连接法兰等效为圆盘单元(其传递矩阵见1.3节),将联轴器等效为两端具有集中质量(考虑其转动惯量影响时则需等效为圆盘单元)、中间为角向刚度和径向刚度的力学单元。根据弹性联轴器左右两端状态向量之间的传递关系,推导出膜片联轴器的传递矩阵为
| ${{T}_{j}}=\left[ \begin{matrix} \frac{{{m}_{j}}{{\omega }^{2}}}{2{{k}_{c,j}}}+1 & 0 & 0 & \frac{1}{{{k}_{c,j}}} \\ 0 & 1 & \frac{1}{{{k}_{a,j}}} & 0 \\ 0 & 0 & 1 & 0 \\ {{m}_{j}}{{\omega }^{2}}+\frac{{{\left( {{m}_{j}}\omega \right)}^{2}}}{4{{k}_{c,j}}} & 0 & 0 & \frac{{{m}_{j}}{{\omega }^{2}}}{2{{k}_{c,j}}}+1 \\ \end{matrix} \right]$ | (6) |
式中:m为膜片、螺栓和垫片等部件的等效质量;ka,j和kc,j分别为第j个联轴器的角向刚度和径向刚度,ω为进动角速度。令式(6) 中的角向刚度ka,j和径向刚度kc,j为0,则得到集中质量单元的传递矩阵。
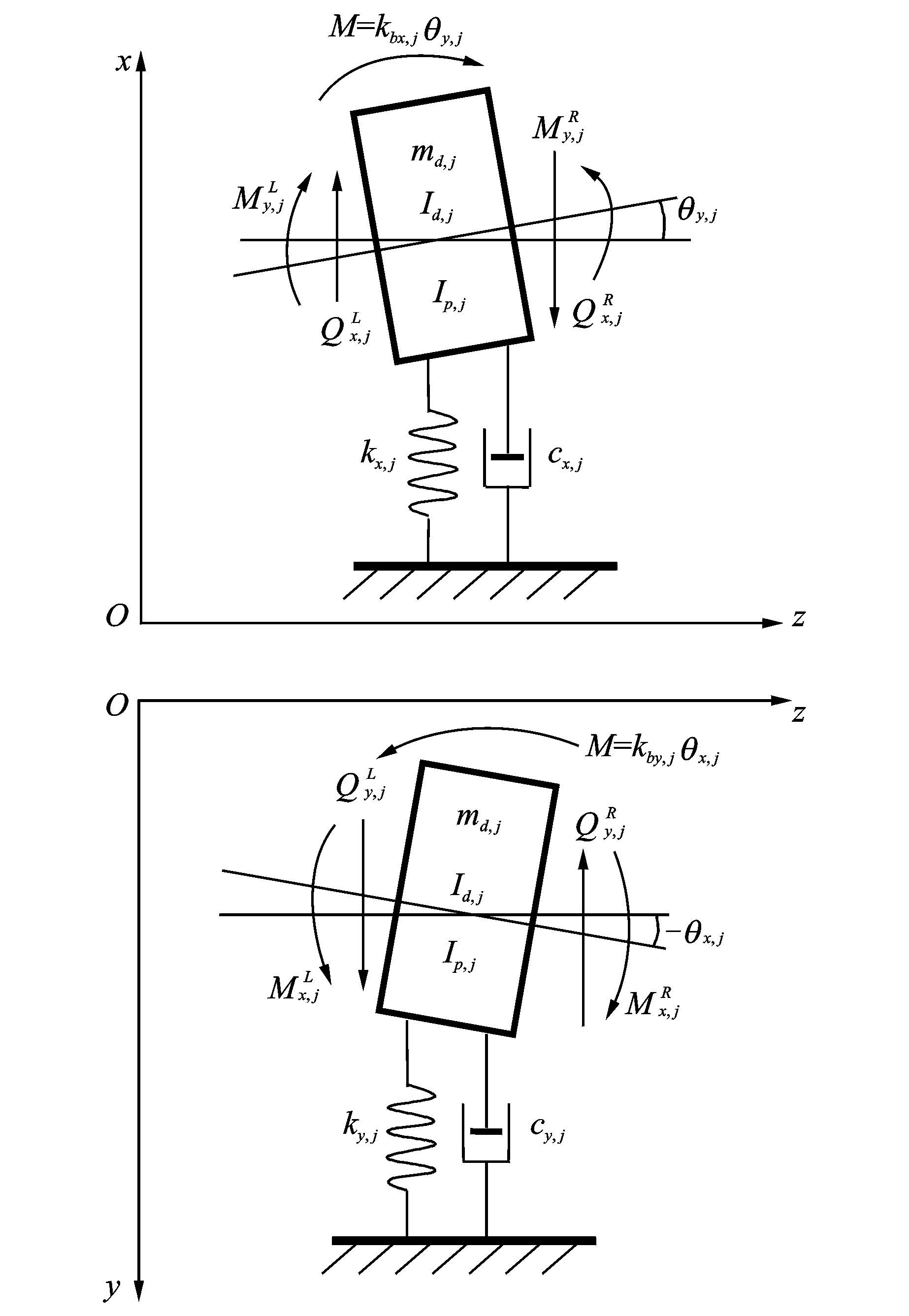
1.3 支承若轴承与轴承座刚度的量级与传动轴相当,则需将其视为弹性支承(本文将刚性支承当作刚度无限大的弹性支承处理)。若轴承座为刚性,则支承刚度仅由轴承提供。直升机服役时,尾传动轴系除对轴承产生径向载荷外还会作用一个弯矩,使得轴承的内外圈之间除了产生径向位移外还产生相对转角。所以,轴承除了提供径向刚度kr外还提供角向刚度kb(弯曲刚度)。鉴于通用性的考虑,将支承系统简化为支撑在弹性和阻尼元件上的圆盘单元,其受力关系如图 2所示。经推导,支承单元的传递矩阵为
| ${{T}_{j}}=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0{{k}_{b,j}}+\left( {{I}_{p,j}}{{\omega }_{\varphi }}-{{I}_{d,j}}\omega \right)\omega & 1 & 0 \\ {{m}_{d,j}}{{\omega }^{2}}-i{{c}_{r,j}}\omega -{{k}_{r,j}} & 0 & 0 & 1 \\ \end{matrix} \right]$ | (7) |
式中:md,j,Ip,j和Id,j分别为第j个支承的等效圆盘的集中质量(包括轴承、轴承座和转轴的参振质量)、极转动惯量和直径转动惯量;cr,j为第j个支承的等效阻尼。令式(7) 中支承的刚度和阻尼为0,则得到圆盘的传递矩阵。
|
图 2 具有圆盘的弹性支承系统的力学模型 Figure 2 Mechanical model of elastic supporting system carrying disc |
2 临界转速计算方法
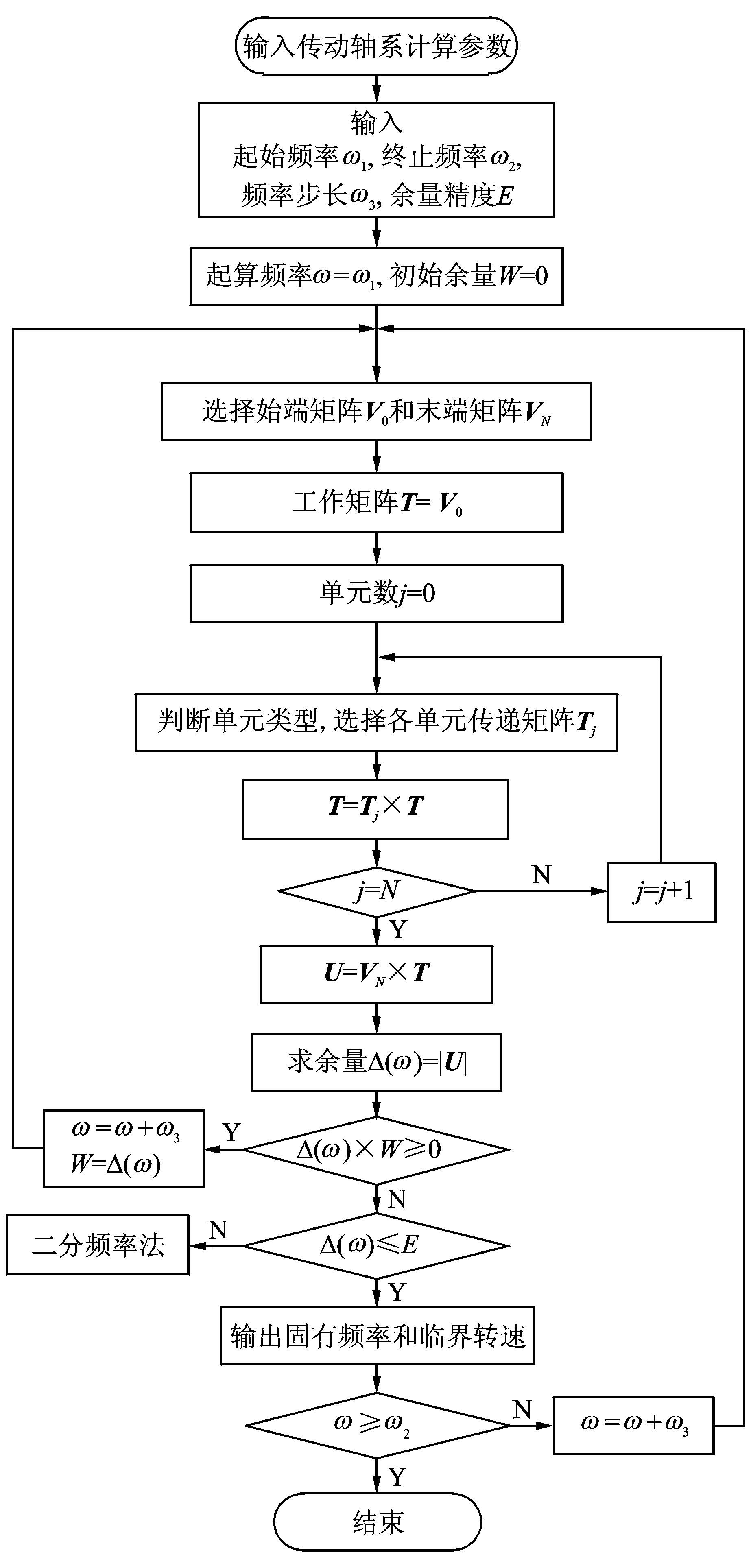
由上节推导的传递矩阵建立尾传动轴系首末两端状态向量之间的传递关系,根据系统两端支承的边界条件推导出其频率方程,在给定的频率范围内,对满足所有边界条件的进动频率进行搜索,所得结果即为待求的临界转速。基于传递矩阵法的尾传动轴系临界转速计算流程如图 3所示[12],其中,常见支承条件下的始端矩阵V0和末端矩阵VN见表 1。
|
图 3 传动轴系临界转速的传递矩阵法计算流程 Figure 3 Calculation flow chart of transfer matrix method for critical speed of drive shaft system |
| 表 1 常见支承条件下的始端矩阵V0和末端矩阵VN Table 1 Initial matrix V0 and terminal matrix VN under common supporting condition |
当待求解的临界转速数值过大或者传递矩阵的数目过多时,受计算机字长限制,传统传递矩阵法的累积误差较大,计算精度将大幅度降低,甚至存在漏根现象。采用改进的Riccati传递矩阵法可以提高计算的数值稳定性和精度,其频率方程的具体推导过程可参见文献[13]。由于本文不存在此种情况,故不再骜述。
传动轴的涡动有正向进动与反向进动之分,其临界转速亦如此。令各部件传递矩阵中的ωΦ=ω,所得结果即为正向同步进动时的临界转速;若令ωΦ=-ω,则为反向同步进动临界转速。由于正进动更常见,且对应于传动轴偏心激励下可能激发的临界转速[14],本文取ωΦ=ω。
3 计算与分析传动轴采用超临界设计可以减少支承数量,对减重十分有利。某直升机水平传动轴系超临界方案由两段轴、3个膜片联轴器和3个支承组成(额定工作转速为4 115 r/min),其简化分析模型如图 4所示。

|
图 4 水平传动轴系的简化计算模型 Figure 4 Simplified calculation model of horizontal drive shaft system |
水平轴系的主要计算参数如表 2所示。由于水平轴系采用滚动轴承,阻尼很小,故本文忽略其影响。为优化水平轴系的设计参数(轴长l2和l3),对其进行多方案设计,3种方案的轴长l2和l3取值见表 3。
| 表 2 水平传动轴系的计算参数 Table 2 Calculation parameters of horizontal drive shaft system |
| 表 3 水平传动轴系临界转速的计算结果 Table 3 Calculation results of critical speed of horizontal drive shaft system |
分别采用本文传递矩阵法和有限元法(SAMCEF分析软件)对该水平传动轴系的临界转速进行计算分析,计算结果的对比情况如表 3所示。表中的误差定义如下
| $误差=\left| \frac{本文传递矩阵法计算结果-有限元法计算结果}{本文传递矩阵法计算结果} \right|\times 100%$ | (8) |
由于有限元法充分考虑了联轴器、法兰盘和支承等细节的影响,所以本文传递矩阵法的计算结果与之相比存在一定误差。由表 2可知,第二阶临界转速的计算误差最大,最大值为4.1%。然而,有限元法的计算精度取决于有限元网格模型的好坏,需要专业的分析人员才能胜任,且计算工作量大,对计算机性能要求高,时间成本高。本文传递矩阵法的计算结果虽然有误差,但只要合理简化分析模型,完全能满足设计人员在方案设计阶段的计算精度要求。本文传递矩阵法易于掌握,计算速度快,设计人员可以快速分析各影响因素对传动轴系临界转速的影响规律,从而获得最优的设计方案,加快研制进度。
尾斜轴的重力会对其产生轴向力分量,中间减速器和尾减速器均采用螺旋锥齿轮传动,也会对传动轴产生轴向力,对传动轴的临界转速有一定的影响。本文推导的传动轴传递矩阵可以考虑轴向力的影响,能分析外力对尾传动轴系临界转速的影响。
4 结论本文研究了基于分布质量轴模型的尾传动轴系临界转速分析方法,主要工作及成果如下:
(1) 对尾传动轴系的结构特点进行了分析,将其等效为传动轴单元、集中质量单元、圆盘单元、联轴器单元和支承单元等构成的链状结构模型。
(2) 建立了尾斜轴的分布质量传递矩阵模型,模型中考虑了弯矩、横向位移、剪切变形、转动惯量、陀螺力矩和轴向力等因素对传动轴横向运动的综合影响。
(3) 建立了膜片联轴器单元和弹性支承单元的传递矩阵模型,同时将集中质量单元看成膜片联轴器单元的一种特例,将圆盘单元看成弹性支承单元的一种特例。
(4) 在上述传递矩阵模型的基础上,编制了尾传动轴系临界转速的计算程序,并以三支点传动轴系为实例对象,对比了本文传递矩阵法与有限元法分析结果的计算精度。本文传递矩阵法相对于有限元法的最大计算误差为4.1%,其计算精度较高,计算速度快,易于程序化,结合灵敏度分析,可以快速获得尾传动轴系临界转速对各影响因素的敏感度。
| [1] | Ma Lei, Rui Xiaoting, Abbas Laith, et al. Free vibration analysis and physical parameter identification of non-uniform beam carrying[J]. Transactions of Nanjing University of Aeronauties and Astronautics, 2012, 29(4): 345–353. |
| [2] |
丛家勇.直升机尾传动系统的动力学分析[D].南京:南京航空航天大学,2008.
Cong Jiayong. Dynamic analysis for helicopter tail rotor transmission system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2008. |
| [3] |
艾平贵.直升机尾传动系统的横向振动和扭转振动分析[D]. 南京:南京航空航天大学, 2009.
Ai Pinggui. Analysis of lateral vibration and torsional vibration of helicopter tail drive system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009. |
| [4] |
朱自冰.直升机尾传动系统动力学关键问题研究[D].南京:南京航空航天大学, 2012.
Zhu Zibing. Research on key problems of dynamics of helicopter tail-drive transmission system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. |
| [5] | Wu J S, Chen C T. A continuous-mass TMM for free vibration analysis of a non-uniform beam with various boundary conditions and carrying multiple concentrated elements[J]. Journal of Sound and Vibration, 2008, 311(3/4/5): 1420–1430. |
| [6] | Wu J S, Chen C T. A lumped-mass TMM for free vibration analysis of a multiple-step beam carrying eccentric tip masses with rotary inertias[J]. Journal of Sound and Vibration, 2007, 301(3/4/5): 878–897. |
| [7] | Aleyaasin M, Ebrahimi M, Whalley R. Vibration analysis of distributed-lumped rotor systems[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 189(2): 545–558. DOI:10.1016/S0045-7825(99)00308-4 |
| [8] |
张小龙, 何洪庆.
涡轮泵转子的临界转速研究(Ⅳ)分布质量轴的传递矩阵法[J]. 推进技术, 2000, 21(2): 52–55.
Zhang Xiaolong, He Hongqing. Critical rotational speed of turbo pump rotor(IV) transfer matrix method for the distributed mass shaft[J]. Journal of Propulsion Technology, 2000, 21(2): 52–55. |
| [9] |
倪德, 朱如鹏, 陆凤霞, 等.
考虑空间机动飞行的直升机尾传动轴建模与临界转速分析[J]. 航空动力学报, 2015, 30(6): 1520–1528.
Ni De, Zhu Rupeng, Lu Fengxia, et al. Modeling and analysis of critical speed for tail drive shaft of the helicopter considering space maneuvering flight[J]. Journal of Aerospace Power, 2015, 30(6): 1520–1528. |
| [10] | Hutchinson J R. Shear coefficients for timoshenko beam theory[J]. Journal of Applied Mechanics, 2001, 68(1): 87–92. DOI:10.1115/1.1349417 |
| [11] | Rao S S. Mechanical vibrations[M]. Fourth Edition. New Jersey: Pearson Education Inc, 2004:249-253. |
| [12] | 屈维德, 唐恒龄. 机械振动手册[M]. 北京: 机械工业出版社, 2000. |
| [13] |
周瑞, 李宁, 鲍利群, 等.
基于分布质量轴模型的回旋振动计算方法[J]. 船舶力学, 2013, 17(8): 931–936.
Zhou Rui, Li Ning, Bao Liqun, et al. Calculation method of whirling vibration based on the distributed mass shaft model[J]. Journal of Ship Mechanica, 2013, 17(8): 931–936. |
| [14] | Lalanne M, Ferraris G. Rotordynamics prediction in engineering[M]. 2nd Edition. New York: John Wiley & Sons Ltd, 1998. |
 2016, Vol. 48
2016, Vol. 48


