2. 陕西省机电传动与控制工程实验室, 西安, 710072
2. Shaanxi Engineering Laboratory for Transmissions and Controls, Xi′an, 710072, China
功率分流传动系统使用两条(或以上)支路并行地传递功率。得益于所具有的大传动比、高可靠性、低噪声、低重量等特点[1-2],该系统目前被广泛应用于航空、船舶等领域。
确保载荷在各支路均匀分配是功率分流传动系统设计中需解决的关键问题[3-5]。Kahraman等[4-6]通过系统动力学方法对行星轮系的均载特性进行了研究;Krantz[3]最先关注功率分流传动系统的均载问题。在上述文献中,作者通过均载系数来度量传动系统的均载能力。同时,Kahraman等[5-6]对存在于行星轮传动系统中的误差进行了分类,并研究了这些误差与系统均载系数的关系,指出零部件的安装误差对系统均载情况的影响最为显著。Dong 等[7-8]引入统计分析的方法研究了零部件误差对系统均载特性的影响。
已有文献的研究内容主要集中在系统存在的各种误差对其均载性能的影响,但较少提及如何根据分析计算结果指导功率分流传动系统的设计。虽然误差是导致不均载最主要的原因[3],但该传动系统结构参数也会对均载性能有相当程度的影响[5]。本文基于集中质量法建立了功率分流传动系统的动力模型;定义了均载系数来衡量系统的均载能力;研究了齿轮啮合刚度、啮合误差、安装误差和耦合刚度对均载系数的影响,并根据对结果的分析提出了可以提高系统均载能力的若干方式。
1 系统动力学模型功率分流传动系统如图 1所示。该系统使用了两级传动,图 1中同时与两个直齿轮啮合的小齿轮为功率输入端;输出端为大人字齿轮,由两个小人字齿轮共同驱动;分布在左右侧的两个传动轴及其上的齿轮、轴承等零部件具有完全一致的结构。
|
图 1 功率分流齿轮传动系统结构图 Figure 1 Structure of split path transmission system |
图 2为该传动系统简图,用以定义功率流动方向并对齿轮依次进行编号。在对系统进行动力学建模时,直齿轮被处理为螺旋角为零度的斜齿轮。系统中各齿轮位移(量纲为一)构成如式(1) 所示的向量。
| $x={{\left[ {{x}_{1}},{{y}_{1}},{{z}_{1}},{{u}_{1}},{{x}_{2}},{{y}_{2}},{{z}_{2}},{{u}_{2}},\cdots ,{{x}_{6}},{{y}_{6}},{{z}_{6}},{{u}_{6}} \right]}^{T}}$ | (1) |

|
图 2 功率分流齿轮传动系统坐标系与齿轮副编号 Figure 2 Global coordinate system and indexes of gear pairs for split path transmission system |
一对齿轮的啮合刚度矩阵与方向向量如式(2) 所示(下标i,j表示由齿轮i驱动齿轮j)。
| $\begin{align} & {{K}_{m,ij}}={{k}_{m,ij}}{{q}_{ij}}{{q}_{ij}}^{T} \\ & {{q}_{ij}}=\left[ cos{{\beta }_{ij}}sin{{\varphi }_{ij}},-cos{{\beta }_{ij}}cos{{\varphi }_{ij}},sin{{\beta }_{ij}},cos{{\beta }_{ij}}, \right. \\ & {{\left. -cos{{\beta }_{ij}}sin{{\varphi }_{ij}},cos{{\beta }_{ij}}cos{{\varphi }_{ij}},-sin{{\beta }_{ij}},-cos{{\beta }_{ij}} \right]}^{T}} \\ \end{align}$ | (2) |
式中:km,ij为齿轮时变啮合刚度;φij为Y轴正方向与啮合线正向(从主动轮到从动轮)之间形成的角度;βij为基圆螺旋角。
齿轮间的耦合刚度矩阵可写成
| $~{{K}_{c,ij}}=\left[ \begin{matrix} ~{{k}_{b,ij}} & 0 & 0 & 0 & -{{k}_{b,ij}} & 0 & 0 & 0 \\ {} & {{k}_{b,ij}} & 0 & 0 & 0 & -{{k}_{b,ij}} & 0 & 0 \\ {} & {} & {{k}_{a,ij}} & 0 & 0 & 0 & -{{k}_{a,ij}} & 0 \\ {} & {} & {} & \frac{{{k}_{s,ij}}}{R_{b,i}^{2}} & 0 & 0 & 0 & -\frac{{{k}_{s,ij}}}{{{R}_{b,i}}{{R}_{b,j}}} \\ {} & {} & {} & {} & {{k}_{b,ij}} & 0 & 0 & 0 \\ {} & {} & {} & {} & {} & {{k}_{b,ij}} & 0 & 0 \\ {} & sym & {} & {} & {} & {} & {{k}_{a,ij}} & 0 \\ {} & {} & {} & {} & {} & {} & {} & \frac{{{k}_{s,ij}}}{R_{b,i}^{2}} \\ \end{matrix} \right]$ | (3) |
式中:kb,ij,ka,ij,ks,ij分别为弯曲、拉伸和扭转刚度;Rb,i,Rb,j为齿轮i和j的基圆半径。
一对齿轮的啮合刚度矩阵和耦合刚度矩阵由式(4) 进行组装
| ${{K}_{\bigcirc }}=\sum{R_{_{ij}}^{T}{{K}_{\bigcirc ,ij}}{{R}_{ij}}}$ | (4) |
式中:K○,ij (○ = m,c) 分别为啮合刚度矩阵和耦合刚度矩阵;Rij为装配矩阵,是一个2×6的分块稀疏矩阵,每个子矩阵的尺寸一致,详见式(5,6) 。
| ${{R}_{ij}}=\left[ \begin{matrix} 0 & \cdots & {{R}_{1i}} & \cdots & 0 & \cdots & 0 \\ 0 & \cdots & 0 & \cdots & {{R}_{2i}} & \cdots & 0 \\ \end{matrix} \right]$ | (5) |
| ${{R}_{1i}}={{R}_{2i}}=diag\left( \left[ 1,1,1,1 \right] \right)$ | (6) |
式中j为矩阵的列坐标。
系统动力学微分方程为
| $M\ddot{x}+C\dot{x}+Kx=F-F\left( e \right)-F\left( {\dot{e}} \right)$ | (7) |
式中:总刚度矩阵为齿轮副啮合刚度、耦合刚度与轴承支撑刚度的和,即K=Km+Kc+Kxy;C为阻尼矩阵;M为质量矩阵;F为载荷矩阵;F(e)与F(${\dot{e}}$)分别为弹性力和阻尼扭矩。
| $\left\{ \begin{align} & F\left( e \right)=\sum{R_{_{ij}}^{T}\left( {{k}_{m,ij}}{{e}_{ij}}{{q}_{ij}} \right)} \\ & F\left( {\dot{e}} \right)=\sum{R_{_{ij}}^{T}\left( {{c}_{m,ij}}{{{\dot{e}}}_{ij}}{{q}_{ij}} \right)} \\ \end{align} \right.$ | (8) |
式中:eij为啮合误差;cm,ij为啮合阻尼。
2 系统激励参数计算外部激励与内部激励是齿轮传动系统激振的主要来源,其中外部激励由系统工况决定,下文主要讨论两种内部激励,即齿轮副时变啮合刚度和齿轮副的啮合与安装误差。在本文中,直齿轮与斜齿轮的时变啮合刚度分别由线性规划法和有限元法计算获得[9]。啮合误差和安装误差是影响齿轮啮合状态最主要的因素,其位移关系为
| ${{e}_{ij}}={{e}_{a,ij}}+{{e}_{m,ij}}$ | (9) |
式中:ea,ij为啮合误差;em,ij为安装误差在啮合线上的投影。em,ij可表示为
| ${{e}_{m,ij}}={{e}_{m,i}}sin\left( {{\varphi }_{ij}}-{{\theta }_{m,i}} \right)-{{e}_{m,j}}sin\left( {{\varphi }_{ij}}-{{\theta }_{m,j}} \right)$ | (10) |
式中:em为理论安装位置与实际安装位置的距离差;θm为由安装误差形成的相位角。
3 传动系统参数设置本文研究的功率分流系统输入功率为Pk=100 kW,输入转速n=3 800 r/min. 齿轮副参数列于表 1。
| 表 1 功率分流系统齿轮副参数 Table 1 Parameters of gear pairs for split path transmission system |
根据表 1所示数据,由线性规划法和有限元法计算的直齿轮和斜齿轮的啮合刚度如图 3所示。

|
图 3 齿轮副啮合刚度曲线图 Figure 3 Time-depended meshing stiffness of gear pairs |
4 均载系数的影响因素分析 4.1 均载能力的影响因素与评估方法
本文研究齿轮啮合刚度、啮合误差、安装误差以及耦合刚度对功率分流传动系统均载性能的影响,着重关注此4项影响因素的原因是:(1) 齿轮的啮合刚度是系统总刚度的重要组成部分,其变化将直接影响系统的总刚度,进而改变系统振动特性;(2) 啮合误差是该系统内部动态激励的来源之一,将非线性振动特征引入了该系统;(3) 安装误差广泛存在于各种传动系统中,对于本文所研究的功率分流传动系统,零部件较多,结构复杂,导致误差逐级累积;(4) 耦合刚度表征了两级齿轮传动之间的相互影响,关系到动态激励在系统内部的传递。因此,对齿轮啮合刚度、啮合误差、安装误差以及耦合刚度与系统振动特性的关系进行敏感度分析具有十分重要的意义。
本文着重讨论功率分流齿轮传动系统的均载特性,该特性由均载系数表示,均载系数值越小,系统均载能力越优。均载系数的具体定义为
| ${{k}_{u}}=\frac{\max \left( {{F}_{FWD}},{{A}_{FTT}} \right)}{{{T}_{in}}/2{{r}_{b,S1~}}}$ | (11) |
式中:FFWD和FAFT 为两个传动支路的平均啮合力;Tin为输入扭矩;rb,S1为小齿轮基圆半径。
动态载荷系数反映了系统载荷振幅与理论均载情况下的载荷的关系,定义为
| $\Delta {{k}_{v}}\frac{=max\left( {{F}_{m}} \right)-min\left( {{F}_{m}} \right)}{{{T}_{in}}/2{{r}_{b,S1}}}$ | (12) |
式中Fm为时变动态啮合力。
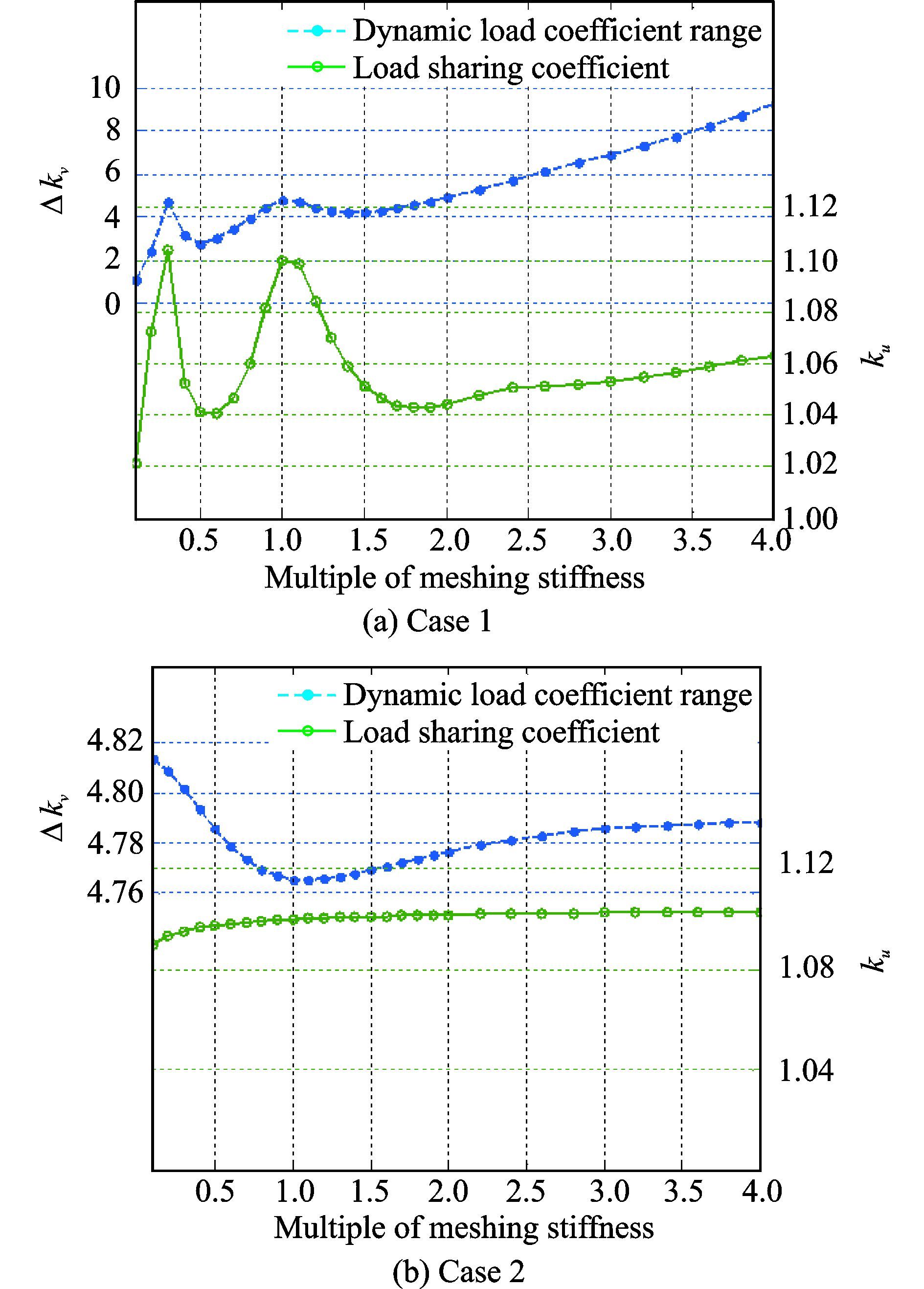
4.2 均载能力影响因素分析为了研究啮合刚度对系统均载性能的影响,对两组算例进行了计算:(1) 第一级齿轮的啮合刚度分别乘以比例因子,从0.1~4.0,第二级齿轮啮合刚度保持不变;(2) 第二级齿轮的啮合刚度分别乘以比例因子,从0.1~4.0,第一级齿轮啮合刚度保持不变。计算结果如图 4所示。
|
图 4 啮合刚度对均载性能的影响分析 Figure 4 Effects of meshing stiffness on load-sharing characteristics |
由图 4(a)可知:(1) 动态载荷系数范围和均载系数对第一级齿轮的啮合刚度较敏感;(2) 随着啮合刚度的上升,动态载荷系数范围上升,意味着更高的第一级齿轮啮合刚度将引起更显著的系统振动;(3) 随着第一级齿轮啮合刚度的上升,均载系数出现了两个峰值。由图 4(b)可知:(1) 动态载荷系数范围和均载系数对第二级齿轮啮合刚度的敏感性不显著;(2) 随着第二级齿轮啮合刚度的上升,动态载荷系数范围先降后升,意味着适当地降低该啮合刚度有利于减轻系统的振动。因此,合理地搭配此二级齿轮副啮合刚度将有助于获得更优的均载特性。
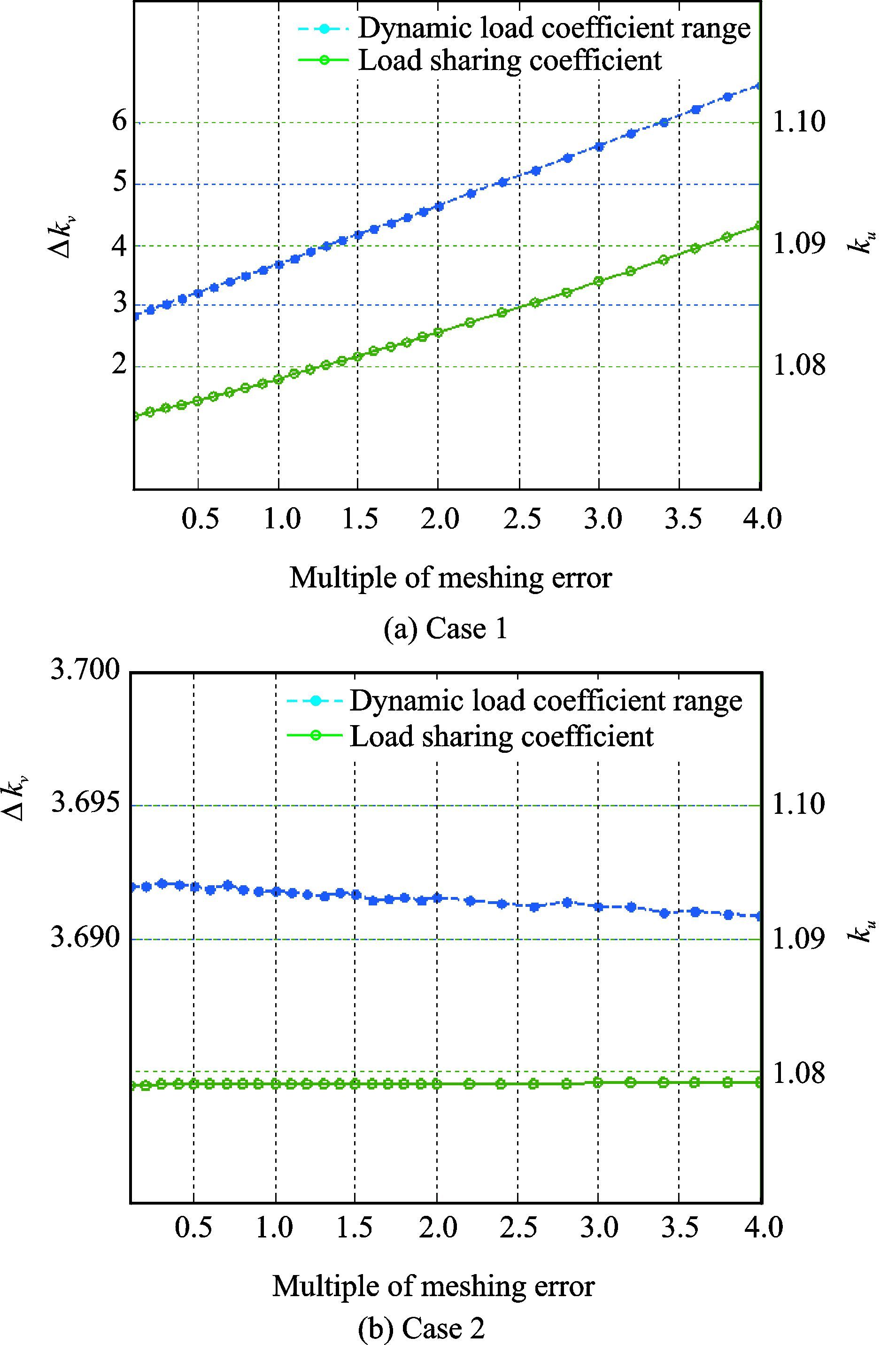
为研究齿轮啮合误差对系统均载性能的影响,对以下两组算例进行了计算:(1) 第一级齿轮啮合误差分别乘以比例因子,从0.1~4.0,第二级齿轮啮合误差保持不变;(2) 第二级齿轮啮合误差分别乘以比例因子,从0.1~4.0,第一级齿轮啮合误差保持不变。计算结果如图 5所示。
|
图 5 啮合误差对均载性能的影响分析 Figure 5 Effects of meshing error on load-sharing characteristics |
由图 5(a)可知:(1) 动态载荷系数范围和均载系数对第一级齿轮啮合误差均比较敏感;(2) 随着第一级齿轮啮合误差的上升,动态载荷系数范围和均载系数均线性上升。由图 5(b)可知:动态载荷系数范围和均载系数对第二级齿轮啮合误差均不敏感,几乎不随啮合误差的变化而变化。由此可知,第一级齿轮加工精度的提高将显著改善系统的振动特性和均载性能;对第二级齿轮加工精度的提高无法获得与之成本匹配的减振、均载效果。
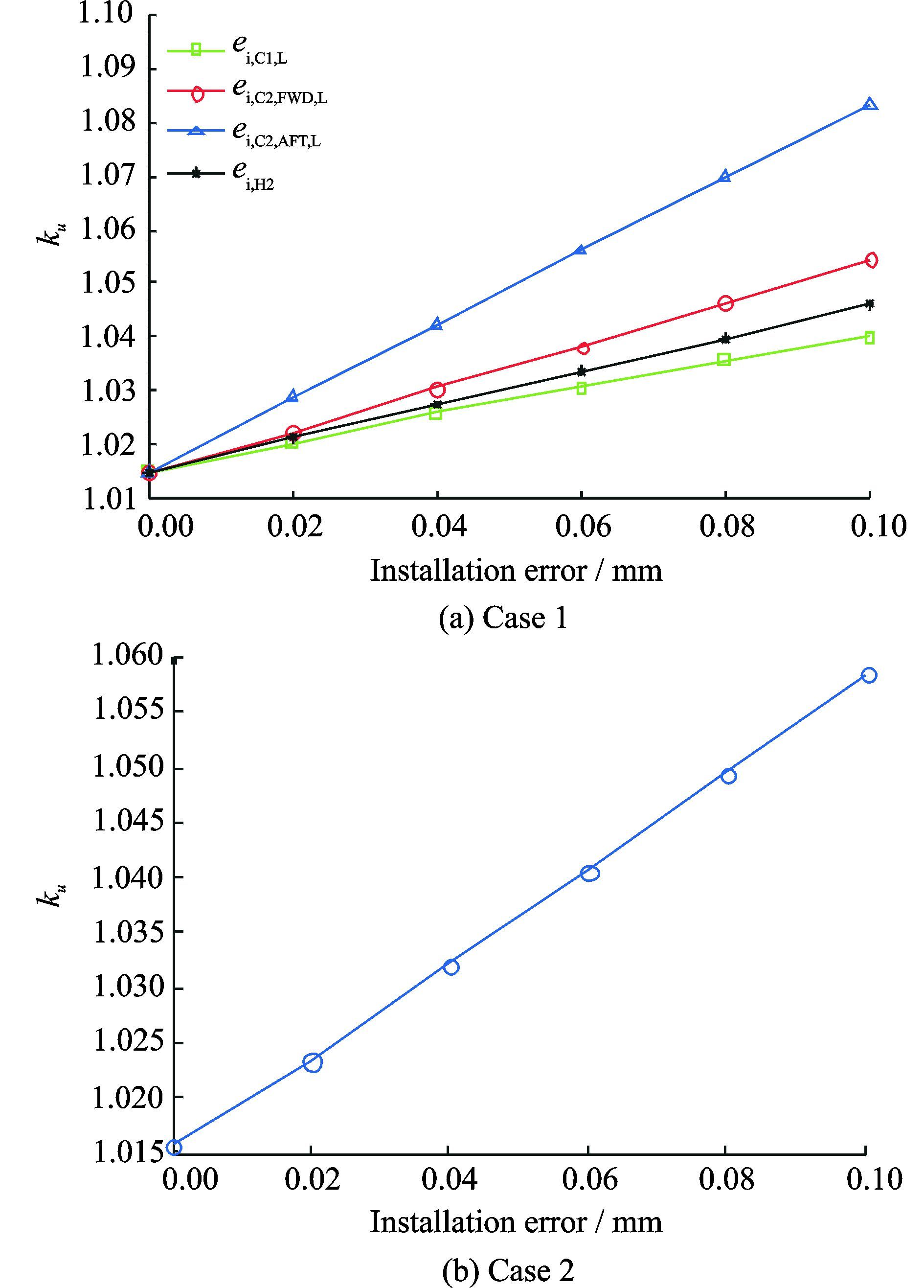
当安装误差分别为0,0.02,0.04,0.06,0.08和0.1 mm时,系统均载系数的变化绘于图 6。图 6(a)为均载系数与某单一部件安装误差的关系;而图 6(b)中,设所有部件具有相同的安装误差。
|
图 6 不同安装误差下的均载系数 Figure 6 Effects of installation error on load-sharing characteristics |
此处安装误差的相位角为0°。当安装误差为0 mm时,仍然不均载,说明功率分流齿轮传动系统是一种非平衡系统,与文献[3]结论一致。
由图 6(a)可知:均载系数与安装误差成线性关系;且均载系数与各个部分安装误差之间的关系并不一致,大直齿轮与小双斜齿轮对均载系数的影响最大,而输入端小齿轮影响最小。由图 6(b)可知:均载系数与安装误差成线性关系。与图 6(a)相比,系统整体安装误差对均载系数的影响要小于大直齿轮和小双斜齿轮安装误差对均载系数的影响。因此,当系统内部件均存在安装误差时,这些误差产生的影响不应直接叠加。
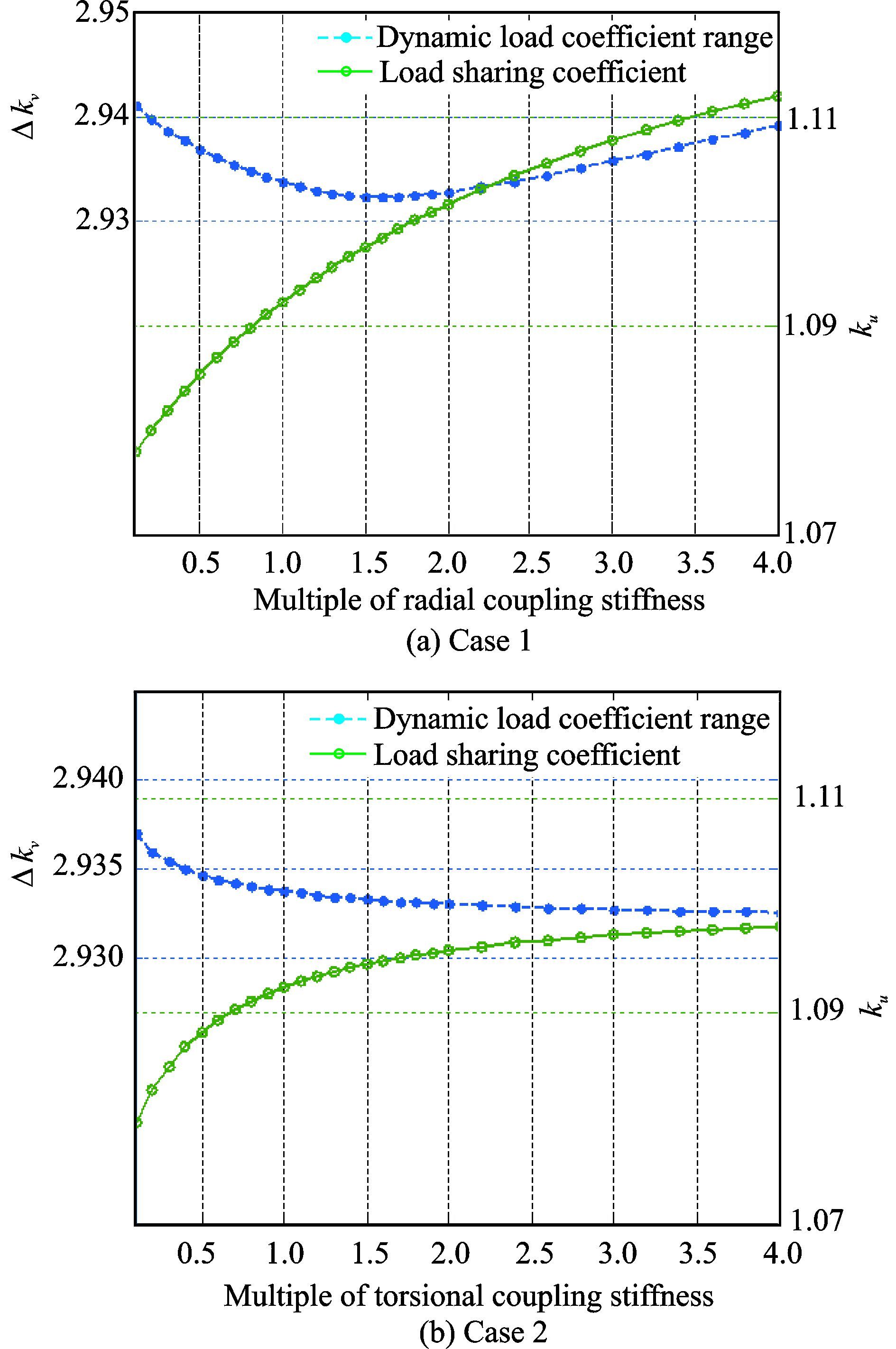
为研究耦合刚度与系统均载能力的关系,对两组算例进行了计算:(1) 径向耦合刚度乘以比例因子,从0.1~4.0,扭转耦合刚度不变;(2) 扭转耦合刚度乘以影响因子,从0.1~4.0,径向刚度不变。
由图 7(a)可知:(1) 动态载荷系数范围和均载系数都对径向耦合刚度不敏感;(2) 随着径向耦合刚度的上升,均载系数单调上升,说明适当地降低径向耦合刚度有利于系统均载能力的提高。由图 7(b)可知:(1) 动态载荷系数范围和均载系数都对扭转耦合刚度不敏感;(2) 随着扭转耦合刚度的上升,均载系数单调上升,说明适当地减小扭转耦合刚度有益于系统均载能力的提高。
|
图 7 耦合刚度对均载系数的影响分析 Figure 7 Effects of coupling stiffness on load-sharing characteristics |
5 结论
本文建立了基于集中质量法的功率分流传动系统的动力学模型,研究了齿轮啮合刚度、啮合误差、安装误差以及耦合刚度对系统均载性能的影响。在此基础上得到以下结论:
(1) 对于本文研究的功率分流传动系统,第一级齿轮副的啮合刚度、啮合误差对系统均载性能的影响最为显著;而第二级齿轮副的啮合刚度、啮合误差,以及双联齿轮的轴向、径向耦合刚度对系统均载性能的影响相对较弱。
(2) 由参数分析可知,提高系统均载能力的可行方式为:根据实际工况优选适当的啮合刚度,应取较小的双联齿轮耦合刚度,并尽可能控制制造与安装误差。
(3) 齿轮副啮合刚度的优化选取方法和误差的控制方法是提高功率分流传动系统均载能力的关键。
| [1] | White G. Split torque helicopter transmissions with widely separated engines[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 1989, 203(1): 53–65. |
| [2] | Heath G F, Bossler Jr R B. Advanced rotorcraft transmission (ART) program [R]. NASA CR-191057, 1993. |
| [3] | Krantz T L. Dynamics of a split torque helicopter transmission [R]. National Aeronautics and Space Administration Cleveland oh Lewis Research Center TM-206410, 1994. |
| [4] | Ligata H, Singh A, Kahraman A. An experimental study of the influence of manufacturing errors on the planetary gear stresses and planet load sharing[J]. Journal of Mechanical Design, 2008, 130(4): 041701. DOI:10.1115/1.2885194 |
| [5] | Singh A, Kahraman A, Ligata H. Internal gear strains and load sharing in planetary transmissions: model and experiments[J]. Journal of Mechanical Design, 2008, 130(7): 072602. DOI:10.1115/1.2890110 |
| [6] | Bodas A, Kahraman A. Influence of carrier and gear manufacturing errors on the static load sharing behavior of planetary gear sets[J]. JSME International Journal Series C, 2004, 47(3): 908–915. DOI:10.1299/jsmec.47.908 |
| [7] | Dong Hao, Fang Zongde, Wang Baobin. Load sharing characteristics of double power split gear system based on deformation coordination[J]. South China University of Technology (Natural Science Edition) Journal, 2012(5): 006. |
| [8] | Dong Hao, Fang Zongde, Wang Baobin, et al. Analysis of load sharing characteristics of double power split system based on deformation coordination and gap floating[J]. Journal of Aerospace Power, 2013(4): 872–877. |
| [9] | Bu Zhonghong, Liu Geng, Wu Liyan, et al. Improved method for calculating gear meshing stiffness and load distribution based on linear programming method[J]. Mechanical Science and Technology, 2008, 27(11): 1365–1368. |
 2016, Vol. 48
2016, Vol. 48


