2. 北京航天控制仪器研究所, 北京, 100854;
3. 中航工业沈阳发动机设计研究所, 沈阳, 110015;
4. 中航工业哈尔滨东安发动机(集团)有限公司, 哈尔滨, 150066
2. Beijing Institute of Aerospace Control Devices, Beijing, 100854, China;
3. Shenyang Aero Engine Research Institute, Aviation Industry Corporation of China, Shenyang, 110015, China;
4. Harbin Dongan Engine(Group Corporation Limited, Aviation Industry Corporation of China, Harbin, 150066, China
齿轮旋转带动周围的空气运动,会形成气体压力场,对其中的喷油射流产生影响。当齿轮工况与喷油参数不匹配时,会阻碍润滑油射流按预先设计的方向喷射[1-2],导致润滑与冷却失效,造成齿轮点蚀、胶合甚至断裂[3-4]。随着现代齿轮传动转速越来越高,形成的压力场对射流的影响越发显著,在我国某型航空附件机匣试车中发现,当喷孔与齿轮距离比较近时,润滑油无法从喷孔流出,在此称之为高速齿轮的气障作用。因此,在对新一代高速齿轮进行喷油润滑设计时就必须对气障作用进行充分考虑。
目前针对高速齿轮的旋转流场与压力场的研究主要集中在其产生的风阻损耗方面,Seetharaman[5],Voeltzel[6]利用数值算法对齿轮旋转的风阻损耗进行了计算,Diab[7],Handschuh[8]对齿轮的风阻进行了试验研究,并提出了降低齿轮风阻的方法[9],他们的研究结果表明,齿轮的风阻与转速呈现正比关系。赵宁等[10-12]采用计算流体动力学(Computational fluid dynamics,CFD)方法对齿轮旋转产生的风阻进行了计算,并且得到了周围的流场分布情况。在喷油射流的流形方面,何志霞等[13-14]对喷油嘴结构参数及流体在供油管路内部流动状态参数对喷出射流流形的影响进行了分析,得到了使射流不发生偏离的设计规律。在齿轮喷油润滑方面,Akin[15-16]利用几何计算方法,对齿轮喷油润滑的喷射冲击及深度进行了较为详细的分析与讨论,并且通过试验发现当齿轮转速及齿宽较小时旋转对射流的影响较小。对于高速齿轮的喷油润滑,王延忠等[17-19]对高速齿轮旋转流场对喷油射流的影响进行了深入的分析,但未能对啮出侧齿形的影响进行充分考虑。
本文利用先进的计算流体动力学方法,建立了齿轮高速旋转在周围产生的流场与压力场计算模型,对不同的齿轮工况参数进行了计算与分析,得到了压力场强度的影响因素与规律。在此基础上,将润滑油射流考虑在内,建立了齿轮喷油润滑的二相流模型,对喷油参数与齿轮工况的匹配进行了研究,并对压力场计算结果进行了对比仿真验证。本文的研究成果将用于指导新一代高性能齿轮传动的喷油润滑设计,对我国相关装备发展具有十分重要的意义。
1 高速齿轮旋转流场计算模型 1.1 齿轮旋转流场数学模型空气在高速旋转齿轮周围的运动可以用计算流体动力学的方法进行求解,本文用有限容积法对其进行建模与数值计算,控制方程如下。
(1) 连续性方程
| $\frac{\partial \rho }{\partial t}+\nabla \cdot \left( \rho U \right)=0$ | (1) |
式中:ρ为密度;U为流体速度。
(2) 动量守恒方程(N-S方程)
| $\partial \frac{\left( \rho U \right)}{\partial t}+\nabla \cdot \left( \rho UU \right)=-\nabla p+\nabla \cdot \tau +{{S}_{M}}$ | (2) |
式中:p为压力;SM为外部体积力,在此为零;τ为应力张量。
| $\tau =\mu \left( \nabla U+{{\left( \nabla U \right)}^{T}}-\frac{2}{3}\delta \nabla \cdot U \right)$ |
式中μ为流体黏度。
(3) 湍流模型
考虑模型的计算效率及准确度,选用普遍的标准k-ε模型[18]求解湍流,模型的湍流黏度为
| ${{\mu }_{t}}={{C}_{\mu }}\rho \frac{{{k}^{2}}}{\varepsilon }$ | (3) |
式中:Cμ为模型常数,在此为0.09;k为湍流动能;ε为其耗散率。分别由其微分输运方程求解得到
| $\begin{align} & \frac{\partial }{\partial t}\left( \rho k \right)+\frac{\partial }{\partial {{x}_{j}}}\left( \rho {{U}_{j}}k \right)=\left[ \frac{\partial }{\partial {{x}_{j}}}\left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{k}}} \right)\frac{\partial k}{\partial {{x}_{j}}} \right]+ \\ & {{P}_{k}}-\rho \varepsilon +{{P}_{kb}}+{{S}_{k}} \\ \end{align}$ | (4) |
| $\begin{align} & \frac{\partial }{\partial t}\left( \rho \varepsilon \right)+\frac{\partial }{\partial {{x}_{j}}}\left( \rho {{U}_{j}}\varepsilon \right)=\left[ \frac{\partial }{\partial {{x}_{j}}}\left( \mu +\frac{{{\mu }_{t}}}{{{\sigma }_{\varepsilon }}} \right)\frac{\partial \varepsilon }{\partial {{x}_{j}}} \right]+ \\ & \frac{\varepsilon }{k}\left( {{C}_{\varepsilon 1}}{{P}_{k}}-{{C}_{\varepsilon 2}}\rho \varepsilon +{{C}_{\varepsilon 1}}{{P}_{\varepsilon b}} \right)+{{S}_{\varepsilon }} \\ \end{align}$ | (5) |
式中:Cε1和Cε2为模型常数,通常分别取为1.44和1.92;Pk是由平均速度梯度产生的湍流动能;Pkb是由浮力产生的湍流动能,在此模型中为零;σk和σε分别为k方程和ε方程的普朗特数;Sk和Sε为用户自定义的源项。
1.2 CFX计算模型在三维建模软件中建立一对相啮合的齿轮模型,由于分析的是齿轮旋转对周围流体的影响及其产生的气体压力场,因此在齿轮三维模型的基础上运用布尔运算建立周围空气的计算流体域,如图 1(a)所示。模型中两个齿轮的尺寸参数相同:模数m=2.5、压力角α=20°、齿数z=20。计算域宽150 mm、高100 mm,经分析此计算域大小对计算偏差无影响。

|
图 1 啮合齿轮对流体域三维模型与网格划分 Figure 1 Three-dimensional and grid models |
在网格划分软件ICEM中对三维模型进行分网,网格采用六面体主导单元,最大网格边长为1 mm,对啮合点附近设置网格加密,最大网格为0.1 mm,划分后的网格偏度小于0.4(如图 1(b)所示)。将划分好的网格模型导入计算流体动力学分析软件CFX前处理模块CFX-Pre中,给定齿轮转速以及空气环境等边界条件,设置收敛条件RMS为1E-5,运行CFX-Solver求解,求解完成后在后处理软件CFX-Post中查看计算结果。
2 气体压力场计算及影响高速齿轮的喷油润滑通常有啮入侧喷油和啮出侧喷油两种方式。当采用啮入侧喷油时,两齿轮产生的流体压力场主要使射流发生角度偏离,对此问题文献[17]进行了详细的讨论。当喷油嘴布置在齿轮对啮出侧时,由于齿轮在喷油嘴直线上的线速度与喷油方向相反,能够形成阻碍喷油射流运动的气障,因此,本文主要对此种情况进行分析。
建立如图 1所示的一对相啮合的齿轮,分别对不同的齿轮转速与齿宽条件进行计算,分析齿轮转速与齿宽对齿轮旋转产生的气体压力场的影响。
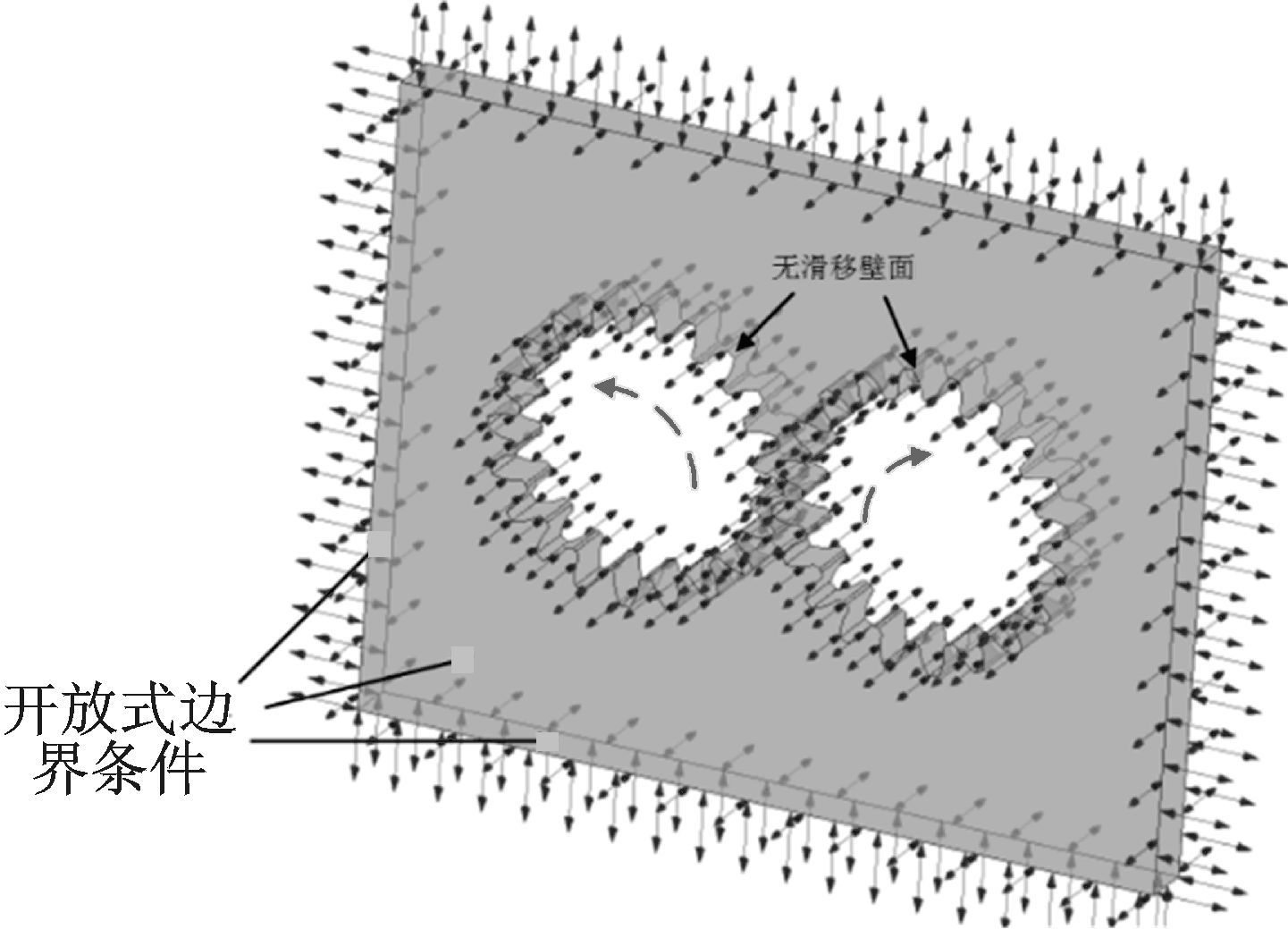
2.1 齿轮转速对气体压力场的影响高速齿轮的转速一般在6 000 r/min以上,因此在计算模型中设置齿轮转速变化范围为6 000~30 000 r/min,齿轮齿面为无滑移壁面边界条件,计算域的其余面为开放式边界条件(相对压力为0) ,如图 2所示,模型中的齿宽固定为10 mm。 不同转速的计算结果如图 3所示。
|
图 2 有限元计算边界条件 Figure 2 Finite element boundary conditions |

|
图 3 不同转速的计算结果 Figure 3 Calculation results of different speed |
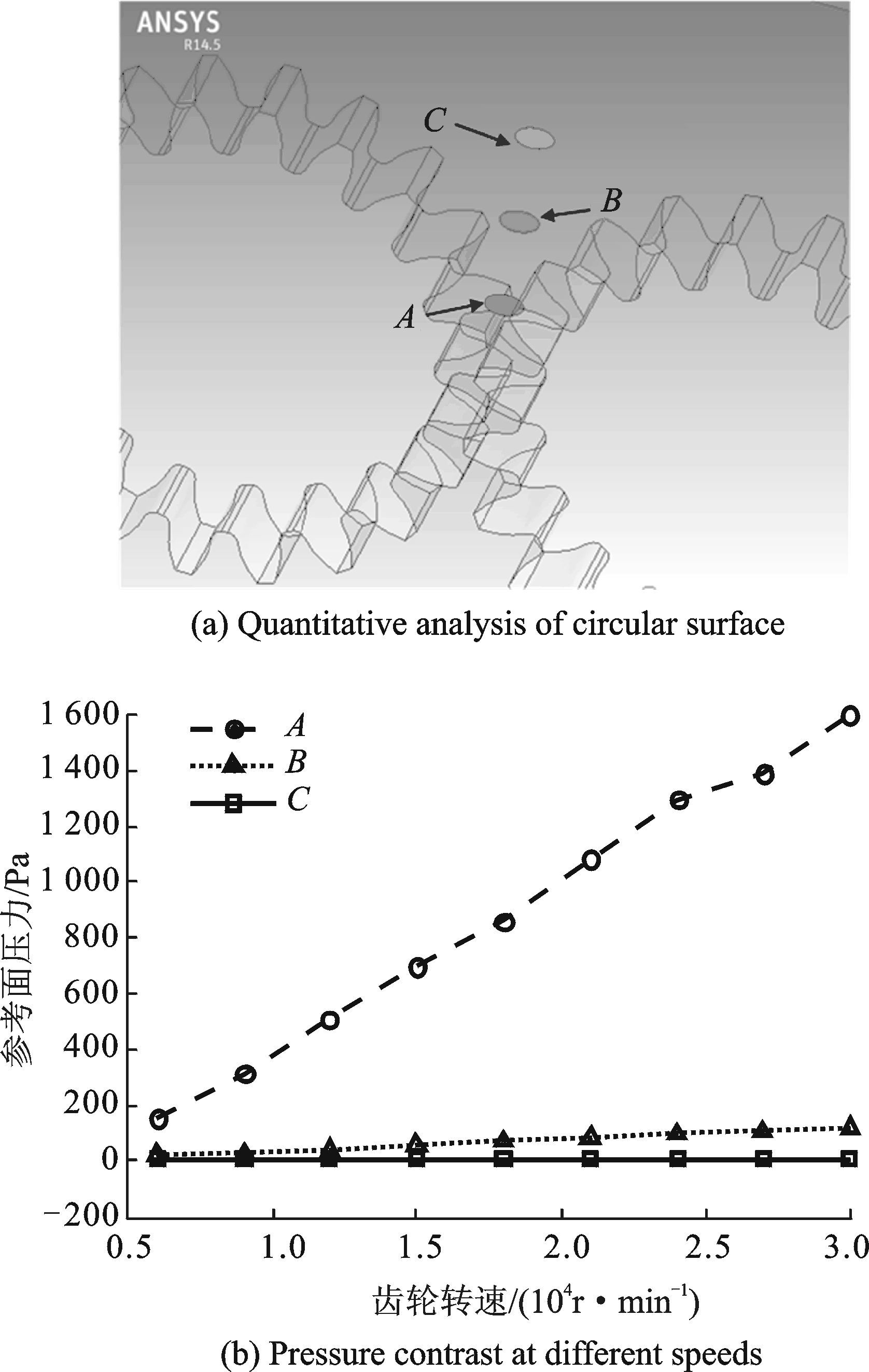
为了对不同转速齿轮产生的气体压力场进行定量的分析,在两齿轮齿宽中心分度圆切点上方分别距离10 mm、20 mm及30 mm处取半径为2 mm的小圆面,分别用A、B、C标识(如图 4(a)所示),并用此小圆面上的压力对不同的转速进行比较,结果如图 4(b)所示。
|
图 4 不同转速的比较分析 Figure 4 Comparative analysis of different speed |
从图 4(b)可以看出,高速齿轮旋转产生的气体压力场强度随着齿轮转速的增加近似呈现线性增加的趋势。同时由分度圆切点上方不同距离的压力计算结果可以看出,越靠近齿轮的压力越大,齿轮旋转对较远距离的气体影响较小。
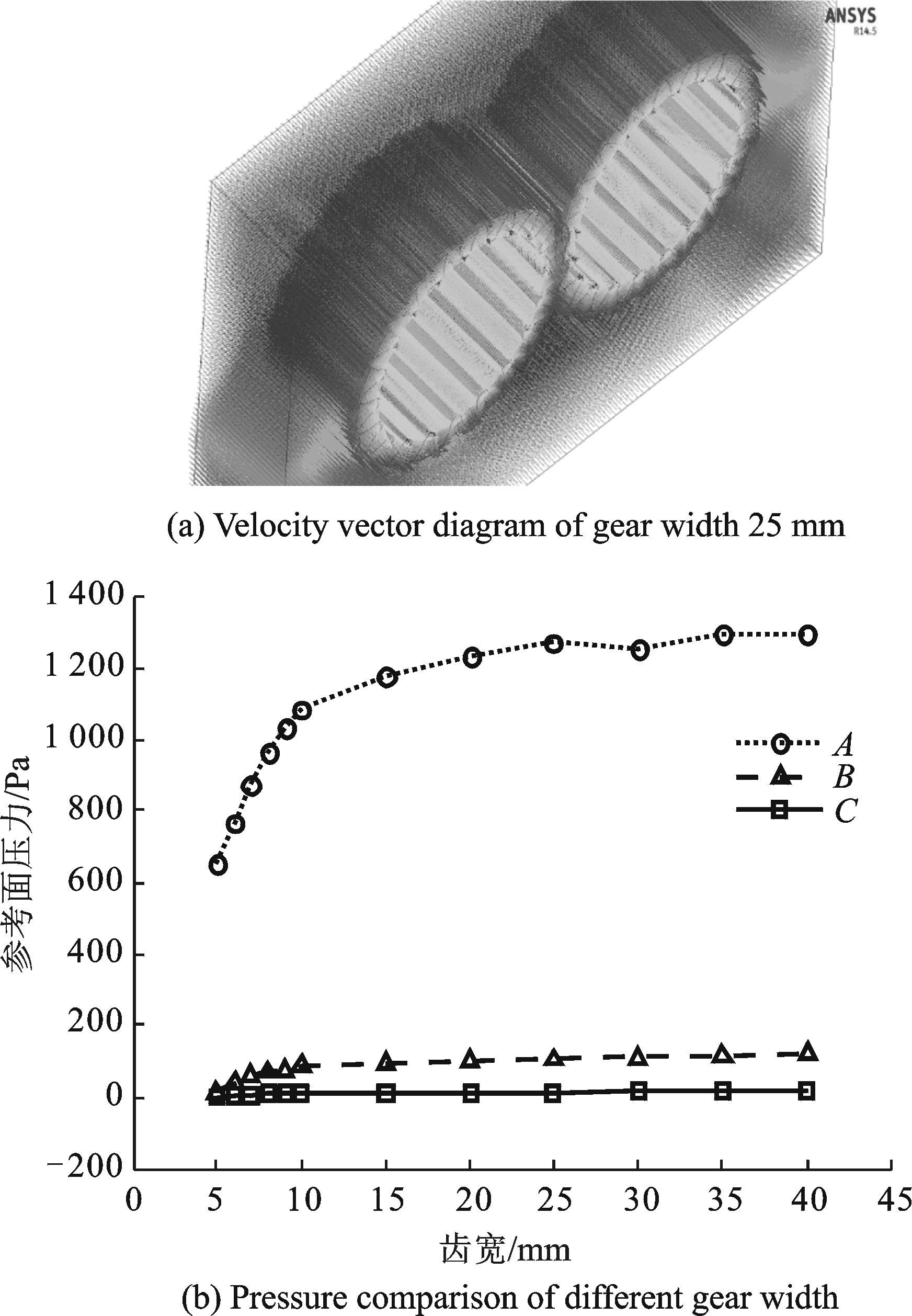
2.2 齿宽对气体压力场的影响建立不同齿宽的三维计算模型,齿宽变化范围为10~40 mm,计算中齿轮转速固定为21 000 r/min。计算结果如图 5所示。
|
图 5 不同齿宽的计算结果 Figure 5 Comparative analysis of different gear width |
采用图 4(a)相同的方法,对不同齿宽齿轮产生的气体压力场进行定量的计算与比较,结果如图 5(b)所示。从图 5(b)可以看出,随着齿轮齿宽的增加,其产生的气体压力场强度也逐渐增加,但是参考面上的压力增加越来越不明显,这是因为齿宽的增加主要影响的是气体压力场的范围,增大的部分齿宽距离如图 4(a)所示的参考面越来越远,因此对其影响越来越小。
3 喷油射流仿真与试验验证建立喷油射流在齿轮高速旋转流场中的计算模型,验证气障的计算结果。齿轮喷油润滑时,从喷嘴喷出的润滑油射入空气中,与空气相互作用并混合,是二相流问题,因此,在做喷油射流仿真验证时必须首先建立高速齿轮喷油润滑的二相流模型。
3.1 喷油射流的二相流模型采用Eular多相流模型对喷油润滑下的气液二相射流进行数学建模,模型中忽略重力影响,喷油润滑过程中不存在传热与化学反应,不考虑润滑油流体的密压及黏压效应。
模型控制方程为
(1) 体积率归一方程
| ${{r}_{air}}+{{r}_{oil}}=1$ | (6) |
式中:rair和roil分别为空气与润滑油的体积率。
(2) 连续方程
| $\frac{\partial ({{r}_{air}}{{\rho }_{air}}+{{r}_{oil}}{{\rho }_{oil}})}{\partial t}+\nabla \cdot \left( ({{r}_{air}}{{\rho }_{air}}+{{r}_{oil}}{{\rho }_{oil}})U \right)=0$ | (7) |
二相流模型的动量守恒方程与湍流模型的形式与式(2~5) 一致,但是计算过程中需要对润滑油和空气两相进行分别求解。两相之间的动量传输采用均相流方法[19]进行考虑。
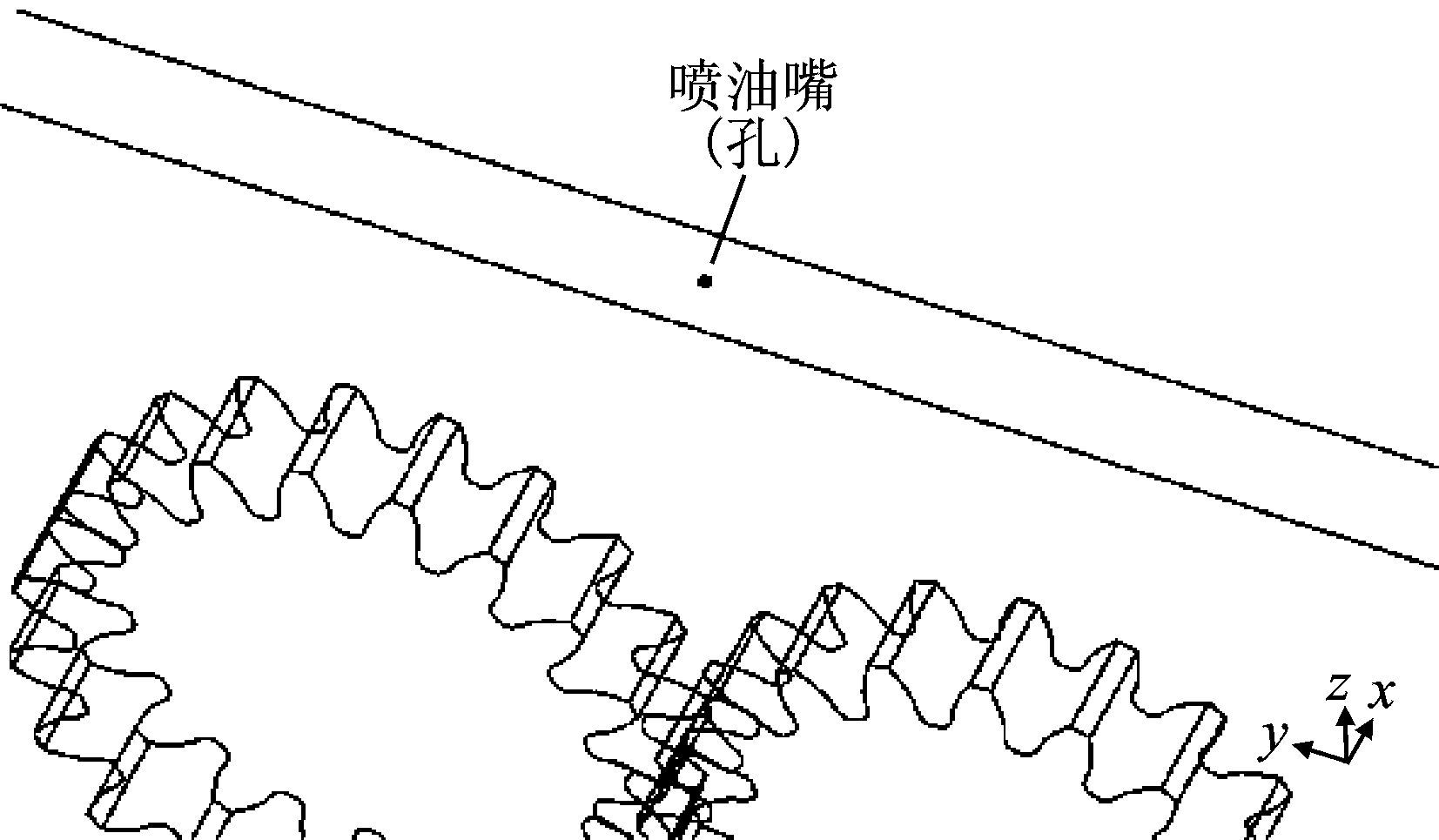
3.2 仿真验证设计与结果分析建立包含喷油嘴的齿轮转动三维模型,将喷油嘴布置在两齿轮分度圆的公切线上,如图 6所示,喷孔直径为1 mm,采用四面体网格并对喷油嘴处进行网格加密处理。模型中开始充满空气,计算采用航空4109润滑油,润滑油密度959 kg/m3、黏度0.01 Pas,喷油嘴出口处为压力边界条件,其余边界条件设置与第2节中相同。
|
图 6 喷油嘴模型 Figure 6 Nozzle model |
为了验证第2节气体压力场的计算结果,建立如表 1所示的两对相互啮合的齿轮,在不同喷油嘴出口压力条件下进行计算,得到喷油射流在高速齿轮旋转产生的气体压力场中的运动状态。表中的喷油压力参考图 4(a)中距离两齿轮分度圆公切点上20 mm圆面的压力,分别为大于和小于参考压力。
| 表 1 计算齿轮对参数 Table 1 Parameters of gear pair |
对以上齿轮对分别进行计算,得到喷油射流流线结果如图 7所示。

|
图 7 不同齿轮对的喷油射流流线 Figure 7 Jet stream lines with different gear pairs |
从图 7可以看出,当喷油压力大于参考面压力时,润滑油从喷嘴喷出后能够喷射较长的一段距离并最终到达齿轮啮合齿面,而当喷油压力小于参考面压力时,润滑油从喷嘴喷出后由于气障作用,受到较强的反向气体压力场的影响,在未到达齿轮齿面时就发生了射流逆流,无法对啮合齿轮进行润滑或冷却。
3.3 原理试验验证设计并搭建超高速齿轮射流试验台,试验台如图 8所示。试验过程中电马达无负载,最高转速为60 000 r/min,齿轮材料为尼龙、模数0.5、齿宽3.5 mm。

|
图 8 试验台 Figure 8 Test rig |
试验结果如图 9所示。

|
图 9 试验结果 Figure 9 Test results |
试验表明,随着齿轮转速的增加,齿轮的气障特性越来越明显,射流出现明显的逆流。
4 结论(1) 航空齿轮的高速旋转会在其周围产生流体压力场,影响射流的运动及其对啮合齿轮的润滑与冷却。当喷油嘴布置在齿轮啮出侧时,齿轮产生的压力场方向与射流方向相反,形成气障阻碍喷油射流运动,当喷油速度(射流压力)不能克服高速齿轮旋转产生的压力场时,射流会发生逆流,无法对齿轮进行润滑和冷却。
(2) 齿轮的转速越高,其产生的气体压力场强度越大,喷油射流越容易发生逆流,因此对此对齿轮进行喷油润滑时需要增大供油管路压力与喷油嘴出口速度。
(3) 齿轮旋转产生的气体压力场强度与齿轮齿宽正相关,然而随着齿宽增大到一定限度时,压力场强度的增大越来越不明显,对较宽的齿轮进行喷油润滑时不需增大供油管路压力与喷油嘴出口速度。
本文通过对齿轮旋转产生的流场(压力场)的建模与分析,揭示了高速齿轮气障现象的机理,在此基础上对齿轮转速与齿宽的影响进行了分析,对航空附件机匣等齿轮传动系统的喷油润滑设计具有指导意义。
| [1] | Höhn B R, Michaelis K, Otto H P. Minimised gear lubrication by a minimum oil/air flow rate[J]. Wear, 2009, 266(3/4): 461–467. |
| [2] |
王延忠, 牛文韬, 唐文, 等.
喷油方位参数对航空直齿轮喷油润滑过程的影响分析[J]. 航空动力学报, 2015, 30(7): 1605–1610.
Wang Yanzhong, Niu Wentao, Tang Wen, et al. Influence of spray orientation parameters on spray lubrication process of aero spur gears[J]. Journal of Aerospace Power, 2015, 30(7): 1605–1610. |
| [3] | Blok H. The flash temperature concept[J]. Wear, 1963, 6(6): 483–494. DOI:10.1016/0043-1648(63)90283-7 |
| [4] | Castro J, Seabra J. Global and local analysis of gear scuffing tests using a mixed film lubrication model[J]. Tribol Int, 2008, 41(4): 244–255. DOI:10.1016/j.triboint.2007.07.005 |
| [5] | Seetharaman S, Kahraman A. A windage power loss model for spur gear pairs[J]. Tribol Trans, 2010, 53(4): 473–484. DOI:10.1080/10402000903452848 |
| [6] | Evans H P, Snidle R W, Sharif K J. Deterministic mixed lubrication modelling using roughness measurements in gear applications[J]. Tribology International, 2009, 42(10): 1406–1417. DOI:10.1016/j.triboint.2009.05.025 |
| [7] | Diab Y, Ville F, Changenet C, et al. Windage losses in high speed gears: Preliminary experimental and theoretical results[D]//ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.[S.l.]:American Society of Mechanical Engineers, 2003:941-947. |
| [8] | Handschuh R F, Hurrell M J. Initial experiments of high-speed drive system windage losses[R]. NASA/TM-2011-216925, 2011: E-17421-1. |
| [9] | Li Yuansheng, Yu Ming. Thermohydrodynamic lubrication analysis on equilibrium position and dynamic coefficient of journal bearing[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2012, 29(3): 227–236. |
| [10] | Wang Liqin, Li Wenzhong, Gu Li, et al. Reducing vibration with friction-damping in high-speed rotor system[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2007, 24(1): 48–53. |
| [11] | Hill M J, Kunz R F, Medvitz R B, et al. CFD analysis of gear windage losses: Validation and parametric aerodynamic studies[J]. J Fluids Eng, 2011, 133(3): 031103. DOI:10.1115/1.4003681 |
| [12] | Gorla C, Concli F, Stahl K, et al. Hydraulic losses of a gearbox: CFD analysis and experiments[J]. Tribol Int, 2013, 66(10): 337–344. |
| [13] |
何志霞, 袁建平, 李德桃, 等.
柴油机喷嘴结构优化的数值模拟分析[J]. 内燃机学报, 2006, 24(1): 35–41.
He Zhixia, Yuan Jianping, Li Detao, et al. Numerical simulation analysis of diesel engine nozzle structure optimization[J]. Journal of Internal Combustion Engines, 2006, 24(1): 35–41. |
| [14] |
王延忠, 牛文韬, 唐文, 等.
喷油嘴喷射方向偏离的影响因素[J]. 航空动力学报, 2015, 30(7): 1605–1610.
Wang Yanzhong, Niu Wentao, Tang Wen, et al. Research on deflection of nozzle spray direction[J]. Journal of Aerospace Power, 2015, 30(7): 1605–1610. |
| [15] | Akin L S, Mross J J, Townsend D P. Study of lubricant jet flow phenomena in spur gears[J]. J Tribol, 1975, 97(2): 283–288. |
| [16] | Akin L S, Townsend D P. Into mesh lubrication of spur gears with arbitrary offset oil jet J. Part 1: For jet velocities less than or equal to gear velocity[J]. J Mech Trans, and Automation, 1983, 105(4): 713–718. DOI:10.1115/1.3258541 |
| [17] | Wang Yanzhong, Niu Wentao, Wei Song, et al. Influence of spinflow on lubricating oil jet - Design method of oil spray parameters to high speed spur gears[J]. Tribo Int, 2015(92): 290–300. |
| [18] | Murphy J, Schmidt D, Wang S P, et al. Multi-dimensional modeling of multiphase flow physics: high-speed nozzle and jet flow-a case study[J]. Nuclear Engineering and Design, 2001(204): 177–190. |
| [19] | Okajiama M, Kato M, Kano H. Contribution of optimum nozzle design to injection rate control[R]. SAE Paper 1991, 910185: 232-245. |
 2016, Vol. 48
2016, Vol. 48


