2. 江南大学人文学院,无锡,214122
2. School of Humanities, Jiangnan University, Wuxi, 214122, China
2009年,伊朗的克曼大学提出了基于牛顿物理学的引力搜索算法[1](Gravitational search algorithm,GSA),它是一种源于牛顿万有引力定律和质量互作用理伦的群体智能优化方法。它的搜索粒子是质量的集合,即它的群体是一个质量的孤立系。在孤立系中,每个质量可以通过万有引力观察其他质量的状态,因此万有引力是不同质量间交换信息的途径。文献[1]将GSA算法与粒子群算法(Particle swarm optimization,PSO)、中心力优化算法(Central force optimization,CFO)以及实数遗传算法(Real genetic algorithm,RGA)做比较,研究结果表明GSA算法在收敛速度和收敛精度上都体现出明显优势。
GSA算法的不足之处在于容易早熟和收敛停滞,以致陷入局部最优的状态。原因在于所有粒子都向种群中质量大的其他粒子学习,那么随着迭代次数的增加,种群渐渐向局部最优解靠拢,搜索空间变小的同时,多样性减少,算法不可避免地陷入局部最优状态。近年来,为了提高种群多样性和抑制早熟,学者们提出了多种改进的引力搜索算法,如文献[2]在GSA算法中引入了量子行为,文献[3]运用混沌策略对算法进行局部搜索,文献[4]模仿PSO算法保存粒子的历史最优值提高算法的开发能力和收敛精度, 而文献[5, 6]均是将PSO算法和GSA算法融合。尽管改进算法各有优势,改善GSA算法的性能仍然是难点,如文献[2]改善了开发能力却没有明显提高探索能力。
针对GSA算法善于开发而劣于探索的特点,本文提出一种基于小生境技术[7]的改进引力搜索算法(Niching behavior based advanced gravitational search algorithm, NAGSA)。小生境技术是指能够搜索并且保存多稳定小生境的技术,或者是指将种群维持在多解的周围,避免种群收敛到单解。小生境技术可以使进化算法的种群维持多样性并且搜索到不同的局部最优解。目前,多种小生境技术被陆续提出,包括拥挤度[8]、适应值共享[9]、物种形成[10]、限制锦标赛选择法[11]等策略。本文为每个粒子定义质量吸引度和欧式距离吸引度两个属性,并且通过线性公式计算出粒子的吸引概率。运用吸引概率和小生境拥挤度技术,使种群同时在多个局部最优解和全局最优解的周围进行细致搜索;此外,通过分析GSA算法的公式,根据指数递减函数将kbest值有效控制在10%~5%之内,使得开发与探索得到平衡。
由于NAGSA对多峰问题的求解效果显著,因此用该算法解决柔性作业调度问题[12-14] (Flexible job-shop scheduling problem, FJSP)。FJSP包含工序排序和机器分配两个问题。工序排序必须遵守工序先后次序的约束,而机器分配指每道工序可在不同的机器上加工,并且加工时间各不相同。因此FJSP是NP (Non-deterministic polynomial)难问题。算法在4个柔性模型算例上测试取得较好的结果,验证了本算法解决实际问题的可行性和优越性。
1 引力搜索算法 1.1 万有引力法则牛顿万有引力的作用被称为“在一定距离内的作用”,这意味着两个不同粒子之间的引力是没有延迟和间隔的。根据牛顿万有引力定律,每一个粒子由于万有引力的作用而彼此相互吸引,吸引力的大小与粒子的质量成正比,与他们之间欧式距离的平方成反比
| $F=D\frac{{{M}_{1}}{{M}_{2}}}{{{R}^{2}}}$ | (1) |
式中:
F代表万有引力的大小;G代表引力常数;M1和M2分别代表两个粒子的惯性质量;R为两个粒子之间的欧氏距离。根据牛顿第二定律,当物体受到力F的作用时,加速度a的大小取决于物体的惯性质量M和力F的大小
| $a=\frac{F}{M}$ | (2) |
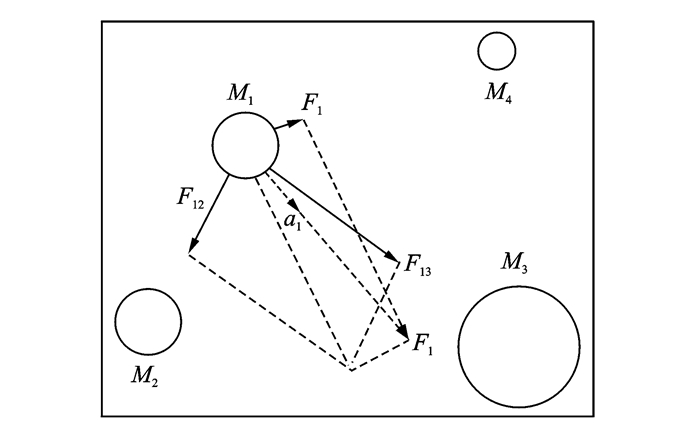
根据式(1,2),两个粒子的质量越大,距离越短,它们的相互吸引力就越大。图 1为力与加速度作用图, 图中F1j表示Mj对M1的作用力,F1表示M1的受力总和,a1表示F1对M1的加速度。此外由于引力常数取决于宇宙的年龄,引力常数呈递减趋势。主动引力质量Ma:衡量引力场强度,与引力场强度成正比;被动引力质量Mb:衡量被引力场影响的强度,在同一个引力场中,Mb越小,受到引力场的作用越小。惯性质量Mi:衡量质量在受力时抑制改变当前运动的强度,Mi越大,越难于改变现状。
|
图 1 力与加速度作用图 Figure 1 Action diagram of force and acceleration |
考虑到上述方面,质量Mj对质量Mi的作用力Fij与Mi的主动引力质量Maj和Mi的被动引力质量Mbi的乘积成正比,且与两者之间的距离R的平方成反比。而加速度ai与力Fij成正比,与惯性质量Mii成反比。因此式(1,2)可改写为
| ${{F}_{ij}}=G\frac{{{M}_{\text{a}j}}{{M}_{\text{b}i}}}{{{R}^{2}}}$ | (3) |
| ${{a}_{i}}=\frac{{{F}_{ij}}}{{{M}_{\text{i}i}}}$ | (4) |
在引力搜索算法中,所有的粒子均受到引力吸引,这就使得种群向质量较大的粒子做全局靠拢。因此引力是粒子之间传递信息的媒介,质量越大的解,移动的越少,这有助于算法的开发能力。GSA算法有4个要素:位置、惯性质量、主动引力质量和被动引力质量。质量的位置表示问题的解,惯性质量和引力质量由适应值决定。
假设在一个D维的搜索空间中有N个粒子,定义第i个粒子的位置为
| ${{X}_{i}}=\left( X_{i}^{1},X_{i}^{2},\cdots ,X_{i}^{D} \right)\ \ \ i=1,2,\cdots ,N$ | (5) |
式中:Xid表示粒子Xi的第d维。
在t次迭代, 定义粒子j对粒子i作用力Fijd(t)为
| $F_{ij}^{d}\left( t \right)=G\left( t \right)\frac{{{M}_{\text{b}i}}\left( t \right)\times {{M}_{\text{a}j}}\left( t \right)}{{{R}_{ij}}\left( t \right)+\varepsilon }\left( X_{j}^{d}\left( t \right)-X_{i}^{d}\left( t \right) \right)$ | (6) |
式中:G(t)表示t时刻的引力常数(式(7));ε为很小的常数;Rij表示粒子之间的欧式距离(式(8))
| $G\left( t \right)={{G}_{0}}\exp \left( -\beta *t/{{t}_{\max }} \right)$ | (7) |
式中:G0设为100,β为20(参考文献[1]); tmax为最大迭代次数。
| ${{R}_{ij}}\left( t \right)={{\left\| {{X}_{i}}\left( t \right),{{X}_{j}}\left( t \right) \right\|}_{2}}$ | (8) |
为了增加随机性,假设粒子Xi的第d维的总作用力为其他所有粒子的作用力之和,Xi的受力和加速度定义分别为
| $F_{i}^{d}\left( t \right)=\sum\limits_{j=1,j\ne i}^{k\text{best}}{\text{ran}{{\text{d}}_{j}}F_{ij}^{d}\left( t \right)}$ | (9) |
式中:randj为0, 1之间的随机数。
| $a_{i}^{d}\left( t \right)=\frac{F_{i}^{d}\left( t \right)}{{{M}_{\text{i}i}}\left( t \right)}$ | (10) |
那么,粒子Xi的更新速度为部分当前速度与加速度之和,因此位置和速度更新公式为
| $v_{i}^{d}\left( t+1 \right)=\text{ran}{{\text{d}}_{i}}\times v_{i}^{d}\left( t \right)+a_{i}^{d}\left( t \right)$ | (11) |
| $X_{i}^{d}\left( t+1 \right)=X_{i}^{d}\left( t \right)+v_{i}^{d}\left( t+1 \right)$ | (12) |
式中:randi为[0,1]之间的随机数,它可以增加搜索的随机性。
物体的惯性质量依据其适应度值的大小来计算,惯性质量越大表明它越接近最优值,同时意味着该物体的吸引力越大,但其移动速度却越慢。假设引力质量与惯性质量相等,物体的质量可以通过适当的运算规则去更新,更新算法为
| ${{M}_{\text{ai}}}={{M}_{\text{b}i}}={{M}_{\text{i}i}}={{M}_{i}}\ \ \ \ i=1,2,\cdots ,N$ | (13) |
| ${{m}_{i}}\left( t \right)={{m}_{i}}\left( t \right)=\frac{\left( \text{fi}{{\text{t}}_{i}}\left( t \right)-\text{worst}\left( t \right) \right)}{\left( \text{best}\left( t \right)-\text{worst}\left( t \right) \right)}$ | (14) |
| ${{M}_{i}}\left( t \right)={{m}_{i}}\left( t \right)/\sum\limits_{j=1}^{N}{{{m}_{j}}\left( t \right)}$ | (15) |
式中:fiti(t)表示第t次迭代时Xi的适应值;针对极小化问题时,worst (t)和best (t)的定义见式(16),极大化问题见式(17)
| $\left\{ \begin{align} & \text{best}\left( t \right)=\underset{j\in \left\{ 1,\cdots ,N \right\}}{\mathop{\min }}\,\text{fi}{{\text{t}}_{j}}\left( t \right) \\ & \text{worst}\left( t \right)=\underset{j\in \left\{ 1,\cdots ,N \right\}}{\mathop{\max }}\,\text{fi}{{\text{t}}_{j}}\left( t \right) \\ \end{align} \right.$ | (16) |
| $\left\{ \begin{align} & \text{best}\left( t \right)=\underset{j\in \left\{ 1,\cdots ,N \right\}}{\mathop{\max }}\,\text{fi}{{\text{t}}_{j}}\left( t \right) \\ & \text{worst}\left( t \right)=\underset{j\in \left\{ 1,\cdots ,N \right\}}{\mathop{\min }}\,\text{fi}{{\text{t}}_{j}}\left( t \right) \\ \end{align} \right.$ | (17) |
为了避免陷入局部最优,算法在初期必须处于探索阶段,随着迭代次数的增加,探索能力渐渐减弱,而开发能力逐步增强。GSA通过控制开发和探索能力提高收敛速度,因此迭代过程中,只有kbest个质量较好的粒子对种群中的其他粒子产生引力,kbest的初始值为种群数量,并随着迭代次数的增加而线性减少,因此粒子Xi的受力公式为
| $F_{i}^{d}\left( t \right)=\sum\limits_{j=k\ \ \text{best,}j\ne i}{\text{ran}{{\text{d}}_{j}}F_{ij}^{d}\left( t \right)}$ | (18) |
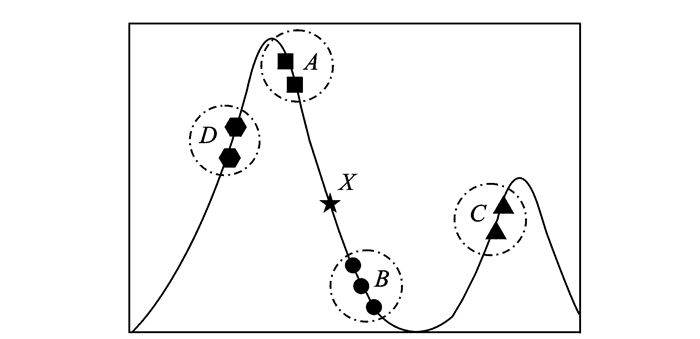
在引力搜索算法中,每个粒子通过万有引力吸引其他粒子,粒子间的吸引力与质量和欧式距离有关。假设种群处于初期阶段(kbest=N,换言之,所有粒子都对当前粒子有吸引力)。图 2为引力搜索算法粒子移动选择图,图中X为当前粒子,种群被划为4个区域:A,B,C,D。粒子X运用式(6,10)计算引力和加速度后更新速度时,有以下推断:
|
图 2 引力搜索算法粒子移动选择图 Figure 2 Particle selected moving of GSA |
(1) 4个区域中的粒子对X的吸引力相差不大。以A区为例,虽然质量最大,但是因为距离最远,吸引力变小;同样B区中的粒子虽然质量最差,但是因为距离最近,吸引力反而变大,因此X的更新充满随机性。
(2) 对于A区的粒子而言,应该在本区域做进一步开发,以便搜索到极值点,然而如果B区的粒子足够多的话,A区的粒子会向B区移动,这反而降低了精度。
从以上分析可以看出:
(1) 在迭代初期,当所有的粒子都有引力时,种群更新不合理,也就是说,kbest的取值是不合理的,这会降低种群的开发能力。
(2) 粒子之间的欧式距离对粒子的更新是否有效起到很大的作用,应该提高欧式距离影响力。
(3) 种群采用质量排序法选择粒子,在迭代后期种群容易陷入局部最优。
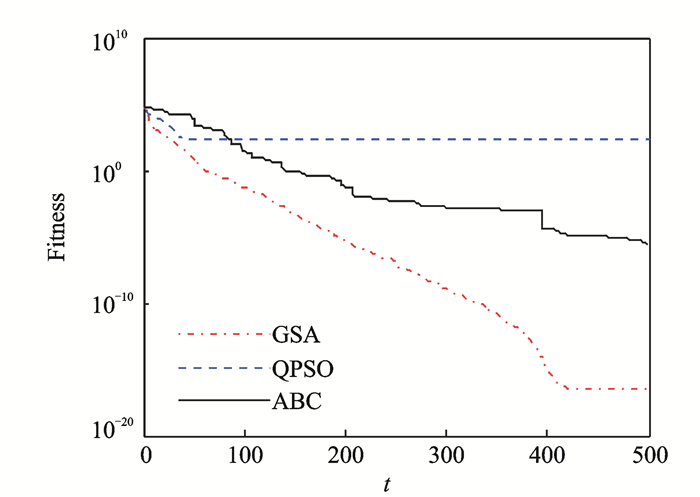
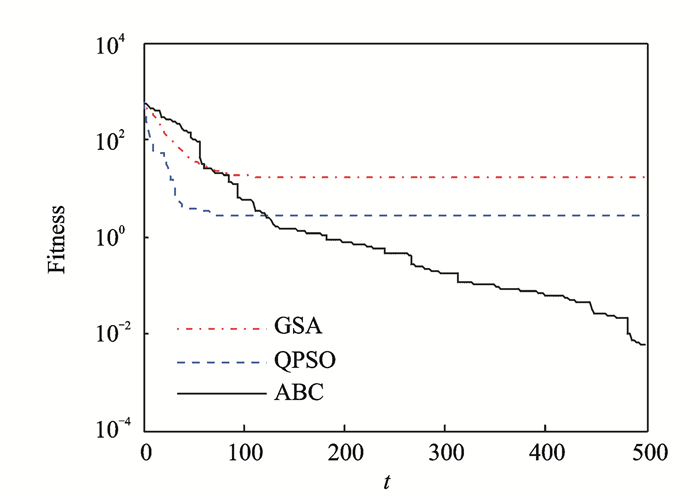
以Sphere函数(单峰)和Griewank函数(多峰)为例(设种群大小为60,维度为30,迭代次数为500),将GSA算法、人工蜂群算法(Artificial bee colony, ABC)和量子粒子群算法(Quantum particle swarm optimization, QPSO)进行比较,收敛曲线见图 3, 4。通过对比可以看出,在Sphere函数中,GSA算法的收敛精度和收敛速度都优于ABC算法和QPSO算法;而对于Griewank函数,GSA算法陷入早熟。因此,GSA算法在单峰问题上表现出很好的开发能力,然而探索多峰问题的能力较差,证明了上述推断。
|
图 3 Sphere函数收敛曲线 Figure 3 Convergence of Sphere function |
|
图 4 Griewank函数收敛曲线 Figure 4 Convergence of Griewank function |
2 基于小生境技术的改进引力搜索算法
从第1.3节的分析可以看出,GSA算法需要改进两点:(1)引入吸引概率;(2)有效控制kbest取值。
2.1 改进的引力搜索算法(1) 引入吸引概率
不同于GSA算法采用质量排序法,本文同时考虑质量和欧式距离两个要素,为每个粒子赋予质量吸引度MA和距离吸引度EA,则
| $\text{M}{{\text{A}}_{ij}}=\frac{\exp \left( 0.1\times \left( {{M}_{j}}-{{M}_{i}} \right) \right)}{\sum\limits_{j=1}^{N}{\exp \left( 0.1\times \left( {{M}_{j}}-{{M}_{i}} \right) \right)}}$ | (19) |
| $\text{E}{{\text{A}}_{ij}}=1-\frac{{{R}_{ij}}}{\sum\limits_{j=1}^{N}{{{R}_{ij}}}}$ | (20) |
式中:MAij和EAij分别为j粒子对i粒子的质量吸引度和距离吸引度; Rij表示两者之间的欧式距离。j粒子对i粒子的吸引概率AP为
| $\text{A}{{\text{P}}_{ij}}=\tau \times \text{E}{{\text{A}}_{ij}}+\left( 1-\tau \right)\times \text{M}{{\text{A}}_{ij}}$ | (21) |
式中:τ为选择参数,τ值越大表示对欧式距离的依赖性越强,τ越小表示对质量的依赖性越强。本文取τ为0.7,已欧式距离的影响为主,质量影响为辅。APij越大,被选中的概率越高。通过AP选择吸引粒子,对种群的开发和探索能力起到平衡的作用。
(2) 改进的kbest取值
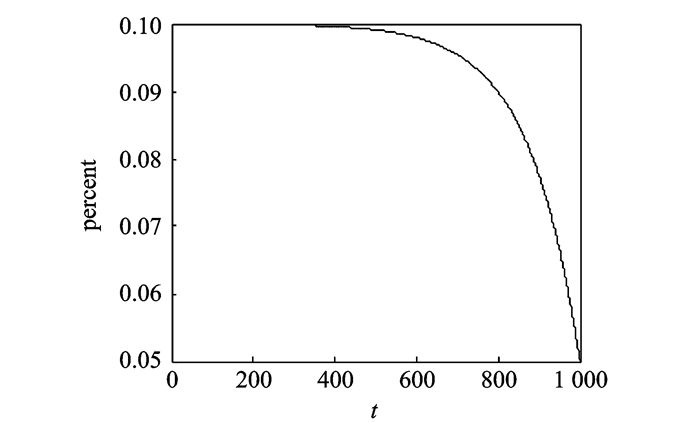
kbestm根据指数函数递减,见式(22)(其中
|
图 5 kbestm的取值百分比 Figure 5 Percent of kbestm |
| $\begin{align} & k\text{bes}{{\text{t}}^{m}}= \\ & \left\lceil N\times \left( 10-5\times \left( \frac{\exp \left( 8*t/{{t}_{\max }} \right)-1}{\exp \left( 8 \right)-1} \right) \right)/100 \right\rceil \\ \end{align}$ | (22) |
因此,式(9)改为
| $F_{i}^{d}\left( t \right)=\sum\limits_{j=k\text{,}j\ne i}^{k\text{bes}{{\text{t}}^{\text{m}}}}{\text{ran}{{\text{d}}_{j}}F_{ij}^{d}\left( t \right)}$ | (23) |
本文采用拥挤度小生境技术,使进化算法的种群维持多样性并且搜索到不同的局部最优解。拥挤度技术是一种最简单的小生境技术,它的思想源于对自然种群中的有限数量的相似个体进行竞争(相似度通常用欧式距离衡量)。拥挤度技术能够保持种群的多样性,它需要将更新后的粒子与从种群中随机选择的子群体进行对比,因此它需要用拥挤度因子(Crowding factor, CF)对对比个体的数量进行控制,本文中CF等于种群的数量。
为了保持种群的稳定性,本算法在每次迭代过程中,将更新得到的新粒子暂存在记忆矩阵Mx中,在本次迭代完成后,找出种群中与Mx最相似的粒子,运用贪婪算法进行选择[12]。
2.2.2 NAGSA算法伪代码算法的初始条件设置完成后,算法可概括为以下步骤:
步骤1 生成初始种群Xi=(Xi1, …, Xid, …, XiD), i=1, 2, …,N。
步骤2 在每一次的迭代过程中:
① 根据式(21,22)分别求出AP, kbest;
② 对种群中的每个粒子而言,首先运用式(23,10)计算粒子的加速度;其次运用式(11)计算粒子的速度;最后运用式(12)得到更新粒子Xi(t+1);
③ 将Xi(t+1)保存到记忆矩阵Mx中;
④ 对于记忆矩阵Mx中的每一个粒子mx:根据欧式距离找出种群中与其最相似的粒子Xinbest:Xinbest←
步骤3 判断是否满足迭代结束条件,如果满足则输出全局最优解,否则返回(2)。
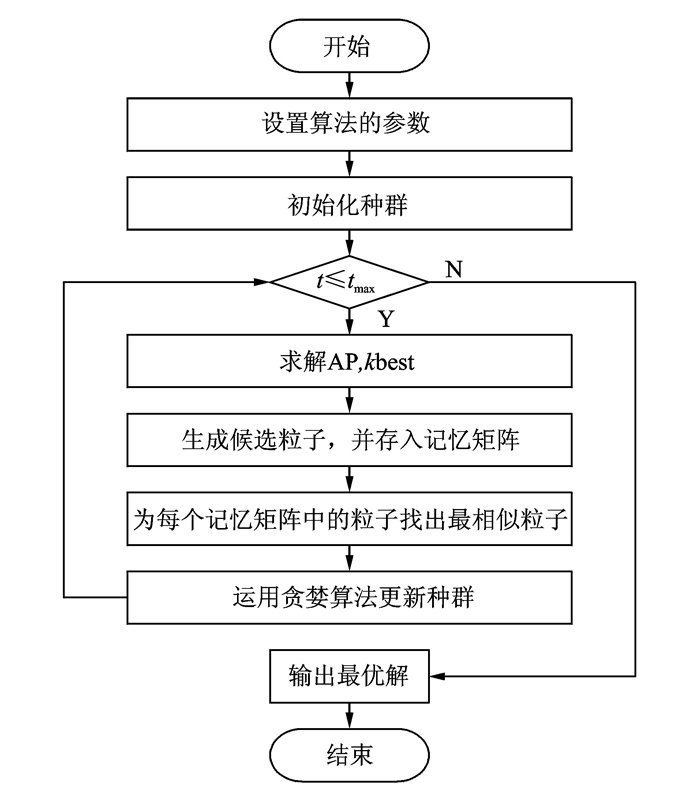
算法的流程图如图 6所示。
|
图 6 NAGSA算法流程图 Figure 6 Flowchart of NAGSA |
3 实验结果与分析
实验种群规模SN设为75,维度D为30,迭代次数t为2 000(最大函数评估次数为150 000),运行次数Nrun为30。NAGSA算法在10个benchmark函数上进行测试,结果见表 1。f1~f5为连续单峰模型函数,f6为步进函数。f7~f10为多峰模型函数,且多峰局部极值点随着维度的增加成指数增长。为测试NAGSA算法的性能,本文将NAGSA算法、GSA、HPSO-GSA[5]和BPSOGSA[15]仿真结果进行比较,表 2记录了4种算法在10个函数下的均值(Mean)和方差(S.D.)。从表 2中的数据可知,在处理单峰问题时,该算法对函数f1, f2, f3, f5的优化效果明显优于其他算法,尤其是对函数f1和f3,收敛精度有较大幅度的提高,只是对函数f4的精度略低于HPSO-GSA。图 7~10给出了函数f1, f2, f8, f9在不同算法下的收敛进化曲线。在图 7,8中NAGSA的收敛进化曲线稳定递减,这表明该算法在处理单峰问题时,能很好地平衡开发和探索能力,保证收敛速度的同时,不失多样性和稳定性。值的注意的是,4个算法对函数f6的优化都能取得最小值,表明引力搜索算法能很好地处理步进函数。
| 表 1 10个标准测试函数 Table 1 Ten standard test functions |
| 表 2 实验数据比较 Table 2 Comparison of experimental data |

|
图 7 函数f1收敛进化曲线 Figure 7 Convergence of function f1 |
|
图 8 函数f2收敛进化曲线 Figure 8 Convergence of function f2 |
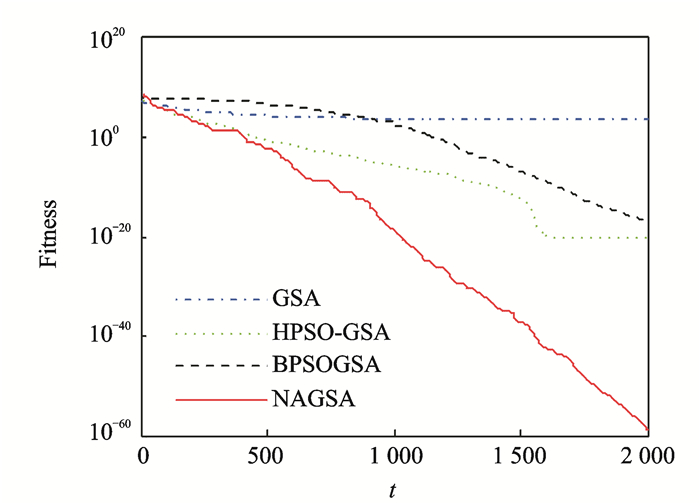
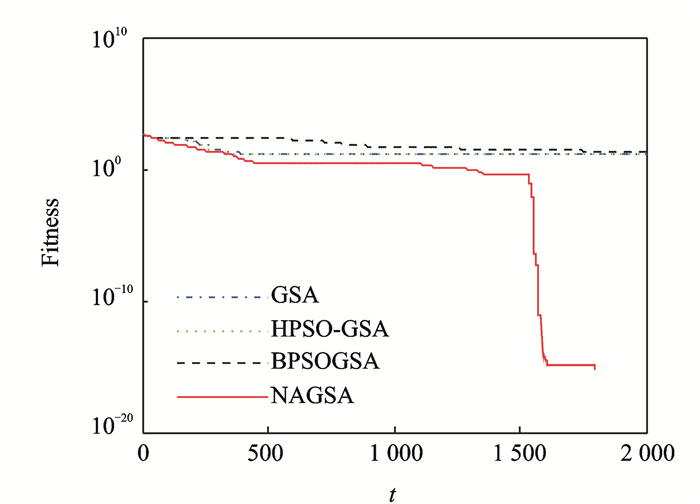
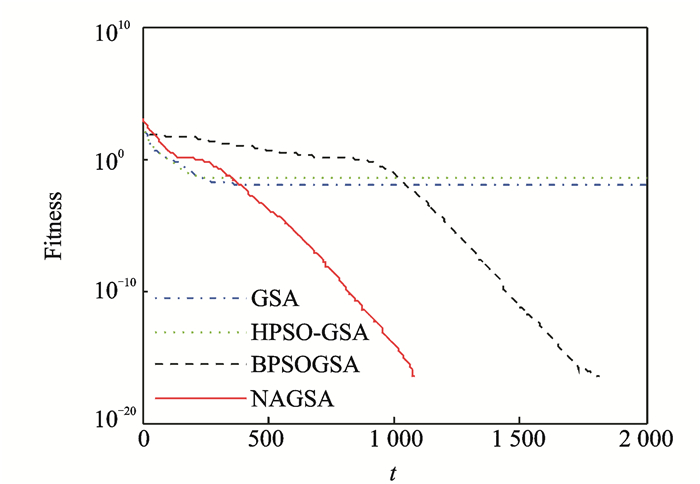
在处理多峰问题时,对于函数f7和f10,NAGSA优化效果略高于其他算法,尤其是对f7的效果不甚明显,然而对函数f8和f9的优化却能进化到全局最小值,优化效果明显提高。在图 9中,NAGSA在迭代初期的收敛效果不明显,然而在迭代后期却快速收敛,这表明,算法在初期具有很强的探索能力,能够搜索全局找出多个极值峰,而在后期,算法拥有很强的开发能力,能够对潜力峰进行深度优化,进而找出全局最优解。NAGSA和BPSOGSA算法都能将函数f9优化到最小值。从图 10可以看出,NAGSA的收敛速度比BPSOGSA快,且NAGSA的进化曲线更加稳定。综上所述,NAGSA能够很好地处理数值优化问题,在单峰和多峰问题上都取得了较好的效果,能够在提高收敛精度和加快收敛速度的同时,确保种群的多样性。
|
图 9 函数f8收敛进化曲线 Figure 9 Convergence of function f8 |
|
图 10 函数f9收敛进化曲线 Figure 10 Convergence of function f9 |
4 NAGSA算法在柔性作业车间调度问题中的应用
FJSP问题是组合优化问题,其适应值地形是非常复杂的,包括大山谷、多峰值、或者大山谷和多峰值并存等。因此,群智能算法解决FJSP问题,必须考虑算法的多峰优化能力。多峰优化问题主要致力于两部分内容,一方面需要搜索空间中的多个全局和局部峰值点,另外需要在保存各峰值点信息的同时,对各个峰进行进一步搜索,以便找到更好的解。因此,如果在迭代过程中,能够保存峰值点,那么迭代进程结束时,将会得到多个最优解,而不是单峰问题中的一个解,这与NAGSA的迭代过程相同。
4.1 编码和解码为了检验NAGSA算法在实际问题中的有效性,本文将NAGSA算法运用到FJSP问题中,目标函数为最大完工时间。此时需要考虑到算法的参数AP,AP是质量吸引度MA和欧式距离吸引度EA的线性相加。根据式(14, 15, 19)可求出质量吸引度MA;FJSP问题采用文献[16]提供的编码和解码方式,运用每个解编码的位置计算欧式距离吸引度EA, 进而可以求出吸引度AP。
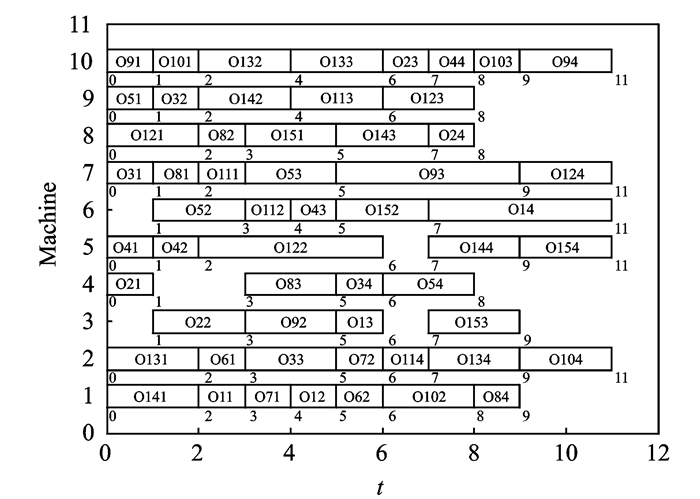
4.2 仿真结果采用MATLAB2013a开发环境,在标准测试模型中采用4个算例进行测试[12]。表 3为比较结果(其中Opt表示算法的最优结果),种群规模为100,迭代次数为50,给出了均衡蜂群算法(FER-ABC)[17]、GSA和NAGSA三种算法的比较。其中3种算法的种群规模均为100,迭代次数分别为100, 100, 50。从对比结果上看,NAGSA算法的效果优于GSA算法,并且在15×10模型上的性能比FER-ABC算法优越。但是, NAGSA算法的迭代次数是FER-ABC算法的两倍,因此算法的复杂度较高。图 11给出了NAGSA算法15×10模型上最优解的甘特图。
| 表 3 实验结果对比 Table 3 Comparison of experimental result |
|
图 11 15×10模型的甘特图 Figure 11 Gantt of 15×10 module |
5 结束语
本文分析了GSA算法的性能和优缺点,提出一种基于小生境技术的改进引力搜索算法。为每个粒子定义了引力吸引度和欧式距离吸引度属性,并且基于两个属性采用线性叠加的方法定义了吸引概率,替换原有的质量排序法进行粒子选择。此外对kbest取值范围做了改进。在10个benchmark函数上的优化结果表明,该算法表现出很大的优势,收敛速度和收敛精度都有明显提高,能够做到探索和开发的均衡。本文将该算法用于求解柔性作业车间调度问题,在与其他算法的比较中体现其优势。
| [1] | Rashedi E, Nezamabadi-Pour H, Saryazdi S. GSA: A gravitational search algorithm[J]. Information Sciences, 2009, 179(13): 2232–2248. DOI:10.1016/j.ins.2009.03.004 |
| [2] | Soleimanpour-Moghadam M, Nezamabadi-Pour H, Farsangi M. A quantum inspired gravitational search algorithm for numerical function optimization[J]. Information Sciences, 2014, 267(5): 83–100. |
| [3] | Gao S, Vairappan C, Wang Y, et al. Gravitational search algorithm combined with chaos for unconstrained numerical optimization[J]. Applied Mathematics and Computation, 2014, 231(11): 48–62. |
| [4] | Jiang S H, Wang Y, Ji Z C. Convergence analysis and performance of an improved gravitational search algorithm[J]. Applied Soft Computing, 2014, 24: 363–384. DOI:10.1016/j.asoc.2014.07.016 |
| [5] | Jiang S H, Ji Z C, Shen Y X. A novel hybrid particle swarm optimization and gravitational search algorithm for solving economic emission load dispatch problems with various practical constraints[J]. International Journal of Electrical Power & Energy Systems, 2014, 55(2): 628–644. |
| [6] | Mirjalili S, Wang G G, Coelho L. Binary optimization using hybrid particle swarm optimization and gravitational search algorithm[J]. Neural Computing and Applications, 2014, 25(6): 1423–1435. DOI:10.1007/s00521-014-1629-6 |
| [7] | Mahfoud S W. Niching methods for genetic algorithms[D]. Urbana: University Illinois Urbana-Champaign, 1995.http://dl.acm.org/citation.cfm?id=240028 |
| [8] | Thomsen R. Multimodal optimization using crow-ding-based differential evolution[C]// Proceedings of the IEEE 2004 Congress on Evolutionary Computation. Portland: IEEE Xplore, 2004. 1382-1389. |
| [9] | Kim H, Liou M S. New fitness sharing approach for multi-objective genetic algorithms[J]. Journal of Global Optimization, 2013, 55(3): 579–595. DOI:10.1007/s10898-012-9966-4 |
| [10] | Chevin L M, Decorzent G, Lenormand T. Niche dimensionality and the genetics of ecological speciation[J]. Evolution, 2014, 68(5): 1244–1256. DOI:10.1111/evo.2014.68.issue-5 |
| [11] | Harik G R. Finding multimodal solutions using restricted tournament selection[C]//Proceedings of 6th International Conference of Genetic Algorithms. San Francisco, CA:[s.n.], 1995: 24-31.http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.51.9292&rep=rep1&type=pdf |
| [12] | Brandimarte P. Routing and scheduling in a flexible job shop by tabu search[J]. Annals of Operations Research, 1993, 41(3): 157–183. DOI:10.1007/BF02023073 |
| [13] |
高亮, 张国辉, 王晓娟.
柔性作业车间调度智能算法及其应用[M]. 武汉: 华中科技大学出版社, 2012: 3-26.
Gao Liang, Zhang Guohui, Wang Xiaojuan. Intelligent algorithm and application of flexible job shop scheduling[M]. Wuhan: Huazhong University of Science And Technology Press, 2012: 3-26. |
| [14] | Li J Q, Pan Q K, Chen J. A hybrid Pareto-based local search algorithm for multi-objective flexible job shop scheduling problems[J]. International Journal of Production Research, 2012, 50(4): 1063–1073. DOI:10.1080/00207543.2011.555427 |
| [15] | Biswas S, Kundu S, Das S, et al. Inducing niching behavior in differential evolution through local information sharing[J]. IEEE Transactions on Evolutionary Computation, 2014, 19(2): 1–16. |
| [16] |
白俊杰, 王宁生, 唐敦兵.
一种求解多目标柔性作业车间调度的改进粒子群算法[J]. 南京航空航天大学学报, 2010, 42(4): 447–453.
Bai Junsheng, Wang Ningsheng, Tang Dunbing. Improved PSO algorithm for multi-objective optimization flexible job shop scheduling problems[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(4): 447–453. |
| [17] |
张明, 田娜, 纪志成.
基于适应值欧式距离比的均衡蜂群算法[J]. 系统仿真学报, 2015, 27(5): 980–989.
Zhang Ming, Tian Na, Ji Zhicheng. Balanced bee colony algorithm based on fitness Euclidean-distance ratio[J]. Journal of System Simulation, 2015, 27(5): 980–989. |
 2016, Vol. 48
2016, Vol. 48


