电路故障诊断一直是现代电路理论的研究热点和难点。近年来,集成电路设计技术和生产工艺得到了快速发展,但与之相匹配的电路测试和故障诊断却一直停滞不前,混合信号电路中的模拟部分的测试与故障诊断问题成了阻碍模拟集成电路工业快速发展的技术难题[1]。虽然近几年在模拟电路测试和诊断方面取得了重要的进展[2-5],但开关电流电路作为一种数字工艺的模拟技术,在电路的故障诊断方面一直进展缓慢,这也使得SI技术的发展受到极大的阻碍,加上SI电路中MOS场效应管的非理想性能、开关电荷流入等因素,这些决定了开关电流电路的测试和故障特征提取等方面还存在很多问题需要解决。
20世纪90年代,已报道了一些开关电流电路测试和故障诊断方法。如:文献[6]通过开关电流电路时钟顺序的变化,使二分电路改变为串联电流镜结构,最后对输入和输出直流信号作了比较。在该方法中,要实现时钟的正确转换非常复杂,仅仅应用在特殊的二分电路结构中。文献[7, 8]方法对开关电流四乘幂滤波器振荡能力进行了测试。文献[9]方法对同样的开关电流存储单元电路进行了内建自测试,在开关电流电路内部插入独立时钟电路,并对级联电流镜的输入与输出直流信号进行了对比。文献[10]以直流信号为基础对SI流水线结构AD转换器进行了测试,有效地降低了测试时间。但是这会导致电路中器件参数不匹配而产生新的偏移电压,降低了测试精度,需要调整片外的高精度电阻。以上方法仅适用于特殊电路结构或仅能诊断到部分电路功能,而很少讨论软故障的诊断、信号的容差等。
近年来,在开关电流电路测试和故障诊断方法研究领域的研究成果较少。文献[11]参考模拟电路测试与诊断方法简单讨论了开关电流基本存储单元的测试,对无MOS开关的基本存储单元电路进行了硬故障测试。由于测量的是电流参数,造成用于测试和诊断的相关故障信息量不完整,以致于不能准确地进行故障定位。文献[12, 13]提出了开关电流电路的伪随机测试方法,但该方法的误判率较高。文献[14]提出了基于故障标识的伪随机隐式功能测试方法,有效克服了文献[12, 13]的缺点,减少了误判率。文献[15]提出了基于粒子群支持向量机(Support vector machine, SVM)的信息熵和峭度预处理的开关电流电路测试和诊断方法,但是由于峭度对野值较敏感导致对大规模开关电流电路故障诊断率不高。文献[16]提出了开关电流电路小波神经网络诊断方法,该方法虽能正确无误地诊断出所有硬故障,但对于低灵敏度晶体管的软故障却达不到好的诊断效果。
针对以上问题,本文提出了一种基于小波变换和核主元分析(Kernel principal component analysis, KPCA)的SVM开关电流电路故障诊断新方法。首先对开关电流节点信号蒙特卡罗分析,再对节点信号进行小波分解和分形,然后利用KPCA提取最优故障特征值,最后通过粒子群优化(Particle swarm optimization, PSO)的SVM实现故障模式分类。并通过六阶切比雪夫低通滤波器加以仿真验证,与其他方法进行比较的实验结果验证了该方法的有效性。
1 基于小波的分形分析 1.1 小波变换原理小波变换广泛应用于信号分析和图像处理领域。一个原始信号经小波变换后可以分解为低频细貌(近似信息)caj和高频细貌(细节信息)cdj。因而信号的特征可以由低频细貌获得。小波一维分解定义为
| ${{\psi }_{\left( a,b \right)}}\left( x \right)=\frac{1}{\sqrt{\left| a \right|}}\psi \left( \frac{x-b}{a} \right)$ | (1) |
| $W\left( a,b \right)=\int\limits_{-\infty }^{\infty }{f\left( x \right){{\psi }_{a,b}}\left( x \right)}\text{d}x$ | (2) |
式中:ψ(x)称为母小波或基本小波;a为进行缩放的缩放参数,反映特定基函数的宽度(或者叫做尺度);b为进行平移的平移参数,指定沿x轴平移的位置;W(a, b)为信号f(t)的小波系数,它能够反映信号的内在特征。
在每一尺度都对信号的小波分解系数W(a, b)进行计算工作量非常大。为解决这一问题,可以采用离散时间等间隔采样的方式,得到离散小波。离散小波定义为
| $W\left( m,n \right)={{a}^{-\frac{m}{2}}}\sum\limits_{k}{x\left( k \right)\psi \left( {{a}^{-m}}k-n \right)}$ | (3) |
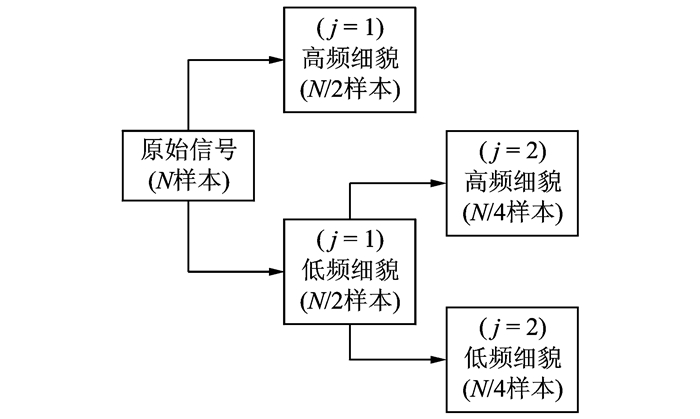
式中:m,n为整数;ψ(k)为ψ(t)的离散形式;x(k)为离散信号。每一次分解信号样本数目减少一半。因此可以在正常提取信号特性的前提下,有效地减少样本数目,缩短SVM训练所需时间。小波分解示意图如图 1所示。
|
图 1 信号的小波分解示意图 Figure 1 Diagram of signals in wavelet decomposition |
选取合适的母小波能够更好地取提信号特征。可以从现有的小波函数中进行有针对性的选取。常见的小波函数的有:Haar小波(Haar)、Daubechies N(dbN)小波、Morlet小波和紧支集样条小波等。其中Morlet小波函数在满足可容许性条件方面不是很理想,还有紧支集样条小波因为是非正交的样条小波,所以不是我们采纳的小波基。在Haar小波和dbN小波中,选取dbN小波,这是因为后者要比前者在反映信号的特征方面更为细腻,而且更适合信号的多尺度分析[8]。
常用的dbN小波有db5,db3,db2三种小波变换基函数。在这3种小波中,信号特征的提取有所区别。在第一层系数的分解中,db5小波包含的内容要比db3包含的丰富,变化特征多。用db2和db5比较,用db2的效果要比db5的效果更好,尤其是在第二层和第三层细节方面,db2比db5的突变特征多,由此反映的故障信号特征也会丰富许多。通过反复的实验验证,db2小波的效果是3个中最好的。因此,本文采用db2小波作为小波分解基函数。
1.2 分形维数在分形学中,分形维数起的作用至关重要,是分形理论中最重要的应用之一。分形维数是以定量的方式刻画分形特征的参数,是分形的数量表示。分形的维数反映对物体表面粗糙程度的感受,同时具有尺度变换下不变性等性质。因此,分形维数作为图形图像形态特征参数,广泛应用于图像分割、特征提取等方面。在实际应用中,分形维数是描述波形信号特征的重要参数。
计算分形维数的算法有许多,常用的有Higuchi算法,Katz算法和Sevcik算法等。其中由Katz等人提出的算法具有简单、高效、占用内存少以及对噪声不敏感等特性,因此本文使用Katz提出的信号分形维数计算方法[17-18]来对故障信号进行计算,从而获得相应的分形维数。
设信号f(x)是具有如下序列[p1, p2, …, pN]的波形,表示序列的点数。信号f(x)的分形维数计算公式如下
| $\text{FD}=\frac{\log \left( n \right)}{\log \left( \frac{d}{L} \right)+\log \left( n \right)}$ | (4) |
| $d=\max \left( \text{dist}\left( {{p}_{1}},{{p}_{i}} \right) \right)$ | (5) |
式中:n=L/a为信号波形步长数,其中L为信号波形曲线的总长度即相继两点之间的距离和,a为相继两点之间的平均距离;d为序列的第一个点与其余点的距离取最大值。
对原始信号f(x)用小波变换的方法,在不同的尺度上进行分解,分解为逼近信号和细节信号。分别计算原始信号和各尺度分解后的逼近信号的分形维数,得到故障信号的特征值。
2 核主元分析假设x1, x2, …, xM为训练样本,用{xi}表示输入空间。KPCA首先通过非线性映射函数Φ:RN→F,将输入空间{xi}映射到特征空间F:Φ(xi), i=1, 2, …, M中,然后在该特征空间中进行主元分析[19]。
设Φ(xi), i=1, 2, …, M已经去均值,即
| $\mathit{\boldsymbol{C}} = \frac{1}{M}\sum\limits_{i = 1}^M {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_i}} \right){\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( {{x_i}} \right)} $ | (6) |
对应的特征方程为
| $\mathit{\boldsymbol{Cv}} = \lambda \mathit{\boldsymbol{v}}$ | (7) |
要求解式(7)中特征值λi>0和对应特征向量vi∈RN, v≠0。将每个样本与式(7)作内积,可得
| $\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_i}} \right) \cdot \mathit{\boldsymbol{Cv}}} \right) = \lambda \left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_i}} \right) \cdot \mathit{\boldsymbol{v}}} \right)$ | (8) |
考虑到所有的特征向量可表示为Φ(x1), Φ(x2), …, Φ(xM)的线性构成,即
| $\mathit{\boldsymbol{v}} = \sum\limits_{j = 1}^M {{\alpha _j}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_j}} \right)} $ | (9) |
则有
| $\begin{gathered} \lambda \sum\limits_{j = 1}^M {{\alpha _j}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_i}} \right) \cdot \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_j}} \right)} \right)} = \hfill \\ \frac{1}{M}\sum\limits_{j = 1}^M {{\alpha _j}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_k}} \right) \cdot \sum\limits_{i = 1}^M {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_i}} \right)\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_i}} \right) \cdot \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_j}} \right)} \right)} } \right)} \hfill \\ \end{gathered} $ | (10) |
定义一个M×M的方阵K
| ${\mathit{\boldsymbol{K}}_{ij}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_i}} \right) \cdot \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_j}} \right)$ | (11) |
则式(10)可以简化为
| $M\lambda \mathit{\boldsymbol{K\alpha }} = {\mathit{\boldsymbol{K}}^2}\mathit{\boldsymbol{\alpha }}$ | (12) |
显然满足
| $M\lambda \mathit{\boldsymbol{\alpha }} = \mathit{\boldsymbol{K\alpha }}$ | (13) |
求解式(13)就能得到特征值λ1, …, λM和对应的特征向量v1, …, vM。首先将特征值按降序排序得λ1′>…>λM′,对特征向量进行相应调整得v1′, …, vM′,然后通过施密特正交化归一化特征向量,得到α1, …, αM,提取前个主分量α1, …, αt。因此测试样本在特征向量空间Vk的投影为
| $\begin{gathered} \left( {{\mathit{\boldsymbol{v}}^k} \cdot \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( x \right)} \right) = \sum\limits_{i = 1}^M {{{\left( {{\alpha _i}} \right)}^k}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{x_i}} \right),\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( x \right)} \right)} \hfill \\ k = 1, \cdots ,t;i = 1, \cdots ,M \hfill \\ \end{gathered} $ | (14) |
将内积(Φ(xi), Φ(x))用高斯径向基核函数,即k(xi, x)=exp (-||xi-xj||/(2σ2))替换则有
| $\begin{gathered} y\left( k \right) = \left( {{\mathit{\boldsymbol{v}}^k} \cdot \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( x \right)} \right) = \sum\limits_{i = 1}^M {{{\left( {{\alpha _i}} \right)}^k}\mathit{\boldsymbol{K}}\left( {{x_i},x} \right)} \hfill \\ k = 1, \cdots ,t;i = 1, \cdots ,M \hfill \\ \end{gathered} $ | (15) |
SVM作为一种基于统计学习理论的模式分类方法,在模式识别领域应用广泛。但是,SVM学习参数的选取对其性能的好坏有很大影响,其参数的选取只能依靠模型建立者的经验。PSO作为一种近年发展起来的进化算法,具有极强的全局搜索能力。本文将其引入到SVM参数的选取中,建立起一种基于PSO-SVM模型的开关电流电路故障分类。
在PSO中,每个问题的解都是搜索空间中的一只鸟,称为“粒子”,所有的粒子都有一个适应值,适应值是用适应值函数得出的。所有的粒子都有一个速度用来决定粒子飞行的方向和距离[20]。分散在解空间中任何位置的粒子,彼此通过直接或间接的沟通,使粒子相互影响,而渐渐移动到可能为最优解的位置上。PSO是粒子在解空间中追随当前最优粒子所进行的一种最优解搜索方法。PSO初始化产生的粒子是一群随机的粒子,通过迭代找到近似最优解,在每次迭代中,粒子的移动受到自身目前为止所搜索到的最好位置pbest,以及种群中所有粒子目前为止所搜索到的最好位置pbest影响。
粒子位置和速度的更新公式如下
| ${s_m}\left( {t + 1} \right) = {s_m}\left( t \right) + {v_m}\left( {t + 1} \right)$ | (16) |
| $\begin{gathered} {v_m}\left( {t + 1} \right) = \omega {v_m}\left( t \right) + {c_1}{r_1}\left( t \right)\left( {{p_m}\left( t \right) - {s_m}\left( t \right)} \right) \hfill \\ + {c_2}{r_2}\left( t \right)\left( {{p_{gm}}\left( t \right) - {s_m}\left( t \right)} \right) \hfill \\ \end{gathered} $ | (17) |
式中:ω为惯性权重;vm(t)为粒子原来的速度;vm(t+1)为粒子的新速度;pm为粒子的最优位置;pgm为整个种群的最优位置。sm(t)为粒子原来的位置;sm(t+1)为粒子的新位置;c1和c2为学习因子;r1(·)和r2(·)为0到1的随机数。
粒子群优化算法的详细步骤如下:
步骤1 粒子位置与速度的初始化。首先确定粒子群体的大小,然后根据SVM模型确定优化的参数:惩罚系数C和核函数参数g。设定搜索空间的维度。
步骤2 适应度函数确定。采用粒子个体对应的惩罚系数和核函数参数建立支持向量机的学习模型,并带入训练样本,计算每个粒子的适应度值。
步骤3 极值更新。将粒子个体适应度和pbest比较,如果适应度比pbest好,则用新适应度的位置更新pbest。将搜索到的适应值和与所有群体中的pbest比较,如果适应度比pbest好,则更新pbest这个最优点位置。
步骤4 用式(16,17)更新粒子的速度和位置。
步骤5 迭代终止判断。判断是否达到最大迭代次数,如果未达到最大迭代数则返回到步骤3;否则将最优参数C,g赋给SVM。
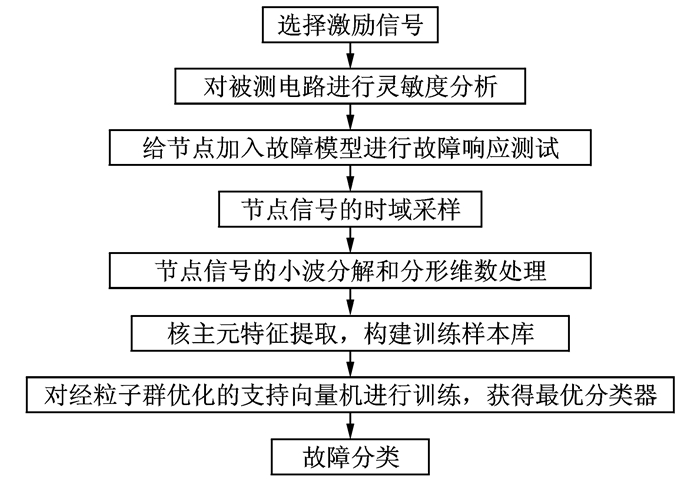
4 基于小波变换和核主元分析的SVM故障诊断首先定义软故障模式,采用一个数据采集板在实际电路输出端节点采集到结点数据。然后利用db2小波作为采集数据的预处理系统,获得原始响应数据的小波高频细貌和低频细貌,接着计算分形维数,利用核主元分析提取最优故障特征,构建训练样本库,最后通过粒子群优化的支持向量机完成故障分类。其故障诊断流程图如图 2所示,该方法的具体实现步骤如下:
|
图 2 基于小波分形和KPCA的SVM故障诊断流程图 Figure 2 Flow chart of wavelet-fractal-and-KPCA-based fault diagnosis of SVM |
步骤1 时钟频率选为1 MHz,输入激励为频率为100 kHz的正弦信号,输出端Iout为唯一可测试点,并提取响应数据。
步骤2 定义故障模式。为了获得元器件参数的变化对电路系统特征的一阶改变,对电路进行灵敏度分析,实现故障元件的定位。
步骤3 db2小波分解和分形维计算。db2利用小波作为采集信号的预处理系统,获得原始响应数据的低频细貌和高频细貌信息,再计算低频细貌小波系数的分形维,从而获得特征值。
步骤4 故障核主元特征提取。利用核主元分析提取最优故障特征值,构建训练样本库,这一步骤也是能正确、高效分类的基础。
步骤5 粒子群优化的支持向量机进行故障分类。将训练样本库送入粒子群优化的支持向量机进行训练,从而构建最优分类器,即可利用该分类器进行故障分类。
5 仿真实验本文采用基于小波分形分析和KPCA的SVM开关电流电路故障诊断方法。首先对原始信号即故障响应信号进行5层db2小波分解获得小波逼近系数,然后再计算出小波分形维特征信息,接着通过KPCA对获得的小波分形维进行特征提取从而得到最优特征模式,最后将最优特征模式输入粒子群优化的SVM训练,获得最优分类器,从而实现正确而有效的分类。
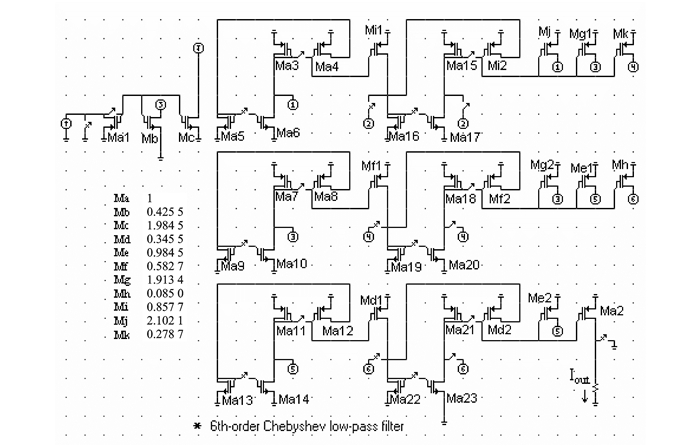
5.1 诊断电路和故障设置开关电流电路的故障诊断针对灾难性(硬)和参数性(软)故障两种。硬故障相对于软故障而言,诊断起来相对容易,因而本节为了验证所提出方法的有效性,以六阶切比雪夫低通滤波器电路软故障诊断实例来验证本文提出的方法,电路如图 3所示。
|
图 3 六阶切比雪夫低通滤波器电路 Figure 3 Six-order Chebyshev low-pass filter circuit |
图中晶体管的归一化跨导值为:Ma=1,Mb=0.425 5,Mc=1.984 5,Md=0.345 5,Me=0.984 5,Mf=0.582 7,Mg=1.913 4,Mh=0.085,Mi=0.857 7,Mj=2.102 1,Mk=0.278 7。电路截止频率为5 MHz,截止频率与时钟频率之比是1:4,时钟频率为20 MHz,带内纹波0.5 dB。
设跨导gm的容差范围为5%,通过灵敏度分析,可知电路中可能发生故障的晶体管为5个,分别为Mg,Mf,Me,Md和Mj。当其中一个晶体管跨导gm值偏移了标称值50%,而其他4个晶体管在其容差范围内变化,电路即为发生软故障,这时所得到的时域响应为有故障类。如表 1所示,可形成共10种软故障模式,其中↑和↓意味着高于或低于标称值50%。
| 表 1 切比雪夫低通滤波器软故障类 Table 1 Classes of soft fault in Chebyshev low-pass filter |
5.2 小波分形分析方法特征计算
首先通过ASIZ软件对开关电流电路故障进行模拟,在电路的输出端获得对应于每个故障类别的60个故障响应信号。接着,对这些故障响应信号进行5层db2小波分解,提取1~5层小波变换的小波逼近系数,再计算相应的分形维数,从而获得每个故障响应信号的6个候选特征值。
图 4给出了6阶切比雪夫低通滤波器电路的MOS管Md发生Md↓即F2故障时,对其中的一个故障响应信号进行5层db2小波分形分析而产生的低频细貌示意图。6个子图分别对应于原故障响应信号及1~5层的逼近系数ca1~ca5。对原始信号和5个小波逼近系数进行分形维计算分别得到各自的分形维数为1.182 4,1.153 6,1.090 3,1.374 3,1.648 7,1.000 1,从而得到了一个侯选特征向量。对所有的故障响应信号进行以上分析,从而得到侯选特征向量集。再依据第3节提出的KPCA方法对每一故障类的所有特征向量提取主元。

|
图 4 Md↓故障信号5层db2小波分解低频细貌意示图 Figure 4 Low frequency schematic diagram of five-layer-db2 wavelet decomposition of Md↓ fault signals |
5.3 核主元分析特征提取
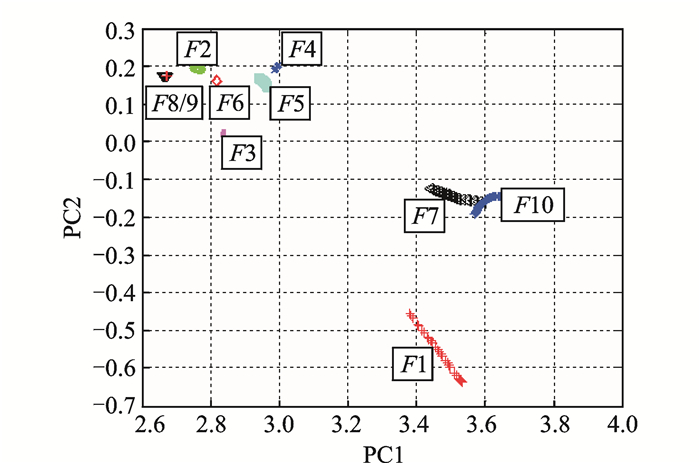
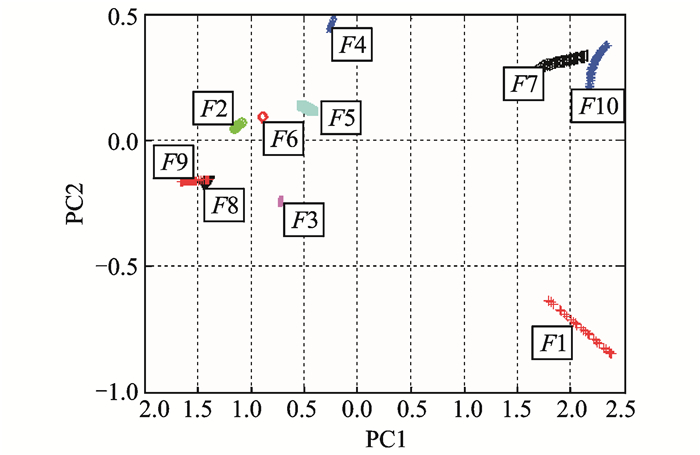
本文以开关电流故障电路的10类故障状态各30组数据,共300组数据的分形维特征向量作为训练样本,用KPCA进行特征提取。经过多次取值试验,KPCA中的核函数采用径向基函数,当σ=1.2时,KPCA可以达到较好的降维和分类效果。为了突出本文所采用的特征提取方法的优势,本文还同时采用PCA方法对侯选特征矢量进行提取。图 5,6分别给出了采用基于PCA和KPCA提取后的前2个主元(PCi)表征的故障类别分布图。在图 5中,F8和F9以及F7和F10故障类别之间发生了比较严重的类别重叠,而在图 6中,只有F8和F9故障类之间发生了重叠,其余各个故障类别都得到了比较好的分离,并且不属于同一类别的故障分得更开。由此可见,基于KPCA的主元特征提取方法获得了比较好的效果,非常有利于后续SVM进行高精确性的故障识别。
|
图 5 PCA的二维分类效果 Figure 5 Effects of 2-D classification of PCA |
|
图 6 KPCA的二维分类效果 Figure 6 Effects of 2-D classification of KPCA |
5.4 仿真结果分析
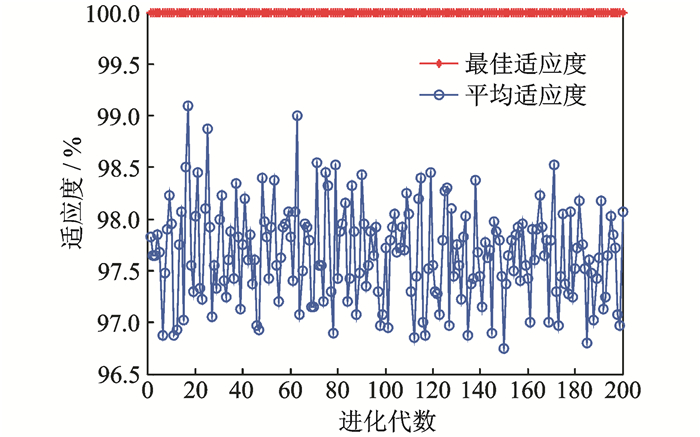
本文通过PSO算法对SVM模型进行参数选取,为了突出PSO算法选取参数的必要性,将基于遗传算法(Genetic algorithm, GA)的SVM模型参数选取和PSO方法进行比较。考虑到GA和PSO算法中r(·)对最终结果的影响,分别对两种优化算法分别运行10次。图 7,8分别为GA和PSO算法在SVM十次优化过程优化结果最好的一次适应度变化曲线,参数c1=1.5,c2=1.7,终止代数200,种群数量20。从图中可以看出,PSO算法的最好适应度达到了100%,GA最好达到98%,因此引入PSO算法进行参数选取效果更好。

|
图 7 GA算法适应度变化曲线 Figure 7 Curve of GA fitness change |
|
图 8 PSO算法适应度变化曲线 Figure 8 Curve of PSO fitness change |
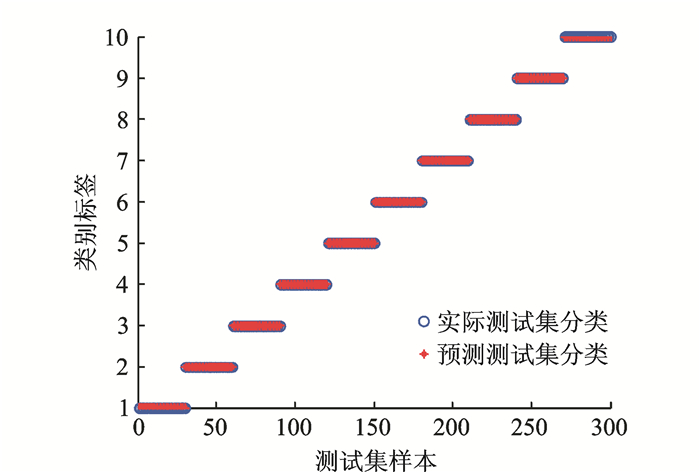
根据PSO-SVM分类器的分类性能来验证本文特征提取方法的有效性。以30组故障数据作为训练样本数据,另选30组数据作为测试数据,计算并提取相应的主元特征。SVM的核函数选用径向基函数,C和g经过PSO优化后分别取22.96和1 000。表 2给出了在小波分解计算出分形维数后,采用PCA和KPCA实施特征提取时的SVM的正确分类率。在二维和三维特征维数的情况下,采用PCA进行特征提取时的粒子群SVM正确分类率分别为96.32%和99.04%,而采用KPCA正确分类率均达到了100%。可知,基于KPCA特征提取的分类效果优于使用PCA的特征提取的分类效果。如图 9所示,KPCA主元特征提取后的最优特征向量输入SVM分类器后所有的故障得到了完全的分类。
| 表 2 采用PCA和KPCA进行特征提取时的粒子群SVM正确分类率 Table 2 Correct rate of classification with particle-swarm-SVM in feature extraction |
|
图 9 基于PSO-SVM的预测分类结果 Figure 9 Results of PSO-SVM prediction-based classification |
本文提出的方法有效地解决了文献[21]中因出现熵的模糊集重叠而影响故障的正确分类,因为作者是只采用熵作为唯一提取的特征,当遇到故障类别之间重叠的时候,无法采用更多的特征来提高诊断系统的性能。
文献[16]的故障晶体管和产生的故障模式和本文一样,有5个晶体管发生故障产生,文献[16]中Mg1↓故障类下50个数据38个诊断正确,12个被误诊断为Mi↑,另外对于Mi↑,Mg1↑和Mi↓故障也有误分类。所以该方法故障诊断率只有95%。而本文方法的故障诊断效率达到了100%。通过与文献[16]的比较结果可以看出,采用本文方法可获得比文献[16]中更高的诊断正确率,且可以成功诊断区分Mg1↓, Mj↑, Mg1↑和Mi↓故障状态,这是在文献[16]中无法成功区分的。同时,该方法可以根据故障数据的复杂程度的高低和故障类别的重叠程度的大小,选取合适数量的特征用于故障分类器进行故障诊断,以获得令人满意的诊断结果。另外,此方法对于开关电流电路多故障类问题的诊断提供了研究方向。
6 结束语本文提出的基于小波分形分析和核主元分析特征提取方法的支持向量机故障诊断系统能有效地对开关电流电路进行故障诊断,得到了较高的故障诊断正确率,并将核主元特征提取法和主元特征提取法做了比较,体现了本文所提出的故障诊断方法的优越性。该方法有效地区别了不同重叠程度的故障类别,获取的特征对分类器具有较强的鲁棒性,可以将此方法推广到多故障开关电流电路的诊断中去。
| [1] |
杨智明, 俞洋, 乔立岩, 等.
基于偏置经验特征映射的电路故障诊断方法[J]. 仪器仪表学报, 2013, 34(7): 1595–1602.
Yang Zhiming, Yu Yang, Qiao Liyan. Electronic circuit fault diagnosis method based on biased empirical feature mapping[J]. Chinese Journal of Scientific Instrument, 2013, 34(7): 1595–1602. |
| [2] |
胡梅, 胡列峰, 明德祥.
模拟电路统一软故障诊断的研究[J]. 电子测量与仪器学报, 2013, 27(11): 1060–1066.
Hu Mei, Hu Liefeng, Ming Dexiang. Study on unified soft fault diagnosis of analog circuits[J]. Journal of Electronic Measurement and Instrument, 2013, 27(11): 1060–1066. |
| [3] | Yuan L, He Y, Huang J. A new neural-net-work-based fault diagnosis approach for analog circuits by using kurtosis and entropy as a preprocessor[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(3): 586–595. DOI:10.1109/TIM.2009.2025068 |
| [4] | EI-Gamal M A, Mohamed M D A. Ensembles of neural networks for fault diagnosis in analog circuits[J]. Journal of Electronic Testing, 2007, 23(4): 323–339. DOI:10.1007/s10836-006-0710-1 |
| [5] |
孙健, 王成华, 杜庆波.
基于小波包能量谱和NPE的模拟电路故障诊断[J]. 仪器仪表学报, 2013, 34(9): 2021–2027.
Sun Jian, Wang Chenghua, Du Qingbo. Analog circuit fault diagnosis based on wavelet packet energy spectrum and NPE[J]. Chinese Journal of Scientific Instrument, 2013, 34(9): 2021–2027. |
| [6] | Sether G E, Toumazou C, Taylor G. Built-in self test of S2I switched current circuits[J]. Analog Integrated Circuits and Signal Processing, 1996, 9(1): 25–30. DOI:10.1007/BF00158849 |
| [7] | Taylor G E, Toumazou C, Wrighton P, et al.Mixed signal test considerations for switched current signal processing[C]// Proceedings of the 35th Midwest Symposium on Circuits and Systems. [S.l.]:IEEE, 1992: 756-759. |
| [8] | Wrighton P L, Taylor G E, Bell I M. Test for switched-current circuits[M]. London: Peter Peregrinus Ltd, 1993: 487-507. |
| [9] | Renovell M, Azais F, Bodin J C. BISTing switched-current circuits[J]. Proceedings of the Asian Test Symposium, 1998, 43(11): 372–377. |
| [10] | Wey C L. Built-in self-test design of current-mode algorithmic analog to digital converters[J]. IEEE Transactions on Instrumentation and Measurement, 1997, 46(3): 667–671. DOI:10.1109/19.585427 |
| [11] |
黄俊, 何怡刚.
开关电流电路故障诊断技术的初步研究[J]. 现代电子技术, 2007, 30(9): 76–78.
Huang Jun, He Yigang. Pilot study on the fault diagnosis of switched current circuits[J]. Modern Electronics Technique, 2007, 30(9): 76–78. |
| [12] | Guo J, He Y, Tang S. Switched-current circuits test using pseudo-random method[J]. Analog Integrated Circuits and Signal Processing, 2007, 52(1/2): 47–55. |
| [13] | Guo J, He Y, Cai X.PRBS test signature analysis of switched curent circuit[C]// 2009 1st International Conference on Information Science and Engineering (ICISE).[S.l.]:IEEE, 2009: 627-630. |
| [14] | Long Y, He Y, Liu L. Implicit functional testing of switched current filter based on fault signatures[J]. Analog Integrated Circuits and Signal Processing, 2012, 71(2): 293–301. DOI:10.1007/s10470-011-9723-5 |
| [15] | Zhang Z, Duan Z, Long Y, et al. A new swarm SVM based fault diagnosis approach for switched current circuit by using kurtosis and entropy as a preprocessor[J]. Analog Integrated Circuits and Signal Processing, 2014, 81(1): 289–297. DOI:10.1007/s10470-014-0373-2 |
| [16] | Guo J, He Y, Liu M. Wavelet neural network approach for testing of switched current circuits[J]. Journal of Electronic Testing, 2011, 27(5): 611–625. DOI:10.1007/s10836-011-5248-1 |
| [17] | Kartz M. Fractals and the analysis of waveforms-Computers in Biology and Medicine[J]. Computers in Biology & Medicine, 1988, 18(18): 145–156. |
| [18] | Scholkopf B, Smola A, Muller K R. Nonlinear component analysis as a kernel eigenvalue problem[J]. Neural Computation, 1998, 10(5): 1299–1319. DOI:10.1162/089976698300017467 |
| [19] |
胡金海, 谢寿生.
核函数主元分析及其在故障特征提取中的应用[J]. 振动、测试与诊断, 2007, 27(1): 48–52.
Hu Jinhai, Xie Shousheng. Kernel principal component analysis and its application to fault feature extraction[J]. Journal of Vibration, Measurement and Diagnosis, 2007, 27(1): 48–52. |
| [20] |
何怡刚, 祝文姬, 周炎涛, 等.
基于粒子群算法的模拟电路故障诊断方法[J]. 电工技术学报, 2010, 25(6): 163–171.
He Yigang, Zhu Wenji, Zhou Yantao, et al. An analog circuit diagnosis method based on particle swarm optimization algorithm[J]. Transactions of China Electrotechnical Society, 2010, 25(6): 163–171. |
| [21] | Long Y, He Y, Yuan L. Fault dictionary based switched curent circuit fault diagnosis using entropy as a preprocessor[J]. Analog Integrated Circuits and Signal Processing, 2011, 66(1): 93–102. DOI:10.1007/s10470-010-9514-4 |
 2016, Vol. 48
2016, Vol. 48


