2. 南京航空航天大学自动化学院,南京,210029;
3. 丽水学院工程与设计学院,丽水,323000
2. College of Automation Engineering, Nanjing University of Aeronautics & Astro nautics, Nanjing, 210016, China;
3. College of Engine ering and Design, Lishui University, Lishui, 323000, China
开关磁阻电机(Switched reluctance motor,SRM)具有结构简单、维护方便、低成本、耐高温、高容错性和固有的高速适应性等特点,在航空航天、军事、民用等领域具备重要应用特色[1-3]。集径向磁轴承和电机功能于一体的无轴承开关磁阻电机(Bearingless switched reluctance motor,BSRM)在实现磁悬浮运行的同时,由于不需独立的径向磁轴承,体积和重量大为减小,可进一步提高功率密度,强化了SRM在全电/多电飞机、舰船、坦克等高速领域的应用基础。
BSRM的研究起始于20世纪90年代,根据每个定子齿上缠绕的绕组数量差异,有单绕组和双绕组两种结构形式。双绕组BSRM的概念最早由日本东京理工大学研究人员提出,在传统SRM的基础上,定子额外增加了一套绕组,即一套传统意义上的转矩绕组,另一套为悬浮绕组,通过控制两套绕组的电流大小和方向,使得悬浮绕组磁通打破转矩绕组磁通,同时产生大小和方向可控的悬浮力和转矩,进而实现其悬浮运行[4-5]。单绕组BSRM,与传统SRM结构完全相同,通过独立控制每相绕组电流的大小,同时产生所需要的转矩和悬浮力,以实现电机的自悬浮和旋转[6-8]。
BSRM是一个多变量、非线性且强耦合的复杂系统,为实现电机的稳定悬浮与旋转,及提升电机性能,必须考虑铁心磁饱和、两个径向悬浮力、以及转矩与径向悬浮力间的耦合等因素。研究初期,为实验验证BSRM的运行和悬浮机理,及降低数学模型推导和控制的复杂度,忽略了磁饱和和耦合特性,并把主、悬绕组电流控制为方波形式,最早成功实现了12/8极双绕组BSRM的悬浮运行[9-11]。
然而,由于磁饱和及电磁参数间的强耦合,尤其转矩负载较大时,BSRM的悬浮精度和运行性能显著下降。为此,国内外学者在数学模型和控制方法等方面的非线性和解耦问题上做了大量的研究[12-37]。日本东京理工大学在数学模型推导中考虑了边缘磁通以及两个径向悬浮力间的交叉耦合,从而使BSRM可稳定悬浮运行在饱和区域和全转矩负载工况[12-14]。
南京航空航天大学把有限元电磁场分析结果应用到BSRM的数学模型中以及计磁饱和,推导出了更为精确的转矩和悬浮力模型[15-20];并相继提出了平均悬浮力、最小损耗、双相导通以及独立控制等新型控制策略,以削弱悬浮力间的耦合强度,提高悬浮精度及运行性能[21-27]。江苏大学在BSRM的全角度拓展模型、解耦控制模型和智能控制算法等方面取得了一些研究成果[28-32]。北京交通大学在悬浮控制机理及滑膜变结构控制方法等方面做了深入的工作[33-35];华中科技大学则研究了BSRM转矩和悬浮力的新型控制方法,并探索将神经网络方法应用于其数学建模中的可行性[36-37]。
上述研究侧重于解决径向悬浮力间的耦合以及铁心的非线性问题;却较少涉及到悬浮力与转矩间的耦合,以及悬浮绕组电流跟踪及斩波控制问题。而这两个问题是决定BSRM高速悬浮精度和运行性能的关键。然而,受限于BSRM的悬浮运行机理,采用新型控制算法和改进数学模型等传统方法,在解决这两个问题时,取得的成效有限。为此,国内外研究人员开始把大量精力投向BSRM新型结构探索上,力图在结构上实现转矩和悬浮力的解耦。逐渐发展了一些新型、具有自解耦功能的BSRM拓扑形式[38-60]。
韩国庆星大学提出了一种两相工作制、定子为宽窄混合结构的8/10极单绕组BSRM[38-40],该电机悬浮和旋转功能分别由宽、窄定子上的绕组独立控制,且在结构上实现转矩和悬浮力的解耦。另外,基于降低铁心损耗和进一步降低转矩和悬浮力间耦合度的考虑,又提出了一种12/14极定子变齿宽的单绕组BSRM[41-44],该电机因磁路变短,悬浮和转矩的解耦度明显提升。为在结构上彻底解决转矩和悬浮力耦合,又发展出了一种双定子单绕组BSRM[45-47],该电机的悬浮力和转矩分别由相互隔离的内、外两个定子上的绕组独立控制,磁路之间完全隔离,故解耦性和容错性高。江苏大学基于8/10、12/14极宽窄定子BSRM,通过在窄定子上又增加一套绕组,提出了两种发电运行的结构拓扑[48-49],均可实现悬浮和发电系统间的解耦控制。北京航空航天大学利用轴向充磁的永磁体作为偏置磁通,并采用隔离的宽窄定子齿结构,提出一种并列式双12/12极BSRM[50-51]。该电机同样可实现解耦控制,还因永磁体提供偏置磁通,即使在较小电流励磁下,也能产生较大的悬浮力。
北京交通大学提出了一种12/8极定子平行齿双绕组BSRM[52-53],南京航空航天大学提出了一种12/8极三相悬浮绕组串联式BSRG[54-56]。这两种电机均是基于电励磁双凸极电机的励磁绕组的构造方式,通过改变悬浮绕组横跨的定子极数,使得悬浮绕组电感恒定不变,致使悬浮绕组不产生转矩,进而实现转矩和悬浮力的解耦。另外,该类电机能够有效降低功率控制器成本和简化电机控制。
除此之外,南京航空航天大学和南京邮电大学针对不同的应用场合,通过改变转子结构以及定、转子极数配合,分别提出了12/4,16/4,12/8极宽转子结构的单绕组BSRM[57-60]。该类电机通过增加转子极弧宽度,使绕组电感在定转子齿与齿对齐位置附近形成一定宽度的平顶区域,并以此作为每相绕组的悬浮励磁区间。因此,该类电机具有悬浮力/电流比大、径向承载能力强和悬浮损耗小等优点,并且由于悬浮励磁区间内绕组电感为恒值,不产生转矩,故也能实现解耦控制。
上述关于BSRM的解耦结构探索与研究,虽然取得了一些成果,但仍存在的一些共性问题:或由于机理的制约不能有效解决悬浮力和转矩的协调控制,以及高速时绕组电流的跟踪和斩波控制;或受限于自身结构形式,不能充分发挥电机的潜力及提高功率密度;或因过分复杂的拓扑结构,弱化了其在高速领域的应用基础,拖延了工程实践的进程。
因此,发展可实现解耦控制、又可解决高速时绕组电流斩波跟踪的新型BSRM结构,是一个值得科学探索的方向。本文拟对现有结构上可解决转矩和悬浮力耦合问题的BSRM的结构、磁路、控制方法进行解析;按其磁路特点及实现方式,对这些结构进行归纳分类,并总结其优缺点。拟基于BSRM解耦拓扑的构造思想,提出双凸定子齿BSRM、宽转子齿BSRM、复合结构BSRM、锥形结构BSRM等4类新型结构,丰富无轴承电机的实现形式。着重分析每类拓扑实现转矩和悬浮力解耦控制的不同实施方式及其结构上的自解耦特性。
1 现有解耦结构拓扑 1.1 不等宽定子齿BSRM该类电机通过重构定、转子极数配合,并利用不同宽度的两种定子齿单独产生转矩和悬浮力,进而实现二者的解耦。具体实现方式为:悬浮绕组所在的宽齿极弧等于一个转子极弧,从而使得悬浮绕组电感在每个转子周期内均恒定不变;基于此,悬浮绕组在悬浮励磁时不产生转矩和运动电动势,进而使该类电机具有自解耦能力。
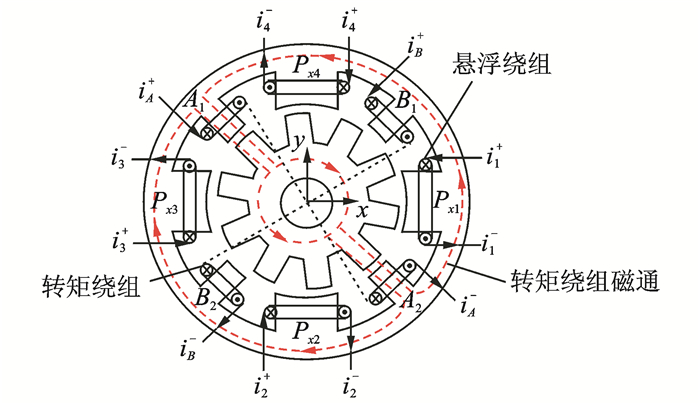
1.1.1 不等宽定子齿BSRM文献[38~40]提出了一种新型的8/10极不等宽定子齿BSRM。该电机定子由宽、窄两种定子齿构成,且每个定子齿上仅绕有一套绕组,如图 1所示。悬浮和旋转的功能分别由宽齿绕组(悬浮绕组)和窄齿绕组(转矩绕组)独立控制。由于宽齿极弧等于一个转子周期角,悬浮绕组的磁导为一恒值,不随转子位置变化,悬浮绕组电流不产生转矩,故该电机在结构上实现了悬浮力和转矩的解耦。另外,由于悬浮绕组电感为恒值,不产生反电动势,故可消除其对电流斩波控制的影响,提升电流跟踪效果。
|
图 1 8/10极不等宽定子齿BSRM Figure 1 8/10 BSRM with hybrid stator poles |
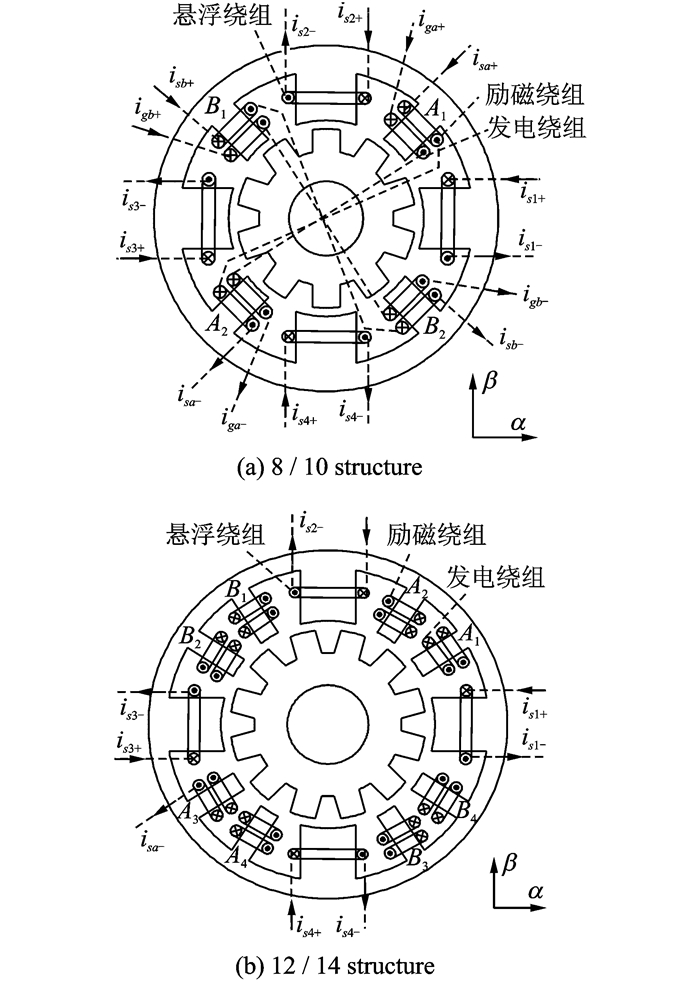
然而,由于转矩绕组磁路较长且定子轭磁通存在翻转现象,定子铁心损耗较高,文献[41~44]通过对8/10结构优化改进,又提出了一种具有短磁路的12/14极不等宽定子齿BSRM,如图 2所示。该结构转矩绕组磁通仅经过窄定子齿、气隙和转子闭合,而不与宽定子齿交链,因此进一步降低了转矩和悬浮力磁路的耦合关系,具有更高的解耦性。

|
图 2 短磁路12/14极BSRM Figure 2 12/14 BSRM with short flux |
不等宽定子齿BSRM,由于宽定子占据大量空间,且电机仅为两相工作制,自起动困难,功率密度较低,另外转子极数较多,且大于定子极数,高速适应性较差。
1.1.2 不等宽定子齿BSRG文献[45, 46],基于8/10和12/14极不等宽定子齿BSRM,在窄定子齿又增加了一套发电绕组,提出了两种新型不等宽定子齿无轴承开关磁阻发电机(Bearingless switched reluctance generator, BSRG),如图 3所示。采用有限元方法分析了悬浮力产生机理和发电电压分布规律。研究发现,这两种结构除了可有效解决转矩与悬浮力的耦合外,还能有效削弱发电系统和悬浮系统之间的耦合效应。
|
图 3 两种不等宽定子齿BSRG Figure 3 Two types of BSRGs with hybrid stator poles |
1.1.3 轴向永磁偏置式BSRM
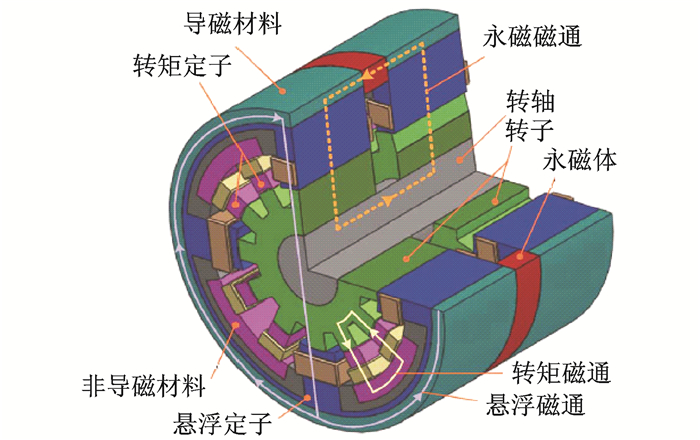
文献[47, 48]利用轴向充磁的永磁体作为偏置磁通,并采用隔离的宽窄定子结构,提出一种双12/12极BSRM, 如图 4所示。该电机两转子轴向错开一定角度,以形成两相工作制。永磁体一侧的位置相对的两宽齿绕组反向串联为一个悬浮绕组,共形成4个;通过与永磁偏置磁通作用,以实现4自由度悬浮。由于转矩磁路与悬浮磁路相互隔离,该电机在结构上完全实现了转矩和悬浮力的解耦,但结构较为复杂,制造成本较高。
|
图 4 轴向永磁偏置式双12/12BSRM Figure 4 12/12 BSRM with axial magnet flux |
1.2 双定子BSRM
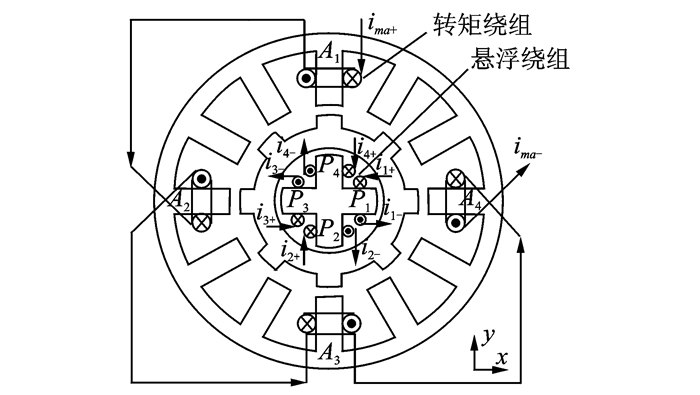
上述不等宽定子齿BSRM虽然在结构上显著地削弱了转矩和悬浮力的耦合,但由于旋转和悬浮始终存在共磁路现象,耦合问题未得到彻底解决。为此,文献[40~42]提出了一种双定子单绕组BSRM,如图 5所示。该电机通过在12/8极SRM转轴内部增加一个具有4个齿的内定子,通过独立控制4个内定子上的绕组,以产生悬浮力;而转矩则由12/8极SRM单独产生。只要转子轭能保证一定的厚度,悬浮力和转矩的耦合问题可完全解决,但因其结构复杂,对加工和装配要求较高。
|
图 5 双定子BSRM Figure 5 BSRM with double stators |
1.3 类双凸极电机BSRM 1.3.1 定子平行齿BSRM
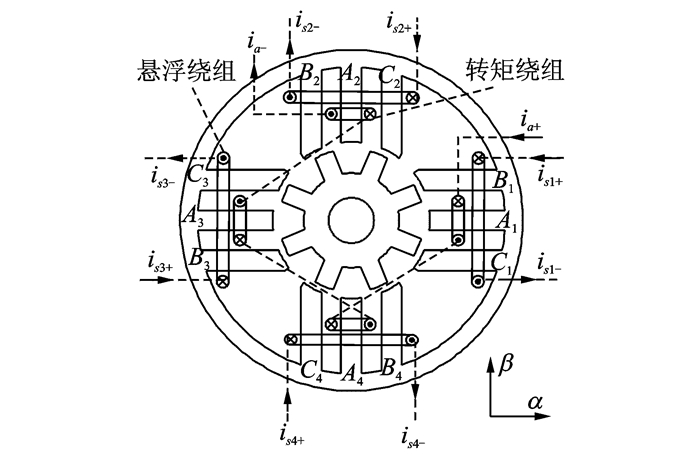
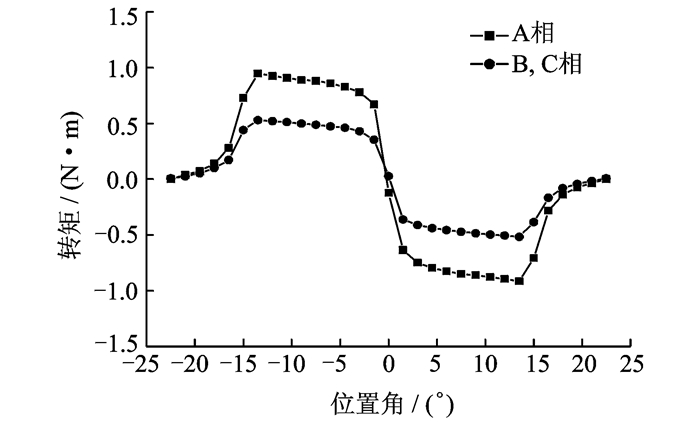
文献[47, 48]提出了一种12/8极定子平行齿双绕组BSRM,如图 6所示。4个悬浮绕组分别横跨紧邻的3个平行定子齿,每个定子齿还绕有一套转矩绕组。当定、转子极弧角均为15°时,悬浮绕组的磁导为一恒值,其电感也不随转子位置变化,因此悬浮绕组不产生转矩,进而可实现转矩和悬浮力的解耦。然而,平行定子齿改变了原电机的磁路分布,处于中间齿的转矩绕组产生的转矩约为另两齿绕组的2倍,如图 7所示(零度角为对齐位置)。因此该结构各相转矩绕组产生的转矩不平衡,脉动大。
|
图 6 12/8极平行定子齿BSRM Figure 6 12/8 BSRM with parallel stator poles |
|
图 7 平行定子齿BSRM各相产生的转矩 Figure 7 Torque of 12/8 BSRM with parallel stator poles |
1.3.2 串励式BSRG
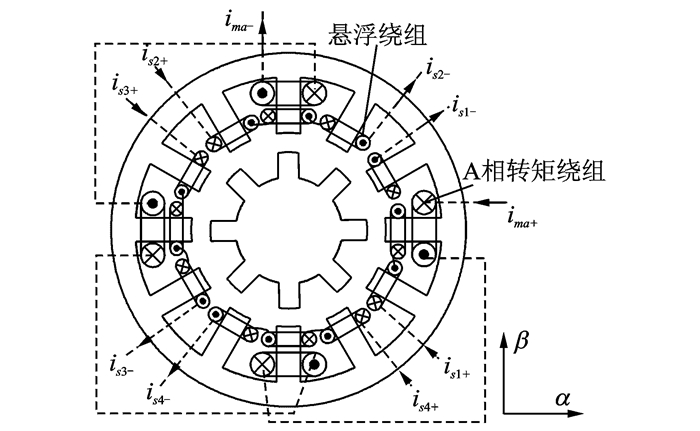
文献[49~51]将传统12/8极双绕组BSRM的相邻三相悬浮绕组串联在一起,提出了一种串励式BSRG (见图 8)。由于相邻3个定子齿上的悬浮线圈串联为一套悬浮绕组,其磁阻不随转子位置变化,因此悬浮绕组不产生转矩。该电机可有效降低功率控制器成本和简化电机控制,另外因所需励磁功率较小,利于励磁系统的设计与控制。但受悬浮运行机理制约,悬浮绕组的磁利用率较低,并且其电动性能较差,更适合作为发电机。
|
图 8 12/8极串励式BSRG Figure 8 12/8 series-excitation BSRG |
2 BSRM的新型结构拓扑 2.1 双凸定子齿BSRM
双凸定子齿BSRM的定子由悬浮定子齿和转矩定子齿构成,悬浮绕组和转矩绕组分别绕在悬浮定子齿和转矩定子上。悬浮定子齿数恒定为4,转矩定子齿数为电机相数的4m倍(m为相数),转子齿数为4的整数倍。
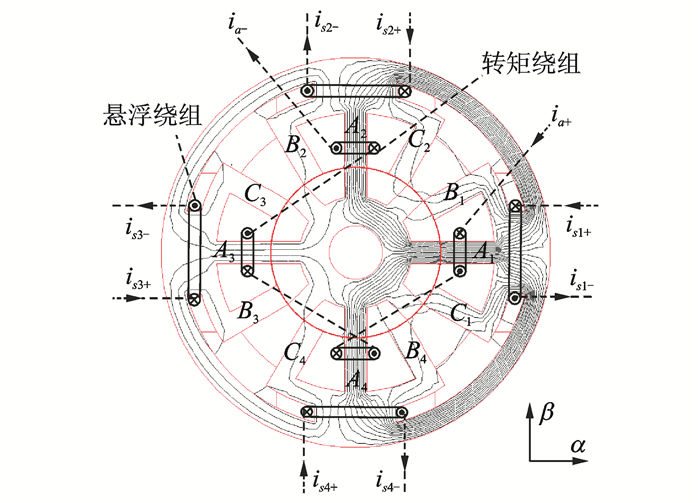
表 1为三相12/8极双凸定子齿BSRM的结构参数。图 9为其结构和绕组连接方式示意图。4个悬浮线圈单独为一套绕组,且独立控制;4个相差90°的转矩定子齿上的线圈串联为一相转矩绕组,图 9中仅给出A相转矩绕组,B, C相的转矩在空间与A相相差30°,-30°。
| 表 1 12/8极双凸定子齿BSRM的结构参数 Table 1 Parameters of 12/8 double-stator BSRM |
|
图 9 12/8极双凸定子齿BSRM Figure 9 12/8 double-salient-stator BSRM |
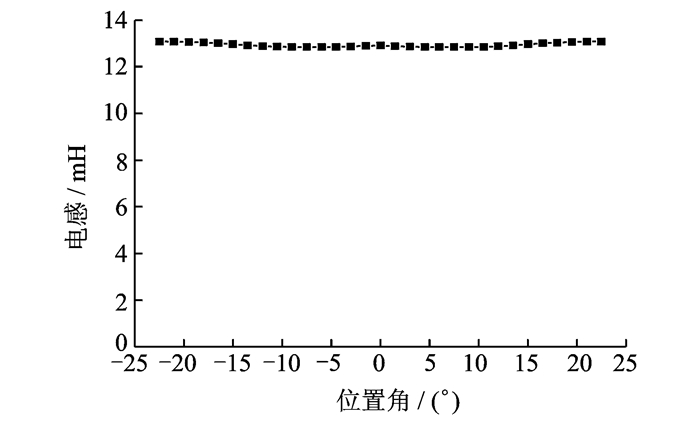
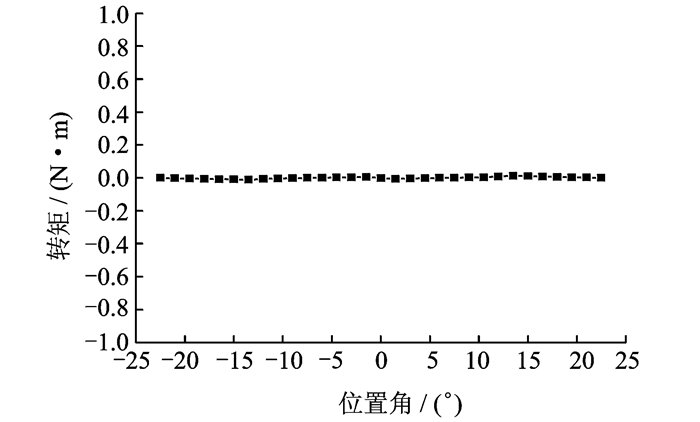
该电机的悬浮控制与磁轴承相似,4个悬浮绕组恒导通,通过不对称励磁,以产生径向悬浮力。而转矩电流的控制方法则与传统SRM相同。由于悬浮绕组在每个转子周期的磁导近似为恒值,悬浮绕组电感也为恒值,悬浮绕组电流不产生转矩,如图 10, 11所示,故可解决转矩和悬浮力间的耦合。另外,该类电机可有效解决平行齿BSRM的转矩不对称问题,克服串励式BSRM悬浮绕组磁利用率不高的缺点。
|
图 10 悬浮绕组电感的有限元仿真值 Figure 10 Simulation on inductance of suspended winding for 12/8 double-salient-stator BSRM |
|
图 11 悬浮绕组单独产生转矩的有限元仿真值 Figure 11 Simulation on torque of suspended winding for 12/8 double-salient-stator BSRM |
2.2 宽转子齿BSRM
宽转子齿BSRM则是利用较大的转子极弧,以改变绕组电感的变化特性,从而在对齐位置处形成一定宽度的平顶区域。采用双相导通策略,利用分时分区域产生转矩和悬浮力的运行模式,以实现转矩和悬浮力的解耦。该电机在电感变化区域产生转矩,在电感平顶区域产生悬浮力;另外,由于电感平顶区域内悬浮力/电流比最大,径向承载力大,且有利于减小悬浮功耗。
为保证绕组的最大电感平顶区足够宽,转子极弧角需显著增大,且定、转子极弧角还需满足
| ${{\beta }_{\text{r}}}\ge {{\beta }_{\text{s}}}+\frac{360{}^\circ }{m\cdot {{Z}_{\text{r}}}}$ | (1) |
式中:βs,βr分别为定、转子极弧角;Zr为转子极数;m为相数。
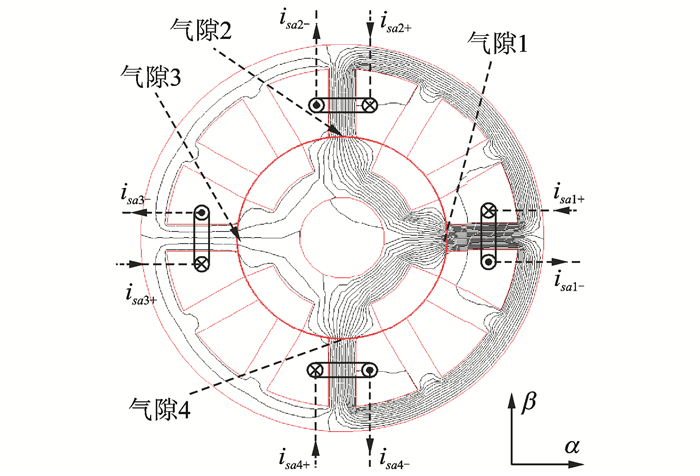
2.2.1 12/4极宽转子单绕组BSRM图 12为三相12/4极宽转子单绕组BSRM的结构示意图,仅给出了A相绕组。12个定子齿均绕有1个绕组,相隔90°的4个绕组共同构成一相绕组;每相4个绕组均独立控制,在电感变化区域对称励磁,产生转矩,在最大电感平顶区域内不对称励磁,以产生悬浮力。B,C相绕组连接方式与A相相同,只是在空间上相隔30°和-30°。
|
图 12 12/4极单绕组BSRM的结构示意图 Figure 12 12/4 single-winding wider-rotor-pole BSRM |
A相α方向两个绕组不对励磁,且isa1>isa3,β方向两个绕组对称励磁时,磁力线分布如图 12所示。此时,气隙2和气隙4处的磁通相等,不产生悬浮力;而气隙1处的磁通大于气隙3处,产生一个α正方向的悬浮力。因此,只需控制一相四套绕组电流的大小,即可产生任意大小和方向的悬浮力,从而实现转子的自悬浮。
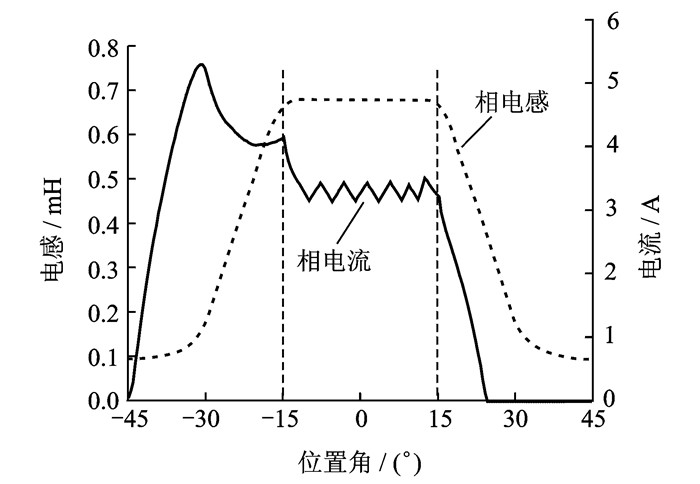
12/4极BSRM的一个转子周期角为90°,对单相悬浮励磁策略而言,每相悬浮励磁区间至少为30°时,才能满足转子的稳定悬浮。为实现转矩和悬浮力的解耦,相绕组最大电感平顶区也必须大于等于30°。图 13为12/4极单绕组BSRM的相绕组电感和电流有限元仿真值,在A相悬浮励磁区内,即[-15°,15°]区间,相绕组最大电感为一恒值,且区间为30°。
|
图 13 相电感和电流的有限元仿真值 Figure 13 Simulation on inductance and current for 12/4 single-winding wider-rotor-pole BSRM |
2.2.2 12/8极宽转子双绕组BSRM
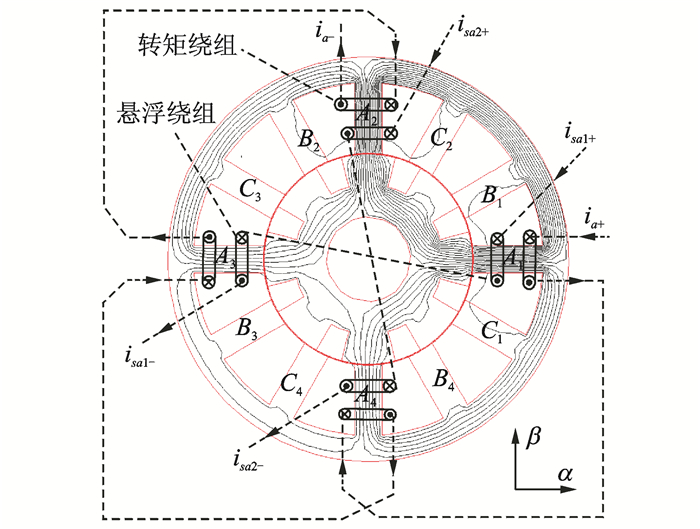
图 14为三相12/8极宽转子双绕组BSRM的结构示意图,也仅给出了A相绕组。该电机绕组连接方式与传统12/8极双绕组BSRM相同,即每相转矩绕组由4个转矩线圈正向串联而成,形成一个四极对称磁通;α方向和β方向悬浮绕组由相对极上的悬浮线圈反向串联而成,分别形成一个二极磁通。
|
图 14 12/8极双绕组BSRM的结构示意图 Figure 14 12/8 double-winding wider-rotor-pole BSRM |
该电机转矩绕组的电流控制方式与12/4极单绕组相似,在电感上升区域,采用SRM的电流控制方式;而在最大电感平顶区域内(15°),转矩绕组电流采用斩波控制方式。悬浮绕组仅在最大电感区域励磁导通,与转矩绕组产生的偏置磁通共同作用,在气隙中形成不对称磁场,进而产生悬浮力。由于悬浮区间内的转矩绕组和悬浮绕组的电感为均恒值,不产生转矩,故可实现转矩和悬浮力的解耦。
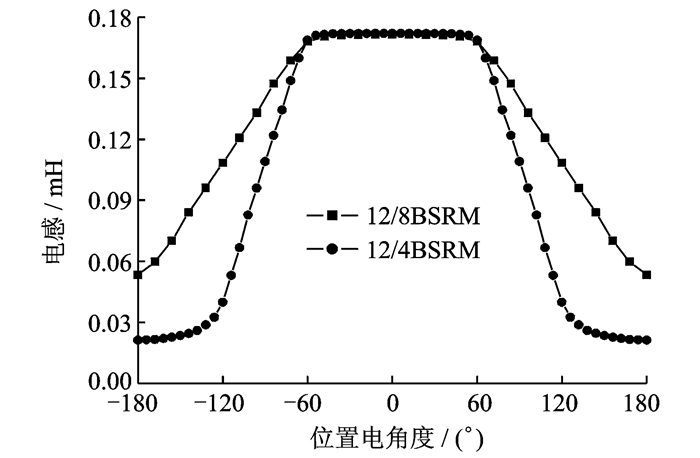
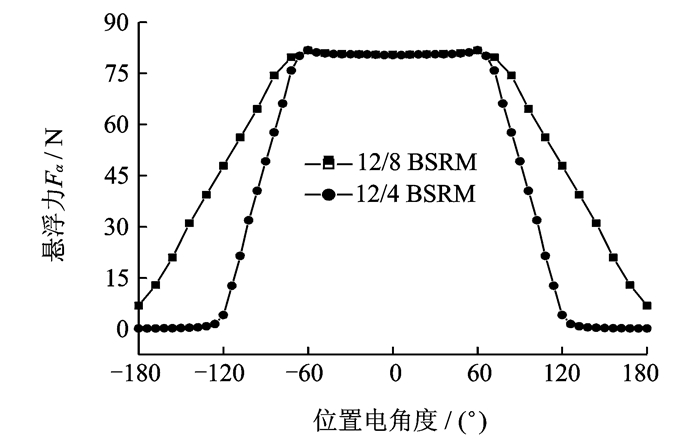
2.2.3 两种宽转子BSRM的解耦特性分析具有相同尺寸(表 2)的两种宽转子BSRM电感、悬浮力和转矩的计算结果分别如图 15~17所示。为便于比较,计算结果中转子位置的机械角度已转换为电角度。结果显示,定、转子极弧角在满足式(1)的最小值时,绕组电感和悬浮力均可产生一个120°电角度的恒值区域,该区域内可实现转矩和悬浮力的解耦。12/4极BSRM的转矩输出宽度仅为12/8极BSRM的二分之一,因此12/8极BSRM具有更好矩角特性。但12/4结构转子极数少,其高速适应性更好。宽转子齿BSRM可有效解决不等宽定子齿BSRM启动能力弱的问题,并且便于优化设计和制造工艺更为简单。
| 表 2 12/4和12/8极宽转子BSRM的结构参数 Table 2 Parameters of 12/4 and 12/8 wider-rotor-pole BSRMs |
|
图 15 两种宽转子齿BSRM的绕组电感 Figure 15 Simulation on inductances for two kinds of BSRMs with wider rotor poles |
|
图 16 两种宽转子齿BSRM的α方向悬浮力Fα Figure 16 Simulation on α-axial suspending forces for two kinds of BSRMs with wider rotor poles |

|
图 17 两种宽转子齿BSRM的转矩 Figure 17 Simulation on torques for two kinds of BSRMs with wider rotor poles |
2.3 复合结构BSRM
文献[61]提出了一种复合转子结构的新型无轴承开关磁阻电机,也称Morrison电机。Morrison电机,是以8/6极SRM为基础,利用一个圆柱转子和凸极转子叠加而成的复合转子,替代原SRM转子,从而构建成的一种新型电机。该电机的悬浮控制类似于磁轴承,相隔90°的4个定子上绕组独立控制且恒导通,用于产生悬浮力;而转矩控制则与传统SRM相同,由剩余4个定子上的线圈两两连接为两相绕组,用于产生转矩。因为圆柱转子和凸极转子均产生悬浮力,该电机径向承载能力强,在径向负载要求高的应用场合具有独特优势。但是该电机同样存在单绕组BSRM结构研究遇到的一些共性问题有待解决:如两相工作制,存在起动死区;悬浮控制采用恒导通模式,势必会运行在负转矩工作区,转矩脉动大,且功率密度不高;不能实现转矩和悬浮力的解耦控制等。
这部分拟基于Morrison电机的构造理念,提出3种新型12/8极复合结构BSRM,既有单绕组形式,又有双绕组结构,逐个分析了每种结构的解耦运行机理,并利用有限元分析结果验证其解耦性。
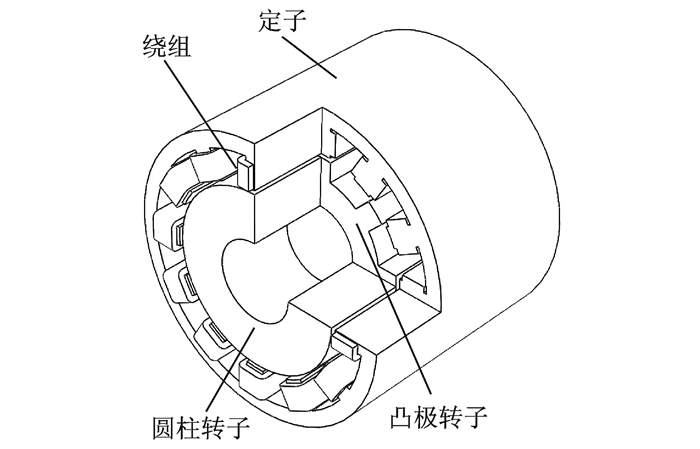
2.3.1 复合转子单绕组BSRM图 18为三相12/8极复合转子单绕组BSRM的三维剖视图。其控制方式与12/4极宽转子齿单绕组BSRM相似,每相4个绕组独立控制;不同之处在于悬浮励磁区间不同,该电机是通过在最小电感平顶区域不对称励磁,以产生悬浮力。表 3为其结构参数。
|
图 18 12/8极复合转子单绕组BSRM Figure 18 12/8 hybrid-rotor single-winding BSRM |
| 表 3 12/8极复合转子单绕组BSRM的结构参数 Table 3 Parameters of 12/8 hybrid-rotor single-winding BSRM |
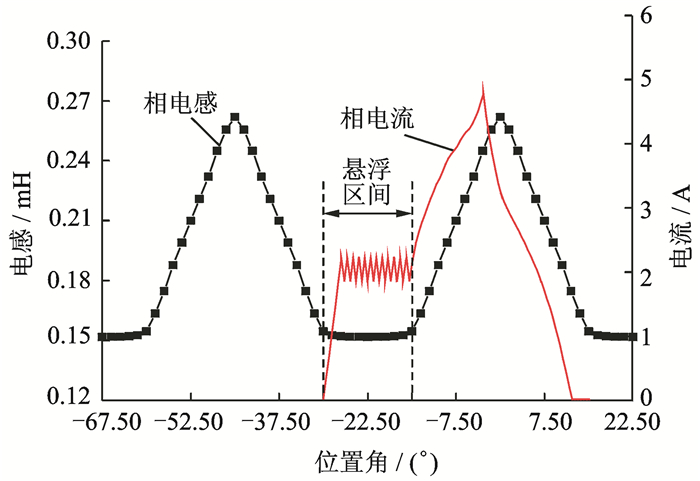
图 19为三相12/8极复合转子单绕组BSRM的A相绕组电感和电流波形有限元仿真值,A相绕组在区间[-30°,-15°]不对称励磁产生悬浮力,且悬浮励磁阶段绕组电流斩波控制为恒值;然后在[-15°,0°]区间,通过对称励磁产生正转矩。
|
图 19 12/8极复合转子BSRM的相电感和电流有限元仿真值 Figure 19 Simulation on inductance and current for 12/8 hybrid-rotorsingle-winding BSRM |
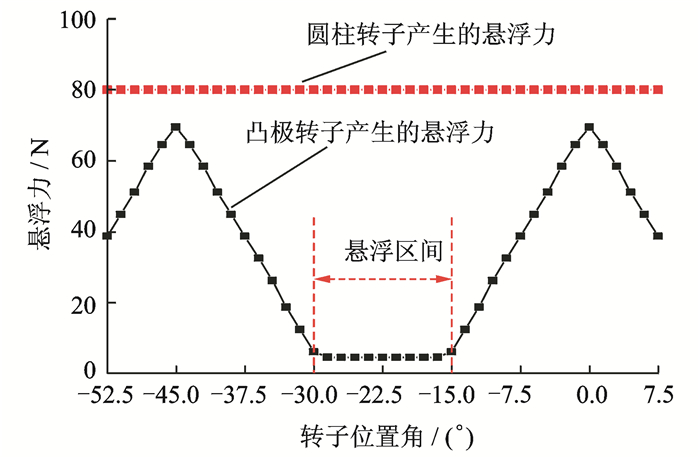
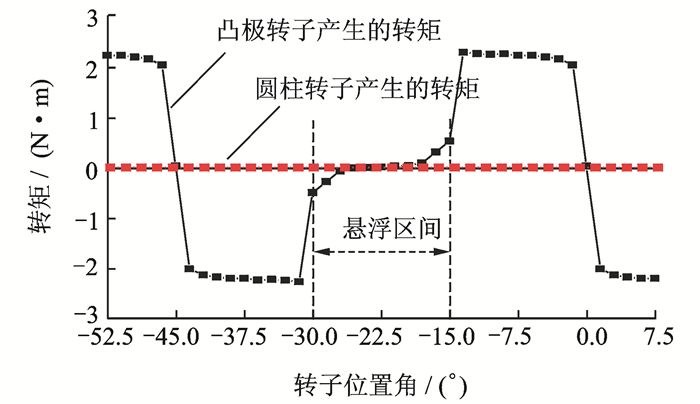
在悬浮区间内,由于凸极转子的磁阻较大,产生的悬浮力相对于圆柱转子可忽略不计,因此该电机的悬浮力可认为由圆柱转子独立产生,如图 20所示。另外,悬浮区域内绕组电感变化平缓,产生的转矩可忽略不计,如图 21所示。因此,采用双相导通策略,利用分时分区域产生转矩和悬浮力的运行模式,即一相绕组在电感变化区域对称励磁,产生转矩,另外一相在最小电感平顶区不对称励磁,产生悬浮力,便可实现12/8极复合转子单绕组BSRM转矩和悬浮力的解耦。
|
图 20 圆柱转子部分和凸极转子部分单独产生的悬浮力有限元仿真结果 Figure 20 Simulation on suspending forces for 12/8 hybrid-rotor single-winding BSRM with individual cylindrical rotor or salient rotor |
|
图 21 圆柱转子部分和凸极转子部分单独产生的转矩有限元仿真结果 Figure 21 Simulation on torques for 12/8 hybrid-rotor single-winding BSRM with individual cylindrical rotor or salient rotor |
2.3.2 复合结构双绕组BSRM
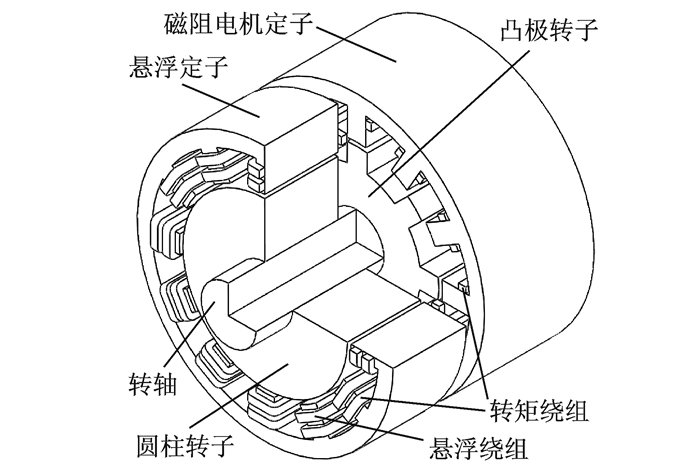
图 22为三相12/8极复合转子双绕组BSRM的三维剖视图。其转矩绕组横跨磁阻电机定子和悬浮定子,且每相转矩绕组由4个转矩线圈串联而成,形成一个四极对称磁通;悬浮绕组仅绕在悬浮定子上,每相两套悬浮绕组均由相对极上的悬浮线圈反向串联而成,产生一个二极磁通。
|
图 22 12/8极复合结构双绕组BSRM Figure 22 12/8 double-winding BSRM with hybrid structure |
该电机的控制方式与12/8极宽转子双绕组BSRM相似;在电感上升区域,转矩绕组采用与SRM相同的电流控制方式;悬浮绕组电流采用斩波控制方式,悬浮励磁区域则由最大电感平顶区(宽度为15°)变为最小电感平顶区(宽度也为15°);悬浮绕组仅在转矩绕组的最小电感区域内励磁导通,与转矩绕组产生的偏置磁通作用,打破气隙中磁通的平衡,进而产生作用于圆柱转子的悬浮力。
由于转矩绕组始终对称励磁,故转矩绕组仅产生转矩,而不产生悬浮力,在悬浮区间产生偏置磁通;而悬浮绕组仅产生悬浮力,而不产生转矩,因此该电机可实现转矩和悬浮力的解耦。另外,隔离的磁路使该电机的容错性更好。
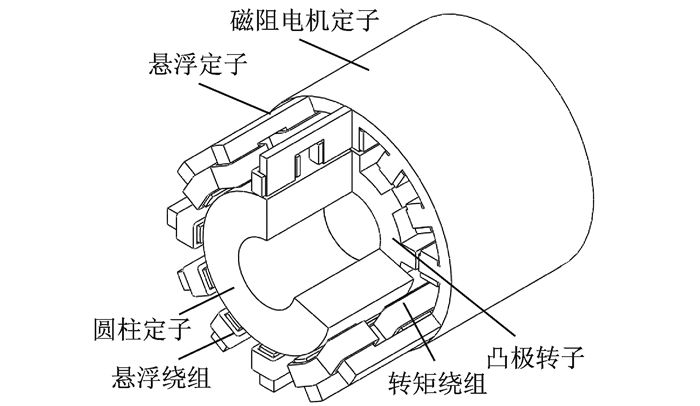
2.3.3 轴向悬浮磁通复合结构BSRM图 23为三相12/8极轴向悬浮磁通复合结构BSRM的三维剖视图。转矩绕组缠绕在磁阻电机定子和与之相邻一个悬浮定子齿上,而远离磁阻电机定子的悬浮定子齿上绕有一个悬浮线圈。悬浮绕组和转矩绕组的连接方式均与上述12/8极复合结构双绕组BSRM相同。
|
图 23 12/8极轴向悬浮磁通复合结构BSRM Figure 23 12/8 hybrid-structure BSRM with axial flux |
该电机的运行原理和解耦控制方式与12/8极复合结构双绕组BSRM相同。不同之处在于,该电机悬浮绕组和转矩绕组在悬浮定子中的磁通具有轴向磁路,且二者共同作用将在每个悬浮定子轴向的两处气隙形成不对称磁通,从而产生悬浮力。因其存在轴向磁路,加工装配难度较大。
2.4 锥形结构BSRM上述BSRM,仅具有径向悬浮功能,若要形成一个稳定磁悬浮系统,至少还需要一个轴向磁悬浮轴承与其配合,以构成五自由度悬浮系统;而这势必会增加轴向长度,降低临界转速,并将导致悬浮系统复杂度进一步提高。
因此,如果将上述所有拓扑中实现悬浮功能的部分设计成锥形结构,衍生出的新型拓扑将具有轴向悬浮功能,有助于系统集成度提升。由于每种结构衍生锥形结构的实施方式相似,限于篇幅,仅以三相12/8极复合结构单绕组BSRM衍生为锥形结构拓扑以例,来说明锥形结构磁悬浮电机的特点。
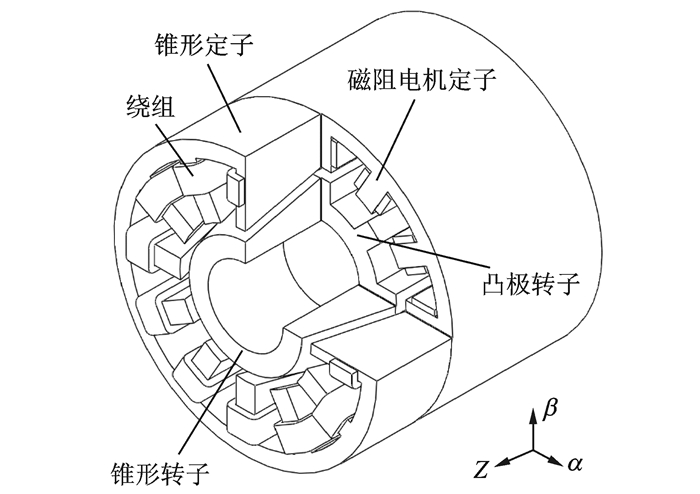
图 24为三相12/8极锥形复合结构单绕组BSRM的三维剖视图。其绕组连接方式、控制策略及悬浮原理与12/8极复合结构单绕组BSRM基本相同;不同之处在于,其产生的悬浮力垂直于锥形转子表面,除了具有径向分量外,还有一个轴向分量。轴向悬浮力方向始终由粗锥形转子端指向细锥形转子端(即图 24中的Z轴正方向),故锥形BSRM仅具有2.5自由度的悬浮能力。因此,要构成一个稳定的五自由度磁悬浮系统,需集成两个2.5自由度的锥形BSRM。因其不再需要轴向磁轴承,由两个锥形BSRM组成的五自由度悬浮系统,具有更高的集成度。
|
图 24 12/8极锥形复合结构单绕组BSRM Figure 24 12/8 single-winding BSRM with hybrid conical structure |
3 结束语
根据现有BSRM实现自解耦的机理和构造特点,本文把其归纳为不等宽定子齿结构、双定子结构和类双凸极电机结构等3类,总结了每种结构的优缺点,并解析了其实现解耦控制的电磁本质。
本文提出了双凸定子齿BSRM、宽转子齿BSRM、复合结构BSRM及锥形结构BSRM等4类结构上具有自解耦功能的无轴承电机。每类结构又衍生出不同的拓扑形式,在相应的工作模式下,均可实现转矩和悬浮力的解耦,有限元仿真结果验证了其解耦悬浮机理的可行性。提出的新型无轴承开关磁阻电机的结构拓扑,丰富了无轴承电机的悬浮理论,拓宽了其实现形式。
| [1] | MacMinn S R, Jones W D.A very high speed switched reluctance starter/generator for aircraft engine application[C]//Proceedings of the IEEE 1989 National Aerospace and Electronics Conference.[S.l.]:IEEE, 1989:1758-1764.http://www.oalib.com/references/7434002 |
| [2] | Ferreira C A, Jones S.R, Heglund W S. Detailed design of a 30-kW switched reluctance starter generator system for agas turbine engine application[J]. IEEE Trans on Ind Applicat, 1995, 31(3): 553–561. DOI:10.1109/28.382116 |
| [3] |
严仰光, 秦海鸿, 龚春英, 等.
多电飞机与电力电子[J]. 南京航空航天大学学报, 2014, 46(1): 11–18.
Yan Yangguang, Qin Haihong, Gong Chunying, et al. More electric aircraft and power electronics[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(1): 11–18. |
| [4] | Chiba A, Chida K, Fukao T.Principles and characteristics of a reluctance motor with windings of magnetic bearing[C]//Proceedings of IEEE IPEC.Tokyo:[s.n.], 1990:919-926. |
| [5] | Chiba A, Rahman M A, Fukao T. Radial force in a bearingless reluctance motor[J]. IEEE Transactions on Magnetics, 1991, 27(2): 786–790. DOI:10.1109/20.133292 |
| [6] | Choi B B, Siebert M.A bearingless switched reluctance motor for high specific power applications[C]//Proceedings of 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit.Sacramento, California:[s.n.], 2006:1-14.http://www.oalib.com/references/16612532 |
| [7] | Lin F C, Yang S M.Radial force control of a switched reluctance motor with two-phase sinusoidal excitations[C]//Proceedings of IEEE IAS Annual Meeting.Tampa, FL:[s.n.], 2006:1171-1177. |
| [8] | Lin F C, Yang S M. Self-bearing control of a switched reluctance motor using sinusoidal currents[J]. IEEE Transac tions on Power Electronic, 2007, 22(6): 2518–2526. DOI:10.1109/TPEL.2007.909274 |
| [9] | Takemoto M, Shimada K, Chiba A, et al.A design and characteristics of switched reluctance type bearingless motors[C]//Proceedings of 4th International Symposium on Magnetic Suspension Technology.Gifu, Japan:[s.n.], 1998:49-63. |
| [10] | Takemoto M, Chiba A, Fukao T. A method of determining advanced angle of square-wave currents in a bearing less switched motor[J]. IEEE Transactions on Industry Application, 2001, 37(6): 1702–1709. DOI:10.1109/28.968181 |
| [11] | Takemoto M, Chiba A, Fukao T.A new control method of bearingless switched reluctance motors using square-wave currents[C]//Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting.Singapore:[s.n.], 2000:375-380.http://www.oalib.com/references/16826438 |
| [12] | Takemoto M, Suzuki H, Chiba A, et al. Improved Analysis of a Bearingless Switched Reluctance Motor[J]. IEEE Transactions on Industry Application, 2001, 37(1): 26–34. DOI:10.1109/28.903123 |
| [13] | Takemoto M, Chiba A, Suzuki H, et al. Radial force and torque of a bearingless switched reluctance motor operating in a region of magnetic saturation[J]. IEEE Transactions on Industry Application, 2004, 40(1): 103–112. DOI:10.1109/TIA.2003.821816 |
| [14] | Michioka C, Sakamoto T, Ichikawa O, et al. A decoupling control method of reluctance-type bearingless motors considering magnetic saturation[J]. IEEE Transactions on Industry Application, 1996, 32(5): 1204–1210. DOI:10.1109/28.536884 |
| [15] |
邓智泉, 杨钢, 张媛, 等.
一种新型的无轴承开关磁阻电机数学模型[J]. 中国电机工程学报, 2005, 25(9): 139–146.
Deng Zhiquan, Yang Gang, Zhang Yuan, et al. An innovative mathematical model for a bearingless switched reluctance generator[J]. Proceedings of the CSEE, 2005, 25(9): 139–146. |
| [16] |
张媛, 邓智泉.
无轴承开关磁阻电机控制系统的设计与实现[J]. 航空学报, 2006, 27(1): 77–81.
Zhang Yuan, Deng Zhiquan. Design and realization of bearingless switched reluctance motor control system[J]. Acta Aeronauticaet Astronautica Sinica, 2006, 27(1): 77–81. |
| [17] |
曹鑫, 邓智泉, 杨钢, 等.
新型无轴承开关磁阻电机双相导通数学模型[J]. 电工技术学报, 2006, 26(22): 97–103.
Cao Xin, Deng Zhiquan, Yang Gang, et al. Novel mathematical model of bearingless switched reluctance motors with two-phase excitation[J]. Transactions of China Electrotechnical Society, 2006, 26(22): 97–103. |
| [18] |
曹鑫, 邓智泉, 杨钢, 等.
无轴承开关磁阻电机麦克斯韦应力法数学模型[J]. 中国电机工程学报, 2009, 29(3): 78–83.
Cao Xin, Deng Zhiquan, Yang gang, et al. Mathematical model of bearingless switched reluctance motors based on maxwell stresstens or method[J]. Proceedings of the CSEE, 2009, 29(3): 78–83. |
| [19] | Cao Xin, Deng Zhiquan, Yang gang, et al. Independent control of average torque and radial force in bearingless switched-reluctance motors with Hybrid Excitations[J]. IEEE Trans on Power Electronics, 2009, 24(5): 1376–1385. DOI:10.1109/TPEL.2009.2016568 |
| [20] |
杨艳, 邓智泉, 曹鑫, 等.
12/8极无轴承开关磁阻电机定子振动特性分析[J]. 南京航空航天大学学报, 2010, 42(4): 454–500.
Yang Yan, Deng Zhiquan, Cao Xin, et al. Characteristic analysis of stator vibration for 12/8 bearingless switched reluctance motors[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(4): 454–500. |
| [21] |
曹鑫, 邓智泉, 杨钢, 等.
一种无轴承开关磁阻电机独立控制策略[J]. 中国电机工程学报, 2008, 28(24): 94–100.
Cao Xin, Deng Zhiquan, Yang Gang, et al. An independent controlsc heme of bearingless switched reluctance motors[J]. Proceedings of the CSE, 2008, 28(24): 94–100. |
| [22] |
杨钢, 邓智泉, 曹鑫, 等.
无轴承开关磁阻电机平均悬浮力控制策略[J]. 航空学报, 2009, 30(3): 505–511.
Yang gang, Deng Zhiquan, Cao Xin, et al. Control strategy of average levitated force of a bearingless switched reluctance motor[J]. Acta Aeronauticaet Astronautica Sinica, 2009, 30(3): 505–511. |
| [23] |
杨钢, 邓智泉, 张媛, 等.
无轴承开关磁阻电机实验平台的设计与实现[J]. 中国电机工程学报, 2006, 26(22): 97–103.
Yang Gang, Deng Zhiquan, Zhang Yuan, et al. The design and realization of experimen tplatform of a bearingless switched reluctance motor[J]. Proceedings of the CSEE, 2006, 26(22): 97–103. |
| [24] |
杨钢.无轴承开关磁阻电动机的基础研究[D].南京:南京航空航天大学, 2008.
Yang Gang.Basic research on bearingless switched reluctance motors[D].Nanjing: Nanjing University of Aeronautics & Astronautics, 2010.http://www.oalib.com/references/16612538 |
| [25] |
刘泽远.无轴承开关磁阻电机的电磁基础研究[D].南京:南京航空航天大学, 2010.
Liu Zeyuan.Basic electromagnetic research on bearingless switched reluctance motors[D].Nanjing: Nanjing University of Aeronautics & A stronautics, 2010.http://cdmd.cnki.com.cn/Article/CDMD-10287-1011291517.htm |
| [26] |
杨艳.无轴承开关磁阻电机振动分析与抑制的基础研究[D].南京:南京航空航天大学, 2010.
Yang Yan.Basic research on vibration analysis and suppression of bearingless switched reluctance motors[D].Nanjing:Nanjing University of Aeronautics & Astronautics, 2010.http://www.oalib.com/references/16826451 |
| [27] |
曹鑫.12/8极无轴承开关磁阻电机的研究[D].南京:南京航空航天大学, 2010.
Cao Xin.Research on 12/8 bearingless switched reluctance motors[D].Nanjing: Nanjing University of A eronautics & Astronautics, 2010.http://www.oalib.com/references/16605998 |
| [28] |
孙玉坤, 刘羡飞, 王德明, 等.
基于有限元分析的磁悬浮开关磁阻电机数学模型的全角度拓展[J]. 电工技术学报, 2007, 22(9): 34–39.
Sun Yukun, Liu Xianfei, Wang Deming, et al. Extension of mathematical model to full angle for bearingless switched reluctance motors based on finite-element analysis[J]. Transactions of China Electrotechnical Society, 2007, 22(9): 34–39. |
| [29] |
项倩雯, 嵇小辅, 孙玉坤, 等.
单绕组磁悬浮开关磁阻电机的原理与解耦控制[J]. 电机与控制学报, 2012, 16(11): 22–28.
Xiang Qianwen, Ji Xiaofu, Sun Yukun, et al. Principle and decoupling control of single-winding bearingless switched reluctance motors[J]. Electric Machines and Control, 2012, 16(11): 22–28. |
| [30] | Liu G, Sun Y, Shen Y, H, et al.Dynamic decoupling control of bearingless switched reluctance motors based on neural network inverse system[C]//Proceedings of the 8th International Conference on Electric Machines and Systems (ICEMS 2005).Nanjing:[s.n.], 2005:1811-1815. |
| [31] |
孙玉坤, 吴建兵, 项倩雯.
基于有限元法的磁悬浮开关磁阻电机数学模型[J]. 中国电机工程学报, 2007, 27(12): 33–40.
Sun Yukun, Wu Jianbing, Xiang Qianwen. The mathematic model of bearingless switched reluctance motor based on the finite-element analysis[J]. Proceedings of the CSEE, 2007, 27(12): 33–40. |
| [32] |
刘羡飞, 孙玉坤, 王德明, 等.
磁悬浮开关磁阻电机径向位置解耦及仿真研究[J]. 系统仿真学报, 2007, 19(7): 1527–1530.
Liu Xianfei, Sun Yukun, Wang Deming, et al. Decoupling and simulat ion study for radial position of bearingless switched reluctance motor[J]. Journal of System Simulation, 2007, 19(7): 1527–1530. |
| [33] |
王喜莲, 葛宝明.
磁浮开关磁阻电机径向悬浮逆系统方法控制[J]. 电机与控制学报, 2009, 13(3): 356–360.
Wang Xilian, Ge Baoming. Radial suspending inverse-system method control for magnetic suspending switched reluctance motor[J]. Electric Machines and Control, 2009, 13(3): 356–360. |
| [34] |
王喜莲, 葛宝明.
磁浮开关磁阻电机悬浮力的变结构控制[J]. 北京交通大学学报, 2010, 34(2): 119–123.
Wang Xilian, Ge Baoming. Variable-structure suspending control for magnetic suspending switched reluctance motor[J]. Journal of Beijing Jiaotong University, 2010, 34(2): 119–123. |
| [35] |
王喜莲, 葛宝明, 赵楠.
磁浮开关磁阻电机悬浮力的反馈线性化PI D控制[J]. 中国电机工程学报, 2009, 29(15): 114–118.
Wang Xilian, Ge Baoming, Zhao Nan. Ax ial suspending feedback linearization PID control for magnetic suspending switched reluctance motor[J]. Proceedings of the CSEE, 2009, 29(15): 114–118. |
| [36] |
曹家勇, 周祖德, 陈幼平.
开关磁阻型动力磁轴承瞬时转矩控制策略的研究[J]. 机械工程学报, 2004, 40(5): 23–29.
DOI:10.3901/JME.2004.05.023 Cao Jiayong, Zhou Zhude, Chen Youping, et al. Instantaneous torque control of an switched reluctance-type power magnetic bearing[J]. Chinese Journal of Mechanical Engineering, 2004, 40(5): 23–29. DOI:10.3901/JME.2004.05.023 |
| [37] | Sun J, Zhan Q, Liu L.Modelling and control of bearingless switched reluctance motor based on artificial neural network[C]//Proceedings of 31st Annual Conference on Industrial Electronics Society (IECON'05).North Carolina, USA: [s.n.], 2005:1638-1643. |
| [38] | Lee D H, Wang Huijun, Ahn J W.Modeling and control of novel bearingless switched reluctance motor[C]//2009 IEEE Energy C onversion Congress and Exposition.San Jose, CA, USA:[s.n.], 2009:276-281. |
| [39] | Park T H, Liang Jianing, Lee D H, et al.Suspending force control scheme for bearingless SRM[C]//2009 IEEE 31st International Telecommunications Energy Conference.Incheon, South Korea:[s.n.], 2009:1-5. |
| [40] | Guan Z, Zhang F, A hn J W.High speed direct current compensation control for 8/10 bearingless SRM [C]//IEEE International Symposium on Industrial Electronics (ISIE).Hangzhou, China:[s.n.], 2012. |
| [41] | Wang H, Wang Y, Liu X, et al. Design of novel bearingless switched reluctance motor[J]. Iet Electric Power Applications, 2012, 6(2): 73–81. DOI:10.1049/iet-epa.2010.0229 |
| [42] | Xu Z, Lee D H, Zhang F, et al.Hybrid pole type bearingless switched reluctance motor with short flux path[C]//2011 IEEE International Conference on Electrical Machines and Systems.Beijing, China:[s.n.], 2011:1-6. |
| [43] | Xu Z, Lee D H, Ahn J W.Suspending force control of a nove l 12/14 hybrid stator poletype bearingless SRM[C]//2012 IEEE 15th International Conference on Electrical Machines and Systems.Sapporo, Japan:[s.n.], 2012:1-5 |
| [44] | Xu Zhenyao, Lee D H, Ahn J W.Modeling and control of a bearingless switched reluctance motor with separated torque and suspending force poles[C]//2013 I EEE International Symposium on Industrial Electronics.Taipei, Taiwan:[s.n.], 2 013:1-6. |
| [45] | Peng W, Lee D H, Zhang F, et al.Design and characteristic analysis of anovel bearingless SRM with double stator[C]//2011 IEEE International Conference on Electrical Machines and Systems.Beijing, China:[s.n.], 2011 :1-6. |
| [46] | Peng Wei, Zhang Fengge, Ahn Jin-Woo.Design and control of a novel bearingless SRM with double stator[C]//2012 IEEE International Symposium on Industrial Electronics.Hangzhou, China:[s.n.], 2012:1928-1933.http://www.oalib.com/references/16826843 |
| [47] | Xu Zhenyao, Lee D H, Ahn J W.Comparative analysis of bearingless switched reluctance motors with decoupled suspending force control[C]//2012 IEEE Industry Applications Society Annual Meeting.Las Vegas, USA:[s.n.], 2012:1-8. |
| [48] |
周云红, 孙玉坤, 嵇小辅, 等.
一种新型的磁悬浮开关磁阻发电机[J]. 中国电机工程学报, 2012, 32(15): 107–113.
Zhou Yunhong, Sun Yukun, Ji Xiaofu, et al. A novel bearingless switched reluctance generator[J]. Proceedings of the CSEE, 2012, 32(15): 107–113. |
| [49] |
孙玉坤, 王丽平, 朱志莹, 等.
一种12/14极短磁路磁悬浮开关磁阻发电机[J]. 电工电能新技术, 2014, 33(5): 38–43.
Sun Yukun, Wang Liping, Zhu Zhiying, et al. 12/14-poles bearingless switched reluctance generator with short flux path[J]. Advanced Technology of Electrical Engineering and Energy, 2014, 33(5): 38–43. |
| [50] | Wang Huijun, Liu Jianfeng, Bao Junfang, et al. A novel bearingless switched reluctance motor with a biased permanent magnet[J]. IEEE Transactions on Industry Electronics, 2014, 61(12): 6947–6955. DOI:10.1109/TIE.2014.2317144 |
| [51] | Liu Jian Feng, Zhang Xinbin, Wang HuiJun, et al.Iron loss characteristic for the novel bearingless switched reluctance motor[C]//2013 IEEE International Conference on Electrical Machines and Systems.Busan, Korea:[s.n.], 2013:1-6. |
| [52] |
王喜莲, 葛宝明, 王旭东.
一种无轴承开关磁阻电机悬浮性能分析[J]. 电机与控制学报, 2013, 17(1): 7–12.
Wang Xilian, Ge Baoming, Wang Xudong. Magnetic suspension perfo rmance analysis of a bearingless switched reluctance motor[J]. Electric Machines and Control, 2013, 17(1): 7–12. |
| [53] | Wang Xilian, Ge Baoming, Wu Zhaoli, et al. A novel bearingless switched eluctance motor[J]. COMPEL: The International Journal for Computation and Mathematics in Electrical and Electronic Engine ering, 2012, 31(6): 1681–1695. DOI:10.1108/03321641211267065 |
| [54] |
曹鑫, 邓智泉, 庄铮, 等.
三相串联励磁式无轴承开关磁阻发电机原理与实现[J]. 电工技术学报, 2013, 28(2): 108–116.
Cao Xin, Deng Zhiquan, Zhuang Zheng, et al. Principle and implementation of a bearingless switched reluctance generator with three adjacent excitation-windings connected in series[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 108–116. |
| [55] |
刘泽远, 杨艳.
串联式无轴承开关磁阻发电机的悬浮力特性[J]. 微特电机, 2015, 43(3): 14–16.
Liu Zeyuan, Yang Yan. Radial force characteristic of a bearingless switched reluctance generator with the adjacent three excitation-windings connected in serie based on different magnetomotive forces[J]. Small & Special Electrical Machines, 2015, 43(3): 14–16. |
| [56] |
庄铮.无轴承开关磁阻发电机的优化控制[D].南京:南京航空航天大学, 2012.
Zhuang Zheng.Optimal control of a bearingless switched reluctance generator[D].Nanjing:Nanjing University of Aeronautics & Astronautics, 2012.http://cdmd.cnki.com.cn/Article/CDMD-10287-1012041449.htm |
| [57] |
曹鑫, 邓智泉, 刘泽远, 等.一种12/4极单绕组无轴承开关磁阻电机及其控制方法[P].中国, 201310244349.5, 2013.
Cao Xin, Deng Zhiquan, Liu Zeyuan.A novel 12/4 single-winding be aringless switched reluctance motor[P].China, 201310244349.5, 2013. |
| [58] | Yang Yan, Liu Zeyuan, Deng Zhiquan, et al. Design and characteristic analysis of anovel bearingless srm considering decoupling between torque and suspension force[J]. Mathematical Problems in Engineering, 2014, Article ID 101626. |
| [59] |
杨艳, 刘泽远, 邓智泉.
一种新型无轴承开关磁阻电动机性能分析[J]. 微特电机, 2014, 42(11): 14–17.
Yang Yan, Liu Zeyuan. Perfermance analysis of a new bearingless switched reluctance motor[J]. Small & Special Electrical Machines, 2014, 42(11): 14–17. |
| [60] | Yang Yan, Liu Fangfang, Liu Chengwei.A new bearingless switched reluctance motor with wide rotor polearc[C]//IEEE Conference on ICIEA.Hangzhou:IEEE, 2014:374-378. |
| [61] | Morrison C R, Siebert M W, Ho E J. Electromagnetic forces in a hybrid magnetic-bearing switc hed-reluctance motor[J]. IEEE Transactions on Magnetics, 2008, 44(12): 4626–4638. DOI:10.1109/TMAG.2008.2002891 |
 2016, Vol. 48
2016, Vol. 48


