未知辐射源的精确定位在定位跟踪、搜寻和营救中具有广泛的应用^[1-2]。低轨双星定位系统具有平台少、成本低、降低了系统实现难度等优势，因此得到了广泛的应用^[3]。但是，由于主星转发器通常存在未知信号的转发时延和频率搬移，导致时差(Time difference of arrival, TDOA)测量和频差(Frequency difference of arrival, FDOA)测量存在较大的系统误差，使得低轨双星定位系统的定位精度一般在3~10 km的范围^[3-5]。近年来，为了提高低轨双星无源定位系统的定位精度，文献[6~8]提出了一种基于4个或4个以上已知位置的地面合作辐射源对未知辐射源TDOA/FDOA误差以及星历误差进行改正的方法。文献[6, 8]主要是利用地面4个或4个以上且位置已知的参考站首先求出两颗卫星的相对星历误差，然后再利用修正后的卫星星历对未知幅射源定位。文献[7]首先定义一个能够反映辐射源定位后所有位置的代价函数，然后使该代价函数最小，求出两颗卫星的相对星历误差。然而上面所提出对未知辐射源系统误差进行改正的方法至少需要4个或4个以上的地面参考站，并且改正的误差是相对误差，同时也需要考虑参考站的布站方式，因此，这将限制该方法的应用。

为了提高低轨双星无源定位系统的定位精度以及减少对未知辐射源定位时所需要的参考站数量，文中借鉴GP S中虚拟参考站(Virtual reference station, VRS)的思想，提出了一种基于VRS的时频差精密修正的方法。该方法不仅可以消除未知辐射源测量时频系统误差，还可以在很大程度上减小双星系统的星历误差，提高了低轨双星无源定位系统的定位精度。此外，由于该方法实现一次定位最少只需要3个参考站且改正的误差都是绝对误差，因此文中所提的方法也可以看成是利用多站对低轨双星TDOA/FODA系统误差改正方法的进一步完善。

1 低轨双星无源定位系统误差分析

根据常规误差理论，低轨双星定位系统的误差来源是：星历误差、转发时延、电离层误差、对流层误差、多路径效应、测量系统误差(TDOA和FDOA)。上述误差可以分为空间相关误差和非空间相关误差。

(1)空间相关误差：星历误差、电离层误差、对流层误差。

(2)非空间相关误差：转发延时、测量误差(TDOA和FDOA)、多路径效应。

转发延时和测量系统误差主要是由两颗卫星的钟差引起。下面详细分析影响低轨双星无源定位系统的主要误差。

假设主卫星测得地面辐射源的到达时间(Time of arrival, TOA)、到达频率(Frequency of arrival, FOA)分别记为t₂，f₂；辅卫星测得地面辐射源的到达时间、到达频率分别为t₁，f₁；假设在地心低固坐标系中，主卫星的位置和速度分别为S₂，Ṡ₂；辅卫星的位置和速度分别为S₁，Ṡ₁；未知辐射源坐标u=(x y z)。因此，主卫星对地面辐射源的TOA和FOA分别写为t₂=$\frac{1}{c}$‖u-S₂‖和f₂=$\frac{{{f_0}}}{c}\frac{{{{\left({{\mathit{\boldsymbol{S}}_2} - \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_2}}}{{\left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_2}} \right\|}}$，其中f₀为未知辐射源载波频率，c为信号传播速度，‖x‖表示向量x的2范数，上标T表示转置运算。由于受到卫星钟差、星历误差以及电离层和对流层等因素的影响，因此主卫星TOA和FOA分别为t₂=‖u-S₂‖+δ_t2+O_t2+T_t2+I_t2+ζ_T，f₂=$\frac{{{f_0}}}{c}\frac{{{{\left({{\mathit{\boldsymbol{S}}_2} - \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_2}}}{{\left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_2}} \right\|}}$+${\dot \delta }$_f2+Ȯ_f2+Ṫ_f2+İ_f2+ζ_F，辅卫星的TOA和FOA也具有和主卫星相同的表达式。因此，对于地面辐射源，其时差方程可以写为

$ \begin{array}{l} {\rm{TDOA}}\left(\mathit{\boldsymbol{u}} \right)={t_2} - {t_1}=\frac{1}{c}\left({\left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_2}} \right\| - \left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_1}} \right\|} \right)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\delta _T}+{O_{{T_{21}}}}+\Delta {T_T}+\Delta {I_T}+{\xi _T} \end{array} $

(1)

式中：δ_T中包含了转发时延和两卫星测量误差之差；O_T21为两卫星的轨道误差之差；ΔT_T为两卫星的对流层之差；ΔI_T为两卫星的电离层之差；ζ_T为时差方程中的其他微小误差。由于卫星到地面的距离远大于两卫星之间的距离，因此，可以认为ΔT_T≈0，ΔI _T≈0。对于地面辐射源u，其频差方程可以写为

$ \begin{array}{l} {\rm{FDOA}}\left(\mathit{\boldsymbol{u}} \right)={f_2} - f=\frac{{{f_0}}}{c}\frac{{{{\left({{\mathit{\boldsymbol{S}}_2} - \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_2}}}{{\left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_2}} \right\|}} - \\ \;\;\;\;\;\;\frac{{{{\left({{\mathit{\boldsymbol{S}}_1} - \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_1}}}{{\left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_1}} \right\|}}+{\delta _F}+{{\dot O}_{{F_{21}}}}+\Delta {{\dot T}_F}+\Delta {{\dot I}_F}+{\zeta _F} \end{array} $

(2)

式中：^δ_F为两卫星测量频偏；Ȯ_F21为两卫星星历误差之差；ΔṪ_F和Δİ_F为两卫星对流层和电离层之差，且基本可以认为等于零；ζ_F为频差方程中的其他微小误差。经简化后，对于地面辐射源的时差、频差方程分别为

$ \left\{ \begin{array}{l} {\rm{TDOA}}\left(\mathit{\boldsymbol{u}} \right)=\frac{1}{c}\left({\left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_2}} \right\| - \left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_1}} \right\|} \right)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\delta _T}+{O_{{T_{21}}}}+{\xi _T}\\ {\rm{FDOA}}\left(\mathit{\boldsymbol{u}} \right)=\frac{{{f_0}}}{c}\left[{\frac{{{{\left({{\mathit{\boldsymbol{S}}_2}-\mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_2}}}{{\left\| {\mathit{\boldsymbol{u}}-{\mathit{\boldsymbol{S}}_2}} \right\|}}-\frac{{{{\left({{\mathit{\boldsymbol{S}}_1} - \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_1}}}{{\left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_1}} \right\|}}} \right]+\\ \;\;\;\;\;\;\;\;\;\;\;\;{\delta _F}+{{\dot O}_{{F_{21}}}}+{\zeta _F}\; \end{array} \right. $

(3)

从式(3)可以看出，在低轨双星无源定位系统中，TDOA/FDOA误差主要由空间相关误差，如星历误差和非相关误差，如转发延时和测量系统误差引起。

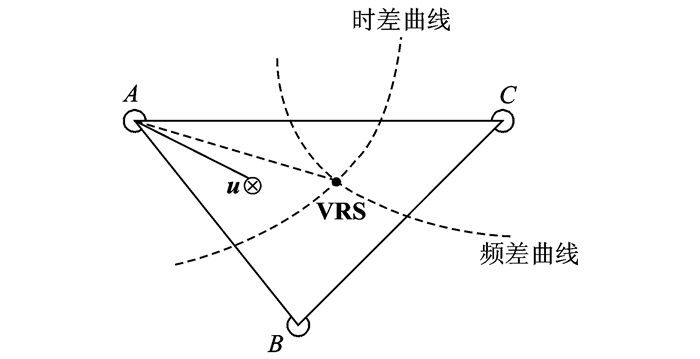
2 低轨双星无源定位中VRS差分原理

将差分全球定位系统(Differential GPS, DGPS)中的VRS技术应用于低轨双星无源定位，关键问题是如何在未知辐射源附近生成虚拟观测值，包括虚拟时差和虚拟频差观测值。图 1是将VRS原理应用于双星无源定位中的系统模型，假设在双星覆盖范围内有6个位置已知的合作辐射源，合作辐射源可以是各个省会的电视塔，也可以是在已知位置临时架设的合作辐射源。图中未知辐射源坐标为u，未知辐射源附近建立的虚拟参考站其坐标定义为VRS。文中分析了影响时频差误差的主要因素，因此可以采用站间差分消除非空间误差，只剩下空间相关误差，这就为VRS技术在双星无源定位中的实现提供了可能性。

DGPS中VRS的运行包含4个步骤^[9]，参考站数据整合、参考站间差分、误差源建模和虚拟参考站建立。而在双星定位中数据处理都是在星上直接完成或者待卫星过境后转发给地面处理，因此双星无源定位中VRS技术的实现要比GPS中简单，可以把双星无源定位中VRS的运行划分为3个阶段。

2.1 参考站基线间的改正数生成

由式(3)可得，对某个坐标为ref_k的参考站k的时差频差方程为

$ \begin{array}{l} {\rm{TDOA}}\left({{\bf{re}}{{\bf{f}}_k}} \right)=\frac{1}{c}\left({\left\| {{\bf{re}}{{\bf{f}}_k} - {\mathit{\boldsymbol{S}}_2}} \right\| - \left\| {{\bf{re}}{{\bf{f}}_k} - {\mathit{\boldsymbol{S}}_1}} \right\|} \right)+\\ \;\;\;\;\;\;{\delta _T}+{O_{{T_{21}}}}+{\xi _T}=\frac{1}{c}\left({r_2^k - r_1^k} \right)+{\delta _T}+{O_{{T_{21}}}}+{\xi _T} \end{array} $

(4)

$ \begin{array}{l} {\rm{FDOA}}\left({{\bf{re}}{{\bf{f}}_k}} \right)=\frac{{{f_0}}}{c}\left[{\frac{{{{\left({{\mathit{\boldsymbol{S}}_2}-{\bf{re}}{{\bf{f}}_k}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_2}}}{{\left\| {{\bf{re}}{{\bf{f}}_k}-{\mathit{\boldsymbol{S}}_2}} \right\|}}-} \right.\\ \;\;\;\;\;\;\;\;\;\;\left.{\frac{{{{\left({{\mathit{\boldsymbol{S}}_1} - \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_1}}}{{\left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_1}} \right\|}}} \right]+{\delta _F}+{{\dot O}_{{F_{21}}}}+{\zeta _F}\;=\frac{{{f_0}}}{c}\left({\dot r_2^k - \dot r_1^k} \right)+\\ \;\;\;\;\;\;\;\;\;\;\;{\delta _F}+{{\dot O}_{{F_{21}}}}+{\zeta _F} \end{array} $

(5)

式中：$r_i^k=\left\| {{\bf{re}}{{\bf{f}}_k} - {\mathit{\boldsymbol{S}}_i}} \right\|$，$\dot r_i^k=\;\frac{{{{\left({{\mathit{\boldsymbol{S}}_i} - {\bf{re}}{{\bf{f}}_k}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_i}}}{{\left\| {{\bf{re}}{{\bf{f}}_k} - {\mathit{\boldsymbol{S}}_i}} \right\|}}$，i=1, 2；对于地面任意两个坐标为ref_m，ref_n的参考站m，n求差后对应的时差频差方程为

$ \begin{array}{l} {\rm{TDO}}{{\rm{A}}^{m, n}}\left({{\bf{ref}}} \right)={\rm{TDOA}}\left({{\bf{re}}{{\bf{f}}_m}} \right)- {\rm{TDOA}}\left({{\bf{re}}{{\bf{f}}_n}} \right)=\\ \;\;\;\;\frac{1}{c}\left({\mathit{\boldsymbol{r}}_2^m - \mathit{\boldsymbol{r}}_1^m - \mathit{\boldsymbol{r}}_2^n+\mathit{\boldsymbol{r}}_1^n} \right)+O_{{T_{21}}}^{m, n}+{\zeta _T} \end{array} $

(6)

$ \begin{array}{l} {\rm{FDO}}{{\rm{A}}^{m, n}}\left({{\bf{ref}}} \right)={\rm{FDOA}}\left({{\bf{re}}{{\bf{f}}_m}} \right)- {\rm{FDOA}}\left({{\bf{re}}{{\bf{f}}_n}} \right)=\\ \;\;\;\;\frac{{{f_0}}}{c}\left({\mathit{\boldsymbol{\dot r}}_2^m - \mathit{\boldsymbol{\dot r}}_1^m - \mathit{\boldsymbol{\dot r}}_2^n+\mathit{\boldsymbol{\dot r}}_1^n} \right)+\dot O_{{F_{21}}}^{m, n}+{\zeta _F} \end{array} $

(7)

式中：O^{m, n}_T21，Ȯ^{m, n}_F21表示参考站m，n相对于双星的卫星星历之差，从表达式可以看出经过参考站m，n之间的差分后，影响参考站间差分后时频差误差的主要因素是星历误差。

如果将星历误差和其他误差记为V^{m, n}，那么对于参考站m，n的时差方程和频差方程，其基线间的综合误差改正数可以表示为

$ V_{{\rm{TDOA}}}^{m, n}={\rm{TDO}}{{\rm{A}}^{m, n}}\left({{\bf{ref}}} \right)- \frac{1}{c}\left({r_2^m - r_1^m - r_2^n+r_1^n} \right) $

(8)

$ V_{{\rm{FDOA}}}^{m, n}={\rm{FDO}}{{\rm{A}}^{m, n}}\left({{\bf{ref}}} \right)- \;\frac{{{f_0}}}{c}\left({\dot r_2^m - \dot r_1^m - \dot r_2^n+\dot r_1^n} \right) $

(9)

在双星无源定位中，可以选定一个主参考站，其他参考站的所有时频综合误差改正数都是相对于主参考站这条基线上；而VRS处的时频综合误差也是建立在主参考站与VRS之间的。

2.2 VRS上观测值的生成

利用主参考站上的观测数据，通过加入一个几何改正量和误差项，就可以将主参考站上的观测数据归算到VRS上，而加入的几何改正量实际上就是在VRS处计算的理论时差和理论频差。如果在某时刻主参考站时差频差观测方程为

$ \left\{ \begin{array}{l} {\rm{TDOA}}\left({{\bf{re}}{{\bf{f}}_m}} \right)=\frac{1}{c}\left({r_2^m - r_1^m} \right)+{O_{{T_{21}}}}+\left({{\bf{re}}{{\bf{f}}_A}} \right)+{\xi _T}\\ {\rm{FDOA}}\left({{\bf{re}}{{\bf{f}}_m}} \right)=\frac{{{f_0}}}{c}\left({\dot r_2^m - \dot r_1^m} \right)+{{\dot O}_{{F_{21}}}}+\left({{\bf{re}}{{\bf{f}}_A}} \right)+{\xi _F} \end{array} \right. $

(10)

那么，在相同时刻VRS处的观测方程具有相同形式，将两组方程分别对相应的时频方程求差后有

$ \left\{ \begin{array}{l} {\rm{TDO}}{{\rm{A}}^{m, {\rm{VRS}}}}=\frac{1}{c}\left({r_2^m - r_1^m - r_2^{{\rm{VRS}}}+r_1^{{\rm{VRS}}}} \right)+V_{{\rm{TDOA}}}^{m{\rm{, VRS}}}\\ {\rm{FDO}}{{\rm{A}}^{m, {\rm{VRS}}}}=\frac{{{f_0}}}{c}\left({\dot r_2^m - \dot r_1^m - \dot r_2^{{\rm{VRS}}}+\dot r_1^{{\rm{VRS}}}} \right)+V_{{\rm{FDOA}}}^{m{\rm{, VRS}}} \end{array} \right. $

(11)

将VRS处的时频差观测值移到等式左边，有

$ \left\{ \begin{array}{l} {\rm{TDOA}}\left({{\bf{VRS}}} \right)={\rm{TDOA}}\left({{\bf{re}}{{\bf{f}}_m}} \right)- \left[{\frac{1}{c}\left({r_2^m-r_1^m-} \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left.{\left.{r_2^{{\rm{VRS}}}+r_1^{{\rm{VRS}}}} \right)+{V^{m, {\rm{VRS}}}}} \right]\;\\ {\rm{FDOA}}\left({{\bf{VRS}}} \right)={\rm{FDOA}}\left({{\bf{re}}{{\bf{f}}_m}} \right)- \left[{\frac{{{f_0}}}{c}\left({\dot r_2^m-\dot r_1^m-} \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left.{\left.{\dot r_2^{{\rm{VRS}}}+\dot r_1^{{\rm{VRS}}}} \right)+{V^{m, {\rm{VRS}}}}} \right]\; \end{array} \right. $

(12)

由式(12)可以看出，只要将基准站与VRS之间的时频差综合误差确定后，那么VRS处的时频差观测值也可以构建出来。

2.3 内插改正数的生成和未知辐射源位置确定

基线间改正数生成的模型有很多种，比较常见的是线性组合模型、距离反比例模型及低阶曲面模型等。文献[10]指出在GPS中除了距离反比例模型内插效果稍差外，其余几种内插模型效果基本相当。同时文中考虑到线性组合模型能够减小多路径效应、测量噪声等非空间相关误差，因此，文中采用该模型对基线间的改正数进行内插，更多内插模型参考文献[11, 12]。

2.3.1 内插改正数的生成

假设有N个参考站，其坐标分别为ref_i=(x_i，y _i，z_i)，i=1，…，N，第i个参考站与主参考站1之间的时频综合误差改正数分别为V_TDOA^{1, i}，V_FDOA^{1, i}。因此根据线性组合法原理，VRS与主参考站之间的综合误差改正数可以记为

$ \left\{ \begin{array}{l} V_{{\rm{TDOA}}}^{1, {\rm{VRS}}}={\alpha _1}V_{{\rm{TDOA}}}^{1, 2}+{\alpha _2}V_{{\rm{TDOA}}}^{1, 3}+\cdots+{\alpha _{N - 1}}V_{{\rm{TDOA}}}^{1, N - 1}\\ V_{{\rm{FDOA}}}^{1, {\rm{VRS}}}={\beta _1}V_{{\rm{FDOA}}}^{1, 2}+{\beta _2}V_{{\rm{FDOA}}}^{1, 3}+\cdots+{\beta _{N - 1}}V_{{\rm{FDOA}}}^{1, N - 1} \end{array} \right. $

(13)

显然，VRS与主参考站之间的时频综合误差改正数是第i个参考站与主参考站1之间综合误差改正数的线性组合，且待求参数α=(α₁，α₂，…，α_N)^T, β=(β₁，β₂，…，β_N)^T满足以下条件

$ \left\{ \begin{array}{l} \sum\limits_{i=1}^N {{\alpha _i}=1} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i=1}^N {{\beta _i}=1} \\ \sum\limits_{i=1}^N {{\alpha _i}\left({{\mathit{\boldsymbol{X}}_{{\rm{VRS}}}} - {\mathit{\boldsymbol{X}}_i}} \right)=0} \;\;\;\;\;\sum\limits_{i=1}^N {{\beta _i}\left({{\mathit{\boldsymbol{X}}_{{\rm{VRS}}}} - {\mathit{\boldsymbol{X}}_i}} \right)=0} \\ \sum\limits_{i=1}^N {\alpha _i^2=\min } \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i=1}^N {\beta _i^2=\min } \end{array} \right. $

(14)

式中：X_VRS和X_i分别为VRS所在位置与第i个参考站所在位置的高斯平面坐标系中的分量^[13]。将式(14)以α为例写为矩阵形式

$ \begin{array}{l} \left({\begin{array}{*{20}{c}} 1&1&\cdots &1&1\\ {\Delta {X_{1, 2}}}&{\Delta {X_{1, 3}}}&\vdots &{\Delta {X_{1, N - 1}}}&0\\ {\Delta {Y_{1, 2}}}&{\Delta {Y_{1, 3}}}&\cdots &{\Delta {Y_{1, N - 1}}}&0 \end{array}} \right)\left(\begin{array}{l} {\alpha _1}\\ {\alpha _2}\\ \vdots \\ {\alpha _N} \end{array} \right)=\\ \;\;\left(\begin{array}{l} 1\\ \Delta {X_{{\rm{VRS, }}1}}\\ \Delta {Y_{{\rm{VRS, }}1}} \end{array} \right) \end{array} $

采用条件平差的方法可以求出(α₁，α₂，…，α_N)。可见，线性组合法所需要的参考站最少是3个，且α的取值与参考站位置相关。在同一时刻，参与平差的参考站增加，α的值将会越准确，但是由误差传播理论知识可以知道，参考站的增加，将会引入更多的误差来影响α的值，因此参与求解的参考站数量不能无限制的增加。通过仿真发现，VRS与主参考站之间的时差综合误差求解，一般采用3个参考站就可以获得比较满意的结果；而VRS与主参考站之间的频差综合误差求解，可以采用多个参考站。

2.3.2 辐射源位置的确定

假设双星系统对未知辐射源和参考站在相同时刻进行了观测，则未知辐射源时频差方程与式(3)相同。一般而言，未知辐射源经过初次定位后，未知辐射源与VRS相距不远。因此，将未知辐射源时频差方程与VRS处的时频差观测方程作差分后，有

$ \begin{array}{l} {\rm{TDOA}}\left(\mathit{\boldsymbol{u}} \right)- {\rm{TDOA}}\left({{\bf{VRS}}} \right)=\frac{1}{c}\left[{\left\| {\mathit{\boldsymbol{u}}-{\mathit{\boldsymbol{S}}_2}} \right\|-} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left\| {\mathit{\boldsymbol{u}}-{\mathit{\boldsymbol{S}}_1}} \right\| - \left({\left\| {{\bf{VRS}} - {\mathit{\boldsymbol{S}}_2}} \right\|} \right.- \\ \;\;\;\;\;\;\;\;\;\;\;\left.{\left.{\left\| {{\bf{VRS}} - {\mathit{\boldsymbol{S}}_1}} \right\|\;} \right)} \right] \end{array} $

(15)

$ \begin{array}{l} {\rm{FDOA}}\left(\mathit{\boldsymbol{u}} \right)- {\rm{FDOA}}\left({{\bf{VRS}}} \right)=\frac{{{f_0}}}{c}\left[{\frac{{{{\left({{\mathit{\boldsymbol{S}}_2}-\mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}{{\dot S}_2}}}{{\left\| {\mathit{\boldsymbol{u}}-{\mathit{\boldsymbol{S}}_2}} \right\|}}} \right.-\\ \;\;\;\;\;\;\;\;\;\;\;\left.{\frac{{{{\left({{\mathit{\boldsymbol{S}}_1}- \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}{{\dot S}_1}}}{{\left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_1}} \right\|}}} \right] - \frac{{{f_0}}}{c}\left[{\frac{{{{\left({{\mathit{\boldsymbol{S}}_2}-{\bf{VRS}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_2}}}{{\left\| {{\bf{VRS}}-{\mathit{\boldsymbol{S}}_2}} \right\|}}} \right.-\\ \;\;\;\;\;\;\;\;\;\;\;\left.{\frac{{{{\left({{\mathit{\boldsymbol{S}}_2}- {\bf{VRS}}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_1}}}{{\left\| {{\bf{VRS}} - {\mathit{\boldsymbol{S}}_1}} \right\|}}} \right] \end{array} $

(16)

利用式(15，16)结合WGS-84椭球模型，采用文献[1, 3, 14]中提出的方法可以解算出未知辐射源的位置。

3 影响VRS处虚拟时频差构建误差因素分析

由于VRS处虚拟时频差构建的误差将会直接影响未知辐射源的定位精度，因此有必要分析低轨双星无源定位中引起时频差还原误差的因素。同时，虚拟时频差的构建误差主要是由内插误差决定，所以本节详细分析影响时频差内插误差的原因。

由误差分析可知，经过两参考站间的差分后，测量系统误差和转发时延被消除，而影响差分后时差和频差观测方程误差的主要因素是星历误差。假设卫星i到地面辐射源的几何距离r_i⁰=‖S _i⁰-u‖，i=1, 2。其中，S_i⁰表示卫星的真实位置。将r _i⁰在S_i处展开同时忽略高次项，有r_i⁰=‖S_i⁰-u‖=‖S _i -u‖-ρ^T_{Si, k}Δ S_i其中，ρ_{Si, k}=$\frac{{\left({{\mathit{\boldsymbol{S}}_1} - \mathit{\boldsymbol{u}}} \right)}}{{\left\| {\left({{\mathit{\boldsymbol{S}}_1} - \mathit{\boldsymbol{u}}} \right)} \right\|}}$，ΔS_i为卫星i的位置误差。对于地面任意两个参考站m, n，由式(6)可知，单差时差方程为

$ \begin{array}{l} {\rm{TDO}}{{\rm{A}}^{m, n}}\left({{\bf{ref}}} \right)=\frac{1}{c}\left({r_2^m - r_1^m - r_2^n+r_1^n} \right)- \\ \;\;\;\;\;\;\frac{1}{c}\left({\mathit{\boldsymbol{\rho }}_{{{\rm{s}}_{\rm{2}}}{\rm{, }}m}^{\rm{T}}\Delta {\mathit{\boldsymbol{S}}_2} - \mathit{\boldsymbol{\rho }}_{{{\rm{s}}_1}{\rm{, }}m}^{\rm{T}}\Delta {\mathit{\boldsymbol{S}}_1} - \mathit{\boldsymbol{\rho }}_{{{\rm{s}}_{\rm{2}}}{\rm{, }}n}^{\rm{T}}\Delta {\mathit{\boldsymbol{S}}_2}+\mathit{\boldsymbol{\rho }}_{{{\rm{s}}_1}{\rm{, }}n}^{\rm{T}}\Delta {\mathit{\boldsymbol{S}}_1}} \right) \end{array} $

(17)

同理，对于卫星i到地面辐射源的理想径向速度为ṙ_i⁰=$\frac{{{{\left({\mathit{\boldsymbol{S}}_i^0 - \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}}}{{\left\| {\mathit{\boldsymbol{S}}_i^0 - \mathit{\boldsymbol{u}}} \right\|}}\mathit{\boldsymbol{\dot S}}_i^0$。其中，Ṡ_i⁰表示卫星真实速度。同样地，将ṙ⁰ _i同时在S_i和Ṡ_i处展开并忽略高次项，有ṙ_i⁰=$\frac{{{{\left({\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_i}} \right)}^{\rm{T}}}{{\mathit{\boldsymbol{\dot S}}}_i}}}{{\left\| {\mathit{\boldsymbol{u}} - {\mathit{\boldsymbol{S}}_i}} \right\|}}$，其中D_i(u)=$\;\frac{1}{{\left\| {\left({{\mathit{\boldsymbol{S}}_i} - \mathit{\boldsymbol{u}}} \right)} \right\|}}$(S_i-(ρ_i^T(u)S_i)ρ_i(u))^T+ρ_i^T(u)ΔṠ_i，ΔṠ_i为卫星i的速度误差。对于地面任意两个参站m, n，由式(7)可知单差频差方程为

$ \begin{array}{l} {\rm{FDO}}{{\rm{A}}^{m, n}}\left({{\bf{ref}}} \right)=\frac{{{f_0}}}{c}\left({\mathit{\boldsymbol{\dot r}}_2^m - \mathit{\boldsymbol{\dot r}}_1^m - \mathit{\boldsymbol{\dot r}}_2^n+\mathit{\boldsymbol{\dot r}}_1^n} \right)- \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{{f_0}}}{c}\left({{D_2}\left(m \right)- {D_1}\left(m \right)- {D_2}\left(n \right)- {D_1}\left(n \right)} \right)\; \end{array} $

(18)

由上面分析可以看出，对于地面任意两个参考站m, n之间的时差和频差空间误差分别为

$ \begin{array}{l} {\rm{TSC=- }}\frac{1}{c}\left({\mathit{\boldsymbol{\rho }}_{{{\rm{s}}_{\rm{2}}}{\rm{, }}m}^{\rm{T}}\Delta {\mathit{\boldsymbol{S}}_2} - \mathit{\boldsymbol{\rho }}_{{{\rm{s}}_1}{\rm{, }}m}^{\rm{T}}\Delta {\mathit{\boldsymbol{S}}_1} - \mathit{\boldsymbol{\rho }}_{{{\rm{s}}_{\rm{2}}}{\rm{, }}n}^{\rm{T}}\Delta {\mathit{\boldsymbol{S}}_2}} \right.\\ \;\;\;\;\;\;\;\;\;\;\left.{\mathit{\boldsymbol{\rho }}_{{{\rm{s}}_1}{\rm{, }}n}^{\rm{T}}\Delta {\mathit{\boldsymbol{S}}_1}} \right)\\ {\rm{FSC=- }}\frac{{{f_0}}}{c}\left({{D_2}\left(m \right)- {D_1}\left(m \right)- {D_2}\left(n \right)- {D_1}\left(n \right)} \right) \end{array} $

(19)

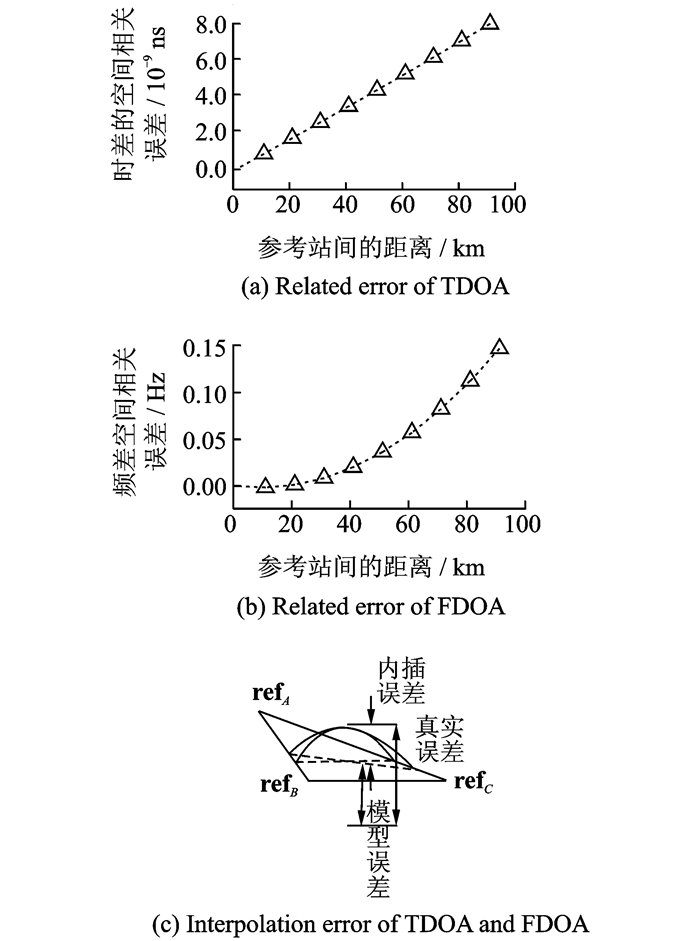
对式(19)进行分析后可以得到，参考站间的时差空间相关误差近似呈线性关系，如图 2(a)所示；而参考站间的频差空间相关误差呈非线性关系，如图 2(b)所示；对于线性插值而言，正是由于前两者这种近似线性和非线性的关系，才导致了时差和频差内插误差的存在，如图 2(c)所示，从而使得虚拟时差和虚拟频差的还原值存在误差，并且，在VRS处的时差构建误差要小于频差构建误差。

4 仿真分析

为了验证文中所提出方案的有效性，需要对其进行仿真分析。假设两颗卫星同轨运行且轨道高度为800 km，两个卫星间距50 km，未知辐射源载频f₀=10 GHz，时差测量系统误差80 ns，转发时延20 ns，频差测量系统误差10 Hz，两卫星的轨道误差为10 m，速度误差为0.1 m/s。如果在双星覆盖的范围内选取其中3个参考站作为合作辐射源，见图 1中A, B, C，且合作辐射源之间的最大基线长度为500 km。首先分析VRS处时频差的构建误差，然后再分析VRS对未知辐射源时频差方程的改正效果。文中对于虚拟参考站处时频差的构建精度定义为${\gamma _k}=\frac{{\left| {C - {C_0}} \right|}}{{{C_0}}}$, 其中，C表示时差/频差的构建值；C₀表示时差/频差的真实值，k∈(T, F)。对于整体构建精度采用对γ_κ的绝对值求均值的方法。

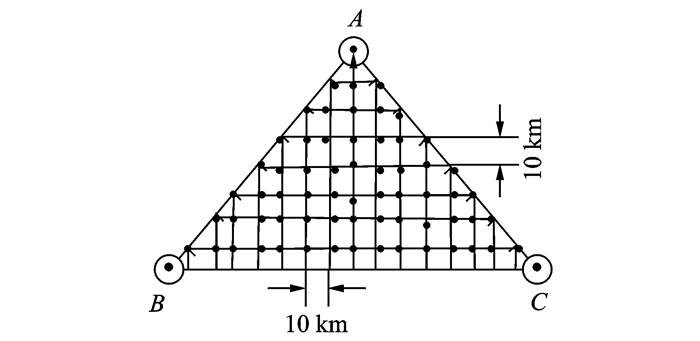
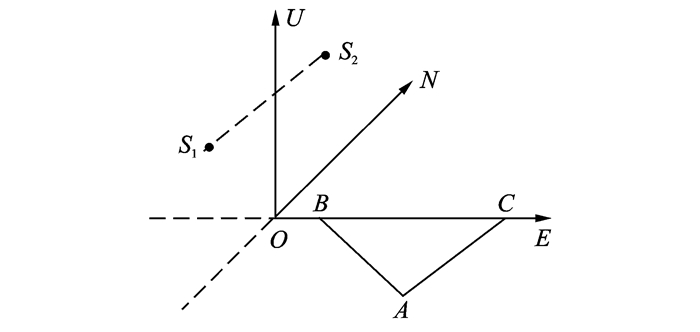
以图 1中A为主参考站，B和C为辅参考站，同时在3个参考站范围内选取足够多的点作为虚拟参考站VRS的坐标。3个参考站与各个VRS之间的相对位置关系如图 3所示，图 3中每两个VRS之间的横向和纵向距离相差10 km；每一个VRS的坐标都是在以低轨双星连线中点的星下点建立的站心坐标系(见图 4)，图 4中参考站B的坐标为(100 km, 0, 0)，同时为了便于分析，将VRS按照一定的顺序进行标号并且将此标号定义为VRS的“位置”。

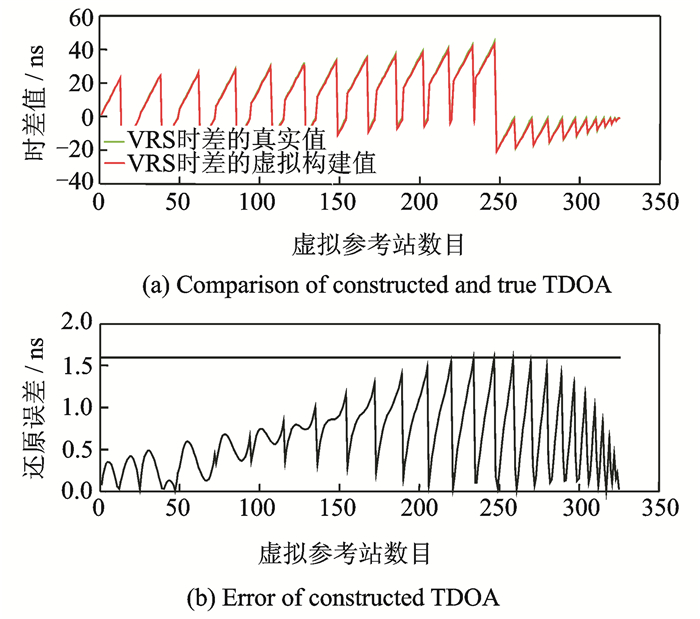
图 5, 6为VRS处构建的虚拟时差、频差与真实值的比较。从图 5, 6可以看出，当VRS位于3个参考站中间区域时(如参考站数目在180~280之间)，时频差构建误差将达到最大。从图 5(b)可以看出，时差构建误差最大可以达到1.8 ns；从图 6(b)可以看出，频差构建误差最大为1.08 Hz，并且从整体构建误差上来说，时差还原精度为0.087，而频差还原精度为0.59。因此，时差还原精度要高于频差还原精度，这与前面的理论分析一致。因此，利用3个参考站能使VRS处虚拟时差值基本达到要求，而虚拟频差值可以利用多个参考站来提高VRS处的频差还原精度。

VRS与未知辐射源之间的基线长度在很大的程度上决定了VRS对未知辐射源系统误差的改正效果。为了评估VRS对未知辐射源时频差的改正效果，表 1列出了在不同基线长度时，VRS对未知辐射源测量时差和测量频差的修正效果，如表 1所示。

由表 1可知：

(1) VRS能够比较有效地改正未知辐射源时频差误差，但是未知辐射源与VRS之间距离越大，VRS对未知辐射源时差和频差修正效果越差。

(2)基线长度在10 km以内时，VRS对未知辐射源时频差的修正效率分别达到97%和95 %。

在对未知辐射源实际定位过程中，为了减小VRS与未知辐射源之间的基线长度，可以对未知辐射源初次定位时采用单站差分定位(一般选用主参考站)，这样就可以尽量减小未知辐射源与VRS之间的基线长度，从而使得VRS对未知辐射源时频差的修正效果变好。

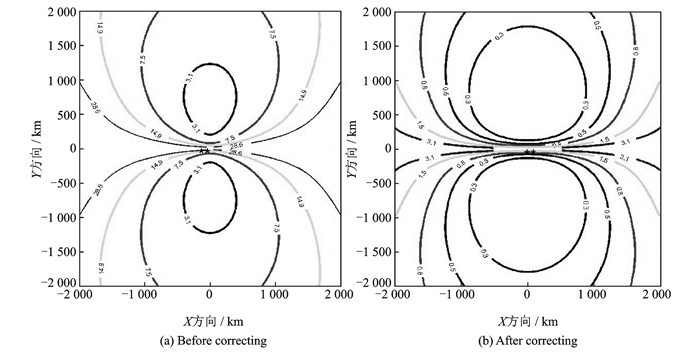
图 7是在双星覆盖范围内，未知辐射源没有利用VRS改正和利用VRS改正后的几何精度因子(Geometric dilution of precision, GDOP)分布。由于未知辐射源定位精度最差可以达到10 km，因此文中假设未知辐射源经过初次定位后，未知辐射源与VRS相距10 km，误差设置与仿真条件相同。

从图 7可以看出，经过VRS差分后定位误差为3.1 km的范围，相对于没有利用VRS差分的定位误差范围有很大提高，同时说明文中所提方案的可行性。由于在仿真时文中固定了VRS与未知辐射源的基线长度，然而在实际情况中，未知辐射源经过一次差分后其定位误差一般小于10 km，因此，未知辐射源经过VRS差分后的定位误差可能还会稍好一些。

5 结束语

文中研究了一种基于VRS的低轨双星时差频差精密修正的方法。通过理论和仿真分析，得出了VRS处虚拟时差还原精度要高于虚拟频差的还原精度，并从理论上分析了影响时频差内插误差的原因。通过仿真得出：(1) VRS对未知辐射源时频差系统误差的修正精度分别可以达到97%和95%；(2)利用修正后的时频差去对未知辐射源进行定位，其定位精度优于3 km的范围有很大幅度的提高。因此，文中所提的方法对提高低轨双星无源定位系统的定位精度具有一定的参考意义。