实际中,一些系统除了“正常工作”和“完全失效”两种状态外,可以在多个性能水平下运行,这样的系统可称为多态系统(Multi-state system, MSS)[1],与二态系统模型相比,多态系统模型能够准确定义部件的多态性,能够更加灵活精确地表征部件性能变化对系统性能和可靠性的影响。
20世纪70年代,MSS的概念被提出后,MSS可靠性的研究得到了学者们的广泛关注。在理论方法方面,文献[1]对多态系统可靠性的基本概念、评估方法和优化设计等方面进行了详细的阐述。在工程应用方面,多态系统可靠性的相关理论已经应用到电力[2]、网络[3]和机械[4]等领域。
对于高可靠部件构成的系统,短时间内很难得到准确有效的部件或系统的状态性能信息。因此,通过获得精确的失效数据去评估系统的精确概率和性能水平显得十分困难。针对上述问题,一些学者对传统的多态系统理论进行推广。Ding等[5-6]在模糊状态及其概率给定的前提下,给出了模糊多态系统的通用定义和可靠性分析方法。鄢民强等[7]提出了一种考虑不完全覆盖的模糊多状态系统的可靠性计算方法。Li等[8]利用区间分析理论和通用生成函数方法分析了多态系统的区间可靠性。Sebas tien等[9]将随机集理论和通用生成函数方法相结合,对考虑认知不确定性的多态系统可靠性进行分析。但是对高可靠性部件构成的MSS进行可靠性分析时,由于对部件性能分布信息的认知存在一定的不确定性,无法准确地对其性能分布进行描述。鉴于上述不足,本文提出了考虑认知不确定的多态系统模糊可靠性分析方法,并以仿真实例进行了验证分析。
1 多态系统模糊状态性能分析 1.1 退化部件状态性能分析实际工程中,对于一些高可靠、性能退化部件,由于短时间内无法得到精确和有效的数据,难以获得足够的性能分布信息。鉴于此,可假定部件的性能分布参数为模糊数,在对其进行分析之前,先对如下假设和结论进行描述:
(1)部件只有一个性能参数x,对应一个性能退化过程,且退化过程不可逆。
(2)假定在任意时刻t,部件的性能x(t)服从为均值
(3)给定任意时刻t和置信水平β,根据假设(2)分析,部件的均值μx(t)、方差σx2(t)分别为在[
| $ \begin{array}{l} {F_\beta }\left(Y \right){\rm{=}}\int_{ - \infty }^y {\int_{_{\mu \alpha }^{ - {\rm{L}}}\left(t \right)}^{_{\mu \alpha }^{ - {\rm{U}}}\left(t \right)} {\int_{\left({{\sigma ^{ - 2}}} \right)_\alpha ^{\rm{L}}\left(t \right)}^{\left({{\sigma ^{ - 2}}} \right)_\alpha ^{\rm{U}}\left(t \right)} {f\left({x\left| {{u_x}\left(t \right), \sigma _x^2\left(t \right)} \right.} \right)} } } \cdot \\ \;\;\;\;\;\;\;\;\;\;\;h\left({{u_x}\left(t \right)} \right)m\left({\sigma _x^2\left(t \right)} \right){\rm{d}}{u_x}{\rm{d}}\sigma _x^2{\rm{d}}x \end{array} $ | (1) |
式中:
| $ \begin{array}{l} f\left({x\left| {{u_x}\left(t \right), \sigma _x^2\left(t \right)} \right.} \right)=\frac{1}{{\sqrt {2\pi \sigma _x^2\left(t \right)} }}\exp \left({\frac{{ - {{\left({x - {u_x}\left(t \right)} \right)}^2}}}{{2\sigma _x^2\left(t \right)}}} \right), \\ \beta \in \left[{0, 1} \right];\\ h\left({{u_x}\left(t \right)} \right)=\left\{ \begin{array}{l} \frac{1}{{\tilde u_\beta ^{\rm{U}}\left(t \right)- \tilde u_\beta ^{\rm{L}}\left(t \right)}}\;\;\;\;\;\;\tilde u_\beta ^{\rm{L}}\left(t \right)<{u_x} <\tilde u_\beta ^{\rm{U}}\left(t \right)\;\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{else}} \end{array} \right.;\\ m\left({\sigma _x^2\left(t \right)} \right)=\\ \left\{ \begin{array}{l} \frac{1}{{\left({{{\tilde \sigma }^2}} \right)_\beta ^{\rm{U}}\left(t \right)- \left({{{\tilde \sigma }^2}} \right)_\beta ^{\rm{L}}\left(t \right)}}\;\;\;\;\;\;\left({{{\tilde \sigma }^2}} \right)_\beta ^{\rm{L}}\left(t \right)<\sigma _x^2\left(t \right)<\left({{{\tilde \sigma }^2}} \right)_\beta ^{\rm{U}}\left(t \right)\;\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{else}} \end{array} \right.. \end{array} $ |
(4)最后,根据模糊集合分解定理[11]可得部件的模糊性能分布为:
(1)假定部件的状态性能为模糊数,定义部件i的模糊状态性能排序准则:如果{
(2)定义部件i第ki个状态性能模糊数区间形式为:[
(3)定义部件i的第ki个状态模糊区间的α-截集形式为:[
(4)定义部件性能时,随着部件状态数的增加,能够提高通用生成函数的计算精度,但是随着状态数的增加,计算量也会随之剧增,从而产生“维数灾难”问题。为了不增加状态数,而尽可能地提高计算精度,以状态模糊区间的形式对状态进行划分。假设t时刻部件ki个状态模糊区间形式为[
| $ \left\{ \begin{array}{l} \tilde p_\alpha ^{\rm{L}}\left(t \right)={F_{\min }}\left({y\left(t \right), u, \sigma } \right)- {F_{\max }}\left({x\left(t \right), u, \sigma } \right)\\ \tilde p_\alpha ^{\rm{U}}\left(t \right)={F_{\max }}\left({y\left(t \right), u, \sigma } \right)- {F_{\min }}\left({x\left(t \right), u, \sigma } \right) \end{array} \right. $ | (2) |
式中:
| $ \begin{array}{l} {F_{\alpha, \min }}\left({{y_i}\left(t \right), u, \sigma } \right)=\mathop {\min }\limits_{{y_i}\left(t \right)\in \left[{y_{i, {k_i}, \alpha }^{-{\rm{L}}}, y_{i, {k_i}, \alpha }^{-{\rm{U}}}} \right]} {F_\beta }\left({{y_i}\left(t \right)} \right), \\ {F_{\alpha, \max }}\left({{x_i}\left(t \right), u, \sigma } \right)=\mathop {\max }\limits_{{x_i}\left(t \right)\in \left[{x_{i, {k_i}, \alpha }^{-{\rm{L}}}, x_{i, {k_i}, \alpha }^{-{\rm{U}}}} \right]} {F_\beta }\left({{x_i}\left(t \right)} \right), \\ {F_{\alpha, \max }}\left({{y_i}\left(t \right), u, \sigma } \right)=\mathop {\max }\limits_{{y_i}\left(t \right)\in \left[{y_{i, {k_i}, \alpha }^{-{\rm{L}}}, y_{i, {k_i}, \alpha }^{-{\rm{U}}}} \right]} {F_\beta }\left({{y_i}\left(t \right)} \right), \\ {F_{\alpha, \min }}\left({{x_i}\left(t \right), u, \sigma } \right)=\mathop {\min }\limits_{{x_i}\left(t \right)\in \left[{x_{i, {k_i}, \alpha }^{-{\rm{L}}}, x_{i, {k_i}, \alpha }^{-{\rm{U}}}} \right]} {F_\beta }\left({{x_i}\left(t \right)} \right). \end{array} $ |
则t时刻部件第ki个状态模糊区间[
为使模糊通用生成函数分析更加简单、计算方法更具有通用性,首先对模糊性能区间的边界进行确定。根据模糊集合分解定理,将模糊数转化为α-截集,然后对α-截集通用生成函数的定义和运算法则进行定义,最后,也可将所得α-截集通用生成函数转换为模糊通用生成函数, 在此不再详述。在分析时状态模糊区间具有α-截集上边界、中值、下边界3种情况,因状态模糊区间的α-截集上边界和下边界均不能充分的表征部件在状态模糊区间上特性,因此本文分析时采用部件状态模糊区间的α-截集中值方法。
2.1 模糊区间边界确定对模糊数区间进行边界确定时,先将模糊数区间以其特殊形式隶属度为1的情况进行分析,将复杂的模糊数区间转化成传统的精确值区间,进行状态性能区间划分。
对部件性能区间进行划分时,采用系统最低任务需求与部件性能分布特性相结合的方法进行区间划分。具体如下:
(1)以部件i的性能区间个数Mi=4为例进行详细说明,其中{xi}={[xi, 1], [xi, 2], [xi, 3], [xi, 4]},[xi, 1]=[xi, 1, xi, 1],[xi, 2]=[x i, 2, xi, 2],[xi, 3]=[xi, 3, x i, 3],[xi, 4]=[xi, 4, xi, 4]。
①在给定t时刻,部件i的性能服从均值为[μi(t)],方差为[σi2(t)]正态分布。以标准差[σi(t)]为间隔将部件的整个性能分布区间划分为8部分,具体如图 1所示。
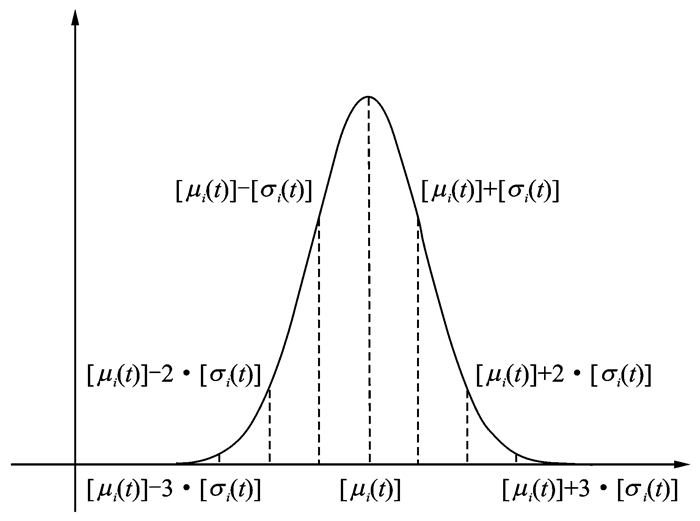
|
图 1 部件性能参数分布 Figure 1 Performance distribution of components |
②根据系统的最小任务性能需求和系统结构函数确定分配到部件的近似最小任务性能区间为[wx],且其中值为wxc,并在该区域附近尽量将其细化,便于系统状态与系统的最小任务性能参数需求区分。
③假定部件i的最大性能为x i, max,为了便于表示假定[xi, ε1]=[μi]-3·[σi],[xi, ε2]=[μi]-2·[σi],[xi, ε3]=[μi]-[σi],[xi, ε4]=[μi],[xi, ε5]=[μi]+[σi],[xi, ε6]=[μi]+2·[σi],[xi, ε7]=[μi]+3·[σi]。假定部件的性能区间族有3个性能区间构成,对部件的性能区间进行划分时,结合①和②根据[wx]与{[xi, ε1], …, [xi, ε7]}中各元素的大小关系进行划分。
④采用区间可能度的定义[12],对区间的大小进行排序,假定[wx]与[xi, ε1], …, [xi, ε7]中各元素的可能度分别为pi, ε1, …, pi, ε7 。
Ⅰ.当0 < pi, ε1≤1时
| $ \left\{ \begin{array}{l} \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline x }_{i, {\varepsilon _1}}}} \right], \left[{{{\underline x }_{i, {\varepsilon _1}}}, {{\overline x }_{i, {\varepsilon _1}}}} \right], \left[{{{\overline x }_{i, {\varepsilon _1}}}, {{\overline w }_x}} \right], } \right.\\ \;\;\;\;\;\;\;\;\;\left.{\left[{{{\overline w }_x}, {x_{i, \max }}} \right]} \right\}\;\;\;\;{\underline w _x} \le {\underline x _{i, {\varepsilon _1}}} \le {\overline x _{i, {\varepsilon _1}}} \le {\overline w _x}\\ \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline x }_{i, {\varepsilon _1}}}} \right], \left[{{{\underline x }_{i, {\varepsilon _1}}}, {{\overline w }_x}} \right], \left[{{{\overline w }_x}, {{\overline x }_{i, {\varepsilon _1}}}} \right], } \right.\\ \left.{\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{{{\overline w }_x}, {x_{i, \max }}} \right]} \right\}\;\;{\underline w _x} \le {\underline x _{i, {\varepsilon _1}}} \le {\overline w _x} \le {\overline x _{i, {\varepsilon _1}}}\\ \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline w }_x}} \right], \left[{{{\underline w }_x}, w_x^c} \right], \left[{w_x^c, {{\overline w }_x}} \right], } \right.\\ \left.{\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{{{\overline w }_x}, {x_{i, \max }}} \right]} \right\}\;\;\;{\underline x _{i, {\varepsilon _1}}} \le {\underline w _x} \le {\overline w _x} \le {\overline x _{i, {\varepsilon _1}}}\\ \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline w }_x}} \right], \left[{{{\underline w }_x}, {{\overline x }_{i, {\varepsilon _1}}}} \right], \left[{{{\overline x }_{i, {\varepsilon _1}}}, {{\overline w }_x}} \right], } \right.\\ \left.{\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{{{\overline w }_x}, {x_{i, \max }}} \right]} \right\}\;\;\;{\underline x _{i, {\varepsilon _1}}} \le {\underline w _x} \le {\overline x _{i, {\varepsilon _1}}} \le {\overline w _x} \end{array} \right. $ |
Ⅱ.当pi, εj-1=0,0 < pi, εj≤1时
| $ \left\{ \begin{array}{l} \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline w }_x}} \right], \left[{{{\underline w }_x}, {{\underline x }_{i, {\varepsilon _j}}}} \right], \left[{{{\underline x }_{i, {\varepsilon _j}}}, {{\overline x }_{i, {\varepsilon _j}}}} \right], } \right.\\ \;\;\;\;\;\;\;\;\;\left.{\left[{{{\overline x }_{i, {\varepsilon _j}}}, {x_{i, \max }}} \right]} \right\}\;\;\;\;{\underline w _x} \le {\underline x _{i, {\varepsilon _j}}} \le {\overline x _{i, {\varepsilon _j}}} \le {\overline w _x}\\ \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline w }_x}} \right], \left[{{{\underline w }_x}, {{\underline x }_{i, {\varepsilon _1}}}} \right], \left[{{{\underline x }_{i, {\varepsilon _1}}}, {{\overline w }_x}} \right], } \right.\\ \left.{\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{{{\overline w }_x}, {x_{i, \max }}} \right]} \right\}\;\;{\underline w _x} \le {\underline x _{i, {\varepsilon _j}}} \le {\overline w _x} \le {\overline x _{i, {\varepsilon _j}}}\\ \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline w }_x}} \right], \left[{{{\underline w }_x}, w_x^c} \right], \left[{w_x^c, {{\overline w }_x}} \right], } \right.\\ \left.{\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{{{\overline w }_x}, {x_{i, \max }}} \right]} \right\}\;\;\;{\underline x _{i, {\varepsilon _j}}} \le {\underline w _x} \le {\overline w _x} \le {\overline x _{i, {\varepsilon _j}}}\\ \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline w }_x}} \right], \left[{{{\underline w }_x}, {{\overline x }_{i, {\varepsilon _j}}}} \right], \left[{{{\overline x }_{i, {\varepsilon _j}}}, {{\overline w }_x}} \right], } \right.\\ \left.{\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{{{\overline w }_x}, {x_{i, \max }}} \right]} \right\}\;\;\;{\underline x _{i, {\varepsilon _j}}} \le {\underline w _x} \le {\overline x _{i, {\varepsilon _j}}} \le {\overline w _x} \end{array} \right. $ |
其中,j=2, …, 6。
Ⅲ.当pi, ε6=0,0 < pi, ε7≤1时
| $ \left\{ \begin{array}{l} \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline w }_x}} \right], \left[{{{\underline w }_x}, {{\underline x }_{i, {\varepsilon _7}}}} \right], \left[{{{\underline x }_{i, {\varepsilon _j}}}, {{\overline x }_{i, {\varepsilon _7}}}} \right], } \right.\\ \;\;\;\;\;\;\;\;\;\left.{\left[{{{\underline x }_{i, {\varepsilon _7}}}, {x_{i, \max }}} \right]} \right\}\;\;\;\;{\underline w _x} \le {\underline x _{i, {\varepsilon _7}}} \le {\overline x _{i, {\varepsilon _7}}} \le {\overline w _x}\\ \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline w }_x}} \right], \left[{{{\underline w }_x}, {{\underline x }_{i, {\varepsilon _1}}}} \right], \left[{{{\underline x }_{i, {\varepsilon _1}}}, {{\overline w }_x}} \right], } \right.\\ \left.{\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{{{\overline w }_x}, {x_{i, \max }}} \right]} \right\}\;\;{\underline w _x} \le {\underline x _{i, {\varepsilon _7}}} \le {\overline w _x} \le {\overline x _{i, {\varepsilon _7}}}\\ \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\underline w }_x}} \right], \left[{{{\underline w }_x}, w_x^c} \right], \left[{w_x^c, {{\overline w }_x}} \right], } \right.\\ \left.{\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{{{\overline w }_x}, {x_{i, \max }}} \right]} \right\}\;\;\;{\underline x _{i, {\varepsilon _7}}} \le {\underline w _x} \le {\overline w _x} \le {\overline x _{i, {\varepsilon _7}}}\\ \left\{ {{x_i}{, _k}_{_i}} \right\}=\left\{ {\left[{0, {{\overline x }_{i, {\varepsilon _7}}}} \right], \left[{{{\overline x }_{i, {\varepsilon _7}}}, {{\underline w }_x}} \right], \left[{{{\underline w }_x}, {{\overline x }_{i, {\varepsilon _j}}}} \right], } \right.\\ \left.{\;\;\;\;\;\;\;\;\;\;\;\;\;\left[{{{\overline x }_{i, {\varepsilon _j}}}, {x_{i, \max }}} \right]} \right\}\;\;\;{\underline x _{i, {\varepsilon _7}}} \le {\underline w _x} \le {\overline x _{i, {\varepsilon _7}}} \le {\overline w _x} \end{array} \right. $ |
Ⅳ.当[wx]>[xi, max]时,表明部件i的性能大小已不满足系统的需求,对其进行性能参数区间的划分已经没有实际的工程意义,故此时可直接认为部件i失效。
(2)部件i的状态数为Mi时,其中2≤Mi≤7,{xi}={[xi, 1], …, [x i, ki], …, [xi, Mi]},对其性能区间进行划分时,其划分思路与Mi=4相同。在近似最小任务性能[wx]附近,结合{[xi, ε1], …, [xi, ε7]},按照距离[wx]由近到远的原则,将其不断细化,进一步增加系统状态在最小任务性能需求附近的区分度,在多态系统的可靠性分析中,随着状态数的增加,系统的状态呈指数型增长,易产生“状态爆炸”问题,计算过于繁杂,因此本文不予考虑。
最后对得到的精确值区间上限边界进行模糊化得到模糊数区间具体如下:
①假定部件i在状态ki的状态性能偏移量为Δxi, ki,且服从均值为0,均方差为Δ σi(t)的标准正态分布,满足Δxi, ki~N(0, Δσ(t))。
②根据正态分布的“3·Δσi(t)法则”,即从概率的角度说明Δxi(t)的值落在(-3·Δσi(t), 3·Δσi(t))外的可能性几乎为0,进一步可得σi(t) <
③假定t时刻部件i的第ki个状态性能水平为xi, ki、状态性能偏移量为Δxi, ki,根据概率论中参数区间估计方法,在偏移量方差Δσ2(t)已知的情况下,则状态偏移量可定义为Δxi(t)=z1-α/2·
④以Δxi和{xi}={ [xi, 1], …, [xi, ki], …, [xi, Mi]}为基础,以三角模糊数为例,对模糊状态性能区间
(a)对ỹi, ki进行求解可得ỹ i, ki=
(b)对
Ⅰ.当ki=1时,
Ⅱ.当1 < ki≤Mi时,
(1)定义部件i的状态模糊区间族形式为:
(2)定义部件i的状态性能α-截集族形式为:
(3)定义部件i的第ki个状态模糊区间α-截集中值的形式为:
(4)定义部件i的状态模糊概率形式为:
(5)定义部件i的状态模糊概率的α-截集形式为
| $ \begin{array}{l} \mathit{\boldsymbol{\tilde p}}{\;_{i, \alpha }}=\left\{ {{{\tilde p}_{i, 1, \alpha }}, \cdots, {{\tilde p}_{i, {k_i}, \alpha }}, \cdots, {{\tilde p}_{i, {M_i}, \alpha }}} \right\}=\left\{ {\left[{\tilde p_{i, 1, \alpha }^{\rm{L}}, } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\left.{\left.{\tilde p_{i, 1, \alpha }^{\rm{U}}} \right], \cdots, \left[{\tilde p_{i, {M_i}, \alpha }^{\rm{L}}, \tilde p_{i, {M_i}, \alpha }^{\rm{U}}} \right]} \right\} \end{array} $ | (3) |
式中:i=1, 2, …, n;ki=1, 2, …, Mi。
(6)定义部件i的α-截集通用生成函数为
| $ {i_{i, \alpha }}\left(z \right)=\sum\limits_{{k_i}=1}^{{M_i}} {{{\tilde p}_{i, {k_i}, \alpha }} \cdot {z^{\overline {\tilde g} _i^I, {k_i}, \alpha }}} $ | (4) |
式中:i=1, 2, …, n;ki=1, 2, …, Mi。
2.3 α-截集通用生成函数运算法则假设部件i和i′,其状态模糊区间中值分别为
| $ \begin{array}{l} U\left({z, t} \right)=\Omega \left({{u_i}\left(z \right), {u_i}'\left(z \right)} \right)=\sum\limits_{i=1}^{{M_i}} {\sum\limits_{i'=1}^{{M_i}'} {{{\tilde p}_{i, {k_i}, \alpha }} \cdot {{\tilde p}_{i', {k_i}', \alpha }} \cdot } } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{z^{f\left({\overline {\tilde g} _i^I, {k_i}, \alpha, \overline {\tilde g} _{i'}^I, {k_{i'}}, \alpha } \right)}} \end{array} $ | (5) |
根据系统结构特点定义如下运算符:
(1)当
| $ \begin{array}{l} {\delta _1}\left({{U_i}\left({z, t} \right), {U_{i'}}\left({z, t} \right)} \right)=\sum\limits_{i=1}^{{M_i}} {\sum\limits_{i'=1}^{{M_i}'} {{{\tilde p}_{i, {k_i}, \alpha }} \cdot {{\tilde p}_{i', {k_i}', \alpha }} \cdot } } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{z^{\overline {\tilde g} _i^I, {k_i}, \alpha, \overline {\tilde g} _{i'}^I, {k_{i'}}, \alpha }} \end{array} $ |
(2)当
| $ \begin{array}{l} {\delta _2}\left({{U_i}\left({z, t} \right), {U_{i'}}\left({z, t} \right)} \right)=\sum\limits_{i=1}^{{M_i}} {\sum\limits_{i'=1}^{{M_i}'} {{{\tilde p}_{i, {k_i}, \alpha }} \cdot {{\tilde p}_{i', {k_i}', \alpha }} \cdot } } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{z^{\min \left\{ {\overline {\tilde g} _i^I, {k_i}, \alpha, \overline {\tilde g} _{i'}^I, {k_{i'}}, \alpha } \right\}}} \end{array} $ |
根据上述运算法则的分析,假定得到的多态系统α-截集通用生成函数为
| $ {U_a}\left({z, t} \right)=\sum\limits_{{k_s}=1}^{{M_s}} {{{\tilde p}_{{k_s}, \alpha }} \cdot {z^{{{\tilde g}_{{k_s}, \alpha }}}}} $ | (6) |
式中:
定义多态系统的最小模糊性能需求
| $ \begin{array}{l} {R_a}\left(t \right)=P\left\{ {\mathit{\boldsymbol{\tilde G}}\left(t \right)\ge \left[w \right]} \right\}=\sum\limits_{{k_s}=1}^{{M_s}} {{{\tilde p}_{{k_s}, \alpha }} \cdot p\left({{{\tilde g}_{{k_s}, \alpha }}\left(t \right)- } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left.{\left[w \right] \ge 0} \right) \end{array} $ | (7) |
式中:P{
如果
(1)若
(2)若
(3)若
| $ p\left({{{\tilde g}_{{k_s}, \alpha }}\left(t \right)- \left[w \right] \ge 0} \right)=\frac{{\tilde g_{{k_s}, \alpha }^{\rm{U}}\left(t \right)- \underline w }}{{\tilde g_{{k_s}, \alpha }^{\rm{U}}\left(t \right)- \underline w+\tilde g_{{k_s}, \alpha }^{\rm{L}}\left(t \right)- \underline w }}. $ |
综合上述3点,可以将
| $ \begin{array}{l} p\left({{{\tilde g}_{{k_s}, \alpha }}\left(t \right)- \left[w \right] \ge 0} \right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{{\max \left\{ {\tilde g_{{k_s}, \alpha }^{\rm{U}}\left(t \right)- \underline w, 0} \right\}}}{{\max \left\{ {\tilde g_{{k_s}, \alpha }^{\rm{U}}\left(t \right)- \underline w+\tilde g_{{k_s}, \alpha }^{\rm{L}}\left(t \right)- \underline w, \tilde g_{{k_s}, \alpha }^{\rm{U}}\left(t \right)- \underline w } \right\}}}. \end{array} $ |
因此,系统的α-截集可靠度为
| $ \begin{array}{l} {R_a}\left(t \right)=P\left\{ {{{\mathit{\boldsymbol{\tilde G}}}_a}\left(t \right)\ge \left[w \right]} \right\}=\sum\limits_{{k_s}=1}^{{M_s}} {{{\tilde p}_{{k_s}, \alpha }} \cdot p\left({{{\tilde g}_{{k_s}, \alpha }}\left(t \right)- } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left.{\left[w \right] \ge 0} \right)=\sum\limits_{{k_s}=1}^{{M_s}} {{{\tilde p}_{{k_s}, \alpha }} \cdot } \\ \frac{{\max \left\{ {\tilde g_{{k_s}, \alpha }^{\rm{U}}\left(t \right)- \underline w, 0} \right\}}}{{\max \left\{ {\tilde g_{{k_s}, \alpha }^{\rm{U}}\left(t \right)- \underline w+\tilde g_{{k_s}, \alpha }^{\rm{L}}\left(t \right)- \underline w, \tilde g_{{k_s}, \alpha }^{\rm{U}}\left(t \right)- \underline w } \right\}}} \end{array} $ | (8) |
最后可以根据模糊集合分解定理[10],可得系统的模糊可靠度
如图 2所示的多态串-并联系统由3个分系统组成,包含6个性能退化部件。其中,部件1和部件2属于同型部件,部件3,4,5属于同型部件。假设部件退化性能和分布参数分别如表 1,2所示。系统的最小模糊性能任务需求
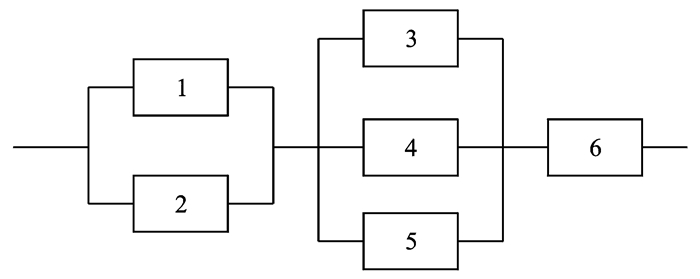
|
图 2 多态串-并联系统 Figure 2 Multi-state serial-parallel system |
| 表 1 部件退化性能、分系统结构函数和系统结构函数 Table 1 Component degraded performances, subsystems structure functions, and system structure functions |
| 表 2 部件性能退化分布参数 Table 2 Performance degradation distribution parameters of components |
4.1 部件和分系统α-截集通用生成函数
假设部件1和部件2可分为4个状态,对应的状态模糊性能区间为:
部件3,4和5可分为3个状态,其状态模糊性能定义为
在t=10 000 h,以β=0.9,α=0.9为例进行分析说明,首先根据2.2节退化部件状态概率分析,得到部件各状态模糊性能对应的概率区间
下面采用部件状态性能模糊区间α-截集的中值方法,对部件α-截集通用生成函数和分系统α-截集通用生成函数进行分析。
根据状态模糊区间族定义和退化部件状态概率求解方法,可得部件1-6的区间通用生成函数为
u1(z, t)=[0.004 5, 0.004 6]·z[26.2, 26.3]+[0.013 7, 0.014 7]·z[53.1, 53.2]+[0.005 3, 0.008 1]·z[53.9, 54.0]+[0.969 3, 0.972 6]·z [62.0, 62.1],u2(z, t)=u1(z, t)
u3(z, t)=[0.033 4, 0.035 9]·z[17.48, 17.52]+[0.099 9, 0.138 0]·z [35.9, 3 6.3]+[0.740 9, 0.826 1]·z[48.4, 48.8]
u3(z, t)=u4(z, t)=u5(z, t),
u6(z, t)=[0, 70]·z0.051 9+[70, 100]·z0.948 1
由图 1可知分系统1是由部件1和部件2构成,且分系统1的性能为部件1和部件2性能的和,根据第3节运算法则定义的δ1运算符,可得分系统1的区间通用生成函数为
Usub1(z, t)=δ1(u1(z, t), u2(z, t))=[0.000 1, 0.000 1]·z[79.3, 79.4]+[0.008 9, 0.009 0]·z[80.1, 80.2]+[0.000 2, 0.000 2] ·z[88.3, 88.4]+[0.000 1, 0.000 2]·z[106.2, 106.4]+[0.026 6, 0.0 28 6]·z[107.0, 108.0]+[0.010 2, 0.015 7]·z[115.2, 1 15.3]+[0.939 5, 0.945 9]·z[124.0, 124.4]
分系统2是由部件3,4和5构成,且其性能为部件3,4和5性能的和,同理可得分系统2的区间通用生成函数为
Usub2(z, t)=δ1(u3(z, t), u4(z, t), u5(z, t))=[0.000 3, 0.000 5]·z[70.9, 71.3]+[0.002 5,0.003 2]·z[78.4, 78.8]+[0.009 9, 0.016 4]· z[89.4, 90.1]+[0.004 9, 0.008 2]·z[96.8, 97.6]+[0.055 0, 0.073 4]·z[104.4, 105.1]+[0.007 4, 0.015 7]·z[107.8, 10 8.9]+[0.014 8, 0.031 5]·z[115.3, 116.4]+[0.164 6, 0.282 6]·z[115.3, 123.9]+[0.406 8, 0.563 8]·z[122.8, 123.9]
4.2 系统区间可靠性分析将分系统1和分系统2采用第3节运算法则定义的δ2运算符,可得分系统1,2综合后的分系统区间通用生成函数为
| $ {U_{1 - 2}}\left({z, t} \right)={\delta _2}\left({{U_{{\rm{sub1}}}}\left({z, t} \right), {U_{{\rm{sub2}}}}\left({z, t} \right)} \right) $ |
因此,根据公式(8)可得分系统1和2的区间可靠度为
| $ {R_{1 - 2}}=\left[{{\rm{0}}{\rm{.576 8, 0}}{\rm{.880 1}}} \right] $ |
分系统3的可靠度为:
| $ {R_3}=0.9481 $ |
最后可得t=10 000h时系统的区间可靠度为
| $ R\left(t \right)={R_{1 - 2}}\left(t \right)\cdot {R_3}\left(t \right)=\left[{{\rm{0}}{\rm{.546 9, 0}}{\rm{.834 5}}} \right] $ |
在t=10 000h时采用M onte Carlo (MC)仿真方法进行分析,在分析过程中为了充分表述MC仿真方法在每次仿真计算过程中所得计算结果的可能性,取L=1 000次仿真结果的最大值和最小值,将其作为区间可靠度的最大值和最小值,可得MC仿真方法的区间可靠度为[0.667 5, 0.788 4],在仿真规模为L=1 000次仿真的耗时大约40.8 638 h,而本文方法耗时约为0.3290h。
如果采用传统的方法进行系统可靠性分析,则一般假设部件仅有两个状态,根据系统总的性能输出要求,确定部件的失效阈值。对于部件1, 2性能不小于[54.75, 55.25]时分系统1正常,部件3, 4, 5性能不小于[36.75, 37.25]时分系统2正常,部件6的性能不小于70时,分系统3正常,因此,采用传统方法可得系统的区间可靠度为[0.453 6, 0.516 3]。
采用本文所提方法、传统可靠性方法、MC仿真方法所得系统的区间可靠性对比关系如表 3所示。
| 表 3 3种方法所得系统区间可靠性对比分析结果 Table 3 Comparison of system interval-valued reliabilities obtained with three methods |
通过对表 3进行分析可以得出以下结论:
(1)传统方法、本文方法和MC仿真方法3者所得结果进行对比,传统方法与后两者相比误差较大,且采用传统方法进行系统可靠性估计时,部件的失效阈值通常是根据部件自身的统计规律确定的,不能根据系统不同任务需求而具体分析,有时可能会出现较大偏差。
(2)取状态模糊区间α-截集中值方法与MC仿真方法相比结果具有重叠部分,且不完全重叠,故存在一定误差,但是两者结果的均值非常接近,所以在一定程度上可以表征系统的可靠性水平,因此在误差允许的范围内,本文方法不仅解决了传统方法误差大的问题,而且克服了MC仿真方法仿真规模大、耗时长的不足,方法简单,便于实现。
4.3 传统点区间通用生函数法为了充分分析本文所提方法的优缺点,在t=10 000h,β=0.9时,将部件状态按传统的点区间进行划分,部件的通用生成函数为
u1(z, t)=u2(z, t)=0.004 6·z[0, 52.5]+0.014 6·z[52.5, 53.7]+0.3 12 9·z[53.7, 57.5]+0.667 9·z[57.5, 70]
u3(z, t)=u4(z, t)=u5(z, t)=0.034 6·z[0, 35]+0.113 7·z[35, 36.7]+0.851 7·z[36.7, 50]
分系统1和分系统2的区间通用生成函数分别为
Usub1(z, t)=δ1(u1(z, t), u2(z, t))=0.00 0 1·z[52.5, 106.2]+0.002 9·z[53.7, 107.5]+0.006 2·z[57.5, 1 10]+0.000 2·z[105, 111.2]+0.009 1·z[106.2, 115]+0.009 8·z[10 7.5, 122.5]+0.019 5·z[110, 123.7]+0.418 0·z[111.2, 127.5]+0.44 6 1·z[115, 140]
Usub2(z, t)=δ1(u3(z, t), u4(z, t), u5(z, t))=0.000 4·z[35, 106.7]+0.003 1·z[36.7, 108.4]+0.001 3·z[70, 110.1]+0.0 201·z[71.7, 120]+0.075 3·z[73.4, 121.7]+0.001 5·z[105, 123.4]+0.033 0·z[106.7, 135]+0.247 4·z[108.4, 136.7]+0.617 8·z[110.1, 150]
同理,将分系统1和分系统2采用第3节运算法则定义的δ2运算符,可得分系统1-2的通用生成函数为
| $ {U_{1 - 2}}\left({z, t} \right)={\delta _2}\left({{U_{{\rm{sub1}}}}\left({z, t} \right), {U_{{\rm{sub2}}}}\left({z, t} \right)} \right) $ |
当系统的最小性能需求[w]=[105, 115],则分系统1-2的可靠度为:R1-2=0.708 0。最后可得系统的可靠度为
| $ R\left(t \right)={R_{1 - 2}}\left(t \right)\cdot {R_3}\left(t \right)={\rm{0}}{\rm{.6713}} $ |
为了分析置信水平α,β变化对系统可靠性的影响,以t=10000 h为例进行分析,首先在给定α=0.9时,可以根据模糊集合分解定理可得部件的模糊可靠度为
其中,R0.1(t)=[0.500 2, 0.762 9],R0.2(t)=[0.521 4, 0.769 4],R0.3(t)=[0.542 3, 0.775 0],R0.4(t)=[0.578 8, 0.824 2],R0.5(t)=[0.454 0, 0.829 7],R0.6(t)=[0.47 2 8, 0.834 0],R0.7(t)=[0.491 4, 0.837 3],R0.8(t)=[0.519 8, 0.8 39 5],R0.9(t)=[0.550 4, 0.840 7],R0.9(t)=[0.443 5, 0.806 6]。
同理在β=0.9时,可得部件的模糊可靠度为
其中,R0.1(t)=[0.602 4, 0.810 7],R0.2(t)=[0.596 0, 0.814 8],R0.3(t)=[0.589 6, 0.818 8],R0.4(t)=[0.583 2, 0.822 7],R0.5(t)=[0.576 7, 0.826 5],R0.6(t)=[0.570 2, 0.830 2],R0.7(t)=[0.563 6, 0.833 8],R0.8(t)=[0.557 0, 0.837 3],R0.9(t)=[0.550 4, 0.840 7],R0.9(t)=[0.844 1, 0.844 1]。
参数α,β变化时与系统区间可靠度均值的关系如图 2所示。通过对图 3的分析,可得区间可靠度的最大值点和最小值点分别为(α, β, Rmax)=(0.9, 1.0, 0.844 1),(α, β, Rmin)=(0.9, 1, 0.5283),从而得到一个合理的系统可靠度,为系统的预防性维修提供一定的参考,降了系统运行的风险。

|
图 3 参数变化与系统区间可靠度均值的关系 Figure 3 Relationship between parametric variation and mean of system interval reliability |
4.5 对比分析
本文在α=[0, 1],β∈ [0, 1]时,对取状态模糊区间α-截集中值方法进行分析,得到在α,β不同取值时系统的区间可靠度。为了进一步对比分析,本文方法(α,β不同取值系统的区间可靠度)、传统方法、MC仿真方法3种方法结果的均值和点区间方法结果进行比较,见图 4。

|
图 4 不同方法所得可靠性结果对比 Figure 4 Comparison of reliabilities obtained by three methods |
由图 4可以得出以下结论:
(1)传统方法与其他方法相比,由于部件失效阈值的选择存在一定盲目性,从而误差较大。
(2)本文方法与传统点区间通用生函数法相比,在状态数相同的情况下,本文方法要比点区间方法的更符合系统可靠性性能的退化规律(通常随着时间增加系统的退化速率将增大),此外本文方法所得结果与MC仿真方法结果比较接近,因此本文方法精度更高、更合理。
5 结论本文针对模糊多态系统,提出了考虑认知不确定的多态系统模糊可靠性评估方法。给出了多态串-并联系统可靠性的分析流程,并采用仿真实例进行验证,并得到以下结论:
(1)本文方法与传统点区间通用生函数方法相比不仅克服了由于认知不确定对部件状态划分不准确的不足,且在相同的状态数时,本文方法要比其计算精度高;
(2)与传统的系统可靠性评估方法相比,降低了对部件的失效阈值确定的不准确而对系统可靠度产生的影响;
(3)与MC仿真方法相比,克服了其仿真规模大、耗时长的不足,为系统预防性维修提供了新方法。
| [1] | Natvig B. Multistate systems reliability theory with applications[M]. Hoboken, NJ, USA: Wiley, 2010. |
| [2] |
史新红, 齐先军, 王治国.
基于UGF的发电系统区间可靠性评估及其仿射算法改进[J]. 合肥工业大学学报(自然科学版), 2014, 37(3): 286–291.
Shi Xinhong, Qi Xianjun, Wang Zhiguo. Interval reliability estimation of power generating system based on UGF method and its modification by using affine arithmetic[J]. Jouranl of Heifei University of Technology, 2014, 37(3): 286–291. |
| [3] | Wei G, Wang Y, Piatkiewicz L. A simple universal generating function method for estimating the reliability of general multi-state node networks[J]. Iie Transactions, 2009, 41(1): 3–11. |
| [4] |
尚彦龙, 蔡琦, 赵新文, 等.
基于UGF和Semi-Markov方法的反应堆泵机组多状态可靠性分析[J]. 核动力工程, 2012, 33(1): 117–123.
Shang Yanlong, Cai Qi, Zhao Xinwen, et al. Multi-state reliability for pump group in nuclear power system based on UGF and semi-Markov process[J]. Nuclear Power Engineering, 2012, 33(1): 117–123. |
| [5] | Ding Y, M J Z. Fuzzy multi-state systems: General definitions, and performance assessment[J]. IEEE Transactions on Reliability, 2008, 57(4): 589–594. DOI:10.1109/TR.2008.2006078 |
| [6] | Ding Y, Lisnianski A. Fuzzy universal generating functions for multi-state system reliability assessment[J]. Fuzzy Sets and Systems, 2008, 159(3): 307–324. DOI:10.1016/j.fss.2007.06.004 |
| [7] |
鄢民强, 杨波, 王展.
不完全覆盖的模糊多状态系统可靠性计算方法[J]. 西安交通大学学报, 2011, 45(10): 109–114.
Yan Minqiang, Yang Bo, Wang Zhan. Reliability assessment for multi-state system subject to imperfect fault coverage[J]. Journal of Xi′an Jiao tong University, 2011, 45(10): 109–114. |
| [8] | Li C Y, Chen X, Yi X S, et al. Interval-valued reliability analysis of multi-state systems[J]. IEEE Transactions on Reliability, 2011, 60(1): 323–330. DOI:10.1109/TR.2010.2103670 |
| [9] | Destercke S, Sallak M. An extension of universal generating function in multi-state systems considering epistemic uncertainties[J]. Reliability Engineering and System Safety, 2013, 62(2): 504–514. |
| [10] |
王光远, 张跃.
模糊随机过程论[M]. 贵阳: 贵州科技出版社, 1994.
Wang Guangyuan, Zhang Yue. The theory of fuzzy stochastic processes[M]. Guiyang: Guizhou Science and Technology Press, 1994. |
| [11] | Wu S, Da C. Theorems of interval fuzzy set and its operation rules[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2012, 29(2): 136–144. |
| [12] |
高峰记.
可能度及区间数综合排序[J]. 系统工程理论与实践, 2013, 33(8): 2033–2040.
Gao Fengji. Possibility degree and comprehensive priority of interval numbers[J]. Systems Engineering-Theory and Practice, 2013, 33(8): 2033–2040. |
| [13] |
茆诗松.
统计手册[M]. 北京: 科学出版社, 2003.
Mao Shisong. Statistics hand book[M]. Beijing: Science Press, 2003. |
| [14] |
邱志平.
非概率集合理论凸方法及其应用[M]. 北京: 国防工业出版社, 2005.
Qiu Zhiping. Convex method of non-probabilistic set-theory and its application[M]. Beijing: National Defense Industry Press, 2005. |
 2016, Vol. 48
2016, Vol. 48


