在可靠性及可靠性灵敏度分析过程中，点估计方法由于不需要求功能函数的导函数和寻找设计点而得到了广泛的应用。该类方法直接利用功能函数在一些特征点处的函数值及权函数来近似计算功能函数的低阶矩(主要是一到四阶矩)，然后由功能函数的各阶矩来近似失效概率^[1]。基于函数矩的可靠性灵敏度分析则依据灵敏度的定义，将失效概率对基本变量分布参数的偏导数转化成功能函数的各阶矩对基本变量分布参数的偏导数的形式，再将此偏导数转化成特征函数矩的形式。常用的点估计方法有两点估计、三点估计及稀疏网格积分等.Rosenblueth首先提出了两点估计法^[2-3]，用以计算单变量或多变量函数三阶(包括三阶)以下的概率矩；随后Gorman推导出了考虑输入随机变量前四阶矩的三点估计法(Three-point estimate，TPE)^[4]；Seo和Kwak利用试验设计技术也得到了相同的计算公式^[5]；然而Gorman和Zhao在实际使用中发现了TPE的一些不足，例如当功能函数的非线性程度较高时，TPE的精度会很低^{[4, 6]}，因此该方法不适合高度非线性的情况；文献[7]通过用Nataf变换替代传统方法中的Rosenblatt变换，将上述点估计方法推广到输入变量相关情况下的前四阶矩求解当中。近年来，以Smolyak准则为基础的稀疏网格方法(Sparse grid，SG)被广泛地应用到数值积分^{[8, 9]}、插值^[10-11]、微分方程的求解^[12]、区域重要性测度估计^[13]以及随机不确定性的传递中，并且已经被证明是一种特别适用于高维情况的有效离散化方法，但对于高度非线性问题，由于功能函数的复杂性，往往需要采用高精度的稀疏网格，这将导致计算量，即模型调用次数大幅度增加。由此可见对于高度非线性问题，SG方法的效率仍然有待提高。

如果能够降低功能函数的复杂性和非线性程度，则可以利用SG方法来进行有效的可靠性及相应的灵敏度分析，而空间分割则可以有效降低子空间中功能函数的复杂性和非线性程度，因此采用空间分割与低精度稀疏网格相结合的方法来进行相应的可靠性及可靠性灵敏度分析。空间分割的关键是分割策略，合理的分割策略才可以提高可靠性及其灵敏度分析的效率。由于实际工程问题中的失效概率一般非常小，使用输入变量的联合概率密度函数进行等概率空间分割时，会导致失效域中的子空间数量远远小于在安全域中的子空间数量，这将使得求解可靠性及其灵敏度的效率非常低下。本文将利用文献[14]中的方法来近似求得用于空间划分的重要抽样密度函数，其思想是在输入变量可能的取值区域进行均匀抽样，将落入失效域中的联合概率密度函数值最大的点作为重要抽样密度函数的密度中心，从而构造一个近似优化的重要抽样密度函数，并且在功能函数具有复杂性和高度非线性时，能够有效避免“多值”问题导致的寻找优化重要抽样密度函数的困难。本文按照此优化后的重要抽样密度函数对输入空间进行分割，使得对失效概率贡献较大的区域的子空间划分得较为密集，对失效概率影响小的区域的子空间划分得比较稀疏，从而达到了节约计算成本的目的。

在实际的工程应用中所面对的往往是高维高度非线性的复杂问题。目前已经存在多种降维技术可以有效地解决高维问题，比如渐进空间法^[15]等可以将任意的高维模型降至低维，然而这种降维的代价是非线性程度的进一步增大。因此解决低纬高度非线性问题就显得非常必要，这类问题的解决再结合有效的降维技术就有望解决工程中的高维高度非线性难题，这也是本文研究的背景和所提方法的价值所在。

1 可靠性及可靠性灵敏度分析的矩方法

对于功能函数g(x)，x=(x₁, x₂, …, x_n)为不确定性输入变量，其失效概率可以表示成积分的形式

$ {P_f}=\int_F {{f_X}\left(\mathit{\boldsymbol{x}} \right)} {\rm{d}}\mathit{\boldsymbol{x=}}\int_{{R^n}} {{I_F}{f_X}\left(\mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} $

(1)

式中：f_X(x)表示X的联合概率密度函数；F={x:g(x)≤0}为g(x)定义的失效域；${I_F}=\left\{ \begin{array}{l} 1, \mathit{\boldsymbol{x}} \in F\\ 0, \mathit{\boldsymbol{x}} \notin F \end{array} \right.$为失效域F的指示函数；Rⁿ表示整体n维输入变量空间。在数学上可靠性灵敏度是由失效概率P_f对基本变量x_i的分布参数θ_xi的偏导数予以表达的

$ \frac{{\partial {P_f}}}{{\partial {\theta _{{x_i}}}}}=\int_{{{\bf{R}}^n}} {{I_F}\left(x \right)\frac{{\partial {f_X}\left(\mathit{\boldsymbol{x}} \right)}}{{\partial {\theta _{{x_i}}}}}{\rm{d}}\mathit{\boldsymbol{x}}} $

(2)

1.1 功能函数矩的计算

功能函数g(x)的前四阶概率矩α_mg(m=1, 2, 3, 4)为

$ \begin{array}{l} {\alpha _{1g}}=\int {g\left(\mathit{\boldsymbol{x}} \right){f_X}\left(\mathit{\boldsymbol{x}} \right)} {\rm{d}}\mathit{\boldsymbol{x}}\\ {\alpha _{2g}}={\left[{\int {{{\left({g\left(\mathit{\boldsymbol{x}} \right)-{\alpha _{1g}}} \right)}^2}{f_X}\left(\mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} } \right]^{\frac{1}{2}}}\\ {\alpha _{mg}}\alpha _{2g}^m=\int {{{\left({g\left(\mathit{\boldsymbol{x}} \right)- {\alpha _{1g}}} \right)}^m}{f_X}\left(\mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} \;\;m=3, 4 \end{array} $

(3)

TPE和稀疏网格积分法是常用的计算前四阶矩的点估计方法，TPE的具体内容见文献[4, 5]，SG方法由于其高效性而得到了广泛的应用^{[8-12, 16]}，它的思想及实现过程可归纳如下：

设S₁^i_j和w₁^i_j表示第j个变量一维空间中的第i_j个积分点和权重，则n维空间中k精度下所有稀疏网格积分点的集合S_n^(k)由以下Smolyak准则选取

$ \mathit{\boldsymbol{S}}_n^{\left(k \right)}=\mathop \cup \limits_{k+1 \le \left| i \right| \le q} \mathit{\boldsymbol{S}}_{{1^1}}^i \otimes \mathit{\boldsymbol{S}}_{{1^2}}^i \otimes \cdots \otimes \mathit{\boldsymbol{S}}_{{1^n}}^i $

(4)

式中：ⓧ表示张量积计算；q=k+n；|i|=i1+i2+…+in为多维指标之和。依据Smolyak准则，集合Snk中相应于第l个积分点ξl=[ξi1ji1, …, ξinjin]∈Sn(k)的权重w(l)为

$ {w^{\left(l \right)}}={\left({ - 1} \right)^{q - \left| i \right|}}\left(\begin{array}{l} n - 1\\ q - \left| i \right| \end{array} \right)\left({w_{{j_{{i_1}}}}^{{i_1}} \cdots w_{{j_{{i_n}}}}^{{i_n}}} \right) $

(5)

则对非线性函数g(x)的积分可以由式(6)求得，并且能够达到2k+1阶多项式精度^[8]

$ \begin{array}{l} \int {g\left(\mathit{\boldsymbol{x}} \right){f_X}\left(\mathit{\boldsymbol{x}} \right)} {\rm{d}}\mathit{\boldsymbol{x}} \approx \sum\limits_{l=1}^{M_{^n}^{\left(k \right)}} {{w^{\left(l \right)}}} g\left({{T^{ - 1}}\left({{{\bf{ \pmb{\mathsf{ ξ}} }}^{\left(l \right)}}} \right)} \right)=\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{l=1}^{M_{^n}^{\left(k \right)}} {{w^{\left(l \right)}}} g\left({{s^{\left(l \right)}}} \right) \end{array} $

(6)

式中：M_n^(k)表示k阶精度下相应的积分点个数；T^-1(·)为任意分布的变量x向积分点空间变换函数的反函数，且在积分点ξ^l处的函数值为s^l，则SG方法求解功能函数g(x)的前四阶矩的积分^[16]可以表示为

$ \begin{array}{l} {\alpha _{1g}}=\int {g\left(\mathit{\boldsymbol{x}} \right){f_X}\left(\mathit{\boldsymbol{x}} \right)} {\rm{d}}\mathit{\boldsymbol{x}} \approx \sum\limits_{l=1}^{M_{^n}^{\left(k \right)}} {{w^{\left(l \right)}}} g\left({{s^{\left(l \right)}}} \right)\\ \;\;\;\;\;{\alpha _{2g}}={\left[{\int {{{\left({g\left(\mathit{\boldsymbol{x}} \right)-{\alpha _{1g}}} \right)}^2}{f_X}\left(\mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} } \right]^{\frac{1}{2}}} \approx \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{\left[{\sum\limits_{l=1}^{M_{^n}^{\left(k \right)}} {{w^{\left(l \right)}}} {{\left({g\left({{s^{\left(l \right)}}} \right)-{\alpha _{1g}}} \right)}^2}} \right]^{\frac{1}{2}}}\\ {\alpha _{mg}}\alpha _{2g}^m=\int {{{\left({g\left(\mathit{\boldsymbol{x}} \right)- {\alpha _{1g}}} \right)}^m}{f_X}\left(\mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}} \approx \\ \sum\limits_{l=1}^{M_{^n}^{\left(k \right)}} {{w^{\left(l \right)}}} {\left({g\left({{s^{\left(l \right)}}} \right)- {\alpha _{1g}}} \right)^k}\;\;\;m=3, 4 \end{array} $

(7)

基于Smolyak准则的稀疏网格能够在一定程度上克服传统数值积分计算量随变量维数呈指数级增长的维数灾难问题，对高维积分问题有很好的适用性，通过调整精度k可以方便地提高积分精度。但是对于非线性程度很高的模型，即使提高精度k也未必可以达到理想的精度。

1.2 基于前四阶矩的失效概率近似方法

基于功能函数概率矩近似失效概率的四阶矩方法包含高阶矩标准化技术法(High-order moment standardization technique，HO M ST)^[17]、Edgeworth级数法^[17]和频率曲线法^[17-21]等。本文采用HOMST方法，可靠度指标β_4M和失效概率P_f分别为

$ {\beta _{4M}}=\frac{{3\left({{\alpha _{4g}} - 1} \right){\beta _{2M}}+{\alpha _{3g}}\left({\beta _2^2M - 1} \right)}}{{\sqrt {\left({5\alpha _{3g}^2 - 9{\alpha _{4g}}+9} \right)\left({1 - {\alpha _{4g}}} \right)} }} $

(8)

$ {P_f}=\Phi \left({ - {\beta _{4M}}} \right) $

(9)

式中：${\beta _{2M}}=\frac{{{\alpha _{1g}}}}{{{\alpha _{2g}}}}$，且当α_3g=0时，β_4M=β_2M。

1.3 可靠性灵敏度分析的点估计方法

根据可靠性灵敏度的定义，由失效概率P_f与可靠度指标β_4M的关系，以及β _4M与α_mgm=1, …, 4的关系，可以采用函数求导法则推出考虑前四阶矩时P_f对基本变量X_i的第r个分布参数θ^(r)_xi的灵敏度为

$ \begin{array}{*{20}{c}} {\frac{{\partial {P_f}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}=\frac{{\partial {P_f}}}{{\partial {\beta _{4M}}}}\frac{{\partial {\beta _{4M}}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}=}\\ {\frac{{\partial {P_f}}}{{\partial {\beta _{4M}}}}\left({\frac{{\partial {\beta _{4M}}}}{{\partial {\beta _{2M}}}}\left({\frac{{\partial {\beta _{2M}}}}{{\partial {\alpha _{1g}}}}\frac{{\partial {\alpha _{1g}}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}+\frac{{\partial {\beta _{2M}}}}{{\partial {\alpha _{2g}}}}\frac{{\partial {\alpha _{2g}}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}} \right)} \right.}\\ {\left.{\frac{{\partial {\beta _{4M}}}}{{\partial {\alpha _{3g}}}}\frac{{\partial {\alpha _{3g}}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}+\frac{{\partial {\beta _{4M}}}}{{\partial {\alpha _{4g}}}}\frac{{\partial {\alpha _{4g}}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}} \right)} \end{array} $

(10)

式中：${\frac{{\partial {P_f}}}{{\partial {\beta _{4M}}}}}$，${\frac{{\partial {\beta _{4M}}}}{{\partial {\beta _{2M}}}}}$，${\frac{{\partial {\beta _{4M}}}}{{\partial {\alpha _{3g}}}}}$和${\frac{{\partial {\beta _{4M}}}}{{\partial {\alpha _{4g}}}}}$以及α_kg对θ^k_xi的偏导数${\frac{{\partial {\alpha _{mg}}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}}$的具体表达形式在文献[1]中有详细说明，此处不再赘述。

2 基于空间分割的改进点估计法 2.1 基本思想

基于空间分割的点估计方法通过空间分割后的子空间来降低功能函数的复杂性和非线性程度，从而达到提高计算效率的目的，其基本思想是：首先利用文献[14]中所介绍的方法使用少量样本近似最可能失效点(Most probable point，MPP)，并以该点为密度中心构造近似优化的重要抽样密度函数h_X(x)；然后按照h_X(x)对输入空间进行划分(Space parti tion，SP)，进而在每个子空间中使用低精度的SG积分法探索功能函数的概率响应特性；最后组合所有子空间中的信息得到所需的可靠性及可靠性灵敏度结果。本文以下部分用SG-SP表示本文方法。

2.2 空间划分策略及划分后的失效率概率和可靠性灵敏度

空间划分策略总体上可分为两步：

步骤1    借鉴文献[14]中提出的MPP近似方法，构造重要抽样密度函数h_X(x)。

(1)对系统的可靠度指标作出保守的假设，然后根据MPP估计中生成样本的最小区间(表 1)使用输入变量的累积分布函数的反函数确定“合适区间”的边界；

(2)在这些“合适区间”内均匀抽取N_MPP个样本x^（j）（j=1, …, N_MPP）；

(3)对于n维独立随机变量X，根据W_j=$\prod\limits_{i=1}^n {{f_{{X_i}}}\left({{x_{i \cdot j}}} \right)} $分别计算这些样本的权重系数W=(W₁, …，W_NMPP)，其中f_xi表示第i维变量的边缘概率密度函数；

(4)失效域中权重系数最大的样本点即为MPP的近似值；

(5)将输入变量联合密度函数f_X(x)的中心平移至MPP处，形成重要抽样密度函数h_X(x)。

步骤2    根据h_X(x)等概率划分输入变量空间，生成子空间。

这种划分策略的结果是：对失效概率贡献较大的地方空间分割比较密集，在影响小的地方则较为稀疏，提高了后续失效概率计算的效率。

根据式(1, 2)，失效概率和可靠性灵敏度在空间分割后可以表示为

$ \begin{array}{*{20}{c}} {{P_f} = \int {{I_F}\left( \mathit{\boldsymbol{x}} \right){f_X}\left( \mathit{\boldsymbol{x}} \right)} {\rm{d}}\mathit{\boldsymbol{x = }}}\\ {\;\int {{I_F}\left( \mathit{\boldsymbol{x}} \right)\frac{{{f_X}\left( \mathit{\boldsymbol{x}} \right)}}{{{h_X}\left( \mathit{\boldsymbol{x}} \right)}}} {h_X}\left( \mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}} = }\\ {\sum\limits_{{i_1} = 1}^{{N_1}} {\sum\limits_{{i_2} = 1}^{{N_2}} { \cdots \sum\limits_{{i_n} = 1}^{{N_n}} {\int {_{{U_{{i_1}}}}\int {_{{U_{i2}}} \cdots \int {_{{U_{{i_n}}}}{I_F}\left( \mathit{\boldsymbol{x}} \right)\frac{{{f_X}\left( \mathit{\boldsymbol{x}} \right)}}{{{h_X}\left( \mathit{\boldsymbol{x}} \right)}}} } } } } } }\\ {\frac{{{h_X}\left( \mathit{\boldsymbol{x}} \right)}}{{\int {_{{U_{{i_1},}}{i_2}, \cdots ,{i_n}}} {h_X}\left( \mathit{\boldsymbol{t}} \right){\rm{d}}\mathit{\boldsymbol{t}}}}\left( {\int {_{{U_{{i_1},}}{i_2}, \cdots ,{i_n}}} {h_X}\left( \mathit{\boldsymbol{t}} \right){\rm{d}}\mathit{\boldsymbol{t}}} \right){\rm{d}}\mathit{\boldsymbol{x}} = }\\ {\sum\limits_{{i_1} = 1}^{{N_1}} {\sum\limits_{{i_2} = 1}^{{N_2}} { \cdots \sum\limits_{{i_n} = 1}^{{N_n}} {{P_{_{{i_1},}{i_2}, \cdots ,{i_n}}}{E_{_{{i_1},}{i_2}, \cdots ,{i_n}}}\left( {{I_F}\left( \mathit{\boldsymbol{x}} \right)\frac{{{f_X}\left( \mathit{\boldsymbol{x}} \right)}}{{{h_X}\left( \mathit{\boldsymbol{x}} \right)}}} \right)} } } } \end{array} $

(11)

$ \begin{array}{*{20}{c}} {\frac{{\partial {P_f}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}=\int {_{{R_n}}{I_F}\left(\mathit{\boldsymbol{x}} \right)\frac{{\partial {f_X}\left(\mathit{\boldsymbol{x}} \right)}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}} {\rm{d}}\mathit{\boldsymbol{x=}}}\\ {\;\int {_{{R_n}}\frac{{{I_F}\left(\mathit{\boldsymbol{x}} \right)}}{{{f_X}\left(\mathit{\boldsymbol{x}} \right)}}\frac{{\partial {f_X}\left(\mathit{\boldsymbol{x}} \right)}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}\frac{{{f_X}\left(\mathit{\boldsymbol{x}} \right)}}{{{h_X}\left(\mathit{\boldsymbol{x}} \right)}}} {h_X}\left(\mathit{\boldsymbol{x}} \right){\rm{d}}\mathit{\boldsymbol{x}}=}\\ {\sum\limits_{{i_1}=1}^{{N_1}} {\sum\limits_{{i_2}=1}^{{N_2}} { \cdots \sum\limits_{{i_n}=1}^{{N_n}} {\int {_{{U_{{i_1}}}}\int {_{{U_{i2}}} \cdots \int {_{{U_{{i_n}}}}\frac{{{I_F}\left(\mathit{\boldsymbol{x}} \right)}}{{{h_X}\left(\mathit{\boldsymbol{x}} \right)}}\frac{{\partial {f_X}\left(\mathit{\boldsymbol{x}} \right)}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}} } } } } } }\\ {\frac{{{h_X}\left(\mathit{\boldsymbol{x}} \right)}}{{\int {_{{U_{{i_1}, }}{i_2}, \cdots, {i_n}}} {h_X}\left(\mathit{\boldsymbol{t}} \right){\rm{d}}\mathit{\boldsymbol{t}}}}\left({\int {_{{U_{{i_1}, }}{i_2}, \cdots, {i_n}}} {h_X}\left(\mathit{\boldsymbol{t}} \right){\rm{d}}\mathit{\boldsymbol{t}}} \right){\rm{d}}\mathit{\boldsymbol{x}}=}\\ {\sum\limits_{{i_1}=1}^{{N_1}} {\sum\limits_{{i_2}=1}^{{N_2}} { \cdots \sum\limits_{{i_n}=1}^{{N_n}} {{P_{_{{i_1}, }{i_2}, \cdots, {i_n}}}{E_{{h_{_{{i_1}, }{i_2}, \cdots, {i_n}}}}}\left({\frac{{{I_F}\left(\mathit{\boldsymbol{x}} \right)}}{{{h_X}\left(\mathit{\boldsymbol{x}} \right)}}\frac{{\partial {f_X}\left(\mathit{\boldsymbol{x}} \right)}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}} \right)} } } } \end{array} $

(12)

式中：U_ij(i_j=1, 2, …, N_j, j=1, 2, …, n)表示第j个变量的第i_j个小区间；N_j表示第j个变量被划分的总区间数；h_{i1, i2, …, in}(x)=${\frac{{{h_X}\left(\mathit{\boldsymbol{x}} \right)}}{{\int {_{{U_{{i_1}, }}{i_2}, \cdots, {i_n}}} {h_X}\left(\mathit{\boldsymbol{t}} \right){\rm{d}}\mathit{\boldsymbol{t}}}}}$表示基本变量X₁, X₂, …，X_n的第i₁, i₂, …，i_n个小区间形成的输入变量子空间U_{i1, i2, …, in}=U_i1∩U_i2∩…∩U_in的联合概率密度函数；E_{hi1, i2, …, in}(·)表示以h_{i1, i2, …, in}(x)为密度函数所求得的期望；P_{i1, i2, …, in}=∫_{U i1, i2，…，in}h_X(t) dt。

2.3 SG-SP方法的实现步骤及计算量

结合前面介绍的SG方法，可以按照以下步骤估计失效概率和可靠性灵敏度：

步骤1    根据近似优化的重要抽样概率密度函数h_X(x)将输入空间等概率划分成若干个子空间。

步骤2   在子空间U_{i1, i2, …, in}中，产生M^(k)_n个稀疏网格积分点s^(l)_{i1, i2, …, in}(l=1, 2, …, M_n^k)和对应的权重系数w^(l)_{i1, i2, …, in}。

步骤3   按照式(13, 14)计算P_f和$\frac{{\partial {P_f}}}{{\partial \theta _{{x_i}}^{\left(k \right)}}}$

$ \begin{array}{*{20}{c}} {{P_f}=\sum\limits_{{i_1}=1}^{{N_1}} {\sum\limits_{{i_2}=1}^{{N_2}} { \cdots \sum\limits_{{i_n}=1}^{{N_n}} {{P_{_{{i_1}, }{i_2}, \cdots, {i_n}}} \cdot } } } }\\ {\left({\sum\limits_{l=1}^{M_{^n}^{\left(k \right)}} {w_{_{{i_1}, }{i_2}, \cdots, {i_n}}^{\left(l \right)}{I_F}\left({s_{_{{i_1}, }{i_2}, \cdots, {i_n}}^{\left(l \right)}} \right)\frac{{{f_X}\left({s_{_{{i_1}, }{i_2}, \cdots, {i_n}}^{\left(l \right)}} \right)}}{{{h_X}\left({s_{_{{i_1}, }{i_2}, \cdots, {i_n}}^{\left(l \right)}} \right)}}} } \right)} \end{array} $

(13)

$ \begin{array}{*{20}{c}} {\frac{{\partial {P_f}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}=\sum\limits_{{i_1}=1}^{{N_1}} {\sum\limits_{{i_2}=1}^{{N_2}} { \cdots \sum\limits_{{i_n}=1}^{{N_n}} {{P_{_{{i_1}, }{i_2}, \cdots, {i_n}}} \cdot } } } }\\ {\left({\sum\limits_{l=1}^{M_{^n}^{\left(k \right)}} {w_{_{{i_1}, }{i_2}, \cdots, {i_n}}^{\left(l \right)}\frac{{{I_F}\left({s_{_{{i_1}, }{i_2}, \cdots, {i_n}}^{\left(l \right)}} \right)}}{{_X\left({s_{_{{i_1}, }{i_2}, \cdots, {i_n}}^{\left(l \right)}} \right)}}\frac{{\partial {f_X}\left({s_{_{{i_1}, }{i_2}, \cdots, {i_n}}^{\left(l \right)}} \right)}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}} } \right)} \end{array} $

(14)

从式(13, 14)可以看出，SG-SP方法的总计算量为$M_n^{\left(k \right)} \cdot \prod\limits_{i=1}^n {{N_i}+{N_{{\rm{MPP}}}}} $，式中N_MPP表示用来估计MPP的样本量。尽管每个子空间中SG方法产生的积分点数M_(n)^k比较小，但是总的计算量却与维数成指数关系，所以该方法只适合低维的情况。

3 算例

在以下算例中，将蒙特卡洛(Monte Carlo，MC)数字模拟方法的结果作为参考解，分别使用TPE，SG积分方法和本文SG-SP方法来估计失效概率和可靠性灵敏度，从计算结果精度和总模型调用次数两方面来比较。

在使用SG-SP方法计算时，为了方便比较，对同一功能函数g(x)，假定每一维输入变量X_j划分段数N_j相同，即N₁=N₂=…=N_n=N。同时为了充分证明本文所提方法的优势，在使用SG积分方法计算前四阶矩时，精度k₁取结果稳定时的最小值。根据式(8~10)，这些稳定的结果用来计算P_f和${\frac{{\partial {P_f}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}}$，而${\frac{{\partial {P_f}}}{{\partial \theta _{{x_i}}^{\left(r \right)}}}}$包含的其他积分运算由精度为k₂的稀疏网格估计, P_f不随k₂变化。

3.1 算例1

假设功能函数为g(x₁, x₂)=a+0.004 63·(x₁+x₂-20)^q-0.235 7(x₁-x₂)，其中独立的输入随机变量x服从正态分布，即x_i~N(10, 3)(i=1, 2)。功能函数中指数q，常数a和使用SG-SP方法估计MPP时均匀抽取的样本量N_MPP如表 2所示。

a和q取不同值时前四阶中心矩和失效概率及可靠性灵敏度的计算结果见表 3~10，其中计算量表示总的模型函数调用次数。

结果分析：q=1和q=2时，功能函数的非线性程度比较低，SG方法在计算量小于SG-SP方法的最低计算量时已经得到了精度略高于后者的结果，在这种情况下SG方法无疑更具有优势。TPE方法在q=1时具有和SG方法相当的计算效率，但是在q=2时该方法的部分计算结果出现较大的偏差。

从q=3和q=4时的计算结果来看，随着非线性程度的增加，在前四阶矩的计算中，TPE方法的计算结果已经部分错误，而SG方法的精度高于TPE方法。在表 8，10中，两种对照方法的结果几乎完全错误，即使提高SG方法的精度水平，也无法得到与MC解接近的结果。而SG-SP方法所得结果随着k的增加而逐渐收敛，且k=1时就已经达到了可用的精度。q=4时的情况同时也表明了所提方法在失效概率数量级较小时的良好适用性。需要说明的是，当q=4时，由于模型的可靠性及可靠性灵敏度过小，使用MC方法无法得到稳定的结果，并且前面3种情况已经证明了SG-SP方法的计算结果随着N和k的增加收敛于真实解，所以此情况下可以取N=40, k=8时的计算结果作为参考解。

以q=4时的情况为例，简要说明SG-SP方法中N与k的选取方法。显然，为了获得要求的计算精度，可以通过增大N和k的取值来实现。N的取值越大，则在划分的子空间中功能函数的复杂性和非线性程度越低，这时就可以采用较小的k值来达到要求的精度。相反，N的取值越小，则要达到要求的精度就需要采用较大的k值来实现。一般来说k值较小时的结果较稳定。图 1给出了本算例在k取1，2，3和4时计算失效概率的均方误差随总计算次数变化的曲线，从图 1中可以看出：在相同计算量下，k=1时的均方误差最小，而相同均方误差情况下，k=1时的总计算量最小。因此一般情况下，在SG-SP方法中建议k取1或2，然后通过增加N来达到要求的计算精度。

3.2 算例2

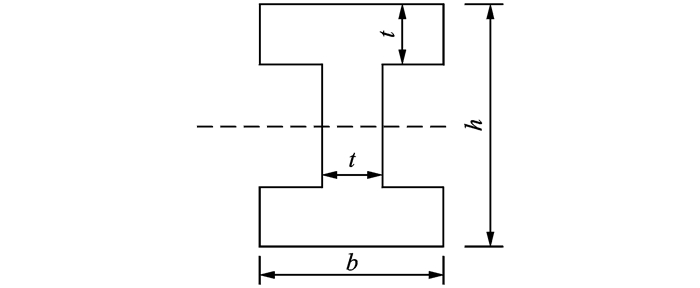
在汽车工程领域中，前轴承载着车辆前部的重力，所以必须保证其有足够的可靠性。工字梁由于具有良好的抗弯性能和质量较轻的特点而被广泛地应用于前轴的设计中。图 2为汽车前轴示意图，工字梁危险截面形状如图 3所示。已知危险截面的最大正应力为σ=M/W_x和τ=T/W_ρ，其中M=2.5×10⁶ N·mm和T=2.1×10⁶ N·mm分别为前轴所受的弯矩和扭矩，W _x和W_ρ分别为结构的截面系数和极截面系数，且有

$ {W_x}=\frac{{{{\left({h - 2t} \right)}^3}}}{{500h}}+\frac{b}{{6h}}\left[{{h^3}-{{\left({h-2t} \right)}^3}} \right] $

(15)

$ {W_\rho }=0.8b{t^2}+\frac{{100}}{3}{t^3}\left({h - 2t} \right) $

(16)

根据前轴的材料特性，给定前轴的静强度极限为σ_s=600 MPa，故由静强度分析并构件模型的功能函数为g=${\sigma _s} - \sqrt {{\sigma ^2}+3{\tau ^2}} $，工字梁的几何参数b，t，h为相互独立的正态输入变量，其分布参数如表 11所示。采用TPE和SG方法作为对照，表 12为这两种方法对前四阶中心矩的估计结果。使用SG-SP方法对该结构进行可靠性及可靠性灵敏度分析时，将变量空间分割成8³=512个子空间，均匀抽取400个样本估计MPP。失效概率及可靠性灵敏度的计算结果如表 13所示。

结果分析：从以上计算结果可以发现两种对照方法SG和TPE估计的前四阶矩与参考值差别不大，但是基于前四阶矩的可靠性及可靠性灵敏度分析结果却几乎全部错误，而使用本文中所建立的SG-SP方法在k=2时已经具有良好精度，计算量为3 984。可靠性灵敏度反映了基本变量分布参数对失效概率的影响程度，无量纲正则化的可靠性灵敏度可以用于基本变量分布参数对可靠度的重要性排序。为了把失效概率控制在理想的范围，研究者可以依据这种重要性排序来决定哪些变量应该被重点考虑，这在工程上具有重要意义。

4 结束语

本文将空间分割思想，SG积分方法和最可能失效点估计方法结合在一起，提出了一种适合低维高度非线性模型可靠性及可靠性灵敏度分析的新方法。常用的传统点估计方法在非线性程度逐渐增加的情况下所计算的结果的误差也逐渐增大，甚至出现了严重的错误，而SG-SP方法却使用不大的计算量即可获得稳定的结果。需要再次强调的是在高维情况下，该方法的计算量会随着维数呈指数增加，在非线性程度低的情况下，与传统的点估计方法相比并不占有优势，但是在低维度、非线性程度较高的问题上本文方法体现出了明显的高效率和高精度的优势，与降维技术相结合将有望解决高维高度非线性问题。在SG-SP方法中，有关计算量随着维数呈指数增长问题将有望采用自适应空间剖分的方法加以解决，这将是作者后续的研究工作。