多属性决策是在考虑多个属性(指标)的情况下，如何有效地协助决策者理性(逻辑性)地从多个备选方案中选择出最合适方案的决策过程^[1]。近几十年来，多属性决策在理论研究和案例应用方面均获得了迅猛的发展，成为管理学科中一个重要的研究分支。随着信息社会带来的信息公开性、透明性和全面性，很多经济社会问题的参考信息量不断增加、利益相关者决策参与度不断提升、相应解决问题的复杂度不断增大。呼应于这一现实问题，考虑多个决策者参与的多属性群决策问题逐渐成为该方向的研究热点^[2-9]。

由于涉及相关研究内容较庞杂，本文只能按照研究演化路径简述一些相关研究：(1)基于经典多属性决策方法在群决策条件下拓展研究，如多属性效用理论(Multiattribute utility theory，MAUT)^[2]、层次分析法(Analytic hierarchy process，AHP)^[3]、TOPSIS (Technique for order preference by similarity to an ideal solution)^[4]等在群决策下的拓展；(2)考虑不确定性现代多属性群决策方法研究，如基于模糊理论^[5]及其拓展、直觉模糊^[6]、一致性理论^[7]、灰色理论^[8]、OWA (Ordered weighted averaging)算子^[9]等。

基于案例学习的多属性决策是指决策者针对特定典型案例集的决策结果，进行学习推理，计算出部分或全部决策参数，从而构建出对应的决策模型，再应用于对所有方案进行评价的方法。其代表性模型有优势粗糙集^[10]、UTADIS (Utility Additives Discriminates)^[11]以及Chen提出的基于案例距离(Case-based Distance Approach)决策模型^[12-14]等方法。这类多属性决策方法在分类决策中有广泛的应用，如“European Journal of Operational Research”期刊主编Slo winski教授就指出，人类的大量决策就是通过学习已有的案例进行推理分析的，基于案例学习的决策易于理解、贴近人类的日常决策过程^[15]。

目前基于案例学习的方法在单个决策者的决策问题中应用广泛，如在文献[12~14]中通过案例学习解决多属性决策中的选优问题、筛选问题及分类问题，Ma对案例学习的距离方法作了进一步拓展^[16-17]。而基于案例学习群决策方法的研究并不多见，文献[18]提出确定多属性排序问题协调权的方法，文献[19]在此基础上引入偏好关系重要度的概念，当协调权不存在时，识别出最不重要的偏好序关系进行调整，文献[20]定义案例信息的一致性和可信度，构建整数规划模型确定群体一致案例信息，并利用该信息构建分类模型。

本文是针对基于案例学习的方法，在考虑群决策分类问题下的拓展研究。其主要思路为：给出多属性决策的分类原则，根据决策者的权重计算案例信息的重要度，从所有的案例信息中挑选出重要度最大的一致案例集，在此基础上确定多属性分类问题的协调权及分类阈值，最后对全部方案进行分类。

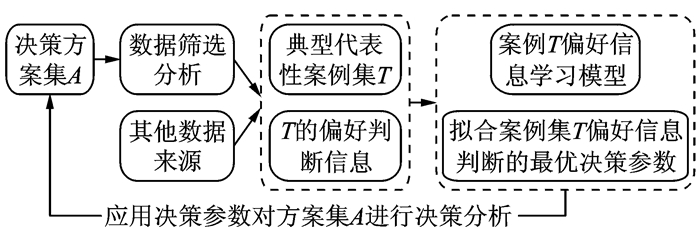
1 基本问题描述 1.1 基于案例学习多属性决策方法概述

为了有效展示本文的研究范畴，图 1为基于案例学习的多属性决策方法流程。其主要包括：

(1)典型代表性案例集T的获取：通过对决策方案集A的聚类分析，或其他类似历史数据、虚拟案例构造等方案，形成案例集T，并邀请决策者对T进行整体性偏好判断如排序、分类等。

(2)决策参数的优化拟合：通过对T构建案例优化学习模型，获得最佳的拟合参数如指标权重信息等。

(3)决策参数的全局应用：将学习获得的参数应用于对全体方案集A的分析。

1.2 多属性群分类问题设定

在本文研究的多属性群决策分类问题中，待分类方案的属性值已知，指标权重信息及分类阈值不确定，各决策者根据自身的决策经验和相关知识，分析部分方案并给出各自的分类结果，即案例信息。本文的主要决策任务是利用各决策者提供的案例信息，确定群体的一致案例集，获取分类问题的决策参数。对于群决策分类问题，引入如下变量：

方案集A，A={a¹, …, aⁱ, …, a^丨A丨}，其中aⁱ为第i个方案，A包含丨A丨个元素；

指标集C, C={c₁, …, c _j…, c_|C|}, 其中c_j为第j个指标，C包含|C|个元素，c_j(a_i)表示方案a_i在指标c_j下的属性值，可简写为c_jⁱ；

基于C针对A的多属性分类决策：根据指标集C，可以对方案集A进行分类决策，形成分类集合G, G={G¹, …, G^s, …, G^|G|}, 其中G¹代表最差的一类，G^s代表第s类，s越大G^s越好，G^|G|为分类集合的第|G|类；

指标权重集W, W={w₁, …, w_j…, w_|W|}, 其中w _j为c_j的权重，满足$\sum\limits_{j=1}^{\left| W \right|}{{{w}_{j=1}}}$, 0≤w _j≤1，且|C|=|W|，权重集W未知；

E={e₁, …, e_k, …, e_|E|}，表示群决策问题中的|E|个决策者的集合，其中e_k为第k个决策者；进一步设定决策者权重集λ，λ=λ₁, …, λ_k, …, λ_|E|，其中λ_k为第k个决策者的权重，满足$\sum\limits_{k=1}^{\left| E \right|}{{{\lambda }_{k}}=1}$, λ_k>0；

案例集T_k，T_k={t_k¹, …t_k^p, …, t|^T_k|_k}，表示由决策者e_k提供的且给出了分类结果的案例信息，令∪T_k表示所有决策者提供的个体案例的集合。案例集的选取可以是决策者过去的类似决策信息，也可以是从方案集A中提炼出的典型案例。

1.3 决策问题效用函数的定义

本文采用文献[20]中线性效用函数表示决策者对案例的偏好，即方案的效用值越大，决策者(或决策群体)认为该方案越好。首先给出以下的指标效用设定：

(1)根据方案集的属性值，∀j=1, 2, …, |C|，c_j^max$\underset{{{a}_{i}}\in A}{\mathop{\max }}\, \left\{ {{c}_{j}}\left({{a}^{i}} \right)\right\}$，c_j^min=$\underset{{{a}_{i}}\in A}{\mathop{\max }}\, \left\{ {{c}_{j}}\left({{a}^{i}} \right)\right\}$分别表示指标c_j下的最大值和最小值。(2)对于∀j=1, 2, …, C，令u_j^max作为所有|E|个决策者或整个决策群体统一的属性值归一化参数，u^max _j=c_j^max-c_j^min。(3)对于∀j=1, 2, …, |C|，当c_j为效益型指标时，即方案在c_j下越大越好，令u_j(aⁱ)为c_j的边际效应函数，u_j(aⁱ)=[c_j(aⁱ)-c_j^min]/u_j^max。(4)对于∀j=1, 2, …, |C|，当c_j为成本型指标时，即方案在c_j下越小越好，关于c_j的边际效应函数，u_j(aⁱ)=[c_j^max-c_j(aⁱ)]/u_j^max。

由此，令U(aⁱ)为决策群体对于方案aⁱ的效用函数，U(aⁱ)=$\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}$·u _j(aⁱ)。U(aⁱ)的值越大，表示决策群体对aⁱ偏好越强。

2 群分类问题协调权构建 2.1 基于效用函数的分类原则

根据效用函数对方案进行分类，满足如下性质：类别越高的方案，效用值越大。令G(aⁱ)表示方案aⁱ所在的类别，若G(a) < G(b)，须满足U(a) < U(b)。由于决策者对于方案的偏好是用效用函数表示，故群体对于案例的一致判断及基于效用函数的分类结果应该满足这个基本性质。

定义1对于∀a, b∈A，已知分类情况G(a) < G(b)，如果存在效用函数U(·)使得U(a) < U(b), 则称方案集A的分类结果满足一致性^[20]。

借鉴基于案例距离分类方法的思想^[12-14]，形成定理1。

定理1如果存在效用函数U(aⁱ)及分类阈值R _s，s=1, 2, …，|G|-1，

(1)若U(aⁱ)≤R₁，则方案aⁱ划为G¹类；

(2)若U(aⁱ)≤R_s+1且U(aⁱ)>R_s，1 < s < |G|-1, 则aⁱ划为G ^s类；

(3)若U(aⁱ)>R_G-1，则aⁱ划为G|^G|类；其中R_s < R_s+g，1≤g≤G-s-1, 则方案集A通过该规则获得的分类结果满足一致性。

证明：∀a, b∈A，如果a∈^Gs，^b∈G^s+g，1 < ^s < |G|-2且1≤g≤|G|-s-1，即G(a) < G(b)，则有U(a)≤R_s+1且U(a)>R_s，U(b)≤R_s+g+1且U(b)>R_s+g，又R_s < R_s+g，1≤g≤|G|-s-1，可以得到U(b)>R_s+g≥R_s+1≥U(a)；对于a∈G^s，b∈G^s+g，s=1或G-2，1≤g≤G-s-1，同理可以得到U(b)>R _s+g≥R_s+1≥U(a)，根据一致性定义，定理1得证。

证毕。

定理1提供了本文基于效用函数和分类阈值进行分类的原理，且通过该分类原则，方案集A的分类结果满足一致性，该原理的优点是方法简单且易于理解。

2.2 多属性群决策分类问题的协调权

对于群决策分类问题，存在不一致的案例偏好信息，目前针对多属性群决策排序问题已有相关研究^[3-4]，通过构建指标协调权，来识别是否存在一组指标权重，满足所有的决策者案例偏好。本文借鉴该思想，构建了如下针对群决策分类问题的协调权。

定义2如果存在β≥0，W={w₁, …, w_j…, w _|W|}及分类阈值R_s, 使得所有决策者对于案例的判断满足如下关系：

(1)$\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}$·u_j(t^p)+β≤R₁, ∀t^p∈G¹；

(2)$\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}$·u_j(t^p)+β≤R_s+1且$\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}$u_j(t^p)-β>R_s，∀t^p∈G^s，1 < s < |G|-1；

(3)$\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}$ ·u_j(t^p)-β>R_G-1，∀t^p∈G^|G|；

其中R_s < R_s+g，1≤g≤|G|-s-1，β为案例的效用函数远离相应阈值的程度，则称W为群决策分类问题的协调权。

考虑如下的线性规划问题P₁，模型P₁的决策变量是β, w_j, R_s。

$ \begin{matrix} \text{max}\beta \\ \text{s}\text{.t}\text{.} \\ \left\{ \begin{align} &\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}\cdot {{u}_{j}}\left({{t}^{p}} \right)+\beta \le {{R}_{1}}\ \ \ \ \forall {{t}^{p}}\in {{G}^{1}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(1\text{a} \right)\\ &\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}\cdot {{u}_{j}}\left({{t}^{p}} \right)+\beta \le {{R}_{s}}\ \ \ \ \forall {{t}^{p}}\in {{G}^{s}}, 1<s<\left| G \right|\ \ \ \ \ \ \ \left(1\text{b} \right)\\ &\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}\cdot {{u}_{j}}\left({{t}^{p}} \right)-\beta >{{R}_{s}}_{-1}\ \ \ \ \forall {{t}^{p}}\in {{G}^{s}}, 1<s<\left| G \right|\ \ \ \left(1\text{c} \right)\\ &\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}\cdot {{u}_{j}}\left({{t}^{p}} \right)-\beta \le {{R}_{\left| G \right|}}_{-1}\ \ \ \ \ \forall {{t}^{p}}\in {{G}^{\left| G \right|}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(1\text{d} \right)\\ &\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}=1\ \ \ \ 0\le {{w}_{j}}\le 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(1\text{e} \right)\\ &0\le {{R}_{s}}\le 1, \forall s=1, 2, \cdots, \left| G \right|-1 \\ \end{align} \right.\\ \end{matrix} $

定理2    令(β^*, W^*, R_s^*)为线性规划模型P₁的最优解，β^*≥0是群决策分类问题存在协调权的充分必要条件。

证明：(1)令β_p^s表示各决策者对于案例t^p的效用函数远离相应阈值的程度，∀t^p ∈∪T_k，s=1, …, |G|，根据模型P₁的目标函数可知，β_p^s≥β^*≥0，∀t^p∈∪T_k，s=1, …, |G|，由定义2，W^*为群决策分类问题的协调权；

(2)假设群决策问题存在协调权W*，β* < 0，又β*=min{ βps|∀tp∈∪Tk, s=1, …, |G|}，故存在βposo=β* < 0，其中βposo∈βps，与定义2中β≥0矛盾，故模型P1的最优解β*≥0。

证毕。

定理2表明可以通过求解线性规划模型P₁确定群决策分类问题的协调权及相应的分类阈值，即若β^*≥0，可确定协调权存在。但是如果直接利用各决策者提供的案例信息构建模型P₁，虽然可得最优解(β^*, W^*, R_s^*)，由于决策者判断的差异性，β^*值很可能小于0，由此不满足协调权存在的条件，故本文构建了以下确定群体一致案例集模型以及基于该案例信息的分类优化模型。

3 基于一致案例集的多属性群分类方法 3.1 确定群体一致案例集的模型构建

在多属性群决策中，各决策者基于自身的知识和思维方式，或者由于自身的认知缺陷，提供的案例信息一般不满足定义1的一致性要求，甚至对于案例的分类结果会出现冲突的情况。在这种情况下，直接利用原始的案例信息确定的群体效用函数，将无法同时满足全部决策者的判断，得到的分类结果自然会有争议。为此，需要从各决策者提供的案例集中尽可能多地挑选出满足群体一致性要求的案例集，在此基础上确定合适的效用函数及分类阈值对待评价方案进行分类。

此外，不同决策者的地位、能力等不同，导致他们在决策过程中的重要程度不同，故在多属性群决策中设定决策者的权重，权重越大通常意味着决策者对群体决策的影响越大。对于某个案例分在某一类，可能是部分决策者的看法，也可能是全部决策者的意见，甚至也会出现部分决策者的不同看法，考虑到决策者们的权重，下面给出案例被分在某一类的重要度的定义。

定义3   令μ_ps表示案例t ^p划为G^s类的重要度，μ_ps=$\sum\limits_{k:{{I}_{kp}}\text{=}s}{{{\lambda }_{k}}}$，0≤μ_ps≤1，∀t^p∈∪T_k，s=1, 2, …, |G|-1。

从定义3可以看出，μ_ps为所有认为案例t^p应划为G^s类的决策者的权重之和，μ_ps的值越大，表示对应的案例分类关系重要性越高，μ_ps=1表示|E|个决策者全部认为t^p应划为G^s类。为了获得群体的一致案例集，尽可能多的利用决策者提供的案例信息，面对决策者给出的案例信息不满足一致性甚至出现冲突的情况，应该使案例满足群体一致性分类关系的重要度之和最大，即使案例不满足群体一致性分类关系的重要度之和最小。为此，构建{0, 1}混合整数线性规划模型P₂，令T^*为群体案例集。

$ \begin{matrix} \max Z=\sum\limits_{p, s:{{t}^{p}}\in {{G}^{s}}}{\mu _{p}^{s}\cdot h_{p}^{s}} \\ \text{s}\text{.t}\text{.} \\ \left\{ \begin{align} &\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}\cdot {{u}_{j}}\left({{t}^{p}} \right)-h_{p}^{1}\le {{R}_{1}}\ \ \ \ \forall {{t}^{p}}\in {{G}^{1}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(\text{2a} \right)\\ &\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}\cdot {{u}_{j}}\left({{t}^{p}} \right)-h_{p}^{s}\le {{R}_{s}}\ \ \ \ \forall {{t}^{p}}\in {{G}^{s}}, 1<s<\left| G \right|\ \ \ \ \ \ \ \left(\text{2b} \right)\\ &\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}\cdot {{u}_{j}}\left({{t}^{p}} \right)+h_{p}^{s}>{{R}_{s}}_{-1}\ \ \ \ \forall {{t}^{p}}\in {{G}^{s}}, 1<s<\left| G \right|\ \ \ \ \ \left(\text{2c} \right)\\ &\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}\cdot {{u}_{j}}\left({{t}^{p}} \right)h_{p}^{\left| G \right|}>{{R}_{\left| G \right|}}_{-1}\ \ \ \ \ \forall {{t}^{p}}\in {{G}^{\left| G \right|}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(2\text{d} \right)\\ &\sum\limits_{s:{{t}^{p}}\in {{G}^{s}}}{\left(1-h_{p}^{s} \right)}\le 1\ \ \ h_{p}^{s}\in \left\{ 0, 1 \right\}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(2\text{e} \right)\\ &{{t}^{p}}\in \cup {{T}_{k}}, k=\left\{ 1, 2, \cdots \left| E \right| \right\} \\ &\sum\limits_{j=1}^{\left| c \right|}{{{w}_{j}}}=1\ \ \ 0\le {{w}_{j}}\le 1 \\ &0\le {{R}_{s}}\le 1, \forall s=1, 2, \cdots, \left| G \right|-1 \\ \end{align} \right.\\ \end{matrix}$

模型P₂的决策变量是h_p^s, w_j, R_s，边际效用函数u_j(t^p)的计算公式在1.2节中给出，目标函数$\max Z=\sum\limits_{p, s:{{t}^{p}}\in {{G}^{s}}}{\mu _{p}^{s}\cdot h_{p}^{s}}$含义为寻找一个案例集能最小化群体案例集的不一致分类偏好关系，其中h_p^s是0-1变量，h_p^s=1表示案例t^p的群体分类结果不是G^s，若∀s={1, 2, …，G}，都有h_p^s=1，表示t^p不能放入群体案例集；h_p^s=0表示案例t^p的群体分类结果是G^s。令通过模型P₂，所有满足h_p^s=0的案例t^p将被选入群体案例集中，即T^*={t^p| h_p^s=0, t^p∈∪T_k, 1≤s≤|G|}，对应的分类关系为群体一致案例信息。

式(2a)用于分析决策者给出的案例信息中被分在G¹类的案例，若案例t^p被正确地分在G¹类，则h_p^s=0，即未考虑约束条件式(2a)的作用，U(t^p)≤R₁，否则h_p^s=1。对于式(2b, 2c)，若案例t^p被正确地分在G ^s类，∀s={2, 3, …，|G|-1}，则h_p^s=0，即R_s-1 < U(t^p)≤R_s，否则h_p^s=1。同理对于式(2d)，若案例t^p被正确地分在G^|G|类，则h_p^s=0，即U(t^p)>R_|G|-1，否则h_p^s=1。

式(2e)表示对于同一案例t^p，∀s={1, 2, …, G}，不能出现两个或以上h_p^s同时等于0，即案例t^p不能被同时分到不同的类，确保案例集对应的分类的结果唯一，但h_p^s可同时等于1。

模型P₂在文献[17]中模型Obj1的基础上进行改进，将解决的问题从单个决策者拓展到群决策，用于确定群体一致案例集。

定理3    设模型P₂的最优值Z^*，最优解为({h_p^s*}, W^*, R_s^*)，则群决策分类问题存在协调权的充分必要条件为Z^*=0。

证明：(1)充分性。若群分类问题存在协调权，由定义2可知，至少存在一组β≥0, W, R_s，则各案例的效用函数满足：U(t^p)≤R₁，∀t^p∈G¹；R_s-1 < U(t^p)≤R_s，∀s={2, 3, …，|G|-1}；U(t ^p)>R_G-1，∀t^p∈G^|G|。故({ 0}, W, R_s)为P₂的可行解，Z^*≤0，又μ_ps≥0, h_p^s∈{0, 1}，Z^*≥0，所以Z^*=0。

(2)必要性。若模型P₂的最优值Z^*=0，则∀t^p∈∪T_k, 1≤s≤G, h_p^s=0，等价于定义2中β=0的情况，满足协调权存在的条件，故此时群分类问题存在协调权。

证毕。

定理3表明若模型P₂的最优值Z^*=0，则群分类问题的协调权及分类阈值存在，若Z^*>0，群分类问题的协调权及分类阈值不存在。

前文总结如下：通过模型P₂可获取群体的一致案例集及相应的一致案例信息。3.2节中进一步设计了利用获得的一致性案例信息构建案例学习的分类模型。

3.2 基于案例的分类模型构建

在群决策问题中，由于各决策者给出的案例信息通常不满足一致性，直接利用原始案例集将无法确定群分类问题的协调权，为此通常情况下首先确定群体一致案例集，再利用群体一致案例信息确定协调权。

定理3    若模型P₁中t^p全部来自群体案例集T ^*，则群决策问题一定存在协调权。

证明：设模型P₂的最优解为(W^*, R_s^*, {h_p^s*})，对于h^s* _p=0，下列关系同时成立：

(1)R₁-$\sum\limits_{j=1}^{\left| c \right|}{w_{j}^{*}}$·u_j(t^p)≥0，h_p^1*=0；

(2)R_s-$\sum\limits_{j=1}^{\left| c \right|}{w_{j}^{*}}$·u_j(t^p)≥0且$\sum\limits_{j=1}^{\left| c \right|}{w_{j}^{*}}$·u_j(t^p)-R_s-1>0，h_p^s*=0；

(3)R_|G|-$\sum\limits_{j=1}^{\left| c \right|}{w_{j}^{*}}$·u_j(t^p)≥0，h_p^G*=0。

若模型P₁中t^p全部来自群体案例集T^*，即t^p∈T^*，令如此变形后的模型为P₃, P₃等价于P₁且t^p∈T^*，其决策变量为(W, R_s, β)。

由上述不等式关系(1~3)可知((W^*, R_s^*, 0)为P₃的可行解，故P₃的最优值β^*≥0，由定理2，群分类问题一定存在协调权。

证毕。

关于模型P₁，P₂和P₃的承接关系总结如下：P₃中的案例集为群体一致案例集，P₁中的案例集为决策者提供的原始案例集，即P₃舍弃了原始案例信息中不满足群体一致性的分类关系。另外当模型P₂的最优值Z^*=0时，即对应β=0，可以得到一组协调权及分类阈值，但是本文期望案例的效用函数能远离分类阈值，根据模型P₃得到的最优值β ^*≥β=0，故采用模型P₃确定协调权及分类阈值，再利用决策参数W^*确定全部方案的效用函数U(aⁱ)，根据定理1，将U(aⁱ)与R_s^*进行比较，可将全部方案进行分类。

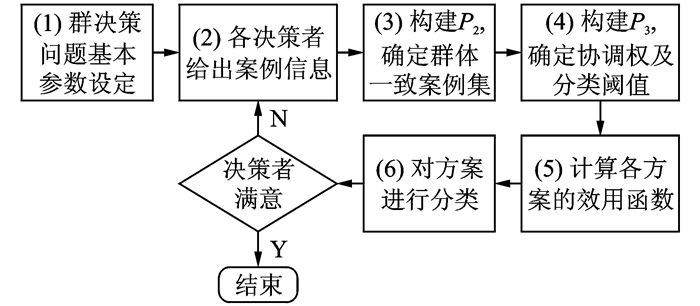
3.3 多属性群决策分类方法的基本步骤

归纳前文的相关内容，本文方法的一般步骤如图 2所示：

步骤1    分析问题，确定群决策分类问题的评价方案集A及指标集C，决策参与者的集合E及决策者权重集λ，并定义分类集合G，见1.2节。

步骤2   给出案例信息，各决策者基于自身的判断，给出部分方案(案例)的分类信息。

步骤3   根据案例信息，计算各案例的分类结果的重要度，构建模型P₂，确定群体的一致案例集及相应的案例信息，如3.1节所示。

步骤4   基于模型P₂得到的群体一致案例信息，构建模型P₃，群定群分类问题的协调权及分类阈值，见本文3.2节。

步骤5   根据1.3节中的定义，计算决策群体对于方案aⁱ的效用函数U(aⁱ)。

步骤6   将效用函数U(aⁱ)与分类阈值进行比较，根据2.1节中基于效用函数的分类原则，可确定各方案的精确分类。

如果决策群体对于最终的分类结果满意，则决策终止，否则返回步骤2，调整案例信息。

4 案例分析 4.1 基本参数设定

本文的案例将文献[20]中30所高校的MBA项目分为5类，其评价数据见表 1，有：

(1) MBA项目的3个指标：c₁=“职业前景”，c₂=“多远化”，c₃=“创新性”，均为效益型指标，方案集A={a¹, a², …, a³⁰}。

参与评价的专家3名，专家集E={e₁, e₂, e₃}，专家权重(λ₁, λ₂, λ₃)=(0.2, 0.35, 0.45)。

分类集合G={G¹, G², G³, G⁴, G⁵}, 其中G¹=“差”，G²=“一般”，G³=“较好”，G⁴=“好”，G⁵=“很好”。

(2)决策者给出的案例信息如表 2所示，其中案例均取自待评价方案，故∪T_k={a₁, a₂, a₃, a₄, a₅, a₆, a₇, a₈, a₁₂, a₁₄, a₂₉}。

(3)各指标的边际效用函数为：${{u}_{1}}\left({{a}^{i}} \right)=\frac{\left[{{c}_{1}}\left({{a}^{i}} \right)-50.4 \right]}{33.4}, {{u}_{2}}\left({{a}^{i}} \right)=\frac{\left[{{c}_{2}}\left({{a}^{i}} \right)-18.69 \right]}{52.05}, $${{u}_{3}}\left({{a}^{i}} \right)=\frac{\left[{{c}_{1}}\left({{a}^{i}} \right)-14.45 \right]}{39.46}$.

将各方案的属性值带入边际效用函数便可得到相应的边际效用值。

4.2 群体一致案例集确定

根据定义2及表 2，计算出全部案例分类结果的重要度：μ₁⁵=0.2，μ₂⁴=0.2，μ₁₂³=0.2，μ₁₄⁵=0.2，μ₃⁴=0.35，μ₄³=0.35，μ₅³=0.35，μ₂₉⁴=0.35，μ₆²=0.45，μ₇²=0.45，μ₈¹=0.45，μ₁₂⁴=0.45，μ₂₉¹=0.45。

利用Lingo11.0求解模型P₁，有h₁⁵=h₂⁴=h₃⁴=h₄³=h₅³=h₆²=h₇²=h₈¹=h₁₂⁴=h₁₄⁵=h¹ ₂₉=1，h₁₂³=h₂₉⁴=0；故群体一致案例集T^*={a₁, a₂, a₃, a₄, a₅, a₆, a₇, a₈, a₁₂, a₁₄, a₂₉}，案例的分类结果如表 3所示，并与文献[20]中结果进行比较。

从表 3可以看出，本文与文献[20]的案例分类结果除案例a₄外，其余均一致，本文将a₄放入群体案例集，而文献[20]相反，这表明本文的群体一致案例集信息更丰富。

4.3 方案的群体分类

基于群体的一致案例信息构建模型P₃，利用Lingo11.0求解，有β^*=0.004 8，表明决策问题的协调权存在，可确定该问题的决策参数：w₁^*=0.259 3，w₂^*=0.274 6，w₃^*=0.466 1，R₁^*=0.372 0，R₂^*=0.434 1，R₃^*=0.443 7，R₄^*=0.529 3。

将权重w₁^*，w₂^*，w₃^*用于计算各方案的效用函数，再与分类阈值R₁^*，R₂^*，R₃^*，R ₄^*比较，根据定理1可确定各方案的精确分类，如表 4所示。

由表 4可知，本文与文献[20]给出的分类结果有6处不同，分类不同的方案分别为：a₄，a₁₆，a₁₇，a₂₆，a₂₇，a₃₀，除方案a₂₇外，其余4个方案的分类结果相邻。根据协调权w₁^*，w₂^*，w₃^*的大小，决策群体对于指标“创新性”的偏好最强，具有一定的合理性。

本文与文献[20]的案例信息及属性值处理方式相同，同样考虑决策者权重及信息的不一致性，但两种方法核心部分具有差异性，群体一致案例集的确定及方案的分类方法完全不同，文献[20]的处理方式是比较两案例的效用函数，而本文的思路是比较各案例的效用函数和分类阈值，对于决策者而言，本文的方法相对易于理解。

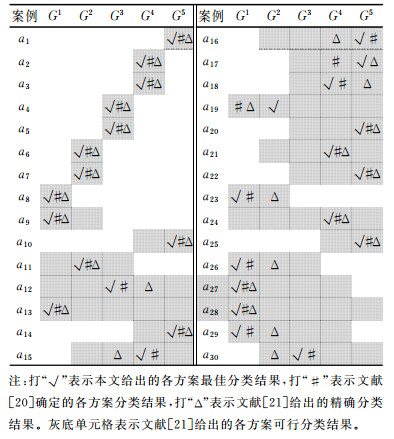
4.4 方法的比较分析

为了进一步说明方法的合理性，现扩大实例分析的比较范围，由于文献[21]只针对单个决策者，为比较不同研究方法的结果，假设4.1节的实例中仅有一名决策者，其提供的案例信息如表 5所示。按照本文所述的方法，仍可获得方案的分类结果，如表 6所示。

本文方法与文献[20, 21]中方法的整体思路一致，都是利用案例分类信息进行决策信息学习，不需要设置指标权重及分类边界。由于不同方法采用的分类规则和模型不同，这是导致最终分类结果有所差异的主要原因。本文采用的分类规则将效用函数与分类阈值进行比较，文献[20]采用的分类规则是将不同案例的效用函数两两比较，文献[21]采用的分类规则是级别优于关系。

由表 6可知，首先本文方法确定的各方案分类结果全部在文献[21]的可行分类区间中，故3种方法的分类结果在一定程度上是一致的；其次3种方法的方案精确分类结果的一致程度如表 7所示。这两方面可在一定程度上反映本文方法的合理性。

5 结束语

基于案例学习的决策方法，直接利用案例信息，通过优化的方法确定决策参数(指标权重及分类阈值)，具有决策信息要求低、易于理解和操作的特点。本文考虑了案例信息提供为多人，即群决策环境下的案例学习分类问题。由于决策者们对于案例的群体分类很可能不一致，为此先确定群体的一致案例集，即重要程度最高的案例分类信息，该过程中体现了决策者权重及案例信息的重要程度。本文定义了分类问题的协调权，期望决策者对于案例的效用函数远离分类阈值，并证明了基于群体一致案例集，协调权一定存在，同时可确定分类阈值。最后通过与其他模型比较验证了所提方法的有效性。