可靠性数据是装备可靠性评估的基础,产品可靠性的信息来源于对失效数据的分析。传统的可靠性评估方法均属于统计方法,评估出测试性指标需要样本量足够大才能获得较可信的评估结果[1]。对于高端装备制造领域的高可靠性、长寿命的产品零部件,寿命试验中往往只有少量失效或者没有失效出现,即使采用加速寿命试验方法,在规定时间也难以取得大量样本;商用装备出于成本等原因,更不可能进行大量的系统级可靠性试验。现场试验数据具有较高的可信性[2],对系统可靠性进行精确的评估需融合现场失效数据和系统的各种试验信息,许多学者就如何利用这些信息、提高系统可靠性评估准确性进行了探索[3]。
目前,系统可靠性建模方法主要有可靠性框图[4-6](Reliability block diagram, RBD),故障树分析法[7-9](Fault tree analysis, FTA),贝叶斯网络[10](Bayesian networks)等技术,这些模型都属于静态分析模型,在定量分析过程中常以给定的可靠度为基础,忽略了系统的故障发生过程是一个受环境应力冲击影响的随机过程,可靠性随时间变化这一问题。Markov[11]状态转移法能够分析系统故障情况下各状态变化过程的可靠性,但其状态空间的规模与系统规模呈指数型关系,状态组合空间容易出现指数爆炸问题。
本文引入图示评审技术(Graphic evaluation and review technique, GERT)进行系统可靠性分析动态建模,将故障的发生视为一个随机过程[12],装备系统运行状态和状态转移传递关系采用服从一定的概率分布的网络进行表征,同时融合现场失效数据与历史经验信息,实现较少失效数据情形下装备可靠性试验寿命估计,进而通过GERT网络拓扑结构进行系统的可靠性评估。
1 模型构建思路与步骤装备失效的发生与受到的各种来自环境的应力冲击强度及装备固有可靠性有关。环境应力冲击反映了环境的严苛程度,如高温、高压、高电磁辐射和海水腐蚀等环境都会降低装备的使用可靠性[13];装备固有可靠性则体现了装备抵抗冲击应力的一种能力,因此每一次冲击作用后装备并不一定失效,而是以一定的概率失效。在装备运行过程中,由于受到各种随机因素的影响,环境应力冲击到达的次数及其发生时间都是随机的[14],根据冲击应力发生特点,从理论上应满足下列条件:(1)在不相重叠的时间区间内应力的到达是互相独立的,即无后效性;(2)对充分小的Δt,在时间区间[t, t+Δt]内装备受到冲击的概率与区间端点无关,而与区间长度Δt成正比,即具有平稳性;(3)对于充分小的Δt内,装备受到多于1次应力冲击的概率极小,即具有普通性。因此,装备受外界冲击的次数可用泊松分布来描述,冲击在某一时间区段内为泊松过程的“质点流”。对于冲击应力受控的加速可靠性试验,由温度、湿度和振动构成综合环境应力,只需测得装备在每次冲击下的失效概率即可进行寿命估计。
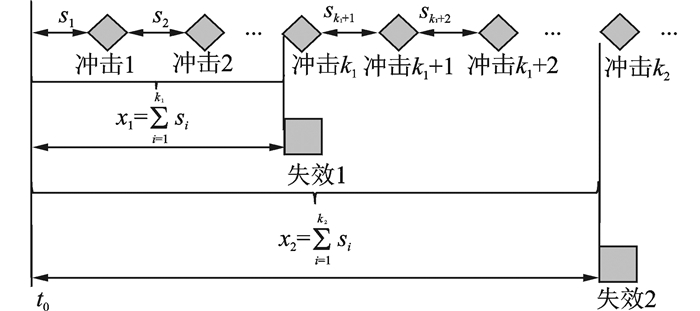
理论上讲,如果知道应力到达时间与装备在受到应力冲击后的失效概率,就可以对装备的可靠性进行评估,预测其平均使用寿命。在影响装备可靠性的应力冲击不容易观测的情形下,通常得到的是失效观测数据,如失效的发生时间和发生次数。失效的发生可以看作装备在受到多次应力冲击后发生状态转移的外在表现,因此可以利用对失效的观测替代对应力的观测,实现对装备的平均寿命的预测,如图 1所示。
|
图 1 图 1装备在应力冲击下的失效示意图 Figure 1 Schematic diagram of equipment failure under impact stress |
图 1描述了装备在冲击应力下的由正常状态到失效状态的情形,试验开始时装备处于正常工作状态,每次冲击后,装备以一定概率选择维持其正常状态或转移到失效状态,若维持其正常工作状态,则其一直正常工作到下一次冲击时刻再做选择,直到第k次冲击到达,装备转移到失效状态。对一批装备进行可靠性试验,可以认为它们所受到的环境应力相同,并且每一装备的寿命是独立同分布的随机变量,冲击到达时装备进行独立选择。当观测到失效时,其实是观测到了若干次冲击的结果,通过对多个失效数据的观测,可以近似求得装备对冲击应力的响应情况,从而测算出装备正常状态保留时间和与之对应的状态转移概率,进行可靠性评估。在冲击应力受控的加速可靠性试验中,则只需测得在每次冲击下的失效概率即可进行寿命估计。
为方便研究,需将上述过程转化为数学语言易处理的模型,考虑到GERT模型可表征多种系统运行状态,状态转移之间具有概率性质,并且允许自环存在,因此这里将上述过程转化为GERT网络模型,模型构建基本步骤如下:
步骤1 依据装备系统结构画出系统的可靠性框图,将其转化为可靠性评估GERT网络模型。
步骤2 根据专家经验或历史统计信息确定部件的寿命分布函数,对部件状态进行观测,记录部件的失效时间序列、试验样本总数和已失效样本数,计算每一个部件正常状态保留时间及相应的部件状态转移概率。
步骤3 确定装备可靠性评估GERT网络模型中的参数,依据网络结构写出系统的等价传递函数。
步骤4 根据模型进行求解,对装备寿命进行评估。
2 装备可靠性评估GERT网络模型结构定义1 装备可靠性评估GERT网络模型由节点、箭线和状态转化流3个要素组成:节点表示装备的某种状态;箭线用于描述装备运行状态之间的传递关系;流为网络中传递关系的定量化描述,网络基本构成单元如图 2所示。图 2中Uij表示装备或部件由状态i到状态j的状态转化流;pij表示状态转移的发生概率;tij表示状态转移时间。
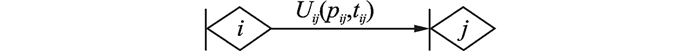
|
图 2 基本单元构成示意图 Figure 2 Schematic diagram of elementary unit in GERT |
在实际工程应用中,装备及其元部件具有除完全正常与故障之外多种运行状态,如:(1)系统部件均正常工作(完美状态);(2)系统部分元件故障或整体性能退化;(3)系统完全故障。其中退化的工作状态又可以有多种情形,这些系统状态可用GERT网络的节点来表征。考虑实际情况,对于部件一般仅考虑其正常工作和失效两种状态,系统则表现为多种运行状态。考虑系统连接方式,装备可靠性评估GERT网络模型主要有3种结构,下面以定义形式给出。
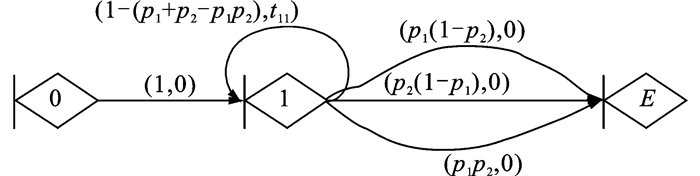
定义2 单部件装备系统是指装备仅含一个部件或不再对装备系统进行拆分,视作一个整体进行可靠性试验的系统,其基于失效选择机制的可靠性评估GERT网络结构如图 3所示。图 3中t11为装备保持正常状态的时间,p为装备受到冲击后由正常状态到失效状态的转移概率,节点0是一个虚拟节点,表示试验开始,节点1表示装备正常运行,即在应力冲击下装备如果不失效,它将保持这种正常工作状态直到下次冲击到达,节点E表示装备失效状态,试验结束。

|
图 3 单部件装备系统可靠性评估GERT网络模型 Figure 3 Structure of reliability evaluation GERT network for equipment with single component |
定义3 对于一个双部件串联型装备系统,若部件的运行状态相互独立,则根据可靠性框图将其转化而来的基于失效选择机制的可靠性评估GERT网络结构如图 4所示。
|
图 4 双部件串联型装备系统可靠性评估GERT网络模型 Figure 4 Structure of reliability evaluation GERT network for series structural system with two components |
图 4所示系统保持正常工作的时间为t11,双部件串联型系统有3种失效模式,故节点1到节点E有3条箭线,分别表示装备在冲击应力下只有A失效,只有B失效,和AB同时失效,系统状态由正常转为失效。对于含N个部件的串联型装备系统,若部件运行状态相互独立,其可靠性评估GERT网络模型有相似结构,且节点1到节点E有2N-1条箭线。
定义4 对于一个双部件并联型装备系统,若部件的运行状态相互独立,则根据可靠性框图将其转化而来的基于失效选择机制的可靠性评估GERT网络结构如图 5所示。

|
图 5 双部件并联型装备系统可靠性评估GERT网络模型 Figure 5 Structure of reliability evaluation GERT network for parallel structural system with two components |
对于图 5所示并联系统,系统由正常工作状态转为失效状态需A, B都失效,即节点E的实现有3种路径:AB同时失效、A先失效后B失效和B先失效后A失效。对于含N个部件的并联型装备系统,若部件运行状态相互独立,其可靠性评估GERT网络模型有相似结构,且节点1到节点E有2N-1条路径,节点2, 3表示系统处于退化的工作状态,在可靠性评估GERT网络中,同样可以求得系统从某一种退化的工作状态到完全失效的相关参数。
3 装备可靠性评估GERT网络模型求解 3.1 装备状态转移过程矩母函数设计结合图示评审技术理论,类似地给出装备可靠性评估GERT网络模型中状态转移过程有向弧(ij)的矩母函数,其定义如下:
定义5 在基于失效选择机制的装备可靠性评估GERT网络模型中,假设装备受到的应力冲击到达时间间隔tij服从某种概率密度函数为f(x)的分布,则状态转化有向弧(ij)的矩母函数为
| $ {{M}_{ij}}\left(s \right)=\int_{-\infty }^{\infty }{{{e}^{st}}ijf\left({{t}_{ij}} \right)\text{d}{{t}_{ij}}} $ |
在可靠性评估GERT网络中,分布函数f(x)可为任意分布形式,具体分布需依据装备特点选取。令pij为装备到达某状态i时弧(ij)被执行的概率,则定义弧(ij)的等价传递函数为Wij(s)=pij·Mij(s)。
设系统的等价传递函数为WE(s),等价概率pE就是等价传递函数WE(s)在s=0处的数值,即pE=WE(s)丨s=0,其等价矩母函数为ME(s)=
由矩母函数的基本性质,即随机变量的原点矩就是矩母函数的n阶导数在s=0处的数值,可知装备平均寿命E(t)和寿命方差V(t)分别为
| $ E\left(t \right)=\frac{\partial {{M}_{E}}\left(s \right)}{\partial s}\left| _{s=0}=\right.\frac{\partial }{\partial s}\left[\frac{{{W}_{E}}\left(s \right)}{{{W}_{E}}\left(0 \right)} \right]\left| _{s=0} \right. $ | (1) |
| $ \begin{matrix} V\left(t \right)=E\left({{t}^{2}} \right)-{{\left(E\left(t \right)\right)}^{2}}=\\ \frac{{{\partial }^{2}}}{\partial {{s}^{2}}}\left[\frac{{{W}_{E}}\left(s \right)}{{{W}_{E}}\left(0 \right)} \right]\left| _{s=0} \right.-{{\left\{ \frac{\partial }{\partial s}\left[\frac{{{W}_{E}}\left(s \right)}{{{W}_{E}}\left(0 \right)} \right]\left| _{s=0} \right.\right\}}^{2}} \\ \end{matrix} $ | (2) |
定理1 本文所构建的装备可靠性评估GERT网络模型终结点的实现概率为1。
证明:本文所构建的可靠性评估GERT网络模型仅有一个终结点,所有活动都以一个正概率流向终结点,故终结点必定实现,即pE=WE(0)=1,证毕。
定理2 对于单部件装备系统,若装备保持正常状态的时间t11的期望为E(t11),那么装备平均寿命为
| $ E\left({{t}_{E}} \right)=\frac{1-p}{p}E\left({{t}_{11}} \right) $ | (3) |
证明:设f(t11)为装备保持正常状态的时间t11的概率密度函数,系统的等价矩母函数为
| $ {{M}_{E}}={{W}_{E}}=\frac{p}{1-\left(1-p \right){{M}_{11}}} $ |
装备平均寿命为
| $ \begin{align} &E\left(t \right)=\frac{\partial {{M}_{E}}\left(s \right)}{\partial s}\left| _{s=0}=\right.\frac{\partial }{\partial s}\left[\frac{p}{1-\left(1-p \right){{M}_{11}}\left(s \right)} \right]\left| _{s=0} \right.=\\ &\ \ \ \ \ \ \ \ \ \ \ \left\{ \frac{p\left(1-p \right)}{{{\left[1-\left(1-p \right){{M}_{11}}\left(s \right)\right]}^{2}}}\cdot \frac{\partial }{\partial s}{{M}_{11}}\left(s \right)\right\}\left| _{s=0} \right.\\ \end{align} $ |
又有
| $ \begin{matrix} \frac{\partial }{\partial s}{{M}_{11}}\left(s \right)\left| _{s=0}=\frac{\partial }{\partial s}\int_{0}^{\infty }{{{e}^{s{{t}_{11}}}}f\left({{t}_{11}} \right)\text{d}{{t}_{11}}\left| _{s=0} \right.=} \right.\\ \int_{0}^{\infty }{{{t}_{11}}\cdot {{e}^{s{{t}_{11}}}}f\left({{t}_{11}} \right)\text{d}{{t}_{11}}\left| _{s=0} \right.=} \\ \int_{0}^{\infty }{{{t}_{11}}f\left({{t}_{11}} \right)\text{d}{{t}_{11}}=E\left({{t}_{11}} \right)} \\ {{M}_{11}}\left(s \right)\left| _{s=0}=\int_{0}^{\infty }{{{e}^{s{{t}_{11}}}}f\left({{t}_{11}} \right)\text{d}{{t}_{11}}\left| _{s=0} \right.=\int_{0}^{\infty }{f\left({{t}_{11}} \right)\text{d}{{t}_{11}}=1}} \right.\\ \end{matrix} $ |
故有
| $ \begin{matrix} E\left(t \right)=\ \left\{ \frac{p\left(1-p \right)}{{{\left[1-\left(1-p \right){{M}_{11}}\left(s \right)\right]}^{2}}}\cdot \frac{\partial }{\partial s}{{M}_{11}}\left(s \right)\right\}\left| _{s=0} \right.=\\ \frac{p\left(1-p \right)}{{{\left[1-\left(1-p \right)\right]}^{2}}}E\left({{t}_{11}} \right)=\frac{1-p}{p}E\left({{t}_{11}} \right)\\ \end{matrix} $ |
证毕。
定理3 在单部件系统可靠性评价GERT网络模型中,对装备进行无替换定数截尾试验,转移概率p只与试验样本数N和观测到的失效数据个数n有关,与装备期望寿命无关。
证明:设装备的期望寿命为θ,试验样本数为N,第r个装备失效时刻为tr,则失效间隔时间
| $ {{x}_{r}}=\left\{ \begin{align} & {{t}_{r}}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ r=1 \\ & {{t}_{r}}-{{t}_{r-1}}\ \ \ \ \ \ \ r=2,3,\cdots ,N \\ \end{align} \right. $ | (4) |
则失效平均间隔时间
| $ {{X}_{r}}=\frac{1}{r}\sum\limits_{i=1}^{r}{{{x}_{i}}=\frac{1}{r}}\left[{{t}_{1}}+\sum\limits_{i=2}^{r}{\left({{t}_{i}}-{{t}_{i-1}} \right)} \right]=\frac{1}{r}{{t}_{r}} $ | (5) |
由式(3)可知,转移概率
证毕。
4 算例研究某型号装备由5个可靠性单元组成,其可靠性框图如图 6所示。单元A为新升级设备,其可靠性试验数据不足,寿命服从指数分布,可应用定义2中的单部件可靠性评估GERT网络模型对其进行参数估计,其完全样本失效数据为:770,1 450,1 589,1 775,2 257,2 325,2 829,3 398,4 835,6 405,6 540,7 292,7 509,7 517,13 934 h,但在一次规定时间内仅取得5个失效数据。

|
图 6 某型号装备系统可靠性框图 Figure 6 Reliability block diagram of a kind of equipment system |
基于失效选择机制的装备可靠性评估GERT模型构建步骤如下:
步骤1 根据装备系统可靠性框图,建立装备系统可靠性评估GERT网络模型如图 7所示。

|
图 7 某型号装备系统可靠性评估GERT网络模型 Figure 7 System reliability evaluation GERT network of a kind of equipment |
步骤2 根据专家经验,单元A寿命服从指数分布,应用如图 3所示的GERT网络模型,其平均寿命为
| $ E\left({{t}_{A}} \right)=\frac{1-{{p}_{r}}}{{{p}_{r}}}\cdot \frac{1}{r}{{t}_{r}} $ | (6) |
式中:r为观测到的失效样本数,tr为第r个样本失效时刻。根据单元A寿命试验数据,截取5个失效数据,可得失效间隔时间序列x={770, 680, 139, 186, 482}和平均失效间隔时间X={770, 725, 529.57, 443.75, 451.4}。
试验测得指数分布定数截尾寿命试验GERT模型转移概率值如表 1所示。
| 表 1 指数分布定数截尾寿命试验GERT模型转移概率 Table 1 Transition probability of Type-Ⅱ censoring life test of exponential distribution |
查表 1可得,15个试验样本下5个失效观测数据时的状态转移概率p5=0.074 8,据此可以对单元A的寿命进行评估,计算结果如表 3所示,θ为完全样本计算的平均寿命。
| 表 2 单元A寿命评估结果比较 Table 2 Comparison of life evaluation results of unit A |
从表 2中可以看出,在小样本情形下,采用本文方法结果优于极大似然估计,单元A的完全样本平均寿命为4 695 h,在5个失效样本情形下,本文方法计算结果为5 583 h,误差18.92%,低于极大似然估计的误差29.55%。
步骤3 依据网络结构及某装备系统各部件状态参数表,可计算此装备系统可靠性评估GERT网络模型的等价传递函数。
结合历史统计与单部件GERT网络模型测算,某装备系统各部件状态保留时间与转移概率如表 3所示。
| 表 3 某装备系统各部件状态参数 Table 3 State parameter of each component of equipment system |
从节点0到节点E的等价传递函数为
| $ \begin{align} &{{W}_{E}}=\frac{1}{1-{{W}_{11}}}\left[{{W}_{1E}}+{{W}_{12}} \right.\frac{{{W}_{2E}}+{{W}_{26}}\frac{{{W}_{6E}}}{1-{{W}_{66}}}+{{W}_{27}}\frac{{{W}_{7E}}}{1-{{W}_{77}}}}{\left(1-{{W}_{22}} \right)}+{{W}_{13}}\frac{{{W}_{3E}}+{{W}_{38}}\frac{{{W}_{8E}}}{1-{{W}_{88}}}+{{W}_{39}}\frac{{{W}_{9E}}}{1-{{W}_{99}}}}{\left(1-{{W}_{33}} \right)}+\\ &\ \ \ \ \ \ \ \left.{{W}_{14}}\frac{{{W}_{4E}}+{{W}_{4, 10}}\frac{{{W}_{10E}}}{1-{{W}_{10, 10}}}+{{W}_{4, 11}}\frac{{{W}_{11E}}}{1-{{W}_{11, 11}}}}{\left(1-{{W}_{44}} \right)}+{{W}_{15}}\frac{{{W}_{5E}}+{{W}_{5, 12}}\frac{{{W}_{12E}}}{1-{{W}_{12, 12}}}+{{W}_{4, 13}}\frac{{{W}_{13E}}}{1-{{W}_{13, 13}}}}{\left(1-{{W}_{55}} \right)} \right] \\ \end{align} $ |
步骤4 根据系统等价传递函数WE,可求得装备系统的平均使用寿命为
| $ E\left({{t}_{E}} \right)=\frac{\partial {{M}_{E}}\left(s \right)}{\partial s}\left| _{s=0}=\right.\frac{\partial {{W}_{E}}\left(s \right)}{\partial s}\left| _{s=0}=\right.5768.0\ \text{h} $ |
根据传统基于故障率的平均失效时间的计算,装备系统的平均寿命为5 581.4 h,GERT网络计算结果与之基本接近,可验证计算结果可信度较好,系统可靠性评估GERT网络能模拟装备在冲击应力作用下的失效过程。此外,还可依据网络结构,计算任意状态之间转换的平均时间,实现对装备运行状态和剩余寿命的评估。
5 结束语本文针对小样本失效数据,基于失效选择机制构建了装备系统可靠性评估GERT网络模型。该模型能够较好地融合历史经验信息和现场试验信息,在失效数据较少情形下取得较好置信度的寿命估计结果;GERT网络可对系统多运行状态进行描述,考虑系统运行的随机性质,根据网络拓扑结构和状态迁移概率,实现对系统可靠寿命、剩余寿命的均值和方差估计。试验结果表明,基于失效选择机制的可靠性试验寿命评估GERT网络模型有效、可行。
| [1] |
赵宇, 杨军, 马小兵.
可靠性数据分析教程[M]. 北京: 北京航空航天大学出版社, 2009.
Zhao Yu, Yang Jun, Ma Xiaobin. Reliability data analysis tutorial[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2009. |
| [2] |
张西山, 黄考利, 闫鹏程, 等.
基于仿真数据的小子样复杂装备系统测试性综合评估[J]. 计算机测量与控制, 2014, 22(4): 1175–1177.
Zhang Xishan, Huang Kaoli, Yan Pengcheng, et al. Complexity equipment system testability integrated evaluation under small sample test based on simulation data[J]. Computer Measurement & Control, 2014, 22(4): 1175–1177. |
| [3] | Langseth H, Portinale L. Bayesian networks in reliability[J]. Reliability Engineering & System Safety, 2007, 92(1): 92–108. |
| [4] | Bistouni F, Jahanshahi M. Analyzing the reliability of shuffle-exchange networks using reliability block diagrams[J]. Reliability Engineering & System Safety, 2014, 132: 97–106. |
| [5] | Kim M C. Reliability block diagram with general gates and its application to system reliability analysis[J]. Annals of Nuclear Energy, 2011, 38(11): 2456–2461. DOI:10.1016/j.anucene.2011.07.013 |
| [6] |
刘哲锋.
航天产品可靠性框图自动评估系统实现与研究[J]. 装备指挥技术学院学报, 2009, 20(6): 65–67.
Liu Zhefeng. Study on automatic estimation system of spaceflight product's reliability black diagram[J]. Journal of the Academy of Equipment Command & Technology, 2009, 20(6): 65–67. |
| [7] | Jong C, Leu S. Bayesian-network-based hydro-power fault diagnosis system development by fault tree transformation[J]. Journal of Marine Science and Technology-TAIWAN, 2013, 21(4): 367–379. |
| [8] | Hyun K, Min S, Choi H, et al. Risk analysis using fault-tree analysis (FTA) and analytic hierarchy process (AHP) applicable to shield TBM tunnels[J]. Tunnelling and Underground Space Technology, 2015, 49: 121–129. DOI:10.1016/j.tust.2015.04.007 |
| [9] |
陶勇剑, 董德存, 任鹏.
基于故障树的系统可靠性估计不确定性分析[J]. 同济大学学报(自然科学版), 2010, 38(1): 141–145.
Tao Yongjian, Dong Decun, Ren Peng. Uncertainty analysis of system reliability estimate based on fault tree[J]. Journal of Tongji University (Natural Science), 2010, 38(1): 141–145. |
| [10] |
戴志辉, 王增平, 焦彦军.
基于动态故障树与蒙特卡罗仿真的保护系统动态可靠性评估[J]. 中国电机工程学报, 2011, 31(19): 105–113.
Dai Zhihui, Wang Zengping, Jiao Yanjun. Dynamic reliability assessment of protection system based on dynamic fault tree and Monte Carlo simulation[J]. Proceedings of the CSEE, 2011, 31(19): 105–113. |
| [11] |
尹晓伟, 钱文学, 谢里阳.
基于贝叶斯网络的多状态系统可靠性建模与评估[J]. 机械工程学报, 2009, 45(2): 206–212.
DOI:10.3901/JME.2009.02.206 Yin Xiaowei, Qian Wenxue, Xie Liyang. Multi-state system reliability modeling and assessment based on Bayesian networks[J]. Journal of Mechanical Engineering, 2009, 45(2): 206–212. DOI:10.3901/JME.2009.02.206 |
| [12] |
于敏, 何正友, 钱清泉.
基于Markov过程的硬/软件综合系统可靠性分析[J]. 电子学报, 2010, 38(2): 473–479.
Yu Min, He Zhengyou, Qian Qingquan. Reliability analysis of combined hardware/software system based on Markov process[J]. Acta Electronica Sinica, 2010, 38(2): 473–479. |
| [13] |
赵涛.
可靠性工程基础[M]. 天津: 天津大学出版社, 1999.
Zhao Tao. Reliability engineering[M]. Tianjin: Tianjin University Press, 1999. |
| [14] |
张勇, 邱静, 刘冠军, 等.
基于非齐次泊松过程和统计仿真的故障样本模拟生成[J]. 机械工程学报, 2012, 48(15): 75–82.
DOI:10.3901/JME.2012.15.075 Zhang Yong, Qiu Jing, Liu Guanjun, et al. Fault sample generation based on nonhomogeneous poisson process and statistical simulation[J]. Journal of Mechanical Engineering, 2012, 48(15): 75–82. DOI:10.3901/JME.2012.15.075 |
 2016, Vol. 48
2016, Vol. 48


