2. 桂林电子科技大学广西可信软件重点实验室, 桂林,541004;
3. 南京邮电大学计算机学院, 南京,210023
2. Guangxi Key Laboratory of Trusted Software, Guilin University of Electronic Technology, Guilin, 541004, China;
3. College of Computer, Nanjing University of Posts and Telecommunications, Nanjing, 210023, China
面向服务计算(Service-oriented computing,SOC)是在现有技术(如面向对象、基于构件的开发、分布式对象计算及Web技术等)基础上,建立了一种基于Internet的软件开发、部署和集成的新模式[1-7]。软件服务的分布性、动态性和自主性等特点,使得面向服务的系统分析、设计、建模和运行等技术仍为目前国内外学者研究热点[6-8]。
关于面向服务计算建模方面,文献[9]提出了一种用于设计面向服务体系结构的参考模型,叙述了参考模型的结构以及其中的服务总线和服务合约的元模型。文献[10]对SOC模型中的约束问题进行了讨论,讨论了约束在服务生成方面的作用。文献[11, 12]充分考虑扭斗对于网络体系结构研究的影响,总结和归纳了在扭斗环境下设计新一代网络体系结构模型的若干原则,在这些设计原则的指导下提出了一种结构分层、功能分面、基于交互、面向服务的新一代网络体系结构模型。文献[13]基于面向服务的体系结构(Service-oriented archite-ture, SOA)给出了一个以企业服务总线为中心的面向服务软件体系架构参考模型。为实现互联网上异种异构的复杂信息资源有序化组织和互操作性服务与共享的目标,文献[14]研究了语义服务的元计算问题,提出了本体元建模理论和方法,定义了本体UML承诺、提倡本体UML表达,给出了本体的元机制。针对在动态、跨组织的网格环境中如何进行适应组织重构、业务变化等动态性要求,文献[15]提出了服务网格动态信息聚合模型,从组织模型、数据模型、协作模型3个维度描述信息聚合中变化的因素。文献[16]利用代数方法(进程代数)对SOA进行形式化建模,并提出多种SOA可信范式,为基于SOA的可信软件开发提供理论支持。本文将单子[17-19]概念引入服务计算中,从另外一个形式化角度为服务计算建模。
基于Web服务的服务计算是面向服务计算的特例,目前Web服务的使用主要是将企业原有信息系统(也称遗留系统)进行封装,通过SOAP、WSDL和UDDI等序列标准发布出来让用户通过网络使用。本文将立足于服务计算的“服务”本质,利用单子技术研究基于Web服务的服务计算形式化模型及其实现:以服务化思想和服务交互观点作为建模基础,以余代数方法和单子技术作为理论基础,建立Web服务的形式化模型,以期大大拓展面向服务计算的形式化研究视野、手段和方法。
本文先简介一些基本理论知识,包括余代数方法和单子技术;然后设计和定义一般余代数单子和相应的单子转换器,并给出一种基于单子技术的Web服务参考模型;最后给出Web服务计算平台系统原型的实现。
1 余代数方法和单子技术 1.1 余代数方法不同于从“构造”角度研究数据结构的代数理论,余代数(coalgebras)[20-22]方法从“观察”角度考察系统及其性质,故其对研究诸如对象、进程和服务等基于状态的系统有独特的优越性。使用余代数理论作为工具,可以对系统的行为等价、不确定性等从数学上进行深入探讨,从而为这些系统建立良好的形式理论基础模型,并方便对其性质进行描述与验证[23]。
一般地,对于自函子(endofunctor)T,T-余代数是一个二元组(U, p),其中对象U称为p的载体,p为U→T U的映射。如果将T-余代数(U, p)看成是一个具有内部状态的系统,则U是其所有可能的状态,映射p: U→T U表示从外部可观察的系统行为,该行为可能会影响系统内部的状态。此外,射p常可分解成几个射,每个射代表系统可观测的一个行为或系统对外部观测的一种响应。更多的有关余代数的基本概念、性质、应用情况参见相关文献(如文献[20~23]等)。
Barbosa及其合作者[24-28]曾理论上深入研究了基于余代数的软件构件形式化建模,给出构件的余代数语义表示。他们指出,软件构件的“黑盒特性”比较适合采用观测语义模型:只要通过观察难以区分的任何两个构件(含配置环境)认为是相同的。这样基于状态的任一构件可由以下形式表示:
| $ f:U \to TU $ |
其中:U为配置环境中所有可能的状态;T为观测行为、计算结构或构件接口。
1.2 单子技术单子技术是一种根据相关类型值及使用这些值的系列计算来构建新计算的方法,其中重要概念包括单子和单子转换器。单子(monad)概念最初是在1950年代作为范畴论里一种函子而被提出的。在1989年由Moggi[17]将之引入到语义框架中。随后,Wadler[19, 29]将Moggi单子方法广泛推广到函数式程序设计中(尤其是Haskell语言)。采用单子这种更加规则的表示法替代λ表示法,可避免定义语义结构时对无关语义成分的引用,从而加强了语义描述的模块性和扩展性。
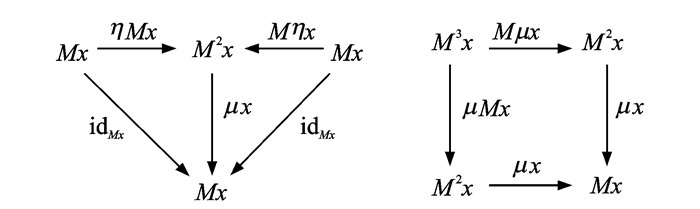
一般地,单子可表示成三元组(M, η, μ),其中M为某范畴C上的自函子;η:Id→M和μ:M2→M为其两个基本自然转换函数,且满足如下等式(或称图 1是可交换的):
| $ \begin{array}{l} \mu x \circ M\eta x = \mu x \circ \eta Mx = {\rm{i}}{{\rm{d}}_{Mx}}:Mx \to Mx\\ \mu x \circ M\mu x = \mu x \circ \mu Mx\;\;\;\;\;\;\;\;\;\;:Mx \to Mx \end{array} $ |
|
图 1 单子中自然转换函数的可交换图 Figure 1 Commute diagram of natural transformations |
其中:x为范畴C中任意对象,id为恒等函数,o为函数复合运算。
单子是一种抽象技术,它可隐藏计算时所需的基本信息,并提供一些(操作)函数允许外界访问这些信息[29]。直观上,对于类型a,类型Ma则表示所有能得到a类型结果的计算,这些计算在范畴理论的同态概念下是一致的[18]。因此,给定一个单子实际上就相当于给定了能够得到某种类型结果的计算类型。目前人们已抽象设计出不少单子,如描述Pi演算的Pi单子[30]、并发单子[31]、Agent单子[32]、描述增量计算的可变单子[33]等。
Ghania等学者[34-36]曾理论说明,余代数演算可以被抽象成一个单子,即余代数单子。Jacobs也曾致力于余代数与单子间关系的理论研究,包括从具体的Java语义表示模型中实例说明余代数表示方法与单子描述方法间的等价性[37]。
单子技术中,为了将两个单子结合成一个新单子,引入了单子转换器(monad transformers)[38],它将给定单子转换成新单子,并增加新操作运算。目前人们已设计了不少单子转换器,如统一描述与程序环境交互计算的环境单子转换器EnvT,表示与状态相关计算的状态单子转换器StateT等[29, 38, 39]。
单子具有高度的抽象性、反射性、重用性和模块化,又具有易于自动实现扩充和修改的特点,这些特性对软件体系结构和软件服务技术带来了积极的影响[19, 40-42]。现在,单子已是独立的概念,掌握它不再需要范畴论的知识,而且大量的研究和实践已证实单子系统具有很强的功能,结合单子表示法的简洁性和易读性,因此将为越来越多的人所接受和应用。现已有不少程序设计语言支持实现单子技术,如Haskell、C++[43]、Java[44]等。
本文采用易于原型开发的函数式语言Haskell作为支持单子相关方法的实现语言。Haskell是一门高级纯函数式编程语言,致力于快速开发可扩展的、可靠的和易维护的软件,并能很好地与其他编程语言集成,具有内建并发性和并行性、调试器、优化器、丰富的类库以及活跃的社区等。在Haskell语言的基本模块Monad中,关于函子、单子和单子转换器分别被定义为:
class Functor f where
fmap :: (a -> b) -> (f a -> f b)
class Monad m where
return :: a -> m a
(>>=) :: m a -> (a -> m b) -> m b
class MonadTrans t where
lift :: Monad m=> m a -> t m a
其中单子的类定义中,return和>>=两个操作函数分别对应于前面提及的两个自然转换函数η和μ。对应于图 1,return和>>=需要满足如下等式(左幺元、右幺元和结合律)[29]:
(return x) >>=f=f x
m >>=return=m
(m >>=f) >>=g=m >>=(λx. f x >>=g)
这里,Haskell本身不保证单子的两个函数所必须满足的上述3个规律,需其设计者事先保证。
2 余代数单子在上节所列述的学者研究成果上,尤其是结合Barbosa等基于余代数的构件形式化模型和Ghania等余代数演算的单子抽象表示,本节将这些理论的形式化表示进一步扩展,给出具体程序语言(如Haskell)表示形式,增加交互操作函数,还进一步提升成余代数单子类和余代数单子转换器,进而方便第3节中将之应用到Web服务实际模型描述上。给出如下的一般余代数类型CoAlg:
newtype CoAlg f=
UnIn | UnOut (f (CoAlg f))
out :: CoAlg f -> f (CoAlg f)
out (UnOut t)=t
in :: CoAlg f a -> a
in (UnIn x)=x
其中:f为一个表示观测操作的函子;a为任意数据类型;UnIn和UnOut为类型构造函子,分别为CoAlg余代数中映射in和out的逆。即一个余代数类型CoAlg要么是所观测到的内部数据信息(包括初始状态情况),要么是对系统的进一步观测行为,该行为可能会影响到系统内部数据或状态等。
其实,上述定义的余代数(CoAlg f, out)中的CoAlg f也可成为函子和单子。下面的两个Haskell实例声明就使得CoAlg f也是函子,且为单子,其所须满足的单子规律可类似文献[45~47]中证明方法进行保证。
instance Functor f=> Functor (CoAlg f) where
fmap f. UnIn=UnIn. f
fmap f. UnOut=UnOut.fmap (fmap f)
instance Functor f=> Monad (CoAlg f) where
return=UnIn
UnIn a >>=k=k a
UnOut t >>=k=UnOut (fmap (>>=k) t)
于是,上述定义的CoAlg f也可称为余代数单子。进一步地,可给出余代数单子类CoAlgMonad,以便对余代数单子与其他单子进行交互转换等。
class (Functor f, Monad m)=> CoAlgMonad f m where
prj :: f (m a) -> m a
instance Functor f=> CoAlgMonad f (CoAlg f) where
prj=UnOut
为了与前面所述一致,这里也给出余代数类CoAlgC,并说明上述所定义的类型CoAlg f也是属于余代数类的。
class Functor f=> CoAlgC f m where
from :: m -> f m
instance Functor f=> CoAlgC f (CoAlg f a) where
from=out
为便于余代数单子与其他单子组合的需要,给出如下的余代数单子转换器CoAlgT定义:
newtype CoAlgT f m a=CoAlgT (m (Either a (f (CoAlgT f m a))))
instance (Functor f)=> MonadTrans (CoAlgT f) where
lift=CoAlgT. liftM Left
其中:Either为“可区分并”联合类型声明,Left为Either类型的投影函数,“.”为函数的复合操作,liftM为一般单子间的提升映射函数。
有了上述的一般余代数单子和单子转换器定义后,任意的服务可抽象描述成其实例,就可自然表示成该服务的单子和单子转换器,以便进行软件服务单子的描述等。
3 服务的单子描述为了更好地体现服务的封装性、松散耦合性、可复用性、高度可集成性和开放性等特性,本节试着利用单子技术形式化研究Web服务中服务实体:将服务抽象成余代数单子(服务单子),通过单子转换器,多个单子可组合成一个新单子,故服务组合可由若干服务单子组合表示。
利用上述的一般余代数单子CoAlg f定义,只要具体化服务相关的函子f定义,就可自然描述该服务单子;类似地可利用CoAlgT方便描述该服务的单子转换器。进一步地,利用单子技术,可自然根据服务单子和单子转换器进行相应服务的合成,以便描述相应功能更强的新单子,如增值服务。
一般地,对于输入类型为ti输出类型为to的服务函数serv: ti → to,其对应的构件单子(余代数单子) M_serv可定义如下:
newtype F_serv=FUN (tin -> tout)
type M_serv=CoAlg F_serv
instance Functor F_serv where
fmap h (FUN f)=FUN (h. f)
M_serv定义中的F_serv为与服务serv对应的函子,也可简称为serv的服务函子。由前节知,任一余代数单子都属于CoAlgMonad类,故可借助于其prj函数,将serv函数转换到M_serv单子统一描述中:
servM :: M_serv tout
servM=prj (fmap return. FUN serv)
进一步地,根据上小节的一般余代数单子转换器定义,可定义serv的服务单子转换器MT_serv:
type MT_serv m=CoAlgT F_serv m
关于上述表示的正确性,主要是要验证上述描述是否满足单子和单子转换器所需规律,因篇幅限制,可借鉴文献[45~47]中证明方法进行验证。为了将系统中各个服务的最后结果再统一描述,给出其统一结果类型ShowOut及其相关的服务调用函数runServ定义:
data ShowOut a b=Finished b | Result a (ShowOut a b)
runServ :: M_serv tout -> tin
-> ShowOut tin tout
runServ (UnIn a) b=Finished a
runServ (UnOut (FUN f)) b
=Result b (runServ (f b) b)
利用runServ调用服务的结果可同时显示输入和输出信息,假设某个服务调用结果为:Result 3 (Finished 12),这表示服务输入为3,服务产生结果为12。
4 Web服务的单子模型及其应用通过前一节的服务单子表示方法,服务被抽象成单子(即服务单子),它可由若干构件单子组合而成。单子技术中的单子转换器不仅可用来组合服务,而且还允许向现有服务单子组合中加入新元素来调整服务以实现相应的Web服务操作。于是,单子转换器可很好描述和处理服务间的交互关系,以此研究Web服务交互行为。
根据单子转换器,可方便进行服务间交互操作,如下面的简单例子给出一种serv1: ti1→to1和serv2: to1→to2两个服务函数组合生成的新服务serv3: ti1→to2,其操作均在余代数单子统一框架下进行。
serv3 :: tin1 ->
MT_serv1 M_serv2 (ShowOut tin1 tout1)
serv3 a=do
let b=3
c < -lift (serv2M b)
let d=... --d由a与c相关计算而得
e=runServ1 serv1M d
return e
实际中,服务发布前,可对遗留系统进行服务抽取并进而对其单子描述;而对已发布的Web服务来说,可直接从其WSDL文档中服务操作的类型信息生成相应的单子库,只是其单子框架下服务的实际操作需通过SOAP远程调用完成。例如上述的serv3服务在其发布后的WSDL文档可能的类型为:Int→IO Int,即serv3操作的结果需要通过SOAP返回,这可由基本输入输出单子IO描述,但最终的M_serv3和MT_serv3描述在形式上还是与上述余代数统一定义一致的。
由单子的可组合性,服务单子可与表示其他计算特性的单子组合起来,以期最终表示服务实体的某类复杂计算。如服务单子与并发单子组合,所形成的新单子可用来描述/建模服务软件的并发行为等。利用余代数方法对研究基于状态系统(如不确定、分布式系统等)的独特优势,可对开放网络环境下的软件服务进行较好的形式化描述。又由单子的抽象性,服务单子可隐藏其计算所需的基本信息,并提供公用接口允许外部有限访问服务的内部状态。因单子具有反射性[40],故服务单子可以在运行时获知实体内部具体的运行信息,并可访问、修改这些信息,从而使得服务单子本身就具有一定应变调节能力。
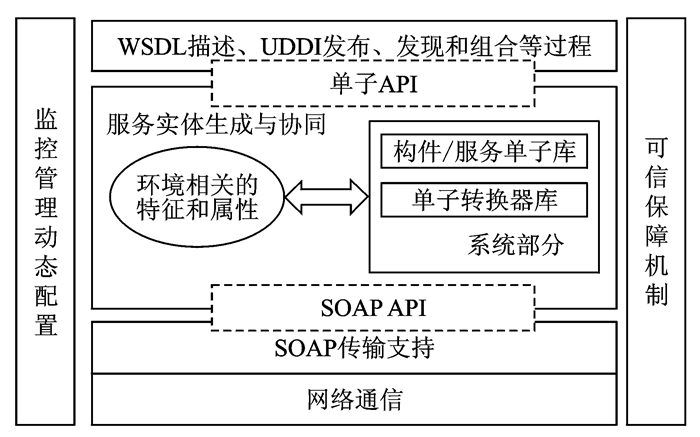
图 2给出了一种基于单子技术的面向服务计算参考模型,主要是针对基于Web服务的服务计算。本文将重点研究图 2模型的中间部分,尤其是Web服务实体的形式化表示等。由于单子的抽象性和可扩展性,该参考模型具有较强的可扩展性,现有的有关服务理论分析技术很容易融入到基于单子的软件服务模型中:先将其相关理论抽象成为单子,然后由单子组合理论安全方便地加入到现有的服务实体中,从而可对现有软件服务进行相关理论分析操作。如要利用现有的描述和验证服务组合的Pi演算技术[48],可先将其抽象成Pi单子[30],再将其组合入所要分析的服务单子中,这样在改动很小的情况下就可对所关注的服务实体进行相应的Pi演算分析操作等。
|
图 2 一种基于单子技术的Web服务参考模型 Figure 2 Web service model based on monads |
上述所提的Web服务的单子框架模型可直接应用的领域包括:(1) Web服务的形式化语义描述;(2) Web服务自动组合与形式化验证;(3)遗留系统的服务化切分与封装;(4) Web服务自动测试;(5) Web服务的发现等。其优势主要体现在:(1)可在统一的形式化描述框架下进行上述相关工作研究,方便其结果的集成融合;(2)文中所提Web服务的形式化框架模型,可以一种黑盒方式考察研究Web服务操作及其协作行为。利用余代数方法对研究基于状态系统(如不确定、并发系统等)的独特优势,以及单子的抽象性、反射性和可组合性,可很好地对开放网络环境下的构件和服务进行形式化描述和深入研究。
关于其在Web服务测试中的应用,文献[49, 50]中利用单子技术开发了一个Web服务自动测试工具,给出了一个Web服务测试单子,这可融入本文的服务计算单子框架中,以便深入研究Web服务的自动测试。此外,文献[51]通过程序切片技术[52],提出一种基于函数依赖图的构件抽取方法,进而将之用到服务的抽取、发布和度量等[53-55]。又因程序切片这类计算也可被抽象成单子[45-47, 56, 57],结合本文的服务计算单子框架,从而能方便对遗留系统进行服务化切片与封装。上述已有工作虽然没有提及服务的单子模型,但这很容易融入到文中单子框架中(如图 2上层所示),即本文的服务单子模型能为这些相关的服务活动提供相应的单子接口。由于篇幅限制,本文中不再赘述。
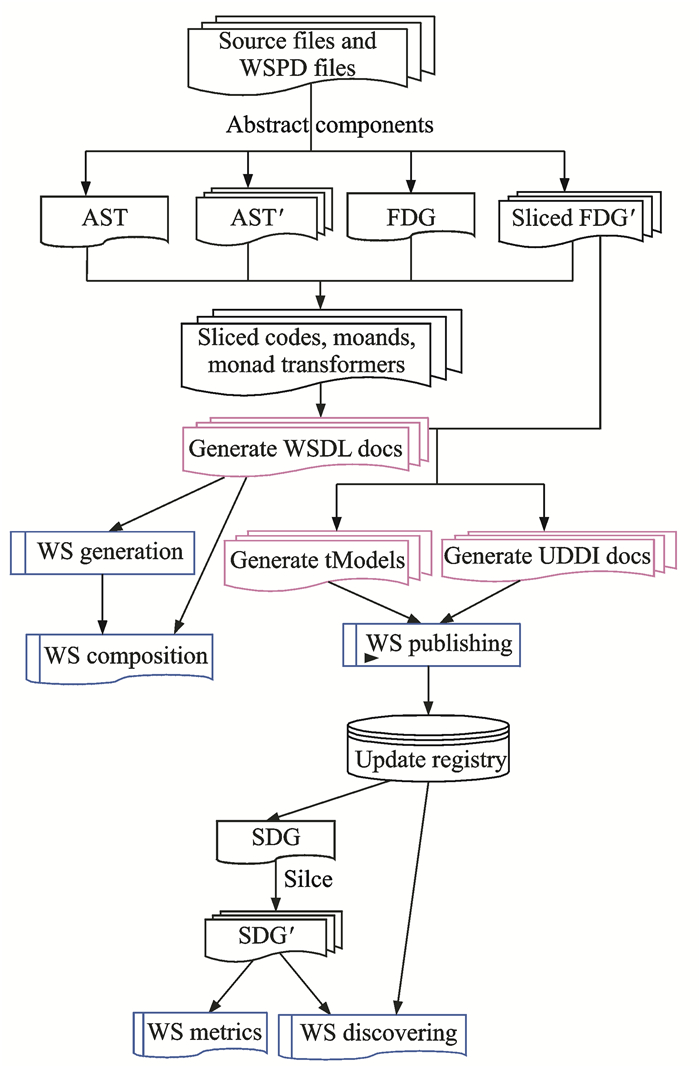
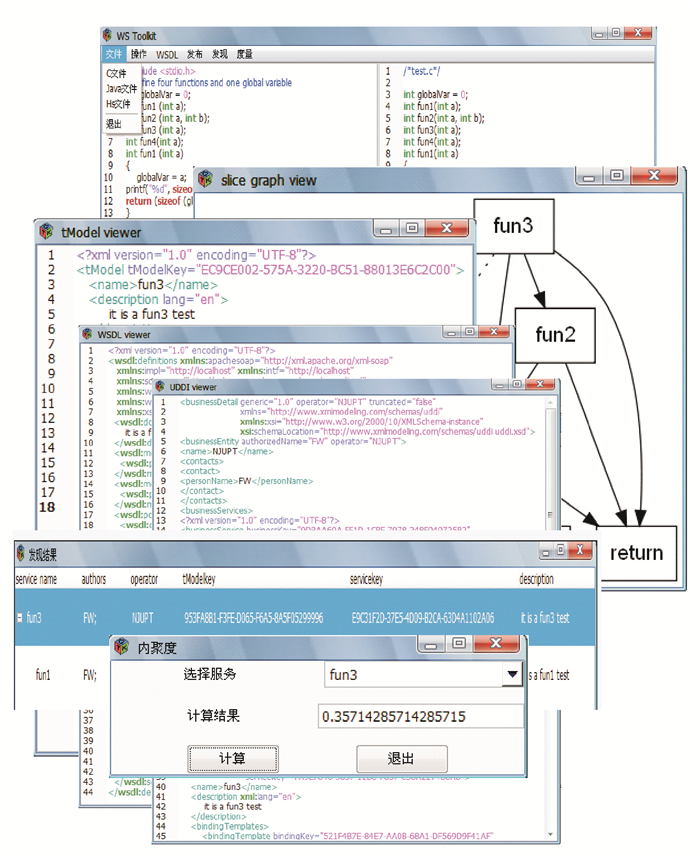
5 Web服务计算平台原型系统针对前面所建立的服务计算单子模型,以及文献[51, 53~55]中对构件抽取、服务生成/发布/发现/度量等方法,文中实现了一个基于Web服务技术的服务计算平台原型系统WS Toolkit,其系统框架图和部分截图分别见图 3, 4。
|
图 3 Web服务计算平台的系统框架 Figure 3 System framework of computing platform for Web service |
|
图 4 平台系统原型WSToolkit部分截图 Figure 4 Some screenshots of platform prototype WToolkit |
WS Toolkit是用Haskell[58]开发的一个实现Web服务框架的原型系统,其中,由HXml来解析所有的XML格式文档,用GTK+来实现GUI界面。系统功能包括Web服务的生成、组合、发布、发现以及度量。在系统启动时,用户需要选择一个服务的源文件(C、Java或者Haskell),WS Toolkit会先自动调用gcc和元编译环境ASF+SDF分别对其中C和Java源码分析并生成中间表示结构。然后系统对中间表示信息进行分析,列出源文件中的主要函数(或类等),此时用户需要指定这些函数中哪些需要被发布成为服务并给出服务的作者,所属公司以及服务描述等信息,再根据这些信息生成WSPD文件。根据WSPD文件中记录的信息,系统接着对源文件进行构件抽取,将要发布成为服务的构件抽取出来,生成切片后的服务代码。同时为每个构件产生相应的单子和单子转换器,并为每个服务生成相应WSDL文档,实现服务的生成。WSDL文档中记录了服务的接口,参数等信息,通过分析WSDL文档,可以对某些服务进行适当的组合并生成新的服务。
接着根据WSDL文档可以为每个服务生成tModel和UDDI文档,实现服务的发布。发布服务的同时对服务注册表进行更新,并根据tModel文档记录的依赖关系为服务注册表中的服务生成服务依赖图,根据服务发现的要求对服务依赖图进行切片生成服务依赖子图,对子图进行分析,列出服务发现的结果。系统还可根据服务依赖图和服务依赖子图对发现的服务进行度量。
6 结束语由于开放环境下的Web服务实体主要来源于不同的第三方提供者,并且其形成与运行过程常处在一种演化的状态之中,故难以采取传统的过程监控、可控测试、白盒分析等方式保障其可靠性。本文将Web服务系统的服务抽象成余代数单子(称为服务单子),从而以一种黑盒方式给出服务的语义模型。利用余代数方法对研究基于状态系统(如不确定、并发系统等)的独特优势,以及单子的抽象性、反射性和可组合性,对开放网络环境下的构件和服务进行形式化描述和深入研究,建立并实现了一种服务计算形式化模型框架。
上述研究中一个重要观点是将服务和服务的交互行为分别抽象描述成单子技术中的单子和单子转换器,由此可在单子框架下方便形式化研究服务相关性质和活动。与本文形式化研究相似工作有文献[16],该文给出了服务的代数定义,并将服务组合解释成服务运算的实现,由此可用进程代数进一步讨论可信SOA的建模问题。
不同点在于,文献[16]从代数语义角度研究服务进而用代数运算解释服务组合等,其抽象层次比较高,有利于服务相关属性的验证等;而本文从另一语义(单子语义)角度探讨服务及其交互组合等,由单子的相关性质可对服务及其相关活动进行较好描述,此外因为单子语义描述具有清晰的操作解释,所以其易于执行实现。例如,本文的服务计算平台原型系统就是利用单子的易于执行性实现的,这便于后续进行服务的生成、发布与发现、组合、服务质量评价、运行等。
未来工作包括:进一步完善服务计算的单子模型,并重点关注服务组合的测试和验证、基于QoS的服务质量评测等。
| [1] | Singh M P, Huhns M N. Service-oriented computing[M]. Chichester: John Wiley & Sons, 2005. |
| [2] | Zoran S, Ajantha D. Service-oriented software system engineering: Challenges and practices[M]. Hershey: Ideal Group Publishing, 2005. |
| [3] | Papazoglou M, Traverso P, Dustdar S. Service-oriented computing: State of the art and research challenges[J]. IEEE Computer, 2007, 12(7): 38–45. |
| [4] | Kreger H. Web services conceptual architecture (WSCA 1.0)[J]. Ibm Software Group, 2001, 5: 6–7. |
| [5] |
喻坚, 韩燕波.
面向服务的计算--原理和应用[M]. 北京: 清华大学出版社, 2006.
Yu Jian, Han Yanbo. Service-oriented computing-Theory and applications[M]. Beijing: Tsinghua University Press, 2006. |
| [6] |
蔡维德, 白晓颖, 陈以农.
浅谈深析面向服务的软件工程[M]. 北京: 清华大学出版社, 2008.
Cai Weide, Bai Xiaoying, Cheng Yinong. Deep analysis of service-oriented software engineering[M]. Beijing: Tsinghua University Press, 2008. |
| [7] |
白晓颖, 赵冲冲, 戴桂兰.
Web服务测试研究[J]. 计算机科学, 2006, 33(2): 252–256.
Bai Xiaoying, Zhao Chongchong, Dai Guilan. Research on web service testing[J]. Computer Science, 2006, 33(2): 252–256. |
| [8] |
廖军.面向服务的计算(SOC)中服务组合的研究[D].成都:电子科技大学, 2006.
Liao Jun. The research on service composition in service-oriented computing[D]. Chengdu: University of Electronic Science and Technology, 2006. |
| [9] |
麻志毅, 陈泓婕.
一种面向服务的体系结构参考模型[J]. 计算机学报, 2006, 29(7): 1011–1019.
Ma Zhiyi, Chen Hongjie. A service-oriented architecture reference model[J]. Chinese Journal of Computers, 2006, 29(7): 1011–1019. |
| [10] | Curbera F. Component contracts in service-oriented architectures[J]. IEEE Computer, 2007, 12(7): 74–80. |
| [11] |
杨鹏.面向服务的新一代网络体系结构及其形式化建模的研究[D].南京:东南大学, 2006.
Yang Peng. Research on service-oriented new generation network architecture and its formal modeling[D]. Nanjing: Southeast University, 2006. |
| [12] |
杨鹏, 吴家皋.
网络服务体系结构及其形式化模型研究[J]. 计算机研究与发展, 2005, 42(7): 1115–1122.
DOI:10.1360/crad20050704 Yang Peng, Wu Jiagao. Research on network service architecture and its formal model[J]. Journal of Computer Research and Development, 2005, 42(7): 1115–1122. DOI:10.1360/crad20050704 |
| [13] |
张广胜, 蒋昌俊, 汤宪飞, 等.
面向服务的企业应用集成系统描述与验证[J]. 软件学报, 2007, 18(12): 3015–3030.
Zhang Guangsheng, Jiang Changjun, Tang Xianfei, et al. Specification and verification of service-oriented enterprise application integration system[J]. Journal of Software, 2007, 18(12): 3015–3030. |
| [14] |
何克清, 何非, 李兵, 等.
面向服务的本体元建模理论与方法研究[J]. 计算机学报, 2005, 28(4): 524–533.
He Keqing, He Fei, Li Bing, et al. Research on service -oriented ontology & meta-modeling theory and methodology[J]. Chinese Journal of Computers, 2005, 28(4): 524–533. |
| [15] |
王桂玲, 李玉顺, 姜进磊, 等.
一种服务网格动态信息聚合模型及其应用[J]. 计算机学报, 2005, 28(4): 541–548.
Wang Guilin, Li Yushun, Jiang Jinlei, et al. A dynamic information aggregation model and its application in service grid environment[J]. Chinese Journal of Computers, 2005, 28(4): 541–548. |
| [16] |
赵会群, 孙晶.面向服务的可信软件体系结构代数模型[J]. 2010, 33(5):890-899.
Zhao Huiqun, Sun Jing. An algebraic model of service oriented trustworthy software architecture[J]. Chinese Journal of Computers, 2010, 33(5):890-899. |
| [17] | Moggi E. An abstract view of programming languages[R]. LFCS Report, ECS-LFCS-90-113, 1989. |
| [18] |
袁琦. Monad理论及其应用研究[D].吉林:吉林大学, 2000.
Yuan Qi. Research on Monad theory and its application[D]. Jilin: Jilin University, 2000. |
| [19] | Wadler P. Comprehending monads[J]. Mathematical Structures in Computer Science, 1992, 2(3): 461–493. |
| [20] | Rutten J. Universal coalgebra: A theory of systems[J]. Theoretical Computer Science, 2000, 249(1): 3–80. DOI:10.1016/S0304-3975(00)00056-6 |
| [21] | Gumm H P. Functors for coalgebras[J]. Algebra Universalis, 2000, 45(2-3): 135–147. |
| [22] | Jacobs B. Comprehension for coalgebras[J]. Electronic Notes in Theoretical Computer Science, 2002, 65(1): 112–134. DOI:10.1016/S1571-0661(04)80362-1 |
| [23] |
周晓聪, 舒忠梅.
计算机科学中的共代数方法的研究综述[J]. 软件学报, 2003, 14(10): 1661–1671.
Zhou Xiaocong, Shu Zhongmei. A survey on the coalgebraic methods in computer science[J]. Journal of Software, 2003, 14(10): 1661–1671. |
| [24] | Meng S, Barbosa L. Refinement of generic software components[R]. UNU/ⅡST Report No.281, 2004. |
| [25] | Sun M, Barbosa L. Components as coalgebras: The refinement dimension[J]. Theoretical Computer Science, 2006, 351(2): 276–294. DOI:10.1016/j.tcs.2005.09.072 |
| [26] | Barbosa L. Towards a calculus of state-based software components[J]. J Universal Comput, 2003, 9(8): 891–909. |
| [27] | Barbosa L. Components as coalgebras[D]. Braga:University of Minho, 2001. |
| [28] | Sun M, Aichernig B K, Barbosa L S, et al. A coalgebraic semantic framework for component based development in UML[C]//Conference on Category Theory and Computer Science (CTCS'04).[S.l.]:ENTCS, Elsevier, 2005, 122: 229-245. |
| [29] | Wadler P. Monads for functional programming[J]. Nato Asi, 2015, 36(2): 24–52. |
| [30] | Fiore M, Moggi E, Sangiorgi D. A fully abstract model for the pi-calculus[J]. Information and Computation, 2002, 179(1): 76–117. DOI:10.1006/inco.2002.2968 |
| [31] | Holyer I, Spiliopoulou E. Concurrent monadic interfacing[C]//Workshop on Implementation of Functional Languages, IFL'98.[S.l.]: Springer Verlag, 1998: 72-87. |
| [32] | Lam E, Sulzmann M. Towards agent programming in CHR[C]//Workshop on Constraint Handling Rules (CHR'06). Heidelberg: Springer, 2006: 17-31. |
| [33] | Carlsson M. Monads for incremental computing[C]//International Conference on Functional Programming (ICFP'02). Pittsburgh, PA:[s.n.], 2002: 26-35. |
| [34] | Ghania N, Lüthb C, De Marchia F. Coalgebraic monads[J]. Electronic Notes in Theoretical Computer Science, 2002, 65(1): 71–91. DOI:10.1016/S1571-0661(04)80360-8 |
| [35] | Ghani N, Lüth C, de Marchi F. Monads of coalgebras: Rational terms and term graphs[J]. Mathematical Structures in Computer, 2005, 15(3): 433–451. DOI:10.1017/S0960129505004743 |
| [36] | Ghania N, Lüthb C, de Marchia F, et al. Algebras, coalgebras, monads and comonads[J]. Electronic Notes in Theoretical Computer Science, 2001, 44(1): 128–145. DOI:10.1016/S1571-0661(04)80905-8 |
| [37] | Jacobs B, Poll E. Coalgebras and monads in the semantics of Java[J]. Theoretical Computer Science, 2003, 291(3): 329–349. DOI:10.1016/S0304-3975(02)00366-3 |
| [38] | Liang S, Hudak P, Jones M. Monad transformers and modular interpreters[C]//22nd ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages. New York: ACM Press, 1995: 333-343. |
| [39] | Liang S. Modular monadic semantics and compilation[D]. Yale: University of Yale, 1998. |
| [40] |
吕江花, 金成植.
Monad的反射性[J]. 吉林大学学报(理学版), 2004, 42(2): 195–199.
Lü Jianghua, Jin Chengzhi. Reflection in monad[J]. Journal of Jilin University (Science Edition), 2004, 42(2): 195–199. |
| [41] |
吕江花, 金成植.
Monad的一种自动生成技术[J]. 软件学报, 2003, 14(12): 1989–1995.
Lü Jianghua, Jin Chengzhi. An automatic generation technique for monad[J]. Journal of Software, 2003, 14(12): 1989–1995. |
| [42] |
袁琦, 金成植.
Monad的面向对象程序的自动生成[J]. 计算机研究与发展, 2000, 37(6): 668–671.
Yuan Qi, Jin Chengzhi. Transforming monad representing to oo programs[J]. Journal of Computer Research and Development, 2000, 37(6): 668–671. |
| [43] | Mcnamara B, Smaragdakis Y. Functional programming with the FC++ library[J]. Journal of Functional Programming, 2004, 14(4): 429–472. DOI:10.1017/S0956796803004969 |
| [44] | Mericli T, Bi P. JFun: functional programming in Java[R]. Technical Report TR-06-65, 2006. |
| [45] |
张迎周, 徐宝文.
一种基于模块单子语义的动态程序切片方法[J]. 计算机学报, 2006, 29(4): 526–534.
Zhang Yingzhou, Xu Baowen. An approach to dynamic program slicing based on modular monadic semantics[J]. Chinese Journal of Computers, 2006, 29(4): 526–534. |
| [46] |
张迎周, 徐宝文.
一种新型形式化程序切片方法[J]. 中国科学, E辑:信息科学, 2008, 38(2): 161–176.
Zhang Yingzhou, Xu Baowen. A novel formal approach to program slicing[J]. Science in China, Series E: Information Sciences, 2008, 38(2): 161–176. |
| [47] |
张迎周.基于模块单子语义的程序切片技术研究[D].南京:东南大学, 2006.
Zhang Yingzhou. Research on program slicing techniques based on modular monadic semantics[D]. Nanjing: Southeast University, 2006. |
| [48] |
廖军, 谭浩, 刘锦德.
基于Pi-演算的Web服务组合的描述和验证[J]. 计算机学报, 2005, 28(4): 635–643.
Liao Jun, Tan Hao, Liu Jinde. Describing and verifying web service using Pi-Caculus[J]. Chinese Journal of Computers, 2005, 28(4): 635–643. |
| [49] | Zhang Y Z, Fu W, Qian J Y. Automatic testing of web services in haskell platform[J]. Journal of Computational Information Systems, 2010, 6(9): 2859–2867. |
| [50] | Zhang Y Z, Fu W, Nie C H. MonadWS: A monad-based testing tool for web services[C]//ICSE Workshop, 6th IEEE/ACM International Workshop on Automation of Software Test (AST 2011).New York, NY:[s.n.], 2011: 111-112. |
| [51] |
符炜, 张迎周, 孙无极, 等.
一种基于函数依赖图的构件抽取方法[J]. 南京邮电大学学报(自然科学版), 2010, 30(6): 78–84.
Fu Wei, Zhang Yingzhou, Sun Wuji, et al. A method of component extraction based on function dependence graph[J]. Journal of Nanjing University of Posts and Telecommunications (Natural Science), 2010, 30(6): 78–84. |
| [52] | Weiser M. Program slicing[J]. IEEE Transactions on Software Engineering, 1984, 16(5): 498–509. |
| [53] | Fu W, Zhang Y Z, et al. Program slicing based web-service generation and composition[C]//2010 IEEE International Workshop on Service-Oriented System Engineering (SOSE'10). Nanjing:[s.n], 2010: 189-192. |
| [54] | Fu W, Zhang Y Z, et al. Program slicing based web service publishing and discovery[C]//2010 International Conference on Web Information Systems and Mining (WISM'10). Sanya, China:[s.n], 2010:144-148. |
| [55] | Zhang Y, Fu W, Leung H. Web service publishing and composition based on Monadic methods and program slicing[J]. Knowledge-Based Systems, 2013, 37: 296–304. DOI:10.1016/j.knosys.2012.08.008 |
| [56] |
张迎周, 吴重强, 钱巨, 等.
含指针程序的单子切片方法[J]. 计算机学报, 2010, 33(3): 473–482.
DOI:10.3724/SP.J.1016.2010.00473 Zhang Yingzhou, Wu Chongqiang, Qian Ju, et al. A Monadic slicing algorithm for a program with pointers[J]. Chinese Journal of Computers, 2010, 33(3): 473–482. DOI:10.3724/SP.J.1016.2010.00473 |
| [57] | Zhang Yingzhou. Program slicing based on monadic semantics[M]//Semantics in Action-Applications and Scenarios.[S.l.]: InTech, 2012: 41-62. |
| [58] |
Simon Thompson. Haskell:函数式编程基础[M].3版, 乔海燕, 张迎周, 译.北京:科学出版社, 2015.
Thompson S. Haskell: The craft of functional programming[M]. Third Edition. Qiao Haiyan, Zhang Yingzhou, tran. Beijing: Science Press, 2015. |
 2016, Vol. 48
2016, Vol. 48


