2. 苏州中科启慧软件技术有限公司,苏州,215500;
3. 南京航空航天大学能源与动力学院,南京,210016
2. Suzhou Chinsdom Co. Ltd., Suzhou, 215500, China;
3. College of Energy and Power Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China
Hash函数是密码学的重要分支, 是一种将任意长度的输入消息压缩成固定长度输出摘要的函数, 它在数字签名、身份认证与密钥交换、数据校验与消息认证及伪随机数生成等领域具有广泛的应用。随着无线通信与网络技术的发展, 普通的Hash函数难以满足无线终端资源受限环境的应用需求, 轻量级Hash函数的设计与分析成为当前的研究热点, 比较有代表性的有SQUASH, DM-PRESENT, H-PRESENT, Vortex, QUARK, PHOTON, SPONGENT, Lesamnta-LW, GLUON和ARMADILLO等。其中, DM-PRESENT, H-PRESENT和SPONGENT的压缩函数均采用轻量级分组密码国际标准PRESENT[1-2], 只是结构不同。
SQUASH[3]是Shamir在FSE 2008上提出的轻量级Hash函数。它是针对射频识别(Radio frequency identification, RFID)标签等资源极端受限环境设计的, 迭代结构采用的是Rabin结构, 压缩函数采用的是非线性反馈移位寄存器(Nonlinear feedback shift register, NFSR)。这种设计使得该算法可以应用于任何资源极端受限的环境, 因为它也可以根据处理器的倍数来调整算法的吞吐率, 例如将算法从8位平台换到32位或者64位平台的话, 它的速率将会大大地提高。
DM-PRESENT[4]和H-PRESENT[5]是Bogdanov等在CHES 2008上提出的轻量级Hash函数。它们都采用轻量级分组密码PRESENT作为压缩函数, 在迭代结构的选择上DM-PRESENT使用DM结构, 而H-PRESENT使用Hirose结构。DM-PRESENT的摘要长度为64 bit, H-PRESENT的摘要长度为128 bit。在硬件实现时, DM-PRESENT最少需要1 600个门电路(GE), 而H-PRESENT最少需要2 330个GE, 都可用于RFID标签等环境。
Vortex[6]是Gueron和Kounavis在ISC 2008上提出的一种轻量级Hash函数。它可将任意长度的消息压缩成256 bit的消息摘要。在设计时采用MD结构, 压缩函数采用类似高级加密标准(Advanced encryption standard, AES)的轮, 在扩散层设计时通过使用有限域GF (2)上的乘法实现, 这种方式提高了扩散的速度。虽然只采用了3个AES型的轮, 但是设计者通过增加压缩函数的密钥编排算法的强度来保证算法的安全。设计者声称该算法的安全性与SHA-256相当, 同时速度是优于SHA-256的。
QUARK[7]是Aumasson等在CHES 2010上提出的一种轻量级的Hash函数。它设计时采用Sponge结构[8], 压缩函数的设计基于轻量级密码Grain和KANTAN。它分为U-QUARK, D-QUARK和T-QUARK, 并且都有着不错的效率。最小的U-QUARK提供264的安全强度, 硬件实现能控制在1 379个GE。最大的T-QUARK能提供2112的安全强度, 也仅需要2 296个GE就可实现。
PHOTON[9]是Guo等在CRYPTO 2011上提出的一种轻量级Hash函数。它设计时采用Sponge结构, 压缩函数采用AES型的设计。一般来说, AES并不适合于资源极端受限环境, 但是设计者采用一种序列化的方法, 巧妙地降低了算法实现时对GE数的需求。在提供264安全强度的情况下, 该算法最少可用1 120 GE实现。
SPONGENT[10]是Bogdanov等在CHES 2011上提出的一种轻量级Hash函数。它设计时迭代结构采用Sponge结构, 压缩函数采用轻量级分组密码PRESENT。这种设计能够大大提高硬件的实现效率。该算法能提供88, 128, 160, 224和256五种不同的摘要长度, 它们的硬件实现的GE数分别为738, 1 060, 1 329, 1 728和1 950。该算法是一种硬件实现效率非常优秀的轻量级Hash函数, 具有很好的前景。
GLUON[11]是Berger等在AFRICACRYPT 2012上提出的一种轻量级Hash函数。它在设计时采用Sponge结构, 并以两个流密码为基础设计压缩函数。设计者声称它的最小版本能用2 071个GE实现, 且能达到264的安全强度。它是个相当有竞争力的轻量级Hash函数, 而且引入流密码的设计理念也是它的一大特色。
ARMADILLO[12]是由Badel等在CHES 2010上提出的一种专门面向硬件设计的迭代的轻量级Hash函数。它在设计时采用了数据依赖置换技术, 该技术因为在RC6和MARS设计时的应用而受到重视, 由于具体过程中采用的更易硬件实现的移位操作, 所以硬件实现效率很高, 最小的硬件实现能达到2 923个GE。
Wu等设计了一个轻量级Hash函数LHash[13], 硬件实现需要989~1 200个GE, 符合超轻量级密码的硬件需求, 性能较好。
总体而言, 现有轻量级Hash函数一般是面向硬件的, 没有兼顾软件效率, 难以满足嵌入式系统和单片机等环境对软件实现的需求。目前轻量级Hash函数尚未制定相应的国际标准。本文设计了一种综合性能较好的轻量级Hash函数。
1 轻量级Hash函数CHF设计为了满足资源受限环境的应用需求, 基于目前比较流行的Sponge迭代结构, 采用轻量级分组密码国际标准CLEFIA-128的变形算法CLEFIA-128*作为压缩函数, 设计了一个轻量级Hash函数CHF。
1.1 符号注释GF (mn)={0, …, m-1}n表示n位m进制有限域;
A×B={ < x, y>|x(A, y∈B}表示集合A与B的笛卡积;
A→B表示集合A到B的映射;
x |→ y表示元素x映射到y;
x(n)表示长度为n-bit的x;
GE表示门电路;
a←b表示用b的值更新a的值;
a⊕b表示按位异或运算;
a|b=(a, b)表示连接运算;
X[a~b]表示X的第a到b比特;
x < < < i表示x循环左移i位;
x>>>j表示x循环右移j位。
1.2 CHF算法参数设计与迭代结构CHF算法设计了3种版本, 对应的消息摘要长度分别为72,88和128 bit。具体设计时, 统一取内部状态宽度b=128 bit; 吞吐率r=8 bit; 容量c=120 bit, 即提供2120的抗原像攻击能力; 迭代轮数R=18轮。
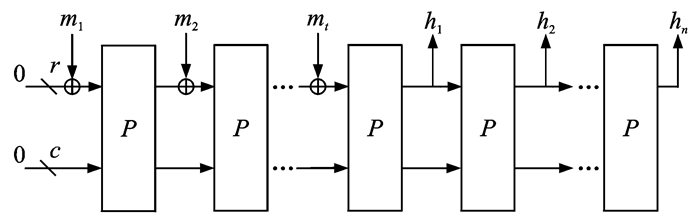
CHF算法的迭代结构采用目前比较流行的Sponge迭代结构[8], 如图 1所示。
|
图 1 Sponge结构 Figure 1 Sponge structure |
Sponge结构采用简单的迭代设计, 通过一个固定b比特长度的内部状态和一个置换函数P将不定长度的消息压缩成任意长度的消息摘要。它的内部状态b=r+c≥n为宽度, r为吞吐率, c为容量, n为消息摘要的长度。Sponge结构因为没有前向反馈, 硬件实现时所需的GE数更少, 更加符合轻量级Hash函数的设计要求。
1.3 CHF算法的压缩函数--变形算法CLEFIA-128*介绍测试和分析表明, 轻量级分组密码国际标准CLEFIA-128算法[14]存在以下可改进空间[15]:首先它需要5轮才能基本实现伪随机性, 扩散效果并不明显; 其次它每一轮使用两个轮函数的设计降低了算法的软硬件实现效率。因此, 可从加密结构和轮函数两个方面对其进行改进。
(1) 修改加密结构
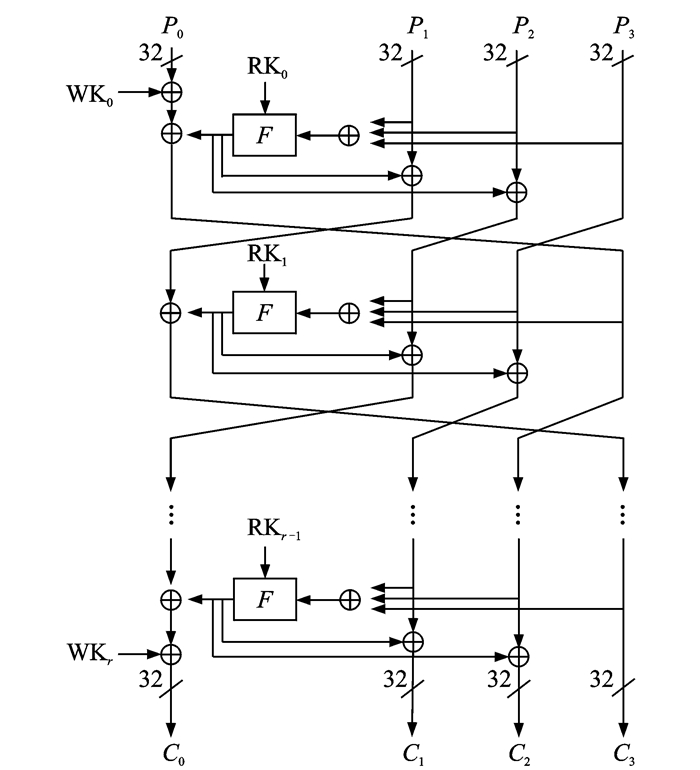
变形算法CLEFIA-128*的加密结构如图 2所示(结合Mars和SMS4, 命名为MS结构), 将原来的加密结构更改为每一轮用3个分支去更新另外一个分支, 然后再用更新结果去更新另外两个分支, 迭代的轮数不变, 即r=18。整个加密过程中共用到了r个32 bit的轮密钥(RK0, RK1, RK2, …, RKr-1)和2个32 bit的白化子密钥(WK0, WK1)。详细过程可参阅文献[15]。
|
图 2 CLEFIA-128*所采用的MS加密结构示意图 Figure 2 MS structure in CLEFIA-128* |
(2) 修改轮函数
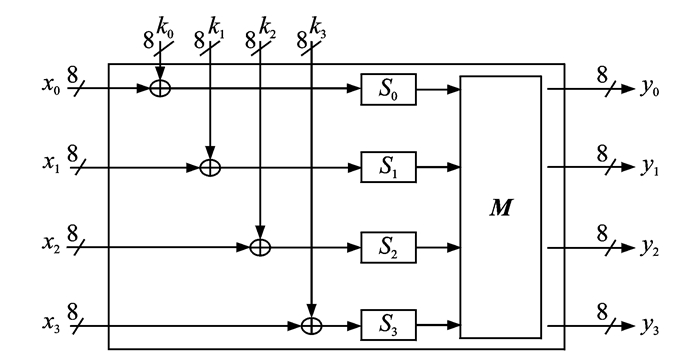
CLEFIA-128使用了两个不同的轮函数F0, F1, CLEFIA-128*只使用一个轮函数F, 如图 3所示。
|
图 3 CLEFIA-128*中轮函数F示意图 Figure 3 Round function F in CLEFIA-128* |
CLEFIA-128选用了两个不同的S盒S0, S1, 各使用两次。由于Camellia算法(欧洲第二代普通型分组密码标准)[16]采用的S盒适用于小硬件设计, CLEFIA-128*轮函数F中混淆层的4个S盒采用Camellia中的4个8位S盒并行, 扩散层矩阵M仍然使用CLEFIA-128中的Hadamard矩阵, 选择CLEFIA-128中M0或M1均可。
Camellia/ CLEFIA-128*算法轮函数F的4个S盒可参阅文献[16]。
2 CHF算法效率分析与测试(1) 硬件实现效率
依据文献[17]所讲述的硬件实现效率的评估方法来计算CHF系列算法的硬件实现效率。CHF算法的硬件实现大约需要2 240.96 GE, 可以较好地应用到RFID等环境。为了进一步降低所需的GE数, 可以采用S盒序列化的方法, 只需约1 640.96 GE就可实现CHF算法。这样做的缺点就是吞吐率将减小, 算法的执行时间延长, 在实际应用时可根据具体需求来决定采用何种实现方式。
文献[6]总结了当前一些轻量级Hash函数的硬件实现效率, 如表 1所示。
| 表 1 一些轻量级Hash函数的硬件实现效率 Table 1 Hardware efficiency of some Hash functions |
(2) 软件实现效率
在Intel (R) Core (TM) i5-2520 M 2.5 GHz Windows 7 64-bit平台下用C语言编程对CHF算法进行了实现, 并将它们与典型轻量级Hash函数SPONGENT-88算法的软件实现效率进行对比, 如表 2所示, CHF的软件效率是SPONGENT的4倍。
| 表 2 CHF系列算法和SPONGENT的软件实现效率对比 Table 2 Software efficiency of CHF and SPONGENT |
(3) 效率分析比较
CHF算法的硬件实现能达到2 000 GE以下的数量级, 与SQUASH, H-PRESENT和GLUON等算法相当, 虽尚不及SPONGENT和PHOTON, 但明显优于C-PRESENT和Lesamnta-LW。通常来讲, 2 000 GE可作为衡量一个轻量级密码是否能够应用RFID环境的标准, 文中设计的超轻量级的U-CHF完全能够达到这一标准。虽然典型轻量级Hash函数SPONGENT算法具有更佳的硬件实现, 但是它采用了PRESENT类型的压缩函数设计, 大量位操作使得它的软件实现效率不高, 而CHF系列算法的压缩函数采用的是广义的Feistel结构, 具有更高的软件实现效率, 如表 2所示。
总的来说, CHF算法兼顾了软件和硬件实现, 既能满足RFID等资源极端受限环境的硬件使用需求, 也可以满足其他的一些诸如嵌入式、单片机等环境对软件实现的需求, 适用范围更广。
3 CHF算法安全性测试与分析(1) 依赖性测试
密码算法的依赖性包括算法的完备性、雪崩效应和严格雪崩准则等方面。一个密码算法具有良好的依赖性是指它满足完备度dc=1, 雪崩效应度da≈1, 严格雪崩效应度dsa≈1。任取100 000个128 bit的样本对CHF算法的依赖性做测试, 结果如表 3所示。
| 表 3 CHF依赖性测试结果 Table 3 Dependency test of CHF |
可以看出, 两种算法的输出改变的平均位数非常接近理想值50%, 即输入几乎每改变一位, 就会引起输出一半的值的改变。因此, 该算法的混淆和扩散效果好。
(2) 抗碰撞、原像和第二原像分析
Bertoni等[18]论证了Sponge结构与随机预言机是不可区别的, 并给出了该结构抗碰撞、原像及第二原像攻击的能力。抗碰撞攻击:min{2n/2, 2c/2}; 抗原像攻击: min{2n, 2c, max{2n-r, 2c/2}}; 抗第二原像攻击: min{2n, 2c/2}。
文献[15]证明了压缩函数CLEFIA-128*的安全性, 因此, CHF-72, CHF-88和CHF-128抗碰撞攻击的能力分别为236,244和260, 抗原像攻击的能力分别为264,280和2120, 抗第二原像攻击的能力均为260。
(3) 差分和线性分析
CLEFIA-128算法在设计轮函数的混淆层时选用了两个不同的S盒S0, S1, 各使用两次, 其中S0的最大差分概率DPmaxS0=2-4.67, 最大线性概率LPmaxS0=2-4.38, 相比之下S1具有更低的最大差分和线性概率, 安全性更高。CHF算法采用的4个8位的S盒都满足DPmaxSi=LPmaxSi=2-6, 0≤i < 4, 安全性都比S0更高, 与S1相当。差分和线性分析表明CHF算法每一轮的最大差分和线性活动S盒的个数如表 4所示。
| 表 4 CHF算法的活动S盒情况 Table 4 Active S-box of CHF |
9轮压缩函数的最大差分概率为DCPmax9r≤224×(-6)=2-144 < 2-128, 7轮压缩函数的最大线性概率为LCPmax7r≤224×(-6)=2-144 < 2-128, 由此可见, 18轮的设计是足以抵抗差分和线性分析的。
(4) 不可能差分分析
运用矩阵的方法对CHF算法的压缩函数CLEFIA-128*进行不可能差分分析[19], 只能攻击到第4轮, 可以找到如下的6条不可能差分路径:
| $ \begin{array}{l} (\alpha, 0, 0, 0)\mathop {\not \to }\limits^{4r} (\alpha, 0, 0, 0)\;\;p = 1;\\ (0, 0, \alpha, 0)\mathop {\not \to }\limits^{4r} (0, 0, \alpha, 0)\;\;p = 1;\\ (0, 0, \alpha, 0)\mathop {\not \to }\limits^{4r} (\alpha, 0, \alpha, 0)\;\;p = 1;\\ (\alpha, \alpha, 0, 0)\mathop {\not \to }\limits^{4r} (\alpha, 0, 0, 0)\;\;p = 1;\\ (\alpha, 0, \alpha, 0)\mathop {\not \to }\limits^{4r} (\alpha, 0, 0, 0)\;\;p = 1;\\ (\alpha, 0, 0, \alpha )\mathop {\not \to }\limits^{4r} (\alpha, 0, 0, 0)\;\;p = 1; \end{array} $ |
其中,α(GF (232)表示非零的差分。因此, CHF系列算法是能够抵抗不可能差分分析的。
4 结束语为了满足能耗等资源受限环境的应用需求, 本文基于Sponge迭代结构, 采用CLEFIA-128*算法作为压缩函数, 设计了一个轻量级Hash函数CHF。其硬件实现能达到2 000GE以下的数量级。与典型轻量级Hash函数SPONGENT相比, CHF算法具有更好的软件实现效率; 其硬件实现效率与现有轻量级Hash函数也可比, 可以说它兼顾了软硬件实现效率, 适用范围更广。最后, 对CHF算法作了依赖性测试和安全性分析, 它具有良好的混淆和扩散效果, 并能抵抗现有的攻击。实际上, CLEFIA-128*与CLEFIA-128总体迭代加密结构并不相同, 只是轮函数结构相同, 轮函数采用的S盒也不相同。之所以采用已有的轮函数结构和S盒, 是为了方便同行感知和验证CLEFIA-128*所采用的迭代加密结构MS及CHF算法的安全性, 而Camellia算法为CLEFIA-128*和CHF算法提供了4个现成的S盒。实际上, 4个S盒可自行设计, 通过伪随机方式产生或通过不可约多项式产生。
| [1] | ISO/IEC 29192-2. Information technology -security techniques -lightweight cryptography -Part 2: Block ciphers[S]. Switzerland: ISO/IEC, 2012. |
| [2] | Bogdanov A, Knezevic M, Leander G, et al. SPONGENT: The design space of lightweight cryptographic hashing[J]. IEEE Transactions on Computers, 2013, 62(10): 2041–2053. DOI:10.1109/TC.2012.196 |
| [3] | Shamir A. SQUASH-A new MAC with provable security properties for highly constrained device such as RFID Tags[C]//FSE 2008, LNCS 5086. Berlin Heidelberg: Springer-Verlag, 2008: 144-157. |
| [4] | Koyama T, Sasaki Y, Kunihiro N. Multi-differential cryptanalysis on reduced DM-PRESENT-80: Collisions and other differential properties[J]. Lecture Notes in Computer Science, 2013, 7839: 352–367. DOI:10.1007/978-3-642-37682-5 |
| [5] | Bogdanov A, Leander G, Paar C, et al. Hash functions and RFID tags: Mind the gap[C]//CHES 2008, LNCS 5154. Berlin Heidelberg: Springer-Verlag, 2008: 283-299.http://www.ei.ruhr-uni-bochum.de/media/crypto/veroeffentlichungen/2010/09/17/hash_and_rfid_ches2008.pdf |
| [6] | Gueron S, Kounavis M K. Vortex: A new family of one-way hash functions based on AES rounds and carry-less application[C]//ISC 2008, LNCS 5222. Berlin Heidelberg: Springer-Verlag, 2008: 331-340. |
| [7] | Aumasson J P, Henzen L, Meier W, et al. QUARK: A lightweight Hash[J]. Journal of Cryptology, 2013, 26(2): 313-339.http://link.springer.com/chapter/10.1007%2F978-3-642-15031-9_1 |
| [8] | Bertoni G, Daemen J, Peeters M, et al. Sponge functions[C]//ENCRYPT Hash Workshop 2007. Berlin Heidelberg: Springer-Verlag, 2007: 1-22. |
| [9] | Guo J, Peyrin T, Poschmann A. The PHOTON family of lightweight hash functions[C]//CRYPTO 2011, LNCS 6841. Berlin Heidelberg: Springer-Verlag, 2011: 222-239. |
| [10] | Bogdanov A, Leander G, Toz D, et al. SPONGENT: A lightweight hash function[C]//CHES 2011, LNCS 6917. Berlin Heidelberg: Springer-Verlag, 2011: 312-325. |
| [11] | Berger T P, Hayer J D, Marquet K, et al. The GLUON family: A lightweight Hash function family based on FCSRs[C]//AFRICACRYPT 2012, LNCS 7374. Berlin Heidelberg: Springer-Verlag, 2012: 306-323. |
| [12] | Badel S, Dagtekin N, Jr JN, et al. ARMADILLO: A multi-purpose cryptographic primitive dedicated to hardware[C]//CHES 2010, LNCS 6225. Berlin Heidelberg: Springer-Verlag, 2010: 398-412. |
| [13] | Wu Wenling, Wu Shuang, Zhang Lei, et al. LHash: A lightweight hash function[J]. Lecture Notes in Computer Science, 2014, 8567: 291–308. DOI:10.1007/978-3-319-12087-4 |
| [14] | Shirai T, Shibutani K, Akishita T, et al. The 128-bit blockcipher CLEFIA (Extended abstract)[C]//FSE 2007, LNCS 4593. Berlin Heidelberg: Springer-Verlag, 2007: 181-195. |
| [15] |
陈帮春.物联网终端系统安全机制研究与设计[D].南京:南京航空航天大学, 2014.
Chen Bangchun. Research and design of terminal system security mechanism in IoT[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014. |
| [16] | Aoki K, Ichikawa T, Kanda M, et al. Specification of Camellia-A 128-bit block cipher[EB/OL]. https://www.cosic.esat.kuleuven.ac.be/nessie/workshop/submissions/Camellia.zip, 2016-10-12. |
| [17] | Axel Y P B. Lightweight cryptography: Cryptographic engineering for a pervasive world [D]. Bochum: Ruhr-University Bochum, 2009. |
| [18] | Bertoni G, Daemen J, Peeters M, et al. On the indifferentiability of the Sponge construction[C]//EUROCRYPT 2008, LNCS 4965. Berlin Heidelberg: Springer-Verlag, 2008: 181-197. |
| [19] | Azimi S A, Ahmadian Z, Mohajeri J, et al. Impossible differential cryptanalysis of Piccolo lightweight block cipher[C]//11th International Conference on Information Security and Cryptology. Berlin Heidelberg: Springer-Verlag, 2014: 89-94. |
 2016, Vol. 48
2016, Vol. 48


