2. 上海卫星工程研究所,上海,200240
2. Shanghai In stitute of Satellite Engineering, Shanghai, 200240, China
频率选择表面(Frequency selective surface, FSS)是指由金属贴片或孔径单元呈周期性排布的二维平面结构,在谐振频率处可以使得电磁波发生全反射(贴片型结构)或者全透过(孔径型结构),是一种具有对电磁波有入射角度选择性、极化方式选择性和频率选择性的空间滤波器,常作为天线的极化器、滤波器和反射板,或者用于天线罩中来降低雷达的散射截面(Radar cross section, RCS)[1]。
对FSS的理论分析可以概括为3种方法:模式匹配发[2-3]、等效电路法[4-6]和谱域法。模式匹配法将自由空间Floquet模式和FSS单元上的电场或电流模式进行匹配,通过求解电流或电场积分方程得到FSS的数值解,但模式匹配法的不足在于求解多层结构式,公式复杂计算量非常大;等效电路法利用无限长金属微带的电感和电容计算公式,分析等效电路参数由此计算出FSS的传输或反射系数,这种分析方法简单、直观,文献[5, 6]中通过等效电路法设计FSS,其等效电路的频响特性与其他方法的频响特性结果有一定的偏差,这主要是由于等效电路法无法计算邻近单元之间以及多层结构之间耦合的影响;本文所提出的FSS为多层缝隙耦合结构,不同介质层以及邻近单元结构之间相互作用的复杂性较高,更适合采用谱域法。谱域法是通过寻求适当的空间和结构的格林(Green)函数,建立周期结构表面电流积分方程,将电流积分方程转化为代数方程进行数值计算求得场分布,在计算多层结构或不规则结构时,谱域法计算结果比较精确。此前Pozar等人已经用周期性矩量法分析了周期性缝隙天线[7-10],本文在此基础上拟采用谱域法对缝隙耦合FSS进行了理论分析。
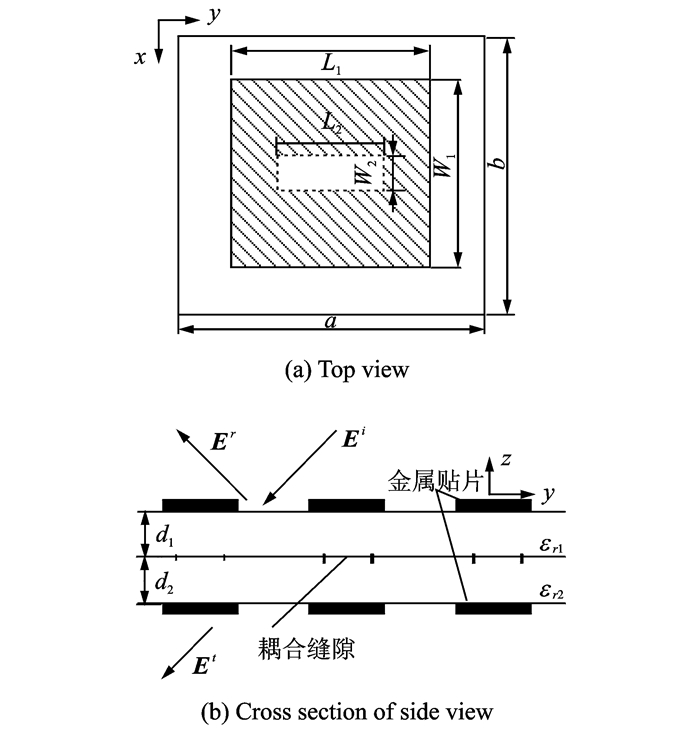
本文基于缝隙耦合贴片天线,提出了一种窄带带通频率选择表面结构。图 1展示了FSS的单元结构,共分为3层结构,其中上下表面分别为L1W1矩形金属贴片,中间层为L2W2耦合缝隙,上下层介质材料厚度和介电常数分别为d1和d2,εr1和ε r2,周期为ab。图 1(a)的中间矩形部分为缝隙结构,阴影部分为上下表面的金属贴片。FSS的频率响应主要由上下表面的贴片决定,缝隙结构则使得贴片型(带阻型)实现了带通特性。
|
图 1 FSS单元俯视图及侧面截面图 Figure 1 Geometry of frequency selective surface |
1 FSS的数值分析 1.1 等效积分方程
在整个求解过程中,假设FSS结构是单一周期无限大阵列。入射波为任意角度和任意极化方式的平面波,记作Ei,Hi。通过谱域周期矩量法求解出FSS的反射系数和透射系数[8]。
对于FSS的中间缝隙,利用等效原则用等效的磁流MS替代缝隙中穿透的电场Eaperture
| $ {\mathit{\boldsymbol{M}}_S} =-\mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over n} }} \times {\mathit{\boldsymbol{E}}_{{\rm{aperture}}}} $ | (1) |
式中
根据式(1),缝隙结构可以由上下表面等幅反向磁流的理想导体替代,这样可以确保切向电场能够透过缝隙结构,但是还需要确定切向磁场的连续性。
接下来,将电场和磁场分解成3个组成部分
| $ \mathit{\boldsymbol{E}} = {\mathit{\boldsymbol{E}}^i} + {\mathit{\boldsymbol{E}}^r} + {\mathit{\boldsymbol{E}}^s} $ | (2) |
| $ \mathit{\boldsymbol{H}} = {\mathit{\boldsymbol{H}}^i} + {\mathit{\boldsymbol{H}}^r} + {\mathit{\boldsymbol{H}}^s} $ | (3) |
式中:Ei和Hi分别表示为入射波的电场和磁场;Er和Hr表示为地平面、上层介质和上表面金属贴片的反射电场和磁场;Es和Hs为散射电场与磁场可以重新表示为
| $ {\mathit{\boldsymbol{E}}^s} = \mathit{\boldsymbol{E}}-{\mathit{\boldsymbol{E}}^i}-{\mathit{\boldsymbol{E}}^r} $ | (4) |
| $ {\boldsymbol{H}^s} = \boldsymbol{H}-{\boldsymbol{H}^i}-{\boldsymbol{H}^r} $ | (5) |
注意到入射场和反射场在沿传播方向上是相互抵消的,而平面的透射场强则是与入射场同向的散射场和与入射场反向的散射场的叠加结果,散射场的激励源是地平面上的磁流和金属贴片表面的电流。因此可以用金属贴片表面的电流来代替金属贴片,但要特别注意,根据麦克斯韦方程组,金属表面的切向电场为零。FSS的透射场和反射场包含3个激励源,顶层金属贴片的表面电流JS1,底层金属贴片的表面电流JS2,缝隙结构的表面磁流±MS3。3个边界条件,即S1顶层金属贴片的切向电场恒为零Etan≡0;S2底层金属贴片的切向电场恒为零Etan≡0;S3穿过缝隙结构的磁场连续Htan。根据上面的边界条件,可以得到3个积分方程[8]
| $ \begin{array}{l} \mathit{\boldsymbol{E}}_{\tan }^i{\left| {_{S1} + \mathit{\boldsymbol{E}}_{\tan }^r} \right|_{S1}} + \int_{S1} {\mathit{\boldsymbol{g}}_{\tan }^{{\rm{EJ}}}} {\mathit{\boldsymbol{J}}_{S1}} \cdot {\rm{d}}\mathit{\boldsymbol{S}}1 + \\ \;\;\int_{S1} {\mathit{\boldsymbol{g}}_{\tan }^{{\rm{EM}}}} {\mathit{\boldsymbol{M}}_S} \cdot {\rm{d}}\mathit{\boldsymbol{S}}3 = 0 \end{array} $ | (6) |
| $ \int_{S2} {\mathit{\boldsymbol{g}}_{\tan }^{{\rm{EJ}}}} {\mathit{\boldsymbol{J}}_{S2}} \cdot {\rm{d}}\mathit{\boldsymbol{S}}2 + \int_{S2} {\mathit{\boldsymbol{g}}_{\tan }^{{\rm{EM}}}} \left( {\mathit{\boldsymbol{-}}{\mathit{\boldsymbol{M}}_S}} \right) \cdot {\rm{d}}\mathit{\boldsymbol{S}}3 = 0 $ | (7) |
| $ \begin{array}{l} \mathit{\boldsymbol{H}}_{\tan }^i{\left| {_{S3} + \mathit{\boldsymbol{H}}_{\tan }^r} \right|_{S3}} + \int_{S2} {\mathit{\boldsymbol{g}}_{\tan }^{{\rm{EJ}}}} {\mathit{\boldsymbol{J}}_{S1}} \cdot {\rm{d}}\mathit{\boldsymbol{S}}1 + \\ \;\;\int_{S3} {\mathit{\boldsymbol{g}}_{\tan }^{{\rm{EM}}}} {\mathit{\boldsymbol{M}}_S} \cdot {\rm{d}}\mathit{\boldsymbol{S}}3 = \;\;\int_{S3} {\mathit{\boldsymbol{g}}_{\tan }^{{\rm{EJ}}}} {\mathit{\boldsymbol{J}}_{S2}} \cdot {\rm{d}}\mathit{\boldsymbol{S}}2 + \\ \;\;\int_{S3} {\mathit{\boldsymbol{g}}_{\tan }^{{\rm{HM}}}} \left( {\mathit{\boldsymbol{-}}{\mathit{\boldsymbol{M}}_S}} \right) \cdot {\rm{d}}\mathit{\boldsymbol{S}}3 \end{array} $ | (8) |
式中:g为空域格林函数;EJ/EM为表面电流和磁流引起的电场;HJ/HM为由表面电流和磁流引起的磁场。通过求解上面积分方程中的3个未知量电流JS1,JS2和磁流±MS3,就可以获得频率选择表面的反射特性和透射特性。
1.2 积分方程的解析解积分方程式(6~8)可以借助格林公式通过谱域伽辽金矩量法求解[7-9]。这种方法是将积分方程转化成矩阵等式求解
| $ \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Z}}^{11}}}&{{\mathit{\boldsymbol{Z}}^{12}}}&{{\mathit{\boldsymbol{Z}}^{13}}}\\ {{\mathit{\boldsymbol{Z}}^{21}}}&{{\mathit{\boldsymbol{Z}}^{22}}}&{{\mathit{\boldsymbol{Z}}^{23}}}\\ {{\mathit{\boldsymbol{Z}}^{31}}}&{{\mathit{\boldsymbol{Z}}^{32}}}&{{\mathit{\boldsymbol{Z}}^{33}}} \end{array}} \right) \bullet \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}^1}}\\ {{\mathit{\boldsymbol{I}}^2}}\\ {{\mathit{\boldsymbol{I}}^3}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}^1}}\\ {{\mathit{\boldsymbol{V}}^2}}\\ {{\mathit{\boldsymbol{V}}^3}} \end{array}} \right) $ | (9) |
式中:Zij为子矩阵,Vi和Ii为子向量,而未知的电流和磁流可以表达为
| $ {\mathit{\boldsymbol{J}}_{S1}}\left( {x, y} \right) = \sum\limits_i {I_i^1\mathit{\boldsymbol{f}}_i^{J1}\left( {x, y} \right)} $ | (10) |
| $ {\mathit{\boldsymbol{J}}_{S2}}\left( {x, y} \right) = \sum\limits_i {I_i^2\mathit{\boldsymbol{f}}_i^{J2}\left( {x, y} \right)} $ | (11) |
| $ {\mathit{\boldsymbol{M}}_{S1}}\left( {x, y} \right) = \sum\limits_i {I_i^3\mathit{\boldsymbol{f}}_i^M\left( {x, y} \right)} $ | (12) |
由于入射和反射波都是平面波,它们的正切分量可以表达成如下形式
| $ {\mathit{\boldsymbol{E}}^i}\left( {x, y} \right) = \mathit{\boldsymbol{E}}_o^i{{\rm{e}}^{{\rm{j}}{k_o}\left( {ux + vy} \right)}} $ | (13) |
| $ {\mathit{\boldsymbol{H}}^i}\left( {x, y} \right) = \mathit{\boldsymbol{H}}_o^i{{\rm{e}}^{{\rm{j}}{k_o}\left( {ux + vy} \right)}} $ | (14) |
| $ {\mathit{\boldsymbol{E}}^r}\left( {x, y} \right) = \mathit{\boldsymbol{E}}_o^r{{\rm{e}}^{{\rm{-j}}{k_o}\left( {ux + vy} \right)}} $ | (15) |
| $ {\mathit{\boldsymbol{H}}^r}\left( {x, y} \right) = \mathit{\boldsymbol{H}}_o^r{{\rm{e}}^{{\rm{-j}}{k_o}\left( {ux + vy} \right)}} $ | (16) |
式中:u=sinθcosφ,v=sinθsinφ,θ和φ分别为俯仰和水平入射角度。同样激励源可以表达为
| $ \begin{array}{l} V_i^1 =-\mathit{\boldsymbol{E}}_0^i \cdot \mathit{\boldsymbol{F}}_i^{J1}\left( {-{k_0}u, -{k_0}v} \right)\mathit{\boldsymbol{E}}_0^r \cdot \\ \;\;\;\mathit{\boldsymbol{F}}_i^{J1}\left( {{k_0}u, {k_0}v} \right) \end{array} $ | (17) |
| $ V_i^2 = 0 $ | (18) |
| $ \begin{array}{l} V_i^3 =-\mathit{\boldsymbol{H}}_0^i \cdot \mathit{\boldsymbol{F}}_i^M\left( {-{k_0}u, -{k_0}v} \right) - \mathit{\boldsymbol{H}}_0^r \cdot \\ \;\;\;\mathit{\boldsymbol{F}}_i^M\left( {{k_0}u, {k_0}v} \right) \end{array} $ | (19) |
式中:FiJ1,FiJ2,FiM分别为JS1,JS2和±MS3的傅里叶表达式。
通过求解矩阵式(9),可以得到电流I1,I2和I3。为了得到FSS的反射系数和透射系数,需要计算出反射场和透射场。这些场是所有传播Floquet模式的叠加结果,同时Flo quet模式的波常数必须满足
| $ k_{xm}^2 + k_{yn}^2 \le k_o^2 $ | (20) |
式中:kx和ky分别为波矢量在x和y方向的分量。
根据上述理论计算得到的透射场和反射场为
| $ \begin{array}{l} {\mathit{\boldsymbol{E}}^{{\rm{trans}}}}\left( {x, y} \right) = \frac{1}{{ab}}\sum\limits_{k_{xm}^2 + k_{ym}^2 \le k_o^2} {\left[{{\mathit{\boldsymbol{G}}^{{\rm{EJ}}}}\left( {{k_{xm}}, {k_{yn}}} \right) \cdot } \right.} \\ \;\;\;\;\;\;\;\;\sum\limits_i {I_i^2\mathit{\boldsymbol{F}}_i^{J2}\left( {{k_{xm}}, {k_{yn}}} \right) + } {\mathit{\boldsymbol{G}}^{{\rm{EM}}}}\left( {{k_{xm}}, {k_{yn}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\left. {\sum\limits_i {I_i^3\mathit{\boldsymbol{F}}_i^M\left( {{k_{xm}}, {k_{yn}}} \right) + } } \right] \cdot {{\rm{e}}^{ -{\rm{j}}\left( {{k_{xm}} + {k_{ym}}y} \right)}} \end{array} $ | (21) |
| $ \begin{array}{l} {\mathit{\boldsymbol{E}}^{{\rm{refl}}}}\left( {x, y} \right) = \frac{1}{{ab}}\sum\limits_{k_{xm}^2 + k_{ym}^2 \le k_o^2} {\left[{{\mathit{\boldsymbol{G}}^{{\rm{EJ}}}}\left( {{k_{xm}}, {k_{yn}}} \right) \cdot } \right.} \\ \;\;\;\;\;\;\;\;\sum\limits_i {I_i^1\mathit{\boldsymbol{F}}_i^{J1}\left( {{k_{xm}}, {k_{yn}}} \right) + } {\mathit{\boldsymbol{G}}^{{\rm{EM}}}}\left( {{k_{xm}}, {k_{yn}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\left. {\sum\limits_i {I_i^3\mathit{\boldsymbol{F}}_i^M\left( {{k_{xm}}, {k_{yn}}} \right) + } } \right] \cdot {{\rm{e}}^{ -{\rm{j}}\left( {{k_{xm}} + {k_{ym}}y} \right)}} + \\ \;\;\;\;\;\;\;{\Gamma _{TM, TE}} \cdot {\mathit{\boldsymbol{E}}^i}\left( {x, y} \right) \end{array} $ | (22) |
式中:GEJ和GEM分别为感应电流和等效磁流引起的电场的谱域格林函数。则透射系数为
| $ {\Gamma _{TM}} = \frac{{\sin {k_z}d + {\rm{j}}\frac{{{\varepsilon _r}{k_{zo}}}}{{{k_z}}}\cos {k_z}d}}{{\sin {k_z}d-{\rm{j}}\frac{{{\varepsilon _r}{k_{zo}}}}{{{k_z}}}\cos {k_z}d}} $ | (23) |
| $ {\Gamma _{TE}} = \frac{{\sin {k_z}d + {\rm{j}}\frac{{{k_z}}}{{{k_{zo}}}}\cos {k_z}d}}{{\sin {k_z}d-{\rm{j}}\frac{{{k_z}}}{{{k_{zo}}}}\cos {k_z}d}} $ | (24) |
| $ {k_{zo}} = {k_o}\cos \theta $ | (25) |
| $ {k_z} = {k_o}\sqrt {{\varepsilon _r}-{{\sin }^2}\theta } $ | (26) |
最后,可以求得频率选择表面的透射和反射系数
| $ {T_{\theta \varphi }} = {\left. {\frac{{{\boldsymbol{E}^{{\rm{trans}}}}}}{{E_\theta ^i}}} \right|_{x = y = 0}} $ | (27) |
| $ {R_{\theta \varphi }} = {\left. {\frac{{{\boldsymbol{E}^{{\rm{refl}}}}}}{{E_\theta ^i}}} \right|_{x = y = 0}} $ | (28) |
式中:θ和φ为入射角。
2 FSS的建模与仿真FSS结构设计上对FSS传输特性影响较大的部分包括:金属贴片的长度与宽度、缝隙结构的长度与宽度、介质材料的介电常数与材料厚度等。其中金属贴片主要影响了FSS的谐振频点,通过改变贴片的长与宽可以有效的控制FSS的谐振频率[11-12]。
本文主要讨论当入射波为垂直入射时,缝隙结构和介质材料对FSS的传输特性影响。缝隙结构主要有两方面作用:电磁场通过缝隙对底层金属贴片进行耦合和它的极化选择特性。对于一条很窄的缝隙,只有当波的电场极化方向垂直于缝隙时才能透过FSS。
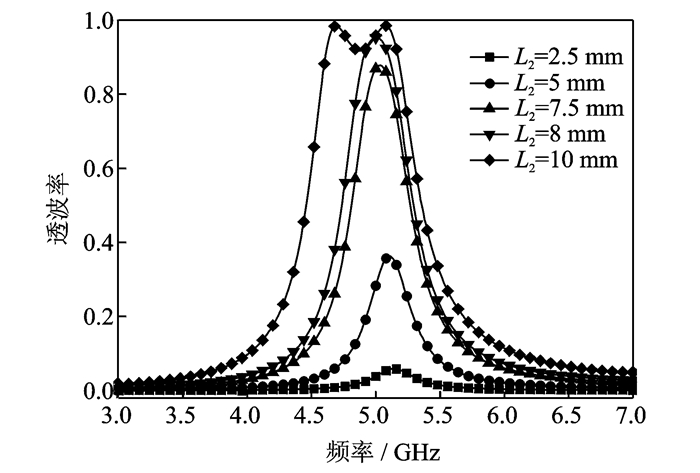
图 2为FSS的频率响应随缝隙结构长度的变化曲线。当缝隙比较短时,FSS频率响应呈带通滤波,谐振频率为5 GHz,但是结构透波率很小。随着缝隙结构的长度增加,透波率逐渐增大,同时FSS的谐振频率略有偏移约为0.4 G Hz,当缝隙长度L2达到8 mm时,FSS的透波率达到最大值约为0.96,且无其他寄生效应FSS透波效果处于最佳状态。随着缝隙长度继续增加,主谐振频率的透波率不再增加,而在低频段出现了新的谐振频点,呈现双频特性[13]。这种双谐振响应是一种典型的耦合谐振器,其中主谐振点是由独立的谐振结构引起的,另外的附带谐振点是由于两个谐振器和耦合缝隙共同作用的结果。为了实现窄带带通响应,应当设置合适的缝隙结构长度,使得两个谐振频点更近。
|
图 2 FSS频率响应随缝隙结构长度的变化 Figure 2 Variation of frequency response of FSS with slot length |
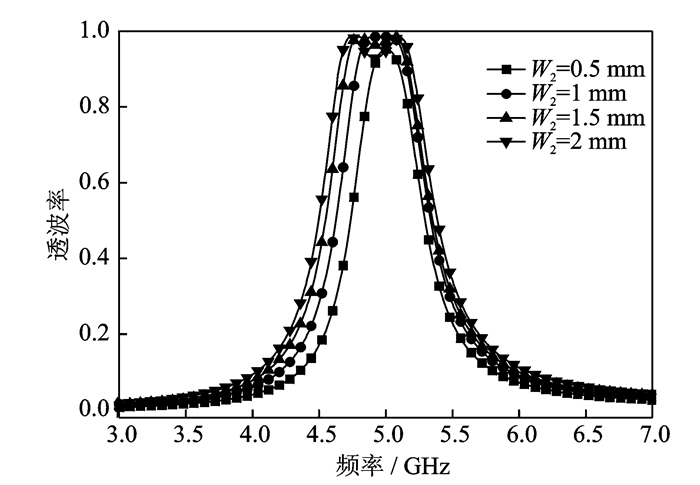
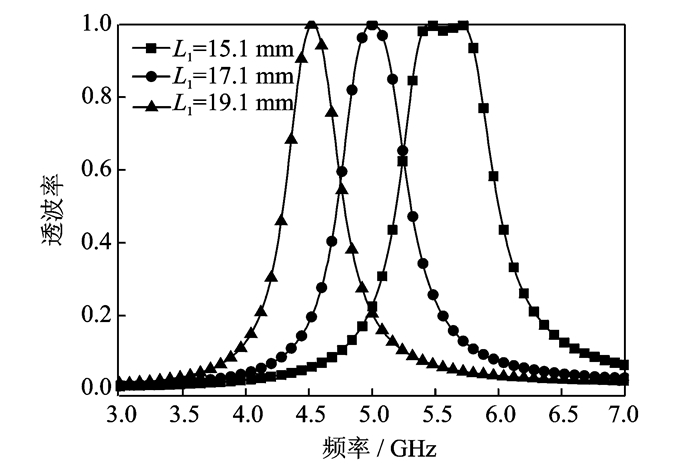
图 3显示了FSS的频率响应随缝隙结构宽度增加的变化。由于缝隙结构宽度增加,上表面贴片与下表面贴片之间的耦合强度增加,FSS的带通带宽也随之拓展,与此同时FSS谐振频率依然保持在5GHz左右。通过对缝隙结构长度和宽度的优化设计以及图 4对贴片单元(方形贴片L1=W1)大小优化仿真表明,在介质板材料和厚度一定时,FSS的谐振频率主要由金属贴片大小决定[14],谐振频点随缝隙结构的变化较小,其中缝隙长度主要影响FSS的透波率,而缝隙宽度主要影响FSS的带宽,同时可以根据不同的使用场景调整缝隙结构,使得FSS呈现不同的滤波效果,因此,缝隙结构的分析与设计相当重要。它的长度优化范围为金属贴片长度的1/4~1/2,它的宽度约为缝隙长度的1/10。单元结构的频响特性对缝隙相对于贴片中心位置并不敏感。当频率在谐振点附近时,金属贴片的表面电流在中心位置最大,所以FSS的频响关于位置的导数为零。
|
图 3 FSS频率响应随缝隙结构宽度的变化 Figure 3 Variation of frequency response of FSS with slot width |
|
图 4 FSS频率响应随贴片大小的变化 Figure 4 Variation of frequency response of FSS with patchsize |
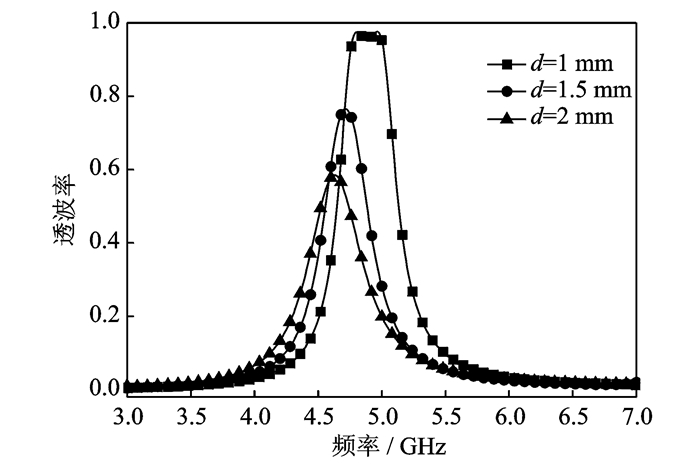
根据贴片天线的频率响应特性,增加介质板的厚度会降低天线的谐振频率,同时可以增加了天线的带宽。图 5为FSS的频率响应随介质材料厚度的变化曲线。由图 4可以看出,增加介质板的厚度同样可以降低缝隙之间的耦合强度。通过计算最终FSS的初始单元结构尺寸如表 1所示。
|
图 5 FSS频率响应随介质材料厚度的变化 Figure 5 Variation of frequency response of FSS with slab thickness |
| 表 1 FSS单元的结构尺寸(εr=2.33) Table 1 Parameters of FSSwith εr=2.33 |
3 双极化频率选择表面的建模与仿真
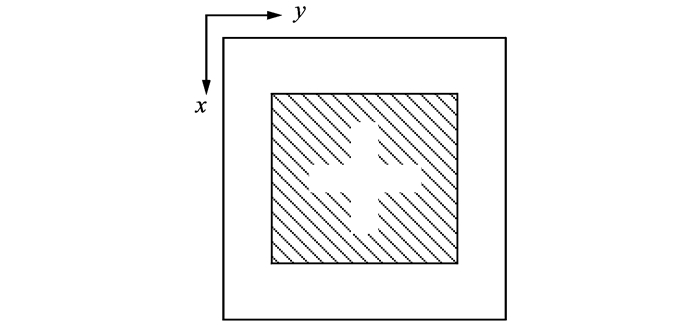
第2节分析了缝隙结构对FSS频率响应的影响。只有当电磁波的电场垂直于缝隙结构时,电场才能透过FSS,所以第2节所提到的单元结构只适用于单一极化,本节将会用一个十字缝隙代替矩形缝隙,具体结构如图 6所示,单元参数参考第2节。
|
图 6 双极化单元结构 Figure 6 Geometry of dual-polarized FSS |
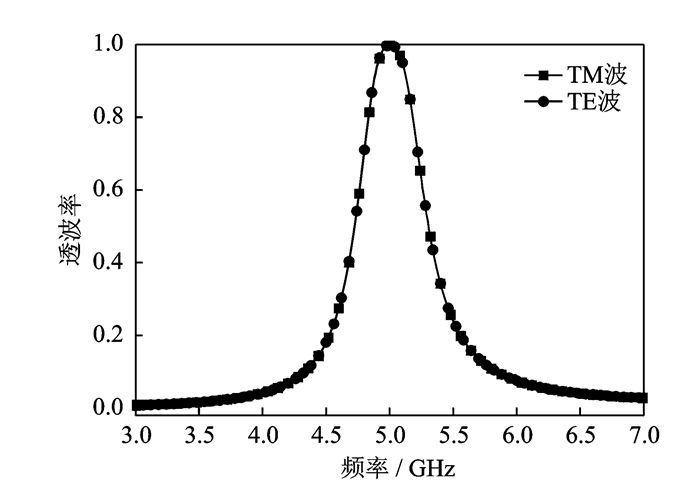
图 7为TE波和TM波极化下垂直入射时FSS的频率响应,从图中可以看出在两种极化下FSS的透波率曲线基本保持一致,所以该多层十字缝隙耦合FSS具有稳定的极化特性。
|
图 7 双极化单元结构频率响应 Figure 7 Frequency re sponse of a dual-polarized FSS |
为了验证多层耦合FSS对极化波入射角度的敏感程度,分别在TE波和TM波入射下进行了仿真(图 8),其中TE波电场保持不变,磁场随入射角度发生变化,而TM波则是磁场保持不变,电场随入射场发生变化。从图 8仿真结果可以看出,入射角变化范围为0°~45°,TE波和TM波谐振频点和通带没有明显变化,但是随着角度增大通带带宽略有减小。这是由于在大角度入射下缝隙结构的等效宽度变小造成的。仿真结果表明,多层缝隙耦合FSS在入射角0°~45°范围内具有角度稳定性。

|
图 8 FSS频率响应随入射角的变化 Figure 8 Frequency response of dual-polarized FSS for different a ngle incident waves TM and TE |
4 结论
本文利用谱域矩量法分析了双层缝隙耦合金属贴片型FSS,通过在两层金属贴片之间增加一层耦合缝隙结构,使得带阻型FSS呈现出带通特性,同时详细分析了缝隙和介质材料对其频率响应特性的影响,经过对频率响应特性曲线的研究,得出以下结论。
(1) 缝隙结构的长度影响FSS的主谐振频率下的透波率,长度越长透波率越大,当达到一定长度后,主谐振点透波率不再变化,在缝隙耦合的作用下呈现双频特性。缝隙结构的宽度对FSS的通带宽度影响不大,同时增强耦合作用,双频特性增强。随着介质板的厚度增加,降低了缝隙结构的耦合作用,双频特性减弱。
(2) 根据耦合缝隙结构的特性,设计出了一款具有极化稳定性和角度稳定性的多层十字缝隙耦合FSS,在实际工程中可根据应用环境和应用要求设计FSS单元,通过对结构参数的调整使得该结构能够应用于不同场合,具有一定的应用前景。下一步的工作中,将通过实物测试验证仿真结果的正确性,同时讨论不同缝隙结构对FSS的频响特性的影响。
| [1] | Mittra R, Chan C H, Cwik T. Techniques for analyzing frequency selective surfaces-A review[J]. Proceedings of the IEEE, 1988, 76(12): 1593–1615. DOI:10.1109/5.16352 |
| [2] | Chen C C. Transmission through a conducting screen perforated periodically with apertures[J]. IEEE Transactions on Microwave Theory & Techniques, 1970, 18(9): 627–632. |
| [3] | Chen C C. Scattering by a two-dimensional periodic array of conducting plates[J]. IEEE Transactions on Antennas & Propagation, 1970, 18(5): 660–665. |
| [4] | Parker E A, Hamdy S M A. Rings as elements for frequency selective surfaces[J]. Electronics Letters, 1981, 17(17): 612–614. DOI:10.1049/el:19810430 |
| [5] | 周传凯, 高正平. 等效电路法在多层频率选择表面中的应用[J]. 材料导报:纳米与新材料专辑, 2014(1): 155–157. |
| [6] | Ghosh S, Srivastava K V. An equivalent circuitmodel of FSS-based metamaterial absorber using coupled line theory[J]. IEEE Antennas & Wireless Propagation Letters, 2015, 14: 511–514. |
| [7] | Pozar D M. Microstrip antenna aperture-coupled to a microstripline[J]. Electronics Letters, 1985, 21(2): 49–50. DOI:10.1049/el:19850034 |
| [8] | Pozar D M. Analysis of an infinite phased array of aperture coupled microstrip patches[J]. IEEE Transactions on Antennas & Propagation, 1989, 37(4): 418–425. |
| [9] | Pozar D M, Schaubert D H. Analysis of an infinite array of rectangular microstrip patches with idealized probe feeds[J]. IEEE Transactions on Antennas & Propagation, 1984, 32(10): 1101–1107. |
| [10] | Aberle J T, Pozar D M. Analysis of infinite arrays of probe-fed rectangular microstrip patches using a rigorous feed model[J]. IEE Proceedings H, 1989, 136(2): 110–119. |
| [11] | 蒙志君, 吕明云, 祝明, 等. 带通FSS结构的插入相位延迟特性[J]. 南京航空航天大学学报, 2010, 42(5): 665–669. |
| [12] | Wang Q, Shao Z H, Cheng Y J, et al. Broadband low-cost reflectarray using modified double-square loop loaded by spiral stubs[J]. IEEE Transactions on Antennas & Propagation, 2015, 63(9): 4224–4229. |
| [13] | 高强, 闫敦豹, 袁乃昌, 等. 双频双极化频率选择表面[J]. 电子与信息学报, 2007, 29(2): 506–508. |
| [14] | Munk B. Frequency selective surfaces : Theory and design[M].[S.l.]:John Wiley, 2000. |
 2016, Vol. 48
2016, Vol. 48


