2. 南京航空航天大学雷达成像与微波光子技术教育部重点实验室,南京,210016
2. Radar Imaging and Microwave Photonic Technology Key Laboratory of Ministry of Education, Nanjing University of Aeronautics & Astronautics, Nanjing, 210016, China
合成孔径雷达[1-2](Synthetic aperture radar, SAR)常用的成像模式有聚束式、条带式和扫描式。极坐标格式算法(Polar format algorithm, PFA)是一种经典的聚束SAR模式成像算法[3]。该算法采用极坐标格式存储数据,有效地解决了远离成像区中心散射点的越分辨单元走动问题,极大地提高了聚束SAR的有效聚焦成像范围[4]。与其他成像算法相比,它具有高效简洁,能自动校正所有目标(包括运动目标)的线性距离走动等诸多优点。但是,经典的PFA算法却不能用于对普通的条带SAR数据进行处理。
通常情况下,条带SAR工作于正侧视模式。但许多应用场合需将波束向前或向后斜视来观察雷达平台前方或后方的场景。斜视模式是重要的条带SAR成像模式之一,在军事方面的应用尤为重要[5-6]。然而,大的斜视角会导致大的距离徙动,必须进行精确距离徙动校正;同时,条带SAR在军事方面的应用又对成像位置的精确性及成像的实时性提出了严格要求。
寻求合适的大斜视条带SAR成像方法已成为当前雷达成像的研究热点:文献[7]提出了基于聚束照射SAR成像算法的条带SAR数据处理方法,但成像仍然存在解决方位耦合困难的问题;文献[8~10]提出了针对条带SAR成像的图像拼接方法,但拼接图像分辨率低,无法达到当前SAR系统对于图像质量的要求;美国Lynx SAR系统对基于子块拼接成像的处理方法进行了验证,但对拼接成像方法如何具体实现,文献中无具体描述 [11]。
本文对大斜视条件下条带SAR提出适用的基于PFA的子孔径拼接成像算法。子孔径PFA成像算法的应用自动校正了大斜视角导致的大的距离徙动,解决了距离方位耦合严重的问题;数据分孔径处理保证了成像的聚焦精度与处理效率。
1 条带SAR子孔径拼接成像处理算法 1.1 成像处理流程条带SAR子孔径拼接算法以聚束经典算法PFA为基础,采用模块式数据处理的方法,对全孔径大数据进行有效成像,其信号处理的流程图见图 1。

|
图 1 条带SAR拼接成像处理流程图 Figure 1 Flow chart of image processing with stripmap SAR mosaic |
大孔径的回波数据经过孔径划分得到子孔径数据,然后由数据转换原理进行条带模式-聚束模式的数据转换,再对转换数据进行PFA成像和几何失真校正处理,最后通过子孔径图像的拼接得到完整的条带SAR图像。
1.2 条带模式-聚束模式数据转换原理条带SAR模式中,天线发射波束与雷达航迹始终保持固定的夹角,波束滑动速度与雷达平台速度一致,照射范围在地面上匀速扫射,形成条形区域。记录数据因天线波束照射区域的变化而分属于不同的子孔径。聚束SAR模式通过对天线指向的控制,使其波束在整个数据记录时间始终照射地面上一小块区域,该区域内的各散射点具有相同的合成孔径[4]。
数据转换几何原理图见图 2,设机载SAR工作于大斜视模式。定义斜视角为θs,合成孔径长度为La,等效聚束照射合成孔径长度为Ls,方位向的波束宽度为β。当L a>Ls时,波束在子孔径CC′处照射时会有宽度为Wa的重叠区域,此部分区域始终处于波束照射之下,可等效为聚束数据。

|
图 2 大斜视条带SAR成像数据转换几何原理图 Figure 2 Data transformation geometry of highly squinted stripmap SAR image |
若将全孔径分成N个子孔径,则当总的回波个数为M时,则需分别对回波个数为MN的子孔径进行成像处理。
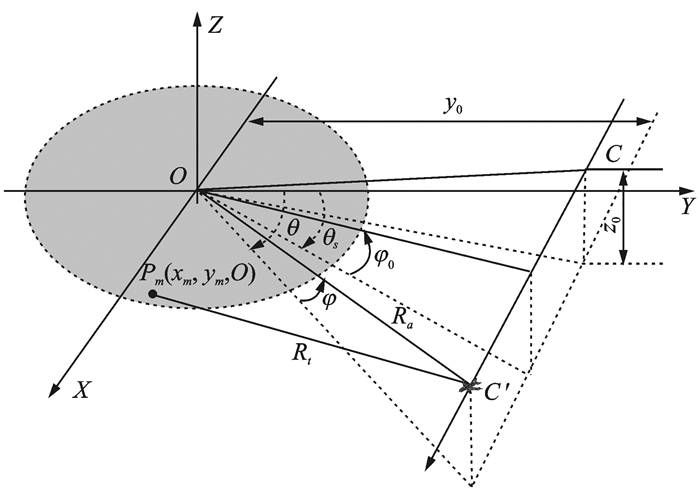
1.3 子孔径PFA成像处理大斜视机载SAR子孔径数据采集几何模型如图 3所示,以场景中心O为坐标原点对子孔径CC′建立如图 3所示坐标系XYZ,雷达航迹相对于正侧视呈现θs的大斜视角,Ra为雷达天线相位中心到场景中心的距离,Rt为雷达天线相位中心到点目标Pm(xm, ym, 0)的距离,雷达瞬时方位角和俯仰角分别为θ和φ(孔径中心时刻为θs和φ0)。
|
图 3 大斜视机载SAR子孔径数据采集几何模型 Figure 3 Subaperture data acquisition geometric model of highly squinted airborne SAR |
设雷达发射宽带线性调频信号(Linear frequency modulation, LFM)
| $s\left( \tau \right) = \exp \left( {{\rm{j2}}\pi {f_0}\tau } \right) \cdot \exp \left( {{\rm{j}}\pi k{\tau ^2}} \right)$ | (1) |
式中:τ为距离向快时间变量;f0为发射信号载频;k为信号线性调频斜率。回波经过距离向脉冲压缩和运动补偿后可表示为
| $s\left( {{f_\tau }, t} \right) = \exp \left[{{\rm{j}}\frac{{4\pi }}{c}\left( {{f_0} + {f_\tau }} \right){R_\Delta }} \right]$ | (2) |
式中:c为电磁波传播速度;fτ为距离频率;RΔ为雷达天线相位中心到场景中心和到目标的差分距离
| ${R_\Delta } = {R_a}-{R_t}$ | (3) |
PFA采用了平面波前假设,在此近似条件下,差分距离Ra-Rt可以表示为
| ${R_\Delta } = {R_a}-{R_t} \approx {x_m}\cos \varphi \sin \theta + {y_m}\cos \varphi \cos \theta $ | (4) |
将式(4)代入式(2)中,可得到回波信号
| $\begin{array}{c} s\left( {{f_\tau }, t} \right) = \exp \left[{{\rm{j}}\frac{{4\pi }}{c}\left( {{f_0} + {f_\tau }} \right)\cos \varphi \left( {{x_m}\sin \theta + } \right.} \right.\\ \left. {\left. {{y_m}\cos \theta } \right)} \right] \end{array}$ | (5) |
或用空间波数表示
| ${s_B}\left( {{k_s}, {k_y}} \right) = \exp \left[{{\rm{j}}\left( {{x_m}{k_x} + {y_m}{k_y}} \right)} \right]$ | (6) |
式中
由式(6)知,雷达回波信号与目标函数间存在简单Fourier变换关系,回波数据经过运动补偿和匹配滤波后再做两维Fourier变换即可成像。PFA通过方位向和距离向两维插值将极坐标格式数据转换为矩形格式,再对重采样后的二维数据作两维FFT变换实现对目标的成像。
1.4 几何失真校正 1.4.1 波前弯曲误差分析实际雷达波前是球面波前,成像处理时,将雷达波前近似为平面,即等相位面由实际的球面假设为平面。但随着分辨率要求的提高、成像场景的增大,或者在近距离成像时,平面波前假设引入的误差变得不可忽略,必须对其进行补偿。
| $\begin{array}{c} {R_\Delta } = \frac{{{r_t} \cdot {R_a}}}{{{R_a}}}-\frac{{r_t^2}}{{2{R_a}}} + \frac{{{{\left( {{r_t} \cdot {R_a}} \right)}^2}}}{{2R_a^3}} + \\ \frac{{\left( {{r_t} \cdot {R_a}} \right)r_t^2}}{{2R_a^3}} + \cdots \end{array}$ | (7) |
则波前弯曲引入的距离误差可表示为
| $\begin{array}{c} {R_e} = {R_\Delta }-\frac{{{r_t} \cdot {R_a}}}{{{R_a}}} =-\frac{{r_t^2}}{{2{R_a}}} + \frac{{{{\left( {{r_t} \cdot {R_a}} \right)}^2}}}{{2R_a^2}} + \\ \frac{{\left( {{r_t} \cdot {R_a}} \right)r_t^2}}{{2R_a^2}} + \cdots \end{array}$ | (8) |
在分辨率要求不高的情况下,可对式(8)所示的距离误差采用保留前两项而忽略高次项的近似,但在近场对大场景范围进行高分辨率成像时,该近似不能满足要求。文献[13]对回波数据(式(2))直接进行了二维泰勒级数展开
| $\begin{array}{c} S\left( {{K_x}, {K_y}} \right) = \exp \left[{{\rm{j}}{K_r}\left( {{R_a}-{R_t}} \right)} \right] = \exp \left\{ {{\rm{j}}\left[{{a_{01}}{K_x} + } \right.} \right.\\ {a_{10}}\left( {{K_y}-{K_c}} \right) + {a_{11}}{K_x}\left( {{K_y}-{K_c}} \right) + \\ \left. {\left. {{a_{20}}K_x^2 + {a_{02}}{{\left( {{K_y}-{K_c}} \right)}^2} + \cdots } \right]} \right\} \end{array}$ | (9) |
再通过对回波相位Kr(Ra-Rt)中各项表示为关于Kx和Ky的显示函数,利用泰勒展开得到一次系数
| $\begin{array}{c} {a_{01}} = {x_m}{r_{c0}} + \left( {{y_0}-{r_{c0}}\left( {{y_0}-{y_m}} \right)/{r_{ct}} + } \right.\\ \left( {{r_{c0}}-{r_{ct}}} \right)\left( {os{\varphi _0} - 1/\cos {\varphi _0}} \right)\tan {\theta _s} \end{array}$ | (10) |
此一次系数a10和a01分别对应点目标在图像中的距离坐标和方位坐标。而目标成像坐标(a10, a01)与真实坐标(xm, ym)在非(0, 0)点处均不相等。由此可知,在平面波前假设条件下,除场景中心点外,其余点目标经PFA成像后均存在一定的几何位置失真[13]。
1.4.2 几何失真校正处理由于平面波前假设,目标的真实位置(xm, ym)在图像中变成了(a01, a10)。几何失真校正通过几何失真映射,由目标真实位置(xm, ym)得到其在PFA图像中的失真像素位置(a01, a10),再通过插值的方法找出该位置所对应的“像”,实现几何失真的校正操作,其流程图如图 4所示。

|
图 4 几何失真校正流程图 Figure 4 Flow chart of geometric distortion correction |
几何失真校正的本质为图像域的重采样。首先,选择校正区为感兴趣的波束扫描区域,然后,将校正区划分为校正点网格,建立XY坐标系,使校正点均匀地分布在所建立的地面XY坐标系内。斜视情况下,为得到校正后沿视线方向的正视图像,需要先对XY坐标系内的校正点(xM, yM)逐个进行如式(11)所示的坐标旋转
| $\left[\begin{array}{l} {x_m}\\ {y_m} \end{array} \right] = \left[{\begin{array}{*{20}{c}} {\cos {\theta _s}}&{-\sin {\theta _s}}\\ {\sin {\theta _s}}&{\cos {\theta _s}} \end{array}} \right]\left[\begin{array}{l} {x_M}\\ {y_M} \end{array} \right]$ | (11) |
通过旋转得到(xm, ym),再对(xm, ym)通过式(10)转换为PFA图像坐标(a01, a10),由该坐标在PFA图像中通过插值找到其“像”,将其放回校正点[14],即完成了单点坐标的几何失真校正。对校正区内所有校正点逐个进行如上校正,就能实现对校正区PFA图像的几何失真校正。
1.5 图像拼接本文的大斜视条带SAR模型中,几何失真校正的校正区选择子孔径波束始终能照射到的区域,此区域数据可等效为聚束数据。当条带SAR全孔径回波脉冲数为M时,根据图 2的数据转换几何原理有
| ${L_s} = M \times \left( {{v_a}/{\rm{PRF}}} \right)$ | (12) |
式中:va为机载SAR平台飞行速度; PRF为雷达脉冲重复频率。再由
| ${W_a} = {L_a}-{L_s}$ | (13) |
可得重叠区域的方位长度。若取XY坐标系内相邻点的横向方位间隔为ρx,纵向距离间隔为ρy,则可根据式(14)计算得到方位向重叠区域需要校正的点数
| ${M_s} = \frac{{{W_a}}}{{{\rho _x}}}$ | (14) |
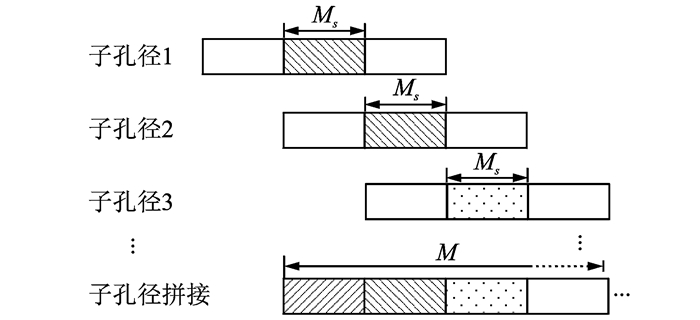
子块图像的数据拼接示意图如图 5所示,取条带SAR方位向总点数为M,分子孔径进行PFA成像处理,由式(12~14)知相邻子孔径重叠点数为Ms。
|
图 5 条带SAR拼接数据示意图 Figure 5 Sketch map of stripmap SAR mosaic data |
对子孔径中能够等效为聚束照射的数据进行PFA成像处理,并取相邻子孔径中波束重叠区域数据进行几何失真校正,得到校正后子孔径图像,将子孔径图像按照图 5所示原理进行首尾拼接即可得到全孔径条带SAR图像[14]。实际处理时,图像拼接还存在天线方向性图的调制问题,很多情况需进行天线方向性图调制校正,否则将存在拼接图像幅度上的不连续。
2 点目标仿真及实测数据验证分析 2.1 点目标仿真分析本文取X波段SAR仿真回波数据进行仿真验证,雷达平台速度150 m/s,工作高度3 000 m,斜视角60°,信号带宽120 MH z。设置地面仿真点目标分布如图 6所示,黑色实心圆点代表点目标位置,总的仿真点个数为57(3×19),相邻点目标距离向距离为100 m,方位向距离也为100 m。

|
图 6 地面点目标位置分布 Figure 6 Location distribution of ground point target |
成像处理时将全孔径数据分成6个子孔径,子孔径数据经过PFA处理后的图像如图 7所示。可以看到,成像场景存在60°的斜视角旋转,且各个子孔径中的点目标均存在不同程度的几何位置失真。

|
图 7 子孔径PFA成像结果 Figure 7 Imaging results of subaperture PFA |
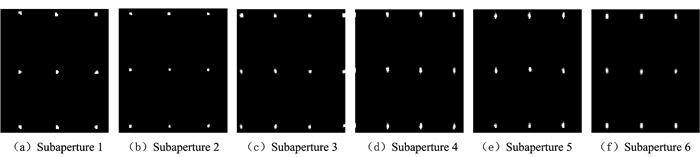
对各个子孔径图像进行几何失真校正处理,得到几何失真校正处理后的子孔径仿真结果如图 8所示。
|
图 8 子孔径图像几何失真校正后结果 Figure 8 Results of subaperture image after geometric distortion correction |
对比图 7, 8可知:用PFA算法对等效聚束子孔径进行成像,结果图中点目标位置均存在一定程度的几何位置失真(子孔径中心点目标除外)。斜视情况下,除了点目标位置的几何失真外,还存在斜视角旋转,导致原始子孔径图像无法直接进行首尾拼接。几何失真校正处理使子孔径场景的斜视角旋转得以恢复,且每个点目标的坐标均得到校正。最后,对几何失真校正后的子孔径图像进行拼接得到如图 9所示的拼接图像。图 9所示拼接图像没有出现折叠、错位等现象,相邻子块目标场景连续变化。

|
图 9 点目标拼接结果图 Figure 9 Image of point target mosaic |
为验证本文算法精度,选取图 6中5个点目标(A, B, C, D, E)进行定量分析。表 1对所选点目标的真实位置与成像位置进行了对比,从中可以看到,通过本文算法成像得到的点目标成像位置接近其真实位置,误差在允许的范围内。
| 表 1 点目标真实位置与成像位置对比 Table 1 Comparison of real position and imaging position of point targets |
2.2 实测数据验证分析
对某型X波段条带SAR的外场试飞实测数据进行了处理验证,该雷达系统主要参数如表 2所示。
| 表 2 SAR主要参数 Table 2 SAR main parameters |
成像处理时,将全孔径原始数据分成10个子孔径,每个子孔径回波脉冲数为8 192个。图 10为实测数据子孔径几何失真校正前后对比图。上行为几何失真校正前子孔径图像,由于场景存在斜视角旋转和目标几何位置失真而不能直接进行拼接;下行为几何失真校正后子孔径图像,各子孔径图像经过几何失真校正后,有效场景连续可拼接。

|
图 10 实测数据子孔径几何失真校正前后对比图 Figure 10 Comparison of measured data before and after subaperture geometric distortion correction |
经子孔径拼接处理后的整幅条带SAR实测数据图像如图 11所示,拼接图像内多处强散射点、植被等目标聚焦良好,相对位置准确。公路拼接完好,没有出现曲折、断层等现象。有效场景均位于条带图像中,图幅大小无损失,保持了原图分辨率,说明了本文方法对于实测场景成像的有效性。

|
图 11 实测数据条带拼接图 Figure 11 Subaperture mosaic image of measured data |
3 结束语
本文提出了一种基于PFA的大斜视条带SAR子孔径拼接成像算法,该算法将改进的经典聚束SAR模式成像算法PFA应用于条带SAR成像模式中,并通过分子孔径处理的方法对全孔径图像进行分步成像及几何失真校正。点目标及实测数据的处理结果表明,该算法适用于大斜视模式,解决了大斜视角导致的距离方位耦合严重及大幅尺寸场景精确实时成像困难等问题,在高分辨率大斜视条带SAR成像处理中具有一定的应用前景。
| [1] | Cumming I G, Wong F H. Digital processing of synthetic aperture radar data algorithms and implementation[M]. Beijing: Publishing House of Electronics Industry, 2012. |
| [2] |
柴建忠, 高旭, 刘学强, 等.
几种载体表面缝隙对雷达目标特性的影响[J]. 南京航空航天大学学报, 2014, 46(4): 567–572.
Chai Jianzhong, Gao Xu, Liu Xueqiang, et al. Effect of gaps in different surfaces on radar target characteristic[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2014, 46(4): 567–572. |
| [3] |
田宵骏, 梁媚蓉, 毛新华.
超高分辨率机载SAR成像算法及其GPU实现[J]. 南京航空航天大学学报, 2015, 47(3): 384–391.
Tian Xiaojun, Liang Meirong, Mao Xinhua. Imaging algorithm and its implementation on GPU for ultra-high resolution airborne SAR[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2015, 47(3): 384–391. |
| [4] |
毛新华. PFA在SAR超高分辨率成像和SAR/GMTI中的应用研究[D].南京:南京航空航天大学, 2009.
Mao Xinhua. Study on the application of PFA in SAR ultra-high resolution imaging and SAR/GMTI [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.http://cdmd.cnki.com.cn/Article/CDMD-10287-2010080027.htm |
| [5] | Wang Shuyan, Su Zhigang, Wu Renbiao. Modified range-Doppler imaging method for the high squint SAR [C]// Proc of the IEEE Radar Conference. Seowl: IEEE, 2010:1450-1453. |
| [6] | Xiao Jing, Hu Xuecheng. A modified RD algorithm for airborne high squint mode SAR imaging [C]// Proc of the 1st Asian and Pacific Conference on Synthetic Aperture Radar. Seoul: IEEE, 2007: 444-448. |
| [7] |
武昕伟, 朱兆达.
基于聚束照射SAR成像算法的条带SAR数据处理[J]. 南京航空航天大学学报, 2002, 34(5): 466–469.
Wu Xinwei, Zhu Zhaoda. Stripmap SAR data processing based on spotlight SAR image formation algorithm[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2002, 34(5): 466–469. |
| [8] | Shimada M, Wakabayashi H, Tadono T, et al. JERS-1 SAR mosaics over the Southeast Asia[J]. Proceedings of IEEE IGARSS 2000. [S.l.]:IEEE, 2000:1-3. |
| [9] | Wei Jie, Zhou Yinqing, Li Chunsheng. The look weighing and mosaic of subimages of spaceborne scan SAR[C]//Proceedings of ICCEA 2004. Beijing: The Chinese Institute of Electronics, 2004:384-387. |
| [10] |
仇志华.基于子孔径处理的SAR高分辨率成像算法研究[D].南京:南京航空航天大学, 2009.
Qiu Zhihua. Study on high-resolution SAR imaging algorithms based on subaperture processing[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009.http://cdmd.cnki.com.cn/Article/CDMD-10287-1011252459.htm |
| [11] | Carrara W G, Goodman R S, Majewski R M. Spotlight synthetic aperture radar:Signal processing algorithms[M]. Boston: Artech House, 1995. |
| [12] | Doerry A W. Wavefront curvature limitations and compensation to polar format processing for synthetic aperture radar images[R]. SAND2007-0046, 2007. |
| [13] |
毛新华, 朱岱寅, 叶少华, 等.
一种基于图像后处理的极坐标格式算法波前弯曲补偿方法[J]. 电子学报, 2010, 38(1): 244–250.
Mao Xinhua, Zhu Daiyin, Ye Shaohua, et al. Image domain space-variant post-processing for wavefront curvature correction in polar format spotlight SAR image[J]. Acta Electronica Sinica, 2010, 38(1): 244–250. |
| [14] | Li Yong, Zhu Daiyin, Zhu Zhaoda, et al. Automatic mosaicing for airborne SAR imaging based on subaperture processing[C]//Proceedings of IEEE IGARSS2005. Seoul: IEEE, 2005:4644-4647. |
 2016, Vol. 48
2016, Vol. 48


