全双工系统可以实现同时同频接收和发送信号，能够大幅度地提升无线通信容量和频谱利用率，因而受到广大学者的关注^[1]。但全双工系统中继的接收端和发送端在传送信号的过程中会产生泄漏，即自干扰，会严重影响系统性能^[2-3]。所以自干扰消除是全双工系统需要解决的主要问题。文献[4]对现有的自扰消除方法做了总结, 包括天线隔离、时域消除和空域抑制等。但是天线隔离只能部分消除自干扰^[2]，时域消除算法复杂度高而且仪器成本高，所以本文主要讨论空域抑制的相关算法。文献[5~7]给出了一些经典的空域自干扰消除方法，如：迫零(Zero forcing, ZF)、最小均方误差(Minimum mean square error，MMSE)和零空间投影(Null-space projection，NSP)。文献[8]提出了梯度投影算法以最大化全双工MIMO中继系统的和速率下界。文献[9]研究了基于译码转发(Decode-and-forward, DF)协议的全双工中继系统误码率，利用特征函数分析性能并给出不同信道衰落下的系统误码率表达式。文献[10]提出了基于放大转发(Amplify-and-forward，AF)的全双工双向中继系统。但以上系统为均采用单用户对模型，如果将系统扩展为多用户对模型，那么多用户对间提供的分集增益会进一步提高系统性能。不过在多用户对系统中，用户对之间存在的干扰也会影响系统性能。文献[11]研究了基于AF的全双工多用户单向中继系统。文献[12]给出了一种基于AF的半双工多用户对双向中继系统的波束成形算法--奇异值分解(Singular value decomposition, SVD)。为了进一步提升频谱利用率，构造了全双工多用户对双向中继模型，并将其应用DF系统。结果表明，文中构造的全双工多用户对双向中继系统在抑制自干扰信号的同时也能够消除用户对之间的干扰，提高了系统性能。并且中继端配置的天线数越多，系统的性能也越好。

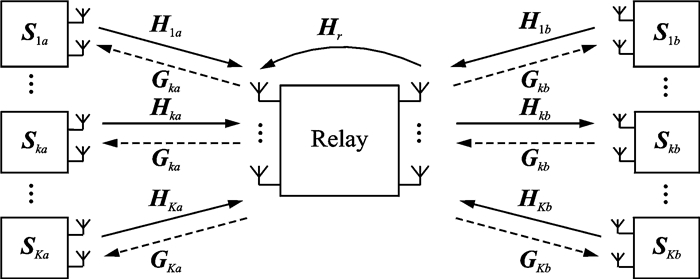
1 系统模型

本文研究的是全双工多用户对双向中继系统, 其模型如图 1所示。由于路径损耗以及阴影衰落，假设不同的用户之间没有直达通道，而是通过中继进行信息交换。中继节点R在接收来自用户当前时隙的信号的同时也向用户节点发送上一时隙的信号。

系统配置为：中继配有N副天线，K个用户对，每个用户配有M根天线。H_ki和G_ki，i∈{a, b}分别表示上行信道和下行信道的信道增益矩阵，H_r为中继自干扰信道增益矩阵。设用户ki发送信号为x_ki，且满足tr{x_kix_ki^H}=P_S，经过上行信道传输以及中继接收信号波束成形，中继接收信号为

${\mathit{\boldsymbol{y}}_r}\left[n \right] = \sum\limits_{k = 1}^K {\sum\limits_{i \in \left\{ {a, b} \right\}} {{\mathit{\boldsymbol{W}}_R}{\mathit{\boldsymbol{H}}_{ki}}{\mathit{\boldsymbol{x}}_{ki}}\left[n \right]} } + {\mathit{\boldsymbol{W}}_R}\left( {{\mathit{\boldsymbol{H}}_r}{\mathit{\boldsymbol{x}}_r} + {z_r}\left[n \right]} \right)$

(1)

式中：W_R表示中继端接收波束成形矩阵; z_r表示中继接收端的加性循环对称复高斯白噪声，满足tr{z_rz_r^H}=σ_r²；x_r为经过中继协议发送波束成形的中继端发送信号，具体表示为x_r=βW_Tx[n-τ]。其中W_T为中继端发送波束成形矩阵；β为功率约束因子；P_RS为中继端发射功率，则β表示为

$\beta = \sqrt {\frac{{{P_{RS}}}}{{{\rm{tr}}\left( {{\mathit{\boldsymbol{W}}_T}\mathit{\boldsymbol{W}}_T^{\rm{H}}} \right)}}} $

(2)

经过中继发送端波束成形以及下行信道传输，用户接收信号表示为

${\mathit{\boldsymbol{y}}_{ki}}\left[n \right] = \mathit{\boldsymbol{G}}_{k\left( { - i} \right)}^{\rm{T}}{\mathit{\boldsymbol{x}}_r} + \sum\limits_{j = 1}^K {{\mathit{\boldsymbol{H}}_j}{\mathit{\boldsymbol{x}}_{ki}}\left[n \right] + z\left[n \right]} $

(3)

式中：H_j为所有ki用户对k(-i)用户的干扰；z为服从零均值高斯分布的用户接收噪声，且tr{zz^H}=σ²。在本文研究的多用户对全双工双向中继系统中，波束成形算法不仅包括对中继的自干扰抑制，也包括用户对内以及用户对间干扰消除。所以，W_R和W_T可以分解为

${\boldsymbol{W}_R} = {\boldsymbol{W}_{sr}}{\boldsymbol{W}_r}\;\;{\boldsymbol{W}_T} = {\boldsymbol{W}_t}{\boldsymbol{W}_{rd}}$

(4)

式中：W_r和W_t分别表示中继接收端和发送端的自干扰消除矩阵，W_sr和W_rd分别表示中继接收端和发送端波束成形矩阵。根据式(1~4)，得到上行链路中继接收的和速率为

${R_{{u_{ki}}}} = {\log _2}{\rm{det}}\left( {{\boldsymbol{I}_{{N_r}}} + {P_{MS}}{\boldsymbol{W}_R}{\boldsymbol{H}_{ki}}{{\left( {{\boldsymbol{W}_R}{\boldsymbol{H}_{ki}}} \right)}^{\rm{H}}}\boldsymbol{R}_W^{-1}} \right)$

(5)

式中：R_W=β²(W_R H_rW_T)·(W_RH_rW_T)^H+σ_r²W_R·(W_R)^H+E_ki, 而${E_{ki}} = \sum\limits_{m = 1, m \ne k}^K {\sum\limits_{n \in \left\{ {a, b} \right\}} {{P_{MS}}{\boldsymbol{W}_{MS}}{\boldsymbol{H}_{mn}} \cdot {{\left( {{\boldsymbol{W}_R}{\boldsymbol{H}_{mn}}} \right)}^{\rm{H}}}} } $。同理，可得下行链路用户接收的和速率表示为

$\begin{array}{c} {R_{{d_{ki}}}} = {\log _2}{\rm{det}}\left( {{\mathit{\boldsymbol{I}}_M} + } \right.\\ \left. {{\beta ^2}{P_{RS}}\mathit{\boldsymbol{G}}_{k\left( {-i} \right)}^{\rm{H}}{\mathit{\boldsymbol{W}}_T}{{\left( {\mathit{\boldsymbol{G}}_{k\left( {-i} \right)}^{\rm{H}}{\mathit{\boldsymbol{W}}_T}} \right)}^{\rm{H}}}\mathit{\boldsymbol{R}}_T^{-1}} \right) \end{array}$

(6)

式中：${\boldsymbol{R}_T} = \sigma _{MS}^2{\boldsymbol{I}_M}$$+ \sum\limits_{m = 1, m \ne k}^K {\sum\limits_{n \in \left\{ {a, b} \right\}} {{\beta ^2}{P_{RS}}{\boldsymbol{G}_{mn}}{\boldsymbol{W}_T}} } $${\left( {{\boldsymbol{G}_{mn}} \cdot {\boldsymbol{W}_T}} \right)^{\rm{H}}} + {\boldsymbol{H}_j}\boldsymbol{H}_j^{\rm{H}}$。由此得出依照DF准则的全双工多用户对双向中继系统的和速率为^[13]

$R = \min \left( {{R_u}, {R_d}} \right)$

(7)

式中：${R_u} = \sum\limits_{k = 1}^K {\sum\limits_{i \in \left\{ {a, b} \right\}} {{R_{{u_{ki}}}}} } $表示上行链路和速率；${R_d} = \sum\limits_{k = 1}^K {\sum\limits_{i \in \left\{ {a, b} \right\}} {{R_{{d_{ki}}}}} } $表示下行链路和速率。

2 波束成形算法

本节讨论全双工多用户对双向中继系统的波束成形算法。首先，需要消除中继端的自干扰，本文采用NSP算法^[6]。依照NSP算法，自干扰消除需满足条件

${\boldsymbol{W}_r}{\boldsymbol{H}_r}{\boldsymbol{W}_t} = 0$

(8)

通过对H_r的SVD分解，H_r=UΣV^H=[U₁  U₂]Σ[V₁  V₂]^H，分别得到了系统的中继接收自干扰消除矩阵和发送自干扰消除矩阵W_r=U₁^H, W_t=V₂。在消除了中继自干扰之后，还需对用户对间的干扰进行处理，所以重新构造了上行和下行信道矩阵

${\mathit{\boldsymbol{W}}_r}\mathit{\boldsymbol{H = \hat H}}\;\;{\mathit{\boldsymbol{G}}^{\rm{T}}}{\mathit{\boldsymbol{W}}_t} = \mathit{\boldsymbol{\hat G}}$

(9)

ZF算法^[14]与SVD算法^[12]均可依据式(9)构造, 在此不作赘述。

由于ZF算法会受到信道相关性的影响，为了提升系统和速率采取块对角化波束成形算法^[14]。首先定义矩阵

$\begin{array}{l} {{\mathit{\boldsymbol{\hat H}}}_{k\left( {- i} \right)}} = \left[{{{\mathit{\boldsymbol{\hat H}}}_{1a}}{{\mathit{\boldsymbol{\hat H}}}_{1b}} \cdots {{\mathit{\boldsymbol{\hat H}}}_{\left( {k-1} \right)b}}{{\mathit{\boldsymbol{\hat H}}}_{ki}}{{\mathit{\boldsymbol{\hat H}}}_{\left( {k + 1} \right)a}} \cdots {{\mathit{\boldsymbol{\hat H}}}_{Kb}}} \right]\\ {{\mathit{\boldsymbol{\hat G}}}_{k\left( { - i} \right)}} = {\left[{\mathit{\boldsymbol{\hat G}}_{1a}^{\rm{T}}\mathit{\boldsymbol{\hat G}}_{1b}^{\rm{T}} \cdots \mathit{\boldsymbol{\hat G}}_{\left( {k-1} \right)b}^{\rm{T}}\mathit{\boldsymbol{\hat G}}_{ki}^{\rm{T}}\mathit{\boldsymbol{\hat G}}_{\left( {k + 1} \right)a}^{\rm{T}} \cdots \mathit{\boldsymbol{\hat G}}_{Kb}^{\rm{T}}} \right]^{\rm{T}}} \end{array} $

(10)

BD算法采用将中继波束成形矩阵映射在的零空间上的方法来消除用户对间的干扰。对上述定义矩阵进行SVD分解

$\begin{array}{l} {{\mathit{\boldsymbol{\hat H}}}_{k- }} = \left[{\mathit{\boldsymbol{U}}_{{\mathit{\boldsymbol{H}}_{k-}}}^{\left( 1 \right)}U_{{\mathit{\boldsymbol{H}}_{k-}}}^{\left( 0 \right)}} \right]{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{\mathit{\boldsymbol{H}}_{k - }}}}\mathit{\boldsymbol{V}}_{{\mathit{\boldsymbol{H}}_{k - }}}^{\rm{H}}\\ {{\mathit{\boldsymbol{\hat G}}}_{k - }} = {\mathit{\boldsymbol{U}}_{{\mathit{\boldsymbol{G}}_{k - }}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{\mathit{\boldsymbol{G}}_{k - }}}}{\left[{\mathit{\boldsymbol{V}}_{{\mathit{\boldsymbol{G}}_{k-}}}^{\left( 1 \right)}V_{{\mathit{\boldsymbol{G}}_{k-}}}^{\left( 0 \right)}} \right]^{\rm{H}}} \end{array}$

(11)

令${L_k} = {\rm{rank}}\left( {{{\mathit{\boldsymbol{\hat H}}}_{k-}}} \right), {R_k} = {\rm{rank}}\left( {{{\mathit{\boldsymbol{\hat G}}}_{k-}}} \right)$，则$\mathit{\boldsymbol{U}}_{{\mathit{\boldsymbol{H}}_{k-}}}^{\left( 0 \right)} \in {{\bf{C}}^{N \times {L_k}}}$和$\mathit{\boldsymbol{V}}_{{\mathit{\boldsymbol{G}}_{k-}}}^{\left( 0 \right)} \in {{\bf{C}}^{2MK \times {R_k}}}$分别为${{{\boldsymbol{\hat H}}_{k-}}}$和${{{\boldsymbol{\hat G}}_{k-}}}$的零空间。将每用户的上下行信道矩阵H_k和G_k分别与U⁽⁰⁾_Hk-和V⁽⁰⁾_Gk-相乘，并对相乘后得到的矩阵进行SVD分解，以达到消除用户对内干扰的目的。

$\begin{array}{l} \mathit{\boldsymbol{U}}_{{\mathit{\boldsymbol{H}}_{k- }}}^{\left( 0 \right)}{\mathit{\boldsymbol{H}}_k} = \left[{\mathit{\boldsymbol{U}}_{{\mathit{\boldsymbol{H}}_k}}^{\left( 1 \right)}\mathit{\boldsymbol{U}}_{{\mathit{\boldsymbol{H}}_k}}^{\left( 0 \right)}} \right]{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{\mathit{\boldsymbol{H}}_k}}}\mathit{\boldsymbol{V}}_{{\mathit{\boldsymbol{H}}_k}}^{\rm{H}}\\ {\mathit{\boldsymbol{G}}_k}\mathit{\boldsymbol{V}}_{{\mathit{\boldsymbol{G}}_{k - }}}^{\left( 0 \right)} = {\mathit{\boldsymbol{U}}_{{\mathit{\boldsymbol{G}}_k}}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{{\mathit{\boldsymbol{G}}_k}}}{\left[{\mathit{\boldsymbol{V}}_{{\mathit{\boldsymbol{G}}_k}}^{\left( 1 \right)}\mathit{\boldsymbol{V}}_{{\mathit{\boldsymbol{G}}_k}}^{\left( 0 \right)}} \right]^{\rm{T}}} \end{array}$

(12)

最后，得到了中继接收端和发送端的BD波束成形矩阵

${\boldsymbol{W}_{sr}} = \boldsymbol{U}_{{\boldsymbol{H}_k}}^{\left( 1 \right){\rm{H}}}\boldsymbol{U}_{{\boldsymbol{H}_{k-}}}^{\left( 0 \right){\rm{H}}}\;\;{\boldsymbol{W}_{rd}} = \boldsymbol{V}_{{\boldsymbol{G}_{k-}}}^{\left( 0 \right)}\boldsymbol{V}_{{\boldsymbol{G}_k}}^{\left( 1 \right)}$

(13)

3 仿真结果及分析

本节通过仿真来评估构造的全双工多用户对双向中继系统的性能，采用SVD算法作为上界, 并用ZF和BD算法对比进行验证。系统参数设置如下：系统用户对数K=2；每用户天线数M=2；中继的发射天线与接收天线的数N=16。用户的平均信噪比为SNR_RS=P_MS/σ_RS²，中继端的平均信噪比为SNR_MS=P_RS/σ_MS²。

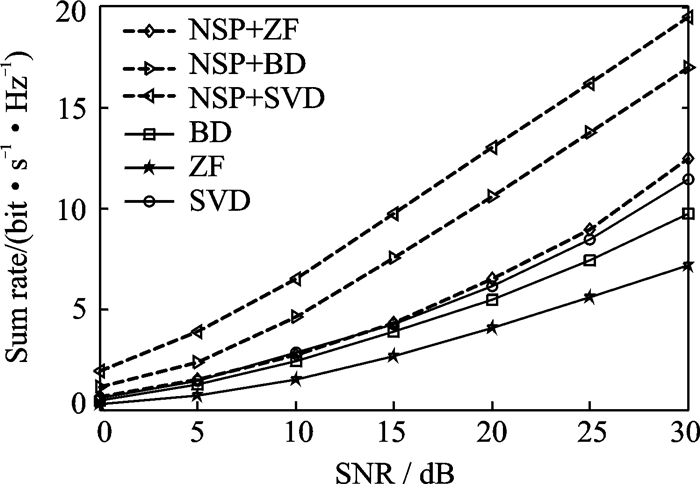
图 2比较了当SNR_RS=SNR_MS，用户对数K=2，用户天线数为M=2时，全双工双向中继模式下NSP+SVD，NSP+BD，NSP+ZF的3种波束成形算法，以及半双工双向中继模式下SVD，BD，ZF三种波束成形算法的和速率。由图 2可知，在本文构造的全双工多用户对双向中继系统中，全双工模式下的3种波束成形算法性能均高于半双工模式下波束成形的算法，且其性能排序为：NSP+SVD>NSP+BD>NSP+ZF >SVD>BD>ZF。ZF算法由于受信道相关性影响较大，其性能次于BD算法。BD算法以牺牲发射信号空间自由度来彻底消除用户对之间的干扰，所以其性能次于SVD算法。理论上全双工双向模式的和速率应该为半双工双向模式的2倍，而文中数据结果(以SNR_RS=SNR_MS=25dB，NSP +BD算法为例)只达到1.78倍。这是因为NSP并不是最优的自干扰抑制方式，因为在其干扰置零过程中会有维度损失，而且在两步波束成形过程中很可能会产生新的干扰，影响系统性能，所以不能达到理想的条件。

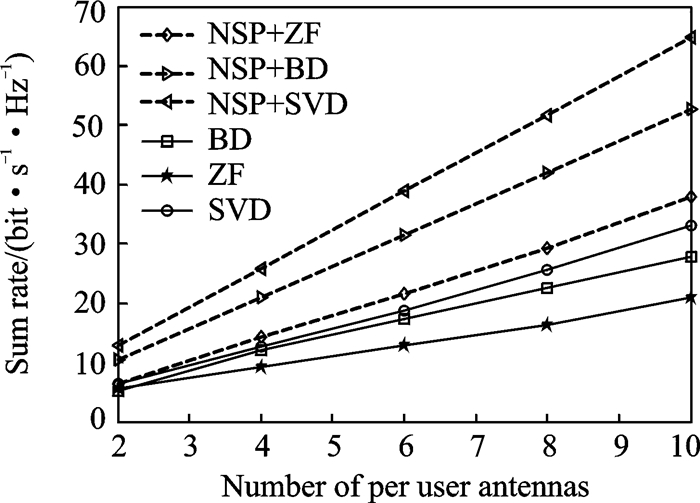
图 3为在SNR_RS=SNR_MS=20 dB时，不同波束成形算法和速率随用户天线数目的变化曲线。由图 3可知，随着用户配置的天线数增加，系统的和速率快速上升，且不同波束成形算法间的差距也逐渐拉大。这意味着采用多天线，甚至达到中大规模的天线数目时，可以带来更高的复用增益。

4 结束语

本文针对基于译码转发的全双工多用户对双向中继系统，设计了NSP+SVD, NSP+ZF, NSP+BD三种波束成形矩阵，以达到同时消除中继自干扰和用户对间干扰的目的。仿真表明，设计的3种波束成形算法既能消除中继自干扰，又能消除用户对间及对内干扰。并且, 随着用户配置天线数目的增多，提出的系统的性能也越好。